Abstract
Despite extended past studies, several questions regarding the resonant structure of the medium-Earth orbit (MEO) region remain hitherto unanswered. This work describes in depth the effects of the \(2g+h\) lunisolar resonance. In particular, (i) we compute the correct forms of the separatrices of the resonance in the inclination-eccentricity (i, e) space for fixed semi-major axis a. This allows to compute the change in the width of the \(2g+h\) resonance as the altitude increases. (ii) We discuss the crucial role played by the value of the inclination of the Laplace plane, \(i_{L}\). Since \(i_L\) is comparable to the resonance’s separatrix width, the parametrization of all resonance bifurcations has to be done in terms of the proper inclination \(i_{p}\), instead of the mean one. (iii) The subset of circular orbits constitutes an invariant subspace embedded in the full phase space, the center manifold \({\mathcal {C}}\), where actual navigation satellites lie. Using \(i_p\) as a label, we compute its range of values for which \({\mathcal {C}}\) becomes a normally hyperbolic invariant manifold (NHIM). The structure of invariant tori in \({\mathcal {C}}\) allows to explain the role of the initial phase h noticed in several works. (iv) Through Fast Lyapunov Indicator (FLI) cartography, we portray the stable and unstable manifolds of the NHIM as the altitude increases. Manifold oscillations dominate in phase space between \(a =\) 24,000 km and \(a=\) 30,000 km as a result of the sweeping of the \(2g+h\) resonance by the  and
and  resonances. The noticeable effects of the latter are explained as a consequence of the relative inclination of the Moon’s orbit with respect to the ecliptic. The role of the phases
resonances. The noticeable effects of the latter are explained as a consequence of the relative inclination of the Moon’s orbit with respect to the ecliptic. The role of the phases  in the structures observed in the FLI maps is also clarified. Finally, (v) we discuss how the understanding of the manifold dynamics could inspire end-of-life disposal strategies.
in the structures observed in the FLI maps is also clarified. Finally, (v) we discuss how the understanding of the manifold dynamics could inspire end-of-life disposal strategies.








Similar content being viewed by others
Notes
One needs to remark, however, that the integrable approximation only serves to obtain quantitative estimates on the allowed maximum size of eccentricity growth inside the resonance. The sensitive dependence of this phenomenon on the initial conditions, discussed in numerical studies, is to be interpreted, instead, in an entirely different context, namely the intricate structure of the asymptotic manifolds emanating from the center manifold of the full (non-integrable) Hamiltonian model, see Gkolias et al. (2019) and Sect. 5.
As discussed by Gkolias et al. (2019), the chaotic nature and the sensitivity on the initial conditions of the orbit solutions leading to eccentricity growth is manifold-drive and determined by the stable and unstable manifolds of the normally hyperbolic invariant manifold \({\mathcal {C}}_{\text {NHIM}}\), as discussed in the sequel. Still, it is numerically verified that Eq. (47) gives the correct estimate for the efficiency of the mechanism, i.e., the maximum eccentricity expected for the chaotic orbits with initial conditions close to the theoretical separatrices of the integrable model (33).
Confer Fig. 5 of Gkolias et al. (2016) for numerical fingerprints of this crossing, slightly above Galileo’s altitude.
A more accurate model for the oscillations in inclination when \(e\ne 0\) can be constructed using few steps of canonical perturbation theory, which however has a different form far from, or near the crossings with the resonances
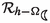 ,
,  ; see Legnaro and Efthymiopoulos (2021).
; see Legnaro and Efthymiopoulos (2021).
References
Aguirre, J., Vallejo, J.C., Sanjuán, M.A.: Wada basins and chaotic invariant sets in the Hénon-Heiles system. Phys. Rev. E 64(6), 066208 (2001)
Alessi, E., Deleflie, F., Rosengren, A., Rossi, A., Valsecchi, G., Daquin, J., et al.: A numerical investigation on the eccentricity growth of GNSS disposal orbits. Celest. Mech. Dyn. Astron. 125(1), 71–90 (2016)
Armellin, R., San-Juan, J.F.: Optimal Earth’s reentry disposal of the Galileo constellation. Adv. Space Res. 61(4), 1097–1120 (2018)
Bleher, S., Grebogi, C., Ott, E., Brown, R.: Fractal boundaries for exit in Hamiltonian dynamics. Phys. Rev. A 38, 930–938 (1988)
Breiter, S.: Lunisolar resonances revisited. Celest. Mech. Dyn. Astron. 81, 81–91 (2001)
Celletti, A., Gales, C.: A study of the lunisolar secular resonance 2 \({\dot{\omega }} +{\dot{\Omega }}= 0\). Front. Astron. Space Sci. 3, 11 (2016). https://doi.org/10.3389/fspas
Celletti, A., Gales, C., Pucacco, G.: Bifurcation of lunisolar secular resonances for space debris orbits. SIAM J. Appl. Dyn. Syst. 15(3), 1352–1383 (2016)
Chao, C., Gick, R.: Long-term evolution of navigation satellite orbits: GPS/GLONASS/GALILEO. Adv. Space Res. 34(5), 1221–1226 (2004)
Chirikov, B.: A universal instability of many-dimensional oscillator systems. Phys. Rep. 52(5), 263–379 (1979)
Cook, G.: Lunisolar perturbations of the orbit of an Earth satellite. Geophys. J. R. Astron. Soc. 6(3), 271 (1962)
Daquin, J., Rosengren, A., Alessi, E., Deleflie, F., Valsecchi, G., Rossi, A.: The dynamical structure of the MEO region: long-term stability, chaos, and transport. Celest. Mech. Dyn. Astron. 124(4), 335–366 (2016)
Dvorak, R., Contopoulos, G., Efthymiopoulos, C., Voglis, N.: “Stickiness” in mappings and dynamical systems. Planet. Space Sci. 46(11–12), 1567–1578 (1998)
Efthymiopoulos, C.: Canonical perturbation theory; stability and diffusion in Hamiltonian systems: applications in dynamical astronomy. In: Workshop series of the asociacion argentina de astronomia, vol. 3, pp. 3–146 (2012)
Ely, T.: Dynamics and control of artificial satellite orbits with multiple tesseral resonances. Ph.D Thesis, Purdue University (1996)
Froeschlé, C., Guzzo, M., Lega, E.: Graphical evolution of the Arnold web: from order to chaos. Science 289(5487), 2108–2110 (2000)
Gkolias, I., Daquin, J., Gachet, F., Rosengren, A.J.: From order to chaos in Earth satellite orbits. Astron. J. 152(5), 119 (2016)
Gkolias, I., Daquin, J., Skoulidou, D.K., Tsiganis, K., Efthymiopoulos, C.: Chaotic transport of navigation satellites. Chaos Interdiscip. J. Nonlinear Sci. 29(10), 101106 (2019)
Guzzo, M., Lega, E., Froeschlé, C.: A numerical study of the topology of hyperbolic manifolds supporting Arnold diffusion in a priori unstable systems (2009)
Henrard, J., Lemaitre, A.: A second fundamental model for resonance. Celest. Mech. 30(2), 197–218 (1983)
Hughes, S.: Earth satellite orbits with resonant lunisolar perturbations i. Resonances dependent only on inclination. Proc. R. Soc. Lond. A Math. Phys. Sci. 372(1749), 243–264 (1980)
Kaula, W.M.: Theory of Satellite Geodesy: Applications of Satellites to Geodesy. Blaisdell Publi. CO. (1966)
Kozai, Y.: Secular perturbations of asteroids with high inclination and eccentricity. Astron. J. 67, 591–598 (1962)
Kudielka, V.W.: Equilibria bifurcations of satellite orbits. In: The Dynamical Behaviour of Our Planetary System, pp. 243–255. Springer (1997)
Lara, M.: Hamiltonian Perturbation Solutions for Spacecraft Orbit Prediction: The Method of Lie Transforms, vol. 54. Walter de Gruyter GmbH & Co KG (2021)
Lara, M., San-Juan, J.F., López-Ochoa, L.M., Cefola, P.: Long-term evolution of galileo operational orbits by canonical perturbation theory. Acta Astronaut. 94(2), 646–655 (2014)
Lega, E., Guzzo, M., Froeschlé, C.: Theory and applications of the fast Lyapunov indicator (FLI) method. In: Chaos Detection and Predictability, pp. 35–54. Springer (2016)
Legnaro, E., Efthymiopoulos, C.: Inclination-dependent lunisolar resonances in the medium-earth orbit region. In: Preparation (2021)
Lemaître, A.: High-order resonances in the restricted three-body problem. Celest. Mech. 32(2), 109–126 (1984)
Lidov, M.: The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies. Planet. Space Sci. 9(10), 719–759 (1962)
Nagler, J.: Crash test for the restricted three-body problem. Phys. Rev. E 71, 026227 (2005)
Rosengren, A.J., Alessi, E.M., Rossi, A., Valsecchi, G.B.: Chaos in navigation satellite orbits caused by the perturbed motion of the Moon. Mon. Not. R. Astron. Soc. 449(4), 3522–3526 (2015)
Rosengren, A.J., Daquin, J., Tsiganis, K., Alessi, E.M., Deleflie, F., Rossi, A., et al.: Galileo disposal strategy: stability, chaos and predictability. Mon. Not. R. Astron. Soc. 464(4), 4063–4076 (2017)
Rosengren, A.J., Skoulidou, D.K., Tsiganis, K., Voyatzis, G.: Dynamical cartography of Earth satellite orbits. Adv. Space Res. 63(1), 443–460 (2019)
Rossi, A.: Resonant dynamics of Medium Earth Orbits: space debris issues. Celest. Mech. Dyn. Astron. 100(4), 267–286 (2008)
Stefanelli, L., Metris, G.: Solar gravitational perturbations on the dynamics of MEO: increase of the eccentricity due to resonances. Adv. Space Res. 55(7), 1855–1867 (2015)
Tremaine, S., Touma, J., Namouni, F.: Satellite dynamics on the Laplace surface. Astron. J. 137(3), 3706 (2009)
Wiggins, S.: Normally Hyperbolic Invariant Manifolds in Dynamical Systems, vol. 105. Springer (2013)
Zaslavsky, G.M.: Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 371(6), 461–580 (2002)
Acknowledgements
J.D. is a postdoctoral researcher of the ‘Fonds de la Recherche Scientifique’—FNRS. J.D. acknowledges the support of the ERC project 677793 ‘Stable and Chaotic Motions in the Planetary Problem’ leaded by Prof. Gabriella Pinzari. I.G. acknowledges the support of the ERC project 679086 COMPASS ‘Control for Orbit Manoeuvring through Perturbations for Application to Space Systems.’ E. L. has been supported by the Marie Curie Initial Training Network Stardust-R, Grant Agreement Number 813644 under the H2020 research and innovation program. C. E. was partially supported by EU-ITN Stardust-R and MIUR-PRIN 20178CJA2B ‘New Frontiers of Celestial Mechanics: theory and Applications.’ The authors acknowledge feedback and discussions with Elisa Maria Alessi.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Leading terms coefficients
Leading terms coefficients
The formal coefficients of the leading terms appearing in the resonant Hamiltonian of Eq. (33), the center-manifold Hamiltonian of Eq. (53) and the coupling terms of Eq. (56) are summarized within Tables 2, 3 and 4, respectively. The physical units adopted in this study read \(\mu _{\odot }=1.32712 \times 10^{11} \text {km}^{3}/\text {s}^{2}\),  , \(\mu _{\text {E}}=398\,600 \, \text {km}^{3}/\text {s}^{2}\), \(J_{2}=1.082 \times 10^{-3}\), \(R_{\text {E}}=6\,387.1 \)km, \(r_{\odot }=1.49579 \times 10^{8}\) km,
, \(\mu _{\text {E}}=398\,600 \, \text {km}^{3}/\text {s}^{2}\), \(J_{2}=1.082 \times 10^{-3}\), \(R_{\text {E}}=6\,387.1 \)km, \(r_{\odot }=1.49579 \times 10^{8}\) km,  km. The shortcuts
km. The shortcuts  and
and  denote the cosine and sinus of the inclination of the Moon to the ecliptic
denote the cosine and sinus of the inclination of the Moon to the ecliptic  . In the same way, \(c_{\varepsilon }\) and \(s_{\varepsilon }\) denote the cosine and sinus of the obliquity of the ecliptic \(\varepsilon =23^{\circ }44\), \(i_{\star }=56^{\circ }06\) and n denotes the mean motion of the test-particle, \(n=\sqrt{\mu _{\text {E}}/a^{3}}\).
. In the same way, \(c_{\varepsilon }\) and \(s_{\varepsilon }\) denote the cosine and sinus of the obliquity of the ecliptic \(\varepsilon =23^{\circ }44\), \(i_{\star }=56^{\circ }06\) and n denotes the mean motion of the test-particle, \(n=\sqrt{\mu _{\text {E}}/a^{3}}\).
Rights and permissions
About this article
Cite this article
Daquin, J., Legnaro, E., Gkolias, I. et al. A deep dive into the \(2g+h\) resonance: separatrices, manifolds and phase space structure of navigation satellites. Celest Mech Dyn Astr 134, 6 (2022). https://doi.org/10.1007/s10569-021-10060-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-021-10060-6



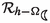 ,
,  ; see Legnaro and Efthymiopoulos (
; see Legnaro and Efthymiopoulos (