Skip to main content
SpringerLink
Log in

Models of Perishable Queueing-Inventory Systems with Server Vacations

  • Published:
Cybernetics and Systems Analysis Aims and scope

Abstract

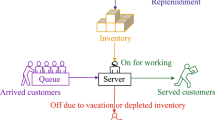
The model of perishable queueing-inventory system with server vacations is studied. Upon service completion, server takes vacation if there are no customers in the queue and it starts service at the end of the vacation if the number of customers in the system exceeds some threshold; otherwise, it takes new vacation. Exact and approximate methods are proposed to calculate the characteristics of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. S. Koroliuk, A. Z. Melikov, L. A. Ponomarenko, and A. M. Rustamov, “Asymptotic analysis of the system with server vacation and perishable inventory,” Cybern. Syst. Analysis, Vol. 53, No. 4, 543–553 (2017).

    Article  MathSciNet  Google Scholar 

  2. J. G. Kemeny and J. L. Snell, Finite Markov Chains, Princeton University Press, Princeton (1960).

    MATH  Google Scholar 

  3. G. Guardabassi and S. Rinaldi, “The problems in Markov chains: A topological approach,” Operations Research, Vol. 18, Issue 2, 324–333 (1970).

    Article  MATH  Google Scholar 

  4. B. N. Feinberg and S. S. Chiu, “A method to calculate steady-state distributions of large Markov chains by aggregating states,” Operations Research, Vol. 35, Issue 2, 282–290 (1987).

    Article  MathSciNet  MATH  Google Scholar 

  5. D. S. Kim and R. L. Smith, “An exact aggregation/disaggregation algorithm for large scale Markov chain,” Naval Research Logistics, Vol. 42, No. 7, 1115–1128 (1995).

    Article  MathSciNet  MATH  Google Scholar 

  6. P. J. Courtois, Decomposability: Queueing and Computer System Applications, Academic Press, New York–London–San Francisco (1977).

    MATH  Google Scholar 

  7. J. R. Koury, D. F. McAllister, and W. J. Stewart, “Iterative methods for computing stationary distribution of nearly completely decomposable Markov chains,” SIAM J. on Algebraic and Discrete Methods, Vol. 5, No. 2, 164–186 (1984).

    Article  MathSciNet  MATH  Google Scholar 

  8. M. Haviv, “Aggregation/disaggregation methods for computing the stationary distributions of a Markov chain,” SIAM J. on Numerical Analysis, Vol. 24, No. 4, 952–966 (1987).

    Article  MathSciNet  MATH  Google Scholar 

  9. W. J. Stewart, Introduction to the Numerical Solution of Markov Chains, Princeton University Press, Princeton (1994).

    MATH  Google Scholar 

  10. D. F. Rogers and R. Plante, “Estimating equilibrium probabilities for band diagonal Markov chains using aggregation and disaggregation techniques,” Computers & Operations Research, Vol. 20, No. 8, 857–877 (1993).

    Article  MATH  Google Scholar 

  11. P. O. Dianne, Iterative Methods for Finding the Stationary Vector for Markov Chain, IMA Preprint Series, No. 932 (1992).

  12. U. Sumita and M. Rieders, “Application of the replacement process approach for computing the ergodic probability vector of large scale row-continuous Markov chains,” J. of the Operations Research Society of Japan, Vol. 33, No. 4, 279–307 (1990).

    Article  MathSciNet  MATH  Google Scholar 

  13. V. S. Koroliuk and A. F. Turbin, Semi-Markov Processes and Their Applications [in Russian], Naukova Dumka, Kyiv (1976).

    Google Scholar 

  14. L. Ponomarenko, C. S. Kim, and A. Melikov, Performance Analysis and Optimization of Multi-Traffic on Communication Networks, Springer, Berlin–Heidelberg (2010).

    Book  MATH  Google Scholar 

  15. A. Melikov and L. Ponomarenko, Multi-Dimensional Queueing Models in Telecommunication Networks, Springer, Heidelberg (2014).

    MATH  Google Scholar 

  16. C. Liang and H. Luh, “Optimal services for content delivery based on business priority,” J. of the Chinese Institute of Engineers, Vol. 36, No. 4, 422–440 (2013).

    Article  Google Scholar 

  17. C. Liang and H. Luh, “Efficient method for solving a two-dimensional Markov chain model for call centers,” Industrial Management & Data Systems, Vol. 115, No. 5, 901–922 (2015).

    Article  Google Scholar 

  18. M. E. Haddad and F. Belarbi, “Approximate analysis of an unreliableM / M /c retrial queue with phase merging algorithm,” New Trends in Mathematical Sciences, Vol. 4, No. 3, 9–21 (2016).

    Article  MathSciNet  Google Scholar 

  19. B. Jajaraman, B. Sivakumar, and G. Arivarignan, “A perishable inventory system with postponed demands and multiple server vacations,” in: Modeling and Simulation in Engineering, Hindawi Publishing Corporation, Vol. 2012, Article ID 620960.

  20. A. Z. Melikov, L. A. Ponomarenko, and S. A. Bagirova, “Markov models of queueing-inventory systems with variable order size,” Cybern. Syst. Analysis, Vol. 53, No. 3, 373–386 (2017).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    V. S. Koroliuk

  2. Institute of Control Systems, Azerbaijan National Academy of Sciences, Baku, Azerbaijan

    A. Z. Melikov

  3. International Research and Training Center for Information Technologies and Systems, National Academy of Sciences of Ukraine and Ministry of Education and Science of Ukraine, Kyiv, Ukraine

    L. A. Ponomarenko

  4. Baku Engineering University, Baku, Azerbaijan

    A. M. Rustamov

Authors
  1. V. S. Koroliuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Z. Melikov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. L. A. Ponomarenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. M. Rustamov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. S. Koroliuk.

Additional information

Translated from Kibernetika i Sistemnyi Analiz, No. 1, January–February, 2018, pp. 35–50

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Koroliuk, V.S., Melikov, A.Z., Ponomarenko, L.A. et al. Models of Perishable Queueing-Inventory Systems with Server Vacations. Cybern Syst Anal 54, 31–44 (2018). https://doi.org/10.1007/s10559-018-0005-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10559-018-0005-4

Keywords

Search

Navigation