1 Introduction

Modelling methods for airflow in complex terrain can be basically divided into diagnostic and prognostic models. They are also called kinematic (mass balance) and dynamic models (Moroney 1990; Pielke and Uliasz 1998; Stage et al. 1999; Seaman 2000; Chung 2002). The division of diagnostic and dynamic models is presented by, inter alia, Finardi et al. (1998), Homicz (2002) and Perez (2018).

Kinematic models adjust the initial wind profile, which is determined by approximation of meteorological data, so that it fulfils a continuity equation. These models, due to their numerical efficiency and accuracy, even when limited data are available, are widely used in dispersion models and research on wind energy.

An essential feature of a kinematic–diagnostic model is the lack of time-dependent equations as opposed to dynamic–prognostic models. The latter use a continuity equation and the Navier–Stokes momentum equation but also state and thermodynamic equations. Sometimes, surface warming, radiative effects, condensation, and evaporation are also considered. These models assess the temporal change of atmospheric variables and they can be used for prediction purposes. Most dynamic models require data referring to the thermodynamic structure of the atmosphere, which means that more data and calculation time is necessary than for kinematic models.

Thus, kinematic models are suitable for defining the wind profile when data necessary for dynamic models are not available. Also, when computational resources are limited, kinematic models are used. Much research (Ratto et al. 1994; Stage et al. 1999; Scire et al. 2000; Burlando et al. 2007a, b; Singh et al. 2008; Lundquist and Katopodes 2013; Gopalaswami et al. 2015) stress the fact that diagnostic models take into account measurements and terrain topography, and they should be equipped with algorithms for parametrization of the flow field. Diagnostic models are not used for predictive purposes. However, a comparison of the use of diagnostic and predictive models (Cox et al. 2003) indicates that both models allow for similar compatibility with the results of the experiment in which concentrations of pollutants were determined. Robe and Scire (1998) concluded that the kinematic model California Meteorological (CALMET) gave results compatible with those from the dynamic model MM5 (Stage et al. 1999; Lundquist and Katopodes 2013).

Gopalaswami et al. (2015) note that there are models combining both kinematic and dynamic approaches (Robe and Scire 1998; Barna et al. 2000; Chandrasekar et al. 2003; Ghannam and El-Fadel 2013), and following such an approach they propose combining the MM5 model (dynamic model) with CALMET (prognostic model).

The dynamic models are used in data-assimilation approaches presented by, among others, Evensen (2009), Gao et al. (2013), Lin and Wang (2013) as well as Chandramouli et al. (2020). The data-assimilation approach, which is applied in relatively large areas for weather forecasting, combines calculations from computational fluid dynamics (CFD) with experimental fluid dynamics. The calculation process from CFD is controlled by the results of measurements. Two approaches can be encountered: segmental data assimilation with the most popular ensemble Kalman filter method (Evensen 2009; Gao et al. 2013; Lin and Wang 2013; Hamrud et al. 2015) or variational data assimilation (VDA) (Lorenc 2003; Chandramouli et al. 2020) with 3DVar and 4DVar formulations.

The diagnostic model and the procedure presented here are similar to the diagnostic version of the WindNinja model (Forthofer et al. 2014) used, inter alia, in Sanjuan et al. (2014, 2015) and Wagenbrenner et al. (2016).

A similar procedure can also be found in the Quick Urban and Industrial Complex dispersion model (QUIC), specifically in the QUIC module for wind-field determination (Singh et al. 2008; Girard et al. 2018). This model allows the wind field to be estimated in urbanized areas similarly to that presented here. Because the diagnostic models approximate measurement data, they are critically dependent on the quality and density of these data.

The procedure for calculating the wind field in diagnostic models is based on adjustment of the wind field resulting from approximation by means of some corrections so that the final wind field fulfils the criterion of mass consistency. Homicz (2002) distinguishes four methods of solving the problem, each using one of the following algorithms: direct-differencing, point-iterative, hybrid, and variational calculus.

The formulation of the variational-diagnostic model used here is presented by Montero et al. (1998, 2005), Montero and Sanín (2001), Sanín and Montero (2007) and Brzozowska (2015a, b). In this formulation, the problem of minimizing the deviation of the wind field and satisfying the continuity equation for initial velocities (obtained by approximation of measurements and parametrization) involves solving the differential equation with partial derivatives. The main difference between the model presented and the WindNinja and QUIC models lies in different approaches to the solution of the differential equations. We use the equidistant finite-difference method, while the finite-element method is applied in WindNinja. Our approach enables us to use a kinematic model, avoiding the situation where the data from meteorological stations, or more precisely, the density of the stations, are too small to be fully used.

Only a short description of the method is given here together with a modification, which enables us, using the finite-difference method, to adjust the wind field into subdomains, by means of a variational method, to meteorological data with consideration of the topographical complexity of the terrain analyzed. In the first step of the algorithm, the wind field, adjusted with experimental measurements to the large domain \({\Omega }_{1}\) including domain \({\Omega }_{2}\), is calculated. The results obtained are treated as the boundary conditions for subdomain \({\Omega }_{2}\). Then, the problem of adjusting the wind field is solved again, but for the new conditions of the initial wind field in subdomain \({\Omega }_{2}\). The algorithm enables us to perform grid refinement in domain \({\Omega }_{2}\) in comparison with the grid in \({\Omega }_{1}\), and thus more precise mapping of the terrain and its architecture. The task of the adjustment of the wind field in subdomain \({\Omega }_{2}\) can be solved several times until the results of calculations become stable.

The main elements of the variational algorithm and description of conformal transformations are presented in Sect. 2. Section 3 presents the solution of an elliptical equation by means of the finite-difference method. The iterative procedure and an application of the algorithms developed for the solution of the task in domain \({\Omega }_{1}\) and subdomain \({\Omega }_{2}\) are described subsequently in Sects. 4 and 5. Section 6 discusses validation of the algorithm proposed and the results of simulations for a selected town. Conclusions regarding the iterative procedure of wind field calculations are presented in Sect. 7.

2 Variational Method, Conformal Variables

The first step is concerned with the definition of the initial wind field. The procedure used in this step is only outlined in broad terms. The details can be found in Brzozowska (2015a, b). This field, which can be obtained either by measurements, parametrization, and approximation (Girard et al. 2018; Bauer 2019; Barbano et al. 2020) or by earlier calculations, is denoted as \({\mathbf{u}}_{0} \left( {x_{1} , x_{2} ,x_{3} } \right)\). Usually it does not ensure mass consistency in the domain analyzed. The next step of the adjustment procedure consists in finding such a wind field \({\mathbf{u}}\left( {x_{1} , x_{2} ,x_{3} } \right)\), which being close to field \({\mathbf{u}}_{0}\), fulfils the continuity equations in the following form in domain \({\Omega }\) (Fig. 1)

$$ \mathop \sum \limits_{l = 1}^{3} \frac{{\partial u^{\left( l \right)} }}{{\partial x^{\left( l \right)} }} = 0, $$

as well as boundary conditions

$$ {\mathbf{n}} \cdot {\mathbf{u}} = 0\; {{\text{over}}\; \Gamma}_{b} , $$

where \({\mathbf{n}}\) is a vector normal to the terrain surface.

Fig. 1
figure 1

Domain \({\Omega }\) and boundaries: \({\Gamma }_{a}\), lateral surface;\({\Gamma }_{b,0} ,{\Gamma }_{b,1}\), bottom and upper surface respectively; \(s\left( {x^{\left( 1 \right)} ,x^{\left( 2 \right)} } \right)\), terrain surface

Full size image

Using Lagrange multipliers, the problem of adjusting the wind field becomes the following minimization problem

$$ L\left( {{\mathbf{v}},\phi } \right) = \mathop {\min }\limits_{u \in K} \left( {\mathop \smallint \limits_{{\Omega }} \left[ {\mathop \sum \limits_{l = 1}^{3} \alpha^{{\left( l \right)^{2} }} \left( {u^{\left( l \right)} - u_{0}^{\left( l \right)} } \right)^{2} + \phi \nabla {\mathbf{u}}} \right]d{\Omega }} \right), $$
(1)

where \( \alpha^{\left( 1 \right)} = \alpha^{\left( 2 \right)} ,\alpha^{\left( 3 \right)}\) are Gaussian precision moduli, \(\phi \left( {x^{\left( 1 \right)} ,x^{\left( 2 \right)} ,x^{\left( 3 \right)} } \right)\) is the Lagrange multiplier, and \(K \) is a set of permissible functions (Montero et al. 2005).

In order to solve the task, the following elliptic equation is obtained (Brzozowska 2015a, b)

$$ \mathop \sum \limits_{l = 1}^{2} \frac{{\partial^{2} \phi }}{{\partial x^{{\left( l \right)^{2} }} }} + \frac{{T^{\left( 3 \right)} }}{{T^{{\left( {1,2} \right)}} }}\frac{{\partial^{2} \phi }}{{\partial x^{{\left( 3 \right)^{2} }} }} = - \frac{1}{{T^{{\left( {1,2} \right)}} }}\mathop \sum \limits_{l = 1}^{3} \frac{{\partial u_{0}^{\left( l \right)} }}{{\partial x^{\left( l \right)} }} , $$
(2)

where \({T^{\left( l \right)}} = 1/\left( {2{\alpha ^{\left( l \right)}}^2} \right)\) are components of the diagonal transmission tensor with the assumption that if \(\alpha^{\left( 1 \right)} = \alpha^{\left( 2 \right)}\) then \(T^{\left( 1 \right)} = T^{\left( 2 \right)} = T^{{\left( {1,2} \right)}}\) Boundary conditions for (2) are in the form of Dirichlet and Neumann conditions. Three-dimensional domain \({\Omega }\), for which the solution is sought, can be reduced by means of conformal coordinates matched to the unit cube \({{\Omega ^{\prime}}}\), in which the terrain surface is a horizontal plane. Such an approach simplifies the grid development process but at the same time complicates the discrete representation of Eq. 2. The procedure is presented in Fig. 2 (Brzozowska 2013; Brzozowska 2015a, b).

Fig. 2
figure 2

Main steps of the procedure applied in the model

Full size image

The following transformation of the spatial coordinates is assumed:

$$ \xi^{\left( l \right)} = \left\{ {\begin{array}{*{20}c} {\frac{{x^{\left( l \right)} }}{{x_{m}^{\left( l \right)} }} \quad for \; l = 1,2} \\ {\frac{{x^{\left( l \right)} - s}}{{x_{m}^{\left( l \right)} - s}} \quad for \; l = 3 } \\ \end{array} } \right., $$
(3)

where \(x_{m}^{\left( 1 \right)} ,x_{m}^{\left( 2 \right)}\) are maximal spatial dimensions of the domain (length, width), \(x_{m}^{\left( 3 \right)}\) is the maximum height of the domain (the height of the mixing layer), and \(s\left( {x^{\left( 1 \right)} ,x^{\left( 2 \right)} } \right)\) is the function describing terrain topography. Coordinate transformations according to (3) lead us to the following form of (2):

$$ \begin{aligned} & \frac{1}{{x_{m}^{{\left( 1 \right)^{2} }} }}\frac{{\partial^{2} \phi }}{{\partial \xi^{{\left( 1 \right)^{2} }} }} + \frac{1}{{x_{m}^{{\left( 2 \right)^{2} }} }}\frac{{\partial^{2} \phi }}{{\partial \xi^{{\left( 2 \right)^{2} }} }} \\ &\quad \quad + \left[ {\left( {\frac{{\xi^{\left( 3 \right)} - 1}}{d}} \right)^{2} \left( {\left( {s^{\left( 1 \right)} } \right)^{2} + \left( {s^{\left( 2 \right)} } \right)^{2} } \right) + \frac{{T^{\left( 3 \right)} }}{{T^{{\left( {1,2} \right)}} d^{2} }}} \right]\frac{{\partial^{2} \phi }}{{\partial \xi^{{\left( 3 \right)^{2} }} }} \\ &\quad \quad + \frac{{2\left( {\xi^{\left( 3 \right)} - 1} \right)}}{d}\left[ {\frac{1}{{x_{m}^{\left( 1 \right)} }}s^{\left( 1 \right)} \frac{{\partial^{2} \phi }}{{\partial \xi^{\left( 1 \right)} \partial \xi^{\left( 3 \right)} }} + \frac{1}{{x_{m}^{\left( 2 \right)} }}s^{\left( 2 \right)} \frac{{\partial^{2} \phi }}{{\partial \xi^{\left( 2 \right)} \partial \xi^{\left( 3 \right)} }}} \right] \\ &\quad \quad + \frac{{\xi^{\left( 3 \right)} - 1}}{d}\left[ {s^{{\left( {11} \right)}} + s^{{\left( {22} \right)}} + \frac{2}{d}\left( {s^{{\left( 1 \right)^{2} }} + s^{{\left( 2 \right)^{2} }} } \right)} \right]\frac{\partial \phi }{{\partial \xi^{\left( 3 \right)} }} \\ &\quad = - \frac{1}{{T^{{\left( {1,2} \right)}} }}\left\{ {\frac{1}{{x_{m}^{\left( 1 \right)} }}\frac{{\partial u_{0}^{\left( 1 \right)} }}{{\partial \xi^{\left( 1 \right)} }} + \frac{1}{{x_{m}^{\left( 2 \right)} }}\frac{{\partial u_{0}^{\left( 2 \right)} }}{{\partial \xi^{\left( 2 \right)} }}} \right. \\ &\quad \quad + \frac{1}{d}\left[ {\left( {\xi^{\left( 3 \right)} - 1} \right)\left( {s^{\left( 1 \right)} \frac{{\partial u_{0}^{\left( 1 \right)} }}{{\partial \xi^{\left( 3 \right)} }} + s^{\left( 2 \right)} \frac{{\partial u_{0}^{\left( 2 \right)} }}{{\partial \xi^{\left( 3 \right)} }}} \right) + \frac{{\partial u_{0}^{\left( 3 \right)} }}{{\partial \xi^{\left( 3 \right)} }}} \right], \\ \end{aligned} $$
(4)

where \(d = x_{m}^{\left( 3 \right)} - s\left( {x^{\left( 1 \right)} ,x^{\left( 2 \right)} } \right)\), \(s^{\left( l \right)} = \frac{\partial s}{{\partial x^{\left( l \right)} }}\) for \(l = 1,2.\) Boundary conditions can be written in the form

$$ \left. \phi \right|_{{\xi^{\left( 1 \right)} = 0}} = 0, \left. \phi \right|_{{\xi^{\left( 1 \right)} = 1}} = 0, $$
(5a)
$$ \left. \phi \right|_{{\xi^{\left( 2 \right)} = 0}} = 0,{ }\left. \phi \right|_{{\xi^{\left( 2 \right)} = 1}} = 0, $$
(5b)
$$ \left. {\frac{\partial \phi }{{\partial \xi^{\left( 3 \right)} }}} \right|_{{\xi^{\left( 3 \right)} = 0}} = \frac{d}{{T^{{\left( {1,2} \right)}} }}\frac{{s^{\left( 1 \right)} \left( {\left. {u_{0}^{\left( 1 \right)} + \frac{{T^{{\left( {1,2} \right)}} }}{{x_{m}^{\left( 1 \right)} }}\frac{\partial \phi }{{\partial \xi^{\left( 1 \right)} }}} \right) + s\left( {\left. {u_{0}^{\left( 2 \right)} + \frac{{T^{{\left( {1,2} \right)}} }}{{x_{m}^{\left( 2 \right)} }}\frac{\partial \phi }{{\partial \xi^{\left( 2 \right)} }}} \right) - u_{0}^{\left( 3 \right)} } \right.} \right.}}{{s^{{\left( 1 \right)^{2} }} + s^{{\left( 2 \right)^{2} }} + \frac{{T^{\left( 3 \right)} }}{{T^{{\left( {1,2} \right)}} }}}} , $$
(5c)
$$ \left. {\frac{\partial \phi }{{\partial \xi^{\left( 3 \right)} }}} \right|_{{\xi^{\left( 3 \right)} = 1}} = 0. $$
(5d)

Differential Eq. 4 with boundary conditions [(5a)–(5d)] can be solved using spatial discretization. To this end, the finite-element method, finite-volume method (Montero et al. 1998; Cascón and Ferragut 2007), or the finite-difference method can be used. Here, the latter method is used for the discretization (Brzozowska et al. 2009; Brzozowska 2015a, b).

3 Discretization of Domain Ω

According to the idea of the finite-difference method, we can assume that Eq. 4 is fulfilled if it is fulfilled at internal points of the domain \({{\Omega ^{\prime}}}\), which are \(\left( {\xi_{{i^{\left( 1 \right)} }}^{\left( 1 \right)} , \xi_{{i^{\left( 2 \right)} }}^{\left( 2 \right)} , \xi_{{i^{\left( 3 \right)} }}^{\left( 3 \right)} } \right)\):

$$ \xi_{0}^{\left( l \right)} = 0; \xi_{{i^{\left( l \right)} }}^{\left( l \right)} = \mathop \sum \limits_{\delta = 1}^{{i^{\left( l \right)} }} {\Delta }\xi_{\delta }^{\left( l \right)}\quad {\text{for }}l = 1,2,3, i^{\left( l \right)} = 1, \ldots ,n^{\left( l \right)} , $$

where \(n^{\left( l \right)} + 1 \) is the number of subintervals in direction of \(x^{\left( l \right)}\), \(\Delta \xi_{\sigma }^{\left( l \right)} = \xi_{\sigma }^{\left( l \right)} - \xi_{\sigma - 1}^{\left( l \right)}\). It is also assumed that discretization points can be spread unevenly (Fig. 3).

Fig. 3
figure 3

Discretization points, notation assumed

Full size image

Partial derivatives occurring in (2) can be approximated using the differences of the second order. As a result we obtain a system of \(m = n^{\left( 1 \right)} n^{\left( 2 \right)} n^{\left( 3 \right)}\) linear algebraic equations with constant coefficients, which can be written in the matrix form as

$$ {\mathbf{A}}_{{\Omega^{\prime}}} {\varvec{\Phi}}_{{{{\Omega^{\prime}}}}} + {\mathbf{B}}_{{{{\Omega^{\prime}}}}} {\varvec{\Phi}}_{{{{\Gamma^{\prime}}}}} = {\mathbf{f}}_{{{{\Omega^{\prime}}}}} , $$
(6)

where \({\varvec{\Phi}}_{{{{\Omega^{\prime}}}}}\) is the vector of values of function \({\varvec{\Phi}}\) inside the domain \({\Omega }^{\prime}\), \(\phi_{{{{\Gamma^{\prime}}}}}\) is the vector of values of function \(\phi\) at the boundaries of domain \({\Gamma }^{\prime}\). Matrix \(\left[ {{\mathbf{A}}_{{{{\Omega^{\prime}}}}} {\varvec{\Phi}}{{{{\Omega^{\prime}}}}} } \right]\) is a sparse matrix. Values of \(\phi\) from 15 nodes of the discretization grid occur in (6).

All the equations obtained from boundary conditions using finite differences can be written as

$$ {\mathbf{A}}_{{{{\Gamma^{\prime}}}}} {\varvec{\Phi}}_{{{{\Omega^{\prime}}}}} + {\mathbf{AB}}_{{{{\Gamma^{\prime}}}}} {\varvec{\Phi}}_{{{{\Gamma^{\prime}}}}} = {\mathbf{f}}_{{{{\Gamma^{\prime}}}}} , $$

where \({\varvec{\Phi}}_{{{{\Omega^{\prime}}}}}\) is the vector consisting of unknown values \(\phi_{{i^{\left( 1 \right)} ,i^{\left( 2 \right)} ,i^{\left( 3 \right)} }}\) for \(i^{\left( l \right)} = 1, \ldots ,n^{\left( l \right)} ,\) \(l = 1,2,3\) and \({\varvec{\Phi}}_{{{{\Gamma^{\prime}}}}} \) is a vector of unknowns \(\phi_{{i^{\left( 1 \right)} ,i^{\left( 2 \right)} ,0}}\) and \(\phi_{{i^{\left( 1 \right)} ,i^{\left( 2 \right)} ,n^{\left( 3 \right)} + 1}}\) for \(i^{\left( 1 \right)} = 1, \ldots ,n^{\left( 1 \right)} ,\) \(i^{\left( 2 \right)} = 1, \ldots ,n^{\left( 2 \right)}\).

Finally, the set of equations discretized by finite differences takes the form

$$ {\mathbf{A}}{\varvec{\Phi}} = {\mathbf{f}}, $$
(7)

where \({\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{A}}_{{{{\Omega^{\prime}}}}} } & {{\mathbf{B}}_{{{{\Omega^{\prime}}}}} } \\ {{\mathbf{A}}_{{{{\Gamma^{\prime}}}}} } & {{\mathbf{B}}_{{{{\Gamma^{\prime}}}}} } \\ \end{array} } \right]\), \({\varvec{\Phi}} = \left[ {\begin{array}{*{20}c} {{\varvec{\Phi}}_{{{{\Omega^{\prime}}}}} } \\ {{\varvec{\Phi}}_{{{{\Gamma^{\prime}}}}} } \\ \end{array} } \right]\), \({\mathbf{f}} = \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{{{{\Omega^{\prime}}}}} } \\ {{\mathbf{f}}_{{{{\Gamma^{\prime}}}}} } \\ \end{array} } \right]\).

Equation 7 forms a set of \(n = n^{\left( 1 \right)} n^{\left( 2 \right)} \left( {n^{\left( 3 \right)} + 2} \right)\) algebraic linear equations.

4 Iterative Procedure

Domain \({\Omega }\) 1 with subdomain \({\Omega }_{2} \subset {\Omega }_{1}\) analyzed is presented in Fig. 4.

Fig. 4
figure 4

Domain \({\Omega }\)1 and subdomain \({\Omega }_{2} \subset {\Omega }_{1}\)

Full size image

Let us consider a general problem of calculating the wind field in \({\Omega }_{2}\) when values of wind velocity are measured in a number of meteorological stations located in domain \({\Omega }_{1}\). Montero et al. (1998), Brzozowska (2015b), and Brzozowska et al. (2009) present a procedure that enables the approximate values of initial wind field \({\mathbf{u}}_{0}\) from (2), (3) to be calculated at nodes of the grid. The values depend on, among others, the distance of the grid nodes from measurements stations, terrain topography, the stability class of the atmosphere, and roughness of the ground. In order to capture the flow features, the parametrization is necessary (Girard et al. 2018; Oettl 2019a, b; Barbano et al. 2020). Having calculated the wind field \({\varvec{u}}_{0}\), Eq. 4 with boundary conditions, (5a–5d) can be solved. Then the solution of algebraic linear Eq. 7 gives us the adjusted wind field \({\mathbf{u}}\) fulfilling the continuity equation at the grid nodes. The calculation time depends on the dimension of the problem. According to (7), the number of unknowns in the system is \(n = n^{\left( 1 \right)} n^{\left( 2 \right)} \left( {n^{\left( 3 \right)} + 2} \right)\) and the calculation time for the solution of such a system is proportional to \(n^{\alpha }\) where \(\alpha > 1\). Then it may be necessary to use a dense mesh in domain \({\Omega }_{2} \subset {\Omega }_{1}\), but the use of such a mesh in the whole domain \({\Omega }_{1}\) is not numerically effective. On the other hand, limitation of calculations to domain \({\Omega }_{2}\) with the use of measurements from meteorological stations situated in \({\Omega }_{2}\) or even in domain \({\Omega }_{1}\) can lead to considerable errors in calculations of the initial wind field \({\mathbf{u}}_{0}\). Thus we propose the following procedure:

  • Stage Z(1) Calculation of wind field \({\mathbf{u}}_{0}\) in domain \({\Omega }_{1}\) using the initial wind field obtained by approximating data from measurement stations and parametrization. The domain is discretized into \(n_{{}}^{\left( l \right)} + 1\) intervals along axes \(x^{\left( l \right)} l = 1, 2, 3\). The resulting wind field is \({\mathbf{u}}_{1}\).

  • Stage Z(2) Calculation of the wind field in domain \({\Omega }_{2}\), assuming that the initial wind field is obtained by interpolating wind field \({\mathbf{u}}_{1}\) obtained as a solution of task Z(1). The wind field obtained in domain \({\Omega }_{2}\) is denoted as \({\mathbf{u}}_{2}\). Domain \({\Omega }_{2}\) is discretized into \(n_{2}^{\left( l \right)} + 1\) intervals along axes \(x^{\left( j \right)} j = 1, 2\) and \(n_{2}^{\left( 3 \right)} = n_{1}^{\left( 3 \right)} = n^{\left( 3 \right)}\), which means that the number and the length of intervals along vertical axis \(x^{\left( 3 \right)}\) is in task Z(2) the same as in task Z(1).

  • Stage Z(i) \(i = 3, 4, \ldots\) Calculation of wind field in domain \({\Omega }_{2}\), assuming that the initial wind field in task Z(i) is the solution of task Z(i—1) and \(n_{i}^{\left( j \right)} = n_{i - 1}^{\left( j \right)} , = 1,2,3\).

The iterative process described in task Z(i) is carried out until the wind field in domain \({\Omega}_2\) stabilizes or other conditions for the accuracy of results are met.

5 Formulation of the Problem in Domain \({{\varvec{\Omega}}}_{2} \subset {{\varvec{\Omega}}}_{1}\)

The solution of the task formulated above in domain \({\Omega }_{1}\) requires an assumption of boundary conditions for \(\xi_{0}^{\left( 1 \right)} = 0, \xi_{{n_{1}^{\left( 1 \right)} }}^{\left( 1 \right)} = 1,\xi_{0}^{\left( 2 \right)} = 0, \xi_{{n_{1}^{\left( 2 \right)} }}^{\left( 2 \right)} = 1\). When there is a relatively small number of discretization points (small \(n_{1} = n_{1}^{\left( 1 \right)}\), \(n_{2} = n_{2}^{\left( 2 \right)}\)), the influence of the boundary conditions on the results can be considerable. Also the procedure of calculating the initial wind field \({\mathbf{u}}_{0}\) with a small number of meteorological stations and a large grid can be the source of errors in the calculated wind field. Thus, let us assume that subdivision \({\Omega }_{2} \subset {\Omega }_{1}\) is placed at a certain distance from borders \({\Gamma }_{{\text{a}}}^{{\left( {{\Omega }_{1} } \right)}}\) of domain \({\Omega }_{1}\) (Fig. 5).

Fig. 5
figure 5

Domain analyzed with boundary conditions

Full size image

The solution of the task in domain \({\Omega }_{1}\) leads us to the determination of values \(u^{\left( 1 \right)} , u^{\left( 2 \right)} , u^{\left( 3 \right)} , \phi\) at points \(\left( {x_{i}^{\left( 1 \right)} , x_{j}^{\left( 2 \right)} , x_{k}^{\left( 3 \right)} } \right)\) for \(i = 0, \ldots ,n_{1}^{\left( 1 \right)} + 1\), \(j = 0, \ldots ,n_{1}^{\left( 2 \right)} + 1\), \(k = 0, \ldots ,n_{1}^{\left( 3 \right)} + 1\). With these values the task of the adjustment of the wind field in domain \({\Omega }_{2}\) (defined above as Z(2)), can be formulated as follows.

The initial conditions for the iteration process in domain \({\Omega }_{2}\) are assumed as

$$ \begin{gathered} {\mathbf{u}}_{0}^{{\left( {{\Omega }_{2} } \right)}} = {\mathbf{u}}_{1*}^{{}} , \hfill \\ \left. \phi \right|_{{{\Gamma }_{{\text{a}}}^{{\left( {{\Omega }_{2} } \right)}} }} = 0, \hfill \\ \left. \phi \right|_{{{\Gamma }_{{\text{b}}}^{{\left( {{\Omega }_{2} } \right)}} }} = \left. \phi \right|_{{{\Gamma }_{{\text{b}}}^{{\left( {{\Omega }_{1} } \right)}} }} , \hfill \\ \end{gathered} $$

where \({\mathbf{u}}_{1*}^{{}}\) is a vector of velocities and the function \(\phi\) at all points of \({\Omega }_{2}\) (together with boundaries) is obtained either directly from \({\mathbf{u}}_{1}\), having solved the task in domain \({\Omega }_{1}\), or from the interpolation formulae of the second order in the case when the grid in \({\Omega }_{2}\) is more dense than in \({\Omega }_{1}\). Domain \({\Omega }_{2}\) is divided into \(n_{2}^{\left( 1 \right)} + 1, n_{2}^{\left( 2 \right)} + 1, n_{2}^{\left( 3 \right)} + 1\) subintervals along directions \(x^{\left( 1 \right)} , x^{\left( 2 \right)}\) and it is assumed that \(n_{2}^{\left( 3 \right)} = { }n_{1}^{\left( 3 \right)}\). This means that the division in the direction of the \(z\) axis in domain \({\Omega }_{2}\) is the same as in domain \({\Omega }_{1}\). When the grid in \({\Omega }_{2}\) is more dense than the one used in \({\Omega }_{1}\), the respective values of the wind field \({\mathbf{u}}_{0} \) can be calculated from the following interpolation formulae

$$ \begin{aligned} f\left( {x^{\left( 1 \right)} ,x^{\left( 2 \right)} ,x^{\left( 3 \right)} } \right) & = a_{0} + a_{{x^{\left( 1 \right)} }} \left( {x^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} } \right) + a_{{x^{\left( 2 \right)} }} \left( {x^{\left( 2 \right)} - x_{j}^{\left( 2 \right)} } \right) \\ &\quad + a_{{x^{\left( 1 \right)} x^{\left( 3 \right)} }} \left( {x^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} } \right)\left( {x^{\left( 3 \right)} - x_{k}^{\left( 3 \right)} } \right) \\ &\quad + a_{{x^{\left( 2 \right)} x^{\left( 3 \right)} }} \left( {x^{\left( 2 \right)} - x_{j}^{\left( 2 \right)} } \right)\left( {x^{\left( 3 \right)} - x_{k}^{\left( 3 \right)} } \right) \\ &\quad + a_{{x^{\left( 1 \right)} x^{\left( 2 \right)} x^{\left( 3 \right)} }} \left( {x^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} } \right)\left( {x^{\left( 2 \right)} - x_{j}^{\left( 2 \right)} } \right)\left( {x^{\left( 3 \right)} - x_{k}^{\left( 3 \right)} } \right), \\ \end{aligned} $$

where \(x^{\left( 1 \right)} \in <x_{i}^{\left( 1 \right)} ,x_{i + 1}^{\left( 1 \right)}>\), \(x^{\left( 2 \right)} \in <x_{j}^{\left( 2 \right)} ,x_{j + 1}^{\left( 2 \right)}>\), \(x^{\left( 3 \right)} \in <x_{k}^{\left( 3 \right)} ,x_{k + 1}^{\left( 3 \right)}>\), \(\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right)\) and \(\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right)\) are nodes of the grid in domain \({\Omega }_{1}\),

$$ \begin{gathered} a_{0} = f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right),\quad \hfill \\ a_{{x^{\left( 1 \right)} }} = \frac{{f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) - f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right)}}{{x_{i + 1}^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} }}, \hfill \\ a_{{x^{\left( 2 \right)} }} = \frac{{f\left( {x_{i}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) - f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right)}}{{x_{j + 1}^{\left( 2 \right)} - x_{j}^{\left( 2 \right)} }}, \hfill \\ a_{{x^{\left( 3 \right)} }} = \frac{{f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right) - f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right)}}{{x_{k + 1}^{\left( 3 \right)} - x_{k}^{\left( 3 \right)} }}, \hfill \\ a_{{x^{\left( 1 \right)} x^{\left( 2 \right)} }} = \frac{{f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) + f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) - f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) - f\left( {x_{i}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right)}}{{\left( {x_{i + 1}^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} } \right)\left( {x_{j + 1}^{\left( 2 \right)} - x_{j}^{\left( 2 \right)} } \right)}}, \hfill \\ a_{{x^{\left( 1 \right)} x^{\left( 3 \right)} }} = \frac{{f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) + f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right) - f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) - f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right)}}{{\left( {x_{i + 1}^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} } \right)\left( {x_{k + 1}^{\left( 3 \right)} - x_{k}^{\left( 3 \right)} } \right)}}, \hfill \\ \end{gathered} $$
$$ \begin{aligned} a_{{x^{\left( 1 \right)} x^{\left( 2 \right)} x^{\left( 3 \right)} }} & = \frac{{ - f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) + f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) + f\left( {x_{i}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) + f\left( {x_{i}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right)}}{{\left( {x_{i + 1}^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} } \right)\left( {x_{j + 1}^{\left( 2 \right)} - x_{j}^{\left( 2 \right)} } \right)\left( {x_{k + 1}^{\left( 3 \right)} - x_{k}^{\left( 3 \right)} } \right)}} \\ &\quad \frac{{ - f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k}^{\left( 3 \right)} } \right) - f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right) - f\left( {x_{i}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right) + f\left( {x_{i + 1}^{\left( 1 \right)} ,x_{j + 1}^{\left( 2 \right)} ,x_{k + 1}^{\left( 3 \right)} } \right)}}{{\left( {x_{i + 1}^{\left( 1 \right)} - x_{i}^{\left( 1 \right)} } \right)\left( {x_{j + 1}^{\left( 2 \right)} - x_{j}^{\left( 2 \right)} } \right)\left( {x_{k + 1}^{\left( 3 \right)} - x_{k}^{\left( 3 \right)} } \right)}}. \\ \end{aligned} $$

It is important to note that the problem of adjustment of the wind field in domain \({\Omega }_{2} \) assumes that:

  1. (1)

    Discretization in the vertical direction is the same in both domains \({\Omega }_{1}\) and \({\Omega }_{2}\). Nodes \(x_{i}^{\left( 3 \right)}\) are identical for both tasks.

  2. (2)

    The initial wind field \({\mathbf{u}}_{0}^{{\left( {{\Omega }_{2} } \right)}}\) is not calculated according to the procedure described in Sect. 3 by means of the algorithm using the results from the measurement stations and parametrization. Values \({\mathbf{u}}_{0}^{{\left( {{\Omega }_{2} } \right)}} \) are the values from the solution of the task for domain \({\Omega }_{1}\) after use of appropriate interpolation formulae.

  3. (3)

    Boundary conditions on \(\phi\) for \({\Gamma }_{a}^{{({\Omega }_{2} )}}\) in a denser grid for domain \({\Omega }_{1}\) are calculated by the approximation of results obtained as a solution for domain \({\Omega }_{1}\).

The task for \({\Omega }_{2}\) can be solved several times using the same grid as before and assuming

$$ {\mathbf{u}}_{0}^{\left( i \right)} = {\mathbf{u}}_{{}}^{{\left( {i - 1} \right)}} ,{\text{ for }}i = 3,{ }4, \ldots $$

The iteration process can be carried out until the wind field converges. In simulations presented in the next section, it is assumed that the wind field in \({\Omega }_{2}\) converges when

$$ {\frac{{\|{\mathbf{u}}_{{}}^{\left( i \right)}\| - \|{\mathbf{u}}_{{}}^{{\left( {i - 1} \right)}} }\|}{{\|{\mathbf{u}}_{{}}^{\left( i \right)}\| }}} < \varepsilon , $$

where \(\|{\mathbf{u}}_{{}}^{\left( i \right)}\| = \left( {\mathop \sum \limits_{{j = {{\text{all points in}} \Omega }_{2} }} \left[ {\left( {u_{j}^{i,1} } \right)^{2} + \left( {u_{j}^{i,2} } \right)^{2} + \left( {u_{j}^{i,3} } \right)^{2} } \right]} \right)^{1/2} \), and \(\varepsilon\) is a relative error. In the sub-areas, the mass continuity equation is also fulfilled.

Results of numerical simulations using the iterative process described are presented and discussed in the next sections. They indicate efficiency and numerical effectiveness of the algorithm proposed as well as a considerable reduction of calculation time.

6 Results of Numerical Simulations

In order to validate the model of the wind field, the usual metrics are used (COST Action 710 1998; Britter and Schatzmann 2007):

  •  − the normalized-mean-square error

    $$ NMSE = \overline{{\frac{{\left( {w_{e} - w} \right)^{2} }}{{\overline{{w_{e} }} \overline{w}}}}} , $$

  •  − the proportion of calculated values within a factor-of-two of the measured values

    $$ FAC2 = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left\{ {\begin{array}{*{20}l} {1\quad {\text{for}}\; 0.5 \le \frac{w}{{w_{e} }} \le 2} \\ {0 \quad {\text{otherwise }}} \\ \end{array} ,} \right. $$

    where \(w\) is the value calculated, \(w_{e}\) is the value measured, \(n\) is the number of measurement data;

  •  − the hit rate \(q\) (VDI 2005)

    $$ q = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} N_{i} , N_{i} = \left\{ {\begin{array}{*{20}l} {1 \quad for \left| {\frac{{w_{i} - w_{0,i} }}{{w_{e,i} }}} \right| \le D_{w} \vee \left| {w_{i} - w_{0,i} } \right| \le W_{w} } \\ {0 \quad {\text{otherwise }} } \\ \end{array} ,} \right. $$

    where \(D_{w}\) is the normalized allowed range (assumed 0.25 for the analysis carried out), \(W_{w}\) is the threshold value accounting for relative uncertainty of the measurements assumed as 8 × 10–3 for the main component of the velocity vector. The lowest acceptable value of the hit rate q for prognostic models is 0.66 (VDI 2005).

6.1 Validation of the Model

Validation of the model is performed for a domain in which there are obstacles disturbing the airflow. Results of numerical simulations obtained using the authors’ own model are compared with the laboratory-scale experimental measurements. The experiment was carried out in a wind tunnel in Hamburg. Geometrical conditions of the Mock Urban Setting Test (MUST) experiment (Harms et al., 2011; Bezpalcová et al. 2006; Bezpalcová 2007; Leitl et al. 2007) have been reflected on a 1:75 scale. Although the experiment was conducted in a wind tunnel, all data provided hereafter relate to the MUST test site, so the length units are not divided by 75. The authors are aware that the mere mapping of real conditions in the tunnel may cause some errors. These issues are considered in the research to which we refer. One hundred and twenty solid blocks imitating real containers (119 cuboid containers with size 12.2 × 2.42 × 2.54 m and one cuboid container of 6.09 × 2.43 × 3.51 m in the middle) were placed in the domain as shown in Fig. 6. The wind field was calculated and compared with the experimental measurements for a flow direction of 45° with respect to the position of the containers.

Fig. 6
figure 6

Arrangements of the containers in the experiment

Full size image

During the experiment the flow velocity was registered for two components of the air velocity during three measurement series. The total number of measurement points was 1721 (series 1–498 points, series 2–847 points, series 3–376 points). The number of measuring profiles (planes) and their location on the \(x^{\left( 3 \right)}\) axis is as follows:

  • for series 1: 18 profiles from 0.45 to 13.5 m;

  • for series 2: three profiles at 1.272; 2.55 and 5.1 m, respectively;

  • for series 3: four profiles at 0.9; 1.275; 1.575; 2.55 m, respectively.

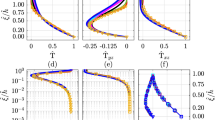
The average number of measuring points in the profile (plane) is 27 for series 1, 282 for series 2 and 94 for series 3. The positions of the measuring points and distribution of profiles (planes) are presented in Figs. 7 and 8.

Fig. 7
figure 7

Distribution of measuring profiles for series 1

Full size image
Fig. 8
figure 8

Distribution of measuring planes in series 2 and 3

Full size image

In order to reflect the airflow in the domain (Fig. 9), at the border of the domain (for \(x^{\left( 1 \right)} = - 140 \,{\text{m}}\), \(x^{\left( 2 \right)} = 0 \) and \(x^{\left( 1 \right)} = 135 \,{\text{m}}\), \(x^{\left( 2 \right)} = 0\)) the input wind field was calculated for the reference speed \(u_{ref} = 5.5 \,{\text{m s}}^{ - 1}\) (registered at \(x_{ref}^{\left( 3 \right)} = 7.29 \,{\text{m}}\)) according to Macdonald (2000)

$$ \begin{gathered} {\text{for}}\;x^{\left( 3 \right)} \le \overline{d}\quad u\left( {x^{\left( 3 \right)} } \right) = u\left( {x_{H}^{\left( 3 \right)} } \right){\text{exp}}\left[ {\alpha \left( {\frac{{x^{\left( 3 \right)} }}{{x_{H}^{\left( 3 \right)} }} - 1} \right)} \right], \hfill \\ {\text{for}}\;x^{\left( 3 \right)} > \overline{d}\quad u\left( {x^{\left( 3 \right)} } \right) = u_{*} k\ln \left( {\frac{{x^{\left( 3 \right)} - \overline{d}}}{{x_{0}^{\left( 3 \right)} }}} \right), \hfill \\ \end{gathered} $$

where \(x_{0}^{\left( 3 \right)} = 0.0165 \,{\text{m}}\), \(u_{*}\) is the friction velocity for \(x^{\left( 3 \right)} = x_{ref}^{\left( 3 \right)}\) and \(u\left( {x_{ref}^{\left( 3 \right)} } \right) = u_{ref}\),\(k = 0.41\),\( \alpha = 0.3\), \(x_{H}^{\left( 3 \right)} = 2.54 \,{\text{m}}\), \(\overline{d} = 0.7x_{H}^{\left( 3 \right)}\).

Fig. 9
figure 9

Initial wind profile

Full size image

The calculations were carried out on a discretized grid with 15 layers in the vertical direction based on trigonometric distribution (Chebyshev nodes). Such a distribution of nodes provides better convergence of the iterative algorithm for the wind field than the parabolic distribution or equal distance method (Brzozowska 2015a). Table 1 presents the results of the quantitative analysis of the main component of the flow velocity vector for each series for different density of the calculation grid in directions \(x^{\left( 1 \right)}\) and \(x^{\left( 2 \right)}\). These are the results of stage Z(1) described in Sect. 4.

Table 1 Metrics NMSE, FAC2, q of the main component of the wind profile for different series
Full size table

Analysis of the metrics presented in Table 1 shows that better results are obtained for measurement series I and II. The change of density of the grid in directions \(x^{\left( 1 \right)}\) and \(x^{\left( 2 \right)}\) below 1 m between the neighbouring nodes does not result in improvement of the quality of the results (reduction of error values). Domain \({\Omega }_{1}\) is defined by (\(x^{\left( 1 \right)} \in< - 150;\break 150 >{\text{m}}; x^{\left( 2 \right)} \in< - 150;150 >{\text{ m}}; x^{\left( 3 \right)} \in <0;21> {\text{ m}} \)).

Below, the results of calculations of the wind field in three smaller subdomains \({\Omega }_{2}\), separated from domain \({\Omega }_{1}\) in such a way that all points of the same measurement series belong to one subdomain, are presented. The results of calculations for domain \({\Omega }_{1}\) with a discretized grid of resolution 5 m are assumed as input data for subdomain \({\Omega }_{2}\). The results of calculations are again compared with the results of the experiment, in this case focusing only on subdomain \({\Omega }_{2}\). The results presented in the Table 2 refer to the first iteration. Even in this case, a considerable improvement in the accuracy can be seen.

Table 2 Metrics NMSE, FAC2, q of the main component of the wind field in each subdomain
Full size table

The errors obtained are similar to those obtained when calculations are carried out for the whole domain. It is important to note that the application of the iterative procedure improved the metrics for series 3. The reason can be seen in the fact that subdomain \({\Omega }_{2}\) lies far from the edges \( <- 150;150 >\) and the initial solution for \({\Omega }_{1}\) with the 5-m grid gives a better approximation of the initial wind field in \({\Omega }_{2}\) than the initial field adopted for the domain \({\Omega }_{1}\) with the 1-m grid according to the parametrization.

A comparison of the calculation times for the analyzed grids for domain \({\Omega }_{1}\) and subdomains \({\Omega }_{2}\) is presented in Table 3.

Table 3 Times t of calculations of wind field in domain \({\Omega }_{1}\) and subdomains \({\Omega }_{2}\)
Full size table

Having analyzed data in Table 3, it can be seen that the calculation time necessary for the subdomains is considerably smaller. When the wind field is determined using the division of the domain into subdomains, the calculation time in subdomain \({\Omega }_{2}\) is several times smaller than the calculation time in domain \({\Omega }_{1}\), which demonstrates the efficiency of the algorithm proposed.

Table 4 shows the results for the iterative process of wind field stabilization. The wind field calculated at a given calculation step is used as the initial data for the solution of the task in the next step. The discretization grid is the same at all steps in the iterative procedure.

Table 4 Metrics in subsequent iterations
Full size table

The results presented indicate that the conformity metrics stabilize after one or two iterations. Subsequent iterations do not significantly improve the metrics.

6.2 Simulations for a Built-Up Area in a Medium-Size Town

In this section, the algorithms presented are used in numerical simulations concerning a real area. Further analysis is concerned with part of a medium-size town (170,000 inhabitants, Bielsko-Biała, Poland) lying near mountains, which means the area has a diversified terrain. The area simulated is shown in Fig. 10.

Fig. 10
figure 10

Area for simulation: a whole domain, b subdomains

Full size image

The area presented in Fig. 10a forms domain \({\Omega }_{1}\), and Fig. 10b shows subdomains \({\Omega }_{2}\) modelled in which P1, P2, and P3 denote three cases analyzed. It is assumed that the flow is from the north-east.

A logarithmic wind profile is assumed at nine points of the area marked in Fig. 10b as \(S_{1} , \ldots ,S_{9}\) (components in directions \(x^{\left( 1 \right)}\), \(x^{\left( 2 \right)}\) of the wind speed at \(h = 10\,{\text{m}}\) are \(u_{{x^{\left( 1 \right)} }} = 4{\text{ m s}}^{ - 1}\), \(u_{{x^{\left( 2 \right)} }} = 3{\text{ m s}}^{ - 1}\)). The coordinates of the points are as follows:

$$ \begin{gathered} S_{{1,x^{\left( 1 \right)} }} = S_{{4,x^{\left( 1 \right)} }} = S_{{7,x^{\left( 1 \right)} }} = 50\; {\text{m,}} \hfill \\ S_{{2,x^{\left( 1 \right)} }} = S_{{5,x^{\left( 1 \right)} }} = S_{{8,x^{\left( 1 \right)} }} = 1500 \; {\text{m}}, \hfill \\ S_{{3,x^{\left( 1 \right)} }} = S_{{6,x^{\left( 1 \right)} }} = S_{{9,x^{\left( 1 \right)} }} = 2950 \; {\text{m}}, \hfill \\ S_{{1,x^{\left( 2 \right)} }} = S_{{2,x^{\left( 2 \right)} }} = S_{{3,x^{\left( 2 \right)} }} = 50 \; {\text{m}}, \hfill \\ S_{{4,x^{\left( 2 \right)} }} = S_{{5,x^{\left( 2 \right)} }} = S_{{6,x^{\left( 2 \right)} }} = 1500 \; {\text{m}}, \hfill \\ S_{{7,x^{\left( 2 \right)} }} = S_{{8,x^{\left( 2 \right)} }} = S_{{9,x^{\left( 2 \right)} }} = 2950 \; {\text{m}}. \hfill \\ \end{gathered} $$

Data for the elevation and hydrodynamic roughness of the terrain are obtained from GIS (geographical information system) (1:10,000 scale topographical map). The parametrization is adopted from Montero et al. (1998, 2005), Macdonald (2000), and Montero and Sanín (2001). Calculations in area \({\Omega }_{1}\) are carried out with the grid resolution \(\Delta_{{x^{\left( 1 \right)} }} = \Delta_{{x^{\left( 2 \right)} }} = 10 \,{\text{m}}\) (notation \({\Omega }_{1}^{10}\)) or the grid resolution \(\Delta_{{x^{\left( 1 \right)} }} = \Delta_{{x^{\left( 2 \right)} }} = 50 \,{\text{m}}\) (notation \({\Omega }_{1}^{50}\)).

In direction \({x}^{\left(3\right)}\), Chebyshev nodes are used with greater density towards the ground, assuming that \({n}^{\left(3\right)}+1=16\). The grid with \({\Delta }_{{x}^{\left(1\right)}}={\Delta }_{{x}^{\left(2\right)}}=10 \,{\mathrm{m}}\) is used for all subdomains in \({\Omega }_{2}^{10}.\) Sub-areas P1, P2, and P3 are denoted as \({\Omega }_{\mathrm{2,1}}^{10}\), \({\Omega }_{\mathrm{2,2}}^{10}\), and \({\Omega }_{\mathrm{2,3}}^{10}\) respectively. Table 5 presents the results of simulations.

Table 5 Comparison of results obtained for domain \({\Omega }_{1}\) and subdomains \({\Omega }_{2}\)
Full size table

The results for sub-areas \({P}_{j} (j=\mathrm{1,2},3)\) in the second iteration (assuming input data from \(\Omega_{1}^{50} )\) are denoted as \({\Omega }_{2,j}^{10}\).

Norms \(\|{\mathbf{u}}_{i}\|\) and \(\|{\mathbf{u}}_{i} - {\mathbf{u}}_{i - 1}\|\) are calculated as

$$\|{\mathbf{u}}_{i}\| = \left[ {\frac{1}{N}\mathop \sum \limits_{p = 1}^{N} u_{i,p}^{2} } \right]^{1/2} , $$
$$ \|{\mathbf{u}}_{i} - {\mathbf{u}}_{i - 1}\| = \left[ {\frac{1}{N}\mathop \sum \limits_{p = 1}^{N} \left( {u_{i,p} - u_{i - 1,p} } \right)^{2} } \right]^{1/2} , $$

where \(u_{i,p}\), \(u_{i - 1,p}\) are absolute velocities of the wind in the \(i\)-th and \(i - 1\) iteration and \(N\) is the total number of points (nodes of the grid in the area analyzed).

The admissible values of the metrics are presented by Chang and Hanna (2004) and the value of the average percentage error is calculated as

$$ MSE = \frac{1}{{{N^{\left( 2 \right)}}}}\mathop \sum \limits_{p = 1}^{{N_2}} \left| {\frac{{{u_p}^{(1)} - {u_p}^{(2)}}}{{{u_p}^{(2)}}}} \right|100, $$

where \(u_{p}^{\left( 1 \right)} , u_{p}^{\left( 2 \right)}\) are velocities calculated in area \({\overline{\Omega }}_{1}^{{\left( {10} \right)}}\) and sub-area \({\Omega }_{2,j}^{{\left( {10} \right)}}\) respectively, \(N^{\left( 2 \right)}\) is the number of points (nodes of the grid in area \({\Omega }_{2,j}^{{\left( {10} \right)}}\)).

If we assume that the input wind field \(u_{0} \left( {{\Omega }_{1}^{{\left( {10} \right)}} } \right)\) is the wind field obtained by the interpolation of results \(u\left( {{\Omega }_{1}^{{\left( {50} \right)}} } \right)\) with results from the first iteration \({\Omega }_{2,j}^{{\left( {10} \right)}}\) obtained for the same initial wind field, the metrics for the comparison of the wind fields obtained for the whole area \({\overline{\Omega }}_{1}^{10}\) are as follows:

  • NMSE = 0.0001 for all cases \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), and \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), while admissible values should be smaller than 4,

  • FAC2 = 1 for all cases \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), and \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), while admissible values should be larger than 0.5,

  • q = 0.9999 for \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), q = 0.9997 for \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), q = 1for \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), and the admissible values should be larger than 0.68,

  • MSE = 0.89% for \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), MSE = 0.52% for \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), MSE = 0.77% for \({\overline{\Omega }}_{1}^{{\left( {10} \right)}} {\text{vs}} {\Omega }_{2,1}^{{\left( {10} \right)}}\), while the admissible values should be smaller than 5.

Resulting wind fields in area \({\Omega }_{1}^{{\left( {10} \right)}}\) and sub-areas \({\Omega }_{2,j}^{{\left( {10} \right)}}\) analyzed are presented in Fig. 11. Analysis of the results indicates that the first iteration step with the grid of 50 m in the horizontal plane already provides correct results (with respect to 10 m mesh in the whole area).

Fig. 11
figure 11

Wind field analyzed: a whole domain, b subdomain P1, c subdomain P2, d subdomain P3

Full size image

The calculation time of wind fields in each sub-area is considerably shorter. The average percentage error for wind fields calculated in area \({\Omega }_{1}\) and sub-areas \({\Omega }_{2,1} ,{\Omega }_{2,2} ,{\Omega }_{2,3}\) with the same mesh does not exceed 1%.

7 Conclusions

The method of subdomains enables us to considerably shorten the calculation time. Validation of the model presented in Sect. 6.1 concerns a standard experiment widely used for the validation of wind field models for built-up areas (with complicated topography). The analysis indicates that the results already converge after the first iteration of the algorithm. The method applied in areas with complex topography makes it possible to obtain more accurate results with a considerably reduced time of calculations. It can be successfully used for typical meteorological conditions in a given area/town (using the database of the wind field) when the wind field and pollutant concentration have to be defined in the microscale. The calculations presented in Sect. 6.2 used a mesh not smaller than 10 m, which is the typical grid size considered in a mesoscale. However, the model, as shown in Brzozowska et al. (2007) and Brzozowska (2016), also enables modelling of the wind field and dispersion of pollutants in the microscale with good accuracy.

In general, it should be noted that dynamic, prognostic models of the CFD class controlled by measurements have the greatest accuracy—as in the data-assimilation approach. However, they require detailed data and high computing power for performing calculations. Diagnostic, stationary models that fulfil the continuity equation, sometimes equivalent to the momentum equation, are less accurate, as in the NinjaWind or QUIC-URB packages.

An interesting comparison of diagnostic and CFD class models (Reynolds-averaged Navier−Stokes and large-eddy simulation) is presented by Hayati et al. (2019). It is shown that diagnostic models (as the model presented in this paper) are definitely cheaper in terms of costs and calculation times. The use of parallel computations can significantly improve computational efficiency. Here, parallel computations were used by means of multithreading. As demonstrated by Bozorgmehr et al. (2021), an additional improvement in the efficiency of computations can be obtained by applying graphic processing units.

The model presented can be used successfully when the prognostic model is not applicable (too much input data is required), when there are no meteorological stations in the analyzed area, or the grid of available data points from meteorological stations is so sparse that it does not cover the area analyzed. The use of the method proposed allows for the initial calculations of the air velocity field and then the calculation of the wind field in any sub-area, at the same time refining the discretization grid. If, additionally, a database of wind fields is created for typical meteorological conditions in a given region, the primary calculations can be avoided each time, and only performed for selected sub-areas. This considerably reduces the time needed to perform simulations, for example, in the case of sudden releases of hazardous substances or episodes related to low emission.