How is the Two-Regime Stable Boundary Layer Reproduced by the Different Turbulence Parametrizations in the Weather Research and Forecasting Model?

Abstract

Five planetary-boundary-layer parametrizations of the Weather Research and Forecasting model are compared with respect to their ability to simulate the very stable and the weakly stable regimes of the stable boundary layer. This is performed for single column models where the large-scale mechanical forcing is represented by geostrophic wind speeds ranging from 0.5 to 12 m $\hbox {s}^{-1}$. The performance of the models is assessed by contrasting the relationships they produce between the turbulence velocity scale and the mean wind speed, between potential temperature gradient and the mean wind speed, and between the flux and gradient Richardson numbers. The level-2.5 Mellor–Yamada–Nakanishi–Niino parametrization simulates the very stable regime the best, mainly because its heat eddy diffusivity decreases with respect to the momentum eddy diffusivity as the stability increases, while the same is not true for the other parametrizations considered.

Appendices

Appendix 1: Numerical Constants

All numerical constants employed in the MYNN, MYJ, QNSE, UWBLS and BouLac parametrizations are presented in Table 4.

Table 4 Numerical constants employed by the PBL parametrizations

Appendix 2: The Mellor–Yamada–Janjic Parametrization

The numerical constants $A_{S_M}$, $B_{S_M}$,$C_{S_M}$,$D_{S_M}$,$F_{S_M}$,$G_{S_M}$,$A_{S_H}$,$B_{S_H}$ and $C_{S_H}$ in Eqs. 15–16 are given by

$$\begin{aligned} A_{S_M}= & {} -3A_1A_2\left( 3A_2+3B_2C_1+12A_1C_1-B2\right) ,\\ B_{S_M}= & {} A_1\left( 1-3C_1\right) ,\\ C_{S_M}= & {} 18A_1^2A_2\left( B_2-3A_2\right) ,\\ D_{S_M}= & {} 9A_1A_2^2\left( 12A_1+3B_2\right) ,\\ F_{S_M}= & {} 6A_1^2,\\ G_{S_M}= & {} 3A_2\left( 7A_1+B_2\right) ,\\ A_{S_H}= & {} 18A_1^2A_2C_1,\\ B_{S_H}= & {} 9A_1A_2^2,\\ C_{S_H}= & {} A_2, \end{aligned}$$

where the values of numerical constants $A_1$, $A_2$, $B_1$, $B_2$, and $C_1$ are given the Appendix 1.

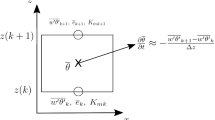
The MYJ PBL parametrization solves a linearized form of a prognostic equation for the ratio between the mixing length and TKE (Eqs. 20–21). This linearization starts with Eq. 19 rewritten as

$$\begin{aligned} \frac{d}{dt}\left( \frac{l_K}{q}\right) =\frac{A\left( \frac{l_K}{q}\right) ^4 +B\left( \frac{l_K}{q}\right) ^2}{C\left( \frac{l_K}{q}\right) ^4 +D\left( \frac{l_K}{q}\right) ^2+1}-\frac{1}{B1}, \end{aligned}$$

(54)

where the right-hand side is defined as R. Its derivative with respect to $l_t/q$ is defined as $R'$, such that

$$\begin{aligned} \frac{dR}{d\left( l_K/q\right) }=R'=-2\frac{\left[ \left( AD-BC\right) \left( \frac{l_K}{q}\right) ^5+2A\left( \frac{l_K}{q}\right) ^3+B \left( \frac{l_K}{q}\right) \right] }{\left[ C\left( \frac{l_K}{q}\right) ^4 +D\left( \frac{l_K}{q}\right) ^2+1\right] ^2}. \end{aligned}$$

(55)

The functions A, B, C, and D are given by

$$\begin{aligned} A= & {} \left\{ \left[ -3A_1A_2\left( 3A_2+3B_2c_1+18A_1C_1-B2\right) \left( \beta g\right) \right] g_M -\left[ B_{S_H}\left( \beta g\right) ^2\right] g_H\right\} g_H, \\ B= & {} B_{S_M}g_M-\left( A_2\beta g\right) g_H,\\ C= & {} \left\{ \left[ C_{S_M}\left( \beta g\right) \right] g_M-\left[ D_{S_H}\left( \beta g\right) ^2\right] g_H\right\} g_H, \end{aligned}$$

and

$$\begin{aligned} D=F_{S_M}g_M-G_{S_H}\left( \beta g\right) g_H, \end{aligned}$$

where the dimensionless vertical gradients of mean wind speed and virtual temperature are defined as

$$\begin{aligned} g_M =\frac{G_M}{\frac{l_K^2}{q^2}}, \end{aligned}$$

and

$$\begin{aligned} g_H=\frac{G_H}{ \frac{l_K^2}{q^2}\beta g}. \end{aligned}$$

Equation 54 is linearized as

$$\begin{aligned} \frac{d\left( l_K/q\right) _{i+1}}{dt}=R_{i}+R'_{i} \left[ \left( \frac{l_K}{q}\right) _{i+1}-\left( \frac{l_K}{q}\right) _{i}\right] , \end{aligned}$$

(56)

whose solution is given by Eq. 21.

Equations 19–22 do not solve TKE transport. It is estimated at a later step through Eq. 23, where coefficients $C_r(z_i)$, $R_Q(z_i)$ and $C_M(z_i)$ are given by

$$\begin{aligned} C_R(z_{i})= & {} -DTZ(z_i)AK_q(z_{i}),\\ C_M= & {} C_R(z_{i-1})C_F(z_{i})+(AK_q(z_{i-1})+AK_q(z_{i}))DTZ(z_i)+1,\\ R_Q(z_i)= & {} R_Q(z_{i-1})C_F(z_i)+q^2(z_i),\\ AK_q(z_{i})= & {} \frac{5\sqrt{q^2(z_{i})}l_K(z_{i})}{z_{i+1}-z_{i+2}},\\ DTZ(z_i)= & {} \frac{2{\Delta } t}{z_{i}-z_{i+2}},\\ C_F= & {} \frac{-DTZ(z_i)AK_q(z_{i-1})}{C_M(z_{i-1})}. \end{aligned}$$

Appendix 3: The Mellor–Yamada–Nakanishi–Niino Level-2 model

Although no level-2 MYNN PBL parametrization is explicitly used in the present study, it is necessary to define its equations before showing those for levels 2.5 and 3.

As defined in Mellor and Yamada (1974, 1982), in level-2 parametrizations, the TKE is estimated through the balance between shear production, buoyant destruction and dissipation

$$\begin{aligned} q_2^2=b_1l_K^2\left\{ s_m\left[ \left( \frac{\partial {\overline{u}}}{\partial z}\right) ^2+\left( \frac{\partial {\overline{v}}}{\partial z}\right) ^2\right] +s_h\frac{g}{\varTheta }\frac{\partial {\overline{\theta }}_V}{\partial z}\right\} , \end{aligned}$$

(57)

where $s_h$ and $s_m$ are the stability functions for heat and momentum, respectively,

$$\begin{aligned} s_h=3a_2\left( g_1+g_2\right) \frac{Ri_{fc}-Ri_f}{1-Ri_f}, \end{aligned}$$

(58)

and

$$\begin{aligned} s_m=\frac{a_1}{a_2}\frac{f_1}{f_2}\frac{r_{f1}-Ri_f}{r_{f2}-Ri_f}s_h, \end{aligned}$$

(59)

which are functions of the level-2 flux Richardson number $Ri_f$, defined as

$$\begin{aligned} Ri_f=\mathrm {min}\left[ ri1\left( Ri_g+r_{i2}-\sqrt{Ri_g^2-r_{i3}Ri_g+r_{i2}^2} \right) ,Ri_{fc}\right] , \end{aligned}$$

(60)

where $Ri_g$ is the gradient Richardson number, and $Ri_{fc}$ is the critical flux Richardson number

$$\begin{aligned} Ri_{fc}=\frac{g_1}{g_1+g_2}. \end{aligned}$$

(61)

The other quantities in Eqs. 58–60 are numerical constants:

$$\begin{aligned} f_1= & {} b_1\left( g_1-c_1\right) +3a_2\left( 1-c_2\right) \left( 1-c_5\right) +2a_1\left( 1-c_2\right) ,\\ f_2= & {} b_1\left( g_1+g_2\right) -3a_1\left( 1-c_2\right) ,\\ r_{f1}= & {} \frac{b_1\left( g_1-c_1\right) }{f_1},\\ r_{f2}= & {} \frac{b_1g_1}{f_2},\\ r_{i1}= & {} \frac{1}{2}\frac{a_2}{a_1}\frac{f_2}{f_1},\\ r_{i2}= & {} r_{f1}\frac{a_1}{a_2}\frac{f_1}{f_2}, \end{aligned}$$

and

$$\begin{aligned} r_{i3}=4r_{f2}\frac{a_1}{a_2}\frac{f_1}{f_2}-2r_{i2}. \end{aligned}$$

A correction that allows a variable critical Richardson number and avoids negative TKE in stable condions uses

$$\begin{aligned} a_2=\frac{a'_2}{1+Ri_g}, \end{aligned}$$

following Canuto et al. (2008) and Kitamura (2010).

Appendix 4: The Mellor–Yamada–Nakanishi–Niino Level-2.5 model

In Eq. 37, $e_2$, $e_4$, $e_5$, and $D_{2.5}$ are given by

$$\begin{aligned} e_2= & {} q^2-9a_1a_2\left( 1-c_2\right) l_K^2\frac{g}{\varTheta } \frac{\partial {\overline{\theta }}_V}{\partial z},\\ e_4= & {} e_1-12a_1a_2\left( 1-c_2\right) l_K^2\frac{g}{\varTheta } \frac{\partial {\overline{\theta }}_V}{\partial z},\\ e_5= & {} 6a_1^2l_K^2\left[ \left( \frac{\partial {\overline{u}}}{\partial z}\right) ^2+\left( \frac{\partial {\overline{v}}}{\partial z}\right) ^2\right] , \end{aligned}$$

and

$$\begin{aligned} D_{2.5}=e_2e_4+e_3e_5, \end{aligned}$$

where the terms $e_1$ and $e_3$ are defined as

$$\begin{aligned} e_1= & {} q^2-3a_2b_2\left( 1-c_3\right) l_K^2\frac{g}{\varTheta } \frac{\partial {\overline{\theta }}_V}{\partial z},\\ e_3= & {} e_1+9a_2^2\left( 1-c_2\right) \left( 1-c_5\right) l_K^2\frac{g}{\varTheta } \frac{\partial {\overline{\theta }}_V}{\partial z}. \end{aligned}$$

The variance of temperature, the variance of total water content, and the covariance of $\overline{\theta _l}$ and ${\overline{q}}_w$ are diagnostically estimated as

$$\begin{aligned} \overline{\theta '^2_{l}}_{2.5}= & {} \alpha _cb_2l_Kqs_{h2.5}\left( \frac{\partial \overline{\theta _l}}{\partial z}\right) ^2, \end{aligned}$$

(62)

$$\begin{aligned} \overline{q'^2_w}_{2.5}= & {} \alpha _cb_2l_Kqs_{h2.5}\left( \frac{\partial {\overline{q}}_w}{\partial z}\right) ^2, \end{aligned}$$

(63)

$$\begin{aligned} \overline{\theta '_lq'_w}_{2.5}= & {} \alpha _cb_2l_Kqs_{h2.5}\frac{\partial {\overline{q}}_w}{\partial z}\frac{\partial {\overline{\theta }}_l}{\partial z}. \end{aligned}$$

(64)

These quantities are not used in the level-2.5 parametrization, but they are necessary for calculating the contergradients and stability functions for the level-3 model. The parameter $\alpha _c$ is defined by Nakanishi and Niino (2009) as

$$\begin{aligned} \alpha _c=\left\{ \begin{array}{ll} q/q_2, \ \ \ \mathrm {if} \ \ q<q_2\\ \ \ \ 1 , \ \ \ \ \mathrm {if} \ \ q \ge q_2 \\ \end{array} \right. . \end{aligned}$$

(65)

Appendix 5: The Mellor–Yamada–Nakanishi–Niino Level-3 model

In Eq. 40, $D_3$ and $e'_6$, are given by

$$\begin{aligned} D_{3}= & {} e'_2e'_4+e'_3e'_5, \\ e'_6= & {} 3a_2\left( 1-c_3\right) \frac{g}{\varTheta }, \end{aligned}$$

where $e'_2$, $e'_3$, $e'_4$, $e'_5$ and $e'_7$ are defined as

$$\begin{aligned} e'_2= & {} q^2-9a_1a_2\left( 1-c_2\right) l_K^2\frac{g}{\varTheta } \frac{\partial {\overline{\theta }}_V}{\partial z}\alpha _c^2, \\ e'_3= & {} q^2 +9a_2^2\left( 1-c_2\right) \left( 1-c_5\right) l_K^2\frac{g}{\varTheta } \frac{\partial {\overline{\theta }}_V}{\partial z}\alpha _c^2, \\ e'_4= & {} q^2 -12a_1a_2\left( 1-c_2\right) l_K^2\frac{g}{\varTheta }\frac{\partial {\overline{\theta }}_V}{\partial z}\alpha _c^2, \\ e'_5= & {} 6a_1^2l_K^2\left[ \left( \frac{\partial {\overline{u}}}{\partial z}\right) ^2+\left( \frac{\partial {\overline{v}}}{\partial z}\right) ^2\right] \alpha _c^2, \end{aligned}$$

and

$$\begin{aligned} e'_7=e'_2+e'_5. \end{aligned}$$

The countergradient contributions in Eqs. 42–44 are given by

$$\begin{aligned} \varGamma _{\theta }= & {} \frac{-e'_7\alpha _ce'_6\left( \overline{\theta _l'\theta _V'} -\overline{\theta _l'\theta '_V}_{2.5}\right) }{D_3}, \end{aligned}$$

(66)

$$\begin{aligned} \varGamma _V= & {} \frac{e'_7\alpha _ce'_6\frac{g}{\varTheta }\left( \overline{\theta '^2_V} -\overline{\theta '^2_V}_{2.5}\right) }{D_3}, \end{aligned}$$

(67)

$$\begin{aligned} \varGamma _q= & {} \frac{-e'_7\alpha _ce'_6\left( \overline{q_w'\theta _V'} -\overline{q_w'\theta _V'}_{2.5}\right) }{D_3}, \end{aligned}$$

(68)

where the terms $\overline{ \theta '_l\theta '_V}$, $\overline{q'_w\theta '_V}$, $\overline{\theta '^2_V}$ are defined as

$$\begin{aligned} \overline{ \theta '_l\theta '_V}=\beta _{\theta }\overline{\theta '^{2}_{l}} +\beta _q\overline{\theta '_lq'_w}, \ \ \overline{q'_w\theta '_V}=\beta _{\theta }\overline{\theta '_lq_w} +\beta _q\overline{q'^2_w} \ \ \mathrm {and} \ \ \overline{\theta '^2_V}=\beta _{\theta }\overline{\theta '_l\theta '_V} +\beta _q\overline{q'_w\theta '_V}. \end{aligned}$$

In the expressions above, $\beta _{\theta }$ and $\beta _q$ are functions related to the condensation process (Nakanishi and Niino 2009). The above equations are also valid for the terms with sub-index 2.5 (present in Eqs. 66–68). Such a sub-index means that these terms are evaluated by the level-2.5 MYNN parametrization. Therefore, the determination of $\overline{ \theta '_l\theta '_V}$, $\overline{q'_w\theta '_V}$, and $\overline{\theta '^2_V}$ demands knowledge of the terms $\overline{\theta '^2_{l}}_{2.5}$, $\overline{q'^2_w}_{2.5}$, and $\overline{\theta '_lq'_w}_{2.5}$, which are presented in Appendix 3.

The other prognostic equations solved in the level-3 model, for $\overline{\theta '^2_l}$, $\overline{q'^2_w}$ and $\overline{\theta '_l q'_w}$ are

$$\begin{aligned} \frac{\partial \overline{\theta '^2_l}}{\partial t}= & {} 2l_Kq\left[ s_{h2.5}\left( \frac{\partial \overline{\theta _l}}{\partial z}\right) +\varGamma _{\theta }\right] \left( \frac{\partial \overline{\theta _l}}{\partial z}\right) +\frac{\partial }{\partial z}\left[ l_Kqs_{m}\frac{\partial \overline{\theta '^2_l}}{\partial z}\right] -\frac{2q\overline{\theta '^2_l}}{b_2l_K}, \end{aligned}$$

(69)

$$\begin{aligned} \frac{\partial \overline{q'^2_w}}{\partial t}= & {} 2l_Kq\left[ s_{h2.5}\left( \frac{\partial \overline{q_w}}{\partial z}\right) +\varGamma _{q}\right] \left( \frac{\partial \overline{q_w}}{\partial z}\right) +\frac{\partial }{\partial z}\left[ l_Kqs_{m}\frac{\partial \overline{q'^2_w}}{\partial z}\right] -\frac{2q \overline{q'^2_w}}{b_2l_K}, \end{aligned}$$

(70)

$$\begin{aligned} \frac{\partial \overline{\theta '_l q'_w}}{\partial t}= & {} l_Kq\left\{ \left[ s_{h2.5}\left( \frac{\partial \overline{\theta _l}}{\partial z}\right) +\varGamma _{\theta }\right] \left( \frac{\partial {\overline{q}}_w}{\partial z}\right) + \left[ s_{h2.5}\left( \frac{\partial \overline{q_w}}{\partial z}\right) +\varGamma _{q}\right] \right. \nonumber \\&\left. \left( \frac{\partial \overline{\theta _l}}{\partial z}\right) \right\} + \frac{\partial }{\partial z}\left[ l_Kqs_{m}\frac{\partial \overline{\theta '_lq'_w}}{\partial z}\right] -\frac{2q \overline{\theta '_lq'_w}}{b_2l_K}. \end{aligned}$$

(71)