1 Introduction

A stable atmospheric boundary layer (SABL) generally occurs with longwave radiative cooling of the land surface when the underlying surface becomes colder than the air above it, or in the case of warm air advection over a colder surface. These processes are followed by the transfer of energy from the atmosphere to the surface and lead to stably stratified inversion layers.

An important challenge for SABL research is understanding the relationships between the mean wind and temperature fields, and the average turbulent fluxes and variances. The increase of computational power has made it possible to use techniques such as large-eddy simulation (LES) to investigate the structure and properties of the SABL, which can help improve turbulence models (Huang et al. 2013). A comparison of LES results is presented in Beare et al. (2006) for an idealized set-up of a SABL in dry conditions with prescribed temperature forcing on a flat homogeneous surface, the so-called first Global Energy and Watercycle Experiment (GEWEX) Atmospheric Boundary Layer Study (GABLS1). The LES results have been utilized in the intercomparison of turbulent closure models typically used both in operational weather forecasting and research (see Cuxart et al. 2006). The study shows large variations among the model results and indicates that the turbulence models have a tendency to overpredict turbulence mixing in the SABL. As pointed out by Holtslag et al. (2013), turbulence models have a significant effect on the overall accuracy of climate and weather numerical models.

Recently, a high-resolution LES study by Sullivan et al. (2016) extended the set-up of the GABLS1 case by modifying the rate at which the surface temperature is changing in time. Varying the cooling rates at the surface produces a set of different stratification levels in the SABL. Turbulence transport weakens with increased stratification and the height of the SABL decreases. These recent LES data make it possible to test different turbulence models to varying levels of stratification. A particularly relevant question is how stratification affects the production of turbulence kinetic energy since many of the turbulence models do not contain the relevant physical processes for capturing the interaction between the turbulence and density stratification. Simpler turbulence models rely on the eddy-viscosity hypothesis (also known as K-theory) in which turbulence kinetic energy is typically modelled using empirical stability correction functions that depend on the gradient Richardson number.

In the present study we investigate the ability of the recently proposed explicit algebraic Reynolds-stress (EARS) model to predict the effects of different levels of stratification in the SABL. A notable difference between the EARS model and simpler models that rely on the eddy-viscosity hypothesis is that, instead of directly modelling turbulent fluxes, these are found by solving algebraic approximations of the transport equations for turbulent momentum and heat fluxes, also known as the Reynolds-stress and scalar-flux equations. The model has been developed by Lazeroms et al. (2013), and since then, a new boundary-condition treatment has been implemented along with a simplified model formulation by Želi et al. (2019). Previously, the result of the EARS model was compared to LES data for the case of the original GABLS1 set-up (Lazeroms et al. 2016). However, simulations with varying cooling rates allow us to study how the EARS model responds to varying stratification levels by comparing the results against the new set of high-resolution LES data from Sullivan et al. (2016).

The following section gives a model description: Sect. 3 explains the set-up of the numerical simulations. In Sect. 4, results of the validation are presented for the EARS model in the model’s standard form. Discussion of possible model modification and improvements are given in Sect. 5, and a summary is given in Sect. 6.

2 Description of the Turbulence Model

The framework of the EARS model is based on Lazeroms et al. (2013). A summary of the EARS model is given in Sects. 2.1 and 2.2, and in subsection 2.3, the general formulation of the EARS model is applied in the framework of a single-column model.

2.1 Generalized Explicit Algebraic Reynolds-stress Model

The EARS model is presented in a frame-invariant form in which the model equations for the Reynolds-stress tensor and the heat-flux vector read

$$\begin{aligned} \frac{\text {D}\,\overline{u_i u_j}}{\text {D} t} - \mathcal {D}_{ij} =&\mathcal {P}_{ij} + {\Pi }_{ij} - \epsilon _{ij} + \mathcal {G}_{ij}, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\text {D}\,\overline{u_i \theta }}{\text {D} t} - \mathcal {D}_{\theta i} =&\mathcal {P}_{\theta i} + {\Pi }_{\theta i} - \epsilon _{\theta i} + \mathcal {G}_{\theta i}, \end{aligned}$$
(2)

where \(\text {D}/\text {D}t \equiv \partial /\partial t + U_m \partial /\partial _m\) is the material derivative in the direction of the mean flow, and the remaining terms represent (from left to right) diffusion, shear production/destruction, pressure redistribution, dissipation, and buoyancy production/destruction. The large number of strongly coupled prognostic equations makes this class of models hard to evaluate in practice.

The system of equations in (1), (2) will be simplified as algebraic relations further below. Additional prognostic equations for scalar properties are then introduced, namely, the model for turbulent kinetic energy (TKE), K, and half the temperature variance, \(K_\theta \),

$$\begin{aligned} \frac{\text {D} K}{\text {D} t} - {\mathcal {D}_K} =&\mathcal {P} - {\epsilon } + \mathcal {G}, \end{aligned}$$
(3)
$$\begin{aligned} \frac{\text {D} K_\theta }{\text {D} t} - \mathcal {D}_{K_\theta } =&\mathcal {P}_{\theta } - \epsilon _{\theta }, \end{aligned}$$
(4)

where \(\mathcal {P}\) and \(\mathcal {G}\) are the production or destruction of TKE due to mean-shear and buoyancy effects, respectively, and \(\epsilon \) is the dissipation rate of TKE; \(\mathcal {P}_\theta \) and \(\epsilon _\theta \) are the production or destruction and the dissipation rate of half the temperature variance; \(\mathcal {D}_K\) and \(\mathcal {D}_{K_\theta }\) are the diffusion terms. It is worth mentioning that (3) is half of the trace of (1), meaning that it does not provide any additional information for the case when the transport equation (1) is solved directly, but will do so here since (1) is solved in an algebraic approximation.

Compared to other atmospheric turbulence models, the EARS model does not explicitly model the turbulent length scale (mixing length). Instead, it adopts the approach of \(K-\epsilon \) models where an additional prognostic equation for \(\epsilon \) is added as

$$\begin{aligned} \frac{\text {D} \epsilon }{\text {D} t} - \mathcal {D}_\epsilon = \, {C_{\epsilon 1} \frac{\epsilon }{K}\mathcal {P}} - {C_{\epsilon 2} \frac{\epsilon }{K} \epsilon } + {C_{\epsilon 3} \frac{\epsilon }{K}\mathcal {G}} , \end{aligned}$$
(5)

where \(C_{\epsilon 1}\), \(C_{\epsilon 2}\), and \(C_{\epsilon 3}\) are model coefficients discussed in Sect. 2.2; \(K / \epsilon \) is the turbulent time scale and \(K^{3/2} / \epsilon \) is the turbulent length scale. The equation for the dissipation rate of TKE is to a lesser extent related to the exact equation compared to (3) but it has the same general form with production, destruction, and diffusion effects.

The diffusion effects for the scalar properties are modelled as gradient diffusion and read

$$\begin{aligned} D_K&= \frac{\partial }{\partial x_i} \left( \frac{\nu _T}{\sigma _K}\frac{\partial K}{\partial x_i} \right) , \end{aligned}$$
(6)
$$\begin{aligned} D_{K_\theta }&= \frac{\partial }{\partial x_i} \left( \frac{\nu _T}{\sigma _{K_\theta }}\frac{\partial {K_\theta }}{\partial x_i} \right) , \end{aligned}$$
(7)
$$\begin{aligned} D_\epsilon&= \frac{\partial }{\partial x_i} \left( \frac{\nu _T}{\sigma _\epsilon }\frac{\partial \epsilon }{\partial x_i} \right) , \end{aligned}$$
(8)

where \(\sigma _K = 1\), \(\sigma _{K_\theta }=1\), \(\sigma _\epsilon =1.3\), and \(\nu _T\) is the eddy viscosity obtained from the EARS model solution. Refer to Appendix 1 in Želi et al. (2019) for the full derivation and details regarding \(\nu _T\) in the EARS model.

To simplify the system of equations in (1), (2) we use the approach of Rodi (1972, 1976) and introduce the weak-equilibrium assumption that states

$$\begin{aligned} \frac{\text {D}\,\overline{u_i u_j}}{\text {D} t} - \mathcal {D}_{ij} = \frac{\overline{u_i u_j}}{K} \left( \frac{\text {D} K}{\text {D} t} - {\mathcal {D}_K} \right) , \end{aligned}$$
(9)

assuming similarity between the different components. The weak-equilibrium formulation is more general than simply neglecting the advection and diffusion of turbulent momentum and heat transport, and can be expressed with the Reynolds-stress anisotropy

$$\begin{aligned} a_{ij} = \frac{\overline{u_i u_j}}{K} - \frac{2}{3} \delta _{ij}. \end{aligned}$$
(10)

Equation 9 is equivalent to the advection and diffusion of \(a_{ij}\) being zero,

$$\begin{aligned} \frac{\text {D} a_{ij}}{\text {D} t} - D_{a_{ij}} = 0. \end{aligned}$$
(11)

Correspondingly, the weak equilibrium for the heat flux is to neglect advection and diffusion of the normalized flux, and can be written as

$$\begin{aligned} \frac{\text {D} \xi _{i}}{\text {D} t} - D_{\xi _i} = 0, \end{aligned}$$
(12)

where

$$\begin{aligned} \xi _i = \frac{\overline{u_i \theta }}{\sqrt{K K_\theta }}. \end{aligned}$$
(13)

Formulation of the weak-equilibrium assumption for heat flux is adopted from Wikström et al. (2000). In Rodi (1972, 1976) the heat flux is not considered.

Applying the weak-equilibrium assumption in (1) and (2) results in

$$\begin{aligned} \frac{\overline{u_i u_j}}{K}(\mathcal {P}-\epsilon +\mathcal {G})&= \mathcal {P}_{ij} + {\Pi }_{ij} - \epsilon _{ij} + \mathcal {G}_{ij}, \end{aligned}$$
(14)
$$\begin{aligned} \frac{\overline{u_i \theta }}{2}\left( \frac{\mathcal {P}-\epsilon +\mathcal {G}}{K} + \frac{\mathcal {P}_\theta -\epsilon _\theta }{K_\theta }\right)&= \mathcal {P}_{\theta i} + {\Pi }_{\theta i} - \epsilon _{\theta i} + \mathcal {G}_{\theta i}. \end{aligned}$$
(15)

These two algebraic relations, with modelling of \({\Pi }_{ij}\), \(\epsilon _{ij}\), \({\Pi }_{\theta i}\), and \(\epsilon _{\theta i}\), replace the eddy-viscosity and eddy-diffusivity hypotheses.

The following source terms in (3), (4), (5), (14), (15) are given in closed form. This implies that these terms are exactly represented without further modelling

$$\begin{aligned} \mathcal {P}_{ij}&= -\overline{u_i u_k}\frac{\partial U_j}{\partial x_k} - \overline{u_j u_k}\frac{\partial U_i}{\partial x_k} \nonumber \\&= -(\overline{u_i u_k}S_{kj} + S_{ik}\overline{u_k u_j}) + (\overline{u_i u_k}{\Omega }_{kj} - {\Omega }_{ik}\overline{u_k u_j}), \end{aligned}$$
(16)
$$\begin{aligned} \mathcal {G}_{ij}&= -\frac{1}{T_0}(g_i \overline{u_j\theta } + g_j \overline{u_i\theta }) , \end{aligned}$$
(17)
$$\begin{aligned} \mathcal {P}&= -\overline{u_k u_m}\frac{\partial U_k}{\partial x_m} = -\overline{u_k u_m}S_{km}, \end{aligned}$$
(18)
$$\begin{aligned} \mathcal {G}&= -\frac{g_k}{T_0}\overline{u_k \theta }, \end{aligned}$$
(19)
$$\begin{aligned} \mathcal {P}_{\theta i}&= -\overline{u_i u_j}\frac{\partial {\Theta }}{\partial x_j} -\overline{u_j \theta }\frac{\partial U_i}{\partial x_j} = -\overline{u_i u_j}\frac{\partial {\Theta }}{\partial x_j} -\overline{u_j \theta } (S_{ij} + {\Omega }_{ij}), \end{aligned}$$
(20)
$$\begin{aligned} \mathcal {G}_{\theta i}&= -2\frac{K_\theta g_i}{T_0}, \end{aligned}$$
(21)
$$\begin{aligned} \mathcal {P}_\theta&= -\overline{u_j \theta } \frac{\partial {\Theta }}{\partial x_j}, \end{aligned}$$
(22)

where \(T_0\) is the reference temperature, \(g_i\) is the acceleration due to gravity, and \(S_{ij}\) and \({\Omega }_{ij}\) are the mean strain and rotation rate tensors defined as

$$\begin{aligned} S_{ij}&= \frac{1}{2} \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i}\right) , \end{aligned}$$
(23)
$$\begin{aligned} {\Omega }_{ij}&= \frac{1}{2} \left( \frac{\partial U_i}{\partial x_j} - \frac{\partial U_j}{\partial x_i}\right) . \end{aligned}$$
(24)

For the remaining terms in (14), (15) we apply the following models,

$$\begin{aligned} \Pi _{ij}-\epsilon _{ij} =&-c_1 \epsilon \left( \frac{\overline{u_i u_j}}{K}-\frac{2}{3}\delta _{ij}\right) + \frac{7 c_2-10}{11} (\overline{u_i u_k}{\Omega }_{kj} - {\Omega }_{ik}\overline{u_k u_j}) \nonumber \\&- \frac{30c_2-2}{55}K S_{ij} + \frac{9 c_2+6}{11}(\overline{u_i u_k}S_{kj} + S_{ik}\overline{u_k u_j} - \frac{2}{3}\overline{u_k u_m} S_{mk} \delta _{ij}) \nonumber \\&- c_3\left( \mathcal {G}_{ij}-\frac{2}{3}\mathcal {G}\delta _{ij}\right) - \frac{2}{3}\epsilon \delta _{ij}, \end{aligned}$$
(25)
$$\begin{aligned} \Pi _{\theta i}-\epsilon _{\theta i} =&-\left( c_{\theta 1}+c_{\theta 1}^*\frac{K}{\epsilon K_\theta } \overline{u_k \theta }\frac{\partial {\Theta }}{\partial x_k}\right) \frac{\epsilon }{K}\overline{u_i\theta }+c_{\theta 2}\overline{u_j\theta }(S_{ij} + {\Omega }_{ij}) \nonumber \\&+ c_{\theta g}\frac{K_\theta g_i}{T_0}, \end{aligned}$$
(26)
$$\begin{aligned} \epsilon _\theta =&\frac{K_\theta \epsilon }{r K}, \end{aligned}$$
(27)

where \(c_1\), \(c_2\), \(c_3\), \(c_{\theta 1}\), \(c_{\theta 1}^*\), \(c_{\theta 2}\), and \(c_{\theta g}\) are model coefficients discussed in Sect. 2.2 and \(r=0.55\) is the ratio of turbulence time scales for the temperature (\(\tau _\theta = K_\theta / \epsilon _\theta \)) and the velocity (\(\tau = K/\epsilon \)). The pressure terms are modelled according to Launder et al. (1975) and also adopted by Wallin and Johansson (2000), Wikström et al. (2000). Aside from the commonly found terms in (26) there is an additional non-linear term related to \(c_{\theta 1}^*\) used to avoid model singularity, see Wikström et al. (2000), where also the modelling of \(\epsilon _\theta \) is discussed in more detail.

Equations 14, 15 are non-linear in the sense that the source terms depend on turbulent momentum and heat flux. Adopting the approach from Lazeroms et al. (2013) and expressed by Želi et al. (2019), it is possible to derive explicit expressions for solutions of the turbulent momentum and heat flux that have the following forms,

$$\begin{aligned} \overline{u_i u_j}&= f_{ij} \left( S_{km}, {\Omega }_{km}, \frac{\partial {\Theta }}{\partial x_m}, K, \epsilon , K_\theta \right) , \end{aligned}$$
(28)
$$\begin{aligned} \overline{u_i \theta }&= f_{\theta i} \left( S_{km}, {\Omega }_{km}, \frac{\partial {\Theta }}{\partial x_m}, K, \epsilon , K_\theta \right) , \end{aligned}$$
(29)

where \(f_{ij}\) and \(f_{\theta i}\) are the functions for the turbulent momentum and heat flux, respectively. For the details of these functions, see Appendix 1 in Želi et al. (2019).

In the context of the Mellor and Yamada (1974) hierarchy of turbulence models, the EARS model belongs to the class of the Mellor and Yamada level-3 closure, see Lazeroms et al. (2016). Computational efficiency of the EARS model is higher than the Mellor and Yamada level-4 models and is comparable to that of the commonly used turbulence models, e.g., the Mellor and Yamada level-2.5 class of models.

2.2 Coefficients of the Explicit Algebraic Reynolds-stress Model

In (5) \(C_{\epsilon 1} = 1.44\), which is a commonly used value for this coefficient and is also found in Lazeroms et al. (2016). However, instead of \(C_{\epsilon 2} = 1.92\) as in Lazeroms et al. (2016), we set \(C_{\epsilon 2} = 1.82\). For the case of neutrally-stratified homogeneous shear flow (i.e. when \(\mathcal {G} = 0\)), this parameter recalibration results in a change of the dimensionless production from \(\mathcal {P} / \epsilon = 2.05\) to \(\mathcal {P} / \epsilon = 1.85\). This is close to the experimental results in the non-stratified homogeneous shear flow reported by Tavoularis and Corrsin (1981) and gives a value of \({\varvec{\varkappa }}= 0.38\) for the von Kármán constant in a neutrally-stratified atmospheric boundary layer.

We require that the EARS model with stratified effects returns to the baseline modelling in the limit of passive scalar flows where the turbulent velocity and density fields are decoupled. Therefore, in (25) and (26) the coefficients \(c_1\), \(c_2\), \(c_{\theta 1}\), \(c_{\theta 1}^*\), and \(c_{\theta 2}\) have the values from Wallin and Johansson (2000) and Wikström et al. (2000). Coefficients associated with the passive scalar are calibrated in Wikström et al. (2000) using DNS data. When calibrating the coefficients in the EARS model for the case of SABL it is important to retain the general behaviour of the EARS model in the limiting case of a passive scalar. Therefore, among the coefficients in (25), (26) only \(c_3\), \(c_{\theta g}\), and \(C_{\epsilon 3}\) are directly related to buoyancy effects in the EARS model and can be recalibrated. In stratified flows, buoyancy is believed to have a lesser influence on the dissipative scales and we set \(C_{\epsilon 3} = 0\). The remaining coefficients \(c_3\) and \(c_{\theta g}\) are then calibrated by considering the critical gradient Richardson number \(Ri_c = 0.2\), and were changed from \(c_3 = 0.3\) and \(c_{\theta g} = 0.75\) to \(c_3 = 0.35\) and \(c_{\theta g} = 1.0\). Increasing \(c_{\theta g}\) decreased the values of K and \(K_\theta \) improving the overall agreement with LES. The current value of \(c_{\theta g}\) is still far from \(c_{\theta g} = 2\) which corresponds to the two-component limit (compare Eqs. 21 and 26). The value of \(Ri_c = 0.2\) is chosen as a compromise between observed extreme conditions and the overall agreement with the present LES. However, it should be noted that the critical gradient Richardson number is an artificial asymptotic state in stratified homogeneous shear flow with a subtle balance between production and dissipation never exactly obtained in reality.

The complete set of the coefficients in (5) comprises \(C_{\epsilon 1} = 1.44,\, C_{\epsilon 2} = 1.82,\) and \(C_{\epsilon 3} = 0\), and in (25), (26) are \(c_1 = 1.8,\,c_2 = 5/9,\,c_3 = 0.35,\,c_{\theta 1} = 4.51,\,c_{\theta 1}^* = 0.5,\,c_{\theta 2} = 1.0,\) and \(c_{\theta g} = 1.0\).

2.3 Explicit Algebraic Reynolds-stress Model in the Framework of Single-column Model

The single-column model approach is commonly used to model a vertical column of the atmospheric boundary layer when statistical variations in the horizontal directions can be neglected. The previously introduced formulation of the EARS model is applied in the framework of the single-column model by setting \(x_1 = x\), \(x_2 = y\), and \(x_3 = z\). The first two coordinates are in the horizontal plane and the third is in the vertical direction.

The main quantities in the single-column model are the mean horizontal wind velocity \(\mathbf {V} = (U,V)\) and the mean potential temperature \({\Theta }\). The main equations under the assumption of horizontal homogeneity and using the Boussinesq approximation are

$$\begin{aligned} \frac{\partial U}{\partial t}&= -\frac{\partial \,\overline{u w}}{\partial z} - f(V_g-V), \end{aligned}$$
(30)
$$\begin{aligned} \frac{\partial V}{\partial t}&= -\frac{\partial \,\overline{v w}}{\partial z} + f(U_g-U), \end{aligned}$$
(31)
$$\begin{aligned} \frac{\partial {\Theta }}{\partial t}&= - \frac{\partial \,\overline{w\theta }}{\partial z}, \end{aligned}$$
(32)

where \(\mathbf {V}_g=(U_g,V_g)\) is the geostrophic velocity, \(f\!=\!2\, {\Omega }\sin \phi \) is the Coriolis parameter depending on the rotation rate \({\Omega }\) of the Earth and \(\phi \) is the latitude. The quantities \(\overline{u w}\) and \(\overline{v w}\) are the vertical components of the turbulent momentum flux and \(\overline{w \theta }\) is the vertical component of the turbulent heat flux.

The complete set of model equations consists of (30), (31), (32), (3), (4), (5) together with (28), (29), where in the latter two \(S_{km}, \, {\Omega }_{km}, \, \partial {\Theta } / \partial x_m\) are replaced by \(\partial U / \partial z, \, \partial V / \partial z\), and \(\partial {\Theta } / \partial z\) (see Želi et al. 2019).

3 Case Description

The modified GABLS1 set-up used herein is taken from Sullivan et al. (2016). The SABL is primarily driven by a steady geostrophic velocity (\(U_g\), \(V_g\)) = (8, 0) \(\mathrm {m} \, \mathrm {s}^{-1}\) and a time-varying surface temperature. The surface temperature is initially set to 265 \(\mathrm {K}\) and thereafter decreases with a constant cooling rate \(C_r = \) (0.25, 0.375, 0.5, 1) \(\mathrm {K} \, \mathrm {h}^{-1}\). Increasing the cooling rate of the surface enhances the overall level of stratification in the SABL as compared to the original GABLS1 set-up (Beare et al. 2006) in which only \(C_r = 0.25\)\(\mathrm {K} \, \mathrm {h}^{-1}\) was studied.

The height of the vertical domain is \(H = 400\)\(\mathrm {m}\) with 231 grid points log-linearly distributed. The height of the first grid cell \({\Delta }\) = 0.9 m. Other parameters are \(g = 9.81\)\(\mathrm {m} \, \mathrm {s}^{-2}\), \(f=1.39 \times 10^{-4}\)\(\mathrm {s}^{-1}\), reference temperature \(T_0 = 265\)\(\mathrm {K}\), and roughness length for momentum and potential temperature \(z_0\) is 0.1 \(\mathrm {m}\).

The initial conditions are set in accordance to the LES in Sullivan et al. (2016). After an initial transient, the flow slowly develops according to the specified surface cooling rate. The initial potential temperature is constant at 265 \(\mathrm {K}\) from the surface up to the initial inversion layer at 100 \(\mathrm {m}\) and increases above it at a rate of 0.01 \(\mathrm {K} \, \mathrm {m}^{-1}\). The initial wind profile is equal to the geostrophic velocity throughout the SABL. At the time of initialization, turbulence is described by the initial profiles of K, \(\epsilon \) and \(K_\theta \). The initial TKE profile is \(K = 0.4(1-z/250)^3\)\(\mathrm {m}^2 \, \mathrm {s}^{-2}\) for \(z < 250\)\(\mathrm {m}\). Above \(z = 250\)\(\mathrm {m}\) it is equal to \(10^{-5}\)\(\mathrm {m}^2 \, \mathrm {s}^{-2}\). The initial \(\epsilon \) profile is not specified in Sullivan et al. (2016). In the present study the initial \(\epsilon \) profile is prescribed through specifying the turbulence time scale \(\tau _0\), which is a diagnostic variable computed from K and \(\epsilon \). The turbulence time scale \(\tau _0 = K/\epsilon = 1\)\(\mathrm {s}\) at \(z_0\) and increases linearly to \(\tau _0 = 550\)\(\mathrm {s}\) at 250 m, above which it is constant. This implies that the turbulence eddies close to the surface are small and the size of the turbulence structures increases with height. The initial profile for \(K_\theta \) is set to \(10^{-4}\)\(\mathrm {K}^2\), resulting in small levels of potential-temperature variance in accordance with a stably stratified atmospheric boundary layer. The effect of the initial conditions for K, \(\epsilon \), and \(K_\theta \) on the model results is negligible compared to the effect of the initial condition for \({\Theta }\).

In contrast to Sullivan et al. (2016), the boundary-condition treatment in the EARS model, with sufficiently small first cell height, does not use Monin–Obukhov functions for calculating friction velocity \(u_*\) and the characteristic temperature scale \(\theta _*\). The boundary-condition treatment is taken from Želi et al. (2019) where it was shown that the EARS model with more general boundary conditions gives the same Monin–Obukhov functions that are used in Sullivan et al. (2016) without a priori imposing such behaviour. For details on the boundary-condition treatment in the simulations, see the Appendix.

4 Results

In order to reach a quasi-steady state solution, the simulations are integrated with the EARS model for the duration of nine physical hours and a timestep of \({\Delta } t = 60\)\(\mathrm {s}\). The atmospheric quantities have been averaged over the last hour of the simulation, as in Sullivan et al. (2016). We explore the possibility of using two different sets of coefficients in the EARS model, and this section discusses the results of the EARS model with the coefficients defined as in Sect. 2. This choice of coefficients is referred to as the EARS model with the standard coefficient values. Section 5 discusses the results of what is referred to as the EARS model with the modified set of coefficients for Eq. 5. Turbulent fluxes in the LES are the total turbulent fluxes, i.e. the sum of the resolved and subgrid-scale contributions.

Figures 1 and 2 show mean profiles of the horizontal wind speed \(\mathbb {V}(z)\), where \(\mathbb {V} = \sqrt{U^2 + V^2}\), and potential temperature \({\Theta }(z)\). The profiles for the EARS model show similar behaviour to those obtained with LES. Both the model and LES predict the existence of a low-level jet and the decrease of the boundary-layer height with increased surface cooling rates. The EARS model predicts a somewhat higher SABL and a higher low-level jet than in the LES model. The model predicts profile bending in the higher part of the SABL at higher cooling rates, i.e. the sharp change of the profile slope close to the inversion layer for the wind-speed and potential-temperature profiles (separating the inversion layer from the interior of the SABL).

A large number of grid points for the simulations of the SABL is used in order to obtain a smooth representation of the vertical profiles of atmospheric variables. However, a high resolution is not a requirement of the EARS model and the present second-order numerical method. Computationally efficient simulations were carried out with 29 log-linearly distributed grid points between \(z_0\) and H, where the height of the first grid cell is \({\Delta }\) = 1.5 m. Figure 1 shows that the solutions for the finer and the coarser grid resolutions, with 231 and 29 grid points respectively, are almost identical, indicating a grid independent solution. The same statement is valid for the second-order statistics (not shown in the figures).

Fig. 1
figure 1

Vertical profiles of horizontal wind speed for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Solutions of the EARS model with standard () and modified coefficients in the equation for \(\epsilon \) () and the LES results () from Sullivan et al. (2016). Addition of markers (\(\times \)) represent solutions at each grid point of the EARS model with standard coefficients and coarse grid resolution

Full size image
Fig. 2
figure 2

Vertical profiles of potential temperature for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1. The scale of the \({\Theta }\) axis varies but the labels and the grid are the same for all the subplots

Full size image
Fig. 3
figure 3

Hodograph of the mean velocity vector for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image

Wind turning is an important effect in the SABL. Figure 3 shows that the wind direction in the EARS model agrees well with the LES. Differences are only observed in the part of the SABL above the centre of the low-level jet where the wind direction in the EARS model approaches the geostrophic wind direction. In the near-surface region, wind direction and speed are strongly influenced by the boundary conditions. Good agreement between the model and LES indicates that the methodology for imposing the boundary conditions presented in Želi et al. (2019) gives an accurate treatment of the near-surface region. Interestingly, and in contrast to eddy-viscosity-based models, the EARS model predicts a non-zero \(\overline{uv}\) component as a result of the wind turning.

Figure 4 shows profiles of TKE. The EARS model with standard values of the coefficients, introduced in Sect. 2, tends to overestimate the amount of TKE in the SABL compared to the LES, and predicts a layer of constant TKE close to the surface. This behaviour is considered to be related to the non-optimal modelling of the \(\epsilon \)-equation (5). The resulting K and \(K_\theta \) profiles are sensitive to the details of the modelling of this equation, as shown later in Sect. 5. This can be expected since generally an underestimated value of \(\epsilon \) leads to overestimated TKE. However, in LES it is not possible to directly evaluate derivatives needed for \(\epsilon \), which means that this quantity will depend on the subgrid-scale model. For this reason \(\epsilon \) profiles are not compared. Section 5 discusses a possible modification of the \(\epsilon \) equation (5) to improve the behaviour of the EARS model. The results of the EARS model with the modified equation for \(\epsilon \) are shown in the figures by the dashed lines and discussed later in Sect. 5.1.

Fig. 4
figure 4

Vertical profiles of turbulence kinetic energy for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image

Profiles of \(K_\theta \), shown in Fig. 5, are directly related to the level of stratification in the SABL and the temperature forcing at the surface. Similar to TKE, \(K_\theta \) is higher in the standard EARS model results than in the LES results. In Eq. 4, \(K_\theta \) is coupled to \(\epsilon \) through \(\epsilon _\theta \). Therefore, changing the way \(\epsilon \) reacts to the level of stratification in the SABL influences \(K_\theta \) (see Sect. 5 for details). Modifying the prediction of the \(K_\theta \) profile is also possible by changing r, as it represents the ratio between the two time scales \(K_\theta /\epsilon _\theta \) and \(K/\epsilon \). However, in the current model, r is considered to be constant (different values of this constant could be considered).

Fig. 5
figure 5

Vertical profiles of half temperature variance for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image

The EARS model allows the individual stresses to be studied. Instead of plotting \(\overline{uw}\) and \(\overline{vw}\) profiles separately, Fig. 6 shows the total turbulent vertical momentum flux profile defined as

$$\begin{aligned} \overline{uw}^{T} = -\sqrt{{\overline{uw}}^2 + {\overline{vw}}^2}. \end{aligned}$$
(33)

Compared to the LES, the character of the profiles is well captured by the model, but the magnitude of the surface stress \(\overline{uw}^T(z=z_0)\) predicted by the model is greater, which is consistent with the greater TKE values. Figure 7 shows profiles of the individual normal stresses scaled with TKE, for the lowest cooling rate. In the LES, the variance is computed by adding the isotropic \((2/3) K_\mathrm {sgs}\) subgrid-scale contribution to the resolved part and the scaling is made with the total TKE. We note the horizontal turbulent momentum variances, \(\overline{uu}\) and \(\overline{vv}\), in the EARS model are dominant and the vertical variance \(\overline{ww}\) is damped due to stratification effects. Qualitatively, the results of the EARS model agree well with the results of LES also for the normal stress components. Additionally, we note that \(\overline{ww}/K\) should have a finite value above the height of the roughness elements. Although this statement is valid for the LES results, close to the surface the profile of \(\overline{ww}\) exhibits unphysical behaviour in the sense that it decreases near the surface, which is probably related to the surface boundary conditions.

Fig. 6
figure 6

Vertical profiles of total turbulent momentum flux for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image
Fig. 7
figure 7

Vertical profiles of (a) \(\overline{uu}/K\), (b) \(\overline{vv}/K\), and (c) \(\overline{ww}/K\) for the surface cooling rate 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image

Figure 8 shows profiles of the vertical turbulent heat flux. The EARS model predicts that the vertical turbulent heat fluxes behave similarly to the vertical turbulent momentum flux, shown in Fig. 6. The predefined temperature forcing in the EARS and the LES is the same but surface fluxes are different, depending on the surface modelling and the way boundary conditions are imposed. As a consequence, the surface flux \(\overline{w\theta } \approx -u_*\theta _*\) in the standard formulation of the EARS model is greater than in the LES, which is related to the larger overall predicted mixing and in the deeper boundary layer.

Aside from the \(\overline{w\theta }\) component of the heat-flux vector, the EARS model predicts the turbulent heat fluxes in x- and y-directions as well, shown in Figs. 9 and 10, respectively. This is an improvement compared to the isotropic atmospheric turbulence models that use the eddy-viscosity concept and which are unable to predict (non-zero) turbulent heat fluxes in the horizontal plane. In the surface layer, the EARS model tends to predict \(|\overline{u\theta }/\overline{w\theta }| < 1\), while Wyngaard et al. (1971) measured \(|\overline{u\theta }/\overline{w\theta }| > 2\), which is closer to the LES result. Above this layer the EARS model performs qualitatively well, changing the sign of the solution in the same way as in the LES model. Results in Figs. 8, 9, and 10 show that the turbulent heat flux in the horizontal plane in the EARS model is comparable to the turbulent heat flux in the vertical direction.

Fig. 8
figure 8

Vertical profiles of turbulent heat flux in the vertical direction for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image
Fig. 9
figure 9

Vertical profiles of turbulent heat flux in the x-direction for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image
Fig. 10
figure 10

Vertical profiles of turbulent heat flux in the y-direction for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image
Fig. 11
figure 11

Vertical profiles of Richardson number for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Legend as in Fig. 1

Full size image

Figure 11 shows profiles of the gradient Richardson number,

$$\begin{aligned} Ri = \frac{g}{T_0} \frac{\partial {\Theta } / \partial z}{(\partial \mathbb {V} / \partial z)^2}. \end{aligned}$$
(34)

This quantity is sensitive to the turbulence modelling, i.e. the prediction of the mean profile for wind speed and potential temperature, which are results of the turbulence fluxes \(\overline{u w}^T\) and \(\overline{w \theta }\). Note that in the EARS model there are no explicitly imposed dependencies between turbulent fluxes and the Richardson number. This is obviously not the case in the eddy-viscosity models where such dependency usually is imposed through the stability functions. The coefficients in the model for \(\epsilon \) are calibrated in the simulation of the homogeneous-shear flow with a constant temperature gradient such that the critical Richardson number is \(Ri_c = 0.20\). In the SABL, however, there are turbulent-transport effects present and it is possible to have regions where \(Ri(z) > Ri_c\).

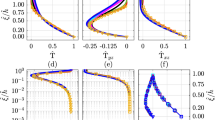
As long as there are no transport or transient effects, the change of TKE is \(\partial K /\partial t \rightarrow 0\) when \(Ri \rightarrow Ri_c\). It is interesting to investigate how the total production of TKE changes as a function of Ri. To study this for different cooling rates, an alignment coefficient \(\mathbb {C}\) is introduced and defined as

$$\begin{aligned} \mathbb {C} = \frac{\mathcal {P}+\mathcal {G}}{K\sqrt{I\!I_a I\!I_S}}, \end{aligned}$$
(35)

where \(I\!I_a = a_{ij}a_{ji}\) and \(I\!I_S = S_{ij}S_{ji}\) are the second invariants of turbulent anisotropy (10) and mean strain-rate tensor (23). Applying the Cauchy–Schwarz inequality on \(\mathcal {P}\) gives \(|\mathcal {P}| \le K\sqrt{I\!I_a I\!I_S}\) where the equality is reached only when \(a_{ij}\) and \(S_{ij}\) are perfectly aligned. Misalignment can significantly reduce the production of TKE and even cause the production to become negative in the rare conditions when the TKE is transferred to the mean flow. Therefore, \(\mathbb {C}\) is a dimensionless measure of local production that relates the alignment between the turbulence anisotropy and the strain-rate tensor with the total production of TKE. Figure 12 shows that \(\mathbb {C}\) has close relation to the Richardson number inside the SABL in all four cases. In the LES, \(\mathbb {C}\) is calculated from the total turbulent quantities (resolved plus sub-grid scale) and reaches zero at \(Ri \approx 0.26\) implying that above \(Ri_c = 0.25\) no turbulence is produced in the LES. Results for the critical Richardson number in the LES agrees with the value reported in Howard (1961) and Miles (1961). One should be aware that \(\mathbb {C}\) becomes singular at this limit and that the SABL is not in steady-state. Results of the EARS model scale and show a nearly linear dependence on the Richardson number. The alignment coefficient tends towards zero in the higher part of the SABL, close to the inversion layer. In the results of the EARS model, however, \(\mathbb {C}\) never reaches zero because above the SABL TKE \(\rightarrow 0\) and \(\mathbb {C}\) becomes singular. For this reason the profiles were cutoff at the height outside the SABL where the turbulence is weak and the condition \(\text {TKE} < 10^{-5}\)\(\text {m}^2 \, \text {s}^{-2}\) is met.

Close to the surface the stratification effects weaken so that \(\mathcal {G} \rightarrow 0\) and \(Ri \rightarrow 0\). Using the data for a neutrally-stratified logarithmic layer from Wallin and Johansson (2000) in (35) results in \(\mathbb {C} \approx 0.76\) near the surface. This agrees with the prediction of the EARS model \(\mathbb {C} = 0.76\), but the LES gives a significantly lower value. The reason for this could be that the LES, in the near-surface region, is strongly influenced by the boundary conditions and the value of \(\overline{ww}/K\) in the surface layer is underpredicted (see Fig. 7) resulting in high values of \(I\!I_a\). This leads to low values of \(\mathbb {C}\).

Fig. 12
figure 12

Alignment coefficient as a function of Richardson number for different cooling rates inside the SABL. Legend as in Fig. 1

Full size image

5 Discussion

The model presented so far is basically calibrated using generic flow cases such as homogeneous turbulence and passive scalars. The terms related to buoyancy were simply calibrated to give a realistic \(Ri_c\). Although the EARS model captures most of the features of the SABL, there are some quantitative differences compared with LES. In general, the heat flux was found to be higher in the model results, leading to a higher SABL. Hence, in this section we will discuss possible modifications and recalibration. However, we avoid any modifications that would influence predictions in the passive scalar limit. We propose two modifications that change the behaviour of the standard model by changing the coefficients in (5) and by introducing the Daly–Harlow transport model.

5.1 Modified \(C_{\epsilon 2}\) and \(C_{\epsilon 3}\)

Equation 5 is modelled in analogy with the exact transport equation for \(\epsilon \) and contains model parameters that need to be calibrated. Different values for \(C_{\epsilon 2}\) and \(C_{\epsilon 3}\) coefficients have been proposed in studies of stratified flows with \(K-\epsilon \) model. Pereira and Rocha (2010) made \(C_{\epsilon 2}\) a function of turbulence anisotropy and set \(C_{\epsilon 3} = 0\). In Goudsmit et al. (2002) \(C_{\epsilon 3} < 0\) was used for stable stratification, and by using data from a direct numerical simulation Venayagamoorthy et al. (2003) suggested that \(C_{\epsilon 2}\) is a function of Ri, and \(C_{\epsilon 3}\) a function of Froude number. Similar to the model suggested by Venayagamoorthy et al. (2003), we here propose to model \(C_{\epsilon 2}\) as a function \(C_{\epsilon 2}(Ri)\) with the following functional dependency,

$$\begin{aligned} C_{\epsilon 2} = {\left\{ \begin{array}{ll} 1.82, &{} \text {for } 0.00\leqslant Ri< 0.13 \\ 1.82 + 2.57(Ri-0.13), &{} \text {for } 0.13\leqslant Ri \leqslant 0.20 \\ 2.00, &{} \text {for } 0.20< Ri, \end{array}\right. } \end{aligned}$$

and use \(C_{\epsilon 3} = -0.70\). The purpose of introducing the functional dependence of \(C_{\epsilon 2}\) on Ri and modifying the value of \(C_{\epsilon 3}\) is to study how such a modification in (5) affects the overall behaviour of the model.

The seemingly higher values of the K and \(K_\theta \), seen in Figs. 4 and 5, respectively, were discussed in Sect. 4. Functional dependency for \(C_{\epsilon 2}\) is chosen such that the value of \(C_{\epsilon 2}\) does not change in the case of neutral stratification and increases linearly up to 2.0 in the Ri range \(0.13\;\)–\(\;0.20\). The critical Richardson number is thereby calibrated to be \(Ri_c = 0.20\), i.e. the same as in the standard EARS model. We note that the total change of \(C_{\epsilon 2}\) is 10%.

Figures 1–11 show the results of the modified EARS model for different stratification levels as dashed curves. Important differences as compared to the standard EARS model are in the levels of K and \(K_\theta \), shown in Figs. 4 and 5. K and \(K_\theta \) are very sensitive to the modelling in (5) and responsible for intensity of the turbulent fluxes, shown in Figs. 6, 8, 9. Weaker turbulent fluxes (also surface fluxes, Figs. 6, 8) lead to the lower height of the SABL. In the simulation with the strongest cooling rate \(Cr = 1\)\(\mathrm {K} \, \mathrm {h}^{-1}\) the model is predicting lower values of all mean atmospheric properties than in the LES. Interestingly, Fig. 11 indicates that the profiles of Ri also get significantly closer to the LES results, as compared to the standard EARS model. The new coefficients do not change the results shown in Fig. 12 and are hence not included there.

5.2 Implementing Daly–Harlow Transport Model

The standard EARS model, described in Sect. 2, models the diffusion in terms of an eddy-viscosity-based diffusivity coefficient. However, this diffusion might be inaccurate because turbulence in the SABL is strongly anisotropic. Therefore, the Daly–Harlow diffusion model (Daly and Harlow 1970) can be used for the modelling of the diffusion terms \(\mathcal {D}_{K}\), \(\mathcal {D}_{ K_\theta }\), and \(\mathcal {D}_\epsilon \) in (3)–(5).

According to the Daly–Harlow transport model:

$$\begin{aligned} \mathcal {D}_{K}^{(DH)}&= \frac{\partial }{\partial z} \left( c_{s_K} \frac{K}{\epsilon } \overline{ww} \frac{\partial K}{\partial z}\right) , \end{aligned}$$
(36)
$$\begin{aligned} \mathcal {D}_{\epsilon }^{(DH)}&= \frac{\partial }{\partial z} \left( c_{s_\epsilon } \frac{K}{\epsilon } \overline{ww} \frac{\partial \epsilon }{\partial z}\right) , \end{aligned}$$
(37)
$$\begin{aligned} \mathcal {D}_{K_\theta }^{(DH)}&=\frac{\partial }{\partial z} \left( c_{s_{K_\theta }} \frac{K}{\epsilon } \overline{ww} \frac{\partial K_\theta }{\partial z}\right) , \end{aligned}$$
(38)

where \(c_{s_K} = c_{s_{K_\theta }} = 0.16\) and \(c_{s_\epsilon } = 0.21\). Modelling of the diffusion terms will have an impact on Ri but will leave \(Ri_c\) unchanged. It should be noted that the Daly–Harlow model does not impose any additional computational cost on the turbulence model.

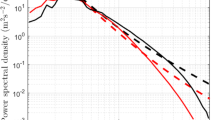
Figure 13 shows the comparison between the simple diffusion models (6) and Daly–Harlow model (36) used for transport of TKE. Particularly, in (6) we use \(\nu _T\) from the EARS model (see Želi et al. 2019) and the standard \(K-\epsilon \) model approach with \(C_\mu = 0.09\). The results are based on the TKE profile shown in Fig. 4. Using the same TKE profile ensures that the transport models are comparable. The results of TKE transport using \(\nu _T\) from the EARS model are closer to the Daly–Harlow model than the model where \(\nu _T\) is computed with the formulation from the \(K-\epsilon \) model. This is probably related to the fact that \(\nu _T\) in the EARS model is a function of buoyancy in the EARS model (see Želi et al. 2019). The difference is consistent across all stratification rates and is similar for the transport of half the temperature variance (not shown).

Fig. 13
figure 13

Transport of TKE in the vertical direction for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Transport of TKE computed with Eq. 6 where \(\nu _T\) is from the EARS model () and the \(K-\epsilon \) model \(\nu _T = 0.09 K^2 \epsilon ^{-1}\) (), and Daly–Harlow transport model in Eq. 36 ()

Full size image

Figure 14 shows vertical profiles of the Richardson number, obtained using the Daly–Harlow model for diffusion and with the coefficients given in Sect. 2.2. The mean profiles are nearly the same as the ones described in Sect. 4, however, subtle differences in the mean profiles lead to qualitatively different profiles of Ri in the region around the low-level jet. Other atmospheric quantities are not significantly affected; this is consistent with the previous observation that there are only small differences between the Daly–Harlow and the current diffusion model, so the results are not shown. Therefore, there is little value of using a more complex diffusion model.

Fig. 14
figure 14

Vertical profiles of Richardson number for surface cooling rates (a) 0.25 \(\mathrm {K} \, \mathrm {h}^{-1}\), (b) 0.375 \(\mathrm {K} \, \mathrm {h}^{-1}\), (c) 0.5 \(\mathrm {K} \, \mathrm {h}^{-1}\), and (d) 1 \(\mathrm {K} \, \mathrm {h}^{-1}\). Solutions of the standard EARS model () and EARS model with the Daly–Harlow transport model () and the LES model () by Sullivan et al. (2016)

Full size image

6 Conclusion

The SABL with weak to moderate stratification is simulated with the EARS model. The results of the model are compared with high-resolution LES results. The mean profiles show that the EARS model is able to predict the general properties and features of stratified turbulence in such situations, including e.g. the low-level jet and wind turning. The mean profiles and vertical turbulent fluxes compare qualitatively well with the LES but the fluxes are greater in the EARS model, which leads to a higher SABL than in the LES. The weakest point in the EARS model is probably the modelling of the \(\epsilon \) equation. It was shown that improvements can be made by modifying the coefficients, although a more general solution to this problem would be preferred. In order to improve the model for the \(\epsilon \) equation it would be helpful to study dissipation in stratified boundary layers by direct numerical simulation and experimental atmospheric measurements.

Unlike many other models, the EARS model predicts all components of the turbulence momentum-flux tensor and heat-flux vector, including horizontal fluxes, without the need for any additional modelling. Apart from the results in the surface layer the horizontal-heat-flux profiles show qualitatively good agreement. This is an advantage compared to the simpler atmospheric turbulence models that are not able to predict horizontal fluxes in the single-column model approach. The model predicts that the horizontal turbulence fluctuations carry more energy than the vertical fluctuations, which is in line with the observations of the SABL.

The study also presents a new type of scaling for the production of TKE as a function of Richardson number in the SABL. Results for different cooling rates in the case of the EARS and LES results collapse well, showing that the scaled production is dependent only on the local Ri and almost independent of the cooling rate. The collapse can be further investigated to see if the scaling has universal features.