1 Introduction

Probabilistic seismic hazard assessment (PSHA) aims to estimate the likelihood of exceeding specific ground motion levels, typically measured by the ground motion parameters such as the peak acceleration (PGA) at individual sites or across a map of locations. This process is accomplished by considering all potential earthquake sources and their average activity rates (Cornell 1968; Field et al. 2003). PSHA involves three primary steps: (1) defining the seismic source model, (2) specifying the ground motion model, and (3) performing the probabilistic calculation to identify the probability of exceeding each ground-motion level at a given site over a specified time period.

The seismic source model for each potential source includes earthquake/seismicity rate and rupture models and describes the distribution of earthquakes in time and space. The rupture model includes information regarding the fault geometry and kinematics, such as location, fault length, rupture depth, strike, dip, rake, seismogenic thickness, magnitude-area scaling relationship, rupture aspect-ratio (length/width), and slip rate (SSHAC 1997; Pagani et al. 2014). These parameters influence the generation of rupture scenarios that consist of the magnitude of the earthquake, the style of faulting, the depth, and the geometric dimensions of the rupture. The generation of rupture scenarios depends heavily on the ground motion model's requirements regarding the specification of the rupture. The earthquake/seismicity rate model specifies the frequency distribution of earthquake magnitudes and determines the total moment rate and relative frequency of earthquakes of various magnitudes (Schwartz and Coppersmith 1984; Field et al. 2003; McGuire 2004; Pagani et al. 2014).

In recent decades, smoothed seismicity models (Frankel 1995) have become some of the most commonly used models for seismic hazard assessment. This widespread adoption is attributed to the simplicity of these models. They utilize the epicenters from a complete seismicity catalog to construct a spatial density of seismic activity. This is achieved through a spatial kernel dependent on a single parameter (Frankel 1995). Consequently, they do not require information about fault geometries or slip rates, as they directly derive the spatial distribution of seismicity and the annual rate of events from the catalog. Despite their simplicity, these models demonstrated very good performance in seismic prospective experiments (Zechar et al. 2013), particularly the adaptive seismicity model of Helmstetter et al. (2007).

These models handle the seismicity in a simplistic 2D manner, using a cutoff depth to select events in the seismic catalog, and then they construct the spatial model based solely on epicentral information, disregarding event depth. This approach can be effective in seismic zones where the earthquake depth exhibits limited variation, such as in California. However, it is not recommended in more complex seismic zones, such as subductions or regions with overlapping seismic structures. Recently, the scientific community is working to overcome this issue. Thingbaijam et al. (2023) proposed a quasi-3D smoothed seismicity approach applied to the intraslab seismicity within the Hikurangi and Puysegur subduction zones in Aotearoa New Zealand.

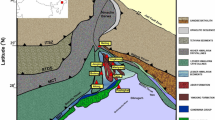
A further step was made in Pandolfi et al. (2023) where the authors developed a novel real 3D version of the smoothed seismicity technique, applied to the Adriatic Basal Thrust (ABT), a seismogenic lithospheric shear zone within the compressional domain of eastern Central Italy. The authors also attempted to integrate the smoothed seismicity modeling with a fault-based approach. The method computes the earthquake rates for each point of a 3D grid used for the smoothing, according to the location in latitude, longitude, and depth. Moreover, the 3D spatial grid aligns with the known fault geometry and depth variability. This integrated approach combines seismotectonic data with earthquake catalogs; strike, dip, and rake of the fault geometry are also incorporated into the model.

Another important issue to address in PSHA computation is the ground motion model (GMM). GMM incorporates one or more prediction equations/models to estimate the intensity of ground shaking as a function of the magnitude and distance between the source and the site of interest. One key aspect that must be carefully considered when assessing seismic hazard is how the site-source distance is defined. The type of distance measurement used in a given ground motion prediction equation (GMPE) (e.g., Repi, Rhypo, and Rjb) can significantly impact the estimated ground shaking, mainly when dealing with locations near the earthquake source. In fact, ground motion amplitude decreases with increasing distance as a result of the geometric spreading and anelastic attenuation. In particular for 3D applications, the selection of the proper distance is fundamental to account for the variability in depth of the seismic source model; for example, Repi cannot be used, because it considers a fixed depth for the seismogenic sources while the Rhypo considers the distance between the hypocenter and the site and preserves the three-dimensional location of the sources.

The present study performs a comprehensive PSHA of the Adriatic Thrust Zone (ATZ) of eastern Central Italy, investigating the combined effect of the ABT and a recently outlined underlying lithospheric thrust, referred to as T2 in de Nardis et al. (2022). Both thrusts deep at low-angle SW-ward with an average distance of 12.5 km between them. The ABT extends from the near-surface Adriatic Thrust front to depths of about 40 km, while T2 ranges from 20 to 60 km. This peculiar regional configuration, characterized by the coexistence of well-defined and overlapping seismogenic compressional volumes within the Marche Adriatic lithosphere, makes it relevant to differentiate and quantify their contributions to ground shaking. This is crucial for accurately assessing seismic hazards.

2 The seismotectonic framework

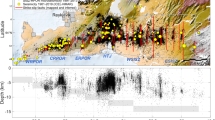
Eastern Central Italy is characterized by an active compressional domain at the outer front of the eastward-growing Apennine fold-and-thrust belt (Fig. 1a). Like the rest of the Outer Thrust System of Italy, the region is marked by intricate structural and seismotectonic complexities, both in the shallow, buried structures deforming the sedimentary crust (Lavecchia et al. 2007; Visini et al. 2010; Casero and Bigi 2013; Maesano et al. 2015; Livani et al. 2018; Ferrarini et al. 2021; Panara et al. 2021; Tibaldi et al. 2023) and in the deep shear zones affecting the underlying crust and uppermost mantle (Petricca et al. 2019; de Nardis et al. 2022).

Fig. 1
figure 1

The seismotectonic setting of eastern Central Italy and the Adriatic Thrust Zone (ATZ) a Quaternary and potentially seismogenic extensional and contractional structures with historical and instrumental earthquakes and related focal mechanisms (Pondrelli et al. 2006; de Nardis et al. 2022; Rovida et al. 2022). The left bottom panel represents the location map of the major structural domains, and the bottom right panel reports the stress tensors for north and south ATZ (de Nardis et al. 2022). b 3D fault model of the Adriatic Basal Thrust and the underlying T2 thrust across the northern ATZ zone from Lavecchia et al. (2023); the hypocenters refer to earthquake activity from 1 August 2009 to 21 December 2022 (ML 1–5.5) (Dataset in Lavecchia et al. 2023)

Full size image

This paper focuses on the Adriatic Thrust Zone extending from the coastal and offshore Marche-Adriatic zone to the Apennine Mountain belt (see inset in Fig. 1a). The Apennine Extensional domain latter comprises late Miocene to Early Pliocene eastward-verging fold-and-thrust structures dissected by a nearly coaxial system of late Pliocene to Quaternary normal faults (Lavecchia et al. 2021). Such extensional deformation in the upper crust geographically overlaps with contractional deformation in the lower crust, due to the westward-deepening of the basal detachments of the Adriatic Thrust belt.

A noteworthy characteristic of the overall Neogene-Quaternary evolution of the Apennine thrust belt is the coexistence of active compression and extensional deformations in both vertical and horizontal directions at the same time. This dynamic interplay progressively shifts over time and space from west to east, resulting in a mixture of neighboring contractional and extensional features in adjacent coastal regions (Lavecchia et al. 1994; Barchi 2010).

The active extensional domain of the Apennines is typified by high-angle, westward-dipping normal faults that detach on eastward-dipping, low-angle basal detachments (e.g., Mirabella et al. 2011; Brozzetti et al. 2017; Lavecchia et al. 2022). In historical and instrumental times, this region has experienced moderate to large-magnitude normal and normal-oblique earthquakes, with intensities reaching up to XI MCS (Mercalli–Cancani–Sieberg) and magnitudes as high as 6.5–7, primarily occurring at shallow depths (< 12–14 km) in the upper crust (Scogliamiglio et al. 2006; Mariucci and Montone 2020; Rovida et al. 2022).

The active compressional domain manifests itself in the eastward-verging Marche-Adriatic arcuate belt whose upper crustal geometry and structural style are well-understood, thanks to petroleum exploration in Italy (Pieri and Groppi 1981; Fantoni and Franciosi 2010; Casero and Bigi 2013). The geometry and kinematics of the underlying deep shear zones, such as the previously introduced Adriatic Basal Thrust (ABT) and the underlying T2 thrust structures, are also relatively well-constrained, being illuminated by diffuse microseismicity and activated by a few moderate earthquakes (de Nardis et al. 2022; Lavecchia et al. 2023) (Fig. 1b). The reconstructed geometries of the two thrusts result from a meticulous integration of various multiscale datasets, including geological and geophysical cross-sections available in the literature used to superficially reconstruct the ABT alignment, and high-quality catalog with associated focal mechanisms used to constrain the surface geometry in depth and define the kinematics (de Nardis et al. 2022; Lavecchia et al. 2023). The seismogenic potential of these structures remains an area of ongoing exploration (Taroni and Carafa 2023).

The ABT portion has an average along-strike length of ~ 210 km and an along-dip length (i.e., width) of ~ 85 km, spanning depths from near-surface to ~ 32 km. It is characterized by an average dip-azimuth of 240° N and a dip-angle of ~ 20°. Earthquake distribution is not uniform along the dip; instead, it is concentrated in the upper crust (up to approximately 10 km, around 10%), in the lower crust (between 10 and 28 km, roughly 85%), and to a lesser extent, at Moho depths (28–35 km, approximately 5%). Since instrumental records have been kept, several small-to-moderate (M < 5.5) instrumental earthquakes and seismic sequences have occurred along the ABT and its hanging-wall splays, with a prevalent compressive kinematic character and local strike-slip deformation. Some examples include the Ancona earthquake 1972 (MW 4.8), Porto San Giorgio 1987 (MW 5.1), Ancona 2013 (MW 5.1), and Alto Adriatico 2022 (MW 5.5) (Lavecchia et al. 2023, with references). In historical times, earthquakes with magnitudes up to approximately 6.0, possibly associated with the ABT have mainly occurred along the coastal areas (e.g., Conero offshore in 1690, MW 5.9; Rimini in 1916, MW 5.7; Senigallia in 1930, MW 5.9) and, to a lesser extent, in the Apennine Foothills area (e.g., Fabriano in 1741, MW 6.2; Sarnano in 1873, MW 6.0) (Rovida et al. 2022). As for T2, it boasts an average along-strike length of ~ 150 km and an along-dip length (i.e., width) of ~ 80 km, spanning depths from − 20 km to − 60 km. It exhibits a mean dip-azimuth of 226° N and a dip-angle of 24°. Microseismic activity is consistently observed from the middle crust to upper mantle depths without interruption. Since T2 thrust has recently been discovered and is still under investigation, there is a lack of knowledge of significant energetic earthquakes directly associated with this domain. However, Lavecchia et al. (2023) advance the hypothesis of associating it to the 1741 Fabriano earthquake. This hypothesis is based on the new estimation of hypocentral depth (around 35 km) and magnitude (MW 6.3–6.4) calculated by Sbarra et al. (2023) using the analysis of macroseismic attenuation curves.

Thanks to the availability of a large number of focal mechanisms covering the Marche-Adriatic and Apennine foothills areas resulting from both local and regional compilations (Pondrelli et al. 2006; de Nardis et al. 2022; Montone and Mariucci 2023), the strain and stress patterns associated with ABT and T2 are rather well-constrained. In the time interval from 1967 to 2020, available focal mechanisms, range in magnitudes from ML 1.4 to 5.8, are located at depths from a few kilometers to ~ 60 km and are predominantly characterized by reverse/oblique solutions. Nearly 76% of the total number of FMs exhibit reverse/reverse-oblique solutions, with horizontal P-axes rotating in azimuth from SW-NE in the northern ATZ sector to WSW-ENE and W-E in the southern ATZ sector. A formal stress inversion of the kinematically compatible focal mechanisms shows a near-pure regional reverse faulting stress regime (see stereoplots in Fig. 1). It confirms the radial orientation of nearly horizontal principal stress axes, with significant implications for the orientation of slip vectors along differently oriented segments of ABT and T2.

3 Constructing seismicity rate models for the ATZ

In this section, we establish seismicity rate and rupture models for the ATZ, taking into account the two distinct seismogenic volumes, ABT and T2, located at different depths (Fig. 1b) following the approach proposed by Pandolfi et al. (2023), known as the 3D smoothed seismicity method. The new 3D smoothed seismicity approach has been developed to include hypocentral depths and create a smoothed earthquake distribution over three-dimensional spatial cell grids using a 3D kernel, which employs a 3D distance (R3). In contrast, the classical smoothed approach relies on a 2D kernel based on 2D distance (R2) and is typically used with earthquake catalogs that provide only latitude and longitude coordinates, without considering the hypocentral depth of each event. In our calculations, we applied a 3D Gaussian kernel

$${K}_{j}=\frac{1}{2\sqrt{2{\pi }^{3/2}{\sigma }^{3}}}\text{exp}\left(\frac{-{{R3}_{ij}}^{2}}{2{\sigma }^{2}}\right)$$
(1)

denoted as Kj to quantify the impact of the j-th earthquake on the i-th cell within the grid. In Eq. 1, σ represents the model parameter that governs the smoothing amplitude based on the number of nearest neighbors. R3ij corresponds to the 3D distance between the j-th earthquake, including its specific hypocentral depth, and the i-th cell's center, which is at a particular depth derived from the 3D geological structure. Once we have computed the effect of the j-th earthquake on the i-th grid cell using the Gaussian kernel, we calculate the total rate within the i-th grid cell (\({K}_{TOT}^{(i)}\)) by summing up the contributions from all N events in the earthquake catalog (\({K}_{TOT}^{(i)}=\sum_{j=1}^{N}{K}_{j}\)).

This method integrates seismotectonic data and earthquake catalogs to predict earthquake rates and smoothes them over a three-dimensional grid that considers the region's complex geometry and depth variations. The procedure can be summarized in several steps:

  1. 1.

    Catalog Selection and Analysis We select the earthquake catalog through a seismotectonic process and analyze it to identify the activity associated with specific seismogenic structures.

  2. 2.

    Seismogenic Volume Characterization The seismogenic structures are parametrized within a 3D grid, including rupture parameters focusing on rupture depth.

  3. 3.

    3D Adaptive Smoothed Seismicity The earthquake rates are computed for each grid point based on the distance between the grid point's location and each earthquake in terms of latitude, longitude, and depth. Additionally, unique smoothing distance are assigned to each earthquake, resulting in spatially variable smoothing distances. These distances are smaller in areas with high seismic activity compared to regions with fewer seismic events.

3.1 Seismicity rate model for the ABT seismogenic volume

The 3D earthquake rate model for the ABT seismogenic volume (Fig. 2a) is constructed using the methodology described previously. First, we employed the relocated high-quality seismic catalog from Lavecchia et al. (2023) (methodologies for relocation and quality of the seismic data are described in de Nardis et al. 2022) selected to identify ABT activity. We performed a spatial selection with 72 serial cross sections with a semiwidth of 2.5 km organized in three sets with N040°, N060°, and N080° directions. This was done to consider the arc shape of the ABT-related compressive structures and ensure an orthogonal projection of the earthquakes. Additionally, we utilized six summary sections with a semiwidth of 20 km. The selected catalog comprises 6939 earthquakes recorded between 2010 and 2021. These earthquakes range in magnitudes from 0.0 to 4.8 ML and occur at depths between 0 and 50 km (Fig. 2b). An analysis of the catalog revealed a Magnitude of Completeness (Mc) of 1.3, computed using the best combination of Mc 95, Mc 90, and maximum curvature (Woessner and Wiemer 2005). After removing all the earthquakes below the Mc, the complete catalog comprises 2333 events with a b-value of 0.91 ± 0.02 computed using the classical maximum-likelihood estimation (Aki 1965). The Gutenberg-Richter plot is shown in Fig. S1a in Online Resource 1. We then converted the ML in MW with the equation presented in Lolli et al. (2020) and declustered the catalog to ensure a time-independent (Poisson) recurrence behavior, following the Gardner and Knopoff (1974), where the time–space window is determined on the size of the mainshock. We adopted the same parameters as those used for California, as they generate a Poisson distribution for the Italian catalog as demonstrated in the work of Taroni and Akinci (2021). The final declustered catalog consists of 179 independent events. It’s worth noting that we chose to compute the b-value of the catalog prior to the declustering procedure, aiming to include all events in the magnitude-frequency distribution and improve the curve's constraints. Some studies have pointed out that using a declustered catalog, which excludes mainly low-magnitude events, yields a low b-value, potentially leading to an inaccurate estimation of the number of higher magnitude events (Taroni and Akinci 2021; Mizrahi et al. 2021).

Fig. 2
figure 2

The ABT and T2 resulting three-dimensional earthquake rate models (expected number of MW ≥ 4.5 events per year in each cell in logarithmic scale) computed with the new 3D adaptive smoothed seismicity, and the ABT and T2 selected catalog used for smoothing computation. a The ABT 3D earthquake rate model and the 3D grid in colored squares with a 0.1° × 0.1° spacing. The earthquake rate model reflects the ABT fault surface. b The ABT selected catalog in colored dots from green to red according to hypocentral depth. c The T2 3D earthquake rate model and the 3D grid in colored squares with a 0.1° × 0.1° spacing. The earthquake rate model reflects the T2 fault surface. d The T2 selected catalog in colored dots from green to red according to hypocentral depth

Full size image

The ABT grid and its associated rupture parameters (the rupture depth, strike, dip-angle, and seismogenic thickness) align with the information outlined in Pandolfi et al. (2023). This grid is characterized by a regular 0.1° × 0.1° spacing pattern, and the rupture parameters are directly derived from the ABT seismotectonic model (Figs. 3a, b, e). We derived the rupture depth and the rake parameter from the depth contour lines spaced one-kilometer apart (Fig. 3a). The dip-angle parameter, on the other hand, was obtained by dividing the ABT fault model into five sectors that represent the main variations in dip angle along the dip direction (Fig. 3a). The seismogenic thickness is inferred from the grouped seismicity associated with ABT activity within approximately ± 5 km from the hypocentral depth of each grid point.

Fig. 3
figure 3

The 3D model of ABT and T2 and their parametrization for PSHA. a The ABT 3D model and its parameterization. The colored sectors represent the surface subdivision for dip-angle computation. The yellow squares are the 3D grid built on the model with a 0.1° × 0.1° spacing. The thin black lines are the depth contour lines of the surface with 1 km spacing. The zoomed portion of the model shows the subdivision in 50 segments of each depth contour line for strike computation. The colors of the segments are random. b The map view of the ABT 3D model. The colored lines are the depth contour lines from green to red according to depth. The sectors and the stress tensors for rake computation are from de Nardis et al. (2022). Figure adapted from Pandolfi et al. (2023). c The 3D model of the underlying T2 thrust and its parametrization. The colored sectors represent the surface subdivision for dip-angle computation. The yellow dots are the 3D grid built on the model with a 0.1° × 0.1° spacing. The thin yellow lines are the depth contour lines of the surface with 2 km spacing. The zoomed portion of the model shows the subdivision in 40 segments of each depth contour line for strike computation. The colors of the segments are random. d The map view of the T2 3D model. The colored lines are the depth contour lines from green to red according to depth. The sectors and the stress tensors for rake computation are from de Nardis et al. (2022). e The resulting Aki-Richards kinematics (Aki and Richards 1983) based on the average rake parameter calculated with the Slicken 1.0 software (Xu et al. 2017) for each ABT grid point. f The resulting Aki-Richards kinematics (Aki and Richards 1983) based on the average rake parameter calculated with the Slicken 1.0 software (Xu et al. 2017) for each T2 grid point

Full size image

For the rake parameter, however, we performed a different procedure. To determine the sense of slip on the fault plane at any grid point and consequently express it as rake (the parameter requested by Openquake), we adopted a direct method developed by Xu et al. (2017) for calculating the resolved shear stress on a planar surface (Figs. 3b, e). This method assumes that the shear stress vector applied to a given fault is parallel to the slip vector on the fault (Wallace 1951; Bott 1959). Specifically, we calculated the average rake at any grid point with the Slicken 1.0 software (Xu et al. 2017). Necessary input data are the unit vector normal to the fault plane, the unit vectors of the three principal stress axes, and the stress ratio. We derived the stress tensor data from the formal inversion performed for the ATZ zone by de Nardis et al. (2022). Two different near-pure reverse regional tensors are used for the northern and southern ATZ sectors, as reported in Fig. 1a.

The inferred rupture parameters geometrically define the construction of ruptures in the Openquake calculations for each grid-point: the strike determines the orientation relative to the north, the dip-angle defines the slope, the rake sets the kinematics, and the seismogenic thickness delimits the rupture propagation both above and below.

In the context of 3D adaptive smoothed seismicity analysis, we used the Neighboring Numbers (NN) parameter set to a value of 2, consistent with previous studies conducted in Italy (Akinci et al. 2018; Pandolfi et al. 2023). The resulting model displays areas of higher earthquake rates. These include a region in the southeastern part of the surface, situated at approximately 20 km depth, a smaller but deeper area in the northwest at about 30 km depth, and a shallower coastal area along the coast near the city of Ancona (Fig. 2a). A 2D map showing the earthquake rates for the ABT region and the corresponding declustered catalog can be found in Fig. S3a.

3.2 Seismicity rate model for the T2 seismogenic volume

Following the same procedure, we constructed the 3D earthquake rate model for the T2 seismogenic volume (Fig. 2c) using the same high-quality seismic catalog (Lavecchia et al. 2023), exclusively selecting events associated with T2 activity with the same serial cross sections and procedures used for the ABT.

The catalog spans from 2010 to 2021 and includes 648 earthquakes with magnitudes ranging from 0.0 to 4.4 ML and depths between 11.35 and 60.46 km (Fig. 2d). The Mc is determined as 1.3, and removing all events below this threshold yelds a complete catalog of 347 events. Due to this limited number of events, the resulting b-value is 0.7 ± 0.04 (the Gutenberg-Richter plot is shown in Fig. S1b) which is lower compared to the recent studies on compressional regime in Italy (0.98 ± 0.03 in Taroni and Carafa 2023). Additionally, analysis of the distribution of possible b-values of the unified catalog ABT + T2, computed following the methodology reported in Taroni and Selva (2021), reveals plausible values vary between 0.9 and 0.98 as reported in Fig. S2. Therefore, since the ABT and T2 belong to the same tectonic regime, we adopted the same b-value as the ABT catalog (0.91) for T2 to ensure robust computation. Finally, we converted the ML in MW (Lolli et al. 2020) and declustered the catalog using the Gardner and Knopoff (1974) method as part of the smoothing process, resulting in a final catalog of 161 events.

In the second step of our process, we established the 3D model for T2 to create a spatial grid on the fault surface. This grid features a regular grid with a spacing of 0.1° × 0.1° to represent the surface variations in depth, strike, dip, and rake (as shown in Figs. 3c, d, f). We used the depth contour lines spaced at two-kilometer intervals to obtain each point's depth and strike parameters. The T2 seismogenic zone is divided into two sectors to account for variations along the dip direction. The mean dip-angle value is obtained for each sector (Fig. 3c) while the rake parameter is obtained with the same procedure as for ABT (Figs. 3d, f). Seismogenic thickness, which delineates the extent of rupture propagation, was inferred based on grouped seismicity associated with T2 around ± 5 km from the hypocentral depth of each grid point.

Finally, we applied the 3D adaptive smoothing algorithm with NN = 2 to the declustered catalog on the T2 3D grid, resulting in a 3D earthquake rate model for events with MW ≥ 4.5 (Fig. 2c). This model reveals a significant area of higher rate values located from northwest to south-east, including various depths. Additionally, a shallower small area with high-rate values is located in the southeastern portion of the surface. The 2D map of the T2 earthquake rates and the declustered T2 catalog are shown in Fig. S3b. Various perspectives of the ABT and T2 3D rate models are described in Fig. S4.

The smoothing process distributes the total annual moment rate of ABT and T2 to each point on the ABT and T2 grids, respectively. For PSHA computation, each point represents a seismogenic source characterized by distributing its total annual rate according to a tapered Gutenberg-Richter magnitude-frequency distribution, constructed with a corner magnitude of 7.3 and a b-value of 0.91 (for Mmin = 4.5 and above). We determined the corner magnitude initially based on the value of 7.1 from Akinci et al. (2018) for the instrumental catalog of Italy. To account for uncertainties, we applied an additional uncertainty of 0.2, following the approach outlined by Visini et al. (2022). The decision was influenced by the complex seismotectonic framework of the area, where the seismogenic potential may be complicated by possible interactions between the ABT and the underlying thrust T2, as emphasized in Lavecchia et al. (2023). Such scenarios can lead to multifault ruptures, which are critical for the definition of seismic hazard and the potential maximum earthquake magnitude. For example, in Hamling et al. (2017), the study of the 14th of November 2016 earthquake with a Mw 7.8 revealed the involvement of 12 major faults across two distinct seismogenic domain in New Zealand.

Finally, at each grid point, we incorporated information about the fault strike, dip angle, rake of the slip direction, and seismogenic layers’ depth for ABT and T2 (Fig. 3).

To assess seismic hazards in the study area, we utilized the open-source software Openquake (version 3.11) for seismic hazard calculations (Pagani et al. 2014). The impact of these compressional seismic sources on ground shaking in the study area will be further examined in the subsequent sections.

4 Probabilistic seismic hazard analysis for the ATZ

To validate our method which assumes that catalogs of small seismicity, such as ABT and T2 catalogs, can model the behavior of the large magnitude events occurred in the ATZ, we first compared the earthquake rates computed with the overall tapered GR to the earthquake rates of the large earthquakes associated to the compressional domain. To perform this, we first calculated the overall GR of the unified ABT and T2 catalogs and estimated the uncertainties following the approach of Taroni and Selva (2021). Then we identified large earthquakes related to the compressional domain through a detailed comparison of detailed literature with the CPTI15 (Rovida et al. 2022), and association made in the Database of Individual Seismogenic Sources (DISS 3.3.0, DISS Working Group 2021). In particular, we considered the associated earthquakes from studies by Lavecchia et al. (2007), and a recent work by Sbarra et al. (2023), where the authors recomputed the hypocentral depth of some historical earthquakes using a novel approach. Additionally, we referred to the work of Gironelli et al. (2023) who proposed a novel approach to investigate the location and parametrization of the seismogenic sources of Fabriano (1741, Mw = 6.2, Imax IX MCS) and Camerino (1799, Mw = 6.1, Imax IX–X MCS) historical earthquakes. We identified two scenarios of association of events with magnitudes greater than 5.6 occurring within a complete time window defined for central Italy from 1650 until 2023: scenario-1 including 9 events and scenario-2 with 7 events. The first scenario (Ass. 1 in Fig. 4) includes the Sarnano and Offida earthquakes, with respect to the second scenario (Ass. 2 in Fig. 4). Since these earthquakes are located at shallower depths by Sbarra et al. (2023) in a depth-range compatible with the extensional domain, their association with the ABT or T2 is uncertain. Therefore, we have explored all possibilities in the two different scenarios. For each scenario, we computed the activity rates from Mw 5.6 and 6.2 and estimated the 95% rate confidence intervals using the approach of Ross (2003). It is important to note that for the GR, we used the ABT + T2 unified catalog since the occurred large earthquakes are historical events with hypocentral depth difficult to constrain. Thus, we cannot discern with certainty the involvement of the ABT or the T2 thrust, as also highlighted by some authors. For instance, in Lavecchia et al. (2023), the authors propose the hypothesis that the strongest earthquake (Fabriano 1741, Mw 6.2) occurred on T2 instead of the ABT, considering the deeper hypocentral depth obtained in Sbarra et al. (2023). Our results in Fig. 4 shows that the occurrence rates of the events (green circle and black square for Mw 5.6 of Ass. 1 and Ass. 2 respectively, and purple rhombus for Mw 6.2 common to both scenarios) for each scenario are very close to those predicted by the tapered GR, reinforcing our assumption and validating the subsequent assessment.

Fig. 4
figure 4

The comparison between the earthquake rates computed with the overall tapered GR of the unified ABT + T2 catalog and the earthquake rates of the large earthquakes associated with the ATZ. a The tapered GR computed with the ABT + T2 catalog and the earthquake rates of large events of the two scenarios of association. Ass. 1 includes all the 9 earthquakes listed in panel c while Ass. 2 excludes Sarnano and Offida earthquakes, whose association to the compressional domain is uncertain. The earthquake rates are computed from Mw 5.6 (green circle for Ass. 1 and black square for Ass. 2) and from Mw 6.2 (purple rhombus for both scenarios) b Map view shows the location of the large earthquakes considered in our associations, obtained from the CPTI15 (Rovida et al. 2022) and the DISS database (DISS 3.3.0, DISS Working Group 2021). c Full table detailing associated ATZ earthquakes with a comparison of depth ranges from different works

Full size image

To emphasize the impact of the compressional domain in ground shaking, we incorporated both the ABT, which is situated at shallow depths near the coast and deeper depths under the Apennine chain, and the T2, located beneath the ABT at depths ranging from 25 to 60 km. These source models were combined into a single point source input data to calculate the overall compressional ground motion in the region.

To assess the ground shaking, we used the ground motion prediction equations (GMPEs) from Bindi et al. (2014) (BIN14) since they ranked highly in the analysis performed for the new seismic hazard model of Italy (MPS19) (Lanzano et al. 2020). Bindi et al. (2014) proposed Pan-European ground-motion prediction equations for the average horizontal component of peak ground acceleration (PGA), peak ground velocity (PGV), and 5% damped pseudo-spectral acceleration at spectral periods up to 3.0 s using the RESORCE dataset (Akkar et al. 2013). To emphasize our multi-depth scenario, we evaluated the hypocentral distance (Rhypo), the distance between the hypocenter and the site where the hypocenter is assumed to be at the center of a rupture (Pagani et al. 2014). In addition, the BIN14 also considers the rake parameter to compute the ground motion, ensuring that the predicted ground shaking reflects both the depth and the rake variations of the ABT and T2. We chose to extrapolate all rupture parameters from the seismotectonic model to provide comprehensive input for different distance metrics. Our model is available in supplementary material as Online Resource 2 (ABT) and Online Resource 3 (T2). The Rjb distance must be excluded from this 3D application, because the events in the ABT and T2 structures will be erroneously projected together into the surface. Another possible correct distance could be Rrup, i.e. the rupture distance, but was not used in this study because it is not available for the Bindi et al. (2014) GMPEs.

Employing the attenuation relationships provided by the GMMs makes it possible to describe the range of potential ground-motion intensities for each specific scenario. Hence, each scenario is defined by an earthquake magnitude, a corresponding annual rate, and the distance between the earthquake source and the site where ground motion levels are assessed. This information calculates the expected distribution of ground-motion levels for that particular earthquake scenario. Our computation employed a straightforward, simple one-branched logic tree approach for both seismic source and ground motion models, with a weight of 1.0 assigned to each (Fig. 5). This choice was made because our primary focus was to show the application of the 3D smoothed seismicity approach in the ATZ where we have access to detailed seismicity catalogs that allow for this specific application. We underline that this work is not a complete hazard analysis of the zone (such type of analysis would have required a logic tree approach and several different models, to explore and capture the epistemic uncertainties around the estimated hazard), but it is simply one possible implementation of the new 3D smoothed seismicity approach.

Fig. 5
figure 5

The PSHA computation workflow for Openquake. The Seismic Source Model combines catalog and seismotectonic data. The Ground Motion Model uses Rhypo distance metric

Full size image

The probability (P) of exceeding each ground-motion level (lnPGA) at a given site over a specified time period (T) is determined through the probabilistic calculation (Eq. 2). This calculation considers the total annual rate (Rtot), which is calculated by summing the rates of all the scenarios considered during the analysis.

$${P}_{pois}\left(>lnPGA, T\right)=1-{e}^{{-R}_{tot} T}$$
(2)

It is important to emphasize that the resulting PSHA map is significantly influenced by the various models and input parameters employed in its determination.

4.1 Resulting PSHA map and hazard curves

Figure 6a presents the final hazard map for the 2% in 50 years exceedance in PGA on rock sites. In this map, we observe higher Peak Ground Acceleration values ranging between 0.175 and 0.2 g, notably located offshore between the cities of Pesaro and Ancona and onshore southeast of the city of Sarnano. In line with what was predicted, the offshore area with higher PGA was recently affected by the Bice seismic sequence of November 9, 2022, which occurred offshore Pesaro and Ancona with two major events of Mw 5.5 and 5.2 enucleated within 1 min and ~ 8 km away in map view (Lavecchia et al. 2023).

Fig. 6
figure 6

The 2% in 50 years PSHA map of the overall compressional domain in eastern Central Italy. The ground motion is computed with the Rhypo distance. a The 2% in 50 years PSHA map of ABT + T2. b The seismic hazard curves computed for the city of Pesaro with the single contribution of ABT and T2 and the overall contribution. c The seismic hazard curves computed for the city of Sarnano with the single contribution of ABT and T2 and the overall contribution

Full size image

To gain insights into the seismic hazard, we generated seismic hazard curves for two specific localities within the study area (Figs. 6b, c). The first locality is Pesaro, located along the coast in the northern sector, while the second is Sarnano, located at the foot of the Apennine chain. A comparison analysis of these curves reveals that the ground motion near Sarnano (Fig. 6c) is predominantly influenced by the ABT, whereas the contribution of the underlying T2 thrust becomes more significant near Pesaro (Fig. 6b). In Fig. S5, the PSHA maps with ABT and T2 contributions computed separately are shown, aiming to highlight the spatial differences in the ground motion of the two sources. Additionally, Fig. S6 depicts the 10% in 50 years map of the overall seismic hazard and of the ABT and T2 separately to illustrate the contribution of smaller magnitude events.

Our model suggests significantly higher resolution due to the integration of a seismotectonic and catalog-based approach. This approach facilitates the association of seismicity rates with detailed rupture depths, thus accurately reflecting the geometries of the underlying structures. Consequently, our PSHA map provides detailed insights into the seismic hazard within the coastal area offshore Pesaro and Ancona. This region has historically experienced several noteworthy earthquakes, including, the Conero offshore earthquake in 1690, (MW 5.9), and the Senigallia earthquake in 1930, (MW 5.9) as shown in Fig. 1a.

5 Discussion

We explore and discuss the impact of different smoothed seismicity approaches (T2 seismicity related to ABT, standard 2D approach with and without the seismogenic structures) on the final ground motion hazard in the ATZ. To accomplish this, we emphasize the capability of our approach, which combines seismotectonic- and catalog-based data, in effectively characterizing the complex, multi-layered, and multi-depth seismotectonic scenario in eastern Central Italy. Furthermore, we provide insights into the importance of precisely defining rate computations and rupture-depth parametrization within the context of seismic hazard analysis.

5.1 Comparison PSHA maps computed with different smoothing methods and models

In this section, we explore various smoothed seismicity approaches, where we combine the seismic activity and the seismic catalogs from distinct seismogenic zones. These zones and their seismic activity are considered individually and in combination with our seismic hazard analysis. Our objective is to evaluate the influence of different input data and methodologies, as well as to compare the ground motion hazard with the methodology proposed in our study, which is based on the work by Pandolfi et al. (2023). These three methods/models considered are as follows:

  1. 1)

    T2 seismicity associated with the ABT seismogenic structure (only the ABT structure is used and the ABT and T2 catalogs are unified),

  2. 2)

    2D adaptive smoothed seismicity computed with seismogenic structures (ABT and T2 structures are considered individually with their associated catalog),

  3. 3)

    2D adaptive smoothed seismicity without seismogenic structures (ABT and T2 structures are represented in a common generic grid and the ABT and T2 catalogs are unified).

The results obtained from the three models are provided for a 2% probability of exceeding ground motion intensity (PGA) over a 50 year period. We also present ratio maps comparing these models with our proposed 3D smoothed approach, referred to as PSHAref, in the following sections. We note that the BIN14 GMM and Rhypo as the distance definition are considered for the 3D approach. The comparisons between models are described in Fig. 7 as PGA values and in Fig. 8 as relative values in percentage of PGA with respect to the final map computed with the catalog- and seismotectonic-based approach proposed in this work (PSHAref, Fig. 7a and Fig. 8a), as reported in Eq. 3.

Fig. 7
figure 7

The comparison between the reference map with ABT + T2 modeled as different sources and three different approaches. All the maps represent the 2% in 50 years scenario computed with BIN14 Rhypo. a The reference map computed with the new catalog- and seismotectonic-based approach of the ABT and T2 as separate sources. b The first model with T2 seismicity is associated with the ABT. c The second model was computed with the 2D adaptive method with the seismogenic structures. d The third model computed with the 2D adaptive method without the seismogenic structures. e The generic grid is used for the third model

Full size image
Fig. 8
figure 8

The relative differences in the percentage of PGA values between the reference map computed with the new approach proposed in this work and three different approaches: \(\frac{\left[{PSHA}_{model(1 to 3)}{- PSHA}_{ref}\right]}{{PSHA}_{ref}} \times 100\). All the maps represent the 2% in 50 years scenario computed with BIN14 Rhypo. a The reference map computed with the new catalog- and seismotectonic-based approach of the ABT and T2 as separate sources. b The relative differences between the reference map and the first model with T2 seismicity associated with the ABT. c The relative differences between the reference map and the second model computed with the 2D adaptive method with the seismogenic structures. d The relative differences between the reference map and the third model with the 2D adaptive method without the seismogenic structures

Full size image
$$\frac{\left[{PSHA}_{model(1 to 3)}{- PSHA}_{ref}\right]}{{PSHA}_{ref}}\times 100$$
(3)

In our first model (PSHAmodel1), we associated T2 seismicity with ABT to investigate the consequences of connecting seismicity to a specific seismogenic volume. We subsequently created an earthquake rate model using the newly compiled ABT + T2 seismicity catalog and applied the 3D adaptive smoothing method on the ABT's 3D grid. The comparison of the first model with our approach, in which ABT and T2 were considered separately (Fig. 7a), reveals significant variations in PGA values (Fig. 7b and Fig. 8b). This finding indicates that the combined seismicity caused considerable amplifications in ground motion with major increases from 40 to 65%, affecting both shallower and deeper depths. Several factors contribute to these variations, including an increased total annual rate of the ABT due to T2 seismicity, and the attribution of T2 seismicity to shallower ABT rupture depths. Attributing T2 seismicity to shallower ABT rupture depths has the greatest impact on PGA values. This effect becomes particularly evident when comparing it with the BIN14 GMM using the Rjb distance, where the contribution to ground motion changes less significantly as rupture depth is not considered (Fig. 9). Therefore, under the Rjb distance metric, increases in PGA primarily depend on variations in rate distribution.

Fig. 9
figure 9

The comparison between the reference map with ABT + T2 modeled as different sources and the first model with T2 seismicity associated with the ABT computed with BIN14 Rjb. a The reference map computed with the new catalog- and seismotectonic-based approach of the ABT and T2 as separate sources. b The first model with T2 seismicity associated with the ABT

Full size image

In the second model (PSHAmodel2), we computed PSHA maps for peak ground acceleration with a 2% probability of exceedance in 50 years in eastern Central Italy using the 2D adaptive smoothing seismicity approach. In the 2D method, we applied separate smoothing to the seismicity associated with the ABT and T2 seismogenic zones based on a predefined grid. This approach excluded depth information, focusing solely on earthquake distributions determined by the latitude and longitude of each event. As shown in Fig. 7c and Fig. 8c, the 3D adaptive approach from the reference map and the 2D adaptive method used in the second model produced similar results, with the exception that the 2D approach yielded higher PGA values, especially near Ancona with a greatest peak of increase from 50 to 85%. This discrepancy can be attributed to the absence of hypocentral depth information as the third dimension in the 2D approach. In the Ancona region, numerous seismic events are well-grouped in terms of latitude and longitude but vary significantly in depth. The 3D adaptive smoothing technique, which considers all three dimensions, provides a more precise rate distribution by accounting for grouped seismic activity and its distance relative to the grid. It is important to note that the quality of the catalog and the seismotectonic model play a role in influencing the results. The 2D approach, which only takes latitude and longitude into account, may inaccurately group earthquakes at different depths, especially when specific seismic volumes are not explicitly defined.

In the third model (PSHAmodel3), we applied a standard 2D approach based solely on the earthquake catalog. In this method, we utilized the overall compressional catalog for the conventional 2D adaptive technique without distinguishing the ABT and T2 seismicity. This traditional approach is typically used when fault data is unavailable. We established a regular grid comprising 306 points, each measuring 0.1° × 0.1°, covering the entire area without taking into account the specific geometries of ABT or T2 (Figs. 7d, e). For the rupture depth of each grid point, we relied on the catalog's average depth, with a hypo average depth of 22 km. When we compared the third model to the reference map, notable differences in the distribution of PGA became evident (Fig. 7d, and Fig. 8d). The 2D standard map indicates higher ground motion in the northwest between Rimini and Perugia, with an increasing range from 20 to 86%. In contrast, it underestimates the coastal area, and the region near Sarnano, with a decreasing range from 10 to 37%. These variations can be attributed to the use of a uniform rupture depth in the standard 2D method, which led to the underestimation of ABT's contribution along the coast and overestimation of T2 in the western parts. This underlines the importance of a multi-layered seismotectonic approach that considers particular seismogenic and kinematic volumes, along with comprehensive rupture parameters, in the process of hazard assessment.

6 Conclusions

In this study, we conducted a probabilistic seismic hazard analysis in the Adriatic Thrust Zone (ATZ) domain of eastern Central Italy using an innovative 3D adaptive smoothed approach. One of our main objectives was to create a seismic source model that could provide reliable earthquake rate data and detailed rupture parameters. We placed particular emphasis on characterizing the complex geometrical aspects of both the ABT and the underlying T2 thrust within our study area.

In our study, we rigorously compared various approaches, considering multiple factors to ensure a robust assessment of seismic hazards in a complex tectonic environment. We demonstrated that the 3D adaptive smoothing approach is more relevant to grouped seismicity than the traditional 2D method. However, it is important to note that the 3D approach is most effective when establishing a well-defined geometric-kinematic fault model and when the seismic data feature high-quality location parameters.

Our findings demonstrated that attributing seismicity to specific seismogenic and kinematic domains has significant implications for parameters like the b-value, the rate distribution, and the rupture-site distance. This approach results in hazard maps that better reflect the underlying seismotectonic framework. We applied a smoothed seismicity approach based on seismotectonic models, which allowed us to work with multi-layered and multi-depth structures, characterizing their contribution to ground motion. This approach is particularly useful when dealing with complex geological features, such as extensive regional or offshore structures, for which geologic, geodetic, or paleoseismological data is limited.

Notably, we conducted a novel analysis by investigating the seismicity of the ABT and T2 structures separately and their respective contributions to seismic hazard. This was particularly significant along the Adriatic coast, where the ABT becomes shallower. Our combined approach, integrating seismotectonic- and catalog-based data, resulted in higher-resolution hazard maps, revealing elevated Peak Ground Acceleration (PGA) values in the coastal area offshore Pesaro and Ancona, known for historical earthquakes and recently hit by the Bice seismic sequence of November 9, 2022, with two major events (Mw 5.5 and 5.2) very close in time and space.

Moving forward, our future objective is to expand our modeling to include the epistemic uncertainties which affect the model and the intra-Apennine extensional domain, enabling the computation of a comprehensive Probabilistic Seismic Hazard Assessment (PSHA) map that considers the contribution of all seismogenic volumes in eastern Central Italy.

In conclusion, our methodology has the potential to be highly effective in other complex seismic regions, particularly in areas where depth is a crucial factor in seismic activity, such as subduction zones. Applying this method to subduction zones, where seismic activity rates and magnitude-frequency distributions vary with depth, could significantly improve the reliability of probabilistic seismic and tsunami hazard assessments.