Pin-supported walls as seismic retrofit for existing RC frames: performance improvement through link removal

Abstract

Pin-supported (PS) walls represent a possible solution for the seismic retrofit of existing reinforced concrete (RC) buildings, enabling linearization of the frame deformation along its height and consequently inhibiting soft storey collapse mechanisms. The effectiveness of this rehabilitation technology is strongly related to the characteristics of the existing frames, especially to the vertical distribution of the frame storey lateral stiffness. Since a larger 1st storey lateral stiffness may lead to a detrimental structural response of the retrofitted system, an alternative solution obtained from removing the connecting link between the 1st floor of the existing building and the pin-supported wall is investigated in this paper. An analytical method is proposed to derive the distribution of the internal actions in a dual 2D RC frame-PS wall system without the link at the 1st floor level, considering both a linear and nonlinear behaviour of the frame. It emerges that some parameters describing the structure type can provide straightforward information on the suitability of this solution in the seismic retrofit of existing RC buildings. As a result, a simplified procedure has been derived to preliminarily define the retrofit system configuration and evaluate the maximum demand in the PS wall. Such a procedure is finally applied with reference to a frame representing a RC building and finite element model analyses are carried out for validation purposes.

1 Introduction

Pin-supported (PS) walls represent a possible innovative seismic retrofit solution for existing reinforced concrete (RC) buildings (Belleri et al. 2016; Casprini et al. 2022; Wada et al. 2011; Wada 2018), particularly for those designed before the enforcement of modern anti-seismic regulations and seismic zonation, featuring low-ductility structural detailing and structural irregularities, which represent a wide portion of the existing heritage (Marini et al. 2017). The introduction of a stiff pin-supported wall (also referred to as “hinged walls” or “rocking cores”) able to linearize the lateral deformation of the existing frame along its height (MacRae et al. 2004), allows spreading the ductility demand, thus inhibiting soft storey collapse mechanisms. Although the first examples of PS walls as retrofit systems are quite recent (Wada et al. 2011; Qu et al. 2012), its application has increased in the last decade in several countries (Balducci and Castellano 2015; Gioiella et al. 2017). Some research studies deal with finite element simulations to investigate the behaviour and effectiveness of 2D wall-frame retrofitted systems (Qu et al. 2015) or to define preliminary design criteria (Blebo and Roke 2015), while others focus on analytical formulations able to derive the dynamic characteristics of the system (Bozdogan and Öztürk 2016), or the displacement and force demand under several lateral load configurations (Sun et al. 2017; Zhou et al. 2021).

The PS wall solution presents several advantages: it can be assembled completely outside the building, or by re-engineering existing structural elements, such as the staircase walls. In many cases (e.g., for the frames examined in the following), such a retrofit solution does not necessarily entail an increase in the global lateral stiffness, so neither of the seismic demand. On the other hand, as presented in this paper, a slight capacity increase in terms of strength is obtained, governed by the capacity of the existing structural elements engaged by the linearization of the deflected shape. This allows reaching a higher serviceability level: in fact, a global elastic behaviour may be obtained for higher intensity earthquakes compared to the as-is condition, therefore leading to a damage reduction. It should be noted that an overall strength increase may also lead to higher loads on the floor diaphragms which need to be carefully assessed (Bull 2004; Rodriguez et al. 2007; Tena-Colunga et al. 2015; Marini et al. 2022). However, the authors preliminarily investigated not only the beneficial effects, but also the weaknesses of PS wall solutions when applied in the retrofit of existing RC frames (Casprini et al. 2019). It was shown that, for some frames typologies (as it will be discussed in Sect. 4), the application of the PS wall system may lead to a global capacity reduction; the PS wall solution should thus be avoided in these cases, since the development of a plastic behaviour may be anticipated with respect to the as-is condition, for the same earthquake intensity.

Based on these preliminary considerations, a closed-form analytical method able to assess the suitability of this solution in relation to the actual configuration and geometrical properties of the existing structures was proposed (Casprini et al. 2022). In this method, differently from most approaches proposed in the former mentioned research works, the frame 1st storey lateral stiffness was set as a key parameter to understand the behaviour of the retrofitted system. A parameter β was defined as the ratio between the lateral stiffness of the 1st storey and the mean lateral stiffness of the upper storeys; it was observed that, even if the PS wall improves the global behaviour, a larger ductility demand is observed on the existing structural elements in the case of β $\ge$ 1.5, which may lead to anticipated local failures and may compromise the global performance of the retrofitted system. In this condition, the global behaviour of the retrofitted system may be improved by changing the configuration of the connecting links by removing the link connecting the frame and the wall at the 1st floor level. The PS wall solution can also be coupled with additional devices acting as dissipators, which allow increasing the lateral stiffness and the energy dissipation, thus reducing the displacement demand.

In this paper, the analytical procedure developed by Casprini et al. (2022) (i.e., with links at each floor level) is extended for the case of the 1st link removal, providing a closed-form solution to estimate the load distribution in the PS wall and the system capacity in terms of strength, both considering a linear and nonlinear behaviour of the frame elements. The post-retrofit deformation demand should be then compared with the capacity of the existing elements; in this paper, such comparison is carried out through nonlinear pushover analyses. A procedure is also provided to determine whether the PS wall is a suitable retrofit solution for existing RC frames, and, if that is the case, if the first connecting link needs to be removed. The maximum internal actions expected in the PS wall can be determined starting from the estimated load distribution, allowing for its preliminary design. The validation of the procedure is finally carried out through a finite element model simulation on a reference 2D RC frame.

2 Description of the PS wall system and model assumptions

The introduction of a pin-supported wall, by forcing the deformation compatibility between the wall and the frame, leads to a change in the static scheme of the frame, thereby to a different internal actions’ distribution. A PS wall may thus lead to an increase of the retrofitted system capacity due to the sharing of the external action between the frame and the wall; while, at a sectional level, the structural elements capacity is not modified.

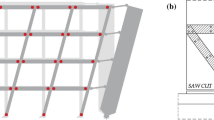
The first parameter which needs to be set in the design of this retrofit solution is the lateral stiffness ratio χ between the PS wall and the frame (MacRae et al 2004), required to linearize the frame lateral deformation. Sensitivity analyses on the behaviour of elastic planar finite element models of 2D regular RC frames varying between 3 and 8-storeys showed that a value of χ ranging between 0.3 and 0.5 is effective in linearizing the frame deformation in the elastic range: the value of 0.3 leads to a maximum 5% difference from a complete linearization, while no further beneficial effects are obtained from taking values higher than 0.5. The frame storey lateral stiffness (K_s) is herein calculated by adopting the formula proposed by Schultz (1992). The PS wall geometrical dimensions can be calculated by setting the design value of χ once the frame layout and the dimensions of the structural elements are known. A complete linearization of the deformed shape of the retrofitted system is inherently assumed in the proposed analytical model, thus considering a lateral stiffness ratio (χ) at least equal to 0.3 in the following applications. The interested reader is referred to Casprini et al. (2022) for further details and for the background of the analytical method presented in this paper. Herein the 1st link removal is investigated in order to improve, when necessary, the efficacy of a PS wall solution. A scheme of a 2D frame-wall system is reported in Fig. 1.

Fig. 1

Implementation of a pin-supported wall retrofit system on an existing frame by removing the 1st connecting link (adapted from Casprini et al. 2022)

This method is based on some general simplifying assumptions allowing the definition of a closed-form solution:

• only planar effects are considered; therefore, the retrofitted system is composed of an existing 2D frame and a retrofit PS wall system.

• n-storey RC frames with a constant inter-storey height H and with constant column cross-sections along the building height are considered; stiff infills are not considered; the intermediate and upper storey lateral stiffness is assumed to be constant for all the storeys except for the first one due to the different boundary conditions.

• a shear-type behaviour of the existing frame is assumed; the axial deformability of the beams is neglected, and each story rigidly translates when subjected to horizontal loads. Corrective factors are then provided to account for non-shear type conditions.

• unlimited ductility at plastic hinges of the existing structural elements is preliminarily assumed in the definition of the analytical model; thus an assessment of the actual deformation capacity and demand of the structural elements are required through, for instance, nonlinear static analyses to check the compliance with design targets and performance objectives.

• the seismic action is described by lumped loads at each floor level, with an inverse triangular pattern due to the deflected shape linearization of the retrofitted system, according to the 1st vibration mode. Therefore, the derived set of equations accounts only for the first fundamental mode shape of the retrofitted system.

3 Elastic load distribution in the retrofitted system in the case of 1st link removal

3.1 Analytical method: background

As in the previously developed solution (Casprini et al. 2022), the derivation of the analytical formulation with the 1st link removal requires the definition of the external load distribution, the storey shear, and the inter-storey displacement (Eqs. 1–4). The system configuration is described in Fig. 2. The seismic load F_i at the ith storey is expressed as in Eq. (1), where α is a load factor and H is the inter-storey height. Such forces are balanced at each floor by the forces N_i transferred between the frame and the wall at the ith level, and globally by the frame and PS wall base shear. The storey shear V_j (at the jth floor) is calculated at each level as the sum of the loads F_i and N_i of the storeys above it (Eq. 2); as for the as-is condition, the equations are still valid by considering N_i = 0 and a linear load distribution assumption. The generic storey lateral stiffness (K_s,i = K_s for i = 2:n) is assumed to be constant for all the storeys but in the 1st one, where it is assumed equal to K_s,1 = βK_s. The obtained formulation is strongly dependent on the parameter β, which governs the load distribution in the elastic phase; the influence of such parameter on the response has been investigated and it will be addressed in Sect. 3.4.

$$F_{i} = i\alpha H$$

(1)

$$V_{j} = \sum\limits_{i = j}^{n} {(i\alpha H + N_{i} )}$$

(2)

Fig. 2

Forces distribution after the PS wall introduction without the 1st connecting link. $\overline{M }$ is the equivalent resisting moment provided by the possible presence of additional devices (adapted from Casprini et al. 2022)

The inter-storey lateral displacement in the elastic range is computed as the ratio between the storey shear and the storey lateral stiffness, both in the as-is condition (${\Delta }_{j}$ in Eq. 3) and after the PS wall introduction ($\overline{{\Delta }_{j}}$ in Eq. 4).

$$\Delta_{j} = V_{j} /K_{s,j}$$

(3)

$$\overline{{\Delta_{j} }} = \frac{{\sum\nolimits_{i = j}^{n} {(i\alpha H + N_{i} )} }}{{K_{s,j} }}$$

(4)

As for the retrofit system configuration, the PS wall can be connected to the existing frame at the storey levels by means of axially rigid links acting as “spacers” or coupled with the frame by introducing additional replaceable devices which represent a further constraint for the structural elements of the existing building. The pinned constraint becomes a non-linear rotational spring when such devices are located between the PS wall and its foundation, which should thus be designed according to the required flexural capacity. If instead they are placed at the floor levels, the capacity of the existing structural elements in transferring the additional shear/bending moment should be verified. The equivalent bending moment $\overline{M }$ considered at the wall base in the case of additional devices is associated with the contribution ΔV_d in terms of base shear, and it can be calculated from the activation loads (yielding forces) in the devices (Casprini et al. 2022).

3.2 Solution for the case with 1st link removal

In the case of 1st link removal, the equations governing the problem are identified in the system of Eq. (5): the first equation represents the condition of equal inter-storey displacements between adjacent storeys, except for the first two, due to the deformed shape linearization in the frame; the second equation represents the sum of the relative displacements of the first two storeys which is equal to twice the inter-storey displacement of any couple of consecutive storeys connected to the PS wall; and the third equation represents the moment equilibrium with respect to the wall pinned connection. The value of N_j (Eq. 6) is derived from the first equation of the system (Eq. 5). From the second and third equations of the system (Eq. 5), it is possible to derive the loads transferred to the PS wall at the 2nd (N₂ in Eq. 8) and at the roof level (N_n in Eq. 9).

$$\left\{ {\begin{array}{*{20}l} {\overline{{\Delta_{j + 1} }} = \overline{{\Delta_{j} }} } \hfill & {{\text{for }}j = 3:n - 1} \hfill \\ {\overline{{\Delta_{1} }} + \overline{{\Delta_{2} }} = 2\overline{{\Delta_{3} }} } \hfill & {} \hfill \\ {\sum\limits_{i = 2}^{n} {N_{i} iH + \overline{M} } } \hfill & {} \hfill \\ \end{array} } \right.$$

(5)

$$N_{j} = - j\alpha H{\text{ for }}j = 3:n - 1$$

(6)

$$\left\{ {\begin{array}{*{20}l} {\overline{{\Delta_{1} }} + \overline {{\Delta_{2} }} = 2 \overline {{\Delta_{3} }} } \hfill \\ {\sum\limits_{i = 2}^{n} {N_{i} iH + \overline{M} } = 0} \hfill \\ \end{array} } \right.\; {\longrightarrow} \;\left\{ {\begin{array}{*{20}l} {\frac{{\sum\nolimits_{i = 1}^{n} {(i\alpha H + \sum\nolimits_{i = 2}^{n} {N_{i} )} } }}{{\beta K_{s} }} + \frac{{\sum\nolimits_{i = 2}^{n} {(i\alpha H + N_{i} )} }}{{K_{s} }} = 2\frac{{\sum\nolimits_{i = 3}^{n} {(i\alpha H + N_{i} )} }}{{K_{s} }}} \hfill \\ {N_{2} 2H - \alpha H^{2} \sum\limits_{i = 3}^{n - 1} {i^{2} + N_{n} nH + \overline{M} = 0} } \hfill \\ \end{array} } \right.$$

(7)

$$N_{2} = \frac{\alpha H}{6}\frac{{(2n^{3} + 3n^{2} )(\beta - 1) - n(11\beta + 19) - 30(\beta - 1) + \frac{{6\overline{M} }}{{\alpha H^{2} }}(\beta - 1)}}{n(\beta + 1) + 2(\beta - 1)}$$

(8)

$$N_{n} = \frac{\alpha H}{6}\frac{{(\beta + 1)(2n^{3} - 3n^{2} ) - n(11\beta - 13) - 6(\beta - 1) - \frac{{6\overline{M} }}{{\alpha H^{2} }}(\beta + 1)}}{n(\beta + 1) + 2(\beta - 1)}$$

(9)

The base shear demand of the PS wall (V_PSW) and of the frame after the retrofit (V_FR,R,) are computed in Eqs. (10) and (11); the former is defined as the sum of all N_i and the latter as the difference between the seismic loads and the PS wall base shear. The contribution of the additional devices in terms of base shear is explicated in Eq. 12. The step-by-step solution is reported in “Appendix 1”.

$$V_{PSW} = \overline{V}_{PSW} + \Delta V_{d} = \frac{\alpha H}{6}\frac{{n^{3} (3 - \beta ) + 3n^{2} (\beta - 1) - 2n(\beta + 3)}}{n(\beta + 1) + 2(\beta - 1)} + \Delta V_{d}$$

(10)

$$V_{FR,R} = \overline{V}_{FR,R} - \Delta V_{d} = \frac{\alpha H}{6}\frac{{2n\beta (2n^{2} + 3n + 4)}}{n(\beta + 1) + 2(\beta - 1)} - \Delta V_{d}$$

(11)

$$\Delta V_{d} = \frac{2}{n(\beta + 1) + 2(\beta - 1)}\frac{{\overline{M} }}{H}$$

(12)

It is observed that the base shear demand of the PS wall and the existing frame in the retrofitted configuration in the elastic phase is dependent on the number of storeys n, the coefficient β and the contribution of additional devices, if any. Because the value of β affects the shear distribution in the frame, possible relevant differences between the storey lateral stiffnesses need to be accurately considered for a reliable prediction of the force distribution (further considerations are carried out in Sect. 3.4).

3.3 Non-shear type conditions: corrective factors

The proposed analytical method provides a solution in the case of an ideal shear type behaviour. Finite element analyses were carried out to derive a corrective factor for non-shear type conditions. Such factor is defined as the ratio between the maximum bending moment in the PS wall (in the elastic phase) obtained from the numerical simulation and from the analytical formulation. Various system configurations were considered: several number of storeys (n = 3, 5, 8), different storey lateral stiffness ratios (β = 1, β = 2), and the difference between the real behaviour and the assumed shear type behaviour (K_s/K_S.T), where K_s is the generic storey lateral stiffness and K_S.T is the storey lateral stiffness in the case of shear type behaviour (Casprini et al. 2022). The corrective factors resulting from the sensitivity analyses are reported in Table 1.

Table 1 Corrective factors for maximum bending moment predictions in a PS wall without the 1st link in the case of non-shear type conditions

The PS wall bending moment obtained from the analytical formulation can be multiplied by the corrective factors to estimate the results of the finite element simulation. A linear interpolation is suggested to account for intermediate values of n and K_s/K_S.T. The corrective factor is greater than 1 (i.e. actual maximum bending moment equal to the one predicted by the model) for β = 2 and by decreasing the storey number or making the frame behaviour further from the ideal shear type.

3.4 Beneficial effects of the 1st link removal

The internal actions distribution depends on the value of β; it was shown that, in regular frames, this parameter may assume values ranging between 1 and 2 (Casprini et al. 2022). Also, in the case of a lower and a higher 1st storey height, a higher and lower value of β can be expected, respectively. The potential benefits of the PS wall introduction in the elastic phase are evaluated through an efficacy factor (frame base shear factor) η_fr,el, defined as the ratio between the frame base shear without (V_FR,0 = αHn(n + 1)/2) and with (V_FR,R from Eq. 11) the PS wall. In detail, η_fr,el > 1 corresponds with a beneficial effect of the retrofit intervention, otherwise a detrimental effect in terms of global capacity may be expected since the PS wall introduction leads to a higher soliciting action on the existing frame for the same external load. Previous analyses showed that, in the case of connecting links at each floor level, a major beneficial effect is obtained when β < 1, but a detrimental effect is found when β > 1.5 (η_fr,el < 1) (Casprini et al. 2022). To highlight the beneficial effects of the 1st link removal, the method is applied to a 3-storey frame (by assuming α = F/H) for β = 2 (Fig. 3).

Fig. 3

Shear distribution in the frame for a total seismic load equal to 6F (α = F/H) in the as-is condition (a); shear distribution in the PS wall and force transferred from the frame to the wall in the case of all links (b) and with the 1st link removal (c)

It is observed that, in the case with all links (Fig. 3b) η_fr,el < 1 (η_fr,el = V_FR,0/V_FR,R = 6/7 = 0.85) while, in the case without the 1st link (Fig. 3c) η_fr,el > 1 ( η_fr,el = V_FR,0/V_FR,R = 6/5.6 = 1.07). Indeed, without the link at the 1st floor, the equivalent lateral stiffness of the first two storeys, acting as springs in series, is lower than the stiffness of a single storey; considering for instance the 1st and 2nd storey stiffness equal to 2K_s and K_s respectively (i.e. β = 2), the resulting equivalent stiffness is 2/3K_s which leads to an equivalent β (ratio between such stiffness and the stiffness of the above storeys) lower than 1. The same results are obtained in the case of PS wall with additional devices at the base (FR + PSW + $\overline{\mathrm{M} }$), as shown in Fig. 4. The external force distribution in the system in the elastic range with all the connecting links and without the first link are compared. The results show that, while in the presence of all the connecting links (PSW_0) an increase in the frame base shear occurs after the retrofit, the solution without the first connecting link (PSW_1) is associated with a decrease of the base shear in the existing frame, thus resulting in a global beneficial effect for the selected values of β. In all cases, the same triangular distribution of the seismic loading was considered, leading to the same total seismic action referred to as 100%; these assumptions do not influence the results because an elastic behaviour of the frame and the wall is assumed in this phase.

Fig. 4

Share of base shear with respect to the total external load (100%) applied to a 3-storey frame (β = 2) in the as-is configuration (FR), after PS wall introduction (FR + PSW) and with additional dissipation (FR + PSW + $\overline{\mathrm{M} }$)

Despite the share of base shear undertaken by the PS wall (6% for β = 2) is quite modest for the considered example, the capacity of the retrofitted system may be increased by adding additional devices (as shown in Fig. 4, case PSW_1 with $\overline{\mathrm{M} }$), and major beneficial effects may also arise in changing the ductility demand and avoiding possible soft-storey mechanisms (see examples in Sect. 5, Fig. 11b, c). To extend the results, Fig. 5 shows the frame base shear factor η_fr,el for a n-storey frame, with n ranging from 2 to 10, obtained from the aforementioned equations. η_fr,el strongly depends on the stiffness ratio β, and not on the geometrical properties of the structural elements; for this reason, such a trend holds also for frames with different number of storeys, even if larger element dimensions would be expected by increasing n. The contribution of additional devices is neglected in this example. For β = 2, the provision of connecting links at each floor (PSW0) always leads to η_fr,el < 1, while the retrofit solution without the link at the 1st floor (PSW1) leads to a beneficial effect. It is observed that, for β = 1, the 1st link removal is not beneficial; however, the difference between the solution with all the links or without the first link is not remarkable and it also reduces by increasing the storey number. In contrast, such difference increases (with an asymptotic trend) for β = 2. An asymptotic trend of η_fr,el is noted when the storey number increases: for β = 1 the maximum value is 1.5 in both solutions (i.e. with and without the 1st link removal), while for β = 2 the maximum and minimum value of η_fr,el are 1.13 and 0.75, with and without the 1st link removal, respectively.

Fig. 5

η_fr,el for frames up to 10 storeys (χ ≥ 0.5) for different values of β: filled symbols represent the solution with links at each floor level while empty symbols the case of no link at the 1st floor level

4 Capacity of the retrofitted system in the case of 1st link removal

4.1 Analytical model: background

According to the shear type hypothesis, the storey shear capacity $\overline{\mathrm{V} }$ is obtained from assuming the development of plastic hinges at each column ends, considering an elastic-perfectly-plastic behaviour. Moreover, in the as-is condition, the existing frame maximum capacity is considered to be achieved upon reaching the maximum shear capacity in the 1st storey. Considering the aforementioned assumption, the shear capacity at each frame level is known. The column capacity varies in relation to the axial load applied and the actual capacity of the columns decreases along the height of the frame (assuming the same geometrical and mechanical properties for all the columns in the structure). The linearly distributed lumped loads F_i represents the seismic action at each storey i (Eq. 13 and Fig. 6), where δ_F is the increase of the applied external seismic load at each floor level until the system maximum capacity is reached, considering the linear deflected shape imposed by the PS wall introduction.

$$F_{i} = (\alpha H + \delta_{F} )i$$

(13)

Fig. 6

Capacity of the retrofitted system without the link at the 1st floor level. Note: $V_{2}^{*}$ is equal to $\overline{V} _{2}$ when the capacity of the 2nd storey is achieved first and V₂ otherwise; $V_{1}^{*}$ is equal to $\overline{V} _{1}$ when the capacity of the 1st storey is achieved first and V₁ otherwise (adapted from Casprini et al. 2022)

4.2 Solution in the case of 1st link removal

The analytical problem is governed by the system in Eq. (14), where the first three equations represent the equilibrium of forces at each floor level (i.e., accounting for both the shear below and above the considered floor and the load transferred to the wall) and the last equation represents the equilibrium of moment with respect to the wall base. In detail, the first one is referred to the top storey nth, the second one to the intermediate storeys from the 3rd to the (n − 1)th, and the third one to the 1st or 2nd storey, depending on which shear capacity is first achieved (Fig. 6). Therefore, n + 1 equations and n + 1 unknowns are defined, being n the number of storeys. The unknowns are the loads N_i transferred in the connecting links and δ_F.

In this case, two different solutions are possible, depending on which storey shear capacity is first achieved. The forces in the connecting link N_i are calculated as in Eq. 15 and the storey shear in the storey which does not reach its capacity as in Eqs. 16–19. The PS wall base shear (V_PSW) and the frame base shear (V_FR,R) are defined in Eqs. 17 and 18, respectively. The term ΔV_d describing the contribution of additional devices is also explicated in Eq. 19. The complete step-by-step solution is reported in “Appendix 2”.

$$\left\{ {\begin{array}{*{20}l} {N_{n} + n(\alpha H + \delta_{F} ) = \overline{V}_{n} } \hfill & {j = n} \hfill \\ {N_{j} + j(\alpha H + \delta_{F} ) + \overline{V}_{j + 1} = \overline{V}_{j} } \hfill & {j = 3:n - 1} \hfill \\ {\left\{ {\begin{array}{*{20}l} {(N_{2} + 2(\alpha H + \delta_{F} ) + \overline{V}_{3} = \overline{V}_{2} )} \hfill & {{\text{if }}\overline{{V_{2} }} {\text{ achieved first}}} \hfill \\ {or} \hfill & {} \hfill \\ {(N_{2} + 3(\alpha H + \delta_{F} ) + \overline{V}_{3} = \overline{V}_{1} )} \hfill & {{\text{if }}\overline{{V_{1} }} {\text{ achieved first}}} \hfill \\ \end{array} } \right.} \hfill & {} \hfill \\ {\sum\limits_{i = 2}^{n} {N_{i} iH + \overline{M} = 0} } \hfill & {} \hfill \\ \end{array} } \right.$$

(14)

$$\begin{array}{*{20}l} {{\mathbf{if}}\;\overline{V}_{2} \;{\mathbf{achieved}}\; \, {\mathbf{first}}} \hfill & {{\mathbf{if}}\;\overline{V}_{1} \;{\mathbf{achieved}} \, \;{\mathbf{first}}} \hfill \\ {\left\{ {\begin{array}{*{20}l} {(\alpha H + \delta_{F} ) = 6\frac{{\sum\nolimits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}}} \hfill \\ {N_{n} = \overline{V}_{n} - n(\alpha H + \delta_{F} )} \hfill \\ \begin{gathered} N_{i} = \overline{V}_{i} - \overline{V}_{i + 1} - i(\alpha H + \delta_{F} ) \, \hfill \\ {\text{for }}i = 2:n - 1 \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.} \hfill & {\left\{ {\begin{array}{*{20}l} {(\alpha H + \delta_{F} ) = 6\frac{{\sum\nolimits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}}} \hfill \\ {N_{n} = \overline{V}_{n} - n(\alpha H + \delta_{F} )} \hfill \\ \begin{gathered} N_{i} = \overline{V}_{i} - \overline{V}_{i + 1} - i(\alpha H + \delta_{F} ) \hfill \\ {\text{for }}i = 3:n - 1 \hfill \\ \end{gathered} \hfill \\ {N_{2} = \overline{V}_{1} - \overline{V}_{3} - 3(\alpha H + \delta_{F} )} \hfill \\ \end{array} } \right.} \hfill \\ \end{array}$$

(15)

$$V_{1} = (\alpha H + \delta_{F} ) + \overline{V}_{2} \quad\quad\quad\quad V_{2} = \overline{V}_{1} - (\alpha H + \delta_{F} )$$

(16)

$$V_{PSW} = (\alpha H + \delta_{F} )\frac{{(n^{2} + n - 2)}}{2} - \overline{V}_{2} \quad\quad\quad\quad V_{PSW} = (\alpha H + \delta_{F} )\frac{{(n^{2} + n)}}{2} - \overline{V}_{1}$$

(17)

$$V_{FR,R} = (\alpha H + \delta_{F} ) + \overline{V}_{2} \quad \quad\quad\quad V_{FR,R} = \overline{V}_{1}$$

(18)

$$\Delta V_{d} = \frac{{\overline{M} }}{H}\frac{{3(n^{2} + n - 2)}}{{2n^{3} + 3n^{2} + n - 6}}\quad\quad\quad\quad \Delta V_{d} = \frac{{\overline{M} }}{H}\frac{{3(n^{2} + n)}}{{2n^{3} + 3n^{2} + n + 6}}$$

(19)

The total base shear in the retrofitted system V_b,T is the sum of V_PSW and V_FR,R (Eq. 20); therefore, according to the proposed formulation, the maximum capacity of the retrofitted system is not dependent on the storeys lateral stiffness but only on the number of storeys and their shear capacity (in case of unlimited ductility); for this reason, once the geometry, the layout and the structural details of the existing building are known, such maximum capacity can be easily estimated.

$$V_{b,T} = (\alpha H + \delta_{F} )\frac{{(n^{2} + n)}}{2}$$

(20)

An efficacy factor η_sys,c aimed at investigating the potential benefit of the retrofitted system in terms of maximum achievable strength (herein named as “capacity factor”) is defined also in the non-linear range by comparing, in this case, the total capacity of the system (in terms of base shear) before and after the retrofit. Since in the as-is condition the seismic capacity of the frame is herein assumed as the capacity of the 1st storey (${\overline{V} }_{1}$), the capacity factor is calculated as η_sys,c = V_b,T /${\overline{V} }_{1}$. The authors showed that, in the case of links at each floor level and assuming a constant shear capacity for all the storeys, η_sys,c depends only on the number of storeys (Casprini et al. 2022). This holds also when the 1st link is removed (see Eqs. 20 and 15). However, in real structures, a different capacity at each storey is usually found. Assuming that the ith storey shear capacity ${\overline{V} }_{i}$ decreases with the height, a parameter λ_i = ${\overline{V} }_{i}$/${\overline{V} }_{i-1}$ is defined. If the same value of λ (i.e. λ_i = λ) is considered for all the storeys (for instance equal to the mean value of all λ_i) the capacity factor η_sys,c depends solely on the number of storeys and on λ. Figure 7 shows the application of the analytical formulation for n-storey frames (n ranging from 2 to 10). For λ < 1, a detrimental effect is observed: if λ = 0.9 or λ = 0.8 (i.e., the storey shear capacity is equal to 90% or 80% of the capacity of the lower storey, respectively) the PS wall introduction, both with and without the 1st link, becomes detrimental for a frame with a number of storeys greater than 8 and 4, respectively.

Fig. 7

Capacity factor η_sys,c in a n-storey frame with different storey capacity distribution: constant capacity (λ = 1), capacity equal to 90% of the lower storey (λ = 0.9) and 80% of the lower storey (λ = 0.8); links at each floor (empty symbol), removal of the first link (filled symbol)

The results obtained from the removal of the link at the 1st floor are represented in Fig. 7, with filled symbols (empty symbols represent the solution with all the connecting links), by evaluating case-by-case in which storey the capacity was first reached, among the 1st and the 2nd storey. The graph shows that such solution does not provide an increase in the total capacity with respect to the case of links at all floors, neither significant difference is observed between the two solutions. Some differences between the considered link configurations could be appreciated only for low-rise frames, although, in general, the maximum achievable global capacity tends to the same value. It is worth noting that, for some configurations of the analysed frames (i.e. λ < 0.9) the PS wall solution is not suitable to perform an effective retrofit. Moreover, the real beneficial effect of the solution without the 1st link may be obtained in terms of global ductility of the retrofitted system (see the following section), and such effect can be preliminarily evaluated through the frame base shear factor η_fr,el in the elastic phase (Sect. 3.4). In this regard, it is further highlighted the importance of the proposed analytical tool to estimate the load distribution in the elastic range, in order to understand whether the maximum reachable capacity may be impaired, due to higher forces (associated with plastic hinges activation) induced at the lower storeys leading to possible premature collapse of the structural elements.

4.3 Non-shear type conditions: corrective factors

The simplified model can be adapted to non-shear type conditions also in the non-linear range, by defining corrective factors through sensitivity analyses. The authors showed that, in the non-linear range, the storey nodal ratio (NR) plays a relevant role in determining the structural behaviour (Casprini et al. 2019). Being NR calculated for each story as the mean value of the ratios of the sum of the bending moment capacity of the beams over the sum of the bending moment capacity of the columns converging in each node, it represents an estimation of the difference from the assumption of strong beams-weak columns frame type. Table 2 reports the corrective factors for the bending moment in the PS wall (ratio between the numerically computed and estimated maximum bending moment) at the system maximum capacity for λ = 1 and λ = 0.9. A linear interpolation is suggested to account for intermediate values of n, λ, and NR.

Table 2 Corrective factor for maximum bending moment prediction for the case without the 1st link (PSW_1)

5 Application and FE validation of the proposed procedure

The analytical method proposed in this paper (set of equations and corrective factors in Sect. 3–4) allows evaluating the suitability of a PS wall retrofit solution and defining preliminary criteria of the intervention, such as the connecting link configuration, the wall dimension and the expected maximum bending moment. A procedure to assess the PS wall efficacy is addressed in the following, applied to a reference case study, and validated through nonlinear numerical analyses (MidasGen 2020).

The procedure to assess the PS wall efficacy (see flow-chart in Figs. 8, 9) is:

• Calculation of the parameter λ to evaluate the capacity factor η_sys,c = V_b,T /${\overline{V} }_{1}$, which indicates the maximum achievable increase in the system base shear capacity (not considering at this stage the ductility demand on the existing structural elements) with respect to the as-is condition due to PS wall introduction. For λ < 0.8 and λ < 0.9 η_sys,c may be lower than 1 for 4-storey frames and 8-storey frames, respectively, thus the PS wall intervention is not suitable.

• Calculation of the parameter β to evaluate the frame base shear factor η_fr,el = V_FR,0/V_FR,R, which indicates the reduction of the base shear undertaken by the frame in the elastic phase. If β >1.5,  η_fr,el is lower than 1 in a PS wall solution with links at each floor, while η_fr,el is greater than 1 for the solution without the link at the 1st floor. Therefore, the evaluation of β allows selecting the retrofit system configuration.

• Definition of the PS wall cross-section to linearize the frame deformation along its height by setting the lateral stiffness ratio between the PS wall and the frame (χ) between 0.3 and 0.5 (Casprini et al. 2022).

• Calculation of corrective factors for non-shear type conditions to estimate both the load distribution in the elastic range and the capacity increase in the inelastic range (also accounting for the possible contribution of additional devices); herein, such evaluation allows validating the set of equations proposed through comparison with non-linear numerical analyses.

• Evaluation of the maximum bending moment demand in the PS wall for preliminary proportioning and detailing.

• Assessment of the actual deformation capacity and demand through nonlinear analysis (e.g., Pushover analysis) and evaluation of the possible introduction of additional devices.

Fig. 8

Schematic representation of the proposed analytical procedure to estimate the PS wall efficacy and preliminary assessment of the PS wall geometry and detailing

Fig. 9

PS wall preliminary design flowchart. Note: Equations and Tables marked with (*) are referred to the solution with all the connecting links described in Casprini et al. (2022)

A typical strong beams-weak columns existing RC frame is considered herein (frame B from Casprini et al. 2019). The frame features 5-storeys and 5-bays, with an inter-storey height (H) equal to 3 m and a bay length of 4.5 m, for a total dimension of 22.5 m × 15 m. Table 3 reports the relevant details for the structural elements. A concrete modulus of elasticity equal to E_c = 31,476 MPa (C25/30 according to EN1992, 2004) is adopted; the flexural elastic stiffness of beams and columns is reduced to 50% and 70%, respectively, to account for concrete cracking. The frame elements and the wall were modelled with beam-type elements; the PS wall was modelled as elastic (E_w = 36,283 MPa, corresponding to C45/55 in EN1992 2004), while the frame non-linear behaviour was accounted for through a lumped plasticity approach. Flexural plastic hinges for columns and beams were defined based on EN1998 (2004): the moment-rotation diagram of the plastic hinges presents an elastic branch up to the yielding moment, a perfectly plastic behaviour, and a drop (at the chord ultimate rotation) to a constant residual moment equal to 20% of the yielding strength. The columns bending moment capacity was calculated considering the axial load due to gravity loading. For the frame’s elements, a concrete cylindrical strength of 30 MPa and a steel yielding stress of 450 MPa were considered in the analyses. A permanent structural (4 kN/m²), non-structural (2 kN/m²), and live (2 kN/m²) load, acting on an influence area of 2.5 m, were assumed. A linear load of 6 kN/m was also included to account for perimetral infills (for a total permanent and live load g = 21 kN/m and q = 5 kN/m distributed on the beams, respectively). In the FE model, an axial stiffness of 6,300,000 kN/m is assigned to the connecting links, associated with the axial stiffness of 3 steel plates (30 × 30 × 1cm), similar to the connection proposed by Steele and Wiebe (2020).

Table 3 Elements cross-section details

The parameters λ and β can be calculated from the geometrical and mechanical characteristics of the frame. In this model, the capacity of each storey is computed assuming the development of plastic hinges at each column end (M_COL), accounting for the axial load due to gravity loading and considering the column’s nominal capacity. Table 4 reports the shear capacity of each storey and the capacity ratio between consecutive storeys (${\lambda }_{i}=\overline{\mathrm{V} }$_i/$\overline{\mathrm{V} }$_i−1). A reference mean value of $\lambda =0.9$ can be assumed. Considering this value and n = 5, the PS wall solution can be adopted and a maximum increase in the global system capacity in terms of base shear equal to about 10% can be ideally obtained (considering unlimited ductility at plastic hinges) with both the all-links condition and without the 1st one (by neglecting the possible additional contribution of $\overline{\mathrm{M} }$), as shown in Fig. 7.

Table 4 Storey shear capacity assessment

The coefficient β describes the stiffness increase at the 1st floor and it is taken equal to 1.67 (Casprini et al. 2022). Being β > 1.5, the solution with links at each floor may result in a detrimental effect on the structural behaviour, while the solution without the 1st connecting link corresponds to a frame base shear factor η_fr,el in the range 1.1 ÷ 1.3 (see the plot in Fig. 6). Therefore, the latter configuration of the retrofit solution is selected.

The dimensions of the PS wall required to linearize the frame deformation are obtained from the procedure reported in Casprini et al. (2022) resulting in a wall-length and thickness equal to L_w = 2.75 m and t_w = 0.40 m, respectively.

The load distribution in the frame and in the PS wall in the elastic range is obtained analytically by following the set of equations proposed in Sect. 3; in this case, the difference from an ideal shear type behaviour is expressed through the ratio K_s/K_S.T = 0.5. The corrective factor related to the maximum bending moment in the PS wall is calculated from Table 1 and assumed equal to 1.20 (1.28 for the solution with all the connecting links, from Casprini et al. 2022). To show the improvement of the system behaviour achieved through the 1st link removal when β > 1.5, the maximum bending moment in the PS wall in the elastic phase is reported in Fig. 10 for both solutions. A value of αH associated with the first yielding equal to 16.1 kN (external load equal to 241.8 kN) and 15.7 kN (external load equal to 235.7 kN) was taken, respectively. The estimated analytical distribution is then corrected (“Analytical-adj”) by multiplying its values by the corrective factor 1.20.

Fig. 10

PS wall bending moment (M) distribution in the elastic range: a PSW_0 and b PSW_1 in the case of β = 1.67

The results of the analytical estimation are then compared with the numerical results obtained from a linear static analysis (MidasGen, 2020). Figure 10 shows a good prediction of the results. The evaluation in the elastic range highlights a possible detrimental effect in the case of links at each floor level. Indeed, the bending moment diagram configuration (Fig. 10a) shows that the PS wall introduction leads to an additional action in the frame at the 1st storey, with respect to the as-is condition. Higher forces are therefore expected to develop in the lower storeys in the case of β $\ge$ 1.5, which may lead to larger displacement and rotation demands, requiring more ductility capacity in the existing elements. If the available ductility does not allow for the development of a full-plastic mechanism, the actual capacity of the retrofitted system will result lower than that predicted by the analytical equations in the nonlinear range, which stems as an upper bound reference value for both link configurations. The nonlinear static (pushover) curves related to the reference frame (Fig. 11a) and the plastic hinges status results in both configurations (Fig. 11c–d) show that an improvement of the global behaviour is obtained from removing the 1st connecting link when a detrimental behaviour is expected in the traditional all-links solution. The 1st link removal allows reducing the constraint corresponding with the 1st storey, and therefore stabilizing the retrofitted system response. Figure 11b–d emphasizes the effect of the PS wall introduction on the distribution of plastic hinges in the frame by comparing the hinge status at the same displacement demand (d = 18 cm, which corresponds to the existing frame failure in the as-is condition) for the three configurations: as-is, PSW_0 and PSW_1. The moment-rotation behaviour at the plastic hinges (see the legend in Fig. 11b) is linear elastic up to B, constant with a maximum capacity between B-C, constant with a residual value equal to 20% of the maximum capacity between D-E. In the as-is condition (Fig. 11b), a soft-storey mechanism at the first level is observed at collapse, while the ductility demand spreads along the system after the PS wall introduction (Fig. 11c–d) for the same displacement demand. However, while a premature failure of beams close to the 1st connecting links is observed in the all-links PSW_0 solution (Fig. 11c), this phenomenon is avoided by removing the 1st link. After the PS wall introduction, the ductility demand and capacity of all the existing structural elements should be verified.

Fig. 11

a Capacity curves for the considered frame in the as-is condition and after introducing a PS wall with χ = 0.5; comparison of the plastic hinge status corresponding with a roof displacement d = 18 cm (red dashed line) for the: b–d as-is condition, PSW_0 and PSW_1 configuration

It is worth noting that the suitability of the solution without the 1st connecting link could be easily evaluated by simply calculating the parameters λ and β. The results shown in Figs. 11 and 12 have been used for validation purposes and to show the variation in ductility demand which cannot be predicted by the proposed analytical method. Once the best retrofit solution (in this case PSW_1) has been selected among the two configurations, the capacity factor η_sys,c can be calculated to evaluate the maximum achievable capacity increase. According to Eq. 20, the total base shear in the retrofitted system estimated by the analytical procedure is V_b,T = 435 kN (in this case the capacity at the 2nd storey is first reached), while the capacity in the as-is condition is assumed as 392 kN (which is the capacity of the 1st storey from Table 4). Therefore, the capacity factor η_sys,c is equal to 1.109 and 1.112 in the analytical and numerical evaluation, respectively.

Fig. 12

Pushover curves in the as-is condition, after the PS wall introduction in the case of 1st link removal (PSW_1) and with the additional devices (PSW_1_$\overline{\mathrm{M} }$). Note: Y (V_b,T = 236 kN); M (V_b,T = 315 kN); C (V_b,T = 364 kN)

In the case of additional devices (as a proof of the concept $\overline{M }$=400kNm), η_sys,c obtained from a pushover analysis is equal to 1.232 (1.204 by following the analytical estimate), as reported in Fig. 12. At the system capacity, the maximum bending moment in the PS wall is estimated by following the analytical procedure and then reduced by the corrective factor (Fig. 13b); by considering a mean nodal ratio of 0.87 (Casprini et al. 2019) and λ equal to 0.9, the corrective factor to account for non-shear type conditions in the nonlinear range is calculated from Table 2 as 0.84.

Fig. 13

a PS wall maximum bending moment recorded in the pushover analysis (Step M in Fig. 12) compared with the moment distribution obtained through the analytical procedure defined for the elastic phase; b bending moment distribution at the system capacity (Step C in Fig. 12) and comparison with the proposed upper-bound estimation (analytical procedure defined for the nonlinear phase)

It is observed that a higher value of the bending moment in the PS wall is recorded in the numerical analyses (step M) between the first yielding (step Y) and the attainment of the maximum capacity (step C, see Fig. 12) associated with the load distribution variation in the connecting links between step Y and C.

The proposed analytical model may also be used to provide such an upper-bound estimate of the maximum bending moment in the PS wall between the elastic phase and the achievement of the system capacity. This can be provided by the elastic load distribution (analytical procedure in Sect. 3) due to an external load associated with the estimated system capacity (i.e. by considering a collapse mechanism according with the strong beam—weak column concept and the corrective factor reported in Table 2). The results are summarized in Fig. 13a.

6 Conclusions

The pin-supported (PS) walls as a rehabilitation technology for existing RC structures has gained interest in the last decades and some applications can be found worldwide. A PS wall can linearize the lateral seismic deflected shape of the frame along its height, thus avoiding high deformation demand lumped at one storey. However, the results presented in this paper show that, in some cases, the efficacy of a such a retrofit system may be jeopardized, due to the geometrical and mechanical characteristics of the existing structure. The main parameters governing the system response were identified, and an analytical procedure to preliminarily assess the suitability of the retrofit system have been proposed. Starting from the number of storeys n and an estimation of the storey shear capacity ratio λ (ratio between upper and lower storey shear capacity), the capacity factor η_sys,c is calculated: η_sys,c < 1 indicates that the total base shear in the system after the PS wall introduction is lower than the frame capacity before the retrofit, thus resulting in a detrimental behaviour; η_sys,c > 1 corresponds to a beneficial effect and its value indicates the maximum achievable strength increase with respect to the as-is condition before assessing the actual rotation demand at plastic hinges.

If η_sys,c > 1, the ratio between the 1st storey lateral stiffness and the mean upper storeys lateral stiffness β is a critical parameter to be considered. It allows calculating the frame base shear factor η_fr,el which indicates the reduction of the base shear undertaken by the frame in the elastic phase due to the PS wall introduction. It is shown that, for β > 1.5, the solution with all connecting links is always detrimental, leading to a larger ductility demand on the existing elements in the elastic phase, which may anticipate the development of a plastic mechanism. In these cases, a PS wall solution in which the link to the 1st floor is removed should be considered. A closed-form solution for the internal action distribution is derived in the paper for such retrofit configuration, by considering equilibrium equations and enforcing the system deformation compatibility, both in the elastic range and after reaching the storey shear capacity.

The method is based on some simplified assumptions such as 2D planar models, shear type behaviour, frame vertical regularity, and unlimited ductility capacity at plastic hinges. Corrective factors obtained through sensitivity analyses have been also provided to adapt the results in the case of non-shear-type conditions. At this stage, the actual ductility demand on the existing elements may be assessed through, for instance, nonlinear static analyses after preliminarily assessing the general beneficial effects of a PS wall introduction in terms of base shear capacity.

In this regard further developments of the research are aimed at treating this aspect analytically and including it in the model. Ongoing research is also focused on addressing performance issues related to the 3D case and to the structural details of the connections. Anyway, the proposed procedure may be effectively used as a preliminary design tool to define the PS wall demand and the capacity of the retrofitted system, also in the case of the provision of additional dissipative devices.

Appendices

Appendix 1: Forces distribution in the elastic range without the link at the 1st floor level

Referring to Fig. 2, the analytical solution of the problem is identified by the following system:

$$\left\{ {\begin{array}{*{20}l} {\overline{{\Delta_{j + 1} }} = \overline{{\Delta_{j} }} } \hfill & {{\text{for }}j = 3:n - 1} \hfill \\ {\overline{{\Delta_{1} }} + \overline{{\Delta_{2} }} = 2\overline{{\Delta_{3} }} } \hfill & {} \hfill \\ {\sum\limits_{i = 2}^{n} {N_{i} iH + \overline{M} } } \hfill & {} \hfill \\ \end{array} } \right.$$

(21)

Condition of equal displacement between consecutive floors (j, j + 1) with j varying from 3 and n − 1:

$$\overline{{\Delta_{j + 1} }} = \overline{{\Delta_{j} }}\; {\longrightarrow} \;\frac{{\sum\nolimits_{i = j + 1}^{n} {(i\alpha H + N_{i} } )}}{{K_{s} }} = \frac{{\sum\limits_{i = j + 1}^{n} {(i\alpha H + N_{i} )} }}{{K_{s} }} + \frac{{j\alpha H + N_{j} }}{{K_{s} }}$$

(22)

$$\frac{{j\alpha H + N_{j} }}{{K_{s} }} = 0 \; {\longrightarrow} \;\quad N_{j} = - j\alpha H\;{\text{for}}\;j = 3:n - 1$$

(23)

In this case N₂ and N_n need to be determined, because no action is transferred at the first floor. The condition of equal displacements of the third storey and the mean displacement of the first two, along with the equilibrium of forces with respect to the rotation at the base of the PS wall are considered.

$$\left\{ {\begin{array}{*{20}l} {\overline{{\Delta_{1} }} + \overline{{\Delta_{2} }} = 2\overline{{\Delta_{3} }} } \hfill \\ {\sum\limits_{i = 2}^{n} {N_{i} iH + \overline{M} } = 0} \hfill \\ \end{array} } \right.\; {\longrightarrow} \;\left\{ {\begin{array}{*{20}l} {\frac{{\sum\nolimits_{i = 1}^{n} {(i\alpha H + \sum\nolimits_{i = 2}^{n} {N_{i} )} } }}{{\beta K_{s} }} + \frac{{\sum\nolimits_{i = 2}^{n} {(i\alpha H + N_{i} )} }}{{K_{s} }} = 2\frac{{\sum\nolimits_{i = 3}^{n} {(i\alpha H + N_{i} )} }}{{K_{s} }}} \hfill \\ {N_{2} 2H - \alpha H^{2} \sum\limits_{i = 3}^{n - 1} {i^{2} + N_{n} nH + \overline{M} = 0} } \hfill \\ \end{array} } \right.$$

(24)

From the first equation of the system in Eq. (24):

$$2\frac{{n\alpha H + N_{n} }}{{K_{s} }} = \frac{{2\alpha H + N_{2} + n\alpha H + N_{n} }}{{K_{s} }} + \frac{{\alpha H + 2\alpha H + n\alpha H + N_{2} + N_{n} }}{{\beta K_{s} }}$$

(25)

$$2\beta (n\alpha H + N_{n} ) = \beta (2\alpha H + N_{2} + n\alpha H + N_{n} ) + (\alpha H + 2\alpha H + N_{2} + n\alpha H + N_{n} )$$

$$N_{n} (2\beta - \beta - 1) + N_{2} ( - \beta - 1) = - 2\beta n\alpha H + 2\beta \alpha H + \beta n\alpha H + 3\alpha H + n\alpha H$$

$$N_{n} (\beta - 1) - N_{2} (\beta + 1) = - \beta n\alpha H + 2\beta \alpha H + 3\alpha H + n\alpha H$$

$$N_{n} (\beta - 1) - N_{2} (\beta + 1) = \alpha H\left[ {n(1 - \beta ) + (2\beta + 3)} \right]$$

(26)

By considering (28), the second equation of the system (24) becomes (29):

$$\sum\limits_{i = 3}^{n - 1} {i^{2} = \frac{n(n - 1)(2n - 1)}{6} - 1 - 4}$$

(28)

$$N_{2} 2H + N_{n} nH + \overline{M} = \alpha H^{2} \left[ {\frac{n(n - 1)(2n - 1)}{6} - 5} \right]$$

(29)

$$N_{2} 2 + N_{n} n + \frac{{\overline{M} }}{H} = \alpha H\left[ {\frac{n(n - 1)(2n - 1)}{6} - 5} \right]$$

$$N_{2} = \frac{\alpha H}{2}\left[ {\frac{{2n^{3} - 3n^{2} + n - 30}}{6}} \right] - \frac{{N_{n} n}}{2} - \frac{{\overline{M} }}{2H}$$

(30)

By substituting in the previous equation:

$$\alpha H\left[ {n(\beta - 1) - (2\beta + 3)} \right] = - N_{n} (\beta - 1) + (\beta + 1)\left( {\frac{\alpha H}{2}\frac{{2n^{3} - 3n^{2} + n - 30}}{6} - \frac{{N_{n} n}}{2} - \frac{{\overline{M} }}{2H}} \right)$$

(31)

$$\begin{aligned} & \alpha H\left[ {n(\beta - 1) - (2\beta + 3)} \right] - (\beta + 1)\left( {\frac{\alpha H}{2}\frac{{2n^{3} - 3n^{2} + n - 30}}{6}} \right) + (\beta + 1)\frac{{\overline{M} }}{2H} \\ & = - N_{n} (\beta - 1) - \frac{{nN_{n} }}{2}(\beta + 1) \\ \end{aligned}$$

$$\begin{aligned} & \frac{\alpha H}{{12}}\left[ {12n\beta - 12n - 24\beta - 36 - \beta (2n^{3} - 3n^{2} + n - 30) - (2n^{3} - 3n^{2} + n - 30)} \right] \\ & + (\beta + 1)\frac{{\overline{M} }}{2H} = - \frac{{N_{n} }}{2}(n\beta + n + 2\beta - 2) \\ \end{aligned}$$

$$\begin{aligned} & \frac{\alpha H}{6}\left[ {(\beta + 1)( - 2n^{3} + 3n^{2} ) + n(11\beta - 13) + 6(\beta - 1)} \right] + (\beta + 1)\frac{{\overline{M} }}{2H} \\ & = - N_{n} \left[ {n(\beta + 1) + 2(\beta - 1)} \right] \\ \end{aligned}$$

$$N_{n} = \frac{\alpha H}{6}\frac{{\left[ {(\beta + 1)(2n^{3} - 3n^{2} ) - n(11\beta - 13) - 6(\beta - 1)} \right] - \frac{{6\overline{M} }}{{\alpha H^{2} }}(\beta + 1)}}{n(\beta + 1) + 2(\beta - 1)}$$

(32)

By substituting the value of N_n in the expression of N₂, the latter is obtained:

$$\begin{gathered} N_{2} = \frac{\alpha H}{{12}}(2n^{3} - 3n^{2} + n - 30) + \hfill \\ - \frac{\alpha Hn}{{12}}\frac{{\left[ {(\beta + 1)(2n^{3} - 3n^{2} ) - n(11\beta - 13) - 6(\beta - 1)} \right] - \frac{{6\overline{M} }}{{\alpha H^{2} }}(\beta + 1)}}{n(\beta + 1) + 2(\beta - 1)} - \frac{{\overline{M} }}{2H} \hfill \\ \end{gathered}$$

(33)

$$N_{2} = \frac{\alpha H}{6}\frac{{(2n^{3} + 3n^{2} )(\beta - 1) - n(11\beta + 19) - 30(\beta - 1) + \frac{{6\overline{M} }}{{\alpha H^{2} }}(\beta - 1)}}{n(\beta + 1) + 2(\beta - 1)}$$

(34)

The equation of the base shear both for the PS wall and for the frame is provided:

$$V_{PSW} = - \sum\limits_{i = 2}^{n} {N_{i} = - } N_{2} - N_{n} + \alpha H\sum\limits_{i = 3}^{n - 1} i$$

(35)

$$N_{2} + N_{n} = \frac{\alpha H}{6}\frac{{4\beta n^{3} - 6n^{2} - 6n - 22\beta n - 36\beta + 36 - \frac{{12\overline{M} }}{{\alpha H^{2} }}}}{n(\beta + 1) + 2(\beta - 1)}$$

$$V_{PSW} = - \frac{\alpha H}{6}\frac{{4\beta n^{3} - 6n^{2} - 6n - 22\beta n - 36\beta + 36 - \frac{{12\overline{M} }}{{\alpha H^{2} }}}}{n(\beta + 1) + 2(\beta - 1)} + \alpha H\frac{{n^{2} - n - 6}}{2}$$

$$V_{PSW} = \frac{\alpha H}{6}\frac{{n^{3} (3 - \beta ) + 3n^{2} (\beta - 1) - 2n(\beta + 3) + \frac{{12\overline{M} }}{{\alpha H^{2} }}}}{n(\beta + 1) + 2(\beta - 1)}$$

(35)

The frame base shear can be obtained as the difference between the total seismic forces and the shear at the PS wall base:

$$V_{FR,R} = \alpha H\sum\limits_{i = 1}^{n} i - V_{HW}$$

(36)

$$V_{FR,R} = \alpha H\frac{{n^{2} + n}}{2} - V_{HW}$$

$$V_{FR,R} = \frac{\alpha H}{6}\frac{{2n\beta (2n^{2} + 3n + 4) - \frac{{12\overline{M} }}{{\alpha H^{2} }}}}{n(\beta + 1) + 2(\beta - 1)}$$

(37)

Appendix 2: Forces distribution at system capacity without the link at the 1st floor level

Referring to Fig. 6, the analytical solution of the problem is identified by the system (38). In this case, the general expression for N_i is valid for i = 3:n − 1. For how concern the force N₂, the equation is different in relation to the storey capacity that is first achieved among the first two floors. Once the system is solved (39), the shear force in the storey which did not reach the ultimate capacity can be simply calculated trough equilibrium consideration (40).

$$\left\{ {\begin{array}{*{20}l} {N_{n} + n(\alpha H + \delta_{F} ) = \overline{V}_{n} } \hfill & {j = n} \hfill \\ {N_{j} + j(\alpha H + \delta_{F} ) + \overline{V}_{j + 1} = \overline{V}_{j} } \hfill & {j = 3:n - 1} \hfill \\ {\left\{ {\begin{array}{*{20}l} {(N_{2} + 2(\alpha H + \delta_{F} ) + \overline{V}_{3} = \overline{V}_{2} )} \hfill & {{\text{if }}\overline{{V_{2} }} {\text{ achieved first}}} \hfill \\ {or} \hfill & {} \hfill \\ {(N_{2} + 3(\alpha H + \delta_{F} ) + \overline{V}_{3} = \overline{V}_{1} )} \hfill & {{\text{if }}\overline{{V_{1} }} {\text{ achieved first}}} \hfill \\ \end{array} } \right.} \hfill & {} \hfill \\ {\sum\limits_{i = 2}^{n} {N_{i} iH + \overline{M} = 0} } \hfill & {} \hfill \\ \end{array} } \right.$$

(38)

Solution of the system
$\overline{{{\varvec{V}} }_{2}}$ achieved first	$\overline{{{\varvec{V}} }_{1}}$achieved first
$\begin{aligned} & \sum\limits_{{i = 2}}^{{n - 1}} {N_{i} i} + N_{n} n + \frac{{\overline{M} }}{H} = 0 \\ & \sum\limits_{{i = 2}}^{{n - 1}} {\left[ {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) - i^{2} (\alpha H + \delta _{F} )} \right]} + \frac{{\overline{M} }}{H} \\ & = - n\left[ {\overline{V} _{n} - n(\alpha H + \delta _{F} )} \right] \\ & \sum\limits_{{i = 2}}^{{n - 1}} {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) - (\alpha H + \delta _{F} )\sum\limits_{{i = 2}}^{{n - 1}} {i^{2} } } + \frac{{\overline{M} }}{H} \\ & = - n\overline{V} _{n} + n^{2} (\alpha H + \delta _{F} ) \\ & \sum\limits_{{i = 2}}^{{n - 1}} {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) + n\overline{V} _{n} + \frac{{\overline{M} }}{H} = (\alpha H + \delta _{F} )\sum\limits_{{i = 2}}^{n} {i^{2} } } \\ \end{aligned}$	$\begin{aligned} & \sum\limits_{{i = 3}}^{{n - 1}} {N_{i} i} + N_{n} n + 2N_{2} + \frac{{\overline{M} }}{H} = 0 \\ & \sum\limits_{{i = 3}}^{{n - 1}} {\left[ {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) - i^{2} (\alpha H + \delta _{F} )} \right]} + \frac{{\overline{M} }}{H} \\ = - n\left[ {\overline{V} _{n} - n(\alpha H + \delta _{F} )} \right] - 2\overline{V} _{1} + 2\overline{V} _{3} + 6(\alpha H + \delta _{F} ) \\ & \sum\limits_{{i = 3}}^{{n - 1}} {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) - (\alpha H + \delta _{F} )\sum\limits_{{i = 3}}^{{n - 1}} {i^{2} } } + \frac{{\overline{M} }}{H} \\ = - n\overline{V} _{n} + n^{2} (\alpha H + \delta _{F} ) + 6(\alpha H + \delta _{F} ) - 2\overline{V} _{1} + 2\overline{V} _{3} \\ & \sum\limits_{{i = 3}}^{{n - 1}} {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) + n\overline{V} _{n} + 2\overline{V} _{1} - 2\overline{V} _{3} + \frac{{\overline{M} }}{H}} \\ & = (\alpha H + \delta _{F} )(\sum\limits_{{i = 3}}^{n} {i^{2} } + 6) \\ \end{aligned}$
$\sum\limits_{{i = 2}}^{{n - 1}} {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) = } \sum\limits_{{i = 3}}^{n} {\overline{V} _{i} - n\overline{V} _{n} } + 2\overline{V} _{2}$	$\sum\limits_{{i = 3}}^{{n - 1}} {i(\overline{V} _{i} - \overline{V} _{{i + 1}} ) = } \sum\limits_{{i = 4}}^{n} {\overline{V} _{i} - n\overline{V} _{n} } + 3\overline{V} _{3}$
$\sum\limits_{{i = 2}}^{n} {i^{2} = \frac{{n(n + 1)(2n + 1)}}{6}} - 1$
$\begin{aligned} & \sum\limits_{{i = 3}}^{n} {i^{2} + 6 = \frac{{n(n + 1)(2n + 1)}}{6}} + 6 - 1 - 4 \\ & = \frac{{n(n + 1)(2n + 1)}}{6} + 1 \\ \end{aligned}$
$\left\{ {\begin{array}{*{20}l} {(\alpha H + \delta _{F} ) = 6\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}}} \hfill \\ {N_{n} = \overline{V} _{n} - 6n\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}}} \hfill \\ \begin{gathered} N_{i} = \overline{V} _{i} - \overline{V} _{{i + 1}} - 6i\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}}{\text{ }} \hfill \\ {\text{for }}i = 2:n - 1 \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.$	$\left\{ {\begin{array}{*{20}l} {(\alpha H + \delta _{F} ) = 6\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}}} \hfill \\ {N_{n} = \overline{V} _{n} - 6n\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}}} \hfill \\ \begin{gathered} N_{i} = \overline{V} _{i} - \overline{V} _{{i + 1}} - 6i\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}} \hfill \\ {\text{for }}i = 3:n - 1 \hfill \\ \end{gathered} \hfill \\ {N_{2} = \overline{V} _{1} - \overline{V} _{3} - 18\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}}} \hfill \\ \end{array} } \right.$	(39)
$V_{1} = 6\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}} + \overline{V} _{2}$	$V_{2} = \overline{V} _{1} - 6\frac{{\sum\nolimits_{{i = 3}}^{n} {\overline{V} _{i} } + 2\overline{V} _{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}}$	(40)

The equation of the base shear both for the PS wall and for the frame is provided; the equation of αH + δ_F is here defined as γ. In case of first achievement of $\overline{{V }_{1}}$, the expression is valid for n > 3.

$\overline{{{\varvec{V}} }_{2}}$ achieved first	$\overline{{{\varvec{V}} }_{1}}$achieved first
$V_{PSW} = - \sum\limits_{i = 2}^{n} {N_{i} = - } N_{n} - \sum\limits_{i = 2}^{n - 1} {N_{i} }$	$V_{PSW} = - \sum\limits_{i = 2}^{n} {N_{i} = - } N_{n} - \sum\limits_{i = 3}^{n - 1} {N_{i} } - N_{2}$	(41)
$\begin{aligned} V_{PSW} & = - \left[ {\overline{V}_{n} - n\gamma + \sum\limits_{i = 2}^{n - 1} {(\overline{V}_{i} - \overline{V}_{i + 1} ) - } \gamma \sum\limits_{i = 2}^{n - 1} i } \right] \\ V_{PSW} & = \gamma \left[ {n + (\frac{{n^{2} + n}}{2} - n - 1)} \right] - \overline{V}_{2} \\ V_{PSW} & = \gamma \left[ {\frac{{n^{2} + n - 2}}{2}} \right] - \overline{V}_{2} \\ \end{aligned}$	$\begin{aligned} V_{PSW} & = - \left[ {\overline{V}_{n} - n\gamma + \sum\limits_{i = 3}^{n - 1} {(\overline{V}_{i} - \overline{V}_{i + 1} ) - } \gamma \sum\limits_{i = 3}^{n - 1} i + \overline{V}_{1} - \overline{V}_{3} - 3\gamma } \right] \\ V_{PSW} & = \gamma \left[ {n + (\frac{{n^{2} + n}}{2} - n - 1 - 2) + 3} \right] - \overline{V}_{1} \\ V_{PSW} & = \gamma \left[ {\frac{{n^{2} + n}}{2}} \right] - \overline{V}_{1} \\ \end{aligned}$
$\begin{aligned} \gamma & = 6\frac{{\sum\limits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}} \\ V_{PSW} & = 6\frac{{\sum\limits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}}\left[ {\frac{{n^{2} + n - 2}}{2}} \right] - \overline{V}_{2} \\ V_{PSW} & = 3\frac{{\sum\limits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}}(n^{2} + n - 2) - \overline{V}_{2} \\ \end{aligned}$	$\begin{aligned} \gamma & = 6\frac{{\sum\limits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}} \\ V_{PSW} & = 6\frac{{\sum\limits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}}\left[ {\frac{{n^{2} + n}}{2}} \right] - \overline{V}_{1} \\ V_{PSW} & = 3\frac{{\sum\limits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{1} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n + 6}}(n^{2} + n) - \overline{V}_{1} \\ \end{aligned}$	(42)
$\begin{aligned} V_{FR,R} & = (\alpha H + \delta_{F} )\sum\limits_{i = 1}^{n} i - V_{HW} \\ V_{FR,R} & = \gamma \frac{n(n + 1)}{2} - \gamma \left[ {\frac{{n^{2} + n - 2}}{2}} \right] + \overline{V}_{2} \\ V_{FR,R} & = \gamma + \overline{V}_{2} \\ V_{FR,R} & = 6\frac{{\sum\limits_{i = 3}^{n} {\overline{V}_{i} } + 2\overline{V}_{2} + \frac{{\overline{M} }}{H}}}{{2n^{3} + 3n^{2} + n - 6}} + \overline{V}_{2} \\ \end{aligned}$	$\begin{aligned} V_{FR,R} & = (\alpha H + \delta_{F} )\sum\limits_{i = 1}^{n} i - V_{HW} \\ V_{FR,R} & = \gamma \frac{n(n + 1)}{2} - \gamma \left[ {\frac{{n^{2} + n}}{2}} \right] + \overline{V}_{1} \\ V_{FR,R} & = \overline{V}_{1} \\ \end{aligned}$	(43)
$\Delta V_{d} = \frac{{\overline{M} }}{H}\frac{{3(n^{2} + n - 2)}}{{2n^{3} + 3n^{2} + n - 6}}$	$\Delta V_{d} = \frac{{\overline{M} }}{H}\frac{{3(n^{2} + n)}}{{2n^{3} + 3n^{2} + n + 6}}$	(42)
$V_{b,T} = (\alpha H + \delta_{F} )\frac{{(n^{2} + n)}}{2}$		(44)