Yield displacement charts for performance-based seismic design

Abstract

A new tool for seismic design is presented, called Yield Displacement Charts (YDC). As with its predecessors, the Yield Point Spectra (YPS) and the Yield Frequency Spectra (YFS), the YDC concept takes advantage of the simple features of yield displacement (u_y), to use u_y in a performance-based design instead of a force-based period-dependent approach. A self-contained and comprehensive approach to YPS and YFS is presented, enabling the novel aspect of YDC to be introduced: a tool for a multi-performance objective design that only depends on the location of the structure to be designed. Once the yield displacement chart has been calculated for a particular place, it can be used for the preliminary design of any structure. For a given value of yield displacement, the YFS are obtained from the Yield Displacement Chart. The suitability of the methodology proposed is illustrated by means of a simple case study of a concrete bridge pier.

1 Introduction

The seismic design process always needs to start with a preliminary design (Aschheim et al. 2019; Palermo et al. 2016). The accuracy of the preliminary design is of paramount importance, since if the final design is similar to the preliminary one, numerous redesign cycles can be avoided. The stiffness of a structure (or equivalently, its natural period) is related to its seismic demand. As structural displacements caused by earthquakes primarily follow the shape of the first mode of vibration, preliminary seismic designs are generally based on the response of single-degree-of-freedom systems (Aschheim et al. 2019). These are characterized by their natural period in the elastic range. Approximate expressions of the natural period of the most common structures are available in the literature and in professional codes. Starting an iteration process between seismic demand and natural period up to convergence (Chopra and Goel 2001) only requires an initial estimation of the value of the natural period.

For design purposes, the natural period can be used in force-based design (e.g. EN1998-1 2004) or in performance-based design (Deierlein 2004). The fundamentals of performance-based design, outlined in the Vision 2000 report (SEAOC 1995), are now widely accepted.

In addition to the natural period, yield displacement (u_y) has proven to be an stable and useful parameter for performance-based design, (Priestley 2000; Aschheim 2002). In this article, yield displacement is used as a primary structural parameter to obtain a first value of the seismic demand of a structure. The objective of this article is to determine the seismic demand for various performance objectives. This will be carried out using Yield Displacement Charts (YDC). The great advantage of YDC is that they only depend on the location of a structure.

The first section of the article is dedicated to describing, in a mathematically compact and simple way, the response of a single degree-of-freedom system in the linear elastic domain and in the plastic domain. The second section presents the seismic hazard curve (peak ground acceleration -PGA- versus probability of occurrence), particularized for Granada –Spain-. For preliminary design, the intensity of ground motion is expressed in terms of the PGA, although it implies conservatism. PGA can be substituted by period-dependent (e.g. the spectral acceleration, S_a(T), (Luco and Bazzurro 2007)) or non-period-dependent describers (e.g. peak ground velocity (Palermo et al. 2014)).

Several spectral representations of the seismic demand of single degree-of-freedom (SDOF) systems are available in the literature, (Chopra 2020). The most common representation is pseudo-acceleration versus the period of the SDOF system. However, yield point spectra (YPS) uses yield displacement (u_y) as an alternative to the period (T) (Mark Aschheim and Black 2000). The great advantage of yield displacement is that, for a given structural configuration, it is a more stable parameter than the elastic period, which is a useful property in preliminary designs. The properties of yield displacement are explained in the third section of this paper.

In the fourth section, the YDC are created. YDC are represented in a reference system whose axes are yield displacement, ductility demand and mean annual frequency. Given its suitability for design purposes, yield displacement has been used instead of the elastic period (Aschheim et al. 2019). Moreover, although it has not been adequately substantiated, the elastic period has not been used with in the article to emphasize the fact that the elastic period loses part of its physical meaning in the plastic range.

Performance-based seismic designs that consider several performance objectives corresponding to different seismic hazard levels are now more commonly used, and they are recommended in (SEAOC 1999 and FIB 2012). In this context, Yield Frequency Spectra (YFS) (Vamvatsikos and Aschheim 2016) are considered to be efficient tools for dealing with this type of analysis. YFS are graphical representations that link the mean annual frequency/rate (MAF) of ductility threshold being exceeded (i.e. a performance objective) to the system yield strength coefficient (C_y). YFS are plotted for a given yield displacement (u_y), and they enable the system demand for different performance objectives to be visualized. The fifth section deduces the YFS from the theoretical framework of conditional probability, and YDC are presented. Like the YFS, the YDC are graphical representations of the system demand for given performance objectives, but unlike YFS, YDC are obtained by considering yield displacement as a variable, so the result is a performance-based seismic design tool that only depends on the geographical location of the structure.

YDC can be considered as the latest member of the family of Yield Displacement Based Design Spectra: Yield Point Spectra (YPS), Yield Frequency Spectra (YFS), and Yield Displacement Charts (YDC). YPS are used for deterministic analysis while YFS and YDC are meant for probabilistic approaches. Given that u_y is a new variable in the definition of YDC, a spectrum that only depends on the location of a structure is obtained. This factor could make them the most attractive member of the family. Finally, in the fifth section the yield displacement chart for the City of Granada is calculated, and a simple example of structural design is developed.

2 The response of the single degree-of-freedom system

The time-history displacement response, u(t), of a linear-elastic SDOF system, for a fixed value of damping, subjected to a given ground motion, $\ddot{u}$ _g(t), is characterized by only one variable, which is usually the elastic period T. From this period, ω = 2π/T and k = ω²m can be computed, with k as the initial stiffness, m the mass and ω the natural circular frequency of the system (see Fig. 1). The maximum displacement of a linear-elastic SDOF for a given ground motion is called elastic spectral displacement S_d = max[u(t)], for which the SDOF develops an elastic force F_e = k S_d. Typically, this elastic force is presented in the literature as being divided by mass m, and, in this case, it is called spectral pseudo-acceleration: S_a = F_e/m. By using the simple relationships above, it can be demonstrated that S_a = ω²S_d. Since T characterizes the SDOF response for a given ground motion, all the variables defined above can be expressed as functions of T, i.e.: S_a(T), S_d(T) and F_e(T). For example, the (pseudo-acceleration) response spectrum of a ground motion can be represented by S_a(T) versus T, as shown in Fig. 2

Fig. 1

Characterization of the linear elastic SDOF and its response

Fig. 2

Pseudo-acceleration response spectra for the Corralitos record of the Loma Prieta Earthquake in October 17, 1989, for 5% damping

.

In structural engineering design, seismic action is not unique (note that Fig. 2 corresponds to a specific seismic accelerogram, $\ddot{u}$ _g(t)). Thus, a probabilistic treatment of seismic action is required. Simple envelope approximations of uniform-hazard response spectra derived from probabilistic seismic hazard analysis (PSHA, Cornell 1968) are used in professional standards (i.e. ASCE7 2022, EN1998-1) for structural design purposes: the design spectra. For a SDOF system of period T and mass m, the design spectrum gives the maximum elastic force that can be developed by the SDOF system, S_a(T)m, for a certain probability of occurrence, e.g. 10% in 50 years.

Likewise, a non-linear SDOF system modeled as elasto-plastic can be characterized by only two variables, usually C_y and u_y, with u_y being the yield displacement and C_y being the yield strength coefficient, defined as C_y = F_y/mg where F_y is the yield strength (see Fig. 3). Note the apparent absence of the elastic period in this characterization, which is defined via C_y and u_y as

$$T=2\pi \sqrt{\frac{{u}_{y}}{{C}_{y}g}}$$

(1)

If for a given ground motion, the maximum displacement of this non-linear system, is u_max so that if u_max > u_y, then the maximum displacement is within the plastic range. It is important to note that once the system is on the yield plateau, the main recovery factor of the system in terms of displacement is the cyclical nature of the seismic action itself, whereby the system alternates between unloading/reloading at elastic stiffness (or near-elastic for non-kinematic-hardening hysteresis rules), and it sustains further damage along the yield plateau. In other words, the importance of a period as a performance-prediction variable is limited when the system enters the post-yield range. The reader should be aware that the authors are looking for a simple preliminary design tool, not a complete and comprehensive description of the response.

Fig. 3

Characterization of the elasto-plastic SDOF and its response

In the time-history analysis, ductility (μ) is defined as u_max/u_y (i.e., ductility demand). Given that demand D should not exceed capacity C (i.e. D < C), it is necessary to ensure that the ductility demanded by the earthquake is lower than the ductility capacity of the structure. In other words, when designing for a certain level of ductility, the designer needs to ensure that the structure is going to allow reliable plastic behavior in the areas of (pre-designated) structural detailing where plasticity is going to occur (i.e., ductility capacity). For the sake of mathematical completeness, values of μ that are lower than 1 are going to be considered (even if they are not proper ductility) in order to also include the cases where u_max is lower than u_y in the study, which refers to the cases where displacement demand does not exceed the yield displacement of the structure. Even though the SDOF can be characterized by one or two variables, depending on whether it is linear or elasto-plastic, the (maximum or worst-case) response of the system can be described by only one variable: the maximum displacement, S_d or u_max. The inelastic displacement ratio C₁ is defined to relate S_d(T) and u_max, so that u_max = C₁S_d(T), FEMA 440 (FEMA 2005).

A simple way to describe the intensity of a ground motion is S_d, because it shows, as no other parameter does, the effect of a specific ground motion on an elastic SDOF of period T. Note that, as previously mentioned, S_a = ω²S_d, lending the same properties of S_d to S_a. As previously discussed, the strength of this relationship is weakened when it enters the non-linear range. This is quantified by the use of inelastic displacement ratios C₁(C_y, Τ), also known as R-μ-T strength ratio/ductility/period relationships (where R is essentially C_y, see Fig. 3), (Veletsos and Newmark 1960; Miranda and Bertero 1994; Ruiz-García and Miranda 2003). Since the connection is no longer deterministic, these relationships convey the statistics of inelastic displacement u_max for systems of a given C_y and T, typically offering the mean estimate, $\overline{{u }_{\mathrm{max}}}$, for use in tandem with the static pushover (FEMA 2005; EN1998-32005):

$$\overline{{u }_{\mathrm{max}}}={C}_{1m}\left({C}_{y},T\right){S}_{d}(T)$$

(2)

where C_1m is the mean inelastic displacement ratio function for a given C_y and T.

The predictive ability of S_d and S_a, as intensity measures (IMs) within the framework of Performance-Based Earthquake Engineering (Cornell and Krawinkler 2000), can be characterized by implementing the associated dispersion of the distribution of C₁(C_y,Τ), as offered by (Vamvatsikos and Cornell 2006) or (Ruiz-García and Miranda 2007). This is known as IM efficiency (Luco and Cornell 2007), and the lower the dispersion, the higher the efficiency and associated predictive capability. The issue of IM sufficiency also arises (Nicolas Luco and Cornell 2007). This characterizes the capability of S_d and S_a to render the distribution of C₁(C_y,Τ), or, equivalently, of u_max conditioned on S_d or S_a, which are independent of other seismological characteristics.

Sufficiency is a particularly useful property, as it negates (or generally reduces) bias when assessing performance (see Sect. 4). S_a(T) is moderately efficient and sufficient, but clearly imperfect whenever large excursions into non-linearity or significantly higher-mode effects are involved (Luco and Bazzurro 2007). At the same time, S_a(T) is clearly better than peak ground acceleration PGA (Kazantzi and Vamvatsikos 2015) for everything but the shortest periods, in which both parameters are practically identical. Despite everything described above, in the YDC presented, the authors are going to use PGA as the intensity measure, emphasizing the fact that it is not period dependent, which makes it more versatile than S_a(T) even though it reduces efficiency and sufficiency. The authors believe this tradeoff is acceptable for practical design applications, where simplicity is important, and conservativeness can be added as needed to make up for the probabilistic deficiencies of PGA. Definitely, new IMs containing elastic and plastic structural properties should be investigated to improve sufficiency and efficiency.

3 Seismic hazard

The intensity of ground motion at a certain site can be measured by IMs that, among other parameters, can be represented, as mentioned, by peak ground acceleration PGA or pseudo-acceleration S_a(T). The level of ground motion intensity expected at a site is associated with a certain frequency/rate of occurrence, and this is calculated by using the total probability theorem, combining several probabilistic distributions, and conveying information about the seismic sources (faults), the site (e.g., soil type), and the source-to-site propagation (Baker 2013). This is known as probabilistic seismic hazard analysis (PSHA), and a representation of the intensity of ground motion, measured by the PGA versus its MAF is the seismic hazard curve λ(PGA).

In this study, YDC was built for the city of Granada (latitude 37.18°, longitude -3.60°) using the site-specific hazard curve, λ(PGA), using the seismic source model (Giardini et al. 2014) as estimated by (EFEHR 2021), considering a soil with an average shear wave speed in the upper 30 m of V_s30 = 250 m/s. The seismic hazard curve is approximated by using a continuous smooth interpolation curve (splines), as shown in Fig. 4.

Fig. 4

Seismic hazard curve (black dots) and the fitting model (red line). Granada (Spain), Vs₃₀ = 250 m/s

4 The use of yield displacement for seismic design

A preliminary design can be made based on the displacement response corresponding to the first mode of the structure, or to a combination of some of the modes, which is known as the equivalent single degree-of-freedom (ESDOF) system (Aschheim et al. 2019).

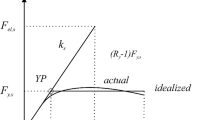
As an alternative, some displacement-based methods for seismic design (Mark Aschheim and Black 2000; Paulay 2002) use an estimation of yield displacement for establishing values of base shear strength. The main advantage of yield displacement, instead of the period, is that it is very stable when there are changes in the stiffness of a structure. This stability has been confirmed both at sectional and global system levels (Hernández-Montes and Aschheim 2003; Priestley et al. 2007; Hernández-Montes et al 2019). As an illustration of this feature, Fig. 5 shows the base shear resultant of two buildings subjected to a monotonic lateral force as a function of the roof displacement. The only difference between the two models in Fig. 5 is the amount of reinforcement. Figure 5 shows that the yield displacement (u_y) remains stable (gray bar in Fig. 5).

Fig. 5

Yield displacement of two models that differ only in component reinforcement quantity

So, the stability of yield displacement converts it into a key performance variable for the seismic design of structures (Aschheim and Montes 2003). Estimations of yield displacement for several structural systems and different cross-sections can be found in Chapter 9 of (Aschheim et al. 2019).

5 Yield displacement charts

The performance of a SDOF system under a seismic action, formulated in terms of conditional probability, can be described as the MAF (λ) by which the maximum displacement (u_max) exceeds a certain limit displacement (δ):

$$\lambda \left(\delta |{C}_{y}, {u}_{y}\right)=P\left[{u}_{\mathrm{max}}>\delta |{C}_{y}, {u}_{y}\right]={\int }_{0}^{\infty }P\left[{u}_{\mathrm{max}}>\delta |PGA, {C}_{y}, {u}_{y}\right]\left|\mathrm{d}\lambda (PGA)\right|$$

(3)

where λ(∙) denotes the MAF of its argument, P[u_max > δ|PGA,C_y,u_y] is the probability of u_max exceeding a threshold of δ conditioned by the yield strength coefficient (C_y), yield displacement (u_y), and on peak ground acceleration (PGA). The second term inside the integral is the differential of the PGA seismic hazard curve. Note that, by assuming the sufficiency of the IM (here PGA), any conditioning on seismological characteristics such as magnitude or distance has been dropped, at least in this term. This is a key assumption of the conditional approach (Bazzurro et al. 1998) that allows this standard treatment of Performance-Based Earthquake Engineering.

The integral above can be solved numerically as:

$$\lambda \left(\delta |{C}_{y}, {u}_{y}\right)=\sum_{j=1}^{N}P\left[{u}_{max}>\delta |{PGA}_{j}, {C}_{y}, {u}_{y}\right]\Delta \lambda ({PGA}_{j})$$

(4)

where Δλ (PGA_j) = λ (PGA_j) – λ (PGA_j+1), with PGA_j+1 > PGA_j.

Since the integral (or summation) is calculated over the IM, here, with the IM as PGA, the variable PGA disappears when the integral is completed. For a particular system, given by C_y and u_y, the above equation can be represented as a curve of λ–δ, see Fig. 6a. It can be observed that when displacement threshold values (δ) increase, the probability that u_max exceeds δ decreases, see Fig. 6a. Additionally, C_y can be considered to be a variable. Curves of a constant value of C_y can be plotted together as in Fig. 6b. It can be observed that as the value of C_y increases, the probability of exceedance decreases.

Fig. 6

Development of the yield frequency spectra

The limit displacement (δ) divided by u_y is the ductility threshold, μ (i.e. μ = δ/u_y). So, if the horizontal axis of Fig. 6b is changed from δ to μ (see Fig. 6c) the Yield Frequency Spectra (YFS) is obtained (Vamvatsikos and Aschheim 2016).

As shown in Fig. 6c, for an elasto-plastic SDOF system whose yield displacement (u_y) is known, the YFS relates the probability of the exceedance of a given displacement threshold at a certain place (where the seismic hazard and the soil characteristics are known). Therefore, YFS are created for a specific location and for a constant value of u_y.

As previously mentioned, the yield displacement, u_y, is very stable when there are stiffness changes, which makes YFS the perfect tool for starting a multi-objective design. A new design tool arises if u_y is considered as a variable: The Yield Displacement Charts, see Fig. 7. The variables of the YDC are yield displacement (u_y) and the ductility threshold (μ) from which the yield strength coefficients (C_y) are obtained. Yield Displacement Charts are functions created in an ad hoc manner for a specific location.

Fig. 7

Yield displacement charts

For a series of values of C_y and u_y within a feasible range, the resulting curves, λ-δ, provide charts that are only dependent on the location of the structure, i.e., the charts are independent of the characteristics of the system. In the next step of design, for the value of u_y corresponding to a particular structural system (Chapter 9 of (Aschheim et al. 2019)), a YFS is obtained from the yield displacement chart. By using the YFS, the base shear for different performance objectives can be obtained (Vamvatsikos and Aschheim 2016).

The values of u_y, approximations are available in the literature for different types of structures (Aschheim, Hernández-Montes and Vamvatsikos 2019). Furthermore, the maximum displacements permitted are given by codes, so once the yield displacement is known, these limitations can be expressed as ductility limitations. Consequently, YDC are represented in terms of ductility and yield displacement.

6 Implementation of yield displacement charts

For a large set of elastic-hardening bilinear SDOF systems defined by C_y and u_y (see Fig. 8), the maximum displacement values u_max are obtained by using a database of 980 earthquakes. For all the SDOFs, as in (Heresi et al. 2018), 5% damping and 3% of post-yield stiffness ratio (γ = 0.03, see Fig. 8) are considered. Additionally, a degraded elastic stiffness is used (k_u), defined as:

Fig. 8

Elastic-hardening bilinear model with stiffness degradation

$${k}_{u}=k{\left(\frac{{u}_{y}}{{u}_{max}}\right)}^{\alpha }$$

(5)

For reinforced concrete structures α ranges from 0.0 to 0.5. In this study α = 0.5 is used (Nielsen and Imbeault 1970).

All the ground motions used in this study have been obtained from (RESORCE 2020). No additional corrections were applied to the downloaded ground motion records. The filtering parameters applied in the process of record selection are as follows:

• Records with a moment magnitude (M_W) greater than 5 are selected (Aschheim, Hernández-Montes and Vamvatsikos 2019).

• Any source-to-site distance

• Both pulse-like and non-pulse-like motions

• Records with V_S30 between 180 and 360 m/s.

• Both of the horizontal component recordings available are considered.

As a sample, Fig. 9 shows, for the case of C_y = 0.3 and u_y = 0.025 m, the u_max obtained for the set of 980 ground motions considered (a dataset of 490 ground motions with two components each). A high dispersion is observed for PGA > 0.2 g, where high structural nonlinearity appears, which few records have. Specifically, there are 952 motions in 0 < PGA ≤ 0.2 g whereas there are only 28 motions in 0.2 g < PGA ≤ 0.9 g. Employing scaled ground motion would populate the higher range of response, but this would be at the expense of introducing issues of scaling bias. Therefore, unscaled motions have been chosen in this work.

Fig. 9

u_max versus PGA (left) and its power-law relationship in logarithmic space (right) for the database of 980 ground motions (C_y = 0.3, u_y = 0.025 m)

The results are treated using cloud analysis (Cornell et al. 2002). The u_max versus PGA data cloud are shown in Fig. 9 left, and they are connected by using linear regression in the logarithmic space: u_max = a·PGA^b, or by applying logarithms: Ln[u_max] = Ln[a] + b·Ln[PGA]. The constants are calculated for each particular system (i.e. C_y and u_y are given), see Fig. 9 on the right for the case that is shown here, for which Ln[a] =  − 2.12 and b = 0.92, with 0.6 as the standard deviation, σ.

The regression analysis provides the mean and the standard deviation for each value of PGA. In this sample, μ =  − 2.12 + 0.92·Ln[PGA] and σ = 0.6. Assuming that Ln[u_max] follows a normal distribution, then u_max follows a lognormal distribution, see Fig. 9 on the right. Note that the lognormal distribution characterizes variables with a tendency to produce frequent extremely high values, and it is often used in earthquake engineering, especially when modelling seismic demand.

The lognormal cumulative distribution function gives the probability of occurrence of a given displacement threshold, for example δ, for given values of PGA, C_y, and u_y: i.e. P[u_max ≤ δ | PGA, C_y, u_y]. Figure 10 shows the lognormal cumulative density function for the sample case (i.e., C_y = 0.3 and u_y = 0.025 m) and for six different values of PGA.

Fig. 10

Log Normal Cumulative Distribution Function (µ =  − 2.12 + 0.92·ln(PGA), σ = 0.6) for u_y = 0.025 m, C_y = 0.3, and different values of PGA

Finally, considering that P[u_max > δ | PGA_j,C_y,u_y] = 1 − P[u_max ≤ δ | PGA_j,C_y,u_y], the integrand of Eq. (3) is obtained.

The λ–δ curve (see Fig. 6a) is numerically obtained by applying Eq. (4). The seismic hazard curve λ(PGA) used in Eq. (4) is the one shown in Fig. 4 (i.e., for the case of Granada).

The displacements (u_max and δ) are divided by the yield displacement (u_y), which obtains the ductility demand and the ductility threshold (i.e., a threshold limit in terms of ductility, also called ductility capacity), respectively. Figure 11 shows curve λ–μ (i.e. the YFS) for the sample system (u_y = 0.025 m and C_y = 0.3) and the location in Granada.

Fig. 11

YFS for u_y = 0.025 m, C_y = 0.3, and the location in Granada

The above methodology is applied for different SDOF systems after the selection of values of C_y (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1) and u_y (0.01 m, 0.025 m, 0.05 m, 0.075 m, 0.1 m). The values of u_max versus the PGA that are obtained are represented in Fig. 12, and the Yield Displacement Chart for the city of Granada is originally shown in Fig. 13a. Three YFS corresponding to u_y = 0.01, 0.05 and 0.1 m are displayed in Figs. 13b, c and d to facilitate the interpretation of the Yield Displacement Chart.

Fig. 12

u_max versus PGA. a u_y = 0.01 m, b u_y = 0.025 m, c u_y = 0.05 m, d u_y = 0.075 m, e u_y = 0.1 m. C_y = (0.1:0.1:1)

Fig. 13

a Yield displacement chart for the city of Granada. b λ–μ section for u_y = 0.01 m. c λ–μ section for u_y = 0.05 m. c λ–μ section for u_y = 0.1 m

7 Example of the design approach

In order to illustrate a design case with multiple performance objectives based on YDC, a simple example has been developed following the flow chart shown in Fig. 14.

Fig. 14

Flowchart of the design approach

The example is a single-column pier of a highway bridge located in Granada (Spain), see Fig. 15. In accordance with (EN1998-1 2004), the design has to fulfill the following two performance objectives:

• 1. Life safety (LS) requirement, associated with a probability of exceedance of 10% in 50 years (return period of 475 years), i.e. λ_LS = −ln(1−0.1)/50 = 2.11×10⁻³ years⁻¹.

• 2. Damage limitation (DL) requirement, associated with a probability of exceedance of 10% in 10 years (return period of 95 years), i.e., λ_DL = 0.0105 years⁻¹.

Fig. 15

Bridge column and single-degree-of-freedom model

The effective yield curvature (ϕ_y) for circular column cross-sections is estimated (Hernández-Montes and Aschheim 2003) as:

$${\phi }_{y}=2.3 \frac{{\epsilon }_{y}}{d}$$

(6)

where ε_y is the yield strain of the reinforcing steel and d is the depth of the extreme tension reinforcing bar. The characteristic strength of B-400 steel is f_yk = 400 MPa, leading to ε_y = 400/E_s = 0.0020 (E_s = 200,000 MPa). The column has a circular cross-section with a diameter of 1.2 m. The cover chosen is 2.5 cm, thus d = 1.2 − 0.05 = 1.15 m. The above assumptions results in an effective yield curvature of ϕ_y = 0.00397 rad/m. If overstrength were considered, the value of ϕ_y would be increased (using pushover analysis or code recommendations).

The yield displacement (u_y) for a cantilever column subjected to a lateral load when shear deformation is neglected can be deduced by integrating the curvature along the length of the column twice with ϕ = ϕ_y for x = 0, see Fig. 16 and Eq. 7.

Fig. 16

Yield displacement of a cantilever beam

$${\phi (x)=\phi }_{y}\frac{L-x}{L}\to {u}_{y}=\int (\int \phi (x)dx)dx={\phi }_{y}{\left.\left(\frac{{x}^{2}}{2}-\frac{{x}^{3}}{6L}\right)\right|}_{0}^{L}={\phi }_{y}\frac{{L}^{2} }{3}=0.048\, m$$

(7)

The DL drift ratio, assumed to be of 2% (EN1998-1 2004), results in a displacement of 0.02∙6.00 m = 0.12 m, and the ductility associated with this displacement is µ = 0.12/0.048 = 2.5.

The target ductility for LS has been chosen following (Mander 1983). According to Figs. 7.10 and 7.11 of (Mander 1983), the ductility capacity goes from 3.0 to 10.0, depending on the confinement and the longitudinal steel ratio. A value of 5.0 has been adopted here for the preliminary design.

The YFS for u_y = 0.048 m (see Eq. 7) is calculated by the linear interpolation between u_y = 0.025 m and u_y = 0.05 m in the Yield Displacement Chart (Fig. 13). This YFS and the two performance objectives are represented in Fig. 17. Both performance objectives are expressed in terms of target MAF and ductility: a ductility of 2.5 associated with a MAF of 0.0105 years⁻¹ (which, from Fig. 17, leads to C_y = 0.51) and a ductility of 5.0 associated with a MAF of 2.11 × 10⁻³ years⁻¹ (for which C_y = 0.49). The highest value of C_y is the design value, which in this case is governed by the first performance objective.

Fig. 17

YFS for u_y = 0.048 m and the two performance objectives

So, as the pier is subjected to a dead load of 6500 kN (see Fig. 15), the column has to be designed for a lateral seismic load of 0.51·6500 kN = 3315 kN.

8 Conclusions

The Yield Displacement Chart tool has been introduced. YDC, as with Yield Point Spectra, are based on the fact that yield displacement remains constant with changes in stiffness, at both sectional and structural levels, thus using the yield displacement of a structure as the design parameter. YDC, like Yield Frequency Spectra, are based on the probability of exceedance of certain performance objectives of equivalent single degree-of-freedom systems. The novel aspect of YDC is that they consider yield displacement as a variable, so the result is a performance-based seismic design tool that only depends on the geographical location of a structure. YDC must be created in an ad hoc manner for a given site, which means that engineers can use the same Yield Displacement Chart for the same place. YDC are a unique tool for performance-based design.

PGA has been used as intensity measure in the presentation of this new tool (YDC), to emphazice that YDC use the yield displacement as preliminary design parameter, instead of the period. Other intensity measures may give more accurate results, as S_a(T). More research is needed, and conservativeness may be added, e.g. trying several different SDOFs, assessing their MAF via PGA and then via S_a(T), and introducing safety factors based on the obtained differences.