STAn: analysis of data traces using an event-driven interval temporal logic

Abstract

The increasing integration of systems into people’s daily routines, especially smartphones, requires ensuring correctness of their functionality and even some performance requirements. Sometimes, we can only observe the interaction of the system (e.g. the smartphone) with its environment at certain time points; that is, we only have access to the data traces produced due to this interaction. This paper presents the tool STAn, which performs runtime verification on data traces that combine timestamped discrete events and sampled real-valued magnitudes. STAn uses the Spin model checker as the underlying execution engine, and analyzes traces against properties described in the so-called event-driven interval temporal logic (eLTL) by transforming each eLTL formula into a network of concurrent automata, written in Promela, that monitors the trace. We present two different transformations for online and offline monitoring, respectively. Then, Spin explores the state space of the automata network and the trace to return a verdict about the corresponding property. We use the proposal to analyze data traces obtained during mobile application testing in different network scenarios.

1 Introduction

Nowadays, many electronic devices play an important role in our daily life, from in-home monitoring systems (Botia et al. 2012) or medical devices (Cameron et al. 2015), to smartphones that also allow interacting with other devices (Espada et al. 2019). Since we increasingly depend on these systems, it is important to check that they satisfy some correctness properties which, in many cases, imply fulfilling different non-functional requirements. In the domain of smartphones, an example of these properties could be “the energy consumed by the device during the download of a given application is always less than a threshold K”. The evaluation of this property involves handling the energy consumption of the device that is usually represented by a magnitude variable whose value evolves over time.

Fig. 1

Runtime verification of event-driven hybrid systems with STAn

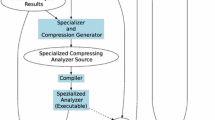
In this paper, we describe an approach to perform runtime verification of non-functional properties of event-driven systems that include magnitude variables and evolve by reacting to internally or externally triggered events. Figure  1 shows our proposal, which has been implemented in the tool STAn. The inputs of STAn are the non-functional properties described in the event-driven temporal logic (eLTL in short) (Gallardo and Panizo 2019), and the data trace under analysis, which is a sequence of observable system states that includes timestamps and sampled real-valued variables.

eLTL is a temporal logic that extends LTL to support the definition of properties with real-valued variables that must be evaluated on sub-traces delimited by events. Thus, intuitively, the eLTL formulae $\Box _{[p,q]} \phi$ and $\Diamond _{[p,q]} \phi$ indicate that the nested formula $\phi$ has to be true in all/some sub-traces of the input data trace satisfying that the first and the last sub-trace states satisfy p and q, respectively. These specifications allow an unknown number of sub-traces of the data trace (of an unknown duration) to be described. In addition, the nested formula $\phi$ can describe properties on the values of any system variable, such as energy consumed or time elapsed, inside the sub-traces provided by the corresponding operator.

Inspired by Pnueli and Zaks (2006), STAn transforms each eLTL operator into an instance of a monitor template; that is, an automaton that analyzes the input data trace. Thus, each eLTL formula is represented by a network of automata that monitors the data trace and determines whether it satisfies the property. This approach is suitable for runtime verification of event traces, but also for system model checking as proposed in Pnueli and Zaks (2006).

The current implementation of STAn is publicly available in GitLab¹ and relies on the Spin model checker (Holzmann 2003) to perform the analysis. To ease the transformation from eLTL to Promela, which is Spin’s modeling language, we provide a parser, called eltl2pml, that transforms a textual representation of a formula into the instantiation of the corresponding monitors.

Although an implementation based on a programming language could be more efficient, Spin and its modelling language Promela introduces several advantages. Firstly, it is possible to easily implement both automata and their composition by means of the Promela process type (proctype). Thus, each eLTL formula is implemented by the synchronized execution of instances of the corresponding proctypes of their nested operators. Second, Promela models can embed C code, which provides high flexibility for the implementation and further extensions. For instance, STAn currently uses C functions to obtain and store data traces, and also to externally monitor the magnitude variables. A similar approach was followed in Gallardo and Panizo (2014), where the embedded C code made it possible to work in a transparent manner with abstractions of the continuous variables for the exploration algorithm.

In Gallardo and Panizo (2019), we presented the eLTL logic and a first version of the implementation. In the current paper, we extend this work with the following contributions: (1) the tool STAn that includes a new offline and online monitoring approaches; (2) an intermediate tree-based implementation of the monitors that demonstrates the correct transformation of eLTL operators into monitors; (3) study of the temporal and space complexities of both implementations; (4) extended case study based on realistic traces.

The rest of the paper is organized as follows. Section 2 presents the syntax and semantics of eLTL. In Sect. 3, we introduce some features of Promela and Spin to facilitate the reading of Sect. 4, which first introduces an intermediate implementation of eLTL monitors and then presents the two approaches to transform eLTL operators into Promela monitor templates. To ease the reading of the paper, most of the Promela code of the online and offline implementations is included in Appendix A. Section 5 presents complexity results of the two monitoring approaches. The proofs of these results are detailed in Appendix B. Then, Sect. 6 presents a case study based on the analysis of non-functional properties of mobile apps in different network scenarios. Section 7 discusses related work on languages and algorithms to analyze data traces in different contexts. Finally, Sect. 8 presents the conclusions and future work.

2 Event-driven systems and the eLTL logic

In this section, we define the behavior of event-driven systems (EDSs) by means of the well-known and classic notion of labeled transition systems. We consider EDSs as black boxes whose states can be observed at some time instants. In particular, states are visible just after an external or internal event occurs or when a certain amount of time has passed. An EDS state contains two types of variables: the discrete variables, whose value only changes as the result of events, and the other of system variables, called magnitudes, whose value may evolve over time. Our aim is to monitor these magnitudes. For instance, assume we are measuring the gasoline consumption (variable $gas$) of a car, which changes depending on the engine $status$ and the car $speed$. The variable $status$ is discrete, since it can only change as the result of a user event to turn the engine on/off, while both $gas$ and $speed$ are magnitudes since their values may evolve over time and also as the result of some user events ($brake$, $speed \ up$ and so on).

Definition 1

(Event-driven systems (EDS)) An EDS is a tuple ${\mathcal H}= \langle \varSigma ,\xrightarrow {-},{E}\cup \{ tick \},s_0 \rangle$ where $\varSigma$ is a non-numerable set of system states. ${E}$ is a finite set of events, $tick$ being a special one used to denote the time passing, $\xrightarrow {-} \subseteq \varSigma \times {E}\cup \{ tick \} \times \varSigma$ is the transition relation, and $s_0 \in \varSigma$ is the initial state.

We now introduce some notation in order to define the semantics of the transition relation $\xrightarrow {-}$ of an EDS ${\mathcal H}$. First, we define the states of $\varSigma$ as tuples of variables as follows. We denote with $Var _d$ and $Var _m$ the ordered sets of the discrete and magnitude variables, respectively. We assume that discrete variables take values in set $Val _\bot$, where symbol $\bot$ represents the unknown value. In contrast, magnitude variables are real-valued, i.e., take values in ${\mathbb {R}}$. We assume that the first variable of $Var _d$ is ev, which registers the last fired event (or $\bot$ if no event has been fired). Similarly, the first variable of $Var _m$ is ts, which contains the timestamp where the corresponding state has been observed. Thus, if $Var _d = \{ev,d_1,\cdots ,d_k\}$ and $Var _m = \{ts,m_1\cdots ,m_n\}$, states $s \in \varSigma$ of ${\mathcal H}$ are 4-tuples of the form $s=\langle v_{ev},\bar{v}_d,v_{ts},\bar{v}_m \rangle$, where $v_{ev} \in Val _\bot$ and $v_{ts} \in {\mathbb {R}}^{\ge 0}$ are the values of ev and ts in state s, and $\bar{v}_d \in Val _\bot ^k$ and $\bar{v}_m \in {\mathbb {R}}^n$ are vectors with the values of the discrete variables and magnitudes in s.

Events of ${E}$ are abstract representations of both internal discrete actions, carried out by the system, and external actions, fired by the environment to change the system operating mode. In any case, events typically update some discrete variables of the system; however, it is also possible that events update some magnitude variables. Continuing with the car example, when the car’s engine is turned off (the discrete event), variable gas is set to zero or, inversely, when the engine is turned on, $gas$ is set to an initial positive value.

We define the intermediate transition relation ${\mathop {\leadsto }\limits ^{-}} \subseteq \varSigma \times {E}\times \varSigma$ that models how a state $\langle v_{ev},\bar{v}_d,v_{ts},\bar{v}_m \rangle$ changes when event $e \in {E}$ occurs:

$$\begin{aligned} \langle v_{ev},\bar{v}_d,v_{ts},\bar{v}_m \rangle {\mathop {\leadsto }\limits ^{e}} \langle e,\bar{v}_d',v_{ts},\bar{v}_m' \rangle \end{aligned}$$

The new state $\langle e,\bar{v}_d',v_{ts},\bar{v}_m' \rangle$ stores in variable ev that e has just happened. We rewrite discrete variables and magnitudes as $\bar{v}_d'$ and $\bar{v}_m'$ to indicate that their values may be modified by the transition. Observe that the value of variable ts does not change, since we are assuming that the transition is instantaneous.

Transition relation $\xrightarrow {-} \subseteq \varSigma \times {E}\cup \{ tick \} \times \varSigma$ models the system evolution by means of the two following rules:

Pure timed transitions

$$\begin{aligned} \frac{\delta >0}{\langle v_{ev},\bar{v}_d,v_{ts},\bar{v}_m \rangle \xrightarrow { tick } \langle \bot ,\bar{v}_d,v_{ts}+\delta ,\bar{v}_m' \rangle } \end{aligned}$$

EDSs may evolve when a pure timed transition occurs, i.e., when the only change in the system is produced by the passing of $\delta > 0$ time units. As commented above, we use the special label $tick$ to identify the timed transitions. Observe that the transition updates the value of variable ts properly. In addition, it rewrites the value of magnitudes as $\bar{v}_m'$ since their values could be changed by the transition. In contrast, transition does not change the value of the discrete variables except for ev that is updated to $\bot$ to indicate that no event has occurred.

Mixed transitions

$$\begin{aligned} \frac{s \xrightarrow { tick } s', s' {\mathop {\leadsto }\limits ^{e}} s'' }{s \xrightarrow {e} s''} \end{aligned}$$

Transitions labeled with an event express both time passing and event firing before the final time instant. In this case, the variable ev registers the event and the other state variables are properly updated. Some discrete and magnitude variables may be updated as the result of the event. We have decided not to deal with discrete transitions in isolation to model the fact that it is not possible to observe two consecutive discrete transitions at the same time instant. This also avoids the Zeno behavior that could occur when infinite discrete transitions take place between two time instants.

Following the car example, assume $Var _d = \{ev, status \}$ and $Var _m = \{ts, speed , gas \}$. If $\langle v_{ev},v_{status}, v_{ts},v_{ speed },v_{ gas } \rangle$ is the state with each variable $var \in Var _m \cup Var _d$ bound to value $v_{var}$, transition $\langle \bot , on, 10, 10, 0.2 \rangle \xrightarrow {tick} \langle \bot , on, 15, 0, 0.5 \rangle$ represents the evolution of speed and gas consumption after passing 5 time units. In this case, the car is reducing its speed from 10 to 0 Km/h but the gas consumption is increased from 0.2 to 0.5 l since the engine is on. Moreover, $\langle \bot , on, 15, 0, 0.5 \rangle \xrightarrow { turnOff } \langle turnOff , off , 20, 0, 0.0 \rangle$ represents that the engine has been turned off (event $turnOff$) at timestamp 20, which causes the change in the status variable but also a reset to 0 of the gas variable.

Given an EDS ${\mathcal H}$, we denote with $\mathcal {O}_ f ({\mathcal H})$ the set of traces of finite length of the form $\pi = s_0 \xrightarrow {e_0} \cdots \xrightarrow {e_{n-2}}s_{n-1}$ with $n>0$ determined by ${\mathcal H}$ produced applying pure timed or mixed transitions. The length of a trace $\pi$ is the number n of states.

2.1 Syntax and semantics of eLTL

In this section, we first describe the syntax of eLTL and then, given ${\mathcal H}= \langle \varSigma ,\xrightarrow {-},{E}\cup \{ tick \},s_0 \rangle$, we present the eLTL semantics on the traces of $\mathcal {O}_ f ({\mathcal H})$.

We assume that events of ${E}$ constitute the state formulae to be checked on states. Recall that given a transition $s \xrightarrow {l} s'$, state $s'$ stores in variable ev the event $l=e \in {E}$ that occurred in the transition, or $\bot$, if no event took place, i. e., $l = tick$. Thus, it is possible to know whether an event has happened by observing a state. We define relation $\vdash \subseteq \varSigma \times {E}$ that associates states and events as follows. Given $s \in \varSigma$, and $e \in {E}$, $s \vdash e$ iff variable ev of state s is equals to e, i.e. if event e has just occurred.

Given a trace $\pi = s_0 \xrightarrow {l_0} \cdots \xrightarrow {l_{n-2}} s_{n-1}$ of length n, and $0\le j<k<n$, $\pi [j,k]$ denotes the sub-trace $s_j \xrightarrow {l_j} \cdots \xrightarrow {l_{k-1}} s_k$ of $\pi$. To simplify the notation, in the following we denote with $ts_j$ the value of variable ts in state $s_j$. Recall that since time evolves in both the pure timed and mixed transitions, we have that $ts_j < ts_k$.

Our proposal is inspired by the duration calculus introduced in Chaochen and Hansen (2004), where the interval logic domain is the set of time intervals ${\mathbb {I}}$ defined as $\{[t_1,t_2] | t_1, t_2 \in {\mathbb {R}}^{\ge 0}, t_1 \le t_2\}$.

To analyze the evolution of magnitude variables (and also discrete variables, if necessary) on intervals, we use the so-called interval formulae as defined below.

Definition 2

An interval formula is a function of the type $\phi : {\mathbb {I}} \rightarrow \{ true , false \}$ that associates each time interval with a truth value.

Let $\varPhi$ be the set of all these interval formulae. We assume that $\varPhi$ contains the special interval formula $True : {\mathbb {I}} \rightarrow \{ true , false \}$ that returns $true$ for all time intervals; that is, $\forall I \in {\mathbb {I}}. True (I) = true$. The elements of $\varPhi$ will be the atomic propositions on which the $\textsf {eLTL}$ logic is constructed.

For instance, consider the real-valued magnitude speed in the car example introduced above. Interval formula $\phi ([t_i,t_ f ]) = speed(t_i) > speed(t_ f )$ can be used to determine whether the speed at the interval end points is decreasing.

The following two definitions are used to determine the time intervals at which the interval formulae should be evaluated. To do this, we use the so-called interval of events of the form [p, q] where $p,q \in {E}$. The idea is that, given a data trace $\pi$, each interval of events [p, q] may determine different sub-traces of $\pi$ and, consequently, different time intervals. Event p fixes the initial timestamp of the interval, and q the final one.

Definition 3

Given a trace $\pi =s_0 \xrightarrow {l_0} \cdots \xrightarrow {l_{n-2}} s_{n-1} \in \mathcal {O}_ f ({\mathcal H})$, two events $p,q \in {E}$ and two states $s_j, s_k$ of $\pi$ such that $j < k$, we say that sub-trace $\pi [j,k]$ satisfies the interval of events [p, q], and we denote it as $\pi [j,k] \Vdash [p,q]$, iff the following four conditions hold: 1) $s_j \vdash p$; 2) $\forall r. j<r<k, s_r \not \vdash q$; 3) $s_k \vdash q$; and 4) if p and q are different events, there is no state $s_h$ with $h < j$, such that $s_h \vdash p$ and $\forall r. h<r\le j. s_r \not \vdash q$.

Intuitively, given $\pi$, $\pi [j,k] \Vdash [p,q]$ holds iff states $s_j$ and $s_k$ occur in different timestamps, $s_j$ satisfies p and $s_k$ is the first state following $s_j$ that satisfies q. In addition, when the events are different, the fourth condition ensures that sub-trace $\pi [j,k]$ is maximal in the sense that it is not possible to find a larger sub-trace ending at $s_k$ satisfying the previous conditions. This notion of maximality guarantees that the evaluation of interval formulae starts at the state when event p first occurs.

Example 1

The following trace $\pi$ tries to clarify Definition 3. Let us first assume that $p,q \in {E}$ are different. Then we have that $\pi [j,k] \Vdash [p,q]$, but $\pi [j',k]\not \Vdash [p,q]$ and $\pi [j',k'] \not \Vdash [p,q]$, since condition (4) does not hold. In addition, $\pi [j,k']\not \Vdash [p,q]$, since condition (2) does not hold.

Now assume that $p,q \in {E}$ are the same event. Then, following Definition 3, we have that $\pi [j,r] \Vdash [p,p]$ and $\pi [r,k] \Vdash [p,p]$. Note that, in this case, condition (4) does not apply.

The following trace $\pi$ has more than one sub-trace satisfying the interval of events [p, q].

The fourth condition in Definition 3 guarantees that the logic manages maximal intervals wrt the first occurrence of event p that makes it easy to represent properties in some application domains. For example, if we are interested in analyzing some property of a network during a video streaming session, the current definition determines that the session is given by the first occurrence of events that initiate and end the video stream, independently of whether the user tries to start the session several times until the video is observed.

Remark 1

It is worth noting that relation $\Vdash$ of Definition 3 could have been differently defined to produce other types of sub-traces. For instance, we could modify condition (2) of Definition to consider the last state where event q occurs (before p appears again) instead of the first one. This would lead us to extract sub-trace $\pi [j,k']$ instead of $\pi [j,k]$ in the first trace of the previous example. In the same line, relation $\Vdash$ could have been defined less restrictively to take into account all sub-traces determined by p and q, including the nested and overlapped ones. In this case, for the same trace of Example 1 just mentioned, we would obtain that $\pi [j,k] \Vdash [p,q], \pi [j,k']\Vdash [p,q], \pi [j',k]\Vdash [p,q]$ and $\pi [j',k']\Vdash [p,q]$.

The next definition is used to simplify the semantics of eLTL given in Definition 6.

Definition 4

Given a trace $\pi =s_0 \xrightarrow {l_0}\cdots \xrightarrow {l_{n-2}}s_{n-1} \in \mathcal {O}_ f ({\mathcal H})$, two state formulae $p,q \in {E}$, we denote with $\mathcal {S}(\pi ,[p,q])$ the ordered set of sub-traces $\{\pi [j,k] |\pi [j,k] \Vdash [p,q]\}$. Similarly, we use $\mathcal {S}(\pi ,p)$ to denote the ordered set of states $\{s_j | s_j \vdash p\}$.

That is, $\mathcal {S}(\pi ,[p,q])$ is the set of sub-traces of $\pi$ satisfying Definition 3. The set $\mathcal {S}(\pi ,[p,q])$ can contain several sub-traces as illustrated in trace (3) of Example 1. In addition, $\mathcal {S}(\pi ,[p,q])$ is ordered with respect to the value of the starting timestamp of each sub-trace. Similarly, $\mathcal {S}(\pi ,p)$ is ordered with respect to the timestamps of their states. Considering this, and given a Boolean condition $\mathcal {C}$, we write $fst (\mathcal {S}(\pi ,[p,q]),\mathcal {C})$ for the first sub-trace in $\mathcal {S}(\pi ,[p,q])$ that satisfies $\mathcal {C}$, if it exists. Otherwise, we define $fst (\mathcal {S}(\pi ,[p,q]),\mathcal {C})$ as the empty trace $\epsilon$. Similarly, we write $fst (\mathcal {S}(\pi , p),\mathcal {C})$ for the first state in $\mathcal {S}(\pi , p)$ that satisfies $\mathcal {C}$ ($fst (\mathcal {S}(\pi , p),\mathcal {C}) = \epsilon$, if no state of $\mathcal {S}(\pi , p)$ satisfies p).

Definition 5

($\textsf {eLTL}$ formulae) Given $p,q \in {E}$, and $\phi \in \varPhi$, the formulae of $\textsf {eLTL}$ logic are recursively constructed as follows:

$$\begin{aligned} \psi {:}{:}= \phi \mid \lnot {\psi } \mid \psi _1 \vee \psi _2 \mid \psi _1\mathcal {U}_{[p,q]}\psi _2 \mid \psi _1\mathcal {U}_{p}\psi _2 \end{aligned}$$

The other temporal operators are defined accordingly as:

$\Diamond _{[p,q]} \psi \equiv True \ \mathcal {U}_{[p,q]} \psi$, $\Box _{[p,q]}\psi \equiv \lnot ( \Diamond _{[p,q]} \lnot \psi )$,

$\Diamond _{p} \psi \equiv True \ \mathcal {U}_{p} \psi$, $\Box _{p}\psi \equiv \lnot ( \Diamond _{p} \lnot \psi )$

The following definition provides the semantics of $\textsf {eLTL}$ formulae given above. Recall that given a trace $\pi \in \mathcal {O}_{ f }({\mathcal H})$ of length n, $\pi [i, f ]$ is the sub-trace of $\pi$ from state $s_i$ to state $s_ f$.

Definition 6

(Semantics of $\textsf {eLTL}$ formulae)

Given $p,q \in {E}$, $\phi \in \varPhi$, and the eLTL formulae $\psi , \psi _1, \psi _2$, the satisfaction relation $\models$ is defined as follows:

(2.1)

(2.2)

(2.3)

(2.4)

(2.5)

Finally, given $\pi \in \mathcal {O}_ f ({\mathcal H})$ a trace of length n and $\psi$ an eLTL formula, $\pi \models \psi$ iff $\pi [0,n-1] \models \psi$.

The semantics given by $\models$ is similar to that of LTL, except that $\models$ manages interval formulae instead of state formulae. For instance, case 2.1 states that the sub-trace $\pi [i, f ]$ of $\pi$ satisfies an interval formula $\phi$ iff $\phi$ holds on the time interval determined by timestamps of states $s_i$ and $s_ f$ ($\phi ([ts_i,ts_ f ])$). Case 2.4 establishes that $\psi _1 \mathcal {U}_{[p,q]} \psi _2$ holds on trace $\pi [i, f ]$ iff we can find two timestamps $ts_j<ts_k$, determined by events p and q, that split the trace into two sub-traces $\pi [i,j]$ and $\pi [j,k]$, each one satisfying $\psi _1$ and $\psi _2$, respectively. Observe that $\psi _1$ must hold in the sub-trace determined by the first interval of events [p, q] on which $\psi _2$ is true. This way, the until operator follows the same semantics of the classical LTL until. However, other alternative approaches are also possible. For instance, in Maler and Ničković (2013) the authors provide a more relaxed definition for until, since they do not require that $\psi _1$ be true the first time $\psi _2$ holds. Nonetheless, we could easily change the until definition to also accept these behaviors if in the future we think this is necessary. Finally, case 2.5 is similar to case 2.4, except that $\psi _2$ is satisfied at a time instant rather than an interval. Similarly, in $\Box _p \psi$ (or $\Diamond _p \psi$) the nested formula $\psi$ will be evaluated at a single point.

Remark 2

Observe that the semantics of operator $\mathcal {U}_{[p,q]}$ completely depends on relation $\Vdash$ of Definition 3. The sub-traces of $\pi [i, f ]$ produced by $\Vdash$ determine the sub-trace $\pi [j,k]$ chosen to evaluate $\psi _2$ (and, consequently, the sub-trace to evaluate $\psi _1$). However, as discussed in Remark 1, relation $\Vdash$ could be differently defined, which would lead to different semantics of operator $\mathcal {U}_{[p,q]}$ and, therefore, to different logic implementations. For instance, if we define $\Vdash$ to produce maximal sub-traces wrt both events p and q, the current definition of $\mathcal {U}_{[p,q]}$ would not change, although the sub-traces on which sub-formulae $\psi _1$ and $\psi _2$ are evaluated would be different. However, to take into account nested or overlapping sub-traces, the definition and the implementation of $\mathcal {U}_{[p,q]}$ would have to change significantly. The current definition of $\Vdash$ preserves the balance between having enough expressiveness in eLTL to describe a set of rich properties and having an efficient implementation as it is shown in Sects. 4 and  5.

Proposition 1

Operators $\Box _{[p,q]}, \Diamond _{[p,q]}, \Box _{p}$ and $\Diamond _{p}$, given in Definition 5 have the following meaning:

(2.6)

(2.7)

(2.8)

(2.9)

Proof

• 1. Cases 2.6 and 2.8 follow from the definition of $\Diamond _{[p,q]}$ and $\Diamond _{p}$, taking into account that the interval formula $True$ holds for all intervals.

• 2. Case 2.7. By definition $\Box _{[p,q]}\psi = \lnot \Diamond _{[p,q]} \lnot \psi$; that is, $\pi [i, f ] \models \Box _{[p,q]}\psi$ iff $\pi [i, f ] \not \models \Diamond _{[p,q]} \lnot \psi$. Using expression 2.6, we have that $\pi [i, f ] \not \models \Diamond _{[p,q]} \lnot \psi$ iff for all $\pi [j,k] \in \mathcal {S}(\pi [i, f ],[p,q])$, $\pi [j,k] \not \models \lnot \psi$ which, according to case 2.2, means that for all $\pi [j,k] \in \mathcal {S}(\pi [i, f ],[p,q])$, $\pi [j,k] \models \psi$.

• 3. The proof for case 2.9 is similar to the one above.

$\square$

Remark 3

At this point it is worth highlighting that eLTL preserves the separation of concerns related to where interval formulae have to be evaluated and what interval formulae must be checked in each sub-trace found. This independence (illustrated in Fig. 1) means that the logic provides, on the one hand, the temporal operators in charge of determining the sub-traces of interest to analyze a given property and, on the other, the interval formulae $\phi$ to be evaluated on these sub-traces.

In addition, the way eLTL deals with interval formulae allows hiding the possible complexity of its evaluation. For instance, consider function $\phi ' \in \varPhi$ defined as $\phi '([t_i,t_ f ])= true$ iff $\forall t_1, t_2 \in {\mathbb {R}}^{\ge 0},\ t_i \le t_1 < t_2 \le t_ f . \ speed(t_1) > speed(t_2)$, that is, iff the speed is decreasing in $[t_i, t_ f ]$. Formally, the eLTL semantics given above just need that the interval formula $\phi '$ can be computed. It is an implementation issue to determine how $\phi '([t_i,t_ f ])$ is calculated in practice. For example, an implementation of $\phi '$ could use only the observable states of the trace under analysis to decide whether speed is decreasing in $[t_i,t_ f ]$, or it could use the actual dynamic behaviour of speed in $[t_i,t_ f ]$, if it is available.

2.2 Examples

Now, we mention some examples of eLTL properties to show its expressiveness and motivate the usefulness of the logic. We specify some properties of interest on data traces of smartphones running applications (apps) in different network scenarios. This case study is further discussed in Sect. 6.

In the Introduction, we stated a non-functional property that must hold when an app is downloaded. The property says that “the energy consumed by a mobile device during the download of a given app is always less than a constant K”. The following eLTL formula represents this property:

$$\begin{aligned}&\Box _{[dStt,dStp]} \phi _e,&where \ \ \phi _e([t_i, t_ f ]) = {\left\{ \begin{array}{ll} true &{} if \ \forall t \in [t_i, t_ f ], \ energy (t) \le K\\ false &{} otherwise \end{array}\right. } \end{aligned}$$

where dStt and dStp are the events raised when the download of an app starts and ends, respectively, and $\phi _e$ is the interval formula that determines whether the energy is below the limit K each time the application is downloaded.

In addition, we can express that “the app is downloaded at least once in less than T time units” using the following formula:

$$\begin{aligned} \Diamond _{[dStt,dStp]} \phi _t, \ \ where \ \ \phi _t([t_i, t_ f ]) = t_ f - t_i < T \end{aligned}$$

The previous property can be refined to express that “the app has to be downloaded at least once, and the download always takes less than T time units and the energy consumed is always less than K” as follows:

$$\begin{aligned} \Diamond _{[dStt,dStp]} \ True \ \wedge \ \Box _{[dStt,dStp]} (\phi _t \wedge \phi _e) \end{aligned}$$

Combining operators with one and two events, we can describe the property “if during the download of an app the mobile raises an overheated event (oh), the device temperature has increased at least C degrees from the download start” as follows:

$$\begin{aligned} \Box _{[dStt, dStp]}(\phi _h \mathcal {U}_{oh} True), \ \ where \ \phi _h([t_i, t_ f ]) = temp(t_ f ) - temp(t_i) > C \end{aligned}$$

Figure 2 shows, for the previous formula, how each temporal operator determines the sub-trace where its nested formula has to be evaluated. For instance, $\Box _{[dStt,dStp]}$ scans the complete trace to find sub-traces delimited by [dStt, dStp]. In each sub-trace, $\phi _h \mathcal {U}_{oh} True$ detects the first occurrence of event oh (this state satisfies True), and then $\phi _h$ can be evaluated in the sub-trace delimited by events dStt and oh. Observe that to satisfy the property, in the second sub-trace determined by [dStt, dStp] the event oh must occur and $\phi _h$ must hold.

Fig. 2

Example of evaluation of $\Box _{[dStt, dStp]}(\phi _h \mathcal {U}_{oh} True)$

3 Background of Promela and Spin

This section introduces the main characteristics of the Spin model checker (Holzmann 2003) and its modeling language Promela. A more complete description of both the tool and the language may be found at Holzmann (1997).

Spin is able to verify the correctness of systems typically composed of concurrent processes against safety and liveness properties described in LTL. Spin is an explicit model checker that works as follows. The system under analysis and the properties to be analyzed are both translated into Büchi automata. Then, the property automaton is executed synchronously with the model automaton, which is exhaustively explored by an efficient double depth-first search algorithm, which builds the system state space on-the-fly. To better understand the interaction between the execution of both automata, we can consider that the property automaton acts as an observer of the system automaton and is able to stop the analysis when an anomalous behavior of the system is observed. Although Spin is a very efficient model checking tool, the exhaustive exploration of the state space can lead to the so-called state space explosion problem when the number of states generated exceeds the available memory. Thus, system abstraction plays an important role in the analysis work.

Promela, Spin’s modeling language, has a syntax similar to language C. A Promela model is composed of a finite set of concurrent processes, whose execution is, by default, interleaved. Promela provides asynchronous/synchronous communication channels, and global/local variables of a non-floating type. System states are given by the values of variables, channels and the program counter (the next statement to be executed) of each process in execution. When some of these elements change, a new state is generated and stored (if it has not yet been visited), building this way the system state space.

Listing 1 shows an example of a Promela process called formula which, in fact, is the instantiation of the eLTL formula $\Box _{[p,q]}(\phi _1 \vee \phi _2)$. The behavior of the process is written in a proctype (line 17), where the keyword active indicates that initially there is a running instance of this process. Promela has a rich syntax that includes enumerate types (lines 3 and 4), variable assignments (line 18), logic operations (line 31), dynamic process creation (line 27) and unconditional jumps (goto) to labeled statements (line 30). Regarding labeled statements, it is worth clarifying that some labels have a special meaning that directly affects the analysis. For instance, labels starting with end mark valid termination states.

Spin simulates the execution a Promela program by interleaving the execution of its processes in a non-deterministic manner. A process can only be selected to continue the execution if it is executable, i.e., if it has an executable statement to be run next. If no executable process exists, the program blocks. Thus, the executability of statements is key to understand how a Promela program may progress. Boolean expressions constitute a special case in the language. A Boolean expression is a basic statement, in the sense that it can be used such as an assignment. The main difference is that a Boolean expression can only be executed if it evaluates to true, while assignments are always executable. This semantics is very useful to easily model the synchronization by shared variables in the language. The executability of the other statements is defined similarly to that of other languages.

Promela provides if selection statements (lines47–52), and do loop statements (lines 29–45). Both statements can be composed of multiple guarded branches (starting with symbols ::) and can exhibit a non-deterministic behavior. If multiple branch guards are executable, one of these branches is non-deterministically selected to be executed. Otherwise, when all guards are non-executable, the process containing the statement is suspended.

In addition to the process synchronization through shared variables, Promela also provides synchronization via messages passing through channels. When the channel size is zero (line 5) the communication is synchronous (rendezvous), which implies that the transmission and reception of a message takes place simultaneously in the two end-point processes. Thus, if one of the processes is not ready to send/receive the message through a synchronous channel, the other process is suspended. Asynchronous channels are used as bounded buffers. The transmitting process can send a message if the channel is not full, while the receiving process can read messages if the channel is not empty. Otherwise, the corresponding process is suspended. Symbols ! and ? after the channel name represent, respectively, the transmission and reception of messages through channels (lines 34 and 39). Observe that messages can comprise multiple values. For example, in line 34, the message includes the value of the integer variable i and the enumerated value START.

From Promela 4.0, the language supports embedded C code in the models. The basic statements to embed C code are c_decl (line 7) to declare C variables or include native libraries, c_expr that allows the use of C expressions in guarded statements, and c_code (line 21) that allows the unconditional execution of C code. As we will see in further examples, Promela variables can be accessed from c_expr and c_code blocks. Global variables are referenced using the notation ${\texttt {now.}}<{\texttt {var}}\_{\texttt {name}}>$, whereas local variables are referenced using $\texttt {P}<\texttt {proctype}\_\texttt {name}>-> <\texttt {var}\_\texttt {name}>$. It is worth mentioning that, by default, the C variables are not part of the system states, and thus changes in the C variables values do not produce new system states. This way, it is possible to keep part of the system behavior in the C variables and maintain an abstract representation in the Promela model (which takes fewer values) and a tractable system’s state space.

4 Implementation

As described in Fig. 1, STAn analyzes execution traces of an EDS against properties described in eLTL. The goal of this section is to show how each eLTL formula is translated into a network of finite automata which are, in fact, Promela processes capable of monitoring and analyzing the input trace. Once the network has been constructed, STAn uses the Spin model checker to determine whether each trace satisfies the formula by analyzing the network of finite automata.

To better understand the approach followed by STAn, in Sect. 4.1 we first introduce an intermediate implementation using the recursive function evalT that makes use of a tree representation of the formulae to be evaluated. Then, we present the implementation of the monitor templates of the eLTL operators described in Sect. 2, which are the patterns of the above mentioned automata. We describe the offline and online implementations of the templates in Sects. 4.2 and 4.3, respectively.

Fig. 3

Tree $\mathcal {T}_\psi$ corresponding to $\psi = \Box _{[p,q]}(\phi _1 \rightarrow \Diamond _{[r,k]}\phi _2)$

4.1 Tree based implementation

We can represent each eLTL formula $\psi$ by means of a binary tree $\mathcal {T}_\psi$ where each node corresponds to an eLTL operator of $\psi$ and branches relate each operator with the sub-trees of its nested formulae. For example, formula $\psi = \Box _{[p,q]}(\phi _1 \rightarrow \Diamond _{[r,k]}\phi _2)$, rewritten as $\Box _{[p,q]}(\lnot \phi _1 \vee \Diamond _{[r,k]}\phi _2)$, induces the binary tree $\mathcal {T}_\psi$ of Fig. 3. As one can see, the tree structure completely matches the structure of $\psi$. Thus, the root node ($\Box _{[p,q]}$) corresponds to the outer operator of $\psi$. As $\Box _{[p,q]}$ is a unary operator, the root node has only one child, and so on.

Now assume that we want to check whether a given eLTL formula $\psi$ holds on a trace $\pi [i, f ]$. Once the tree $\mathcal {T}_\psi$ has been constructed, the role of each tree node is to evaluate a sub-formula of $\psi$ on a sub-trace of $\pi [i, f ]$. For instance, in Fig. 3, the root node $\Box _{[p,q]}$ evaluates sub-formula $\phi _1 \vee \Diamond _{[r,k]} \phi _2$ on each sub-trace of $\mathcal {S}(\pi [i, f ],[p,q])$. Thus, the node $\Box _{[p,q]}$ behaves as an iterator searching for the sub-traces of $\pi [i, f ]$ satisfying [p, q] that, once found, are sent to their child, in this case the node $\vee$. When the node $\vee$ finishes the evaluation of the sub-trace, it returns the result to its parent node ($\Box _{[p,q]}$).

Fig. 4

Definition of $\mathcal {T}_\psi .evalT(\pi [i, f ])$

Figure 4 shows the definition of the Boolean function evalT that, based on a tree $\mathcal {T}_\psi$, evaluates $\psi$ on a trace $\pi [i, f ]$. The left column contains the eLTL operator of the root node of $\mathcal {T}_\psi$, the middle column contains the name of its sub-trees, if any, and finally, the right column shows the algorithm to evaluate $\psi$ on the trace $\pi [i, f ]$. For instance, when $\psi = \phi$ is an interval formula, the tree $\mathcal {T}_\phi$ only has the root node $\phi$, and the function evalT returns the value of $\phi$ on the interval determined by the initial and final states of $\pi [i, f ]$. The cases in which $\psi = \lnot \psi _1$, $\psi = \psi _1 \vee \psi _2$ are simple: the root node $\lnot$ or $\vee$ only has to propagate the trace to its sub-tree $\mathcal {T}_{\psi _1}$ (or sub-trees $\mathcal {T}_{\psi _1}$ and $\mathcal {T}_{\psi _2}$) and wait for the result.

However, when $\psi = \Box _{[p,q]}\psi _1$, $\psi = \Diamond _{[p,q]}\psi _1$ or $\psi = \psi _1 \mathcal {U}_{[p,q]} \psi _2$, the evaluation of $\psi$ involves both an iteration through trace $\pi [i, f ]$ searching for the sub-traces satisfying [p, q] and recursive calls to evaluate the sub-formula $\psi _1$ on the sub-traces using the sub-trees $\mathcal {T}_{\psi _1}$ (and evaluate $\psi _2$ using $\mathcal {T}_{\psi _2}$ for $\mathcal {U}_{[p,q]}$).

In Fig. 4, we use a notation close to the object oriented programming. For example, the statement $\mathcal {T}_{\psi _1}.evalT(\pi [i, f ])$ denotes the tasks carried out by $\mathcal {T}_{\psi _1}$ to evaluate whether trace $\pi [i, f ]$ satisfies $\psi _1$. This way, we emphasize that once the tree $\mathcal {T}_{\psi _1}$ is constructed, it executes method evalT every time its parent ($\mathcal {T}_{\psi }$) asks it.

The following result gives us the correctness of algorithm evalT.

Theorem 1

For each eLTL formula $\psi$ and trace $\pi [i, f ]$,

$$\begin{aligned} \pi [i, f ] \models \psi \iff \mathcal {T}_\psi .evalT(\pi [i, f ]) \ returns \ true \end{aligned}$$

Proof

The proof proceeds by induction of the structure of $\psi$. The base case when $\psi =\phi$ is an interval function is trivial. The other cases hold from the definition of the logic using induction. The most interesting point to be noted is that in all cases iterator $\textbf{for}$ produces the sub-traces of $\pi [i, f ]$ ordered with respect to time instants when the corresponding states have occurred. In consequence, for instance in the $\mathcal {U}_{[p,q]}$ case, when a sub-trace $\pi [j,k]$ is found that satisfies $\psi _2$, it is in fact the first sub-trace of these characteristics in $\pi [i, f ]$, which matches the definition of operator $\mathcal {U}_{[p,q]}$ in the logic. $\square$

The offline and online implementations presented in the next sections, follow this approach; that is, to evaluate an eLTL formula $\psi$ on a trace $\pi [i, f ]$, they construct a tree $\mathcal {T}_\psi$ representing the formula, in which each tree node is a Promela process in charge of evaluating a sub-formula of $\psi$ on a sub-trace of $\pi [i, f ]$, as explained above. Since the behaviour of each tree is completely determined by the operator in its root node, the implementations described below focus on providing the so-called monitor templates for each of the eLTL operators. Once a particular formula $\psi$ is given, the monitor templates can be automatically instantiated into Promela processes organized in a tree like $\mathcal {T}_\psi$. The concurrent execution of all these processes is able to evaluate $\psi$ on any trace.

4.2 Offline implementation in Promela

This section describes how STAn analyzes a trace $\pi [i, f ]$ offline against an eLTL formula $\psi$ using a hierarchical tree of processes. To simplify this section, the Promela implementation of most of these processes is in Appendix A.

Each eLTL operator is represented by an instance of a Promela process (proctype) that is parameterized with a number (id) that identifies the process instance (id=0 is assigned to the outer formula operator) and the identifiers of the nested formulae (c1 and/or c2), if any. In the following, we will call each one of these Promela processes monitor. In addition, STAn always adds an extra monitor called formula connected with the monitor of the outer formula operator. The monitor formula initializes the system execution (including the construction of the tree of monitors) at the beginning of the analysis and receives the result at the end.

To simplify the following discussion, we assume that the monitor id corresponds to an eLTL operator with two nested sub-formulae whose behaviors are implemented by monitors c1 and c2. The case when the operator only has one (or no) nested formula is simpler. The templates also have as parameters the events in which the corresponding monitor is interested (to carry out the iteration work over the trace, as explained in the previous section).

In the offline implementation, monitors inspect the trace when the execution has finished; thus, each monitor knows a priori the end of the trace to be analyzed. This fact is directly reflected in the way in which monitors communicate with each other, which is based on the message passing through different Promela channels (see Sect. 3). Thus, the monitor id receives from its parent, through channel cm[id], the time interval of the sub-trace on which it should perform its analysis work (as a message of the form (ti,tf) with the interval endpoints). Similarly, the monitor id can propagate the time interval information to the monitors of its sub-formulae via channels cm[c1] and cm[c2]. Inversely, the monitor id uses the (output) channel rd[id] to return its evaluation to the outer operator’s monitor (or to the formula monitor, if it is the monitor of the outer formula operator). Both channels are synchronous, which means that the two monitors in communication have to execute the send and receive statements simultaneously. Observe that channels cm and rd correspond, respectively, to the down and up arrows connecting the nodes in the tree of Fig. 3.

As discussed in Sect. 4.1, the monitors of eLTL operators with events (e.g. $\Box _{[p,q]}$ or $\Diamond _{[p,q]}$) have to identify the sub-intervals determined by [p, q] and propagate them to the monitor of its nested operators. In the offline implementation, each monitor makes use of the C function nextEv that, given a complete trace, a time instant t and an event of interest e, returns the next time instant following t when the event e occurs in the trace. $\Box _{[p,q]}$

Fig. 5

Synchronization of offline monitors for formula $\Box _{[p,q]} (\phi _1 \vee \phi _2)$

As an example, we now describe the behavior of the tree of monitors constructed to evaluate the formula $\Box _{[p,q]} (\phi _1 \vee \phi _2)$ by using the Message Sequence Chart (MSC) of Fig. 5 and the Promela code shown in Listings 2 and 3, which show, respectively, the offline Promela implementation of the formula and $\Box _{[p,q]}$ monitor templates.

The proctype formula is the only initially active process (observe the keyword active in Listing 2, line 7). It is in charge of instantiating the monitors of the eLTL operators (Listing 2, line 14) and sending the message with the endpoints of the trace through channel cm[0] (Listing 2, line 15) to the outermost operator’s monitor. In this example, the process ALWAYS_PQ receives this first message (Listing 3, line 5). Then, it searches for the first time sub-interval [tp,tq] $\subseteq$ [ti,tf] that satisfies [p,q] (Listing 3, line 7), propagates the time interval to the monitor OR through cm[1] and waits for OR to return the result of the evaluation. The OR monitor propagates the received time interval to its two nested monitors through cm[2] and cm[3] and waits for their results, which will be received through rd[2] and rd[3], respectively. Monitors PHI_1 and PHI_2 are the functions that implement the interval formulae $\phi _1$ and $\phi _2$ and, for this reason, they do not have any other nested monitor. Thus, if both PHI_1 and PHI_2 evaluate to false, the OR monitor and the ALWAYS_PQ also evaluate to false, and the formula evaluation is finished. Otherwise, ALWAYS_PQ searches for the following sub-interval [tp’,tq’] $\subseteq$ [ti,tf] (after [tp,tq]) satisfying [p,q] and proceeds as previously described. When there are no more sub-intervals in [ti,tf] that satisfy [p,q], ALWAYS_PQ evaluates to true and sends the result via channel rd[0] to the process formula. Observe that the condition result && tq $<=$ tf is needed to stop the execution when the value of result obtained is false or when the sub-trace found is not inside the original trace (in the interval [ti,tf]).

Finally, when the formula receives the evaluation from cm[0] (Listing 2, line 16), it prints the result and executes assert(false) to produce an assertion violation error that stops the analysis. It is worth mentioning that Spin can be configured to produce a counterexample (a trail fail) when assertion violations occur. The counterexample can be reproduced to see how the monitors synchronize to evaluate the formula on the trace.

4.3 Online implementation in Promela

The online implementation follows a similar approach to the offline; that is, there is a hierarchical tree of monitors, each one in charge of analyzing a sub-formula of the original formula. The main difference is that the online monitors scan the trace while it is being produced; thus, the end of the trace is initially unknown. In addition, the online monitors use a slightly different synchronization scheme in order to return a verdict as soon as possible, avoiding if possible the analysis of the complete trace.

However, it is worth noting that the online monitors of eLTL operators with intervals cannot always return the final verdict even though their nested formulae have sent them their results. Assume, for instance, the tree of monitors for formula $\Box _{[p,q]}\psi$. When the monitor of $\Box _{[p,q]}$ detects that event p has occurred, it may start the monitor of $\psi$. However, although the monitor of $\psi$ returns it $false$, it has to wait to know if event q occurs before deciding whether the whole formula holds or not. This is because if no q event occurs in the trace, $\Box _{[p,q]}\psi$ is $true$.

Fig. 6

Synchronization of online monitors for formula $\Box _{[p,q]} (\phi _1 \vee \phi _2)$

We now describe how the online monitors evaluate the formula $\Box _{[p,q]} (\phi _1 \vee \phi _2)$ by using the MSC shown in Fig. 6. Listing 1 shows the online implementation of the process formula. As in the offline version, the proctype formula, which is the only initially active process, is in charge of instantiating the tree of monitors for the eLTL operators.

The first difference in the online monitoring approach is that each monitor receives two different messages, (ti,START) and (tf,STOP), through the channel cm[id], which, respectively, announce the start and the end of the sub-trace evaluate. Between these two messages, the ALWAYS_PQ monitor has to search for the time intervals satisfying [p,q] and propagate them to its nested monitor OR. Finally, as in the offline implementation, the synchronous channel rd[id] is used to return the result of the evaluation to the outer operator’s monitor. Observe that an online monitor could send its result before receiving the message (tf,STOP) (see the left lower diagram of Fig. 6). For instance, the ALWAYS_PQ monitor can send its evaluation when $\phi _1$ and $\phi _2$ evaluate to false. But in any case, the monitor waits for the (tf,STOP) message to be received.

The second difference in the online implementation is that each monitor receives the events through the asynchronous channel ev. A monitor should only consider events between the reception of the (ti,START) and (tf,STOP) messages. Thus, any event received outside this interval is ignored. In Listing 1, the process formula simulates how the system probes transmit the events by using the inline function sendEvent that inserts events in the channel. Since Promela asynchronous channels are buffers of limited size, we have implemented ev channel as a combination of two external C structures (ev and proc), in such a way that the number of events can dynamically grow and each monitor can process the events of its interest independently.

Apart from these changes in the synchronization of monitors, the evaluation of the formulas follows the principles described in Sect. 4.1.

5 Complexity results

In this section, we enunciate two results concerning the asymptotic time and space complexity of the implementation based on the tree of monitors described in Sect. 4.1. Since the actual behavior of the monitors is in Appendix A, the proofs of these results have also been moved to Appendix B.

We will denote as $\mathcal {C}_{s}(\psi ,\pi )$ and $\mathcal {C}_{t}(\psi ,\pi )$ the space and time complexities of the evaluation of the formula $\psi$ by means of the monitor templates on a finite data trace $\pi \in \mathcal {O}_ f ({\mathcal H})$. When necessary, we will distinguish the complexity of the online/offline implementations using super-indexes n and $f$, respectively, as $\mathcal {C}^n_{s}(\psi ,\pi )/\mathcal {C}^ f _{s}(\psi ,\pi )$ and $\mathcal {C}^n_{t}(\psi ,\pi )/\mathcal {C}^ f _{t}(\psi ,\pi )$.

5.1 Space and time complexities of interval formulae

We start by discussing the complexities of the interval formulae and then, we reason on the formula structure to extract the complexities of other eLTL operators.

Given an interval formula $\phi$ and a finite trace $\pi [i, f ]$, the calculation of $\phi ([ts_i,ts_ f ])$ requires two well defined steps: (i) reading of the interval endpoints $ts_i$ and $ts_ f$ from $\pi$ and (ii) evaluating $\phi ([ts_i,ts_ f ])$. This last step is carried out by a C function which is called from the Promela code using the constructor c_code.

In both the offline and online implementations, reading $ts_i$ and $ts_ f$ from $\pi$ involves a spatial constant cost (we only need two variables to store $ts_i$ and $ts_ f$). Regarding the time complexity, the offline implementation also has a constant cost, since the two interval extremes are known at the beginning of the analysis. In contrast, the online implementation has a linear complexity wrt the length of $\pi$ (denoted by n from now on), since the monitor has to wait until the last state of $\pi$ ($s_ f$) occurs to know $ts_ f$.

Evidently, as $\phi$ is a generic interval formula, we cannot estimate exactly the space or time needed to evaluate it. Despite this, in this section, we study the complexity of some interval formulae, and then we establish a condition under which the complexity of eLTL formulae can be approximated. In the following, we discuss some C functions that implement interval formulae with the worst-case time complexity proportional to the length of the trace n, i. e., $\mathcal {C}_{t}(\phi ,\pi ) \in \mathcal {O}(n)$. The space complexity $\mathcal {C}_{s}(\phi ,\pi )$ is usually constant, since the evaluation of $\phi$ normally requires a finite number of variables.

Let us study the complexities of evaluating two eLTL formulae on a finite trace $\pi$ of length n:

• 1. Consider $\phi _{len}$ defined as $\phi _{len}([t_i,t_ f ]) = t_ f - t_i$.

  • Time complexity In this case, we clearly have that $\mathcal {C}^ f _{t}(\phi _{len},\pi ) \in \mathcal {O}(1)$ and $\mathcal {C}^n_{t}(\phi _{len},\pi ) \in \mathcal {O}(n)$ as it was commented above.

  • Space complexity It is similar in both cases, since only a finite number of variables are needed to calculate $\phi _{len}$, i. e., $\mathcal {C}_{s}(\phi _{len},\pi ) \in \mathcal {O}(1)$

• 2. Consider $\phi _{max}^c$ defined as $\phi _{max}^c([t_i,t_ f ]) = \forall \ t_i\le t \le t_ f . \ c(t)\le max$.

  • Time complexity Since trace $\pi$ must be completely traversed to calculate $\phi _{max}^c$, the time complexity of both implementations has to be proportional to the length of the trace, and so $\mathcal {C}^ f _{t}(\phi _{max}^c,\pi ),\mathcal {C}^n_{t}(\phi _{max}^c,\pi ) \in \mathcal {O}(n)$.

  • Space complexity Assuming that the evaluation of $\phi _{max}^c$ only makes use of observable states, as in the previous example, the space complexity of both monitors is constant because a finite number of variables is sufficient to evaluate $\phi _{max}^c$ on any trace. In consequence, $\mathcal {C}_{s}(\phi _{max}^c,\pi ) \in \mathcal {O}(1)$.

We now impose a condition on the functions that measure the time and space complexity of interval formulae to be able to reason on the complexity of more complex eLTL formulae. The intuition behind the condition is the following. Assume that $g_\phi (n)$ gives us an estimation of the time/space complexity of the calculation of $\phi$ over a trace of length n. From the tree based implementation of Sect. 4.1, we know that the monitors for operators $\Box _{[p,q]}$, $\Diamond _{[p,q]}$ and $\mathcal {U}_{[p,q]}$ have to include some kind of iteration on the original trace $\pi [i, f ]$ searching for the sub-traces $\pi [j,k]$ that satisfying [p, q]. The nested interval formulae must be evaluated over these sub-traces. This means that the calculation of the complexity of $\Box _{[p,q]}$, $\Diamond _{[p,q]}$ and $\mathcal {U}_{[p,q]}$ operators typically involves summing up functions of the form $g_\phi (n)$ for each of those sub-traces. Assume we have s sub-traces of this type. The intuition tells us that calculating $\phi$ on the whole trace is more costly than calculating it on each of the sub-traces. That is, if $n_1, \cdots , n_s$ are the length of these sub-traces, the cost of calculating $g_\phi (n_1) + \cdots + g_\phi (n_s)$ should be less than $g_\phi (n)$. In consequence, this is the condition we impose on the complexity functions of interval formulae:

Inverse Triangular Condition(ITC): We assume that worst-case time and space complexities of interval formulae satisfy the inverse triangular condition wrt the trace length, i.e., given $\phi \in \varPhi$ and a finite data trace $\pi$ of length n, if $g_\phi$ is the time/space complexity of calculating $\phi$ and $n_1, \cdots , n_s \in {\mathbb {N}}$ satisfy that $n_1 + \cdots + n_s \le n$ then $g_\phi (n_1) + \cdots + g_\phi (n_s) \le g_\phi (n)$.

5.2 Complexities of eLTL formulae

Now, we enunciate two propositions that establish the time and space complexities of eLTL formulae on traces under the ITC assumption. Proposition 2 shows how the length of the trace, the number of operators of the formula and the time complexity of the nested interval formulae influence the time complexity of the formula. In Proposition 3, we obtain a similar result, but considering the space used by the monitors that implement the formula.

Proposition 2

  Given an eLTL formula $\psi$ with m nested eLTL temporal operators and a data trace $\pi$ of length n, then if $g_\phi$ is the asymptotically worst time complexity of the interval formulae nested in $\psi$ and it satisfies the ITC assumption, and we have that $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(g_\phi (n)+m*n)$.

Proof

The proof may be found in Appendix B. $\square$

Proposition 3

Given an eLTL formula $\psi$ with m nested eLTL operators and a data trace $\pi$ of length n, then if $g_\phi$ and $C_s(\psi )$ are, respectively, the asymptotically worst space complexity of the interval formulae nested in $\psi$ and the monitors implementing $\psi$, we have that $\mathcal {C}_{s}(\psi ,\pi ) \in \mathcal {O}(g_\phi (n)+m*C_s(\psi ))$.

Proof

The proof may be found in Appendix B. $\square$

It is important to remark that polynomial functions trivially satisfy ITC. Thus, we have the following corollary.

Corollary 1

  Given an eLTL formula $\psi$ with m eLTL operators and a data trace $\pi$ of length n, then if the worst time complexity of the interval formulae nested in $\psi$ is in $\mathcal {O}(n^\theta )$ for $\theta \in {\mathbb {N}}$, we have that $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(n^\theta +m*n)$.

Similarly, if the worst space complexity of the interval formulae nested in $\psi$ is in $\mathcal {O}(n^\theta )$, then $\mathcal {C}_{s}(\psi ,\pi ) \in \mathcal {O}(n^\theta +m*C_s(\psi ))$, $C_s(\psi )$ being the worst spatial cost of the monitors implementing the operators of $\psi$.

When complexity functions of interval formulae do not satisfy ITC, the calculation of complexity of the monitors of more complex eLTL formulae must introduce additional linear factors depending on the number of eLTL operators nested in the formula. This case is studied in depth in Appendix B.

6 Use case

In Espada et al. (2019) and Panizo et al. (2020), we presented a model-based testing approach to test mobile applications (apps) under different network scenarios. We used the Spin model checker to generate different test cases, along with the TRIANGLE testbed, which provides a controlled mobile network environment. In Panizo et al. (2020), the complete approach was used to evaluate the performance of Exoplayer, a video streaming app that implements different video streaming protocols. The application is instrumented in order the TRIANGLE testbed can log different events of interest, such as the start and stop of the video playback (events stt and stp, respectively), the video resolution (the event h means that the video is in high resolution, whilst event l marks that the video is in low resolution), or when the first picture is loaded (event $fp$). In addition, the testbed captures network traffic using libpcap² and periodically measures different magnitudes used to compute Key Performance Indicators (KPIs), such as transmitted and received data and data rates, or the strength of the radio signal (rssi).

Using the TRIANGLE testbed we can obtain two types of event traces: first, traces at the app level (Exoplayer) that include video events (e.g. change of video resolution); and second, traces based on the network traffic level that include Tcp protocol events (e.g. connection established or released). In the following sections, we show how STAn can effectively perform the analysis of these two types of traces against different non-functional properties described in eLTL.

6.1 Analysis of video event traces

We have analyzed 5 video event traces produced in a network scenario recreating an internet café at busy hours, and 5 other traces obtained in a network scenario simulating a trip in a high-speed train. In each test, the app tries to play a 2-min long video. Depending on the network conditions, the resulting trace can include (or not) stt, $fp$, stp events and a variable number of resolution changes. Each trace has between 5 and 10 events and around 140 measures of the rssi, received data, and received data rate parameters. Since the length of traces is short and the number of traces is reduced, we have also generated synthetic traces that have between 40 and 120 events and nearly 700–2000 measure points. We analyze these traces against the following properties:

• 1. $\Diamond _{[stt,stp]} True$ This formula checks whether the trace includes a video playback (from stt to stp events). This formula requires an instance of the template EVENTUALLY_PQ and an instance of interval formula TRUE, which is an interval formula monitor that always evaluates to true.

• 2. $\Box _{[stt,stp]} \Diamond _{[stt, fp ]} \phi _{el}$ where $\phi _{el}(t_i, t_f ) = t_f > t_i+1 \wedge t_f < t_i+6$ This formula checks whether in a complete video playback, which is delimited by stt and stp events, the first image ($fp$) is loaded between 1 and 6 s after the video playback starts.

• 3. $\Box _{[stt,stp]} (\Box _{[h,l]} \phi _{rssi})$ where $\phi _{rssi}([t_i,t_ f ]) = \exists t \in [t_i, t_{ f }]. rssi_{min}(t)\le -99$ This formula checks whether a downgrade of resolution is preceded by a fall of the rssi below -99 dB. This formula uses a total of 3 monitors.

• 4. $(\Box _{[h,l]} \phi _{rxRate}) \wedge (\Diamond _{[stt,stp]} \phi _{rxData})$ where $\phi _{rxRate} = \forall t \in [t_i, t_{ f }]. rxRate(t) \le 1 Mbps$ and $\phi _{rxData}$ is defined as follows. We assume that $rxData: {\mathbb {R}}^{\ge 0} \rightarrow {\mathbb {R}}^{\ge 0}$ represents the size of the packets received at each time instant. Thus, given an interval $[t_i, t_{ f }]$, we know that $rxData(t) \not = 0$ for a finite number $\{t_1, \dots , t_k\}$ of $t \in [t_i, t_{ f }]$. Then, the function $\phi _{rxData}$ is defined as follows

  $$\begin{aligned} \phi _{rxData}([t_i,t_{ f }]) = \varSigma _{j=1}^{k} rxData(t_j) \ge 14MB \end{aligned}$$

  The complete formula checks the conjunction of two properties: on the one hand, whether the change in resolution from high to low is preceded by a low reception rate (e.g. the rate is below 1 Mbps) and whether the data corresponding to the video has been received (e.g. it receives more than 14 MB).

Table 1 Analysis of real and synthetic traces

Table 1 summarizes the performance of STAn when analyzing the 4 properties. It shows, for offline and offline implementations, the time to evaluate the property, the state vector size and the number of states stored. In addition, we report the maximum values for the real and the synthetic traces without specifying the result of the evaluation. In all cases, the time to evaluate the property is at most 0.01 sec. (this is the minimum time reported by Spin).

Observe that the size of the state vector only depends on the number of operators in the formula. For instance, formula 4, which requires running 5 monitors, uses 348 bytes in the offline implementation and 372 in the online version. The number of states explored depends on the length of the trace and the number of event intervals scanned to determine whether the property is satisfied or not. The size of the state and the number of states give us an idea of the memory used in each analysis, which depends on both the number of monitors and the length of the trace. These experimental results match the temporal and spatial complexity analysis of both implementations, which is summarized in Sect. 5 and detailed in Appendix B.

Fig. 7

Spin report trace not satisfying F4 (offline implementation)

Figure 7 shows Spin’s report for a synthetic trace that fails formula 3, as stated in the two first lines. The time shown in the second line indicates the timestamp of the trace of events at which the monitors determined the evaluation of the property. It is worth clarifying that the memory usage reported includes the auxiliary structures used by Spin associated to the model checking algorithm (e.g. the hash table and the DFS stack). However, it does not consider the memory used by the external C data structures, since they are hidden to Spin. To obtain this information, we have used the profiling tool included in Valgrind.³ In the real traces, Valgrind reports 50KB more than Spin and, in the longest synthetic trace, it reports 200KB more. This difference is the space needed to load event and measure files, which is done in C structures.

6.2 Analysis of traffic captures

We have also analyzed the network traffic captured during the video sessions using a Dash video server and a mobile phone as client. Network traffic has been captured and exported as cvs files using Wireshark⁴ protocol analyzer, which internally uses the libpcap library. The events of interest are the combination of the Tcp flags activated in each packet (syn, ack, fin, push, reset). In the following, we refer to event as the sequence of active flags. For instance, $SA$ represents an event produced by the reception of a packet with syn and ack flags activated.

The magnitude variables considered are data included in the packet headers, such as the source and destination Tcp ports, and other performance metrics, such as the round trip time calculated by Wireshark. As the traces produced have more than 33.000 events, this example allows us to show the performance of STAn when analyzing long traces.

During a video session, the client and the Dash server establish different connections between different pairs of Tcp ports in order to send video segments with different quality. Each Tcp connection is established using the so-called Tcp 3-way handshake and can be explicitly closed. In both cases, the peers exchange a sequence of messages activating different flags, as shown in Fig. 8.

Fig. 8

Tcp connection establishment and release

We analyze the traces (network traffic) against the following three properties:

• 1. $\Diamond _{[S, S]} \Diamond _{[S, FA ]} \phi _{ports}$ This property determines whether there exists a connection which is closed (message fin,ack) before a new one starts the handshake (message syn). Observe that the outer Eventually operator considers two consecutive occurrences of the event syn (at different time stamps). In addition, $\phi _{ports}$ is an interval formula that checks whether the same Tcp ports are registered in the end points of the sub-trace determined by [s,fa], not necessarily in the same source and destination order. This property requires 2 instances of EVENTUALLY_PQ and one instance of the interval formula.

• 2. $(\Diamond _{[S, SA ]} \phi '_{ports}) \rightarrow (\Diamond _{ FA } \phi '_{ports} \vee \Diamond _{ FPA } \phi '_{ports})$: This property determines whether the establishment of a connection between the ports $p_1$ and $p_2$ (messages with flags syn and syn,ack) implies that, at some point, this connection will be closed using a message fin,ack, or fin,push,ack. The current implementation of STAn does not provide a specific monitor for the implication operator ($\psi _1 \rightarrow \psi _2$). Thus, the property can be analyzed by transforming it into $\lnot \psi _1 \vee \psi _2$. In order to ease the specification of this kind of formulae, the eltl2pml parser, shown in Fig. 1, generates the Promela formula process with the suitable instantiation of 9 monitors.

• 3. $(\Diamond _{[S, RA ]} \phi '_{ports}) \rightarrow (\Diamond _{[S, RA ]} (\phi '_{ports} \wedge \phi _{rtt}))$ with $\phi _{rtt}$ defined as $\phi _{rtt}([t_i, t_{ f }]) = \forall t \in [t_i, t_{ f }]. rtt(t) \ge 35\ ms$: This property determines whether fact that the connection between $p_1$ and $p_2$ ports is reset implies that during this connection the round trip time was greater than $35\ ms$.

Observe that in the second and third formulae, $\phi '_{ports}$ checks the connection between the specific ports p1 and p2 to determine that these events are associated to the same Tcp connection. As we will see in Sect. 7, other specification languages allow free variables associated to events, in such a way that they can express that for any (or for all) ports p1 and p2 the property is fulfilled.

Table 2 Analysis of traffic traces

Table 2 shows the performance metrics of STAn when analyzing the traces of the network traffic generated during the playback of the 2-minute long video against the 3 previous properties. Observe that the online implementation of formula 2 explores 10 times more states than the offline one. In formula 3, the online implementation explores 100 times more states than the offline implementation. This difference is due to the fact that the offline monitor of EVENTUALLY_PQ obtains the end points of the interval of events making two queries, while the online monitor explores the events of the trace one-by-one. Clearly, the online approach explores a greater number of states and consumes more time and memory. In the offline implementation of formula 3, Spin reports 181.7 MB and Valgrind detects 3.5 MB more, which is the memory used to load the event and measure files. In contrast, in the online implementation, Spin reports 669 MB and Valgrind detects 3.5 MB more.

7 Related work

In the last few decades, runtime verification has gained attention in research and industry. As a result, a variety of specification languages, algorithms and tools have appeared to support different types of case studies, such as the analysis of unmanaged vehicles (Reinbacher et al. 2014), mixed signal circuits (Maler and Ničković 2013), or stream processing systems (Espinosa et al. 2019; Awad et al. 2019). This section briefly describes some related works from different perspectives. Some of them have inspired us in the definition of the eLTL logic and the implementation of the monitoring algorithms. In Sánchez et al. (2019), the reader can find an extensive survey on runtime verification work.

7.1 Specification languages for interval properties

Linear temporal logic (LTL) has been traditionally used to describe properties that must hold along the traces of concurrent systems (Rosu and Havelund 2005; Pnueli and Zaks 2006). When execution traces are state sequences with timestamped events, many studies use enriched versions of LTL that are able to capture events or time intervals. For instance, Metric temporal logic (MTL) (Alur and Henzinger 1993) and Signal temporal logic (STL) (Maler and Ničković 2013) are extensions of LTL with real-time intervals. Formulae in MTL can describe what should happen in a (predefined) time interval after (or before) an event occurs. Moreover, STL extends MTL to introduce a dense-time model and real-valued variables. Observe that, unlike these logics, eLTL focuses on describing what should happen in a time interval, determined by two events, of a priori unknown length. In addition, eLTL formulae are evaluated over intervals of states, while the other logics evaluate over single states.

Some of the properties described in the case studies can be also expressed in STL. However, it worth noting that the philosophy behind the two logics is different. In particular, expressing bounded interval determined by events is not natural in STL. For instance, the property “always during a video playback (delimited by events stt and stp) the first picture ($fp$ event) takes place between 1 and 6 s after the start” is expressed as follows in eLTL:

$$\begin{aligned} \Box _{[stt,stp]} \Diamond _{[stt, fp ]} \phi \ \ \ where \ \phi (t_i, t_f) = t_f > t_i + 1 \wedge t_f < t_i+6 \end{aligned}$$

Assuming that there are some signals that rise when events stt, stp and $fp$ take place, a first attempt to express the property in STL will be the following:

$$\begin{aligned} \Box _{[0,\infty )} ( \uparrow stt \rightarrow ((\lnot \uparrow stp \ \mathcal {U}_{[1,6]} \uparrow fp ) \wedge (\Diamond _{(1,\infty )}\uparrow stp))) \end{aligned}$$

We have used the until operator to describe that stp cannot rise before $fp$.

It is also worth noting that in the case of STL, the boolean constraint over signals supported are predicates of the form $x \circ c$, where x is a signal and $\circ \in {<,\le ,=,\ge ,>}$ and $c \in {\mathbb {Q}}$. Thus, the properties defined in Sect. 6.2, which requires comparing the ports involved in two different time instants, would be difficult to define in STL.

Unlike STL and eLTL, which can express properties in future time, other languages such as past-time Metric Temporal Logic (pMTL) (Reinbacher et al. 2014) and Quantified Temporal Logic (QTL) (Havelund and Peled 2020) are suitable to express properties in past time. pMTL is the past fragment of MTL. Thus, pMTL provides past temporal operators defined over time intervals where the nested properties are evaluated. On the contrary, in QTL the logic operators do not explicitly include time intervals, but time is managed as a variable defined in ${\mathbb {N}}$. The key feature of QTL is the use of events parameterized with variables which can be existentially quantified.

Transforming an eLTL property into a past-time logic is not straightforward. We have adapted the first two properties analyzed in Sect. 6.2 to QTL. For instance, we have rewritten the property “if a new connection is open, the previous opened connection is closed” as “if a connection is closed it was previously opened and not closed since then”, which is specified in QTL as follows:

where is the previous operator and interval $\varvec{[}syn, fin \varvec{)}$ is a syntactic sugar for $\lnot fin \ \mathcal {S} \ syn$, $\mathcal {S}$ being the since operator. It is worth noting that in QTL you cannot define events intervals, instead they are a simplified notation of operator since.

The second property establishes whether “if a connection is correctly established then it is closed using $fin$ or $finP$ events”. It could be similarly specified in QTL as follows:

Observe that to simplify the previous QTL formula, we are only checking that the source and destination ports match in the syn and $fin$ events. The original property in eLTL checks that ports can be swapped in the syn and $fin$ events. The third property of Sect. 6.2 cannot be expressed in QTL because it does not support comparing variables with constants or with other variables. Observe that despite eLTL (and STAn) is not currently aimed to support event parameterization; thanks to the interval formulae $\phi _{ports}$ we can express that in the maximal interval of events [syn, $fin$] the source and destination ports are the same (or swapped) without specifying specific ports values, similarly to QTL.

In the same line, Eagle (Barringer et al. 2004) is a more sophisticated framework in which temporal logics with different characteristics can be defined. To do this, Eagle uses parameterized and recursive equations (called rules), quantifiers and the temporal operators next ($\bigcirc$), previous ($\bigodot$) and concatenation ($\cdot$). Rules can be combined to construct monitors which can describe complex properties when properly instantiated.

Although eLTL formulae could be described in Eagle, we think that, from the user point of view, this language is harder to manipulate. For instance, in Eagle the eLTL formula $\Diamond _{[p,q]}\phi$ could be written as $Eventually (\phi ,p,q)$, where $Eventually$ is recursively defined as the minimal fixed point ($\underline{min}$) of the following rule and Form is the predefined type of Eagle formulae:

Similarly, the rule for $Eventually (F,P,Q)$ is constructed as

$$\begin{aligned}{} & {} \underline{min} \ Eventually ( Form \ F, Form \ P, Form \ Q) \\{} & {} \quad =P \wedge Maximal (P,Q) \wedge Search(F,Q,clock) \vee \bigcirc Eventually (F,P,Q) \end{aligned}$$

where clock is a real-time clock that registers the current time, $Maximal$ is a rule that checks whether the interval found is maximal (in the sense given by Definition 3) and Search is a rule that searches for the next occurrence of F2 to evaluate the interval formula F. These two rules can be defined in Eagle as follows where $\underline{max}$ is the maximal fixed point of the corresponding function:

$$\begin{aligned}{} & {} \underline{max} \ Maximal (Form \ P, Form \ Q) \\{} & {} \quad =Q \vee (\lnot P \wedge \bigodot Maximal (P,Q))\\{} & {} \underline{min} \ Search (Form \ F, Form \ Q, float \ t) \\{} & {} \quad =Q \wedge F(t,clock) \vee (\lnot Q \wedge \bigcirc Search(F,Q,t)) \end{aligned}$$

Eagle’s expressiveness implies a huge cost in the implementation of a monitoring algorithm. This is why its authors defined other less expressive languages, such as Ruler (Barringer et al. 2010) or LOGSCOPE (Barringer et al. 2010), that have less complex implementations.

In Kauffman et al. (2016) and Kauffman et al. (2018), the authors define the specification language nfer for the description of properties to be specifically held by streams containing telemetry data produced by spacecraft rovers. The language is based on the Allen’s interval logic (Allen 1983) augmented with rule-based predicates on how the interval must be combined. Although language nfer is constructed from the operators of Allen logics, it is interesting to note the importance of having an interval-based specification language to make the precise description of properties easier for users.

7.2 Monitoring algorithms for interval properties

Regarding the monitoring algorithms, we can find multiple approaches depending mainly on the length of the trace (e.g. bounded or unbounded traces), and when the analysis is performed (e.g. online or offline). Perhaps the most general approach is presented in Kesten and Pnueli (2005), where a compositional transformation of $\textsf {CTL}^*$ formulae is defined using the so-called temporal testers, which are monitors inductively constructed from the formula structure. The tester processes organize according to the formula structure and evolve in a synchronous manner. Later, Pnueli and Zaks (2006) proposed an algorithm based on the composition of these temporal testers to perform online analysis of unbounded traces. In D’Souza and Matteplackel (2012), the authors also apply a compositional approach to construct monitors from $\textsf {LTL}$ formulas inspired by Kesten and Pnueli (2005). However, the monitor construction is more concise in this case, since they focus on LTL instead of the more general $\textsf {CTL}^*$ logic. The hierarchical Büchi automata built in this work are structured in a kind of tree of processes that communicate through synchronous actions, which is similar to our approach. Our current algorithm, which is based on the transformation of the eLTL operators into automata, is similar to Pnueli and Zaks (2006) and the first algorithm presented in Rosu and Havelund (2005), but thanks to Spin, we can deal with abstract representations of the real-valued variables by using external libraries through embedded C code.

Rosu and Havelund (2005) proposed three different algorithms to perform online monitoring of finite traces. The first one synthesizes a monitor of the complete formula solving a dynamic programming problem, while the other two use rewriting techniques to monitor the trace or produce the automata-like monitor. In Reinbacher et al. (2014), the objective is to perform online monitoring of signals bounded by a mission time. In this case the MTL formula is transformed into a pair of observers, which can be implemented in hardware in order to achieve a high performance. In Basin et al. (2015), the proposed algorithm is able to perform online and offline analysis of unbounded signals. It is inspired by relational databases, and it incrementally works out the result of the formula (as a structure) for each point of time. In Maler and Ničković (2013), the authors propose two algorithms to monitor finite continuous signals by interpolating the evolution of the continuous variables between two sampled values; both algorithms are implemented in the tool AMT. More recently, Havelund et al. (2020); Havelund and Peled (2020) presented monitoring algorithms based on BDD to support runtime verification of properties specified in QTL, which are implemented in the DejaVu tool. We have used DejaVu to analyze the traces used in Sect. 6.2 against the QTL properties described in the previous section. DejaVu reports that the time elapsed in the analysis of each property is around 0.45 s, which is more than the time reported by Spin (around 0.05 s in both cases). DejaVu does not report the memory consumed during the analysis, so we cannot compare this metric.

7.3 Stream runtime verification

In the recent years, some works have focused specifically on stream runtime verification (SRV), in which the trace of events is in fact a set of (possibly infinite) streams or signals (numerical or boolean) and the specifications represent the temporal and data manipulation dependencies between input and output streams. These works can be classified into those that assume that the input streams are synchronous (all streams are produced following a global clock and thus the sequence of data is not timestamped), such as Hallé (2016), and those that assume asynchronous input streams, such as Volanschi and Serpette (2019), Faymonville et al. (2019) and Convent18TeSSLa. In general, SRV tools use very expressive specification languages in order to describe the complex relation between input and output streams.

Currently, STAn does not perform SRV, but the eLTL logic could be used as a specification language in this context. For example, we could assume that the trace $\pi$ over which an eLTL formula is evaluated is the result of merging multiple SRV input streams. In addition, the eLTL verdict must be a Boolean output stream instead of a single Boolean value. In this new context, we could design SRV tools based on this extended eLTL.

In the domain of SRV, we have identified two main features. On the one hand, these tools have to deal efficiently with infinite (or very long) streams. Most of them use some operator to define a (fixed or sliding) temporal window in which a property has to be fulfilled (Convent et al. 2018; Espinosa et al. 2019; Faymonville et al. 2019; Awad et al. 2019). In eLTL, we could analyze a property $\psi$ in a time window of fixed size with $\Box _{[p,q]} \psi$ formula, where p and q are events triggered at the beginning and end of each temporal window. On the other hand, some SRV tools (Hallé 2016; Volanschi and Serpette 2019; Gorostiaga and Sánchez 2021) implement monitors in such a way that they can support customized or user-defined operations to deal with their rich input language. In this sense, eLTL maintains a balance between the fixed set of operators and the interval formulae that can be defined by the user.

8 Conclusions

In this paper, we have presented the approach followed by the tool STAn, which performs runtime verification on finite data traces against properties expressed in the Event-driven Interval Logic eLTL.

STAn transforms each eLTL operator into a monitor (automata-like) template that determines the sub-traces in which a property must be satisfied. This way, an eLTL formula is transformed into a tree of monitors, which is the composition of the operators’ templates included in the formula.

We have presented two different transformations of eLTL operators into monitors, and both of them have been implemented in Promela. The online implementation is intended for the analysis of properties during the execution of the system, and the offline implementation is suitable for the analysis of previously produced traces.

We have evaluated both implementations by analyzing the data traces of a real system, a testbed for mobile apps, against some non-functional properties. In particular, we analyze some traces produced during the testing of a streaming video app in different network scenarios (Panizo et al. 2020). Since the traces are published when the tests have completely finished, in the online implementation we have also included an auxiliary mechanism that emulates the reception of events. Both implementations have shown good performance in terms of execution time and memory (measured as states explored).

Although our objective is the analysis of data traces, the use of monitors can also be employed to model check a system against a set of properties described in eLTL. This also justifies the use of Spin as an underlying analysis engine. To model check a system against eLTL properties, we only need a Promela model of the system that is slightly instrumented to inject events in STAn. In addition, in order to model the evolution of real-valued variables, the model can be enriched with embedded C code. In Gallardo and Panizo (2014), we presented an extension of Promela and Spin to model some sub-classes of hybrid systems and analyze them against LTL properties. The combination of this previous work and the current eLTL monitors will allow the analysis of very interesting properties on hybrid systems.

We consider three main future lines of work. First, the integration of STAn in the new testing framework (Díaz Zayas et al. 2020), which is an evolution of TRIANGLE. The objective is to use the results of STAn analysis to refine the generation of new tests. This future work will require enriching STAn results with some degree of quality, similar to the robustness degree introduced in Donzé et al. (2013) to avoid running new tests that will produce the same quality or performance indicators. Second, we would like to improve the reports of STAn in such a way the user has a better understanding of the causes of properties failure. Finally, inspired by related works (Barringer et al. 2004, 2010; Havelund and Pressburger 2000; Convent et al. 2018; Faymonville et al. 2019), we would like to extend eLTL and the monitoring algorithms to support parameterized formulae and also to produce the verdict as a Boolean output stream to perform SRV analysis.

Appendices

Appendix A Offline and online monitors of eLTL operators

This appendix presents the online and offline monitors for different eLTL operators that are used in STAn. We do not explicitly present the monitors of operators over single events (e.g. $\Diamond _{p}$), since they are simplifications of the monitors over intervals of events.

Interval formula $\phi$

Listing 4 shows the offline (left) and online (right) Promela monitor templates of the interval formula $\phi$. An interval formula is evaluated on a time interval [ti,tf] that is communicated via the channel cm.

In the offline case, the complete time interval is received through channel cm (line 4), while in the online case the interval is received in two distinct messages when the sub-trace is identified (lines 4 and 5). In these simple implementations, after receiving the end of the interval, the monitor calls the C function phi (line 7), which implements the evaluation of the interval formula, and the returned value is propagated as the monitor result through the corresponding rd channel.

As commented in Remark 3 in Sect. 2.1, phi hides the complexity of evaluating the behavior of real-valued variables in the interval, and in the implementation this is achieved by using external C code. For instance, we can define a function that determines the maximum or the average of the median value of a continuous variable in the interval, or we can call an external library that interpolates the dynamics of the variables of interest.

Not operator

Listing 5 shows the offline (left) and online (right) monitor templates of the negation operator.

In the offline implementation, the NOT monitor synchronizes with the monitor of the nested formula ($\psi$) as soon as its parent monitor sends the initial and final timestamps through channel cm (lines 5 and 6). When the nested formula $\psi$ has been evaluated, the process NOT negates the result and sends it through the rd channel.

The online implementation behaves in a similar way. The only difference is that the synchronization with the outer and inner operators through channel cm consists of two messages with the START and STOP commands.

Or operator

Listings 6 and 7 present the online and offline monitor templates of the disjunction operator. The proctype OR monitors if any of the two sub-formulae $\psi _1$ and $\psi _2$ holds on the interval [ti,tf] over which OR monitor is being evaluated.

In the online implementation, the OR monitor waits for the successive reception of the START and STOP commands and resends them to its sub-formulae monitors to start and stop their execution, respectively. Then, it waits for the result of the sub-formulae via channels rd[c1] and rd[c2]. If any of the sub-formulae monitors evaluate to true, the OR monitor propagates the result to its parent monitor; if not it waits until both monitors end and returns the disjunction. Observe that the proctype OR finishes its execution at line 6, which is labeled with end_or, in order to mark that it is a valid end state. This way, the monitor can observe new trace intervals, for instance in formulae of the form $\Box _{[p,q]}(\phi 1 \vee \phi 2)$.

Similarly to the NOT and $\phi$ monitor templates, the offline implementation of the OR monitor only differs from the online implementation in the synchronization with inner and outer operators in lines 6 and 8, which are replaced by the corresponding send and receive statements.

Eventually operator

The operator $\Diamond _{[p,q]}$ (and $\Diamond _p$) have to scan the trace to find the sub-traces delimited by events p and q (or just p) in order to determine whether the sub-formula is satisfied. In both implementations, the monitor’s parameters are its identifier (id), the identifier of the monitor for its sub-formula (c1), and the events p and q that delimit the time instants where the sub-formula must be evaluated. However, each implementation uses a different approach to find the sub-traces delimited by events p and q.

Listing 8 shows the offline implementation of the EVENTUALLY_PQ monitor. Similarly to other offline monitors, the time interval [ti,tf] is received in a single message through the channel cm[id] (line 4). In order to determine sub-traces delimited by [p,q], the monitor calls the function nextEv that, given an event e and a timestamp t, returns the timestamp of the next occurrence of e after t, or -1 if no event is found. For example, in line 9, variable tq stores the timestamp of the first event q that occurs after tp. In the label waitC1, the monitor receives the evaluation of the inner sub-formula. If it is true, the eventually formula is satisfied, and thus, it propagates this result to its parent monitor. Otherwise, the monitor continues analyzing the trace (line 18).

Listing 9 shows the online monitor. The identification of the interval of events [p,q] is performed in the two states identified by labels waitP and waitQ. In waitP (lines 8–22), it waits for an event p or for the STOP message. When a valid event p is received (line 14), the monitor sends START to monitor c1 to start evaluating the inner formula. Then, it jumps to waitQ (line 23–35) to wait for the next event q (or STOP message). When a valid event q arrives (line 29), the monitor jumps to waitC1. At this label two tasks happen non-deterministically. On the one hand, the monitor receives the evaluation of the inner formula. On the other hand, the monitor sends the STOP message to c1 monitor. Similarly to the offline monitor, if the sub-formula evaluates to true, the eventually monitor propagates this result to its parent monitor and waits for the STOP message. Otherwise, the eventually monitor continues analyzing the trace.

The other branches in waitP and waitQ define the behavior of the monitor when the events and messages processed are not the expected ones, or when the STOP message is received and therefore there are no more events to process. For instance, in line 31, the monitor has previously received the STOP from its parent (stop is true) and is processing an event with the timestamp greater than tf. This means that no event p occurs in the interval [ti,tf], and consequently, the formula is false. This last event cannot be discarded, since it might be part of the next interval [ti,tf] analyzed by the monitor. For this reason, the event channel goes back to tf in line 62.

Observe that although the monitor c1 could evaluate its formula before EVENTUALLY_PQ receives the event q, the eventually monitor can not decide whether it evaluates true. If no q event occurs before the end of the trace, EVENTUALLY_PQ evaluates to false independently of the c1 result. For this reason, EVENTUALLY_PQ only receives the c1 evaluation when q arrives (line 45) or if the traces ends (line 38).

Clearly, the online implementation is more complex than the offline implementation due to the uncertainty of the end of the sub-trace. In addition, the use of two different channels, cm and the ev C channel, to obtain the end of the trace and the events requires checking whether or not a processed event is part of the current sub-trace.

Always operator

The Always operator over an interval of events is defined as $\Box _{[p,q]}\psi \equiv \lnot ( \Diamond _{[p,q]} \lnot \psi )$. Given the equivalence of eventually and always, the online and offline monitors of the Always operator are modified versions of the Eventually monitors. For example, the offline implementation shown in Listing 3 presents two differences with respect to the eventually monitor (Listing 8). The first one is that the Always operator evaluates to true when the end of the trace is reached and no interval of events is found (line 13). The second difference is in line 18, since the monitor has to continue the analysis of the trace if the sub-formula evaluates to true.

Until operator

The semantics of the Eventually operator relies on the Until operator. We can transform an eventually formula in terms of the Until operator, but the inverse is not possible in all cases. The online and offline monitors of the Eventually operator explained above are simplifications of the until monitor.

To make the presentation simpler, we will briefly explain the offline implementation (UNTIL_PQ) shown in Listing 10. A similar approach is followed in the online version. The UNTIL_PQ monitor (online or offline) has to identify the interval [tp,tq] and determines whether monitor c2 returns true in that interval. If not, the monitor has to find the next interval of events. However, if on the contrary monitor c2 returns true, the UNTIL_PQ monitor returns the same response as monitor c1.

Appendix B Complexity

In this Appendix, we complete Sect. 5, giving all the definitions needed to prove Propositions 2 and 3.

In Sect. 5, we denoted the space and time complexities of the evaluation of an eLTL formula $\psi$ over a trace $\pi \in \mathcal {O}_ f ({\mathcal H})$ with $\mathcal {C}_{s}(\psi ,\pi )$ and $\mathcal {C}_{t}(\psi ,\pi )$. In addition, we added super-indexes n and $f$ as $\mathcal {C}^n_{s}(\psi ,\pi )/\mathcal {C}^ f _{s}(\psi ,\pi )$ and $\mathcal {C}^n_{t}(\psi ,\pi )/\mathcal {C}^ f _{t}(\psi ,\pi )$ to distinguish between the online and offline implementation of the operators, when necessary.

In Appendix A, we have presented the implementation of eLTL operators. Thus, we can now discuss in detail the calculation of these complexities. Recall that the calculation of the cost of each eLTL operator mainly resides in the cost of its nested interval formulae, which is a priori unknown. To get around this, in Sect. 5 we assumed that the worst case complexity of interval functions satisfies the so-called inverse triangular condition (ITC).

In the rest of the section, we study the time and space complexities of eLTL formulae that have Boolean and temporal operators. The space complexity of evaluating each operator depends not only on the monitor template described in Appendix A but also on the Spin memory used to implement the corresponding Promela process instance. Thus, in the following, given $op \in \{\vee ,\lnot ,\Diamond _{[p,q]},\Box _{[p,q]},\mathcal {U}_{[p,q]}\}$, we denote with $C_{s}(\mathcal {M}_{op})$ the memory used by Spin to execute the process instance of the corresponding monitor template. In the following discussion, we assume that n is the length of the trace $\pi$ being analyzed.

Complexities of Not and Or operators

As Listing 5 shows, the offline monitor of $\lnot \psi$ only has to wait for the evaluation of $\psi$ to return the result. In contrast, the online monitor has to wait both the end of the trace $\pi$ and the result provided by the monitor of formula $\psi$. In consequence,

$$\begin{aligned} \mathcal {C}^ f _{t}(\lnot \psi ,\pi )&\in \mathcal {O}(\mathcal {C}^ f _{t}(\psi ,\pi )) \end{aligned}$$

(B.1)

$$\begin{aligned} \mathcal {C}^n_{t}(\lnot \psi ,\pi )&\in \mathcal {O}(\mathcal {C}^n_{t}(\psi ,\pi )+n) \end{aligned}$$

(B.2)

Thus, to simplify the calculations below, we choose the worst case time complexity as:

$$\begin{aligned} \mathcal {C}_{t}(\lnot \psi ,\pi )&\in \mathcal {O}(\mathcal {C}_{t}(\psi ,\pi )+n) \end{aligned}$$

(B.3)

Regarding, the space complexity, both the offline and online monitors of Listing 5 almost use the same memory: the space of the not monitor $C_{s}(\mathcal {M}_{\lnot })$ plus the space needed to calculate the nested formula $\psi$.

$$\begin{aligned} \mathcal {C}_{s}(\lnot \psi ,\pi )&\in \mathcal {O}(\mathcal {C}_{s}(\psi ,\pi ) + C_{s}(\mathcal {M}_{\lnot }) ) \end{aligned}$$

(B.4)

Similarly, in order to evaluate $\psi _1 \vee \psi _2$, the monitor (Listings 6 and 7 depict the online/offline monitors) waits for the monitors of $\psi _1$ and $\psi _2$ to return the result. Thus, the time and space complexities are calculated similarly to those of the $\lnot$ operator. Thus,

$$\begin{aligned} \mathcal {C}_{t}(\psi _1 \vee \psi _2,\pi )&\in \mathcal {O}(max (\mathcal {C}_{t}(\psi _1,\pi ), \mathcal {C}_{t}(\psi _2,\pi ) )+n) \end{aligned}$$

(B.5)

$$\begin{aligned} \mathcal {C}_{s}(\psi _1 \vee \psi _2,\pi )&\in \mathcal {O}(max (\mathcal {C}_{s}(\psi _1,\pi ),\mathcal {C}_{s}(\psi _2,\pi ))+ C_{s}(\mathcal {M}_{\vee })) \end{aligned}$$

(B.6)

where max is the maximum function.

Complexities of Eventually and Always operators

The monitors of $\Diamond _{[p,q]}\psi$ of Listings 8 and 9 mainly differ in that the online monitor has to wait for events p and q to occur in the data trace, which may affect the time complexity. In contrast, the offline monitor can directly access these events in constant time since they are stored in the memory.

Once a sub-trace $\pi [i,j]$ satisfying the interval of events [p, q] i.e. $\pi [i,j] \Vdash [p,q]$ (Definition 3) is found, both monitors behave similarly. They check whether the corresponding timestamps are inside the trace $\pi$ to detect if $\pi [i,j]$ is not really a sub-trace of $\pi$. If the sub-trace is correct, they send the timestamps to the $\psi$ monitor and wait for the result. They iterate by all the sub-traces of the type $\pi [i,j]$ until they receive a positive answer from the $\psi$ monitor or no more sub-traces are found.

According to this description, to calculate $\mathcal {C}_{s}(\Diamond _{[p,q]}\psi ,\pi )$ and $\mathcal {C}_{t}(\Diamond _{[p,q]}\psi ,\pi )$, we have to consider all the sub-traces of set $\mathcal {S}(\pi ,[p,q])$ given in Definition 4. To simplify the following discussion, we denote $\mathcal {S}(\pi ,[p,q]) = \bigcup _{l=1}^k \{\xi _l\}$, with $k \ge 0$ such that, for all $1 \le l \le k$, $\xi _l \Vdash [p,q]$. In addition, we assume that the sub-traces $\xi _l$ are ordered wrt the timestamps of their initial and ending states. Thus,

$$\begin{aligned} \mathcal {C}_{s}(\Diamond _{[p,q]}\psi ,\pi ) \in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{s}(\psi ,\xi _l) + C_{s}(\mathcal {M}_{\Diamond _{[p,q]}})) \end{aligned}$$

(B.7)

since the worst case occurs when all the sub-traces have to be analyzed to produce a result. As in the previous operators, it is necessary to include the memory cost associated to the monitor template instance. With respect to the time complexity, in the worst case, the offline/online monitors traverse the whole trace $\pi$ searching for events p and q to occur. In addition, when a sub-trace determined by p and q has been found, they have to wait until the monitor of the nested formula finishes its evaluation. Thus,

$$\begin{aligned} \mathcal {C}_{t}(\Diamond _{[p,q]}\psi ,\pi ) \in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{t}(\psi ,\xi _l)+n) \end{aligned}$$

(B.8)

Now consider the eLTL formula $\Box _{[p,q]}\psi$. As discussed in Appendix A, the online and offline monitors make use of the corresponding implementations of $\Diamond _{[p,q]}\psi$ monitors with minor changes (see Listing 3). Thus, the worst case time and space complexities of the always operator are similar to those of eventually, i.e.,

$$\begin{aligned} \mathcal {C}_{t}(\Box _{[p,q]}\psi ,\pi )&\in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{t}(\psi ,\xi _l)+n) \end{aligned}$$

(B.9)

$$\begin{aligned} \mathcal {C}_{s}(\Box _{[p,q]}\psi ,\pi )&\in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{s}(\psi ,\xi _l)+C_{s}(\mathcal {M}_{\Box _{[p,q]}})) \end{aligned}$$

(B.10)

Complexities of until operator

Assume that the eLTL formula $\psi _1 \mathcal {U}_{[p,q]} \psi _2$ is evaluated on the data trace $\pi$. The until monitor, shown in Listing 10, searches for a sub-trace where $\psi _2$ holds (such as the eventually monitor template does) and, then, if the sub-trace is found, it checks whether $\psi _1$ is satisfied in the prefix sub-trace. As in the previous section, we use the notation $\mathcal {S}(\pi ,[p,q]) = \bigcup _{l=1}^k \{\xi _l\}$, with $k \ge 0$ to represent the sub-traces of $\pi$ that satisfy [p, q] following Definition 4. Thus,

$$\begin{aligned} \mathcal {C}_{t}(\psi _1 \mathcal {U}_{[p,q]}\psi _2,\pi )&\in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{t}(\psi _2,\xi _l) + \mathcal {C}_{t}(\psi _1,\pi )+n) \end{aligned}$$

(B.11)

$$\begin{aligned} \mathcal {C}_{s}(\psi _1 \mathcal {U}_{[p,q]}\psi _2,\pi )&\in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{s}(\psi _2,\xi _l) + \mathcal {C}_{s}(\psi _1,\pi )+ C_{s}(\mathcal {M}_{\mathcal {U}_{[p,q]}})) \end{aligned}$$

(B.12)

In consequence, the main difference with Eqs. B.7 and B.8 is the additional costs $\mathcal {C}_{s}(\psi _1,\pi )$ and $\mathcal {C}_{t}(\psi _1,\pi )$ to evaluate $\psi _1$ on $\pi$. Observe that these expressions are in fact upper bounds of the actual complexity, since $\psi _1$ is usually evaluated on a sub-trace of $\pi$.

Complexities of eLTL formulae

We can now prove Propositions 2 and 3 enunciated in Sect. 5.

Proposition 2

Given an eLTL formula $\psi$ with m nested eLTL operators and a data trace $\pi$ of length n, then if $g_\phi$ is the asymptotically worst time complexity of the interval formulae nested in $\psi$ and it satisfies the ITC assumption, we have that $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(g_\phi (n)+m*n)$.

Proof

We proceed by induction on the formula structure.

• 1. If $\psi =\phi \in \varPhi$, i.e., $\psi$ is an interval formula, the result $\mathcal {C}_{t}(\phi ,\pi ) \in \mathcal {O}(g_\phi (n))$ is trivially satisfied since $m=0$.

• 2. Assume $\psi = \lnot \psi '$. By induction hypothesis $\mathcal {C}_{t}(\psi ',\pi ) \in \mathcal {O}(g_\phi (n)+(m-1)*n)$. Finally, using Eq. B.3, we obtain $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(g_\phi (n)+m*n)$.

• 3. Assume $\psi = \psi _1 \vee \psi _2$. By induction, we have that $\mathcal {C}_{t}(\psi _i,\pi ) \in \mathcal {O}(g^i_\phi (n)+m_i*n)$, $m_i$ being the number of eLTL operators nested in $\psi _i$ for $i=1,2$. By Eq. B.5, $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(max(g^1_\phi (n)+m_1*n,g^2_\phi (n)+m_2*n)) \subseteq \mathcal {O}(g_\phi (n)+(m_1+m_2+1)*n)=\mathcal {O}(g_\phi (n)+m*n)$, $g_\phi (n)$ being the asymptotically worst function between $g^1_\phi (n)$ and $g^2_\phi (n)$. Observe that the number m of eLTL operators nested in $\psi$ is $m_1 + m_2+1$.

• 4. Assume $\psi = \Diamond _{[p,q]}\psi '$. By Eq. B.8, $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{t}(\psi ',\xi _l)+n)$ where $\xi _l$ (with $1\le l \le k$) are the sub-traces of $\pi$ that satisfy interval [p, q]. Let us denote with $n_l$ the length of each sub-trace $\xi _l$ ($1 \le l \le k$). Then, by the induction hypothesis, we have that $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(\varSigma _{l=1}^k (g^l_\phi (n_l)+(m-1)*n_l)+n)$, $g^l_\phi (n_l)$ being the asymptotic space complexity of calculating $\psi '$ over sub-trace $\xi _l$ for all $1 \le l \le k$.

  Let us denote with $g_\phi (n)$ the function with the worst complexity between $\{g_\phi ^1,\cdots ,g_\phi ^k\}$. Now, using the ITC assumption, since $\varSigma _{l=1}^k n_l \le n$, we have that $\varSigma _{l=1}^k g_\phi (n_l) \le g_\phi (n)$. Thus, $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(g_\phi (n)+(m-1)*n+n)= \mathcal {O}(g_\phi (n)+m*n)$.

• 5. Assume $\psi = \Box _{[p,q]}\psi '$. The proof is similar to that of $\Diamond _{[p,q]}$ since in the worst case this operator has to analyze all the sub-traces satisfying [p, q].

• 6. Assume $\psi = \psi _1 \mathcal {U}_{[p,q]} \psi _2$. Using Eq. B.11 and following the same arguments utilized for $\Diamond _{[p,q]}\psi '$, we obtain that $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(g_\phi (n)+m*n)$, $g_\phi (n)$ being the maximum of set $\{g_\phi ^1(n),\cdots ,g_\phi ^k(n),g'_\phi (n)\}$. Each $g^l_\phi (n)$ is the asymptotic complexity of evaluating $\psi _2$ on each sub-trace of $\pi$ satisfying [p, q], and $g'_\phi (n)$ is the asymptotic complexity for evaluating $\psi _1$ on $\pi$.

$\square$

We have to deal with space complexity in a different proposition taking into account the space cost of storing the instances of monitors, since they affect real storage handled by Spin, as shown in Table 1 of Sect. 6 shows. In the following proposition, given a eLTL formula $\psi$, $C_s(\psi )$ denotes the worst spacial complexity of monitors implementing the eLTL operators nested in $\psi$.

Proposition 3

Given an eLTL formula $\psi$ with m nested eLTL operators and a data trace $\pi$ of length n, then if $g_\phi$ is the asymptotically worst space complexity of the interval formulae nested in $\psi$ and it satisfies the ITC assumption, $\mathcal {C}_{s}(\psi ,\pi ) \in \mathcal {O}(g_\phi (n)+m*C_s(\psi ))$.

Proof

The proof is similar to that of Proposition 2, considering that the space $C_s(\psi )$ is greater than $C_{s}(\mathcal {M}_{op})$ for each eLTL operator op nested in $\psi$. $\square$

The two following propositions deal with the case when the asymptotically worst time complexity of the interval formulae nested in the formula $\psi$ to be analyzed does not satisfy the ITC assumption. In this case, the inductive case for temporal eLTL operators $\Diamond _{[p,q]}, \Box _{[p,q]}$ and $\mathcal {U}_{[p,q]}$ cannot reduce expression $\mathcal {O}(\varSigma _{l=1}^k (g^l_\phi (n_l)+(m-1)*n_l)+n)$ into $\mathcal {O}(g_\phi (n)+m*n)$ and the complexity increases polynomially with the number of nested temporal operators.

Proposition 4

  Given an eLTL formula $\psi$, with m eLTL nested operators, and a data trace $\pi$ of length n, then if $g_\phi$ is the asymptotically worst time complexity of the interval formulae nested in $\psi$, we have that $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(n^m*g_\phi (n)+m*n)$.⁵

Proof

Similarly to Propositions 2 and 3, we proceed by induction on the formula structure. The only different cases are those of the temporal eLTL operators $\Diamond _{[p,q]}, \Box _{[p,q]}$ and $\mathcal {U}_{[p,q]}$.

• 1. Assume $\psi = \Diamond _{[p,q]}\psi '$. By Eq. B.8, $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(\varSigma _{l=1}^k\mathcal {C}_{t}(\psi ',\xi _l)+n)$ where $\xi _l$ (with $1\le l \le k$) are the sub-traces of $\pi$ that satisfy interval [p, q]. Let us denote with $n_l$ the length of each sub-trace $\xi _l$ ($1 \le l \le k$). Then, by the induction hypothesis, we have that $\mathcal {C}_{t}(\psi ',\pi ) \in \mathcal {O}(\varSigma _{l=1}^k (n_l^{m-1}*g^l_\phi (n_l)+(m-1)*n_l)+n)$, $g^l_\phi (n_l)$ being the asymptotic time complexity of calculating $\psi '$ over sub-trace $\xi _l$ for all $1 \le l \le k$.

  Let us denote with $g_\phi (n)$ the asymptotically worst function between $\{g_\phi ^1,\cdots ,g_\phi ^k\}$. We have that $\varSigma _{l=1}^k n_l^{m-1}*g_\phi (n_l) \le \varSigma _{l=1}^k n^{m-1}*g_\phi (n) \le n*n^{m-1}g_\phi (n)$. Thus, $\mathcal {C}_{t}(\psi ,\pi ) \in \mathcal {O}(n^m*g_\phi (n)+m*n)$.

• 2. The cases for $\Box _{[p,q]}$ and $\mathcal {U}_{[p,q]}$ are proved similarly.

$\square$

Proposition 5

Given an eLTL formula $\psi$, with m eLTL nested operators, and a data trace $\pi$ of length n, then if $g_\phi$ is the worst space complexity of the interval formulae nested in $\psi$, and $C_s(\psi )$ is the worst spacial complexity of the monitors implementing the eLTL operators of $\psi$ $\mathcal {C}_{s}(\psi ,\pi ) \in \mathcal {O}(n^m*g_\phi (n)+m*C_s(\psi ))$.

Proof

The proof is similar to that of Proposition 4. $\square$