Long-term perturbations in four-body systems with mutual highly inclined orbits

Abstract

Hierarchical Three Body systems with mutual highly inclined orbits have been well-known since the 1960s. Lidov-Kozai cycles arise within them where the inner orbit eccentricity acquires extreme values. In particular, we focus our research on the motion of exoplanets and exomoons on different Three Body stellar scenarios. Our goal is to study how the LK cycles are perturbed by a fourth body (which we called perturbed LK). We analyze the evolution of the eccentricity and inclination of the inner orbit in two cases: the first involves an exoplanet and the second involves an exomoon. Due to the possible stable configurations of a four-body system, we treat two subcases as well: the Totally Hierarchical Configuration and the 2 + 2 configuration. According to that derived from the particular scenarios of study discussed in the present research, the LK perturbed in exomoon orbits around exoplanets seem to exhibit, in general, way less alterations than the exoplanet orbit around its star.

1 Introduction

The Three Body Problem (TBP) begins with the Lunar problem (Gutzwiller 1998). Their objective was to predict the position of the Moon with the highest possible degree of precision. Undoubtedly, the Lunar problem is the most studied case of the TBP and future, present and past of Celestial Mechanics, in general. Lately, as a result of the Lunar problem, the Stellar TBP emerged (Docobo et al. 2021) which became very relevant, especially in the first half of the twenty-first century. In this scenario, a distant third star perturbs the orbit of a binary star. With these conditions and, unlike in the Moon Problem, the masses of the three bodies are generally comparable and the mutual inclination between the inner and outer orbit is not necessarily small.

We know that the Hamiltonian related to the hierarchical TBP can be expanded as a power series depending on a small parameter, which is equal either to the quotient between the semi-axis of the inner and outer orbits, or the quotient between the inner orbit semi-axis and the pericenter distance of the outer orbit. With that in mind, we can study the problem with different perturbation orders and, at the same time, take into account periodic (short and long period) and secular terms. In that regard, some averaging methods for periodic variables were developed (Lagrange 1782; Laplace 1784).

Some of the most used averaging methods are: Von Zeipel (1916), Krylov and Bogoliubov (1947), and Deprit (1969). In particular, Harrington (1968, 1969, 1970) applied the von Zeipel method to average the short period variables. This author also verified that the perturbations are much larger when the mutual inclination is between $39^{\circ}$ and $141^{\circ}$, as Lidov (1961) and Kozai (1962) had stated some years before, hence the name of these perturbations: the Lidov-Kozai cycles (LK hereafter). These cycles have been observed, for example, in the irregular satellites of Uranus. Later on, Docobo (1977) applied the Deprit method (Deprit 1969) to transform canonical systems into systems that are easier to integrate.

In the 1990s, the detection of the first exoplanets orbiting pulsars (Wolszczan and Frail 1992) and main sequence stars (Mayor and Queloz 1995) promoted, once again, the study of the hierarchical TBP, especially those in which the third body is an exoplanet. In these configurations, there are three types of stable¹ orbits (Dvorak 1984): the S-type (the exoplanet orbits one component of the binary star), the P-type (the exoplanet orbits the two components of the binary star), and the L-type (the exoplanet orbits the L4 or L5 Lagrange point). The stability of an exoplanet in binary star systems has been extensively studied (Harrington 1977; Szebehely 1980; Rabl and Dvorak 1988; Dvorak et al. 1989; Pendleton and Black 1983) and several stability criteria have been proposed, for example, Domingos et al. (2006).

Ford et al. (2000), Takeda and Rasio (2005), Naoz et al. (2013), and Docobo et al. (2021) studied the evolution of the elements of the inner orbit of a hierarchical Three Body system, taking into account the long term effects due to the Lidov-Kozai cycles. In Docobo et al. (2021), the authors utilized the TIDES numerical integrator to study the solution of the equations in the hierarchical TBP. Takeda and Rasio (2005) and Naoz et al. (2013) averaged the Hamiltonian related to that problem, truncating it at the second term (the so-called quadrupole approximation) and at the third term (octupole approximation), respectively.

The main goal of the present work is to analyze how the Lidov-Kozai cycles of the TBP are perturbed when a fourth body is added to the system. We call this as perturbed LK. Although the dynamics of 3 + 1 and 2 + 2 configurations do appear in the literature (Hamers et al. 2015; Hamers and Lai 2017), their authors tackle the problem in a general manner, and no distinctions are made between exoplanets and theoretical exomoons, for example. In this report, we compare the differences in the long-term evolution of the eccentricity and inclination of the inner orbit between the three and four-body systems, which is something that seems to be absent in the literature.

2 Methods

In order to run all of the necessary simulations, we needed to integrate the full n-body problem equations. For that, we used the Mathematica package TIDES, which is specialized software that can solve differential equation systems whose computation time is very long. It was developed in 2011 by Alberto Abad, Roberto Barrio, Fernando Blesa, and Marcos Rodríguez in the Grupo de Mecánica Espacial of the Universidad de Zaragoza (Abad et al. 2011a, 2012, 2015). The code is available at: https://sourceforge.net/projects/tidesodes/.

2.1 TIDES algorithm

This package is based on the Taylor Series Method (TSM) to solve the Initial Problem Value (IPV):

$$ \frac{dy}{dt}= f(t,y(t);p), y(t_{0})=y_{0},\ t\in \mathbb{R}, y\in \mathbb{R}^{n},\ p\in \mathbb{R}^{m}, $$

(1)

$y_{0}$ being the initial conditions, $p$ is the parameters and $t$, the independent variable.

Assuming that $f$ is infinitely differentiable, we can find the approximate solution in a lapse of time $t_{i+1}=t_{i}+h_{i}$, expanding the Taylor series in $y(t)$ around the point $t_{i}$ and evaluating it in $t_{i+1}$:

$$ \begin{aligned} &y(t_{0})=y_{0} \\ &y(t_{i+1})\approx y(t_{i})+\frac{dy(t_{i})}{dt}h_{i+1}+\frac{1}{2!} \frac{d^{2}y(t_{i})}{dt^{2}}h^{2}_{i+1}+ \cdots \\ &+\frac{1}{n!}\frac{d^{n}y(t_{i})}{dt^{n}}h^{n}_{i+1} \stackrel{\text{(1)}}{\approx} y(t_{i})+f(t_{i},y(t_{i}))h_{i+1} \\ &+\frac{1}{2!}\frac{df(t_{i},y(t_{i}))}{dt}h^{2}_{i+1}+ \cdots+ \frac{1}{n!}\frac{d^{n-1}f(t_{i},y(t_{i}))}{dt^{n-1}}h^{n}_{i+1}. \end{aligned} $$

(2)

TIDES calculates the $n-1$ successive derivatives of $f$ to solve the IVP via the so-called automatic differentiation or AD, which permits a very efficient calculation. Since TIDES has an adaptive step, the method is sufficiently robust with no need for a huge amount of integration points. This is a big advantage because, in many cases, we will have to integrate over millions or even tens of millions of years. Hence, the variable step permits a smaller amount of integration nodes without losing precision. This allows TIDES to be very stable because it takes into account the sensitivity of the differential equation with respect to initial conditions and/or parameters.

One advantage of TIDES relative to other typical integration algorithms (such as the Runge-Kutta method) is its efficiency, even when we account for high-precision integrations. It has been applied in several astronomical problems and, when comparing TIDES to other packages such as odex, based on the interpolation method, and dop853, based on the RK method (Hairer et al. 1993), it performs considerably better. Technically, the RK method is found to be faster than TIDES when dealing with relatively small tolerances. It is important to note that the precision error is around $10^{-16}$ (16 digits) in our simulations. For that precision level both odex and dop853 required much more CPU time (Abad et al. 2011a,b, 2012, 2015; Barrio et al. 2011; Simó 2001). In summary, TIDES is capable of dealing with very small precision errors without sacrificing CPU time efficiency.

2.2 TIDES structure

TIDES consists basically of MathTIDES, a Mathematica package that writes the differential equation system, the initial conditions, and the parameters in C code (or Fortran) and the library LibTIDES, which we link and compile to the C (Fortran) code generated by MathTIDES.

Moreover, TIDES includes the GMP and MPFR libraries. These libraries allow double and multiple precision, respectively.

2.3 Other features of TIDES

Other interesting features are:

• Search of the zeros of a function of the IVP solution that we choose.

• Search of the local minima and local maxima.

• Integration of the partial derivatives over the variables or the parameters of the IVP that we choose.

3 Long-term perturbations in Three Body systems

Long-term perturbations in hierarchical, Three Body systems with mutual highly inclined orbits have been well known for several decades (Lidov 1961 and Kozai 1962). The latter observed that some Asteroid Belt objects with orbits inclined with respect to the ecliptic had a remarkable eccentric orbit as well, due to the action of Jupiter. For example, the orbital eccentricity and inclination of (1373) Cincinnati ($a=3.42~\text{au}$) oscillates between $0.25-0.6$ and $25^{\circ}-42^{\circ}$, respectively. This effect has also been noted in the irregular satellites of Uranus, since none of these objects (except one) have an orbital inclination larger than $50^{\circ}$ or smaller than $140^{\circ}$. This coincides significantly with the oscillation range where the LK cycles are maximum: $39.23^{\circ }- 140.76^{\circ}$ (Kozai 1962).

In general, when the inclination of the inner orbit with respect to the outer orbit falls between these range of inclinations, LK cycles can excite initially low eccentricities into almost 1 in the long-term (Lidov 1961; Naoz et al. 2013; Takeda and Rasio 2005; Docobo et al. 2021). In this Section, we will examine the differences between the exoplanet and exomoon orbits undergoing LK cycles.

Since we are interested in studying the exoplanet and exomoon dynamics, we will consider two cases: one where the inner orbit is that of an exoplanet orbiting a star (hereafter, the exoplanet case) and the other, where the inner orbit is that of an exomoon orbiting an exoplanet (hereafter, the exomoon case). The mass choices for the exoplanet and exomoon, which we will maintain through this and the following Section, are 1 $M_{J}$ and 1 $M_{\oplus}$, respectively. In both cases, we will assume the outer orbit is that of a star orbiting the inner pair. We will consider all of the masses to be point-like and we will not take into account tidal or relativistic effects throughout this work.

We have made a series of assumptions, both in the exoplanet and exomoon cases. For the former, a) $e_{\mathit{out}}=0.6$; since, in the observed wide binaries distribution, we noted some considerable eccentric orbits, the average being around 0.59 (Tokovinin and Kiyaeva 2015), b) $a_{\mathit{out}}<100~\text{au}$, just to set an upper limit to the outer semi-axis, c) the eccentricities of the inner orbit are low, d) the initial inclination between the outer and inner orbits is between $60^{\circ}$ and $70^{\circ}$,² and e) the mass of the third body is that of a brown dwarf. With these assumptions in mind, we have carried out several simulations using TIDES for certain initial values of $a_{\mathit{out}}\in \{20, 30, 50, 75, 90\}~\text{au}$, $e_{\mathit{in}} \in \{0.001, 0.1, 0.2\}$ and the mutual inclination between the inner and outer orbits $\in \{60^{\circ}, 65^{\circ}, 70^{\circ}\}$. The initial values of $T$, $\Omega$ and $\omega$ are the same as in Table 1. We noticed two things. On one hand, orbital flips seem to occur in all cases. On the other hand, there are periods of time where the orbital eccentricity of the exoplanet approaches values extremely close to 1.

Table 1 Initial orbital elements of the baseline example for the exoplanet case. In each case, the orbital elements are referenced to the invariable plane of the system

We carried out an analogous study in the exomoon case but, this time, we also used three stellar mass values (brown dwarf, red dwarf, 1 $M_{ \odot}$). We assumed that a) eccentricities of the inner orbit are low, b) eccentricities of the outer orbit can be moderate ($0\leq e_{\mathit{out}} \leq 0.6$), c) the initial inclination between the outer and inner orbits is between $60^{\circ}$ and $70^{\circ}$, and d) the stellar mass is not larger than of the Sun. The different values we used are: $a_{\mathit{out}}\in \{3,5,10\}~\text{au}$, $e_{\mathit{out}}\in \{0,0.1,0.2, 0.4, 0.6\}$, $e_{\mathit{in}}\in \{0.05, 0.1,0.2,0.3\}$, and the inclination between the outer and inner orbits $\in \{60^{\circ}, 65^{\circ}, 70^{\circ}\}$. The initial values of $T$, $\Omega$ and $\omega$ are the same as in Table 2. Unlike the exoplanet case, we have found no orbital flips in the exomoon orbit. Consequently, the eccentricity, although it is highly excited to values close to 0.8 in most cases, hardly ever reached close to 1 values, except when we placed the exomoon very close to the stability limit.³

Table 2 Initial orbital elements of the baseline example for the exomoon case. In each case, the orbital elements are referenced to the invariable plane of the system

As baseline examples upon which we will build the simulations in the next Section, we chose that of Tables 1 and 2. Figure 1 shows the eccentricity and inclination⁴ evolution that undergoes the orbit of a Jupiter-type exoplanet that revolves around a Solar-type star and, at the same time, of a brown dwarf (with mass of 40 $M_{J}$) that orbits the barycenter of both. The eccentricity, initially 0, is excited close to 1 in 5 Myr. The inclination, on the other hand, oscillates between $40^{\circ}$ and $140^{\circ}$, which produces orientation changes in the exoplanet orbit, periodically changing from prograde to retrograde motion, and vice versa. In addition, the argument of the pericenter circularizes.

Fig. 1

Exoplanet initial orbital inclination: $64.7^{\circ}$. Outer orbit initial inclination: $0.3^{\circ}$. Inner initial orbital semi-major axis: 6 au. Outer initial orbital semi-major axis: 100 au. Exoplanet initial orbital eccentricity: 0.001. Outer orbit initial eccentricity: 0.6. Exoplanet initial orbit argument of the pericenter: $45^{\circ}$. Outer orbit argument of the pericenter: $0^{\circ}$. Exoplanet initial orbit ascending node longitude: $240^{\circ}$. Outer orbit ascending node longitude: $60^{\circ}$. All periastron epochs are equal to 0. Example taken from Naoz et al. (2013) to check if the results match and our integration is correct

Figure 2 shows the eccentricity and inclination evolution of the orbit of an Earth-type exomoon revolving around a Jupiter-type exoplanet whose barycenter orbits a brown dwarf. In this example, although the eccentricity of the exomoon orbit does increase significantly from 0 to 0.8, we can see that this increase is less extreme than in the exoplanet case. The same goes for the inclination, where we can see that it never changes its orientation, oscillating between $35^{\circ}$ and $65^{\circ}$. Moreover, the argument of the pericenter, as in the previous case, circularizes in the given examples (Fig. 3). However, it can be proven that is not something characteristic of the LK cycles because, in our exoplanet case, if we assume that both stars are Solar-type with the same initial orbit inclination, the argument of the pericenter librates around $90^{ \circ}$, which indicates that the behavior of the argument of the pericenter will depend on the orbital and physical parameters of the bodies in the system.⁵

Fig. 2

Initial exomoon orbital inclination: $60^{\circ}$. Initial exomoon orbital eccentricity: 0.05. Initial exomoon orbital semi-axis: $0.1~\text{au}$. Initial outer orbit semi-axis: $10~\text{au}$. Initial outer orbit eccentricity: 0. Initial outer orbit inclination: $0.5^{\circ}$. Initial exomoon orbit argument of the pericenter: $45^{\circ}$. Initial outer orbit argument of the pericenter: $0^{\circ}$. Initial exomoon orbit ascending node longitude: $240^{\circ}$. Initial outer orbit ascending node longitude: $60^{ \circ}$. All periastron epochs are equal to 0

Fig. 3

Evolution of the argument of the pericenter for the example in Fig. 1 (exoplanet case, up) and for the example of Fig. 2 (exomoon case, down). In both cases, the argument of the pericenter circularizes

In summary, in all of the examples we have considered throughout this Section, the LK cycles undergoing the exomoon orbit seem to be less extreme than those of the exoplanet orbit. It is worth remarking that this is not a general conclusion but a result obtained from a particular set of initial conditions associated with each case of study.

Now, why do we see such differences in the LK cycles between the exoplanet and the exomoon cases? We consider that it has to do with the difference in the stability regions. Due to the masses of the bodies in the systems, in order for the bodies to be in a stable orbit, the quotient between the inner orbit and outer orbit semi-axis (the small parameter we mentioned in the Introduction, $\epsilon$) has to be much smaller in the exomoon case. Therefore, if we expand the Hamiltonian of the hierarchical TBP as a function of this parameter, we have the next expression (Harrington 1968; Docobo 1977; Ford et al. 2000; Naoz et al. 2013):

(3)

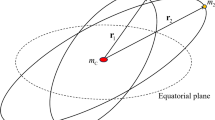
where $r_{1}$ and $r_{2}$ are the radius vectors of the inner and outer orbit, respectively, $\epsilon =a_{1}/a_{2}$, $P_{j}$ is the Legendre polynomial of degree $j$, $\Phi$ is the angle between $r_{1}$ and $r_{2}$, $a_{1}$ and $a_{2}$ are the inner and outer orbit semi-axis, respectively, and

$$ M_{j}= m_{1}m_{2}m_{3} \frac{m_{1}^{j-1}-(-m_{2})^{j-1}}{(m_{1}+m_{2})^{j}}. $$

As usual, in order to handle the Hamiltonian, we need to truncate the sumatory terms. Truncating them at $j=2$, we obtain the quadrupole approximation and, at $j=3$, the octupole approximation.

Obviously, the smaller $\epsilon$, the smaller will be the difference between the quadrupole or octupole approximation and the entire Hamiltonian. So, in the exomoon case, the contribution of the summands such $j\geq 3$ will be negligible and, likewise, the octupole approximation will be very similar to the quadrupole approximation.

On the other hand, if $\epsilon$ is not very small, orbital orientation changes may be absent in the quadrupole approximation but not in the octupole approximation (Naoz et al. 2013). Hence, we deduce that the reason why these changes are non-existing in the exomoon case is because $\epsilon$ is very small and the contribution of the summands such $j>2$ is not enough to change the orbit orientation.

4 Long-term perturbations in four-body systems

Now, we analyze how Lidov-Kozai cycles are perturbed by a fourth body. In order to do that, we add it in both the exoplanet (Fig. 1) and the exomoon case (Fig. 2). In a four-body system, there are at least two possible stable configurations: the Totally Hierarchical Configuration, where the bodies are organized in nested pairs (Fig. 4), and the 2 + 2 configuration, in which the bodies are organized in two separated pairs, where both revolve around their center of mass. Next, we illustrate each system using the decomposition in subsystems depending on their hierarchy, following the methodology described in Abad and Ribera (1984) and Abad and Docobo (1987). This will help us visualize each configuration.

Fig. 4

Diagram of the Totally Hierarchical Configuration

4.1 Exoplanet case

We will assume, for the first three bodies, the same orbital elements as in the example of the Fig. 1 and we will study different examples depending on the mass, eccentricity, and orbital inclination of the fourth body.

We will assume the mass of the fourth body is equal to that of a low-mass star (a red or brown dwarf, depending of the example). The initial eccentricity will be low to avoid orbital instabilities, between 0.1 and 0.3, as well as the initial inclination, which will be between $0.5^{\circ}$ and $40^{ \circ}$.⁶ The initial semi-axis, in the THC (Totally Hierarchical Configuration), will be chosen to be as close as the stability limit as possible. The initial $\Omega$ and $\omega$ will be, in both exoplanet and exomoon cases, always equal to $30^{\circ}$ and $0^{\circ}$, respectively.⁷

4.1.1 Totally hierarchical configuration

We associate each case with another already covered by Campo and Docobo (2014) and Campo (2019) in which they took into account each and every four-body system where one of the bodies is an exoplanet and/or an exomoon (Fig. 5).

Fig. 5

Hierarchical four-body system with an exoplanet orbiting one component of the inner binary. It corresponds to the case 12 of Campo and Docobo (2014)

From all the cases of study (Table 3), we can state some facts:

Table 3 Exoplanet case. Initial orbital elements of the fourth body. In each case, the orbital elements are referenced to the invariable plane of the system

1. The examples 1 and 2, in which the initial orbital inclination of the fourth body is $0.5^{\circ}$ (Figs. 6 and 7, respectively), still preserve the LK mechanism, as in the TBP: the inclination oscillations cause the orbit to change from prograde to retrograde motion, and vice versa. We notice one difference though: the periods in which these orbital flips happen become dramatically larger or shorter in ∼17 Myr (see Figs. 6 and 7). Likewise, its orbital eccentricity undergoes huge oscillations, periodically approaching 1, and the duration of these periods can increase or decrease over time. We think that the presence of the fourth body is the cause of such behavior but a detailed explanation about this will be explored in future studies.

Fig. 6

Temporal evolution of the eccentricity (top panel) and the orbital inclination (bottom panel) for the exoplanet associated with Table 1 in a totally hierarchical four-body system. The mass and the initial semi-major axis, eccentricity, and inclination of the fourth body are 40 $M_{J}$, 2500 au, 0.2, and 0.5 degrees, respectively

Fig. 7

Temporal evolution of the eccentricity (top panel) and the orbital inclination (bottom panel) for the exoplanet associated with Table 1 in a totally hierarchical four-body system. The mass and the initial semi-major axis, eccentricity, and inclination of the fourth body are 40 $M_{J}$, 2500 au, 0.3, and 0.5 degrees, respectively

2. The example 3, in which the initial orbital inclination of the fourth body is $20^{\circ}$ (Fig. 8), still preserves the LK behavior at first, with the exception that, in this case, its inclination undergoes higher amplitude oscillations ($30^{\circ}$ to $180^{\circ}$). However, after 10 Myr, the orientation changes become more chaotic and rapid as its eccentricity constantly oscillates between 0 and 0.9999 in less time.

Fig. 8

Temporal evolution of the eccentricity (top panel) and the orbital inclination (bottom panel) for the exoplanet associated with Table 1 in a totally hierarchical four-body system. The mass and the initial semi-major axis, eccentricity, and inclination of the fourth body are 40 $M_{J}$, 2500 au, 0.2, and 20 degrees, respectively

3. When we modified the initial orbital inclination of the fourth body in both examples 3 and 4 to be greater than $25^{\circ}$, we verified that the exoplanet orbit become unstable. Therefore, in these examples, the orbital inclination of the fourth body cannot be very large.

4. In example 4, when the mass of the fourth body is 209.4 $\mbox{M}_{J}$ (red dwarf), the exoplanet orbit becomes unstable when we modify the initial orbital inclination of the fourth body to be $0.5^{\circ}$. However, when its orbit is initially slightly inclined (between $10^{\circ}$ and $20^{ \circ}$), the exoplanet orbit becomes stable. So, if the initial orbital inclination of the fourth body is $10^{\circ}$ (Fig. 9), the LK mechanism can be noticed in the initial orbital flip (15 Myr). Later on, these flips happen chaotically, without the pattern present in the LK cycles (symmetrical flips with respect to $90^{ \circ}$).

Fig. 9

Temporal evolution of the eccentricity (top panel) and the orbital inclination (bottom panel) for the exoplanet associated with Table 1 in a totally hierarchical four-body system. The mass and the initial semi-major axis, eccentricity, and inclination of the fourth body are 209.4 $M_{J}$, 2500 au, 0.2, and 10 degrees, respectively

5. With regard to the argument of the pericenter, in all cases, periods of libration and circularization alternate over time. Circularization seems to be more frequent (Figs. 10(a), 10(b), 10(c) and 10(d)).

Fig. 10

Evolution of the argument of the pericenter for the examples of the exoplanet case

4.1.2 2 + 2 configuration

In this case, which is illustrated in Figs. 11 and 12, we will assume that the initial exoplanet orbital inclination is $70^{\circ}$. The rest of the initial orbital and physical parameters will be the same as those of the Three Body case for all three bodies (see Fig. 1).⁸

Fig. 11

Diagram of the 2 + 2 configuration

Fig. 12

2 + 2 four-body system with an exoplanet orbiting the distant component. Case 13 of Campo and Docobo (2014)

In examples 5 and 6, where the mass of the fourth body is 40 $M_{J}$, something curious happens: the orbital flips observed in the Three Body case are suppressed. This occurs when $a=3~\text{au}$, $i=0.5^{\circ}$ (Fig. 13), and $a=5~\text{au}$, $i=40^{\circ}$ (Fig. 14). Therefore, the presence of a fourth body in these examples severely restricts the oscillation of the exoplanet orbit inclination with respect to the Three Body case.

Fig. 13

Fourth body initial orbital eccentricity: 0.1. Fourth body initial orbital inclination: $0.5^{\circ}$. Fourth body initial orbital semi-axis with respect to the barycenter: 3 au $\Omega =30^{\circ}$, $\omega =0^{\circ}$. Fourth body mass: 40 $M_{J}$. Exoplanet initial orbital inclination: $70^{\circ}$

Fig. 14

Fourth body initial orbital eccentricity: 0.1. Fourth body initial orbital inclination: $40^{\circ}$. Fourth body initial orbital semi-axis with respect to the barycenter: 5 au. $\Omega =30^{\circ}$, $\omega =0^{\circ}$. Fourth body mass: 40 $M_{J}$. Exoplanet initial orbital inclination: $70^{\circ}$

The argument of the pericenter exhibits behavior analogous to the THC configuration in Example 5. However, in Example 6, the argument of the pericenter librates around 270 degrees (Figs. 10(e) and 10(f)).

4.2 Exomoon case

For the first three bodies, we will assume the same orbital elements as in Fig. 2. In the exoplanet case, we study different examples depending on the mass, eccentricity and orbital inclination of the fourth body. For the exomoon case, the examples are represented in Table 4.

Table 4 Exomoon case. Initial orbital elements of the fourth body. In each case, the orbital elements are referenced to the invariable plane of the system

We also assume that the mass of the fourth body is equal to that of a low-mass star with the eccentricity between 0.1 and 0.3 and the inclination, between $0.5^{\circ}$ and $30^{\circ}$. The semi-axis in the THC configuration is chosen to be as close to the stability limit as possible.

4.2.1 Totally hierarchical configuration

This case is illustrated by Fig. 15.

Fig. 15

Binary star with a planet + satellite system orbiting one component. Case 7 of Campo and Docobo (2014)

In examples 7 and 8 (see Table 4) in which the initial orbital inclination of the fourth body is close to 0 (Figs. 16 and 17), the LK cycles of the exomoon orbit remain practically unaltered, that is, we do not see great differences between the perturbed LK and the LK cycles.

Fig. 16

Fourth body initial orbital eccentricity: 0.1. Fourth body initial orbital inclination: $0.5^{\circ}$. Fourth body initial orbital semi-axis: 80 au. Fourth body mass: 209.4 $M_{J}$

Fig. 17

Fourth body initial orbital eccentricity: 0.2. Fourth body initial orbital inclination: $0.5^{\circ}$. Fourth body initial orbital semi-axis: 80 au. Fourth body mass: 209.4 $M_{J}$

On the other hand, in both examples, the argument of the pericenter changes from libration to circularization and vice versa, but periods of libration are more frequent (Figs. 18(a) and 18(b)).

Fig. 18

Evolution of the argument of the pericenter for the examples of the exomoon case

4.2.2 2 + 2 configuration

This case is illustrated by Fig. 19, and is represented by examples $9 - 12$ (see Table 4). In the first two examples in which the initial orbital inclination of the fourth body is $0.5^{\circ}$ (Figs. 20 and 21), we observe behavior analogous to the cases studied in the Totally Hierarchical Configuration. We do not see great differences between the perturbed LK and the LK cycles. However, when the initial orbital inclination of the fourth is moderate ($10^{\circ}-30^{\circ}$; examples 11 and 12), large and small ranges of oscillations in the eccentricity alternate over time (Figs. 22 and 23, respectively).

Fig. 19

Case 10 of Campo and Docobo (2014)

Fig. 20

Fourth body initial orbital eccentricity: 0.1. Fourth body initial orbital inclination: $0.5^{\circ}$. Fourth body initial orbital semi-axis: 3 au. Fourth body mass: 40 $M_{J}$

Fig. 21

Fourth body initial orbital eccentricity: 0.3. Fourth body initial orbital inclination: $0.5^{\circ}$. Fourth body initial orbital semi-axis: 3 au. Fourth body mass: 40 $M_{J}$

Fig. 22

Fourth body initial orbital eccentricity: 0.1. Fourth body initial orbital inclination: $10^{\circ}$. Fourth body initial orbital semi-axis: 3 au. Fourth body mass: 40 $M_{J}$

Fig. 23

Fourth body initial orbital eccentricity: 0.1. Fourth body initial orbital inclination: $30^{\circ}$. Fourth body initial orbital semi-axis: 3 au. Fourth body mass: 40 $M_{J}$

With regard to the argument of the pericenter, periods of libration and circularization alternate over time, as usual (Figs. 18(c)–18(f)). Unlike in the THC configuration, the oscillations seem to be produced in a very short time, and circularization is substantially more frequent.

5 Conclusions

The perturbation of the LK cycles by a fourth body (perturbed LK) is very complex, and it depends heavily on the orbital and physical parameters. In this report, we carry out a numerical study of this behavior by analyzing the long-term evolution of the orbital eccentricity, the argument of the pericenter and the inclination of an exoplanet and an exomoon. We compare their evolution differences for several examples of the physical and initial orbital parameters of the fourth body (Tables 3 and 4 for the exoplanet and exomoon cases, respectively). From those examples, we draw the following conclusions:

1. There are significant differences in the LK cycles related to the TBP that depend of the nature of the bodies in the system. The difference occurs due to the values in the masses between one case and the other. Therefore, in order for the systems to be Lagrange-stable, the quotient of the inner and outer orbit semi-axes must be smaller in the exomoon case.

2. In many of the examples of the exomoon case, the perturbed LK behavior is similar to the LK cycles in the TBP. However, in the exoplanet case, we always found some long-term differences between the perturbed LK of the exoplanet orbit and its LK cycles in the hierarchical TBP.

3. In some instances, the perturbed LK in the exoplanet case can suppress the orbital flips that are produced by the LK cycles in the TBP. In other cases, it may also accelerate or decelerate them. The acceleration/deceleration of the LK cycles is an interesting topic that may be covered in future studies.

4. The evolution of the argument of the pericenter in the exoplanet and the exomoon cases depends on the orbital and physical parameters of the involved bodies in the system. In 11 of the 12 four-body examples that we studied (all but Example 6), we observe a mixed evolution, where the argument of the pericenter changes chaotically from libration to circularization and vice versa.

5. Regarding all the examples considered in this report, in both three- and four-body systems, we found that the exomoon orbit around the exoplanet generally exhibits less alterations in its orbit than the exoplanet orbit around the star. Nonetheless, we must clarify that our study is focused on a handful of examples based on discrete points in the orbital parameter space. It is not meant to conclude generalizations about the LK perturbed mechanism but to explore particular scenarios of study under several assumptions and to extract features. Further studies will be necessary in order to fully unpack the general behavior of the perturbed LK in four-body systems.