Flow Topology of the Bi-Stable Wake States for the DrivAer Fastback Model

Abstract

For this work, conditional averaging and Proper Orthogonal Decomposition (POD) were used to analyze the salient three-dimensional structures in the wake of a DrivAer fastback model with smooth underbody. Conditional averaging revealed that the bi-stable structure of the wake consists of a ring-like structure with three vortex legs, which includes a vortex pair on the side associated with the bi-stability and one on the opposite side associated with the wheel vortex. POD revealed the entrainment of low-momentum fluid from the wheel wake into the vortex pair leads to an induced spanwise crossflow which drives a feedback loop for the bi-stability. The resultant bi-stable structure was dependent on the state of the wheels. With stationary wheels, the feedback mechanism is enhanced, leading to higher spanwise crossflow that breaks the ring-like vortex. A different structure was observed when the wheels rotate, wherein the ring-like structure is unbroken and pierced by the vortex pair. The feedback mechanism and resultant vortex structure are similar to those found in simplified square-back models. Given the similarity in bi-stability between realistic and simplified vehicles, the suppression of the bi-stability in realistic vehicles could initially be based on the same mechanism as that for simplified square-back models.

1 Introduction

Automotive wake flows have been found to be subject to a wake bi-stability (Grandemange et al. 2013). Characterized by long-period asymmetries, the wake bi-stability has been found to increase drag (Grandemange et al. 2014, 2015; Evrard et al. 2016; Pavia and Passmore 2018; Pavia et al. 2018, 2020; Khan et al. 2022), affect driving stability (Bonnavion et al. 2017, 2019; Brandt et al. 2022), and produce side-force fluctuations which can impact passenger comfort (Aultman et al. 2021). Suppression of wake bi-stability and its corresponding effects have been achieved in varying degrees through flow control methods such as base cavities (Grandemange et al. 2015; Evrard et al. 2016; Fan et al. 2022; Keirsbulck et al. 2023), flaps (Brackston et al. 2016, 2018; Camacho-Sánchez et al. 2023), tapers (Perry et al. 2016; Pavia and Passmore 2018; Pavia et al. 2019; Luckhurst et al. 2019), and suction and blowing (Li et al. 2016; Evstafyeva et al. 2017; Ahmed and Morgans 2022; Khan et al. 2022; Keirsbulck et al. 2023). The majority of these existing studies either focused on highly simplified square-back or “box” models or were performed under “academic” wind-tunnel conditions with a fixed floor, low Reynolds numbers, low inflow turbulence, and zero yaw. They nevertheless provided valuable insight into the occurrence, dynamics, and control of the wake bi-stability phenomenon and therefore served as the necessary building block components to facilitate further progress.

To complement the fundamental studies under academic wind-tunnel conditions, work has been done to analyze the effects of more realistic driving conditions on the wake bi-stability. In particular, changes in Reynolds number have been extensively studied  (Cadot et al. 2015; Volpe et al. 2015; He et al. 2021, 2022a; Fan and Cadot 2023; Su et al. 2023; Grandemange et al. 2015), considering that many tests under “academic” wind-tunnel conditions are done at extremely low Reynolds numbers (e.g., small models at low speeds). The wake bi-stability was found to persist at high Reynolds numbers that are representative of realistic driving conditions (Grandemange et al. 2015). Additionally, the bi-stable switching rate increases substantially with the Reynolds number so that the transitional or symmetric state becomes statistically relevant at high Reynolds numbers. Such a wake was even referred to as a statistical “tri-stable” wake due to its significantly larger amount of time spent switching between the bi-stable states (He et al. 2022a). Similar to the Reynolds number, the development of bi-stability persists at high inflow turbulence levels representative of real world driving conditions (Cadot et al. 2020; Burton et al. 2021; Chen et al. 2023) as well as at the small pitch and yaw angles that may become relevant under driving conditions with relatively small crosswinds (Bonnavion et al. 2017; Bonnavion and Cadot 2018). Furthermore, the addition of a rolling road to reflect real driving only changes the degree of asymmetry within the wake without suppressing it (He et al. 2022b). However, unlike these basic flow conditions, wind-tunnel blockage was found to suppress the bi-stability, but only if a sufficiently small test section is used (He et al. 2021). Therefore, the controlled wind-tunnel conditions in the literature are likely sufficient to represent realistic driving conditions.

In addition to more realistic driving conditions, multiple attempts have been made to increase the complexity of vehicle models to better reflect production vehicles by adjusting various aspects of the geometry. While adjustments to the upstream portion of the vehicle were found to be inconsequential to the development of the bi-stability (Legeai and Cadot 2020), several specifically tuned geometries in the rear end were proven to be impactful, including tapering (Luckhurst et al. 2019; Perry et al. 2016), slant angles (He et al. 2021), and fillets (He et al. 2021). Grandemange et al. (2015) further showed that the inclusion of wheels have not restricted the development of the bi-stability (Grandemange et al. 2015), while the previously observed bi-stability suppression with wheels by Pavia et al. (2020) was actually caused by the influence of the ground boundary layer (Su et al. 2023). Therefore, one can reasonably expect the existence of bi-stable behaviors in a complex automotive vehicle if the vehicle is not specifically tuned to mitigate the bi-stability. Indeed, wake bi-stability has been found to occur for both realistic automotive models (Hesse and Morgans 2021; Aultman et al. 2021; Yu et al. 2022) and production vehicles (Grandemange et al. 2014; Bonnavion et al. 2017, 2019; Yuan et al. 2023).

Although the presence of the wake bi-stability has been confirmed for more realistic car models (Hesse and Morgans 2021; Aultman et al. 2021; Yu et al. 2022) and even for a variety of production vehicles (Grandemange et al. 2014; Bonnavion et al. 2017, 2019), the exact structure and dynamics of the bi-stable behaviors have not been thoroughly characterized. Such information is critical to the deployment of control techniques for suppressing the bi-stability on realistic automotive vehicles. In particular, the bi-stability and its subsequent effects on realistic automotive vehicles could be better targeted if parallels could be drawn with the large volume of existing studies from simplified square-back models. Thus, the goal of this work is to characterize the salient three-dimensional features of the wake bi-stability behind a realistic car model. To achieve this goal, we utilized the DrivAer fastback model with a smooth underbody as our realistic car model at a realistic Reynolds number (Sect. 2.1), along with a well-documented existing database of Lattice-Boltzmann Method (LBM) simulations with a long sampling range of more than 200 seconds (Aultman et al. 2021) to capture the full wake dynamics (Sect. 2.2). In the previous work of Aultman et al. (2021), the LBM simulations were validated against experiments and the existence of bi-stability in the wake of the DrivAer model with and without rotating wheels had been illustrated through the time trace and probability density function (PDF) of the side-force coefficient. However, the previous flow analysis for the DrivAer model was limited in scope in comparison to those for simplified square-back models, preventing parallels being drawn between simplified and realistic vehicle models. The current study filled in the gap by introducing more advanced flow analyses that are similar to those in Pavia et al. (2020) for a simplified square-back model. Specifically, conditional averaging and Proper Orthogonal Decomposition (POD) were introduced to analyze the salient three-dimensional structures and their underlying dynamics as well as to draw comparisons to the studies in the literature for simplified models (Sect. 3). All key findings were then summarized in Sect. 4.

2 Methodology

2.1 Vehicle Model

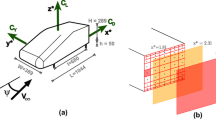
To better represent a realistic vehicle geometry, we utilized the DrivAer fastback model with a smooth underbody (Heft et al. 2012). This model better represents a realistic vehicle model compared to square back models with the inclusion of highly contoured surfaces, side mirrors, complex wheels, etc. Additionally, the use of the smooth underbody provides both a spanwise symmetric geometry to better capture the bi-stability, as well as a better representation of electric vehicles which are becoming more prevalent in the automotive market. To better match realistic driving conditions, we utilized the full-scale DrivAer model with a length $L=4.613$ m, a height $H=1.418$ m, and a width excluding side mirrors of $W=1.753$ m (Fig. 1). All scales given throughout this paper will be non-dimensionalized by the relevant vehicle dimensions.

2.2 Computational Setup

For this work, we utilized the data generated previously in Aultman et al. (2021). A brief summary of the computational setup is given below.

Given the long-period nature of the bi-stability, we utilized LBM simulations due to their high accuracy and computational efficiency in automotive flow field predictions (Forbes et al. 2017; Aultman et al. 2022). Additionally, the method acts as a Very Large-Eddy Simulation (VLES) of which similar methods have been used to capture the bi-stability with lower computational cost than wall-resolved Large-Eddy Simulation (LES) (He et al. 2021). The vehicle was placed in a large rectangular domain with dimensions $38L\times 22L\times 7.5L$ in the streamwise, spanwise, and road-normal directions, respectively (Fig. 2). A uniform freestream inflow of $U_\infty =16$ m/s with a turbulence intensity of $0.1\%$ was placed 12L upstream of the vehicle. This flow speed resulted in a Reynolds number based on vehicle width of $Re=1.86\times 10^6$ ($Re=\rho _\infty U_\infty W/\mu$ where $\rho _\infty$ is the freestream density and $\mu$ is the viscosity). A fixed pressure outlet was applied 25L downstream of the vehicle with the remaining farfield planes (e.g. top and sides) set to symmetry conditions to replicate the freestream. All surfaces of the vehicle were set to a no-slip condition with the exception of the wheels. Two different wheel conditions were tested. In one instance, the wheels were stationary with a stationary ground plane underneath the vehicle. A no-slip portion of the ground extended 1.12L in front of the vehicle, ensuring that the boundary layer did not grow thicker than the minimum height of the underbody which could suppress the bi-stability (Su et al. 2023). This condition is referred to throughout the text as the Stationary Wheels case. In the other case, the wheels were set to rotate at 482.76 rpm to match freestream velocity at the outermost extent of the tires. Wheel rotation was set using a sliding mesh method which fully represents the wheel rotation in comparison to other models (Hobeika and Sebben 2018; Aultman and Duan 2023). Additionally, the ground plane was set to move at the freestream velocity. This case will be referred to as the Rotating Wheels case throughout the remainder of this text.

Fig. 1

Side view (left) and rear view (right) of the DrivAer fastback model with smooth underbody used for analyzing the wake bi-stability

For both simulations, the commercial software PowerFLOW (V6-2020) was used to simulate the flow field. Several grids were tested using 89, 174, and 272 million voxels. Little change was observed in the mean flow time-averaged over $tU_\infty /W=27.4$ (3 s) across the three grids. Additionally, the 174 million voxel grid was run for $tU_\infty /W=465.4$ (50 s) and the bi-stability still appeared to be present, producing similar results to the 89 million voxel grid. If coarsening the grid were to affect the solution, it would be expected to produce different dynamics between the two grids (Zhang et al. 2022). Thus, the coarsest grid was deemed sufficient for the full bi-stability simulations. Full details of the grid refinement study can be found in the work of Aultman et al. (2021). For the full bi-stability simulation, the total simulation time was $tU_\infty /W=1871.2$ (205 s) with flow statistics sampled over $tU_\infty /W=1825.6$ (200 s). Given that the asymmetric switching of the bi-stability has been found to be up to $\sim 1,000W/U_\infty$ (Grandemange et al. 2013), this time length should allow for at least two switching events to be observed. Although this run time is shorter than that of experiments which commonly run up to $t U_\infty /W$ O(10,000) (Hesse and Morgans 2021; Ahmed and Morgans 2022; Evstafyeva et al. 2017; Dalla Longa et al. 2019; He et al. 2021; Su et al. 2023) or even O(100,000) (Volpe et al. 2015; Cadot et al. 2020; Fan and Cadot 2023), it has been found acceptable for capturing the bi-stability with simulations (Hesse and Morgans 2021; Ahmed and Morgans 2022; Evstafyeva et al. 2017; Dalla Longa et al. 2019; He et al. 2021; Su et al. 2023) as well as industrial scales previously (Grandemange et al. 2015; Bonnavion et al. 2019, 2017).

Fig. 2

Computational domain and boundary conditions with grid visualization along the vehicle centerline and ground planes

2.3 Proper Orthogonal Decomposition (POD)

In order to analyze the transient flow field, Proper Orthogonal Decomposition (POD) was used to separate the flow structures into “modes” which has been successfully used to analyze the bi-stability previously (Pavia et al. 2020). In order to use POD, we recorded full flowfield snapshots of the entire domain at a rate of $\Delta tU_\infty /W=0.9$ (or a sampling frequency of $f = 10$ Hz) over the entire sampling range of $tU_\infty /W=1825.6$ (200s), which lead to 2,000 snapshots. Considering that the size of the full flow field snapshots can be as large as terabytes, we first extracted a subdomain in the wake region using a box (Fig. 3a). The box was set to a size of $0.47L\times 0.43L \times 0.31L$ in the streamwise, spanwise, and road-normal directions, respectively. This size was selected to be large enough to capture large-scale wake motions, which include all the regions of large turbulent kinetic energy (with $\overline{k} \ge 0.1\overline{k}_{max}$) in all directions but exclude the region of the ground boundary layer. One should note that the road-normal box size of 0.31L is comparable to the vehicle height ($H = 0.307L$), and the spanwise box size of 0.43L is wider than the vehicle width ($W = 0.38L$). The sampling rate of $f =10$ Hz corresponds to a non-dimensional frequency of $St_W=fW/U_\infty = 1.10$, which is significantly higher than that used by Pavia et al. (2020) with $St_W=0.07$. The flow variables were interpolated onto a uniformly distributed grid with a size of $(0.018W)^3$, which aligns with the voxel size used in the wake refinement region. Thus, the interpolated data is expected to provide sufficient resolution in both space and time to capture the wake bi-stability.

Fig. 3

a Wake volume used for interpolation of the flow field in POD and the average turbulent kinetic energy normalized by the maximum in the wake $\overline{k}/\overline{k}_{max}$ along the b vehicle centerline and c $Z/H=0.45$ planes used to determine the box size

3 Results and Discussion

3.1 Characterization of Bi-Stability

To begin our analysis, we first evaluated the flow field for the presence of the wake bi-stability. Given that the wake bi-stability is characterized as a large, long-period asymmetry of the wake, we considered the pressure footprint such a structure would have on the vehicle base. Extracted roughly halfway up the base ($Z/H=0.45$), we captured the pressure footprint through the time-trace of pressure by taking two probes on opposing sides of the base ($Y/W= \pm 0.3$) (Fig. 4). Three major observations were apparent when looking at the base pressure footprint in time. First, large long-period low-pressure fluctuations developed across the base of the vehicle. These fluctuations in base pressure appeared to be asymmetric, alternating from one side of the vehicle to the other intermittently. Tracking the peaks and troughs of the pressure fluctuations, it is apparent that the two time-traces are out of phase of one another. Such fluctuations align with the expected behavior of the wake bi-stability. Second, although these pressure fluctuations are present for both stationary and rotating wheels, the implementation of wheel rotation reduced both the magnitude and time-period of these fluctuations. This observation aligns with the findings from the previous study of Aultman et al. (2021) who found that wheel rotation reduced the prominent low-frequency peak in the side-force spectra. Third, the transition of pressure between the bi-stable states is not as distinct or rapid as that typically observed for square back models. Given the presence of rounded edges on the base, the separation location is no longer fixed as with square back models. Instead, the separation point is allowed to freely move, which may lead to a drift between states rather than a sudden “switch”. Additional complex vehicle features such as wheel wells and side-body panels can create body contour vortices that will likely affect bi-stable switching by creating greater variability in the wake.

Fig. 4

Comparison of the time-trace of pressure coefficient ($C_p=\frac{P}{q_\infty }$ where P is static pressure and $q_\infty$ is the freestream dynamic pressure) at a $Z/H=0.45$ and $Y/W=\pm 0.3$ for b stationary wheels and c rotating wheels. Note the time-trace was filtered using a sliding average of $tU_\infty /W=15.4$ (1.7s) similar to Perry et al. (2016), Pavia and Passmore (2017) with the faded lines representing the unfiltered signal and the dashed lines representing the time-average

To further characterize the wake asymmetry, the spanwise pressure gradient near the top of the base at a height of $Z/H = 0.70$ at the vehicle centerline ($Y = 0$) was tracked (Fig. 5). This location was selected due to the prominent bi-stable dynamics which will be further discussed in Sect. 3.3. Herein, we calculated the probability density function (PDF) of the gradient by filtering the pressure time trace using a sliding average with a window of $tU_\infty /W=415.4$ (1.7s), similar to the non-dimensionalized filter of Perry et al. (2016) and Pavia and Passmore (2017). A clear asymmetry in the peak is observed in the PDF of the spanwise pressure gradient. This asymmetry indicates the presence of two distinct pressure gradients that are either positive or negative, which is consistent with the previous observations for the long-period fluctuations of the low pressure on the base. However, we observed the lack of a clear second peak expected from the bi-stability. This is not unexpected though, as the reduced signal length of the simulation compared to experiments (Hesse and Morgans 2021; Ahmed and Morgans 2022; Evstafyeva et al. 2017; Dalla Longa et al. 2019; He et al. 2021; Su et al. 2023) is unlikely to capture well converged statistics of the effects of bi-stable switching. Additionally, we noted that the implementation of wheel rotation leads to a wider distribution of the centerline spanwise pressure gradient indicating far more dynamics concentrated near the vehicle centerline compared to the case with stationary wheels.

Fig. 5

Comparison of probability density function (PDF) of the spanwise pressure gradient at $Z/H=0.70$ of the vehicle centerline for a stationary wheels and b rotating wheels. Note the time-trace was filtered using a sliding average of $tU_\infty /W=15.4$ (1.7s) similar to Perry et al. (2016), Pavia and Passmore (2017) and the dashed line marks the average pressure gradient

The aforementioned shifting of low base pressure from one side to another can also create corresponding fluctuations in the side-force coefficient $C_s$ defined as

$$\begin{aligned} C_s=\frac{S}{q_\infty A}, \end{aligned}$$

(1)

where S is the dimensional side-force, $q_\infty$ is the freestream dynamic pressure, and A is the vehicle frontal area. Clear dual peaks are present in the PDF of the side force (Fig. 6). The side-force fluctuations also showed more extreme fluctuations for the stationary wheels than the rotating wheels. Given the greater distribution of centerline pressure gradient for the rotating wheels case and previous observations from Aultman et al. (2021) of the case with stationary wheels producing larger spanwise changes of the wake, the center of the wake is likely far more dynamic for the case with rotating wheels, while the wake undergoes substantially greater structural changes for the case with stationary wheels. Regardless of wheel rotation, the current analysis supports the development of wake bi-stability for the fastback DrivAer model with smooth underbody.

Fig. 6

Comparison of Probability Density Function (PDF) of the fluctuations of the side-force coefficient ($C_s'$) for stationary and rotating wheels. Note the time-trace was filtered using a sliding average of $tU_\infty /W=15.4$ (1.7s) similar to Perry et al. (2016), Pavia and Passmore (2017)

We next consider the effects of the bi-stable wake on the other vehicle forces. Figure 7 shows the time-trace of the three vehicle forces (side-force, drag, and lift) filtered with a sliding average of $tU_\infty /W=15.4$ (1.7s), which is similar to those in Perry et al. (2016) and Pavia and Passmore (2017). For the case with stationary wheels, when the side-force is in an extremely high or low value, corresponding to either the positive or negative bi-stable state, respectively, there is a substantial spike in the time-trace of drag. Several of the most prominent drag spikes have been highlighted in Fig. 7 capturing increases in drag over the average of 5–10 counts ($C_D=0.001$ is one count of drag). Similarly for lift, there are clear spikes as well, although they are not as distinct or as isolated as those for drag likely due to coupling with other flow features around the vehicle. We note that similar observations can be made for the case with rotating wheels. However, the switching between states is far more rapid and less pronounced when rotating wheels are implemented, hence diminished changes in both drag and lift are observed with far more peaks making the effects of wake switching less distinct. Therefore, the effects of the bi-stability only appear to be around 1 count in drag which is supported through the corresponding PDF of the forces (not shown for brevity). It should be noted though, that the base drag is only $\sim 7\%$ of the total drag for the rotating wheels case, and base pressure drag can attribute up to $50\%$ of the total vehicle drag for an SUV style vehicle (Avadiar et al. 2018). Thus, the effects of the bi-stability on a vehicle with a larger base could be up to 7 times greater than those observed herein. Future studies should focus on the development of bi-stability with larger, blunt base vehicles to determine whether or not there is a substantially higher drag penalty under driving conditions than currently observed.

Fig. 7

Correlation of bi-stable switching characterized by side-force coefficient $C_S$ with the drag $C_D$ and lift $C_L$ coefficients. Note the time-trace was filtered using a sliding average of $tU_\infty /W=15.4$ (1.7s) similar to Perry et al. (2016), Pavia and Passmore (2017) with vertical dashed lines marking key spikes in drag associated with the bi-stable switching while horizontal dotted lines mark the time-averaged force coefficients

3.2 Conditional Averaging

In this section, conditional averaging based on the side-force coefficient $C_s$ was used to isolate the extreme states of the wake due to its high correlation with the bi-stability (Perry et al. 2016; Aultman et al. 2021). Specifically, we used $|C'_s| > \sqrt{2}\sigma$ ($\sigma$ is the standard deviation of $C_s$) to separate the central $50\%$ of the data assuming a normal distribution when no filtering operation is applied. The remaining data represent extremely positive or negative side-forces, corresponding to the positive and negative bi-stable wake states, respectively (Fig. 8). With the positive and negative bi-stable states isolated, full snapshots of the flow field were conditionally averaged to obtain the time-averaged flow fields corresponding to the negative state or the positive state.

Fig. 8

Time trace of the side-force coefficient $C_s$ with a $\sqrt{2}\sigma$ band (dashed lines) separating the times in which the wake is in a bi-stable state. Dots show the full flow field snapshots used for conditional averaging of the positive and negative states corresponding to positive and negative side-force, respectively

To infer the exact structure of each state, the conditionally averaged flow fields were subsequently analyzed using critical point theory (Tobak and Peake 1982; Perry and Steiner 1987). The critical point theory analyzes the combinations of global separations (saddles) and local attachments/separations (nodes) along with their connectivity, thereby allowing us to infer the full three-dimensional structure of the wake based on the surface streamline topology (Dallmann 1983). The readers are referred to the table presented in Perry and Steiner (1987) for a review of various types of critical points, and are referred to Dallmann (1983) and Chapman and Yates (1991) for interpreting three-dimensional structures based on the critical point theory.

Figure 9 compares the surface constrained streamlines on the vehicle base for each of the conditionally averaged flow fields against those of the full-time averaged flow field. The full time-averaged flow showed a central node of attachment with streamlines propagating to the edge of the base before reaching two global lines of separation originating from saddles on the top and bottom of the base. These saddles and their separation lines connect with corresponding stable node pairs near the outboard edges of the base which are then connected via two smaller saddles. Such a topology is consistent with the typical topological rules in which there must be two more nodes than saddles, with the additional node being located on the nose of the vehicle (Tobak and Peake 1982). Additionally, this topology aligns with what is expected of two “U-shaped” separations with four legs extending downstream (Dallmann 1983). The presence of two “U-shaped” separations differs from what the traditional time-averaged torus in the literature, although the torus has been noted to purely be a function of time-averaging (Lucas et al. 2017). Focusing on when the wake is in a bi-stable state, the streamline topology in the vehicle base revealed a clear distinction from that of the full-time averaged wake, and there is a distinction in bi-stable states between the two wheel conditions as well. Specifically, there was a saddle-node recombination on the side corresponding to the increased magnitude of side-force for the case with stationary wheels, indicating a reduction in the number of legs to three with a single leg being present on opposing sides depending on the bi-stable state (left for the negative state, right for the positive state). A recombination of the saddle-node pair did not occur for the case with rotating wheels. Instead, the node pair and saddle shifted vertically to a central height on the base for the case with rotating-wheels producing similar connectivity to the time-averaged flow. This difference in surface streamline connectivity between the two wheel conditions is indicative of a change in wake dynamics which was previously observed through reduced time-scales and magnitude of the side-force for the rotating wheels case, as well as base pressure shown in the previous work of Aultman et al. (2021). The change in footprint further indicates a variation in the predicted bi-stable wake structure between the two wheel conditions.

Fig. 9

Surface constrained streamlines on the base of the vehicle using full-time and conditional averaging with stationary wheels (left) and rotating wheels (right): Full-time average (top); Negative state (middle); Positive state (bottom). Critical points are marked with blue circles (nodes) and red squares (saddles)

The wake structures associated with the time-averaged flow and each of the bi-stable states are further visualized using the full three-dimensional streamlines (Fig. 10). Here, the three-dimensional streamlines are seeded from the points of convergence along a streamwise-oriented plane downstream of the vehicle at $X/L=1.15$. Consistent with the base-surface topology as shown in Fig. 9, a three pronged structure is developed for each of the bi-stable states, with a clear singular leg shown on the dominant side of the bi-stable structure. Although the exact nature of these structures is unclear, there exists an apparent entrainment of streamlines from both the upper and lower regions of the wake. Within the lower region of the wake, the legs appear to be connected with a vortex structure emanating from the underbody region. The entrainment of streamlines within the wake may support the notion of a pair of U-shaped vortices on the upper and lower portion of the base with shifting/blending legs, but the two non-dominant legs along with the time-averaged flow may also indicate the blending of vortex pairs with a torus. Such a structure aligns with the wake structures observed by Rao et al. (2019) for a simplified heavy vehicle (GTS model).

To better visualize the number of legs in the wake structure and compare the structures between the two wheel conditions, Fig. 11 plots the surface-constrained streamlines at the same streamwise oriented plane of $X/L=1.15$ for stationary and rotating wheel cases. Two pairs of foci (marked with circles) are observed for the time-averaged flow, which is consistent with the presence of the four legs expected from the base surface topology. When the wake is in a bi-stable state, the number of foci reduces, which indicates a reduction in the number of legs emanating from the base wake. This reduction occurs for both wheel conditions, even for the case with rotating wheels when a saddle-node recombination was not found. These trends are consistent with the visualization of three-dimensional streamlines shown in Fig. 10.

It should be mentioned that the base surface topology associated with a bi-stable state exhibits a different surface streamline connectivity between the two wheel conditions while a similar three-pronged structure is developed regardless of wheel rotation or ground movement. Such an inconsistency may suggest a deficiency in the use of conditional averaging. Indeed, a previous work by Lucas et al. (2017) showed that certain wake structures can arise purely due to time-averaging. Flow analysis techniques other than the conditional time averaging are therefore necessary to confirm the physical presence of such structures in the wake at any instance in time.

Fig. 10

Wake structures captured by full-time (top) and conditional-averaged three-dimensional streamlines seeded from the points of convergence in a streamwise oriented plane at $X/L=1.15$. Conditional averaging captures the negative (middle) and positive (bottom) states with stationary (left) and rotating wheels (right)

Fig. 11

Full-time (top) and conditional-averaged streamlines colored by contours of streamwise velocity $\overline{u}/U_\infty$ in a streamwise oriented plane of $X/L=1.15$. Conditional averaging captures the negative (middle) and positive (bottom) states with stationary (left) and rotating wheels (right)

3.3 Proper Orthogonal Decomposition (POD)

In order to overcome the potential deficiencies of the conditional averaging, we utilized Proper Orthogonal Decomposition (POD) to capture the transient flow features. To perform the POD, we used the snapshot POD method of Sirovich (1987) on the full velocity field (u, v,  and w). Figure 12 shows the energy distribution of the first ten modes of turbulent kinetic energy. Among these ten POD modes, regardless of wheel rotation, the first mode clearly stood out as the dominant mode. A similarly dominant first POD mode was found to correspond to the symmetry breaking wake bi-stability for a simplified square back model (Pavia et al. 2020). Although we observe a dominant first mode for the current DrivAer model, we note that the energy of the first mode for the DrivAer model is far lower than that for a square-back model observed by Pavia et al. (2020). This reduction in energy is not unexpected given the greater geometric complexity of the DrivAer model and the additional flow features contributing to the fluctuations within the wake (e.g., wheel wakes, side-mirror wakes, D-pillar vortices, etc.). It is also apparent that the inclusion of wheel rotation reduced the energy of the bi-stable mode ($\sim 8\%$ for rotating wheels versus $\sim 13.5\%$ for stationary wheels). The reduction of the first mode energy due to wheel rotation aligns well with our previous observations of a less dominant bi-stability found in the base pressure fluctuations and side-force coefficient as shown in Sect. 3.1.

Fig. 12

Distribution of turbulent kinetic energy of the wake across the first ten POD modes

3.3.1 1st POD Mode

To understand the change in timescale of a bi-stable state due to wheel rotation, Fig. 13 plots the time coefficient $A_1$ of the dominant first POD mode for the two wheel conditions. The time coefficient $A_1$ for both cases displays distinct peaks developing for either a positive or negative value. However, these extremes were held for a shorter period of time for the case with rotating wheels. Such an apparent reduction in time-scale due to wheel rotation is consistent with the change in time-scale for the base pressure as shown in Fig. 4 as well as the findings of He et al. (2022b). The different timescale, but similar fluctuating magnitude of $A_1$ at both wheel conditions, further suggests that the reduction in turbulent kinetic energy of the first mode with wheel rotation is not related to the magnitude of the fluctuations within the wake, but rather the time-scale at which those fluctuations are present. Considering the high correlation of the time coefficient $A_1$ with the side-force coefficient $C_s$ ($\rho =0.93$ and 0.80 for the stationary and rotating wheels, respectively where $\rho =\frac{1}{N-1}\sum _{i=1}^{N}(\frac{A_i-\overline{A}}{\sigma _{A}})(\frac{B-\overline{B}}{\sigma _{B}})$), we conclude that the first POD mode corresponds to the wake bi-stability, and the change in time-scale observed in the side-force coefficient is related to the change in wake dynamics captured by the first POD mode.

Fig. 13

Comparison of the time coefficient of the first wake POD mode $A_1$ for the case with a stationary and b rotating wheels

We next isolated the relevant states of the wake again through the side-force coefficient, capturing the positive and negative states, as well as the transitional or symmetric state between the two which we refer to as the neutral state (Fig. 14). Figure 15 shows the reconstructed full wake flow field using the first POD mode from the previous snapshots. Despite the change in time scale, the general wake structure did not appear to be dissimilar for the two wheel conditions. For the case with stationary wheels, a continuous torus formed when the flow is in the neutral state. When the flow is in a bi-stable state, two large vortical structures developed on the dominant side (left for the negative state, right for the positive state). These structures then sweep across the spanwise extent of the vehicle, leading to a breakdown of the base torus and a formation of a “C-shaped” vortex on the opposing side with streamlines entraining into the wheel vortex further downstream. A similar formation of “C-shaped” vortex when the flow is in a bi-stable state was observed by Pavia et al. (2020) in their study of the wake of a simplified Windsor body. When wheel rotation is implemented, the general structure appears to be quite similar. The neutral state shows the same general topology between the two cases. For the bi-stable state, a similar pair of dominant legs is observed for the bi-stable states. Unlike the stationary wheels case, however, the rotating wheels case did not produce the C-shaped base vortex. Rather, the dominant leg appears to entrain the flow from the secondary leg without breaking the torus similar to what was observed for the base surface topology from conditional averaging. The continued presence of the torus for rotating wheels aligns with the observations by Dalla Longa et al. (2019) and Chen et al. (2023).

Fig. 14

Snapshot reference for the reconstructed flowfield from the first POD mode with respect to side-force for the case with a stationary and b rotating wheels

Fig. 15

Snapshots of the reconstructed flowfield from the first POD mode used to create instantaneous streamlines capturing the neutral (top), negative (middle), and positive (bottom) bi-stable wake states for the case with stationary (left) and rotating wheels (right). Note that the snapshots used correspond to the same flow times as Fig. 14

To better analyze these structures we used various planes to isolate the base vortex and vortex legs. For the base vortex, we used a streamise axis located at the vehicle centerline and $Z/H=0.45$ to create a series of planes rotated $0^{\circ }, 60^{\circ }, 90^{\circ },$ and $150^{\circ }$ relative to the vehicle centerline plane. Using these planes to seed streamlines, we better isolated the wake torus (Figs. 16 and 17). When in the neutral state, the streamlines show clear signs of rotation associated with a vortex across all planes for stationary wheels, including the bottom of the centerline where a distinct, albeit small, limit cycle is present. When in a bi-stable state, however, there is a clear lack of a continuous torus present on the side associated with the bi-stability. Although the 3-dimensional streamlines indicated very similar structures, it is apparent from Fig. 17 that the wake is quite different when rotating wheels are implemented. Primarily, the wake is not a torus in any given state, as there is a clear lack of a limit cycle in the lower portion of the wake along the centerline plane for the case with rotating wheels. This indicates that instead of a torus, the wake structure is more in line with a hairpin vortex with the head along the base opening at the bottom portion of the vehicle near the centerline.

Fig. 16

Topology of the wake structure from the first POD mode using surface constrained streamlines on planes centered at $Z/H=0.45$ oriented at $0^{\circ }, 60^{\circ }, 90^{\circ },$ and $150^{\circ }$ for the case with stationary wheels. The neutral, negative, and positive states are shown on the top, middle, and bottom, respectively

Fig. 17

Topology of the wake structure from the first POD mode using surface constrained streamlines on planes centered at $Z/H=0.45$ oriented at $0^{\circ }, 60^{\circ }, 90^{\circ },$ and $150^{\circ }$ for the case with rotating wheels. The neutral, negative, and positive states are shown on the top, middle, and bottom, respectively

For capturing the vortex legs, we used two streamwise normal planes located at $X/L=1.00$ and $X/L=1.26$ (Fig. 18). First considering the neutral state for the case with stationary wheels, there are only two vortices originating from the vehicle underbody near the wheels. These vortices shift toward the ground plane and dissipate as they propagate downstream. Thus, the wake is closed in the neutral state as expected with the presence of a torus. While it is commonly believed that a torus only exists in time-averaged data but not in any instantaneous flowfield (Pavia et al. 2020; Lucas et al. 2017), recent studies by Morgans and her coworkers captured a torus using the instantaneous pressure data in their study of wake bi-stability for the Ahmed body (Ahmed and Morgans 2022; Dalla Longa et al. 2019). Additionally, He et al. (2022a, b) reported that the wake of a square-back configuration has high sensitivity to Reynolds number and ground boundary layer conditions. These studies suggest that the presence of a torus could be dependent on a variety of factors such as the vehicle type and flow conditions, and future studies are therefore necessary to characterizing the wake structures as a function of flow conditions as well as analyzing the effects of vortex identification methods. Although whether a torus exists in the instantaneous flowfield behind a bluff body remains an open question that deserves further study, we refer to the structure topology associated with the neutral state of the DrivAer model as shown in Fig. 18b and c as a torus in this paper, for the purpose of distinguishing it from those associated with the negative and positive bi-stable states.

Focusing on the wake being in a bi-stable state, a vortex pair is observed on the side associated with the bi-stability near the vehicle base. These vortices appear to entrain the streamlines from the wheel vortex, as only one wheel vortex can be observed in the near body plane. The vortices then dominate the downstream flow, with the induced velocity shifting the vortices to the opposing side of the vehicle with the upper vortex showing a more dramatic shift than the lower vortex. Although the vortices initially entrained the fluid from the wheel vortex, this did not prevent the wheel vortex from forming, as both can be observed in the downstream plane. Due to the induced velocities of the base vortex pair, one wheel vortex is shifted toward the ground while the other is pulled upward. This shift of the wake vortices and interaction with the wheel vortex likely accounts for the previously observed three pronged structure from the conditional averaging (Fig. 10). Additionally, the presence of a vortex behind the rotational axis of the base vortex indicates that the previous separation on the base is not a pure “C-shaped” vortex from the torus breaking. Instead, the torus is broken by the pair of vortices forming on the base as a local separation and piercing the torus, entraining the streamlines downstream to form the vortex legs. Such a separation aligns with the previous base surface topology from the conditional averaging (Fig. 9) and resembles the separation of curved bodies referred to as horned vortices (Chapman and Yates 1991; Le Clainche et al. 2016).

Fig. 18

Topology of the wake structure from the first POD mode using surface constrained streamlines on a streamwise-normal planes located at $X/L=1.00$ and $X/L=1.26$ to characterize the b–e neutral state, f–i negative state, and j–m positive for the case with stationary (left) and rotating wheels (right)

Focusing on the vortex legs when the wheels rotate, we observed several key differences from the stationary wheels case as with the base vortex. In the neutral state, minor vortices appear to develop on the lower portion of the vehicle base in addition to the wheel vortices. However, the wheel vortices are much more dominant within the wake flow when the wheels rotate and appear to entrain the weaker vortices along the vehicle base resulting in a downstream vortex pair. Thus, the wake fails to close as it does when the wheels are stationary. This trend carries over for the bi-stable states as well. As was the case with stationary wheels, a predominant vortex pair develops on the side associated with the bi-stability. But, given the increased strength of the wheel vortices, one of the two vortex legs is either entrained or dissipated further downstream of the body leading to there being three wake vortices in the downstream plane instead of four. Despite this difference, the general structure in the near wake appears to align with the structures from the stationary wheels case, but with much weaker vortex legs.

In order to better visualize these structures, we used the local swirling nodes from the previous planes to create a simplified diagram of the wake (Fig. 19). We note that the wheel vortices will not be included for simplicity and focus will be placed just on the immediate base wake structure. In the neutral state, as shown previously, the case with stationary wheels forms a closed torus while the case with rotating wheels instead forms a hairpin vortex with the legs opening at the bottom of the base. Downstream, the two legs of this hairpin vortex are entrained/entrain the wheel vortices resulting in the open wake shown in Fig. 18. In the bi-stable state, regardless of wheel rotation, on the side associated with the bi-stability (left for the negative state, right for the positive state), a pair of vortices form on the base surface. These vortices then pierce the ring-like structure in the wake, creating a dominant vortex pair that propagates downstream. The mechanism for this change is likely similar to the shear layer interactions observed by Haffner et al. (2020) for a square back model. However, instead of the shear layer directly leading to bending of the streamlines resulting in entrainment, the wheel wake produces a similar interaction. The wheels produce low-momentum flow in their wakes which is then entrained by the lower vortex. This wake flow is nearly engulfed when the momentum is extremely low for the case with stationary wheels. Feeding fluid into the lower vortex enhances the strength of the vortex, which then entrains more fluid from the side feeding the upper vortex as well. Both of these vortices then entrain further flow from the side which crosses to feed the vortex on the opposing vehicle side, leading it to swell and increase in strength further enhancing entrainment of fluid into the wake and increasing the wake asymmetry. These crossflows become so high that the torus is eventually broken for the case with stationary wheels. On the other hand, due to the higher momentum in the wheel wake for the case with rotating wheels, this extreme extent of the bi-stable wake does not form. Instead, the wheel vortex combines with the weaker lower vortex further downstream, reducing the feedback of fluid entrainment into the base wake structure.

Fig. 19

Sketch showing the wake in the neutral state (right), negative bi-stable state (middle), and positive bi-stable state (right) using the first POD mode for the case with stationary (top) and rotating wheels (bottom)

These structures can indeed be observed in the instantaneous flow field. Figure 20 plots the instantaneous iso-surface of total pressure coefficient $C_{p_0}$ along with the streamlines in a road-parallel plane of $Z/H=0.45$. Here, the instantaneous flow snapshots were taken at the same flow times as those of the reconstructed POD fields in Fig. 15, and the total pressure coefficient $C_{p_0}$ is defined as

$$\begin{aligned} C_{p_0}=\frac{P+1/2\rho |\textbf{V}|^2-(P_\infty +q_\infty )}{q_\infty }, \end{aligned}$$

(2)

where P is the instantaneous static pressure, $\rho$ is the air density, $|\textbf{V}|$ is the magnitude of the instantaneous local velocity, and $P_\infty$ and $q_\infty$ are the free stream static and dynamic pressures, respectively. The iso-surface of total pressure aligned well with the structure of the streamlines from the first POD mode as shown in Fig. 15. There was an apparent breakdown of torus in the instantaneous flow field, which is similar to the torus breakdown observed in the POD reconstructed flow field for the case with stationary wheels. We also noted that the breakdown of the torus in the case with stationary wheels led to the development of a pair of large low-pressure legs on the dominant side. These legs showed similarity to the hairpin structure observed for a simplified square-back vehicle model (Dalla Longa et al. 2019). There is also great similarity between the structures observed here and those of Rao et al. (2019) for a simplified square-back ground transportation system (GTS) model. Although the low-pressure torus remained intact in a simplified model, the development of low-pressure legs seemed to have a greater effect on the bi-stable wake structure for the current DrivAer model. Similarly, the same structure of the first POD mode was preserved in the instantaneous flow field for the rotating wheels case, as both recirculation bubbles are present in the bi-stable state aligning with the presence of the ring-like structure persisting. Thus, the general structure that we found in the first POD mode reconstruction of the wake is observed in the instantaneous flow.

Fig. 20

Instantaneous iso-surface of total pressure coefficient ($C_{p_0}=-1.05$) capturing the wake structure with streamlines seeded on the $Z/H=0.45$ plane colored with normalized streamwise velocity ($u/U_\infty$) for the case with stationary wheels (left) and rotating wheels (right). Note that the snapshots used correspond to the same flow times as Fig. 14

3.3.2 2nd and 3rd POD Modes

We continue our analysis of the wake by observing the effects of additional POD modes to the flow field reconstruction. In particular, Pavia et al. (2020) noted additional dynamics to the bi-stability by utilizing these additional modes. By using the the first, first and second, and first, second, and third POD modes, we were able to capture the various additional dynamics within the wake. Figure 21 shows the streamlines and z-component of vorticity within the wake on a road-parallel plane at $Z/H=0.45$. The addition of the second POD aligns with a drifting of the wake closure point (saddle) for the case with stationary wheels as evidenced by the dashed lines marking the spanwise position for each of the three flow field reconstructions. Although not shown due to the motion being predominantly spanwise in direction, we do note that the closure point also drifts in the road-normal direction as well, albeit substantially less. In addition to the drifting of the wake closure point, the inclusion of the second mode also leads to a deflection of the shear layer on the vortex side of the bi-stable state. This general deflection of the wake is maintained even when including the third POD mode to the reconstruction. However, additional features of the flow include an increase in vorticity within the shear layer over the vortex side as well as oscillations in the streamlines. These features indicate an additional shear layer flapping being captured by the third POD mode. It should be noted though, that these features are not consistent when analyzing either the neutral or positive states of the wake. Furthermore, these features are not discernible in the flow field for the case with rotating wheels. Additional features observed through animations not shown include further deflections of the vortex legs, shear layer fluctuations around the entire periphery of the base, swelling of the vortex structures, especially the wheel wake vortices, among many others.

Fig. 21

Comparison of the streamlines of the negative bi-stable state in a road-parallel plane at $Z/H=0.45$, colored with road-normal vorticity $\omega _z W/U_\infty$ using the flow reconstructed from a the first POD mode, b the first two POD modes, and c the first three POD modes for the case with stationary wheels

Although such features may align with physical structures within the wake, it is highly unlikely that all these structures align with the same dynamics. Indeed, a deficiency of POD has been that it integrates across all frequencies in time due to its basis in correlations. As such, POD has been noted to not accurately capture so-called "coherent structures" (Weiss 2019; Towne et al. 2018). In order to determine if this issue is resulting in the high inconsistency in the analysis of the additional POD modes, we performed a Fast Fourier Transform (FFT) to analyze the frequency content. The Power Spectral Density (PSD) was captured using Welch’s method with two windows with $90\%$ overlap in order to maintain the low frequency content. We note the doubling or halving the number of windows did not change the predominant frequencies observed, other than those at or below the window size cutoff.

Figure 22 shows the spectral content of the time coefficient A for the first three POD modes for each case of stationary and rotating wheels. It is apparent that the spectral content of the first POD mode is dominated by the extremely low frequency content ($St<10^{-2}$ where $St=fW/U_\infty$ in which f is the frequency in Hertz). Indeed only two frequency peaks can be distinguished for each case with these peaks being at least five times greater than the next peak for the case with stationary wheels and twice that for the case of rotating wheels. The increase in relevance of higher frequency content when using rotating wheels is likely due to the more rapid switching between the bi-stable states when compared to the case of stationary wheels. Regardless of this difference, we note that the higher frequencies of the first POD mode rapidly decay, indicating that only the low-frequency fluctuations in the wake are being well captured in the flow field reconstruction. This is not the case when analyzing the spectral content of the second and third POD modes. Although the same dominant low frequencies are observed in the FFT, we note that there is additional broadband high-frequency content that ultimately has a greater value of PSD than these peak low-frequencies. Thus, the current discrepancies in the reconstruction of the flow field using the second and third POD modes is contaminated by these high-frequency dynamics. Meanwhile, although POD is not known to capture "coherent structures" we can be confident that the structures shown from the first POD mode are coherent given the rapid decay of anything but the extreme low-frequency content. Therefore, in order to distinguish between the variety of features observed previously for the second and third POD modes, spectral based methods such as Spectral POD (SPOD) (Towne et al. 2018) or Dynamic Mode Decomposition (DMD) (Schmid 2010) should be utilized in future analysis of the wake bi-stability.

Fig. 22

Power Spectral Density (PSD) of the time coefficients A for the first three POD modes for the case with a stationary and b rotating wheels

4 Conclusions

In this work, we investigated the bi-stability that develops in the wake of the fastback DrivAer model with a smooth underbody using stationary wheels/ground and rotating wheels/moving ground. The salient three-dimensional features of the wake bi-stability behind the DrivAer model were analyzed in detail through conditional averaging and POD, with the purpose of drawing parallels in wake bi-stability between a realistic vehicle model and multiple simplified square-back models in the literature.

By conditionally averaging the wake, the bi-stable states were found to consist of a ring-like base vortex and three vortex legs. Through the first POD mode, the ring-like structure was further determined to be a torus in the case with stationary wheels, while the bottom of the torus opened to form a hairpin-like vortex structure in the case with rotating wheels. The three vortex legs were determined to be caused by a pair of vortices formed on one side of the vehicle base interacting/entraining with the vortex pair coming from the wheels. Due to the low momentum of the highly separated flow around the wheels, the wheel wakes were entrained into the lower base vortex, which led to increased lower base vortex strength and increased entrainment of fluid from the side of the vehicle into the wake. The increased fluid entrainment from the side then fed the upper vortex, increasing the strength of the upper vortex that subsequently pulled more fluid from the side of the vehicle and fed it across the span of the base into the ring-like vortex structure on the opposite side of the vehicle base. Such a feedback loop closely aligned with the asymmetry-producing mechanism proposed by Haffner et al. (2020) for simplified square-back models. The results suggest that methods aiming to suppress the bi-stability in a realistic car geometry could target regions with the lowest momentum fluid, as fluids with low momentum are more susceptible to entrainment into the base wake. In the case of a DrivAer model, such a low momentum region was determined to be the wheel wakes.

In addition to the mechanism of the bi-stability, the structure of the wake was found to be similar to that of the simplified square-back models as well. When the wheels were stationary, more fluid was entrained into the base wake, which leads to higher spanwise crossflow that breaks down the base torus into a C-shaped vortex on the non-dominant side of the base. Such structures aligned well with those reported in Pavia et al. (2020) and Dalla Longa et al. (2019) for square-back models. In addition to the torus, the presence of three vortex legs and ring-like structure also closely aligns with the structure found on the GTS model by Rao et al. (2019).

Despite the many similarities in the bi-stability between the simplified and DrivAer models, several differences arise due to the different details in the model geometry. The bi-stability for the DrivAer model was found to “drift” between states, which is different from the sudden “switch” typically found for simplified models. Such a difference could be due to a lack of a fixed separation point in the case of the more detailed DrivAer model. Another key difference lies in whether a torus exists in the case of stationary wheels, where controversy exists even among different simplified models. While Pavia et al. (2020) and Lucas et al. (2017) reported the torus being an artifact of averaging in their study for Windsor and Ahmed bodies, respectively, Dalla Longa et al. (2019) found the presence of a low-pressure torus in their analysis of a square-back Ahmed model. Similar to the work of Dalla Longa et al. (2019), the current work found the presence of a torus for the DrivAer model. The lack of consensus on whether a torus exists was likely caused by its high sensitivity to Reynolds number and ground boundary layer conditions as indicated by the work of He et al. (2022a, b). Therefore, further characterization of the bi-stable wake under different conditions would need to be performed to confirm the presence of a torus. Lastly, the presence of a base vortex pair forming behind the ring-like vortex for the current DrivAer model is different from those for simplified square-back models. This feature could be entirely unique to the current configuration, but it could also be present for square-back models, albeit not captured previously due to the difficulty of experimental methods such as Particle Image Velocimetry (PIV) in capturing the flow very near the vehicle surface.

Although conditional averaging and POD analyses served their purpose of connecting the bi-stability for a realistic vehicle model to that for simplified models, one should note that the two methods may not always predict the same bi-stability structures. For example, the full time-averaged four-pronged wake captured by conditional averaging did not resemble the neutral state derived from the first POD mode. Further work may be necessary to reconcile the difference due to the different analysis methods. Furthermore, the POD method was insufficient in revealing spectral information of the wake due to its correlative nature. While work in square-back models by Pavia et al. (2020) found specific additional dynamics to the wake bi-stability with the addition of more POD modes, the current POD analysis did not identify a single key feature with additional POD modes. Including the second and third POD modes to the flow reconstruction revealed a number of dynamics due to the inclusion of high-frequency content in these modes. A spectral analysis of the POD time coefficients revealed that even the first POD mode contained significant high-frequency content in addition to the dominant low-frequency content, although these frequencies showed a rapid decay in power compared to the low-frequency bi-stability. Therefore, spectral based methods should be used in future work to better identify frequency-specific structural features within the wake.