Period-2 Thermoacoustics in a Swirl-Stabilised Partially Premixed Flame Computed Using Large Eddy Simulation

Abstract

A partially premixed swirl-stabilised flame under thermoacoustically unstable conditions is studied using large eddy simulation with an unstrained flamelet model for the filtered reaction rate. The simulation results agree well with measured statistics of velocity, temperature and mixture fraction. Two thermoacoustic modes at approximately 300 and 590 Hz are excited for the case studied. The second mode pressure amplitude is comparable to that of the first mode. However, the second mode of heat release rate fluctuations is not as significant as for the pressure which results in a 2:1 frequency locking behaviour. The analysis offers insights into the physical mechanism involved in the excitation of the two modes and the 2:1 frequency locking behaviour. The index based on the Rayleigh Criterion in frequency domain is analysed to understand the coupling between the heat release rate and pressure fluctuations. It is observed that there is a nonlinear interaction between the two modes resulting in energy exchange across the two modes. The conventional Rayleigh Index has limitations in explaining the observed dynamics and therefore, a modified Rayleigh Index is defined to understand the effects of nonlinear mode interactions on thermoacoustic characteristics. A mode shape analysis using LES and acoustic-modelling reveals that the first mode may be a Helmholtz mode with internal damping that is excited by an acoustic source, and the second mode has the characteristic shape of a chamber mode.

1 Introduction

Stringent regulations for $\textrm{NO}_x$ emissions have forced the use of fuel-lean mixtures for Gas Turbine (GT) combustors, which makes these combustors susceptible to thermoacoustic instabilities (Dowling and Hubbard 2000). These instabilities arise from resonant feedback caused by an overall positive coupling between heat release rate fluctuation and acoustic pressure oscillation (Rayleigh 1878). High amplitude oscillation resulting from this resonant feedback yield loud tonal noise which has the potential to severely damage the combustor components (Zinn and Lieuwen 2005). Mitigation of these instabilities is essential to prolong the combustor life and for smooth operation of GT combustors.

Despite continued research in thermoacoustics, combustion instability is still a major unsolved problem. While the field of thermoacoustics is fundamentally well understood, prediction and control of these instabilities are challenging. One of the challenges comes from the lack of a closed form expression for heat release rate fluctuations as a function of known quantities. A description of the flame dynamics can be obtained either through a nonlinear flame model or Flame Describing Function (FDF) (Dowling 1999). Low-order models using such flame description provide good estimates of amplitudes and stability margins for canonical combustors (Dowling and Stow 2003). However, FDFs are computationally expensive to obtain and rely on the assumption of harmonic acoustics, which may not be amenable to predicting complex dynamical behaviour (Orchini and Juniper 2016). Models based on the G-equation are commonly employed which do not assume harmonic acoustics. While models based on G-equation can capture complex dynamical behaviour they may not be applicable to partially premixed swirl flames (Pitsch 2006).

Common methods to study thermoacoustic behaviour include low-order models and coupling Flame Transfer Function (FTF), which is a linear description of the flame dynamics, with Helmholtz solvers in practical geometries (Camporeale et al. 2011; Selle et al. 2006). Unlike FDFs, FTFs lack amplitude dependence of flame dynamics. Analysis of the eigenspectrum using low-order models based on FTFs reveals only the eigenmodes and mode shapes but not the amplitudes. Exchange of energy across modes requires the knowledge of mode amplitudes, which is unavailable in a linear framework. Low-order models and Helmholtz solvers can be coupled with FDFs which provide a weakly nonlinear framework to obtain information on limit cycle amplitudes (Palies et al. 2011; Laera et al. 2017). However, in the presence of multiple modes FDFs can predict the existence of each mode independently but will fail to estimate the stability of the modes. The stability of multiple co-existing modes depends on the nonlinear coupling between the modes which is missing in FDFs. An alternative approach is using a Flame Double Input Describing Function (FDIDF) as described in Orchini and Juniper (2016) where the describing function is obtained by forcing at two frequencies with a higher penalty in computational cost.

Mode interaction or coupling which is a nonlinear phenomenon resulting from energy exchanges between modes can also be studied using Large Eddy Simulation (LES). Mode interactions have been observed experimentally and addressed theoretically in recent studies (Noiray et al. 2008; Moeck and Paschereit 2012; Acharya et al. 2018; Kim 2017). It was shown in Acharya et al. (2018) that the interaction between closely spaced modes can result in co-existing modes. However, theoretical studies often assume that the acoustic modes are orthogonal (Culick 1976; Acharya et al. 2018) which may not always be true (Nicoud et al. 2007). This may lead to incomplete descriptions of mode interactions. The current study is intended to highlight that modes which are not closely spaced may interact if they are non-orthogonal. Past studies have shown that the interaction between two modes can result in mode hopping, where the limit cycle oscillation “hops" from one unstable mode to another (Noiray et al. 2008). A recent study (Kushwaha et al. 2021) has shown the existence of a period-2 dynamical state in this burner with a 2:1 frequency locking which refers to approximately two acoustic pressure oscillations for every oscillation of heat release rate fluctuation. Co-existing period-2 Limit Cycle Oscillation (LCO) has been studied (Moeck and Paschereit 2012; Acharya et al. 2018; Kim 2017; Agostinelli et al. 2022), but interaction between non-orthogonal longitudinal modes exhibiting 2:1 frequency locking between pressure and heat release rate oscillations have not been investigated, specifically using the LES framework.

Robust and accurate combustion closures within an LES framework can capture the complex flame dynamics, which are crucial for predicting thermoacoustic characteristics. Several past LES studies have accurately predicted thermoacoustic modes and their limit cycle amplitudes (Roux et al. 2005; Franzelli et al. 2012; Lourier et al. 2017; Volpiani et al2017; Fredrich et al. (2021a, b; Agostinelli et al. 2021). Large eddy simulations can also be used to obtain Flame Transfer Functions (FTFs) which can later be employed within a low-order network modelling framework to obtain the thermoacoustic stability map (Jaensch et al. 2018; Kuhlmann et al. 2022). Therefore, LES is a very useful tool to study and predict thermoacoustics of practically relevant GT combustors.

In this study, a presumed Probability Density Function (PDF) based flamelet model (Ruan et al. 2014; Chen and Swaminathan 2020; Chen et al. 2017, 2019a, b, 2020; Langella et al. 2018, 2020; Massey et al. 2022, 2021) is used to study a thermoacoustically unstable case in the PRECCINSTA burner. This model was also used in previous studies (Chen et al. 2019a, b; Chen and Swaminathan 2020) to investigate Period-1 LCO in a model GT combustor. This LCO has a single dominant frequency in both pressure and heat release rate oscillations. Thermoacoustic instabilities in this burner have been studied both experimentally (Meier et al. 2007; Dem et al. 2015; Stöhr et al. 2017) and numerically (Roux et al. 2005; Franzelli et al. 2012; Lourier et al. 2017; Volpiani et al. 2017; Fredrich et al. 2021a, b; Agostinelli et al. 2021) in the past. Period-1 LCO is the most widely studied dynamical state, but a bimodal period-2 LCO having two dominant frequencies in both heat release rate and pressure oscillations, was also studied recently (Agostinelli et al. 2022). The operating conditions of this burner which are of interest to this study have not been considered in the past LES investigations. Period-2 LCO with 2:1 frequency locking is observed in this study and the experimental investigation of Kushwaha et al. (2021) for different operating conditions. There are two dominant frequencies in the pressure oscillation for every dominant frequency of the heat release rate oscillation when there is a 2:1 frequency locking. This has not been investigated in the past LES of the PRECCINSTA burner. Hence, the specific objectives are to (1) test the FlaRe sub-grid scale combustion model (Ruan et al. 2014; Chen and Swaminathan 2020; Chen et al. 2017, 2019a, b, 2020; Langella et al. 2018, 2020; Massey et al. 2022, 2021) for the PRECCINSTA burner with 2:1 frequency locking behaviour, (2) analyse mode interactions between thermoacoustically unstable modes leading to period-2 LCO with 2:1 frequency locking and (3) investigate the acoustic mode shapes and their orthogonality through acoustic-modelling.

This paper is organised as follows. The experimental setup, numerical and acoustic modelling aspects are described in Sect. 2. The comparisons of LES statistics and measurements along with grid dependency for non-reacting flow are presented in Sect. 3.1. The reacting flow structure and comparisons of LES statistics with measurements are presented in Sect. 3.2. The thermoacoustic instability and the period-2 mode coupling are discussed in Sect. 4 and a summary of the key findings is given in the final section.

2 Methods

2.1 Experimental Setup

Fig. 1

a Schematic of the gas turbine model combustor (Meier et al. 2007; Dem et al. 2015) highlighting the locations of pressure probe PP1 and PP2 and b the computational model and grid

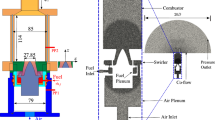
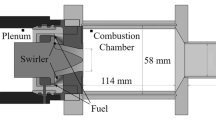
Figure 1a shows the schematic of the PRECCINSTA (Meier et al. 2007; Dem et al. 2015) combustor. Dry air at ambient condition enters the burner nozzle through 12 swirler vanes after passing through an air plenum as shown in Fig. 1a. Methane is delivered to its plenum through three ports, which are $120^{\circ }$ apart. This plenum feeds fuel into the air stream through 12 holes of 1 mm diameter located near the base of the swirler vanes. The conical central body in the convergent nozzle with exit diameter of 27.85 mm has its tip located at the nozzle exit plane (dump-plane).

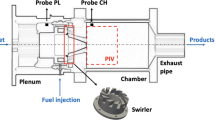
The details of the operating condition are listed in Table 1. The operating condition with global equivalence ratio of $\phi _{\textrm{glob}} = 0.9$, referred to as case TP09 (Dem et al. 2015), is yet to be studied using LES. Case TP07, which is listed as a non-reacting case, is used to validate the computational model setup and grid adequacy using the measured cold flow statistics. The cold flow validation is performed using TP07 since measurements are unavailable for case TP09 (reacting case studied here). The three components of the velocity field were measured using stereoscopic Particle Image Velocimetry (PIV) with a repetition rate of 5 kHz. The details of the PIV system and setup can be found in Dem et al. (2015). The airflow was seeded with ${{\textrm{TiO}}_2}$ particles with a relaxation time of about $5 \mathrm {\mu }$s, which is low enough to follow the flow dynamics accurately. The random uncertainties due to $\pm 0.1$ pixel uncertainty of the peak finding algorithm in the in-plane and out-of-plane velocities are $\pm 0.8~{\textrm{ms}^{-1}}$ and $\pm 2.4~\mathrm {ms^{-1}}$, respectively. Temperature and concentrations of major species ($\mathrm {O_2, N_2, CH_4, H_2, CO, CO_2, H_2O}$) are measured using single-shot laser Raman scattering techniques. The species number density was calculated from the scattering signal using calibration measurements, and the temperature was evaluated using the total number density and the ideal gas law. Measurement uncertainties differ between systematic errors resulting from uncertainties in the calibration process and statistical errors due to noise in the single-shot Raman measurement. The typical systematic and statistical uncertainty in temperature and mixture fraction measurements were ±3% to ±4% and ±3% to ±5%, respectively (Dem et al. 2015).

Table 1 Summary of conditions simulated

2.2 LES Modelling Methodology and Numerical Setup

Fully compressible Favre-filtered transport equations for the mass, momentum and total enthalpy are solved. Thermochemical states are mapped onto mixture fraction-progress variable ($\xi -c$) space using a presumed joint PDF approach with tabulated chemistry (Ruan et al. 2014; Chen and Swaminathan 2020; Chen et al. 2017, 2019a, b, 2020; Langella et al. 2018, 2020; Massey et al. 2022). The mixture fraction tracks the fuel-air mixing and is defined using Bilger’s formula (Bilger 1989). The progress variable describes the extent of reaction and is defined as $c = \psi /\psi ^{\textrm{eq}}$, where $\psi =Y_{\textrm{CO}} + Y_{\mathrm {CO_2}}$ and $\psi ^{\textrm{eq}}$ is the equilibrium value for the local mixture (Fiorina et al. 2003). Thermochemical quantities depend on the Favre-filtered mixture fraction, $\widetilde{\xi }$, progress variable, $\widetilde{c}$, and their respective sub-grid scale (SGS) variances. These four quantities are obtained from their respective transport equations (Ruan et al. 2014; Chen and Swaminathan 2020; Chen et al. 2017, 2019a, b, 2020; Langella et al. 2018, 2020; Massey et al. 2022) which can be written as

$$\begin{aligned} \overline{\rho }\frac{D\widetilde{\varvec{\varphi }}}{Dt} = \nabla \cdot (\overline{\rho \mathcal {D}_{\textrm{eff}}}\nabla \widetilde{\varvec{\varphi }}) + \overline{\varvec{S_{\varphi }}^+} - \overline{\varvec{S_{\varphi }}^-}, \end{aligned}$$

(1)

where the vectors of Favre-filtered scalars, sources and sinks are, respectively, given by

$$\begin{aligned}\widetilde{\varvec{\varphi }} = \Big \{\widetilde{\xi },\hspace{2pt}\sigma ^2_{\xi ,\textrm{sgs}},\hspace{2pt} \widetilde{c},\hspace{2pt}\sigma ^2_{c,\textrm{sgs}}\Big \}, \end{aligned}$$

(2)

$$\begin{aligned} \overline{\varvec{S_{\varphi }}^+} = \Big \{0,\hspace{2pt} 2\frac{\mu _{_t}}{Sc_t}|\nabla \widetilde{\xi }|^2,\hspace{2pt} \overline{\dot{\omega }_c^*},\hspace{2pt} 2\frac{\mu _{_t}}{Sc_t}|\nabla \widetilde{c}|^2\hspace{2pt}+ 2(\overline{c\dot{\omega }_c^*}-\widetilde{c}\overline{\dot{\omega }_c^*})\Big \}, \end{aligned}$$

(3)

$$\begin{aligned} \overline{\varvec{S_{\varphi }^-}} = \Big \{0,\hspace{2pt} 2\overline{\rho }\widetilde{\chi }_{\xi ,\textrm{sgs}},\hspace{2pt} 0,\hspace{2pt} 2\overline{\rho }\widetilde{\chi }_{c,\textrm{sgs}}\Big \}. \end{aligned}$$

(4)

The effective diffusivity is ${{\mathcal D}_{\textrm{eff}}} = {\mathcal {D}} + \nu _{t/Sc_{t}}$ with $Sc_t = 0.7$ for $\widetilde{\varvec{\varphi }}$ and for the total enthalpy transport $Sc_t$ becomes $Pr_t = 0.7$. The turbulent Schmidt and Prandtl numbers are chosen based on past studies (Chen et al. 2020; Langella et al. 2018). Alternatively, a dynamic Schmidt/Prandtl number approach may be used which will be the focus of a future work. The molecular mass diffusivity is obtained as $\overline{\rho \mathcal {D}} = \overline{\rho }\widetilde{\nu }/Sc$ with $Sc = 0.7$. The subgrid eddy viscosity is $\nu _t$ and is modelled using the dynamic Smagorinsky model (Germano et al. 1991; Lilly 1992).

Combustion occurs in partially premixed mode in flames studied here and therefore a sub-grid model accounting for both premixed and non-premixed modes is used. The filtered reaction rate is $\overline{\dot{\omega }_c^*} = \overline{\dot{\omega }}_\textrm{fp} + \overline{\dot{\omega }}_{\textrm{np}}$ given by Ruan et al. (2014), Chen and Swaminathan (2020), Chen et al. (2017, 2019a, 2019b, 2020), Langella et al. (2018, 2020), Massey et al. (2022), Bray et al. (2005)

$$\begin{aligned} \overline{\dot{\omega }_c^*}= & {} \overline{\dot{\omega }}_{\textrm{fp}} + \overline{\dot{\omega }}_{\textrm{np}} = \overline{\rho }\int _0^1\int _0^1\frac{\dot{\omega }_{\textrm{fp}}(\eta ,\zeta )}{\rho (\eta ,\zeta )}\widetilde{P}(\eta ,\zeta ) \mathop {}\!\textrm{d}\eta \mathop {}\!\textrm{d}\zeta \nonumber \\{} & {} \quad\quad + \widetilde{c}\left( \frac{\overline{\mu }}{Sc}|\nabla \widetilde{\xi }|^2 + \overline{\rho }\widetilde{\chi }_{\xi ,\textrm{sgs}}\right) \times \int _0^1\frac{1}{\psi ^{\textrm{eq}}}\frac{\mathop {}\!\textrm{d}^2\psi ^{\textrm{eq}}}{\mathop {}\!\textrm{d}\xi ^2}\widetilde{P}_{\beta }(\eta ) \mathop {}\!\textrm{d}\eta , \end{aligned}$$

(5)

where $\eta$ and $\zeta$ are the sample space variables for $\xi$ and c respectively. The joint Favre filtered density function is approximated as $\widetilde{P}(\eta ,\zeta )\approx \widetilde{P}_{\beta }(\eta ;\widetilde{\xi },\sigma ^2_{\xi ,\textrm{sgs}}) \times \widetilde{P}_\beta (\zeta ;\widetilde{c},\sigma ^2_{c,\textrm{sgs}})$, where the marginal filtered density functions are obtained using the Beta functions. The reaction term, $\overline{c\dot{\omega }_c^*}$, in Eq. (3) is also closed in a similar manner as Eq. (5). An algebraic model for the sub-grid scalar dissipation rate, $\widetilde{\chi }_{c,\textrm{sgs}}$ (Dunstan et al. 2013) that is used in Ruan et al. (2014), Chen and Swaminathan (2020), Chen et al. (2017, 2019a, 2019b, 2020), Langella et al. (2018, 2020), Massey et al. (2022) is employed here, with the scale-dependent parameter $\beta _c$ set to 7.5 following the earlier studies. A linear relaxation model is used for the mixture fraction sub-grid scalar dissipation rate $\widetilde{\chi }_{\xi ,\textrm{sgs}}$ (Pierce and Moin 1998).

All thermo-chemical quantities, such as the specific heat capacity at constant pressure $\widetilde{c}_p$, molecular mass of the mixture $\widetilde{\mathcal {M}}$ and the formation enthalpy $\widetilde{\Delta h}^0_f$, are computed analogous to the premixed term in Eq. (5) as outlined in Ruan et al. (2014) and the local mixture’s filtered density is obtained using $\overline{\rho } = \overline{p}{\widetilde{\mathcal {M}}_{\textrm{mix}}}/(\mathcal {R}_o\widetilde{T})$, where the universal gas constant is $\mathcal {R}_o = 8.314$ J/mol/K. The filtered temperature and molecular mass of the mixture are $\widetilde{T}$ and ${\widetilde{\mathcal {M}}_{\textrm{mix}}}$, respectively. The solution of Eq. (1) gives the control variables $\widetilde{\xi }, \sigma ^2_{\xi ,\textrm{sgs}}, \widetilde{c}$ and $\sigma ^2_{c,\textrm{sgs}}$, which are used to obtain various source terms and thermo-chemical quantities from a lookup table.

The computational grid shown in Fig. 1b consists of 4.5 million unstructured tetrahedral cells with refinement in the swirler region and the combustion zone. A finer grid is required for the swirler to resolve its geometry and to capture the subsequent flow development. The fuel plenum is included in the geometry along with a hemispherical domain as shown in Fig. 1b to mimic the exterior room volume and to avoid spurious acoustic reflections. A small velocity of 0.1 m/s is specified at the base of this hemispherical domain with a wave transmissive boundary condition on its outer boundary. Top-hat profiles of constant mass flow rates listed in Table 1 are specified without turbulence at the inlets, since the turbulence generated by the swirler is stronger than the incoming turbulence. All walls are treated as adiabatic with no-slip conditions and Spalding’s wall function is used for the near-wall flow (Spalding 1960).

Wall temperature measurements are not available for the case considered in this study. As an alternative to adiabatic boundary conditions, one of the three approaches summarised in Kraus et al. (2018) may be considered for treating the thermal boundary condition. The first option is to impose a guessed temperature profile to account for heat loss, which can lead to incorrect flame anchoring and an artificial forcing of the solution. The second option is to link the local wall temperature and heat flux, but this may require several LES runs to tune the heat resistance in the absence of temperature measurements, even though only one iteration was required in Agostinelli et al. (2022). Furthermore, there is uncertainty as to whether the resistance can be treated as a constant across different operating points. Finally, a coupled LES with conjugate heat transfer may be performed, fully accounting for the heat loss via conduction through the walls. Although this approach has the highest fidelity, the computational cost can be about twice that of an adiabatic LES. However, due to the uncertainty and computational expenses involved, the influence of non-adiabatic conditions in conjunction with non-adiabatic flamelets (Massey et al. 2021) on the thermoacoustic aspects is beyond the scope of this study.

All simulations are performed using OpenFOAM v7 with a modified PIMPLE algorithm with density coupling to handle compressibility effects. Second-order central difference schemes are used for the spatial derivatives and a first-order implicit Euler scheme is used for the temporal derivatives. A small time step of $\Delta t = 0.25$ μs is used to ensure numerical stability. The resulting CFL number remains below 0.4 for the entire computational domain. After reaching a stationary state, time-averaged statistics are collected for about 0.2 s which corresponds to approximately 10–12 characteristic flow-through-times based on the entire domain length and the bulk-mean air velocity at the inlet of the domain. The simulations are run on ARCHER2, the UK’s high-performance computing facility, using 1024 cores and requires approximately 120 h of wall clock time to get the statistics reported in this study.

2.3 Acoustic Modelling

The combustor acoustics is computed using the commercial software COMSOL 4.2 in addition to LES to understand the mechanisms of thermoacoustic oscillations. This acoustic model solves the Helmholtz equation in a 3D domain similar to that of the LES, consisting of the flowed-through volume in the combustor and a large atmospheric region downstream of the combustor exit representing the room outside the combustor, as shown in Fig. 2a. Reflecting boundary conditions are applied at the walls inside the combustor and at the air inlet where a sonic orifice is present in the experiment, and non-reflecting conditions are used for the boundaries of the atmospheric region and the fuel inlet. The distributions of density and speed of sound inside the combustor are implemented based on the average temperatures obtained from the LES and correlations between density, speed of sound and temperature obtained using GasEq (Morley 2005) as shown in Fig. 2b, c. The model assumes zero flow velocities throughout the domain. The acoustic model is first used to calculate the acoustic eigenmodes and then to assess the response to an acoustic source in the combustion chamber representing the flame, as discussed in Sects. 4.2 and 4.3.

Fig. 2

Meshed domain and distributions of sound speed and density used for the acoustic analysis with COMSOL

3 Fields of Velocity, Temperature and Mixture Fraction

3.1 Non-reacting Flow Field

As noted earlier the non-reacting case TP07 listed in Table 1 is used to assess the grid dependency using two grids with 4.5 million (4.5 M) and 8 million (8 M) cells. The grid resolution is increased (from $\delta x \approx 1.2$ to 0.8 mm, where $\delta x$ is the edge length) only in the fine cell regions (covering parts of the air plenum, fuel plenum swirler and combustion chamber) visible in Fig. 1b and the cell sizes in the remaining regions are the same in both grids. Profiles of three velocity components in the x-direction were measured at four streamwise, z, locations. Measured time-averaged and root-mean-square (rms) values are compared with the LES results in Fig. 3. Note that the computed rms values are obtained using only the resolved variance ($\langle \widetilde{U}^2 \rangle - \langle \widetilde{U} \rangle ^2$) to isolate the effects of the grid from the sub-grid model.

The grid sensitivity observed between the 4.5M grid and the 8 M grid for all three components is weak, as both give a reasonable agreement with the experimental data. The 8 M grid performs only slightly better than the 4.5M grid; the peaks of the axial velocity profiles shown in Fig. 3a, b are well captured. The 8 M grid also captures the width of the Inner Recirculation Zone (IRZ) better than the 4.5M grid (see Fig. 3a), but the differences are less than $10\%$. The differences in the x-direction and y-direction velocities for the two grids are negligible and they compare well with the experimental data. A discrepancy in the $\sqrt{\langle \sigma ^2_{W}\rangle }$ values close to the IRZ is noticeable in Fig. 3f, but these differences are within the experimental uncertainties of $\pm 2.4~\textrm{ms}^{-1}$. Overall, the 4.5 M grid shows comparable results with the 8 M grid and captures the flow field satisfactorily.

Fig. 3

Cold flow comparison of axial, x-direction and y-direction velocity profiles for four streamwise locations. Symbols: measurements (Steinberg et al. 2013; Oberleithner et al. 2015). Lines: LES using 2 different grid resolutions for TP07

3.2 Reacting Flow Field

Figure 4 shows the contours of the filtered and time-averaged axial velocity fields along with the streamlines in the combustor. A large IRZ that is typically observed in swirling flows can be seen in the right half of Fig. 4. The computed IRZ is approximately 88 mm long in the axial direction, which is in excellent agreement with the measured value of 87.6 mm (Dem et al. 2015). A high-velocity jet (dark contours) enters the combustor and extends outward before impinging on the combustor wall further downstream. The region between the jet stream and the combustor walls encloses an Outer Recirculation Zone (ORZ) which supports the flame stabilised in the vicinity of the outer shear layer. Snapshots of the filtered axial velocity field at an arbitrary time instant depicted in the left-half of Fig. 4 show large regions of reverse flow (light contours) critical for flame stabilisation. The black line corresponds to $40\%$ of the maximum filtered reaction rate contour, which is arbitrarily chosen and shows the typical V-shaped flame. The flame has two branches on either side of the jet stream along the shear layer as noted in the mean structure, but the outer branch of the flame close to the dump plane is due to the adiabatic boundary conditions imposed on the dump plane (Fredrich et al. 2019; Bénard et al. 2019). The flame stabilises in the shear layer and is strongly wrinkled by vortices, as seen on the left half of Fig. 4.

Fig. 4

Filtered and time-averaged axial velocity field on the left and right halves respectively for case TP09. Thick black lines correspond to $0.4\times (\overline{\dot{\omega }_c^*})_{\textrm{max}}$ contours and the thin lines with arrows are the streamlines

Figure 5 shows typical comparisons of time-averaged statistics between computed and measured mean velocities. The magnitude and location of the peaks in the axial velocity corresponding to the jet are well captured at each axial location, as shown in Fig. 5a, b. The velocity gradients in the shear layer are well resolved at all axial locations and the width of computed IRZ compares well with the experiments. The magnitude of the reverse flow velocities near the centreline is underestimated as shown in Fig. 5a with a maximum underestimation of approximately $47\%$, which is quite large at $z=20$ mm. The mean reverse flow is strongly influenced by the thermoacoustic amplitude. This is because of the strong influx of momentum due to the thermoacoustic oscillation which will be shown later in Sect. 4.2. The underestimation in the mean reverse flow velocities could be due to the overestimated thermoacoustic amplitude discussed later in Sect. 4.1. The higher amplitude in the computations results in a higher axial velocities in the positive z-direction (see left half of Fig. 4) during some time instants. This overestimation in the influx of axial velocity results in a lower mean reverse axial velocity. Note that the overestimated amplitude affects influx of momentum more than the efflux because the heat release rate fluctuations are skewed towards positive fluctuations as shown later in Fig. 9b. The rms velocities obtained using only the resolved variance ($\langle \widetilde{U}^2 \rangle - \langle \widetilde{U} \rangle ^2$) are shown in Fig. 6. The axial rms velocities show good comparisons with the measurements, as shown in Fig. 6a with an overestimation of axial velocities at $z = 6$ mm and $z = 10$ mm. The maximum overestimation of the peak axial rms velocities is approximately $15\%$ at $z=10$ mm. The small under prediction of the centreline axial rms velocity at $z = 6$ mm is within the in-plane (x, z) experimental uncertainty of $\pm 0.8~ \textrm{ms}^{-1}$. The computed results for the $x-$direction rms velocity $\Big (\sqrt{\langle \sigma ^2_{V}\rangle }\Big )$ compare well with measured statistics with a maximum under-prediction in centreline and peak velocities of approximately $30\%$, which is quite high. The results for $y-$ direction rms velocity $\Big (\sqrt{\langle \sigma ^2_{W}\rangle }\Big )$ seem to be over predicted, but these are within the out-of-plane uncertainties of $\pm 2.4 \textrm{ms}^{-1}$. The overall agreement between computed and measured rms values is reasonable, suggesting that the grid resolves the flow field to a reasonable degree of accuracy.

Fig. 5

Typical comparisons of measured (symbols) and computed (lines) time-averaged mean of a axial velocity and b x-direction velocity in black and y-direction velocity in red for case TP09

Fig. 6

Typical comparisons of measured (symbols) and computed (lines) time-averaged rms of a axial velocity and b x-direction velocity in black and y-direction velocity in red for case TP09. Black and red error bars correspond to $\pm 0.8$ and $\pm 2.4$ ms respectively

Figure 7 shows the comparisons between computed and measured mean and rms mixture fraction. The jet stream has a higher velocity (see Fig. 4) compared to the ORZ and IRZ. Hence, the residence time there is smaller and leads to higher local unmixedness, since fluid parcels do not have enough time to mix. Therefore, a higher mixture fraction may be expected in the jet region based on these physical arguments. The computed results are consistent with this expectation, but the measured mixture fraction is (unphysically) leaner in this region compared to the surrounding regions (IRZ and ORZ). The unphysical drift of the mixture fraction values has been recognised in the experiments as a systematic inaccuracy of the Raman measurement (Dem et al. 2015). Apart from these discrepancies, the computed mixture fraction compares well with the measurements in the IRZ. The computed values are under predicted in the ORZ by a maximum of about $18\%$. The computed rms profiles of the mixture fraction shown in Fig. 7b capture the qualitative trend of the measurements. The computed rms values in the jet region are larger than those reported from the experiments which may be associated with the spatial averaging effects resulting from the relatively larger probe size (0.6 mm) (Dem et al. 2015) compared to the LES grid size (0.2 mm). Note that there is a systematic error in the mixture fraction measurement (Dem et al. 2015), which could also affect the values of $\sqrt{\langle \sigma ^2_{\xi } \rangle }$. Some uncertainty may arise from the chosen value for turbulent Schmidt number ($Sc_t = 0.7$) based on past studies (Chen et al. 2020; Langella et al. 2020). The results are considered satisfactory to meet the goals of this study. The overall qualitative agreement in the rms values is good, and the fuel-air mixing is well resolved in the computations.

Figure 8 show comparisons of computed and measured mean and rms temperature. The comparisons shown in Fig. 8a show a good agreement between the measured and computed temperatures at locations of $z = 6$mm and $z = 10$mm. The large temperature gradient across the inner and outer jet shear layer are captured well in the simulations. The comparisons at downstream locations show some overestimation especially close to the combustor walls. The temperature is over predicted at the downstream locations, since adiabatic walls are used due to the unavailability of wall temperature measurements. Figure 8b shows the comparisons between measured and computed rms temperature. Some discrepancies may arise from the static value of turbulent Prandtl number, but the simulations resolve the strong gradients in the near field in the rms values and the overall agreement between the computational results and the measurements is reasonable.

Fig. 7

Typical comparisons of measured (symbols) and computed (lines) time-averaged a mean mixture fraction and b rms mixture fraction. Error bars are not shown for rms mixture fraction as they are very small. Red lines approximately indicate the jet region

Fig. 8

Typical comparisons of measured (symbols with error bars) and computed (lines) time-averaged a mean temperature and b rms temperature. Red lines approximately indicate the jet region (see Fig. 4)

4 Thermoacoustic Instability

4.1 Spectra of Pressure and Heat Release Oscillations

Figure 9a shows the measured and computed time series of pressure fluctuations obtained at probe PP2 in the combustor (see Fig. 1a). The pressure fluctuations of the pressure time-series p(t) is given by $p'(t) = p(t) - \langle p \rangle$, where $\langle p \rangle$ is the time-averaged pressure. The fluctuating pressure signal reveals a mild thermoacoustic oscillation with an amplitude of 600 Pa in the computations. The temporal variations of amplitude of the measured pressure fluctuations are higher than the computed signal. The overestimation of this amplitude in the LES may be linked to the absence of the experimental damping due to loosely fitted quartz walls (Lourier et al. 2017). Several past studies on this burner have associated the overestimation in amplitude to the damping due to loosely fitted quartz walls (Agostinelli et al. 2022; Fredrich et al. 2021a) and the tests performed in Lourier et al. (2017) also link the overestimation with the lack of damping. Lack of heat loss also could result in an overestimation of the thermoacosutic amplitude (Agostinelli et al. 2021), but a lack of wall temperature measurements renders the heat loss assessment beyond the scope of the current study. Physical dissipation of the acoustic waves occurs over several acoustic wavelengths and since the combustor length is only about 4% of the acoustic wavelength, failure to capture this may not play a role in the overestimation. Numerical acoustic dissipation is proportional to $\delta x/ \lambda$ and $x/\lambda$, where $\delta x$ is the grid spacing, x is some characteristic length scale (combustor length) and $\lambda$ is the acoustic wavelength (Dickey et al. 2003). Since both these quantities are small, numerical dissipation is irrelevant in this regard giving sufficient confidence to link the overestimation of amplitude to lack of structural damping.

The two signals in Fig. 9a show alternating low and high amplitude peaks, which is a characteristic of signals with two frequencies. Two strong peaks at $f_1=300$ Hz ($f_1=329$ Hz in the experiments) and $f_2=590$ Hz ($f_2=658$ Hz) are visible in the frequency spectrum shown in Fig. 10. The results reveal that the measured and computed amplitude of the first harmonic is comparable to the fundamental mode amplitude, indicating a significant harmonic excitation. The experimental signal has lower amplitude peaks in the frequency spectrum due to averaging over several cycles, which involve low amplitude oscillation at several time instants.

Figures 9b and 10 also show the time series and frequency spectrum of the volume integrated heat release rate fluctuations, $\dot{Q}'(t) = \dot{Q}(t) - \langle \dot{Q}\rangle$, where $\langle \cdot \rangle$ denotes time-averaging and $\dot{Q}(t) = \int _V \dot{q} (\textbf{x},t) \mathop {}\!\textrm{d}V$ with $\dot{q}(\textbf{x},t)$ as the local heat release rate per unit volume at the location $\textbf{x}$ and time t. Figure 9b does not show alternating low and high amplitude peaks unlike Fig. 9a. The positive fluctuations are larger in magnitude compared to the negative fluctuations and therefore the shift of the heat release rate signal towards the positive fluctuations is another noticeable feature of this signal. The positive fluctuation is the result of the overshoot of the flame surface beyond its mean position and subsequent increase in flame volume (not shown). This is induced by the acoustic influx of momentum into the combustion chamber. The flame then shows a tendency to return to its nominal position by the standard kinematic restoration mechanism (Preetham et al. 2008; Blumenthal et al. 2013), but the undershoot of the flame surface is not equal to the initial overshoot since the influx of acoustic momentum for the next cycle has started to increase. The first half ($0< \varphi < \pi$, where $\varphi$ is the phase of the cycle) of the cycle takes shorter time ($\delta t_1 \approx 1.3$ ms) compared to the second half ($\pi< \varphi < 2\pi$, $\delta t_2 \approx 2$ ms) due to the two different physical mechanisms involved - flame surface perturbation by acoustic influx of momentum during $\delta t_1$ and kinematic restoration of flame surface during $\delta t_2$. The frequency spectrum for $\dot{Q}'$ shows two peaks, but the amplitudes of the second mode is lower. The asymmetry in the first and second half of each cycle results in a periodic, but non-sinusoidal signal. The second peak is a harmonic resulting from the FFT of a basic non-sinusoidal signal. This aspect is further explored using Poincaré maps in Sect. 4.3.

A spectrogram, unlike a frequency spectrum, reveals the time-varying amplitude of each mode and this is visible in the spectrogram shown in Fig. 11a. The stripes close to 300 and 600 Hz indicate the presence of a period-2 oscillation. The computed amplitudes (see Fig. 11b) show only a weak variation in time, possibly due to the lack of structural damping in the simulations. The simulations are in good overall agreement with the thermoacoustic behaviour observed in experiments and capture the period-2 LCO behaviour with reasonable accuracy.

Fig. 9

a Measured (dash-dotted) and computed (solid) fluctuating pressure time series at probe PP2 and b computed time series of volume integrated heat release rate fluctuations. The initial time $t_o$ is chosen arbitrarily and $\tau ' = 0.01$ s. The time interval between the first and second half of an arbitrary cycle is denoted by $\delta t_1 \approx 1.3$ ms and $\delta t_2 \approx 2$ ms

Fig. 10

Frequency spectrum of the measured and computed pressure and volume-integrated heat release rate fluctuations. The red solid line corresponds to the volume-integrated heat release rate fluctuations and black lines correspond to the measured (dash-dotted) and computed (solid) pressure fluctuations at probe PP2

Fig. 11

Spectrogram of a measured and b computed pressure fluctuations at probe PP2 (see Fig. 1a)

4.2 Acoustic Eigenmodes

The first two acoustic eigenmodes of the combustor computed using COMSOL (cf. Sect. 2.3) are shown in Fig. 12. The first eigenmode with a frequency of $f=265$ Hz is a Helmholtz resonance that features oscillations of pressure in the plenum and (at a reduced level) in the chamber, and oscillations of acoustic velocity in the burner nozzle, which are shown in more detail in Fig. 13. The eigenmode frequency is close to the frequencies of the combustion instability found in the experiment and the LES at $f=329$ and 300 Hz, respectively, and it is therefore concluded that this mode provides the acoustic feedback for the instability. As shown in previous experimental and numerical studies of combustion instability in this combustor by Stöhr et al. (2017) and Lourier et al. (2017), the oscillations of velocity and pressure in the burner nozzle lead to fluctuations of velocity and equivalence ratio at the flame base that drive the oscillations of heat release and thus also pressure in the chamber. The latter further excite the eigenmode and thereby close the feedback loop of the instability.

The second eigenmode at $f=624$ Hz exhibits strong pressure oscillations in the chamber and velocity oscillations in the exit tube, and therefore corresponds to a Helmholtz resonance of the chamber and the exit tube. For this mode, oscillations of pressure and velocity in the burner nozzle are low, and thus no strong feedback with the flame is expected. The COMSOL analysis yields numerous additional eigenmodes at higher frequencies, including a Helmholtz resonance of fuel plenum and fuel channels at $f=739$ Hz, and longitudinal waves in the plenum and chamber at 2651 and 3441 Hz, respectively, which are not further discussed here.

Fig. 12

Amplitudes of pressure and velocity oscillations shown for the first two acoustic eigenmodes obtained using COMSOL

Fig. 13

Oscillations of pressure and velocity for the acoustic eigenmode at $f=265$ Hz shown at phase angles of $0^\circ$, $90^\circ$, $180^\circ$ and $270^\circ$

When the combustion instability is present in the form of a LCO, the eigenmode at $f=265$ Hz is excited by the pressure oscillations in the combustion chamber caused by the heat release variations of the flame. In order to study the acoustic mechanisms of the eigenmode excitation, additional COMSOL computations are performed where an ellipsoidal acoustic monopole source is included in the combustion chamber as shown in Fig. 14a. The amplitude and phase of pressure oscillations are largely constant within the chamber for $f<1000$ Hz (cf. Figs. 12 and 20), and thus the exact shape and location of the source within the chamber has no major effect on the results of the computations. While for the computation of eigenmodes, the attenuation of acoustic waves inside the combustor was not included in the model as is common practice for eigenmode analyses, the attenuation of acoustic waves becomes relevant when high-amplitude pressure oscillations occur. Strong absorption of acoustic waves typically occurs at the two ends of the neck of a Helmholtz resonator, where periodic shedding of vortices takes place and the vortices then dissipate to heat. In a numerical study of damping in a Helmholtz resonator, Dupere and Dowling (2005) found frequency-dependent values of absorption coefficients of up to 5% and 80% for sound amplitudes between 120 dB and 180 dB, respectively (Dupere and Dowling 2005). It is thus expected that significant acoustic damping occurs near the necks of the present Helmholtz resonances shown in Fig. 12, i.e., near the injector nozzle, swirl channels and exit tube.

For the present combustor, however, no information on frequency- and amplitude-dependent damping that is spatially resolved is available, and thus an approximate representation of damping was adopted here. In principle, the Helmholtz eigenmodes at $f=265$ and 624 Hz can be considered as damped harmonic oscillators that are forced by the acoustic source in the chamber. The frequency-dependent ratio $\mathcal{R}(f)$ (see Fig. 14b for the definition of $\mathcal{R}$) of pressure amplitudes in the plenum and chamber is then the resonance curve of the Helmholtz mode at $f=265$, whose course mainly depends on the amount of damping in the near the neck regions between chamber and plenum as shown below. For the COMSOL computations with an acoustic source, two attenuation coefficients $\alpha$ of $\alpha _1=14.5$ dB/m and $\alpha _2=1$ dB/m have been applied in the regions near necks and the rest of the domain, respectively. The values have been chosen such that the ratio R of pressure amplitudes between plenum and chamber, which is largely governed by the damping near the neck regions, corresponds to the value of $\approx 1.5$ found in the LES at $f=300$ Hz. With this configuration, the Helmholtz equation in the combustor is solved for frequencies of 10, 20, 30,..., 1000 Hz with an arbitrarily chosen source amplitude per unit volume of $Q=1~{\textrm{s}}^{-1}$ inside the ellipsoid. For each frequency, the amplitudes and phases of pressure in the chamber and plenum, and of the velocity in the nozzle is obtained at the respective locations shown in Fig. 14a. In order to highlight the effects of the attenuation coefficients, a second computation with homogeneous $\alpha _1=\alpha _2=1$ dB/m is performed.

Figure 14b shows the resulting ratios $\mathcal{R}(f)$, and the values of the fundamental mode for the LES and the experiment. The plots of $\mathcal{R}(f)$ exhibit typical shapes of a resonance curve for a forced and damped harmonic oscillator, with a maximum near the first eigenmode frequency at $f=265$ Hz. The comparison of the two COMSOL solutions show the strong effect of $\alpha _1$ representing the attenuation in the neck regions, on the pressure ratio R. It can be seen that the COMSOL solution matches well with the values of LES and experiment when $\alpha _1=14.5$ dB/m.

Figure 14c shows the amplitude ratios between velocity in the nozzle and pressure in the chamber. This ratio indicates at which frequencies velocity oscillations in the nozzle are excited by pressure oscillations in the chamber and thereby provide an acoustic feedback to the flame. It is seen that elevated values occur within a range of about $\pm 100$ Hz near the first eigenmode at $f=265$ Hz. This shows that instabilities generally can occur not only exactly at the eigenmode frequency, but within a certain frequency range whose width depends on the amount of acoustic damping. The plot of the associated phase differences in Fig. 14d further shows that in this frequency range, the phase differences between velocity in the nozzle and pressure in the chamber varies significantly, and thereby flames with a considerable range of convective time delays between the nozzle and the flame zone can become unstable. This explains that flames within notable ranges of thermal power, equivalence ratio and hydrogen fuel fraction exhibit combustion instabilities in this combustor (Kushwaha et al. 2021). At frequencies near the second eigenmode at $f=624$ Hz, which is a Helmholtz resonance of the chamber and the exit tube, no variation of signals is seen in Figs. 14b–d.

Fig. 14

COMSOL computations with acoustic source in the combustion chamber: a geometric configuration, b plots of pressure amplitude ratios and c, d plots of amplitude ratios and phase differences between velocity in the nozzle and pressure in the chamber

4.3 Mode Coupling and Period-2 Oscillation

The results presented above have shown that the fundamental flame instability in the LES at $f=300$ Hz is linked to the acoustic Helmholtz resonance with an eigenmode frequency of $f=265$ Hz. It has further been observed that for both the experiment and the LES, additional peaks appear at the respective first harmonic frequency, and the spectrograms in Fig. 11 showed some indications that the oscillations at the fundamental and harmonic frequencies are coupled in the form of a period-2 LCO. Further indications and possible mechanisms for this coupled oscillation are discussed in this section.

At first, further insight into the dynamical behaviour of the unstable modes is obtained through phase reconstructions. In the literature of dynamical systems, often a three-dimensional (3D) phase reconstruction is used to represent all plausible states of a system and their time evolution. A phase reconstruction involves embedding a signal into a higher dimensional phase space by choosing a time delay $\tau$ and dimension d. If $a(t_i) = [a(t_1),a(t_2),\ldots ,a(t_N)]$ is the discrete time-series vector of an arbitrary quantity of interest, a, where N is the signal length, then the d-dimensional phase space involves time delayed vectors expressed as $Z_{ik}(t_i) = [a(t_i), a(t_i+\tau ), \ldots , a(t_i+(d-1)\tau )]$. Therefore, a 3D phase space reconstruction is a 3D plot of $Z_{i0}(t_i) = a(t_i), Z_{i1}(t_i) = a(t_i + \tau )$ and $Z_{i2}(t_i) = a(t_i + 2\tau )$. An optimum time delay will produce independent delayed signals required for a true representation of system dynamics. Average Mutual Information (AMI) is constructed using $a(t_i)$ and a time advanced signal $a(t_i+\tau )$ for a wide range of $\tau$. The optimal time delay $\tau$ for a discrete time series vector $a(t_i)$ is obtained from the first local minima of the AMI (Fraser and Swinney 1986) given by

$$\begin{aligned} I(\tau ) = \sum _{a(t_i),a(t_i + \tau )} P(a(t_i), a(t_i + \tau )) \log _2 \Big [\frac{P(a(t_i),a(t_i + \tau ))}{P(a(t_i)).P(a(t_i + \tau ))}\Big ], \end{aligned}$$

(6)

where $P(a(t_i))$ and $P(a(t_i + \tau ))$ are marginal probabilities and $P(a(t_i),a(t_i + \tau ))$ is the joint probability of occurrence of $a(t_i)$ and $a(t_i+\tau )$. Additional details and a computer code to evaluate AMI can be found in the supplementary material of Juniper and Sujith (2018). The variation of AMI with time-delay is shown in Fig. 15 for the acoustic pressure signal obtained in LES (Fig. 9). Hence the optimal time delay for this signal is $\tau ^* = 6.5$ ms.

Fig. 15

Variation of average mutual information of acoustic pressure signal obtained from the LES shown in Fig. 9. $\tau ^* = 6.5$ ms

A 3D phase reconstruction of the pressure time-series data shown in Fig. 9 reveals a double-loop attractor, as depicted in Fig. 16a for where the outer loop corresponds to $f_1$ and the inner loop corresponds to $f_2$. The double-loop attractor therefore corroborates the presence of a period-2 LCO. The 3D phase reconstruction of the fluctuations in the volume-integrated heat release rate is shown in Fig. 16b. The fluctuations of the volume-integrated heat release rate signal, however, has a single-loop attractor in the three-dimensional phase space and a second loop does not appear. However, a small kink in the single-loop is seen in Fig. 16b. This is associated with the low-amplitude for the second harmonic shown in Fig. 10. This behaviour is similar to the 2:1 frequency locking between acoustic pressure and heat release rate oscillations observed in Kushwaha et al. (2021). A Poincaré map which is the plot of alternate local maxima of the signal also can be used to distinguish between different dynamical states. Poincaré maps of the pressure and volume-integrated heat release rate signal are shown in Fig. 17. The Poincaré map for the pressure shows two distinct clusters confirming the presence of period-2 dynamics, whereas only one cluster is seen for volume-integrated heat release rate which confirms the existence of 2:1 frequency locking behaviour. Note that the second mode is not just a harmonic of non-sinusoidal oscillation, but a distinct second mode of oscillation. The Poincaré map will not produce well separated clusters for harmonics as seen in Fig. 17b. The second peak in the heat release rate spectrum (see Fig. 10) is therefore an artefact of the Fourier transform of a non-sinusoidal periodic function.

Fig. 16

3D phase reconstruction of computed a pressure at probe PP2 (see Fig. 1a) and b volume-integrated heat release rate fluctuations

Fig. 17

Poincaré map of computed a pressure at probe PP2 (see Fig. 1a) and b volume-integrated heat release rate fluctuations

To understand the 2:1 frequency locking behaviour, it is important to understand the coupling between the pressure and heat release rate fluctuations. The coupling between pressure and heat release rate fluctuations can be obtained from the evolution of the acoustic energy equation, which is generally written in the time-domain (Rayleigh 1878). A time-domain analysis does not offer insight into individual contributions from each mode and therefore a frequency-domain analysis is used in this work. A system is unstable if the growth rate of the acoustic energy is positive and this is true when the Rayleigh Criterion in the frequency-domain given in “Appendix 1” is satisfied ($\Re \{\int _V \hat{p}'\hat{\dot{q}}' \mathop {}\!\textrm{d}x\} >0$, where $\hat{p}^{\prime }$ and $\hat{\dot{q}}^{\prime }$ are the respective Fourier coefficients at frequency f).

The swirling flame is approximately axisymmetric and hence the frequency domain Rayleigh Index ($\Re \{\mathrm {\widehat{RI}}(\omega )\} = \Re \{\hat{p}'(\omega )\hat{\dot{q}}(\omega )\}$ as derived in “Appendix 1”) is evaluated in the combustor midplane in this work. The axial distribution of pressure-heat release rate coupling at a frequency $f_j = \omega /2\pi$ is studied using the real part of the discrete $\widehat{\textrm{RI}}$ averaged in x direction. This is given by

$$\begin{aligned} \mathcal {T}(z;2\pi f_j) = \langle \Re \{\widehat{\textrm{RI}}\}\rangle = \frac{1}{b} \int _{-b/2}^{b/2} \Re \{\hat{p}'(x,z;~f_j)~\hat{\dot{q}}'~(x,z;~ f_j)\} \mathop {}\!\textrm{d}x, \end{aligned}$$

(7)

where $\Re \{\hat{p}'(x,z\mathclose {;}\, f_j)\hat{\dot{q}}'(x,z\mathclose {;}\,f_j)\}$ is the real part of the complex correlation of pressure and heat release rate in discrete frequency space $f_j$ and b is the width of the combustor. Figure 18 shows the variation of $\mathcal {T}$ with z for the two modal frequencies $f_1$ and $f_2$. The first mode has a small stabilising region ($\mathcal {T}< 0$) close to the flame root ($0< z< 0.015\mathrel {\textrm{m}}$) and a sizeable destabilising region near the flame tip ($0.015< z< 0.04\mathrel {\textrm{m}}$). This result is consistent with the observation in Agostinelli et al. (2022) where a mode extracted at the fundamental frequency of thermoacoustic oscillation using Dynamic Mode Decomposition (DMD) shows similar destabilising behaviour close to the flame tip. Therefore, the first mode is unstable due to the overall destabilising effect of the flame. The second mode does not reveal significant correlation between the pressure and heat release rate fluctuations, which does not explain the excitation of the second mode and hence the double-loop attractor behaviour in Fig. 16a.

The lack of significant coupling between $p'$ and $\dot{q}'$ suggests that the second mode could be excited through a nonlinear interaction between the first and second modes. Nonlinear modal interactions have been studied in Acharya et al. (2018), and it was shown that modes can be either suppressed or excited by mutual interaction. The Rayleigh Index in the literature is conventionally referred only to terms of the form $\hat{p}'_j\hat{\dot{q}}'_j$ (see Eq. 23), but the acoustic energy may involve contributions from interactive (cross-correlation) terms of the form $\hat{p}'_j\hat{\dot{q}}'_k$ as suggested by Eq. 22. Therefore, a spatially averaged modified Rayleigh Index ($\textrm{mRI}$) is defined in discrete frequency space as follows

$$\begin{aligned} \textrm{mRI}&= \sum \limits _{j=1}^{M}\sum \limits _{k=1}^{N}\textrm{mRI}_{jk}~(z; ~f_j, f_k) \nonumber \\&= \sum \limits _{j=1}^{M}\sum \limits _{k=1}^{N}\frac{1}{W} \int _{-W/2}^{W/2} \Re \{ \hat{p}'~(x,z;~f_j) ~\hat{\dot{q}}'~(x,z;~f_k)\} \mathop {}\!\textrm{d}x, \end{aligned}$$

(8)

where $\textrm{mRI}_{jk} = \langle \mathrm {m\widehat{RI}}_{jk}\rangle$ and $\mathrm {m\widehat{RI}}_{jk}$ is given by Eq. 25. For the case here $M = N = 2$ since there are only two dominant modes observed in Fig. 10. Hence

$$\begin{aligned} \begin{aligned} \textrm{mRI} = \textrm{mRI}_{11} + \textrm{mRI}_{12} + \textrm{mRI}_{21} + \textrm{mRI}_{22} \end{aligned} \end{aligned}$$

(9)

The modified Rayleigh Index is equal to the $\widehat{\textrm{RI}}$ when $j=k$ and is referred as a pure coupling term in this work. The cross-terms of $\textrm{mRI}$ which do not appear in $\widehat{\textrm{RI}}$ are named as interactive coupling terms in this work as indicated by Eq. 9. Figure 19a shows the axial distribution of $\textrm{mRI}$ normalised by its maximum, which peaks close to the flame tip. The positive value in the region $0.02< z < 0.035$ m indicates a strong coupling between pressure and heat release rate fluctuations at the flame tip. The root of the flame has a stabilising effect, but the overall coupling is positive, and hence the combustor is thermoacoustically unstable based on the Rayleigh Criterion (Rayleigh 1878). Figure 19b shows the components of $\textrm{mRI}^*$ at each mode. Terms $\textrm{mRI}^*_{11}$ and $\textrm{mRI}^*_{21}$ show a net positive value across the entire flame length. The terms $\textrm{mRI}^*_{12}$ and $\textrm{mRI}^*_{22}$ show significant oscillation along the axial direction, but the overall effect is negative. The first pressure mode, referred to as a pure mode, is excited purely through coupling at the same frequency since $\int \textrm{mRI}^*_{11} \mathop {}\!\textrm{d}z = 0.012$ but $\int \textrm{mRI}^*_{12} \mathop {}\!\textrm{d}z = -0.002$. The second pressure mode, referred here as an interactive mode, is excited entirely through mode interaction since $\int \textrm{mRI}^*_{21} \mathop {}\!\textrm{d}z = 0.010$ while $\int \textrm{mRI}^*_{22} \mathop {}\!\textrm{d}z = -0.004$. Since the pressure fluctuations have contributions from both pure and interactive modes the resulting three-dimensional phase space representation shows a double-loop attractor as seen in Fig. 16a. The first mode of $\dot{q}'$ is a mixed mode since both $\int \textrm{mRI}^*_{11} \mathop {}\!\textrm{d}z > 0$ and $\int \textrm{mRI}^*_{21} \mathop {}\!\textrm{d}z > 0$. The second mode of heat release rate fluctuations is not significantly excited since $\int \textrm{mRI}^*_{12} \mathop {}\!\textrm{d}z \approx 0$ and $\int \textrm{mRI}^*_{22} < 0$. These features of the individual terms explain the single-loop attractor of the volume integrated heat release rate seen in Fig. 16b. Therefore, the individual modal contributions to the Rayleigh Index are essential to understand the 2:1 frequency locking behaviour. The individual terms of the modified Rayleigh Index indicate that the two modes interact and exchange acoustic energy. This physical mechanism of interaction is still classical in the sense that the dilatation due to heat release rate fluctuations produces acoustic waves that reflect from the boundaries to eventually affect the heat release rate fluctuations, thereby closing the feedback loop. The critical difference is that flame not only couples with the plenum mode, but also with the chamber mode. Since the frequency of the chamber mode is about twice that of the plenum mode, the downstream travelling wave (chamber mode) completes two cycles for every cycle of the upstream travelling wave (plenum mode). The modified Rayleigh Index shows that both these waves (upstream and downstream) are, on average, in phase with the heat release rate fluctuations. Note that the flame may be in phase with the chamber mode only every other cycle due to 2:1 frequency locking and additional cycle-to-cycle variation of phase due to variability in turbulent mixing can result in time-varying amplitude as seen in Fig. 11.

Fig. 18

Axial distribution of the real part of Rayleigh Index of first mode (in black) and second mode (in red)

Fig. 19

Axial distribution of a $\textrm{mRI}^* = \textrm{mRI}/(\textrm{mRI})_{\textrm{max}}$ and b $\textrm{mRI}^*_{jk} = \textrm{mRI}_{jk}/(\mathrm {mRI^*_{jk}})_{\textrm{max}}$

Fig. 20

Amplitudes and phases of pressure oscillations obtained from the COMSOL computations with $\alpha _1=14.5$ dB/m and $\alpha _2=1$ dB/m and an acoustic source in the chamber for $f=300$ and 590 Hz (observed in the LES, see Fig. 10)

Fig. 21

Variation of thermoacoustic amplitudes (top frames in b) and phases (bottom) at mode 1 ($f_1$) and mode 2 ($f_2$) along the path shown in the top figure (a). Mode shapes at $f_1$ and $f_2$ obtained from the COMSOL solver with an acoustic source and two damping coefficients ($\alpha _1$ = 1 dB/m and $\alpha _1$ = 14.5 dB/m) are also plotted. The value of $\alpha _2 = 1$ dB/m for all cases

Fig. 22

Axial variation of the inner product of normalised pressure at mode 1 and 2 obtained from LES and the COMSOL solver (i) with a source and damping ($\alpha _1 = 14.5 \mathrm {dB/m}$) (ii) without source or damping

The amplitudes and phases of pressure oscillations obtained from the COMSOL computations with an acoustic source in the chamber and attenuation coefficients of $\alpha _1=14.5$ dB/m and $\alpha _2=1$ dB/m are shown for $f=300$ and 590 Hz in Fig. 20. While the mode shapes generally look similar to those of the two eigenmodes shown in Fig. 12, the solutions with acoustic source additionally exhibit minima of amplitudes in the region between chamber and plenum.

Figure 21 shows the amplitude and phase (with respect to combustor pressure signal at PP2) for the two pressure modes along the length (path shown in the top frame) of the combustor from the LES together with the two COMSOL solutions with acoustic source. For the COMSOL solution with $\alpha _1=14.5$ and $\alpha _2=1$ dB/m, the normalised distributions of amplitude agree well with the LES. In particular, the amplitude ratios R between plenum and chamber, and the minima at $z\approx -0.02$ m and $z\approx -0.05$ m for $f=300$ and 590 Hz are well reproduced. The COMSOL solution with $\alpha _1=\alpha _2=1$ dB/m, on the other hand, underpredicts the amplitude in the chamber at $f=300$ Hz due to the higher values of R as shown above in Fig. 14b.

It is interesting to analyse the orthogonality of the two modes since the acoustic energy could have contributions from non-orthogonal modes. Two modes are orthogonal if the inner product $\int _{V} \hat{p}'(\omega )\hat{p}'(\omega _1) \textrm{d}V$ (simplifies to $\int _{z} \hat{p}'(\omega )\hat{p}'(\omega _1) \textrm{d}z$ for longitudinal acoustic modes) is zero and it is shown in the “Appendix 1” that this term is non-zero in general and can contribute to the acoustic energy. Figure 22 shows the axial variation of the product of normalised pressure at mode 1 and mode 2 given by $\mathcal {I} = (\hat{p}_1/\hat{p}_{1,\textrm{max}})(\hat{p}_2/\hat{p}_{2,\textrm{max}})$, where $\hat{p}$ is the Fourier transformed pressure and $\hat{p}_{1,\textrm{max}}$ is the maximum value in the axial direction. It is seen that this product is quite low in the combustor for acoustic eigenmodes without a source or damping. However, in the presence of a source and damping ($\alpha _1 = 14.5 \mathrm {dB/m}$), the product is significantly higher and compares reasonably well with the LES result. The inner product $\int _z \mathcal {I} \; \textrm{d}z$ in LES, COMSOL(i) with $\alpha _1 = 14.5 \mathrm {dB/m}$ and COMSOL(ii) without a source or damping are 0.118, 0.123 and 0.042 respectively. Therefore, the common assumption of orthogonal acoustic modes in classical Galerkin expansions (Acharya et al. 2018) is approximately valid only for acoustic eigenmodes without source and damping. However, this assumption does not strictly hold for the case discussed in this study. It is therefore concluded that the acoustic eigenmodes are significantly altered in the presence of acoustic sources and damping which could result in non-orthogonal modes contributing to acoustic energy.

The overall behaviour of the amplitude computed using COMSOL is in good agreement with the LES results. However, it is important to note that the COMSOL acoustic model is used to characterise the thermoacoustic behaviour in terms of Helmholtz acoustic modes but has some limitations. This analysis does not include mean flow effects for simplicity and the acoustic source used in COMSOL is an independent source, but the flame is an acoustic source dependent on the perturbations of acoustic pressure, velocity, equivalence ratio, etc. Therefore, the acoustic source used in the COMSOL lacks coupling among velocity, pressure and equivalence ratio perturbations which were shown to be important for this combustor in earlier studies (Meier et al. 2007; Stöhr et al. 2017). The acoustic source also does not include effects of time-lag, which may be important to capture the thermoacoustic behaviour. Also, a linear model is used for damping due to lack of further information. In general, damping is non-linear, which may have some important effects on the thermoacoustic behaviour of the combustor. The LES captures all these effects except for the structural and heat loss related damping. These effects may play a role in the phase relationships seen in Fig. 21, which are challenging to replicate. Addressing these additional effects in an acoustic model is beyond the scope of this work and may be explored in the future.

5 Conclusions

In this work, large eddy simulation is performed to understand the dynamics of a period-2 thermoacoustic oscillation in the PRECCINSTA burner. A case at $\phi =0.9$ which is not investigated computationally hitherto, is studied, which exhibits a low amplitude period-2 thermoacoustic oscillation. Large eddy simulation is performed using an unstrained flamelet model for the sub-grid scale combustion closure. The simulation results are validated with measured statistics for velocity, temperature and mixture fraction, and the overall agreement is good. The thermoacoustic frequencies are captured quite well with a slight over estimation of amplitudes, which may be due to the lack of structural damping in the simulation while the damping can arise from loosely fitted components in the experiment.

The thermoacoustic behaviour shows several rich features such as period-2 dynamics and 2:1 frequency locking between $p'$ and $\dot{q}'$ through mode interactions. The understanding of the 2:1 frequency locking behaviour and excitation of the second harmonic of pressure oscillations is limited and this work offers insights into the underlying physical mechanisms, such as the mode interactions leading to such frequency locking. Modes are classified as pure, interactive and mixed based on the nature of the interactions between the modes.

Furthermore, the analysis of mode shapes reveals that the first mode shape is a result of a classical Helmholtz mode excited by an acoustic source (flame) with significant flow related damping in the combustor. The second mode resembles an acoustic chamber mode whose amplitude is maximum in the combustor. The two modes are non-orthogonal in contrast to classical acoustic modes, which possibly arises from the presence of an acoustic source with significant flow related damping. It is highlighted that this non-orthogonality between modes is essential for the interaction between two non-closely spaced modes. Period-2 dynamics therefore results from the interaction between these two non-orthogonal modes and is described quantitatively using a modified Rayleigh Index.

Appendix 1: Rayleigh Criterion in the Frequency Space

In this section, the Rayleigh criterion and Rayleigh Index are derived in the frequency space starting from the momentum equation. The Rayleigh Index in frequency space derived previously in Magri et al. (2020) is included here for the sake of completeness and with some additional considerations. Linearised momentum equation is first derived with these additional considerations applicable to the current study. The momentum equation is given by

$$\begin{aligned} \rho \left( \frac{\partial {\textbf {u}}}{\partial t} + {\textbf {u}}\cdot \nabla {\textbf {u}}\right) = - \nabla p + \nabla \cdot \tau , \end{aligned}$$

(10)

where $\tau$ is the viscous stress tensor. Making use of the vector identity

$$\begin{aligned} {\textbf {u}}\cdot \nabla {\textbf {u}} = \Omega \times {\textbf {u}} + \nabla \left( \frac{u^2}{2}\right) , \end{aligned}$$

(11)

where $\Omega = \nabla \times {\textbf {u}}$ is vorticity, the momentum equation can be rewritten as

$$\begin{aligned} \rho \left( \frac{\partial {\textbf {u}}}{\partial t} + \Omega \times {\textbf {u}} + \nabla ( u^2/2)\right) = - \nabla p + \nabla \cdot \tau . \end{aligned}$$

(12)

Linearising 12 and neglecting higher-order terms except $\Omega \times {\textbf {u}}$ results in

$$\begin{aligned} \rho _o\frac{\partial u'}{\partial t} + \nabla p' = \rho _o L + \nabla \cdot \tau \end{aligned}$$

(13)

The first term on the right hand side (RHS) is the Lamb vector ($L = {\textbf {u}}\times \Omega$) which is retained because the present study involves significant acoustic-vorticity interaction arising from flows through apertures, nozzles and across edges (in the swirler). Such flows result in significant acoustic-vorticity mode conversion as shown previously in Fredrich et al. (2021b). Also, acoustic-vorticity interaction at the lip of the combustor exit is an important sink for acoustic energy as shown previously in Howe (1980). The strong velocity amplitude at the combustor exit seen in Fig. 12 suggests that such an interaction is possible in this combustor. For these reasons, the Lamb vector L is not neglected. Similarly, the linearised energy equation in the presence of a heat source is given by Ref. (Dowling 1992)

$$\begin{aligned} \frac{1}{c^2_o}\frac{\partial p'}{\partial t} + \rho _o\nabla .{\textbf {u}} = \frac{(\gamma - 1)}{c_o^2}\dot{q}', \end{aligned}$$

(14)

where $\gamma , \rho _o, c_o, \tau _{ij}$ and $\dot{q}'$ ($\dot{q}' = \dot{q}'(\textbf{x},t)$) are the ratio of specific heat capacities, mean density, speed of sound, viscous stress tensor and heat release rate fluctuation, respectively. The boundary conditions for closed-open end type boundaries are given by

$$\begin{aligned} \nabla p({\textbf {x}}_i) = u({\textbf {x}}_i) = 0, \end{aligned}$$

(15)

$$\begin{aligned} \nabla . u({\textbf {x}}_o) = p({\textbf {x}}_o) = 0, \end{aligned}$$

(16)

where ${\textbf {x}}_i$ and ${\textbf {x}}_o$ are the locations of the inlet and outlet boundaries. The velocity vector can be decomposed as

$$\begin{aligned} {\textbf {u}} = {\textbf {u}}^* + u'_a, \end{aligned}$$

(17)

where ${\textbf {u}}^*$ is the base flow and $u'$ is the acoustic velocity. The Lamb vector can be decomposed similarly as

$$\begin{aligned} L = L^* + L', \end{aligned}$$

(18)

where $L^* = {\textbf {u}}^*\times \Omega$ and $L' = u'\times \Omega$. Substituting Eqs. 17 and 18 in Eqs. 13 and 14 and applying a Fourier transform ($\int _0^{\infty } \cdot \hspace{2pt} e^{-i\omega t} \mathop {}\!\textrm{d}t$, where $\omega = 2\pi f$) on both sides of these equations, results in

$$\begin{aligned}{} & {} -i\rho _o\omega \hat{u}' + \nabla \hat{p}' = \rho _o (\hat{L}^* + \hat{L}') + \nabla \cdot \hat{\tau }, \end{aligned}$$

(19)

$$\begin{aligned}{} & {} -\frac{i\omega }{c^2_o}\hat{p}' + \rho _o \nabla \cdot \hat{u}' = \frac{(\gamma - 1)}{c_o^2}\hat{\dot{q}}', \end{aligned}$$

(20)

where the transformed variables are given by $\hat{u}' = \int _0^{\infty } u' e^{-i\omega t} \mathop {}\!\textrm{d}t$ and are similarly expressed for $\hat{p}'$, $\hat{\dot{q}}'$, $\hat{L}^*, \hat{L}'$ and $\hat{\tau }$. Taking dot product between $\hat{u}'({\underline{\omega }})$ and 19($\omega$) and summing with the dot product between $\hat{p}'(\underline{\omega })$ and 20($\omega$) yields the following equation

$$\begin{aligned} \begin{aligned} -i\omega \left( \rho _o\hat{u}'(\omega )\hat{u}'(\underline{\omega }) + \frac{\hat{p}'(\omega )\hat{p}'(\underline{\omega })}{\rho _oc^2_o}\right) + \hat{p}'(\underline{\omega })\nabla \cdot \hat{u}'(\omega ) + \hat{u}'(\underline{\omega })\cdot \nabla \hat{p}'(\omega )\\ \qquad \qquad \qquad = \frac{(\gamma -1)}{\rho _o c^2_o}\hat{p}'(\underline{\omega })\hat{\dot{q}}'(\omega ) + \rho _o \hat{u}'(\underline{\omega }) \cdot \hat{L}^*(\omega ) + \hat{u}'(\underline{\omega }) \cdot (\nabla \cdot \hat{\tau }(\omega )), \end{aligned} \end{aligned}$$

(21)

where $\underline{\omega },\omega \in [0,\infty )$. Integrating the above equation over the entire volume and using the boundary conditions (Eq. 15 and Eq. 16) gives

$$\begin{aligned} \begin{aligned} -\int _V i\omega \left( \rho _o\hat{u}'(\omega )\hat{u}'(\underline{\omega }) + \frac{\hat{p}'(\omega )\hat{p}'(\underline{\omega })}{\rho _oc^2_o}\right) \mathop {}\!\textrm{d}V = \frac{(\gamma -1)}{\rho _o c^2_o} \int _V \hat{p}'(\underline{\omega })\hat{\dot{q}}'(\omega ) \mathop {}\!\textrm{d}V \\ \qquad \qquad \qquad + \int _V \rho _o \hat{u}'(\underline{\omega }) \cdot \hat{L}^*(\omega ) \mathop {}\!\textrm{d}V + \int _V \hat{u}'(\underline{\omega }) \cdot (\nabla \cdot \hat{\tau }(\omega )) \mathop {}\!\textrm{d}V, \end{aligned} \end{aligned}$$

(22)

which is a general form of the acoustic energy equation. If $\underline{\omega }=\omega$, we recover the well known form of the acoustic energy equation (Dowling 1992; Poinsot and Veynante 2005) with an additional dissipation term due to Lamb vector in frequency space

$$\begin{aligned} -\int _V i\omega \left( \rho _o\hat{u}'^2 + \frac{\hat{p}'^2}{\rho _o c^2_o}\right) \mathop {}\!\textrm{d}V &= \frac{(\gamma -1)}{\rho _o c^2_o} \int _V \hat{p}'\hat{\dot{q}}' \mathop {}\!\textrm{d}V \nonumber \\ & + \int _V \rho _o \hat{u}' \cdot \hat{L}^* \mathop {}\!\textrm{d}V + \int _V \hat{u}' \cdot (\nabla \cdot \hat{\tau }) \mathop {}\!\textrm{d}V. \end{aligned}$$

(23)

The real part of the left hand side of Eq. 22 is the growth rate of the acoustic energy ampltiude which is zero for a thermoacoustically stable case. This quantity is also zero for thermoacoustically unstable case with a limit-cycle oscillation where the amplitudes have saturated due to competing effects of different sources and sinks. A dominant source of acoustic energy that drives a limit cycle oscillation is the first term on the RHS and the other two terms are dissipative terms. The first of the two dissipative terms is due to conversion of an acoustic wave to a vortex at the lip of the combustor exit (Howe 1980). This vortex carries away energy due to convection and therefore cannot positively contribute to acoustic energy. The second dissipative term is due to viscous effects which are usually very small. This study is concerned with only the source term and a significantly strong LCO can be expected if $\Re \{\int _V \hat{p}'\hat{\dot{q}}' \mathop {}\!\textrm{d}V\} >0$ which is the Rayleigh Criterion in frequency space. The Rayleigh Index is therefore given by

$$\begin{aligned} \mathrm {\widehat{RI}}(\omega ) = \Re \{\hat{p}'(\omega )\,\,\hat{\dot{q}}(\omega )\}. \end{aligned}$$

(24)

Eq. 22 shows that the generalised acoustic energy equation may have positive contributions from the cross-correlation between pressure and heat release rate fluctuations. Therefore we define a more general Rayleigh Index called the modified Rayleigh Index given by

$$\begin{aligned} \mathrm {m\widehat{RI}}(\omega ,\underline{\omega }) = \Re \{\hat{p}'(\underline{\omega })\hat{\dot{q}}(\omega )\}. \end{aligned}$$

(25)

It is also common practice to assume that acoustic modes are orthogonal (Culick 1976), which would yield $\int _V \hat{u}'(\omega )\hat{u}'(\underline{\omega })\, \mathop {}\!\textrm{d}V = \int _V \hat{p}'(\omega )\hat{p}'(\underline{\omega }) \mathop {}\!\textrm{d}V = 0,\; {\forall \; \underline{\omega } \ne \omega }$. The modes identified in this work are not orthogonal and this may lead to some contribution to acoustic energy due to non-orthogonality.