Aerodynamics and Wake Flow Characteristics of a Four-Cylinder Cluster

Abstract

The aerodynamic behaviour and wake flow of a cluster of two-dimensional sharp-edged bluff bodies exhibits extremely complex unsteady phenomena in both near and far fields. Due to the high cost of wind-tunnel experiments and numerical simulations, a complete understanding of wake flows and a description of their characteristics are lacking. This paper presents large-eddy simulations (LES) in different flow/wind directions for a cluster of $2 \times 2$ aligned square cylinders, at a separation distance in streamwise and cross-wind directions equal to cylinder side length, and at Reynolds number ${Re}=22,000$ based on the single cylinder side length D. The case at $0^\circ$ incidence shows an evident channel-type flow in the along-wind street/gap, and at its exit an irregularly pulsing jet with an intense shedding of large vortices. The wavelet analyses of the side force/lift coefficient and instantaneous velocities in the wake show that the characteristic length and time scales of the large vortical structures in the far-field wake are close to the cluster size 2D; this is the so called ‘cluster effect’. The cluster effect increases monotonically as the flow incidence angle increases. At a large incidence angle in the near-field wake, the cylinder-scale flow structures are much weaker compared to the cluster-scale structures. At the incidence angle of $45^\circ$, the overall wake flow and the aerodynamic characteristics are well scaled by the scale approximately equal to 2D. Nevertheless, the interaction between cylinders significantly affects the aerodynamics performance of the individual cylinders. The drag and lift coefficients of the individual cylinders differ substantially from each other in the cluster, and are significantly different from observations on a single isolated cylinder too.

1 Introduction

The flow around a single square or rectangular cylinder is a classic bluff body aerodynamic problem, and has been investigated extensively (e.g. Bearman and Obasaju 1982b; Lyn and Rodi 1994; Voke 1997; Rodi 1997; Breuer et al. 2000; Sohankar et al. 2000; Minguez et al. 2011; Trias et al. 2015; Cao and Tamura 2016; Daniels et al. 2016; Ricci et al. 2017; Chen et al. 2020, 2022, ), because of its simple geometry, extremely rich physics, and broad applications. The study on this problem is still ongoing in academia on various challenging issues, such as peak surface pressure, interaction with inflow turbulence, interaction with turbulent boundary layer, and interaction with unsteady motion. This paper is focused on the cluster effect of a group of square cylinders, and does not aim to carry out a review on the single cylinder problem. Readers are advised to start from the non-exhaustive reference papers listed above.

1.1 Aerodynamic Characteristics of a Cluster of Tall Buildings and its Wake Flow

Many cities around the world are growing rapidly bigger and taller. More isolated and clustered tall buildings have been being built or are to be built. This change may significantly affect the urban environment, e.g. street-level winds, the dispersion of pollutants, heat fluxes and the temperature distribution. On the other hand, the changed wind environment affects the aerodynamic performance of the buildings, such as wind loading, surface pressure and indoor ventilation.

Studies on wake flows of a cluster of tall buildings require a domain greater than the neighbourhood scale ($\approx$ 1 km), and a Reynolds number greater than a certain threshold, such as Re $\approx$ $2\times 10^4$, to avoid Re dependency issues. Early studies (e.g. Sohankar 2006; Bai and Alam 2018) found that when Re exceeded such a threshold, the Strouhal number St and the aerodynamic coefficients of a square cylinder reached approximately at constant values. Freestream turbulence increases the effective Reynolds number and consequently reduces this threshold (Bearman and Morel 1983). The requirements of the large domain scale and the necessary building size challenge the available wind tunnel facilities, as well as the computational fluid dynamics approaches, despite the fast growing computing capability. Field experiments are able to provide full-scale data, e.g. at the Reynolds number ${Re} > 10^7$, and the Richardson number ${Ri}\gg 1$, which are nevertheless expensive to obtain, and are usually scattered due to the varying meteorological conditions. Consequently, it remains challenging to understand and quantitatively describe the aerodynamic characteristics (e.g. force coefficients) of a cluster of buildings and its wake flow.

1.2 Aerodynamics of Clusters of Square Cylinders

The wake flow of a cluster of two-dimensional (i.e. infinite in the spanwise/crosswind direction) square cylinders exhibits extremely complex phenomena in both the near and far fields, and lacks of understanding and a quantitative description of its characteristics (e.g. Sau et al. 2007; Burattini and Agrawal 2013; Agrawal et al. 2006; Han et al. 2014; Alam et al. 2011, 2002; Du et al. 2021; Kahil et al. 2019; Zhang et al. 2019). A brief review is given below.

A number of studies (Sau et al. 2007; Burattini and Agrawal 2013; Agrawal et al. 2006) are reported in the literature on a pair of side-by-side cylinders in flows at Reynolds number around 100. Burattini and Agrawal (2013) studied wake interaction of two side-by-side square cylinders at a Reynolds number equal to 73, as a function of the spacing between cylinders. They noticed that the Strouhal number of vortex shedding was almost constant and near 0.16, within a range of spacing 0.5d to 6d, where d is the cylinder side length. Han et al. (2014) studied the wake characteristics of two side-by-side square cylinders at a Reynolds number 22,000.

Alam et al. (2011) experimentally studied wake flow of two side-by-side square cylinders at a Reynolds number 47,000 at a centre-to-centre spacing pitch ratio ranging from P/D 1.02 to 6, where P is the centre-to-centre spacing. They identified four wake flow regions. First, the single-body regime ${\mathscr {A}}$ was identified at $P/D < 1.3$, where the two cylinders were close enough to behave as a single body, forming a single staggered vortex street. The instantaneous velocity in the wake had a primary frequency which was approximately half of the shedding frequency of an isolated cylinder. Second, the two-frequency regime $\mathscr {B}$ occurred at P/D = $1.3-2.2$, where the gap flow between the cylinders was biased with adequate momentum to form one narrow and one wide street, which were respectively associated with a high and a low Strouhal number St. The former and latter were close to 0.5 and 1.5 times of the St of an isolated cylinder, respectively. Third, the transition region $\mathscr {C}$ was identified at P/D = $2.2-3.0$, where the narrow and wide streets were still frequently observed as in the regime $\mathscr {B}$, while they switched from time to time to two anti-phased streets, because of the more energetic gap flow (compared to that in the regime $\mathscr {B}$) between the cylinders injecting into the wake and inducing the symmetry of wake. Consequently, three frequencies were identified from the power spectra of the wake velocities, i.e. 0.5, 1 and 1.5 times of the St of an isolated cylinder. Fourth and last, the coupled vortex shedding regime occurred at $P/D > 3.0$. At $P/D = 3.0-4.6$, the two vortices were shed predominantly in anti-phased pattern, due to the energetic gap flow between the cylinders, which was denoted sub-regime $\mathscr {D}1$. At $P/D > 4.6$, the two vortices were shed both in anti- and in-phase patterns, which was denoted sub-regime $\mathscr {D}2$. In the regime $\mathscr {D}$, the primary frequency of the wake velocities was close to that of the single isolated cylinder.

Alam et al. (2002) studied the aerodynamic interaction of two square prisms in a tandem arrangement with a variation of the centre-to-centre spacing ratio $1.5<P/D<12$, at $Re=56,000$. The Strouhal number St calculated from the power spectrum of the fluctuating lift force acting on the downstream prism was within a very narrow range $0.10<St<0.13$. In particular, Alam et al. (2002) showed ${St}\approx 1.25$ at $P/D=2$. Du et al. (2021) carried out wind tunnel experiments to study aerodynamic interaction of two square cylinders at ${Re}={80,000}$, a centre-to-center spacing ratio $P/D=1.75$ and various incidence angles, in an aligned arrangement. The estimated Strouhal numbers of the lift coefficients of the two cylinders in the aligned arrangement were both greater than 0.1 for small incidence angles ($\alpha \le 20^\circ$). Both the data in Alam et al. (2002) and Du et al. (2021) may suggest that the two square cylinders in tandem do not evidently change the wake flow.

Kahil et al. (2019) reported flows around four circular cylinders in square arrangement at a sub-critical Reynolds number 3000. They detected three distinct biased modes for a ratio of pitch to cylinder diameter ranging from 1.25 to 1.5, where the spacing was the gap width between two in-line cylinders. Mode 1 was defined when the wake of the entire cluster of cylinders drifted to one side within a certain period, while Mode 2 was defined for the reverse of flow topology of Model 1. Mode 3 was defined when the wake had no preferred direction. The authors did not report the separation time of each mode due to the complexity of the physics.

It is worth noting that only a very small number of studies for the 2-by-2 square cylinders arrangement have been reported in the literature (e.g. Abbasi et al. 2014; Liu et al. 2015; Song et al. 2017; Zhang et al. 2019; Shahab et al. 2021). These studies were based either at very low Reynolds numbers (O(100)) (Abbasi et al. 2014; Song et al. 2017; Shahab et al. 2021), or at sub-critical Reynolds numbers (O(1000)) (Liu et al. 2015; Zhang et al. 2019). Zhang et al. (2019) carried out water tunnel experiments to study the wake flow and aerodynamic forces of an array of 2-by-2 aligned square cylinders with a ratio of pitch to cylinder side size P/D ranging from 2 to 5, at incidence angles $\alpha =0^\circ - 45^\circ$ and ${Re}={8000}$. The performance of the unsteady lift and drag was extremely complicated in most of the configurations. Nevertheless, it was evident that the primary frequency of the lift coefficients of the downstream cylinders with $P/D=2$ at $\alpha = 45^\circ$ were $f=1.23~\text {Hz}$, which are almost half of the primary frequency $f=2.57~\text {Hz}$ of the lift coefficients of the four cylinders with $P/D=4$ at $\alpha = 0^\circ$. Zhang et al. (2019) explained that this frequency, which was much lower than the primary vortex shedding frequency, corresponding to the quasi-steady, low frequency ‘galloping and flutter’ type of vibration commonly found in the case of rectangular and square cylinders. It is worth noting that the lower frequency $f=1.23 ~\text {Hz}$ measured in Zhang et al. (2019) corresponds to the Strouhal number ${St}=0.062$, while the higher frequency $f=2.57~\text {Hz}$ corresponds to ${St} = 0.129$, which is very close to the primary vortex shedding frequency ${St} = 0.13$ of an isolated cylinder (see Table 3 and Bearman and Obasaju (1982a); Trias et al. (2015); Chen et al. (2020)). This suggested that the strong cluster effect of four square cylinders at $\alpha = 45^\circ$ is more a fluid-dynamic mechanism, but not a fluid–structure interaction phenomenon.

Du et al. (2021) also studied aerodynamic interaction of two square cylinders in an arrangement with aligned diagonals, at various incidence angles and a centre-to-center spacing ratio $P/D=1.75$. It is highlighted that the narrowest tip-tip gap between the two cylinders was about 0.34D. At $\alpha =35^\circ$, two evident dimensionless frequencies ${St}=0.07$ and 0.21 of the fluctuating lift were observed. Note that the former and the latter were respectively 0.5 and 1.5 times of the shedding frequency of an isolated cylinder. At $\alpha =70^\circ$, two strong peaks in the spectrum of the fluctuating lift were observed at ${St}=0.06$ and 0.27. For $0<\alpha \le 17.5^\circ$, the dominant frequency was identified approximately at ${St} =0.1$. Although it was too early to draw a conclusive remark on the impact of wake flow, these results suggested that a cluster effect did occur at some incidence angles.

1.3 The Current Large-Eddy Simulation Study

Up to the authors’ knowledge, no published study has drawn a conclusive remark of the scaling of the dominant vortex shedding frequency for a cluster of 2-by-2 cylinders at Reynolds numbers equal to or greater than $Re=22,000$. The present large-eddy simulation (LES) study (e.g. Sect. 3) of aerodynamic forces and wake flow is focused on the dominant dimensionless vortex shedding frequency (i.e. the Strouhal number St) to bridge the knowledge gap of the connection between the aerodynamic forces of the cluster and the wake flow. It aims to shed light on the mechanism of flow around a cluster of cylinders and to provide an implication for relevant applications, such as the design of a cluster of tall buildings in cities.

This paper presents large-eddy simulations at a moderately large Reynolds number (${Re}={22,000}$) for single and 2-by-2 square prism arrangements, which are homogeneous in the spanwise direction. Different flow incidence angles were considered. The paper is organised as follows. The computational methods including LES and wavelet analysis are introduced in Sects. 2.1, 2.2. The numerical setup is introduced in Sect. 2.3. The validation and sensitivity tests are presented in Sect. 2.4. Sections 3 and 4 show the characteristics of wake flow and aerodynamic forces, respectively. Conclusions and discussions are presented in Sect. 5.

2 Computational Methods, Numerical Settings and Validations

2.1 Large Eddy Simulations

Large Eddy Simulations (LES) embedded in the open source code OpenFOAM-v2006 was performed to solve the filtered, incompressible Navier-Stokes equations,

$$\begin{aligned} \frac{\partial {\bar{u}}_i}{\partial x_i}= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial {\bar{u}}_i}{\partial t} + \frac{\partial }{\partial x_j} ( {\bar{u}}_i {\bar{u}}_j)= & {} - \frac{\partial {\bar{p}}}{\rho \partial x_i} + \frac{\partial }{\partial x_j} \left( \nu \frac{\partial {\bar{u}}_i}{\partial x_j} \right) + \frac{\partial \tau _{ij}}{\partial x_j}, \end{aligned}$$

(2)

where $\bar{u_i}$ and ${\bar{p}}$ are the filtered velocity and pressure, respectively; $\rho$ is the density; $\nu$ is the kinematic viscosity. The kinematic sub-grid scale (SGS) stresses $\tau _{ij}$ are modelled using the Boussinesq approximation,

$$\begin{aligned} \tau _{ij} = {\bar{u}}_i{\bar{u}}_j-\overline{u_iu_j} = 2\nu _t {\bar{S}}_{ij} - \frac{1}{3} \delta _{ij}\tau _{kk}, \end{aligned}$$

(3)

in which $\delta _{ij}$, $\nu _t$, and ${\bar{S}}_{ij}$ are the delta Kronecker, the kinematic SGS viscosity and the rate-of-strain tensor for the resolved scales, respectively. Rodi (1997) and Sohankar et al. (2000) carried out comparison of various SGS models, such as the Smagorinsky, Dynamic Smagorinsky and One-Equation models, for flows around a squared cylinder at Re =22,000 and at a blockage ratio 6-7% with a span width 4D, The coarse grid resolution used in Rodi (1997) yielded visible discrepancy in drag coefficient, but much less discrepancy in Strouhal number St. Rodi (1997) commented that “it appears that St is not very sensitive to the parameters of the simulation”. The much finer grid resolution used in Sohankar et al. (2000) with the first near wall grid size 0.008D, yielded negligible discrepancy in the Strouhal number St, visible but less than 10% discrepancy in drag coefficient. Early studies (e.g. Xie and Castro 2006) showed that large-eddy simulations for flows around bluff bodies with sharp edges were less sensitive to the SGS model, than those over smooth surfaces. This is because the primary flow structures are determined by the sharp edges, resulting in a reduced influence on the aerodynamic forces and vortex shedding frequency. It is to be noted that the Strouhal number St is around 0.13, suggesting that the time scale of shed vortices are about one order of magnitude greater than the dominant turbulent eddies over the cylinder, and that St is less sensitive to the numerical accuracy than other aerodynamic quantities. Both the Smagorinsky (Rodi 1997; Sohankar et al. 2000; Xie and Castro 2006) and the mixed time-scale (Inagaki et al. 2005; Chen et al. 2020) SGS models were tested in the study, and no significant discrepancy in St was identified. The Van Driest damping function was used to force the Smagorinsky SGS viscosity to vanish in the viscous sublayer.

2.2 Wavelet Analysis

The vortex shedding, wake flow and aerodynamic forces of a cluster of square cylinders display multi-scale behaviour (e.g. Kahil et al. 2019; Zhang et al. 2019). The conventional Fourier analysis is used to process a sufficiently long time series of a stationary process, but can struggle to identify energetic and localised events in short time series. The windowed Fourier analysis splits the time series into a number of short fixed-length segments, and then applies the Fourier transform separately on each segment (Perrier et al. 1995). The pre-defined fixed resolution (i.e. the segment length) constrains the application of the windowed Fourier analysis. In contrast to Fourier transform approaches, the wavelet analysis has the inherent ability to capture local-time spectra of a non-stationary signal (Mahrt 1991; Perrier et al. 1995; Horiguchi et al. 2012; Nguyen et al. 2022), and can be used for identifying multiple scales in wake flows and in the time series of aerodynamic forces.

We noticed that the wake flow and the aerodynamic forces were non-stationary, and decided to use wavelet analysis in this study. Below is a brief of wavelet analysis. The wavelet transformation of a time series signal $\xi (\tau )$ (e.g. a time series of the wake velocity or the aerodynamic force acting on an individual cylinder) is defined as follows

$$\begin{aligned} T_p(a,t)=\frac{1}{\sqrt{a}}\int ^{\infty }_{-\infty }\Psi ^*\left( \frac{\tau -t}{a}\right) \xi (\tau )\text {d}\tau , \end{aligned}$$

(4)

where $T_p$ is the wavelet coefficient (scalogram), $\Psi$ is the mother wavelet with the asterisk denoting the complex conjugate of the function, and a and t are respectively the scale and translation parameters. In this paper, the Morse wavelet function (Olhede and Walden 2002) is employed.

For a clear identification of the energetic scales, the mean wavelet magnitude is used

$$\begin{aligned} {\bar{S}}({\tilde{n}})=\int ^{\infty }_{-\infty }\left| T_p({\tilde{n}},t)\right| \text {d}t, \end{aligned}$$

(5)

where ${\tilde{n}}=fD/U_\infty$ is dimensionless frequency, being $f=1/(2a)$ and $U_\infty$ the frequency and the freestream velocity at inlet. For vortex shedding frequency, ${\tilde{n}}$ is commonly referred to as Strouhal number St.

Again, the time-average wavelet magnitude ${\bar{S}}({\tilde{n}})$ is calculated from the integration over the entire sampled time duration of the wavelet coefficient. It provides an easier tool to identify the representative scales compared to the time-frequency scalogram map (see Fig. 4 as an example).

2.3 Numerical Setup

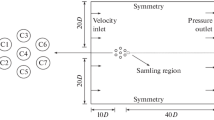
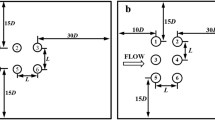
Two arrangements of square cylinders were considered: Case 1, with an isolated square cylinder of size D and infinite spanwise length, and Case 2, with a two by two array of square cylinders with the same dimension as in Case 1 and with a centre-centre spacing of 2D (see Fig. 1). The Reynolds number was ${Re}=22,000$ based on the freestream speed $U_\infty$ and the cylinder size D. Five flow incidence angles, $\alpha =0^\circ , 11.25^\circ , 22.5^\circ , 33.75^\circ$ and $45^\circ$ were simulated for Case 2. Figures 1a and b show the computational domain dimensions and the partition of the structured mesh for Case 1 ($27D \times 20D \times 4D$) and Case 2 ($56D \times 43D \times 4D$), respectively. The dimensions of Case 1 domain are the same as those in Chen et al. (2020) with a blockage ratio 5%, and in the cross-flow direction are slightly greater than those in Rodi (1997) and Sohankar et al. (2000). Case 2 has a slightly less blockage ratio 4.7%. Sohankar et al. (2000) states that the blockage effect on the shedding frequency is significantly less than the effective increase in the oncoming velocity. This is because the mean flow around the trailing edges of the cylinder is probably more directly related to the shedding frequency than the mean velocity in the outer regime of the separating shear layers initiating from the frontal edges (Igarashi 1985). It is to be noted that the key aspect of this study is an analysis of the cluster effect of a group of four square cylinders compared to a single cylinder, rather than a prediction of aerodynamics with an accuracy up to the DNS level. Given the large computational domain and the excessive computational cost for the simulation of a number of vortex shedding cycles, Case 2 was set to have the same span length 4D as in Case 1. Chen et al. (2020) showed that the spanwise integral length scale for the spanwise velocity in the near wake region is approximately D/4, suggesting that a span length 4D with periodic boundary conditions in spanwise direction is sufficient to capture energetic turbulent eddies.

For Case 1, the structured mesh was chosen based on the settings as in the stationary square cylinder case in Chen et al. (2020). Moreover, for the purpose of sensitivity analysis, three resolutions were tested, including coarse mesh with 14 millions cells, medium mesh with 20 millions cells and fine mesh with 24 millions cells. The resolution of the first near wall grid was always equal to D/200, equivalent to less than 5 wall units. Other mesh parameters were the same as those of the stationary case in Chen et al. (2020). For Case 2, the mesh structure for all considered flow directions was based on that of Case 1 with the fine mesh settings, with a fine mesh of 73 million cells and the same near-wall resolution as Case 1.

Fig. 1

A sketch of the computational domain (not to scale) and its partition for structured mesh: a an isolated cylinder; b a cluster of 4 cylinders. The resolution in the near the single cylinder and the cluster region is 200 grid points per cylinder side D, giving the first grid resolution in wall unit less than 5

Uniform velocities were imposed at the inlet (left) and top boundaries (Fig. 1). Outflow boundary condition was imposed at the bottom and outlet (right) boundaries. In the spanwise direction, periodic boundary conditions were used. No-slip boundary condition was applied on the cylinder surfaces. For all simulated cases, the initial duration for LES was more than 150 $t^*$, the duration for average was more 200 $t^*$, where $t^*=tU_\infty /D$ is the non-dimensional time.

2.4 Validation of a Single Square Cylinder and Mesh Sensitivity Tests

Validation simulations for Case 1 were carried out at zero incidence angle and were compared to the LES data in Sohankar et al. (2000), Chen et al. (2020), the experimental data in Bearman and Obasaju (1982a), and the DNS data in Trias et al. (2015). Table 1 shows the time-averaged drag coefficient (${\bar{C}}_D$), the root-mean-square (r.m.s.) value of the fluctuating lift coefficient (${\tilde{C}}_L$) and the Strouhal number (St). The coefficients are hereafter normalised by the freestream speed $U_\infty$ and the cylinder size D.

The three cases of the present study with different resolutions in Table 1 showed an evident convergence of the Strouhal number St. The “fine mesh” case showed excellent agreement with the early LES studies (Sohankar et al. 2000; Chen et al. 2020), as the crucial numerical settings are identical. The data in Chen et al. (2020) were generated from an in-house FORTRAN code with the same domain configuration and grid resolution, but with an immersed boundary condition method for a staggered mesh, and a mixed time scale SGS model. This suggests that the Smagorinsky SGS model and the collocated mesh don’t yield a significant effect.

The present LES slightly under-predicts ${\tilde{C}}_L$ compared to the DNS data, whereas over-predicts it compared to the experimental data. This is likely because ${\tilde{C}}_L$ is sensitive to numerical and experimental conditions, e.g. time and spatial resolutions. As the “fine mesh” provided results in agreement with data in the literature (e.g. Sohankar et al. 2000; Chen et al. 2020), it was used as the base mesh with 74 millions cells for the cluster of four cylinders.

While the structured mesh was kept the same for different flow incidences, a further mesh refinement was carried out for checking the mesh sensitivity. The mesh was further refined from the “fine mesh”, and the total number of cells reached to 159 million. This “finer mesh” was used for flows around the cluster at $\alpha =45^\circ$. Table 2 shows mean and r.m.s. drag (${\bar{C}}_{Di}$ and ${\tilde{C}}_{Di}$, respectively) and mean lift and r.m.s. lift (${\bar{C}}_{Li}$ and ${\tilde{C}}_{Li}$, respectively) coefficients of individual cylinders of the cluster. Overall the mean aerodynamic coefficients and r.m.s. data obtained from two mesh cases are in good agreement. A less-than-10% discrepancy of mean coefficients was visible. For such highly non-stationary flows at $\alpha =45^\circ$ (see Fig. 11), the resolution in the vicinity of the free shear layer initiated from the frontal edges might be coarse for the two cases, resulting in a local non-negligible sub-grid scale and numerical viscosity (Komen et al. 2017). Interestingly, Sohankar et al. (2000) showed a similar discrepancy when comparing different SGS models for flow around a single square cylinder, in which a slightly coarser resolution and a slightly greater blockage ratio were used compared to the current study. Nevertheless, this small uncertainty would not affect the conclusive remarks on cluster effect drawn in this study.

Table 1 Validation for the single cylinder at ${Re}={22,000}$ and $\alpha =0^\circ$

Table 2 Mean and r.m.s drag (${\bar{C}}_{Di}$ and ${\tilde{C}}_{Di}$, respectively) and mean lift and r.m.s lift (${\bar{C}}_{Li}$ and ${\tilde{C}}_{Li}$, respectively) coefficients of individual cylinders of the cluster at ${Re}={22,000}$ and $\alpha =45^\circ$ for two meshes. The subscript ‘i’ denotes the cylinder identification number detailed in Fig. 1

3 Characteristics of Lift Coefficient of the Cluster and the Wake Flow

The fine mesh (Table 2) was used for all the large-eddy simulations reported in the following sections and 8). Again, in the current study we focus more prominently in the region of the wake for $x/D\ge 3.0$, given the extreme complexity of the flow field between the cylinders and in the very near wake (e.g. $x/D<3.0$), where the recirculation and the peak TKE can be identified (e.g. Knisely 1990; Mueller 2012; Cao and Tamura 2016; Chen et al. 2020). In total, we placed ten probes in the wake region (Table 3) to record velocity time series. The spectral characteristics of recorded velocity fluctuations are analysed in the following sections, to elucidate the dynamics of the vortices shed past the cluster.

Table 3 Locations of the velocity probes placed in the wake region. See Fig. 1 for the reference system utilised

3.1 Case at $\alpha =0^\circ$

Figure 2 shows a snapshot of the instantaneous velocity $u_x$ for the case $\alpha =0^\circ$. A strong channelling effect is observed in the along-wind spacing, with separation and reattachment on the inward sides of the front cylinders B1 and B4. This differs from observations around a single isolated square cylinder where flow reattachment does not occur (e.g. Chen et al. 2020). At the exit of the along-wind spacing, a pulsing jet flow is evident with intense vortices shed in a slightly asymmetric pattern. This shedding is slow and irregular, and is shown from the following analysis of the aerodynamic force coefficients and the wake velocity field.

Fig. 2

Example instantaneous velocity field $u_x$ at $\alpha =0 ^\circ$ and locations of velocity probes

Figure 3a shows the time-frequency scalogram map of the lift force coefficient $C_L$ of cylinder B3 at $\alpha =0^\circ$ (left), and its time-averaged wavelet magnitude $\bar{S}({\tilde{n}})$ (right). The force spectrum shows a dominant frequency ${\tilde{n}} = 0.14$, which is close to that of an isolated cylinder. It is worth noting that the lift force coefficient of the upstream cylinder B4 does not show any dominant frequency (not shown). In addition, the lift force coefficients of the cylinders B3 and B4 both show a weak peak at ${\tilde{n}} =0.062$, which is approximately half of that of an isolated cylinder, suggesting a cluster effect.

Figure 3b shows the same as Fig. 3a but for the summation of the lift force coefficients of the four cylinders. The total lift of the four cylinders shows more complex spectrum than that for the cylinder B3. Different from the case of individual cylinder shown in Fig. 3a, no dominant frequency is clearly shown. Instead, large wavelet magnitude occurs within a wide range of frequency (e.g. $0.08 \le {\tilde{n}} \le 0.22$) with a peak at ${\tilde{n}} = 0.162$. The broadband spectrum suggests that multiple-scale vortices act on the cluster, of which the small ones are due to the unsteady channel flow between the cylinders, the pulsing jet at the exit between cylinders B2 and B3, and broken-down vortices from the large ones due to the jet. These structures are associated with the fluctuations of lift force on the individual cylinders.

Fig. 3

Time-frequency scalogram map (left) and the time-averaged wavelet magnitude (right) of a the lift force coefficient $C_L$ of cylinder B3 and b summation of the lift force coefficients of the four cylinders at $\alpha =0^\circ$

Velocity time series sampled in the wake were also used to understand the characteristics of the vortices. Figure 4 shows the time-frequency scalogram map of the fluctuating streamwise velocity component at $\alpha =0^\circ$ (left) and the time-averaged wavelet magnitude $\bar{S}({\tilde{n}})$ (right) at various locations in the wake. The data at the near-cluster probes P4 and P5 show a dominant frequency ${\tilde{n}} =0.14$, which is the same as that of the lift of the downstream cylinder B3 and B2, and is slightly greater than that ${\tilde{n}} ~(\text {i.e.~} St)=0.13$ of an isolated cylinder. This confirms as in Fig. 3 that the vortex shedding frequency and the resultant frequency of lift force of the downstream cylinders are ${\tilde{n}}=0.14$. Figure 4 shows clear secondary frequencies, which are close to the half of the dominant frequency ${\tilde{n}} =0.14$. This is consistent to the secondary (lower) frequencies in the wavelet magnitude of lift coefficient in Fig. 3. At probe $P_{10}$, which is the farthest one to the cluster, only the lower frequency ${\tilde{n}}=0.062$ is visible. One might speculate that the near-cluster vortices at ${\tilde{n}} =0.14$ interact with the slow jet from the along-wind spacing, convert downstream and merge into larger vortices (see Fig. 2).

Fig. 4

Time-frequency scalogram map (left) and the time-averaged wavelet magnitude (right) of the streamwise fluctuating velocity at $\alpha =0^\circ$ at locations a $P_4$; b $P_{5}$; c $P_{10}$

The flow structure at $\alpha = 0^\circ$ is the most complex one compared to the oblique inflow cases, in terms of the identification of the primary frequency of the vortex shedding. Given the extreme complexity of the lift coefficient signal of the individual cylinders, the following sections are focused on the total lift coefficient and the velocity time series sampled from several probes in the wake.

3.2 Case at $\alpha = 11.25^\circ$

At $\alpha =11.25^\circ$, the vortex shedding pattern and the primary vortex shedding frequency were studied as for $\alpha =0^\circ$. As an illustrative example, Fig. 5a shows the time-frequency scalogram map (left) and the time-averaged wavelet magnitude ${\bar{S}}({\tilde{n}})$ (right) of the total lift coefficient $C_L$ of the cluster. Figure 5b shows the same as Fig. 5a, but for the streamwise velocity at probe $P_5$.

For isolated square cylinders, it is known (e.g Knisely 1990; Norberg 1993; Tamura and Miyagi 1999; Mueller 2012; Nguyen et al. 2020) that ${\bar{C}}_L$ and Strouhal number St (i.e. ${\tilde{n}}$) reach their peak values at a critical angle of incidence between $\alpha =12^\circ -14^\circ$. The dominant frequency ${\tilde{n}}=0.076$ shown in Fig. 5 is very close to half of the peak frequency (${\tilde{n}}=0.14-0.155$) of an isolated cylinder at the critical angle of incidence (e.g Tamura and Miyagi 1999; Mueller 2012). This confirms again the strong cluster effect of the flows between the four cylinders, resulting in a dominant vortex shedding frequency ${\tilde{n}}=0.076$. This also suggests that the cluster behaves, as if it was an isolated, solid square cylinder with a width 2D, in terms of the dominant shedding frequency.

Fig. 5

Time-frequency scalogram map (left) and the time-averaged wavelet magnitude (right) of a the sum of lift force coefficients of the four cylinders and b the streamwise fluctuating velocity at location $P_5$ at $\alpha =11.25^\circ$

3.3 Case at $\alpha =22.5^\circ$

Figure 6a shows the time-frequency scalogram map (left) and the time-averaged wavelet magnitude (right) of the total lift coefficient of the cluster at $\alpha =22.5^\circ$. Figure 6b shows the same as Fig. 6a but for the streamwise fluctuating velocity at probe $P_{10}$. Similar to those at $\alpha =11.25^\circ$, the data in Fig. 6 collectively shows a dominant frequency ${\tilde{n}}=0.062$, which is very close to half of the dominant frequency ${\tilde{n}} \approx 0.127$ of an isolated square cylinder at ${Re}={46,000}~\text {and} ~\alpha =20^\circ$ (e.g. Mueller 2012). Again, this suggests that the cluster behaves as a 2D-width solid square cylinder at $\alpha =22.5^\circ$.

The second harmonic frequency ${\tilde{n}}=0.123$ is visible from the two wavelet spectra in Fig. 6. This falls into the range of the dominant vortex shedding frequency $0.123\le {\tilde{n}} ~(\text {i.e.~} St) \le 0.131$ of of an individual isolated cylinder (e.g. Mueller 2012), suggesting that the cylinder scale vortex plays an negligible role on the lift force and the velocities in wake region downstream $x=6.5D$ from the cluster centre.

Fig. 6

Time-frequency scalogram map (left) and the time-averaged wavelet magnitude (right) of a the sum of lift force coefficients of the four cylinders and b the streamwise fluctuating velocity at location $P_{10}$ at $\alpha =22.5^\circ$

3.4 Case at $\alpha =33.75^\circ$

Figure 7 shows the same as Fig. 6 but at $\alpha =33.75^\circ$. The data in Fig. 7a and b collectively show a dominant frequency ${\tilde{n}}=0.054$, equal to half of the secondary frequency ${\tilde{n}}=0.107$. The latter is almost the same as that of an isolated square cylinder at $\alpha =33^\circ ~\text {and~} Re={46,000}$ (Mueller 2012). This is consistent with those at $\alpha =22.5^\circ$ that the incoming flow ‘sees’ a more densely packed cluster than at $\alpha =0, ~\text {and}~ 11.25^\circ$, and the dominant vortex shedding frequency is more pronounced.

The second harmonic frequency, ${\tilde{n}}=0.107$, is weakly visible from Fig. 7a for the lift force data but more visible from Fig. 7b for the fluctuating velocity in the wake. We noticed that the secondary shedding frequency is more evident at the probes closer to the cluster (not shown here). This is perhaps not surprising as the individual cylinders have more impact on the vortices shed at this scale.

Fig. 7

Time-frequency scalogram map (left) and the time-averaged wavelet magnitude (right) of a the sum of lift force coefficients of the four cylinders and b the streamwise fluctuating velocity at location $P_{10}$ at $\alpha =33.75^\circ$

3.5 Case at $\alpha =45^\circ$

Figure 8 shows that the overall flow at $\alpha =45 ^\circ$ is asymmetric to the central plane along the flow direction, similar as the flow around a single isolated square cylinder. Separated flows at the sharp corners of cylinders B1, B3 and B4 are evident, while the separation around B4 is largely constrained by B1 and B3, resulting in nearly steady lift and drag, as discussed later in Fig. 11. Cylinder B2 is entirely in the wake of three upstream cylinders, and is significantly impacted by the oscillatory wakes, as discussed later in Fig. 11.

Fig. 8

Instantaneous velocity field $u_x$ at $\alpha =45 ^\circ$

Figure 9a shows the time-frequency scalogram maps (left) and the time-averaged wavelet magnitude (right) of the total lift coefficient of the cluster at $\alpha =45^\circ$. Figure 9b shows the same as Fig. 9a but for the fluctuating velocity at location $P_{10}$. The data in Fig. 9 collectively shows a dominant frequency of approximately ${\tilde{n}}=0.05$, which is very close to half of the dominant frequency ${\tilde{n}}=0.106$ for an isolated cylinder (Mueller 2012). This again confirms that the cluster at $\alpha =45^\circ$ behaves as if it was an individual isolated cylinder with width equal to 2D. The higher harmonic frequency are hard to discern at $\alpha =45^\circ$ compared to the other incidence angles. It is worth noting that, at $\alpha =45^\circ$, the front area covered by the cylinders is equal to the maximum cross-section of the entire cluster including the spacing between the cylinders, which is aerodynamically the ‘densest’ configuration in all flow directions, and behaves the most like a single larger square cylinder with a width approximately equal to 2D.

Fig. 9

Time-frequency scalogram map (left) and the time-averaged wavelet magnitude (right) of a the sum of lift force coefficients of the four cylinders and b the streamwise fluctuating velocity at location $P_{10}$ at $\alpha =45^\circ$

3.6 Summary and Discussion

Overall, the dominant frequency of the lift force of the cluster of four square cylinders in oblique winds (i.e. $\alpha \ne 0^\circ$) is identical as the dominant frequency of the sampled velocities at probes $x/D>3.0$ downstream from the cluster. These collectively suggest not only that the whole cluster behaves as a single larger square cylinder with a width approximately 2D, and also that the total lift force and the vortex shedding are well correlated. This is unexpected, as one might speculate that the size of the cluster including the spacing is 3D. We argue that the separation between the cylinders, i.e. the ‘permeability’ of the cluster to the incoming flow, determines a change in the dynamics in both the near- and far-wake regions of the cluster, resulting in unsteady flow features whose time scale is well described 2D.

In terms of physical explanations, the wake flow of a 2 × 2 cluster is a combination of the wake of two pairs of side-by-side square cylinders (e.g. Alam et al. 2011) and that of two square cylinders in a tandem (e.g. Alam et al. 2002). The cluster effect is dependent on the “permeability” of the building cluster with respect to the wind incidence, i.e. how the incoming flow “sees” the spacing between the buildings. For a high wind incidence (e.g. $45^\circ$), the effective permeability is much smaller, resulting in “single-body-like wake”, similar as a pair of side-by-side square cylinders (e.g. Alam et al. 2011). For a small wind incidence (e.g. $0^\circ$), the wake flow is more similar to the “two-frequency regime” of a pair of side-by-side square cylinders (e.g. Alam et al. 2011). Albeit the conclusive statistical analysis (i.e. wavelet) for the current LES data, it is worth to explore more physical explanation in the future.

At $\alpha = 0^\circ$, the two downstream cylinders show a dominant vortex shedding frequency ${\tilde{n}}=0.14$, which is slightly greater than that of a single isolated square cylinder, whereas the two upstream two cylinders and the entire cluster do not exhibit any prominent temporal behaviour, demonstrating the higher complexity of flow characteristics compared to the oblique-wind case. Nevertheless, at the farthest downstream probe location (e.g. $P_{10}$) the wavelet variance spectrum showed a dominant frequency ${\tilde{n}}=0.062$, which was nearly half of that of an isolated cylinder, corroborating the observation that the temporal dynamics of vortical structures in the far field can be scaled by 2D.

Table 4 shows the dominant frequencies of the cluster and an isolated cylinder in Knisely (1990) and Mueller (2012). For the cluster, the ${\tilde{n}}(C_L,clus.)$ data are identical to ${\tilde{n}}(u_x,clus.)$ in oblique winds ($\alpha \ne 0^\circ$), while at $\alpha = 0^\circ$, ${\tilde{n}}(C_L,clus.)$ differs slightly from ${\tilde{n}}(u_x,clus.)$ due to the complex wake flow, e.g. the pulsing jet flow from the aloing-flow spacing. The data of ${\tilde{n}}(C_L,sing.)/{\tilde{n}}(C_L,clus.)$ across the entire range of wind directions $0^\circ \le \alpha \le 45^\circ$ are approximately 2, suggesting that the dominant vortex shedding frequencies of the cluster scaled by 2D, are approximately equal to the corresponding dominant frequency of an isolated single cylinder scaled by D.

Table 4 Dominant frequencies of the cluster and an isolated cylinder and the respective ratio. ${\tilde{n}}(C_L,clus.)$ and ${\tilde{n}}(u_x,clus.)$ are the dominant dimensionless frequencies of the cluster, calculated from $C_L$ and $u_x$, respectively. ${\tilde{n}}(C_L,sing.)$ is the dominant dimensionless frequency of an isolated cylinder at Re =46,000 (Mueller 2012), and $22,000\le Re\le 62,000$ (Knisely 1990), calculated from $C_L$. ${\tilde{n}}(C_L,sing.)/{\tilde{n}}(C_L,clus.)$ and ${\tilde{n}}(u_x,sing.)/{\tilde{n}}(C_L,clus.)$ are the frequency ratio between the cluster and the single isolated cylinder, with the data in bracket are corresponding to (Knisely 1990). The values of $\alpha$ in bracket are the closest incidence angles for the isolated cylinder in Knisely (1990); Mueller (2012)

4 Aerodynamic Force Characteristics of the Cylinder Cluster

Fig. 10 shows the time series of the drag and lift coefficients of the four cylinders at $\alpha =0^\circ$. The drag coefficients of cylinders B2 and B3 fluctuate around a small negative average, while the average drag coefficients of cylinders B1 and B4 are positive, and close to that of a single isolated cylinder. On the other hand, the fluctuations of the drag and lift coefficients of cylinders B2 and B3 are more intense than those of B1 and B4, because the rear cylinder constrains the wake of the respective front cylinder. It is worth noting that, different from the single isolated square cylinder, the lift coefficient magnitudes of cylinders B1 and B4 have the average greater than unit. This is because of the channelling effect of the along-flow spacing between the cylinders.

A particular observation is that the drag and lift forces on the four cylinders are highly non-stationary, and different dynamical behaviour is observed in different time periods. During $t^*=150-320$, the fluctuations are moderate, while during $t^*=340-400$ and $t^*=600-680$ they are more intense. This may imply the existence of different flow regimes which are very large in space and very slow in time, resulting from the complex interaction between the jet flow from the along-wind spacing and the vortex shedding from the exterior sides of the array of cylinders. The correlation coefficient of lift forces of B1 and B4 is $-$0.58, while that for B2 and B3 is $-$0.74 (Table 5), both confirming the strong impact of the channelling effect of the the along-wind spacing.

Fig. 10

Time series of drag ($C_{Di}$) and lift ($C_{Li}$) coefficients of each cylinder at $\alpha =0 ^\circ$, where the subscript $`i'$ denotes the cylinder identification number (Fig. 1); $t^*=tU_\infty /D$ is the non-dimensional time, where t is the dimensional flow time

Figure 11 shows the time series of the aerodynamic force coefficients of the individual cylinders at $\alpha =45 ^\circ$. The forces on the B4 cylinder are very different from those on the other three cylinders, with a mean lift coefficient ${\bar{C}}_L \approx 0$ and very small drag fluctuations. One can speculate this is because the other three cylinders, in particular B1 and B3, prevent the B4’s wake from developing to large oscillations. The drag and lift forces on cylinder B1 are highly correlated with those on cylinder B3 with correlation coefficients ${-0.92}$ and 0.53 (Table 5), respectively. This confirms Fig. 9 that the cluster size vortex is shed from the cluster, as if it was an isolated, solid square cylinder with a width 2D. Cylinder B2, which is placed deeper in the wake region than the other cylinders, experiences smaller drag and significantly larger fluctuating lift.

Fig. 11

Same as in Fig. 10 but at $\alpha =45 ^\circ$

Figure 12a and b show the time-averaged aerodynamic coefficients ${\bar{C}}_D$ and ${\bar{C}}_L$, respectively, of each cylinder at various incidence angles. For the drag coefficient ${\bar{C}}_D$ of an isolated square cylinder (e.g. Mueller 2012), the maximum (${\bar{C}}_D \approx 2$) occurs at $\alpha =0^\circ$ and $45^\circ$, while the minimum (${\bar{C}}_D$ $\approx 1.4$) occurs at $\alpha =13^\circ$. For the maximum magnitude of lift coefficient (${\bar{C}}_L$ of an isolated square cylinder, the maximum $\approx 0.9$) occurs at $\alpha =13^\circ$. At $\alpha =0^\circ$ and $45^\circ$, the mean lift coefficient ${\bar{C}}_L$ is approximately zero, as expected. Compared to the lift and drag coefficients of an isolated cylinder, the force coefficients of the individual cylinders of the cluster show very complex interaction between them.

Figure 12c and d show the time-averaged coefficients of the total drag (i.e. summation of the drag forces of the four cylinders) ${\bar{C}}^*_D$ and lift (i.e. summation of the lift forces of the four cylinders) ${\bar{C}}^*_L$, respectively. The ${\bar{C}}^*_D$ of the entire cluster at $\alpha = 45 ^\circ$ is more than twice that at $\alpha = 0^\circ$, whereas the drag of a single isolated cylinder at $\alpha = 45 ^\circ$ is nearly the same as that at $\alpha = 0 ^\circ$. This is because at $\alpha = 45 ^\circ$ both the front area and the solidity (seen by the incoming flow) are substantially increased compared to at $\alpha = 0 ^\circ$. Indeed, the ${\bar{C}}^*_D$ increases monotonically as the incidence angle increases. Figure 12d shows that the critical angle of incidence corresponding to the peak ${\bar{C}}^*_L$ occurs at $11.25^\circ<\alpha <22.5^\circ$. This is somehow consistent with that of an isolated single cylinder, and is also associated with highest dominant frequency ${\tilde{n}}=0.076$ for all the tested incidence angles (i.e. $0^\circ \le \alpha \le 45^\circ$). Again as expected, the total lift coefficient ${\bar{C}}^*_L$ is approximately 0 at $\alpha = 0~ \text {and}~ 45 ^\circ$.

Figure 13 shows the same as Fig. 12 but for the root-mean-squared (r.m.s.) of the fluctuating drag (${\tilde{C}}_D$) and lift ${\tilde{C}}_l$ coefficients. For individual cylinders, the ${\tilde{C}}_D$ and ${\tilde{C}}_L$ of cylinder B4 has small values and is almost unchanged with respect to wind directions. This is because it is always in the most upstream position in the cluster from which the shed vortices are constrained by the downstream cylinders resulting more steady aerodynamic forces of B4. Overall, Fig. 13 shows very complex interactions between the individual cylinders.

In contrast to the extreme complexity of the ${\tilde{C}}_D$ of the individual cylinders shown in Fig. 13, the tendency of the individual ${\tilde{C}}_L$ is simpler. As $\alpha$ increases, ${\tilde{C}}_L$ of cylinder B3 decreases to a small constant close to those of B1 and B4. For α>11.25º, ${\tilde{C}}_L$ of cylinder B2 monotonically increases and has a significant maximum value at $\alpha =45^\circ$. At $\alpha =45^\circ$, cylinder B2 is fully in the wake and is open to the impact of the shed vortices, resulting in intensive fluctuating lift force much greater than that of the other cylinders (also see Fig. 11). As a result, cylinder B2 provides a dominant contribution to the total lift fluctuations, leading to a monotonic increase of ${\tilde{C}}^*_L$ as shown in Fig. 13d.

Fig. 12

Time-averaged aerodynamic coefficients: a drag (${\bar{C}}_D$); b lift (${\bar{C}}_L$); c total drag (${\bar{C}}^*_D$), and d total lift (${\bar{C}}^*_L)$

In term of the dominant vortex shedding frequency, it is evident that the relevant data for the cluster can be scaled by 2D to obtain dimensionless quantities consistent with those for a single isolated cylinder, in particular in oblique incoming flows. Nevertheless, Fig. 13c and d show that the trend against the incidence angle of the r.m.s. data (i.e. ${\tilde{C}}^*_D$, ${\tilde{C}}^*_L$) of total force fluctuations differs evidently from that for a singe isolated cylinder (e.g. Mueller 2012). This suggests the complexity of the flow and aerodynamics of a cluster of cylinders.

Fig. 13

r.m.s. of aerodynamic coefficients: a drag (${\tilde{C}}_D$); b lift (${\tilde{C}}_L$); c total drag (${\tilde{C}}^*_D$), and (d) total lift (${\tilde{C}}^*_L)$

Given the complexity of the interaction between the cylinders, the correlation coefficients of the lift forces might be able to shed light on the interaction and the mechanism of the formation of the total forces. As $\alpha =0^\circ$ and $\alpha =45^\circ$ are respectively the minimum and maximum incidence angles, for which the correlation data are more likely able to show a big map of correlation, Table 5 shows the correlation coefficients between the lift force of individual cylinders at these incidence angles.

At $\alpha =0^\circ$, the correlations of B1-B4 and B2-B3 are respectively $-$0.58 and $-$0.74, while the magnitude of other correlation coefficients are small, again suggesting strong channeling effect and the resulted pulsing jet effect due to the along-flow spacing between the cylinders.

At $\alpha =45^\circ$, all the correlation data show positive, confirming the same tendency of the total lift ${\tilde{C}}^*_L$ and that of B2. It is worth noting that the correlation coefficient 0.53 of the pair B1-B3 suggests alternating cluster-size vortex shedding from B1 and B3 sides. The very small correlation coefficients of the pairs B4-B1 and B4-B3 suggests that the leading edgy vortices generated from B4 are not large enough to reattach on the entire cylinders B1 or B3, of which the lift forces are not correlated to that of B4 (Fig. 8). The correlation coefficients of the pairs B1-B2 and B3-B2 are approximately 0.17. This suggests that the vortices generated from B1 or B3 are large enough to pass over or impact on cylinders B1 and B3. It is interesting that the correlation coefficient of the pair B4-B2 is 0.46. We speculate this is because the structures generated by cylinder B4 pass through the intersection of the cluster and impact on the cylinder B2 (Fig. 8).

Table 5 Correlation coefficients between the lift force of individual cylinders at $\alpha = 0^\circ$ and $45^\circ$. The bold numbers denote those at $\alpha = 45^\circ$

5 Conclusion

This paper addresses the challenges by carrying out large-eddy simulations with wavelet analysis for a 2 × 2 array of square cylinders at a Reynolds number equal to 22,000 at various flow incidence angles. The numerical settings, including the mesh resolution, were first validated extensively for a single isolated cylinder. Following the same settings as for the single isolated cylinder, simulations with further mesh sensitivity tests for a 2 × 2 array of square cylinders were carried out to ensure reliable and consistent data.

We found that the aerodynamic forces of the individual cylinders of the cluster substantially differed from each other, and from a single isolated cylinder. The aerodynamic forces were highly non-stationary suggesting different flow regimes. Engineering practice for estimating wind loading, even for clusters of buildings, is usually based on the aerodynamic coefficients (e.g. force, pressure) from a single isolated building. In addition, quasi-steady and stationary assumptions are often adopted. The current results suggest the importance of an improvement of the assessment of wind loading on densely packed tall buildings, and the impact of the wake flows.

The wavelet data of lift forces and fluctuating velocities in the wake show that the temporal dynamics of vortices shed from the cluster can be scaled by utilising a characteristic cluster size approximately equal to 2D, despite that one might think of the cluster size being 3D. This might be the product of the “permeability” of the cluster to the incoming wind. The shedding of large-scale vortices from the cluster is more intense at larger incidence angles, and relatively weaker at smaller ones. We speculate that this is because of the interaction between the flow developing within the cluster, e.g. the jet flow developing between the front cylinders at small incidence angles, and large-scale vortices shed from the cluster.

It is to be noted that the trend of the mean total aerodynamic forces of the cluster and in particular their r.m.s. data against the flow incidence angle differs evidently from that of an isolated single cylinder. This suggests that these aerodynamic force cannot simply be scaled by 2D for all incidence angles. Likely the width of the wake behind the cluster, and the deficit of the wake velocity, cannot be scaled by 2D, either. This is because of the non-linearity effect of the “permeability” of the cluster, and other more detailed mechanism, such as the pulsing jet within the cluster. Further studies performed for different spacing between the buildings should be conducted to further elucidate the dependence of the characteristic length scale on the cluster parameters including the mean and r.m.s. data of the total aerodynamic forces.