Transient Ignition of Premixed Methane/Air Mixtures by a Pre-chamber Hot Jet: a DNS Study

Abstract

The present study investigates the transient processes controlling ignition by a hot jet issued from a pre-chamber. Direct numerical simulations (DNS) have been performed to study the characteristics of the turbulent jet flow and of the associated flame during the whole ignition process, quantifying the relevant physicochemical interactions between pre-chamber and main chamber. Thanks to a detailed analysis of the DNS results, the transient ignition is found to consist of three main sequential processes: (1) near-orifice local ignition in the main chamber; (2) further flame development supported by the jet flow; and (3) global ignition and propagation of a self-sustained flame in the main chamber, independently from the hot jet. The characteristic time-scale of the hot jet as well as jet-induced effects (local enrichment, supply of radicals and heat) are found to be essential for successful ignition in the main chamber. A more intense turbulence in the main chamber appears to support local ignition. However, it also induces local quenching, thus delaying global ignition. An ignition threshold based on a critical Damköhler number is a promising concept, but is not sufficient to describe the process in all its complexity.

1 Introduction

Pre-chamber turbulent hot jet ignition systems are becoming increasingly popular for lean gas engines. The multiple ignition spots initiated by the hot jet promote burning of leaner mixtures in the main chamber, thus increasing thermal and fuel efficiency (Pitt et al. 1983). A review of pre-chamber hot jet ignition techniques can be found in Toulson et al. (2010).

To figure out the resulting jet structures and to identify the conditions critical for successful ignition by a hot jet, many experimental and numerical studies have been done in the last decades. It was first found in Yamaguchi et al. (1985) that the nozzle diameter and the pre-chamber to main chamber volume ratio strongly influence the structure of the jet. Later, Wallesten and Chomiak (2000) found that a spark location in the pre-chamber farther away from the orifice promotes ignition in the main chamber. The important influence of the hot jet temperature and speed of mixing on the jet ignition process has been investigated in Sadanandan et al. (2007). Malé et al. (2021) extended the work of Sadanandan et al. (2007) with 3D DNS and proved that the jet injection speed and temperature directly govern ignition. Carpio et al. (2013) studied numerically the laminar H$_2$/air jet ignition/extinction. The influence of injection velocity and mixture equivalence ratio on the critical orifice radius (resulting in successful jet ignition) has been discussed. To understand further the ignition mechanism, Ghorbani et al. (2015) found that the turbulent jet ignition (ignition probability, ignition delay time, and ignition location) is strongly influenced by the mixing process and the chemical kinetics employed in the numerical simulations.

Biswas et al. (2016) conducted experiments in a pre-chamber configuration and identified two ignition mechanisms: (1) jet ignition and (2) flame ignition, depending on the relative diameter of the jet orifice compared to the laminar flame thickness. A global Damköhler number was defined; the limiting Damköhler number for a CH$_4$/air flame is found to be around 140, below which ignition probability is almost 0. To reveal the details of the flow and flame through the orifice, both experiments and Large-Eddy Simulations (LES) were conducted in Mastorakos et al. (2017). It was found that the jet flow is composed of a column of hot products surrounded by an annulus of unburnt pre-chamber gases. An estimate of 2$\delta _L/d$ was proposed to classify the jet ignition (2$\delta _L/d>$ 1) and flame ignition (2$\delta _L/d<$ 1) cases, where $\delta _L$ is the laminar flame thickness and d is the orifice diameter.

More recently, Sidey and Mastorakos (2018) simplified the practical configuration and studied the strained layer between a reactive mixture and hot combustion products. The ignition time as a function of strain rate and degree of reaction completion in the stream of hot products have been investigated. Qin et al. (2018) studied the ignition mechanism in a simplified constant-volume divided-chambers system using Direct numerical simulations (DNS). The effect of pre-chamber hot jet on ignition was divided into chemical effect (involving intermediate radicals), thermal effect (high temperature), or enrichment effect (unburned rich mixture issuing from pre-chamber). Allison et al. (2018) investigated the effect of fuel type, orifice diameter and ignition location in the pre-chamber by experiments and LES and found that the strain rate and effective orifice size determine the local quenching of radical species at the orifice. Wang et al. (2018a) found that moving the ignition spark farther from the orifice reduces the 1–10% mass fraction burning period. They identified three regions in the hot jet: (1) extinction region; (2) ignition region and (3) combustion region. In a follow-up study, Wang et al. (2018b) studied the effect of pre-chamber syngas reactivity on hot jet ignition and found that incomplete fuel conversion in the orifice results in a lower hot jet temperature. Malé et al. (2019) used LES to investigate pre-chamber ignition behavior in a real engine. Three regimes were identified in the main chamber: (1) ignition by hot gas ejection; (2) combustion sustained by hot gas ejection; (3) combustion unsustained by hot gas ejection. These results correspond quite well to the original picture of Yamaguchi et al. (1985). Benekos et al. (2020) conducted a parametric 2D DNS study on the effects of wall boundary condition, initial temperature and main chamber composition on pre-chamber ignition. It was found that turbulent jet ignition is associated to two characteristic times: one for ignition of the most reactive mixture fraction, and the second one for ignition of all states created through mixing of the pre-chamber gases with the main chamber mixtures.

These previous studies confirm the importance of orifice diameter, spark location, fuel type, and turbulence on ignition of the main chamber mixtures. Additionally, wall heat losses are quite important for the outcome of the ignition process. Since so many different parameters affect the ignition, the central question is still not completely clarified: What is the interplay between all these phenomena during the transient ignition process? As proposed in Biswas et al. (2016), a global Damköhler number could be used to combine the effect of orifice diameter and turbulence on ignition; this Damköhler number quantifies the competition between turbulent mixing and chemical reactions. However, the connection to other parameters such as spark location, fuel type, pre-chamber mixtures are still unknown. In this study, direct numerical simulations (DNS) have been done in a simplified pre-chamber/ main chamber system with a systematically reduced C/H/O kinetic mechanism to describe methane/air chemistry. The hot jet characteristics in the orifice and the transient ignition process have been investigated in a detailed manner. The underlying physics determining ignition in different setups are then discussed, with consequences regarding the interplay between the features affecting the transient ignition process. The jet time scales (for cold jet and hot jet), as well as the relative intensities of different jet effects (enrichment effect, chemical effect, and thermal effect) are found to determine the success of the transient ignition process, which is composed of near-orifice local ignition (NOLI) and global ignition. Turbulence is found to have different effects on NOLI and global ignition. Note that per definition (see Wang et al. 2018a, b) a NOLI event does not necessarily lead to global combustion, though it shows all features of a successful ignition event. Global ignition corresponds to the development of a self-sustained flame in the main chamber.

2 Numerical Simulations and Configurations

The simulations in this study are performed using the in-house low-Mach DNS flame solver DINO (Abdelsamie et al. 2016). It solves the Navier-Stokes system coupled with detailed physicochemical models. The chemical reactions are described by Goodwin et al. (2015). The spatial derivatives are computed using a sixth-order centered explicit scheme. An implicit Williamson third-order Runge-Kutta time integrator with analytic Jacobian inversion (PyJAC Niemeyer et al. 2017) is employed for temporal integration. The mixture-averaged diffusion coefficients have been used in the transport equations. For the thermodynamic pressure and temperature coupling in the closed domain simulation, the coupling equations of Daru et al. (2010) have been implemented and validated in DINO. The methane/air mechanism from Lindstedt and Vaos (2006) has been used, which contains 14 solved and 15 steady-state species with 141 reactions. DINO has been extensively used in numerous combustion studies, e.g. (Chi et al. 2017, 2018, 2019, 2021; Abdelsamie and Thévenin 2017, 2019), in which the proper coupling between chemical reactions, turbulent transport, and heat exchange has been fully validated.

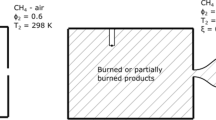
The numerical configurations have been set up as shown in Fig. 1. The orifice diameter d is chosen to be comparable to twice of the laminar flame thickness $\delta _L$ of the pre-chamber mixtures, as shown in Table 1. The geometry is resolved by the novel immersed boundary method from Chi et al. (2020). A uniform grid size of $9.76\,\mu \hbox {m}$ has been used, which is sufficient to resolve correctly the thermal boundary layer and the detailed flame structure (with almost 9 grid points across the minimal laminar flame thickness), especially in the orifice. The minimal value of $\delta _L = 0.09\ \hbox {mm}$ has been calculated for a pressure $p = 10$ bar for stoichiometric mixtures. The maximum $\hbox {y}^+$ value ($\hbox {y}^+ = \frac{\varDelta y\; u_{\tau }}{\nu }$ where $u_{\tau }$ is the friction velocity computed at the wall-adjacent node and $\nu$ is the kinematic viscosity) at the first wall-adjacent node during the jet flow is 0.787.

Fig. 1

Schematic of the computational domain: a 2D domain showing also the three points $\hbox {M}_1$, $\hbox {M}_2$, $\hbox {M}_3$ used for a quantitative analysis of the process as well as the location of the orifice outlet used to compute mass fluxes (white dashed line); b 3D domain showing the iso-surface of Q-criterion at $3\times 10^{10}$ ($1/\hbox {s}^2$) colored by velocity magnitude and iso-surface of temperature at 800 K colored by heat release rate at $t = 0.5\ \hbox {ms}$

All the boundaries are cold walls with initial temperature of 300 K including isothermal wall condition (written ISOT in Case A-G, Case A3D and B3D in Table 1) or adiabatic wall condition (denoted ADIA in Case H in Table 1). The initial ambient temperature is also 300 K. The initial pressure is atmospheric, as has also been used in the pre-chamber study of Wang et al. (2018b). The 2D simplified geometry shown in Fig. 1a resembles the previous DNS study in Qin et al. (2018) with a slightly smaller main chamber volume (volume ratio between pre-chamber and main chamber is 54%), while the 3D geometry shown in Fig. 1b has a volume ratio of 5% between the pre-chamber and main chamber, which is comparable to a practical gas engine (Shah et al. 2014). Detailed dimensions of the 2D and 3D geometries are shown in Fig. 1. The choice of these dimensions was dictated by the best possible compromise between numerical feasibility and connection to practical configurations. The differences in dimensions and ratio between 2D and 3D geometries are due to the different objectives: 1) in 2D, to set up fast DNS simulations for a detailed parametric study; in 3D, going toward more realistic conditions for a few cases. Keeping the same orifice diameter, the surface/volume ratio of the 3D orifice is twice of that in the 2D orifice, resulting in more intensive wall heat losses in 3D. The effect of wall heat losses is studied in Sect. 3.3. It has to be emphasized that the current study intends to reveal the underlying physicochemical mechanisms related to different parameters affecting the transient ignition process. Even though most of the analysis is based on 2D results, the obtained physicochemical mechanism for transient ignition process is validated finally by 3D simulations, confirming its value for realistic pre-chamber combustion system studies. Further 3D simulations are currently running.

The spark is numerically modeled using the energy deposition model from Lacaze et al. (2009), where the energy source is implemented as a Gaussian distribution in both time and space:

$$\begin{aligned} \dot{Q} = \frac{\epsilon }{4\pi ^2\delta _s^3\delta _t} \exp ^{-\frac{1}{2} \left( \frac{r}{\delta _s}\right) ^2} \exp ^{-\frac{1}{2}\left( \frac{t-t_0}{\delta _t}\right) ^2}. \end{aligned}$$

(1)

In the above equation, r is the radial distance to the spark center, t is the current time and $t_0$ is the time instant when the power density function reaches its maximum. The spark is controlled by 3 parameters: the energy deposition $\epsilon$, $\delta _s = \varDelta _s/a$ and $\delta _t = \varDelta _t/a$ where $\varDelta _s$, $\varDelta _t$ and a are characteristic size, time duration of the spark and deposited coefficient, respectively. The value $a = 4\sqrt{\ln (10)}$ is chosen so that 98% of the deposited energy is within the domain $\varDelta _s^3 \cdot \varDelta _t$ (Lacaze et al. 2009). For 2D simulations, the spark distribution equation (Eq. 1) has been adapted accordingly to

$$\begin{aligned} \dot{Q} = \frac{\epsilon }{(2\pi )^{3/2}\delta _s^2\delta _t} \exp ^{-\frac{1}{2}\left( \frac{r}{\delta _s}\right) ^2} \exp ^{-\frac{1}{2}\left( \frac{t-t_0}{\delta _t}\right) ^2}. \end{aligned}$$

(2)

In this study the spark parameters are chosen as: $\varDelta _s = 0.6\ \hbox {mm}$, $\varDelta _t = 0.05\ \hbox {ms}$, $t_0 = 0.05\ \hbox {ms}$ and $\epsilon = 0.12$ mJ, ensuring a stable ignition of the pre-chamber for all conditions considered, and also avoiding local super-adiabatic temperature at the spark.

Table 1 The investigated DNS cases

The details of the investigated cases in this study are shown in Table 1, where $\phi$ is the equivalence ratio of the mixture, $u'$ is the rms velocity of the initial turbulence, $\tau _f$ is the characteristic time of turbulence, $s_L$ is the laminar flame speed of the pre-chamber mixtures, $\delta _{L}$ is laminar flame thickness, and $\eta$ is the Kolmogorov length scale (always larger than the grid resolution for turbulent cases, $9.76\,\mu \hbox {m}$). The turbulence parameters correspond to the initial turbulence. The initial equivalence ratio $\phi$ in the orifice is a step function from pre-chamber to main-chamber. As is seen, $2\delta _L/d > 1$ in Cases A-C and Cases E-B3D. They should thus correspond to the “jet ignition”-regime according to Mastorakos et al. (2017), while Case D corresponds to the “flame ignition”-regime. In Table 1, Case A is a reference configuration to investigate the effect of different parameters; Case B is chosen to study the effect of a different spark location. Note that the spark locations in Table 1 is with respect to the bottom-left of the pre-chamber domain as shown in Fig. 1; Case C is retained to study the effect of varying pre-chamber mixture equivalence ratio $\phi$; Case D is chosen to study the effect of orifice diameter, compared to Case C; Case E is retained to study the effect of main chamber mixture equivalence ratio $\phi$, compared to Case C; by comparison between Case C and Case F, as well as between Case E and Case G, the effect of turbulence is revealed; Case H is chosen to study the effect of the wall condition; Finally, Case A3D and Case B3D are used to check the 3D turbulence effect, and also to validate the 2D results. The normalized power spectrum densities of the initial turbulence as a function of frequency are compared for Case G and Case B3D in Fig. 2, together with the theoretical slope of − 5/3. As expected, differences are seen, but the spectra are sufficiently similar to allow for meaningful comparisons.

Fig. 2

Comparison of the normalized power spectrum density of the initial turbulence as a function of frequency in Case G and Case B3D

As mentioned previously, a low-Mach solver has been used for all simulations. Though no strict rule applies, it is commonly accepted that such solvers should be used for $\hbox {Ma}\le 0.3$. For this reason, the Mach number has been systematically monitored. The peak Mach number has been measured as $\hbox {Ma} = 0.78$ (in Case A3D), close to the outlet of the orifice. However, the total time duration showing local values of $\hbox {Ma} > 0.3$ never exceeded $60\ \mu \hbox {s}$, which is a very short time compared to the whole simulation; the high-Mach region was limited to a very small area close to the orifice; no instabilities were observed on any fields. For all those reasons, using a low-Mach solver to keep acceptable numerical costs is considered acceptable for this study.

3 Results and Discussion

The following results and discussion are first presented for 2D parametric studies (Case A-H). In Sect. 3.6, 3D results will be presented and analyzed to validate the conclusions obtained by 2D studies.

3.1 Phases Identification

Fig. 3

Time evolution of the normalized progress variable $\bar{c}$ at point $\hbox {M}_1$, $\hbox {M}_2$ and $\hbox {M}_3$ (solid lines) and mass flow rate of $\hbox {CH}_2\hbox {O}$, $\hbox {CH}_3$, $\hbox {HO}_2$ and OH (dashed lines) through the orifice outlet for Case A. A positive mass flux is from pre-chamber to main chamber

To clearly identify and distinguish different ignition and combustion phases in the pre-chamber/main chamber systems, the time evolution of the progress variable $\bar{c}$ based on $c=Y_{\mathrm{CO}_2} + Y_{\mathrm{H}_{2}\mathrm{O}}$ (Pierce and Moin 2004) at three points in the orifice ($\hbox {M}_1$, $\hbox {M}_2$ and $\hbox {M}_3$ shown in Fig. 1) has been plotted in Fig. 3, exemplarily for Case A. The local value of $\bar{c}$ at each point is obtained by normalizing c between 0 and 1 using the spatially and temporally peak value in the whole domain over time. After a detailed analysis, four phases have been identified during ignition for all configurations. For a quantitative analysis, these different phases have been finally defined as follows:

$$\begin{aligned} \text {Phase} = {\left\{ \begin{array}{ll} 1 \text { if } \bar{c}_{M_1} < 1\times 10^{-5}\\ 2 \text { if } \bar{c}_{M_1} \ge 1\times 10^{-5} \text { and } d\bar{c}_{M_3}/dt \ge 0 \text { and } \bar{c}_{M_1}> \bar{c}_{M_3}\\ 4 \text { if } \bar{c}_{M_3}> \bar{c}_{M_2} > \bar{c}_{M_1} \text { and } d\bar{c}_{M_1}/dt \ge 0 \\ 3 \text { otherwise} \end{array}\right. } \end{aligned}$$

under the condition that phase 1, 2, 3, and 4 are in sequence and continuous.

To analyze in more detail these four characteristic phases, the fields of velocity, OH mass fraction and temperature have been plotted in Fig. 4. Figure 4a shows the velocity field at 0.13 ms, corresponding to the end of Phase 1 (see again Fig. 3). Figures 4b, c and d present the OH mass fraction distribution at 0.58 ms, 1.0 ms and 1.7 ms, corresponding to Phase 2, 3, and 4, respectively.

Fig. 4

a Velocity field (gray colour scale) with single temperature isolevel (red, 1500 K) at 0.13 ms, corresponding to the end of Phase 1; b Heat release rate (gray colour scale) at 0.58 ms, close to the end of Phase 2; c OH mass fraction (gray colour scale) with single temperature isolevel (red, 1500 K) at 1.0 ms, Phase 3; and d OH mass fraction (gray colour scale) with isolevels of normalized progress variable $\bar{c}$ (solid coloured lines) and velocity vectors (scaled proportional to magnitude, peak velocity 6.15 m/s) at 1.7 ms, Phase 4. All these results correspond to Case A

Combining the data shown in Figs. 3 and 4, the four different phases can be described as follows:

• 1. Phase 1: spark ignition leading to stable flame development in pre-chamber. The spark ignites the mixtures, leading to the establishment of a flame. The cold mixtures in the pre-chamber are driven toward the main chamber through the orifice, as shown in Fig. 4a.

• 2. Phase 2: hot jet propagates through the orifice. The flame in the pre-chamber has now reached the orifice. This leads to the generation of a hot jet, penetrating into the main chamber. This hot jet soon leads to the ignition of the gas located in the main chamber near the orifice. The ignition delay of the main chamber mixtures is defined as the time duration between the hot-jet injection (start of Phase 2) and the rapid increase of OH mass fraction ($dY_{\mathrm{OH}}/dt > 0.1\ \hbox {ms}^{-1}$) due to reaction in the main chamber, following (Zhou et al. 2018). A detailed discussion of the ignition delay time is proposed in Sect. 3.2.

• 3. Phase 3: radicals quench within the orifice. As the combustion in the pre-chamber is almost completed, the velocity of the hot jet through the orifice decreases. Due to excessive heat loss to the cold wall (a constant temperature of 300 K is imposed there), the hot jet structure is broken, as shown in Fig. 4c, leading to two disconnected high-temperature regions.

• 4. Phase 4: back-propagation from main chamber to pre-chamber. As the flame develops significantly in the main chamber while pre-chamber combustion is almost completed, the pressure in the main chamber becomes higher than in the pre-chamber (see later Fig. 7 in Sect. 3.3). This leads to a back-flow through the orifice from main chamber to pre-chamber, as clearly visible in Fig. 4d. Obviously, the occurrence of this last phase and the time at which it starts strongly depend on the relative volume of main chamber and pre-chamber.

These four phases are consistent with previously published studies, e.g. (Mastorakos et al. 2017; Qin et al. 2018), which confirms the representativity of the present numerical configurations. However, the classification and the distinction between the different phases are different. In the present study, a clear distinction based on the normalized progress variable in the orifice has been proposed, as explained at the beginning of this section.

The state of the fluid at the orifice is of crucial importance for the pre-chamber/ main chamber system. Figure 5 shows the temperature, axial velocity, mass fraction of OH, and heat release rate profile across the orifice at the level of point $\hbox {M}_3$ at different time instants. As is seen, the profiles in the orifice are smooth and symmetric. The time evolution of the profiles confirms the previous statements concerning the 4 phases. From Figs. 4a and 5b, it is observed that the jet structure is symmetric in the orifice and in the main chamber. This symmetric structure can obviously be broken by initializing asymmetric fluctuations. Later, the spontaneous transition to turbulence also leads to a rupture of symmetry. This issue is considered later in more details for 3D cases.

Fig. 5

a Temperature, b axial velocity, c mass fraction of OH and d heat release rate profile across the orifice at the level of point $\hbox {M}_3$ at $\hbox {t} = 0.13\ \hbox {ms}$, 0.58 ms, 1.00 ms and 1.70 ms in Case A

3.2 Characteristic Time-Scales of the Jet Flow

According to Qin et al. (2018), the effect of the hot jet on main-chamber ignition can be subdivided into (1) enrichment effect, (2) chemical effect, and (3) thermal effect. All three effects are coupled together during the overall ignition process. As the enrichment effect is mostly associated to the cold jet flow, while the chemical and thermal effects come with the hot jet flow, the time duration of the cold versus hot jet flow is critical in this regard.

To quantify the duration of the cold jet and hot jet in the main chamber, the characteristic time-scales of the cold jet $\tau _{cj}$ and hot jet $\tau _{hj}$ are defined as the time duration of Phase 1 and Phase 2 discussed in Sect. 3.1, respectively. Even if the hot jet continues after Phase 2, its contribution to ignition rapidly becomes negligible: for (1) Chemical effect, the mass flow rates of the radicals decrease to a very low level, as can be seen in Fig. 3; regarding now (2) Thermal effect, heat convection by the hot jet from the orifice to the main chamber stops rapidly, as will be discussed in Sect. 3.3. Table 2 lists the characteristic time-scales of the cold jet $\tau _{cj}$ and hot jet $\tau _{hj}$ for the first seven cases (Case A-G) in Table 1. (Case H is only designed to study the effect of wall heat loss on radical quenching in the orifice as will be discussed in Sect. 3.3, so it is not compared here.) By comparing all these cases, it can be assumed that ignition or misfire in the main chamber depends on the combination of four factors:

• 1. Main chamber equivalence ratio $\phi$ (Case C vs. Case E);

• 2. Intensity of chemical, enrichment and thermal effects (controlled by orifice diameter in Case C vs. Case D, or by pre-chamber equivalence ratio $\phi$ in Case A vs. Case C);

• 3. Hot-jet characteristic time-scale $\tau _{hj}$ (controlled by spark location in Case A vs. Case B);

• 4. Turbulence intensity (comparing Case G to Case E, and Case F to Case C).

The main chamber usually contains leaner mixtures in real engines, in order to enhance fuel efficiency. Thus, the first important factor in this list is not really a free parameter, since it is process-oriented. By increasing the orifice diameter, the hot jet width is larger, bringing more heat into the main chamber, and promoting thermal effect. On the other hand, a too large orifice diameter will ultimately destroy the pre-chamber/main chamber system, resulting in no hot jet generation. Using a richer pre-chamber mixture enhances the enrichment effect. And the pre-chamber flame (determined by its equivalence ratio $\phi$ and fuel type) affects both chemical effect and thermal effect. Finally, orifice diameter and pre-chamber mixtures determine if ignition or misfire will occur by changing the intensity of the transfer processes between pre-chamber and main chamber. The spark location, on the other hand, can impact ignition by changing the hot-jet characteristic time-scale. A spark location farther away from the orifice decreases the hot-jet characteristic time-scale, and can thus lead to misfire. Note that the main chamber volume would also affect the characteristic time-scales and influence ignition, but this parameter has not been investigated in the present study. Finally, turbulence is also known to influence ignition (Chi et al. 2018), and its effect will be discussed in Sects. 3.5 and 3.6.

Table 2 Time-scales and global Damköhler number for Cases A-G considered in this study. The value of Da is computed at $t=\tau _{cj} + \tau$ for ignition cases and at $t = \tau _{cj} +\tau _{hj}$ for misfire cases at the exit of the orifice (white dashed line in Fig. 1). Remember that the ignition delay is computed after the end of the cold-jet phase, so that ignition takes place indeed at $\tau _{cj}+\tau$

As mentioned, the ignition delay time is associated with fast OH radical generation by reaction in the main chamber. To distinguish whether the OH mass fraction is increasing because of reaction or of advection, Fig. 6 has been plotted, which shows the maximum OH mass fraction over all vertical cross-sections from pre-chamber (left boundary) to main chamber (right boundary) as a function of time, exemplarily for Case A and Case G. In Fig. 6a, NOLI event can be observed at time $t=\tau _{cj}+\tau =0.52\ \hbox {ms}$, when the OH mass fraction increases rapidly ($dY_{\mathrm{OH}}/dt>0.1\ \hbox {ms}^{-1}$) at location $y = 3.4\ \hbox {mm}$. This is even more obvious in Fig. 6b for Case G, where NOLI happens at $t=\tau _{cj}+\tau = 0.63\ \hbox {ms}$ near location $y = 3.8\ \hbox {mm}$. Soon after, a region with local flame quenching appears at $t = 0.67\ \hbox {ms}$, with a decrease in OH mass fraction. Finally, slightly after $t = 0.7\ \hbox {ms}$, global ignition happens leading to self-sustained combustion. The corresponding ignition delay $\tau$ (computed using the time instant of the NOLI after end of the cold-jet phase) is listed in Table 2 for Case A-G. The global Damköhler number is computed at the orifice exit (white dashed line in Fig. 1) as defined in Biswas et al. (2016). It is computed for the ignition cases at $t = \tau _{cj}+\tau$, and for the misfire cases at $t = \tau _{cj}+\tau _{hj}$, using:

$$\begin{aligned} \hbox {Da} = \frac{s_L l}{u' \delta _{L}}, \end{aligned}$$

(3)

where $s_L$ and $\delta _{L}$ are respectively computed as the laminar flame speed and laminar flame thickness for the laminar premixed flame corresponding to the initial main-chamber mixtures and pressure found there at the time when Da is computed, while the velocity fluctuations $u'$ and the integral length scale l are estimated as in Biswas et al. (2016) at the orifice exit. The effect of global Damköhler number on hot jet ignition is discussed in Sect. 3.5.

Fig. 6

Time evolution of maximum OH mass fraction along all vertical cross-sections (from left–pre-chamber–to right–main chamber–, the two vertical dashed lines marking the position of the orifice), exemplarily for a Case A and b Case G. For a better visibility, the beginning of the process is not shown, and the time-scales vary

3.3 Radical Quenching in Orifice

Radical quenching is observed in the orifice during Phase 3. Figure 7 shows the time evolution of the different terms controlling heat balance in the orifice: reaction, advection and diffusion, exemplarily for Case A. The axial velocities at points $\hbox {M}_1$ and $\hbox {M}_3$ and the pressure difference between these two points are also plotted. The different terms of the heat balance in the orifice are computed as (using Einstein summation convention):

$$\begin{aligned}&H_{\mathrm{diffusion}} =\sum \limits _{V}^{in\,orifice} \left[ \frac{\partial }{\partial x_j}\left( \lambda \frac{\partial T}{\partial x_j}\right) -\frac{\partial T}{\partial x_j}\rho C_{p,k}Y_k V_{k,j}\right] dV, \end{aligned}$$

(4)

$$\begin{aligned}&H_{\mathrm{advection}} = -\sum \limits _{V}^{in\,orifice} \rho C_p u_j \frac{\partial T}{\partial x_j} dV, \end{aligned}$$

(5)

$$\begin{aligned}&H_{\mathrm{reaction}} = -\sum \limits _{V}^{in\,orifice} h_k \dot{\omega }_k dV. \end{aligned}$$

(6)

Here, $C_p$, $h_k$, $\dot{\omega }_k$, $\lambda$, $V_{k,j}$ represent the specific heat capacity at constant pressure, specific enthalpy, mass reaction rate, heat diffusion coefficient and jth component of the species molecular diffusion velocity, respectively. From Fig. 7, it can be seen that the flow velocity increases as the hot jet enters the orifice (due to thermal expansion, as discussed in Short and Kessler (2009)); heat accumulation by advection is dominating at this early stage. Later on, the heat generation by reaction strongly increases, until the end of Phase 2. It is interesting that the velocity at the inlet of the orifice (point $\hbox {M}_1$) is slightly smaller than that at the outlet (point $\hbox {M}_3$) during the hot jet injection process, due to the establishment of the boundary layer in the orifice, resulting in higher axial velocity at the centerline. After Phase 2, the hot jet velocity decreases, resulting in decreased supply of radicals and hot gases from the pre-chamber. The heat generation by reaction also decreases rapidly due to reactions’ quenching.

Fig. 7

Time evolution of the different terms controlling heat balance in the orifice (left scale, lines with markers), together with (right scale) axial velocity at points $\hbox {M}_3$ (red) and $\hbox {M}_1$ (blue) as well as pressure difference between $\hbox {M}_3$ and $\hbox {M}_1$ (black). The different phases are labelled on the top. All these results are shown exemplarily for Case A

Fig. 8

Time evolution of the progress variable $\bar{c}$ at points $\hbox {M}_1$, $\hbox {M}_2$, $\hbox {M}_3$ and contribution of reaction to heat balance within the orifice for Case H. The different phases are labelled on the top

To check the effect of the cold wall on radical quenching in the orifice, Case H has been simulated. Figure 8 shows the time evolution of the progress variables $\bar{c}$ at points $\hbox {M}_1$, $\hbox {M}_2$ and $\hbox {M}_3$ for Case H. Heat generation by reaction has also been plotted. As can be seen from the evolution of the progress variable in Fig. 8, the reaction front is not interrupted in the orifice for adiabatic wall condition ($\bar{c}_{M_1}> \bar{c}_{M_2} > \bar{c}_{M_3}$), compared to the case considering a cold isothermal wall (with $\bar{c}_{M_2} < \bar{c}_{M_3}$ immediately after Phase 2 in Fig. 3). Additionally, heat generation by reaction does not show a very rapid decrease, indicating that reactions are not completely quenched in the orifice, confirming the importance of wall heat loss to explain radical quenching. The decrease in heat generation seen in the right part of Fig. 8 simply represents the passage of the flame front through the orifice outlet. As a conclusion, radical quenching in the orifice is explained by two effects, mostly combined: (1) reduced radical supply from the pre-chamber, and (2) quenching of the reactions in the orifice mostly due to wall heat loss. In reality, the orifice wall is neither adiabatic nor isothermal. The wall heat loss might not be enough for radical quenching. A detailed wall heat transfer model is critical for practical investigation on the radical quenching event in industrial chambers. Apart from the above two effects, radical destruction at the walls also plays a crucial role for radical quenching in a realistic orifice. To simulate accurately such a process, a detailed wall reaction model would be necessary. This is the subject of future studies.

3.4 Transient Ignition Process

Figure 9 shows the time evolution of the maximum OH mass fraction in the main chamber for Case A-G. For each curve, the time is normalized by the characteristic time-scale of the jet ($\tau _{cj} + \tau _{hj}$) in order to facilitate comparisons. As is seen in Fig. 9, confirming previous discussions connected to Fig. 6, the global ignition process in the main chamber can be divided into: (1) NOLI event (first rapid increase of OH mass fraction due to reaction); (2) flame development supported by the jet flow (OH mass fraction increases slowly and propagates downstream); (3) development of a self-sustained flame, independent from the hot jet (OH mass fraction increases further or stays at a high level after the hot jet stopped). These three steps are consistent with the recent findings in Malé et al. (2019), where a real engine geometry was simulated by LES. All three steps must be successful to achieve overall ignition in the main chamber. The start of the third process is called “global ignition”, distinguishing it from the NOLI event in the initial stage (Ghorbani et al. 2015).

Fig. 9

Time evolution of the maximum OH mass fraction in the main chamber for Case A-G. For each curve, the time is normalized by the characteristic time-scale of the jet ($\tau _{cj} + \tau _{hj}$), so that normalized time 1 corresponds to the end of the jet flow from pre-chamber to main chamber

It is interesting to note that NOLI is observed in Cases B and F; however, global ignition does not happen. For Case B, the increase in OH mass fraction shows at first qualitatively a similar shape to Case A, but shifted toward a later normalized time (remember that the horizontal scale in Fig. 9 is normalized by ($\tau _{cj} + \tau _{hj}$)). However, the hot jet characteristic time $\tau _{hj}$ is much shorter for Case B, resulting in less radicals and hot gases penetrating into the main chamber; for this reason, global ignition cannot be initiated. Concerning Case F, $\tau _{hj}$ becomes longer due to intense turbulent mixing compared with Case C. Chemical effect and thermal effect become more prominent, resulting in NOLI near the orifice (at the difference of Case C, where no ignition at all as found). However, global ignition still does not happen, because of turbulent quenching in the main chamber. The impact of turbulence is discussed in more detail in the next section.

3.5 Turbulence Effect

Different from previous studies (Biswas et al. 2016; Wang et al. 2018a) where there is no initial turbulence, the present work investigates as well the impact of initial turbulence on hot jet ignition. As already mentioned in Table 1, a homogeneous isotropic turbulence has been initially super-imposed on the flow field in Case G (to be compared to Case E) and in Case F (to be compared to Case C).

By comparing Case E and Case G in Table 2 and Fig. 9, the ignition delay in Case G (with initial turbulence) is longer, while the characteristic jet scales $\tau _{cj}$, $\tau _{hj}$ are almost unchanged, the sum $(\tau _{cj}+\tau _{hj})$ being exactly the same. After this effective jet flow duration, local quenching (indicated by the decrease of maximum OH mass fraction in Fig. 9) is more intense in Case G. This result matches well with the observations discussed in Chi et al. (2018) regarding the influence of turbulence on ignition.

A stronger turbulence (due to initial, homogeneous turbulence as well as jet-induced turbulence) results in faster mixing, so that hot-jet radicals diffuse more rapidly; as a consequence, local quenching is observed shortly after the effective jet duration ($\tau _{cj} + \tau _{hj}$). When the turbulence intensity increases further, local quenching ultimately becomes global quenching, since all local ignition kernels are quickly dissipated. This is consistent with the concept of a critical Damköhler number for successful hot-jet ignition as proposed in Biswas et al. (2016), Wang et al. (2018a). From Table 2, it is observed that higher global Damköhler numbers result in easier NOLI event and shorter ignition delay times. This is reasonable since the global Damköhler number is computed using the turbulence characteristics near the orifice exit (Biswas et al. 2016). However, the Damköhler number limit for ignition (estimated as 140 for $\hbox {CH}_4/\hbox {air}$ in Biswas et al. (2016)) is not the same as in the present study. This confirms that the critical Damköhler number is a useful concept but is not the only parameter determining ignition or misfire.

Comparing now Case C and Case F (same as Case C, adding initial turbulence) in Fig. 9, no ignition appears at all in Case C, while NOLI is observed in Case F with the assistance of turbulence. Turbulence is expected to dissipate the reactive radicals and species from the pre-chamber jet flow into the main chamber more efficiently, thus generating local spots with more reactive conditions for ignition events.

Therefore, under the investigated conditions, it is observed that: (1) a more intense turbulence will lead to more intensive local quenching of the flame, which is defavorable for global ignition; while (2) a higher turbulence intensity enhances the NOLI probability, and plays therefore a positive role.

3.6 3D Validation

Since the energy cascade and the generation of fluctuations are indeed different for real 3D turbulence, the validity of the previous conclusions should be checked using 3D DNS. Cases A3D and B3D in Table 1 are proposed for this purpose.

Figure 10 shows the scatter plots of reactive species ($\hbox {CH}_3$ and $\hbox {HO}_2$) versus progress variable from the 2D and 3D DNS cases at the NOLI time. Since the geometry is different, quantitative differences are expected and are clearly observed. In particular, the reactive species are at a lower level in 2D compared to 3D. Still, the shapes of the profiles remain similar.

Fig. 10

Scatter plot of a mass fraction of $\hbox {CH}_3$ vs. progress variable and b mass fraction of $\hbox {HO}_2$ vs. progress variable in the main chamber for Case A (red circles) at $t= 0.52\ \hbox {ms}$ and Case A3D (black dots) at $t = 0.545\ \hbox {ms}$

Figure 11 shows the flame evolution represented by the OH mass fraction equal to 0.001 for Case B3D at 3 sequential time instants. As is seen, at $t = 0.545\ \hbox {ms}$, there is a local ignition spot in the main chamber. Later at $t = 0.755\ \hbox {ms}$, the flame develops further with the support of the hot jet flow. At $t = 0.864\ \hbox {ms}$, the hot jet flow entering the main chamber starts to be quenched, but the flame is self-sustained and propagates further in the main chamber. This results confirm the transient ignition process observed in the 2D simulations.

Fig. 11

Iso-surface of OH mass fraction at 0.001 colored by heat release rate for Case B3D at 3 different time instants a $t=0.545\ \hbox {ms}$, b $t = 0.755\ \hbox {ms}$, and c $t=0.864\ \hbox {ms}$

The 3D turbulence effect on NOLI event has also been investigated. Figure 12a shows the scatter plot between temperature and HO$_2$ mass fraction for Case A3D and Case B3D at $t = 0.545\ \hbox {ms}$, when NOLI happens. As is seen, the HO$_2$ mass fraction is distributed more broadly in Case B3D, especially at higher temperature. This indicates that a more intensive turbulence transports more efficiently the reactive radicals from the hot jet flow into the main chamber mixtures. As is known, local ignition is determined by the most reactive mixtures (Benekos et al. 2020). Thus, turbulence leads to an easier local ignition. Figure 12b shows the scatter plot between temperature and local equivalence ratio. As is seen, the local equivalence ratio is also distributed much more broadly in Case B3D. More spots exist where there is a rich mixture at high temperature, leading to easier NOLI events in Case B3D. This finding confirms the previous 2D analysis based on comparisons between Case C and Case F. It can be concluded that a higher turbulence intensity will enhance the chemical effect (by transporting more efficiently the reactive radicals into the main chamber) and the enrichment effect (by mixing more efficiently the richer mixtures from the pre-chamber jet flow with the lean gases in the main chamber), resulting in easier local ignition in the main chamber.

Fig. 12

Scatter plot of a mass fraction of $\hbox {HO}_2$ versus temperature and b local equivalence ratio vs. temperature in the main chamber for Case A3D (red circles) and Case B3D (black dots) at $\hbox {t} = 0.545\ \hbox {ms}$

Finally, the 3D turbulence effect on global ignition has been investigated. Figure 13 shows the time evolution of the volume in the main chamber where the OH mass fraction is larger than 0.001. As is seen, there are two rapid increases of the OH volume for both Case A3D and Case B3D. The first rapid increase indicates the injection of the pre-chamber hot jet flow into the main chamber, while the second rapid increase indicates the global ignition event (stable flame propagation). Compared to Case A3D, in Case B3D, the global ignition delay is longer. In Case B3D, more and stronger fluctuations of the signal reveal local quenching events. A higher turbulence intensity results in faster dissipation of some local ignition spots, leading to a longer global ignition delay. This result confirms the 2D analysis based on comparisons between Case E and Case G. Thus, the turbulence effect on the transient ignition process is consistent for both 2D and 3D DNS simulations: turbulence facilitates NOLI event, but delays—or could even hinder—global ignition.

Fig. 13

Time evolution of the volume in the main chamber where OH mass fraction is larger than 0.001 in Case A3D and Case B3D

In realistic, 3D turbulence, the aerodynamic strain rates and the flame-strain rate alignment in the main chamber are particularly interesting. These quantities are shown in Fig. 14. The strain rate tensor $s_N$ can be decomposed in 3 principal directions $s_N = s_1 \text {cos}^2\theta _1 + s_2 \text {cos}^2\theta _2+ s_3 \text {cos}^2\theta _3$, where $s_1, s_2$, and $s_3$ are the most extensive, intermediate and most compressive principal strain rates, respectively, and $\theta _1, \theta _2$, and $\theta _3$ are the corresponding angles between the flame normal unit vector and the eigenvectors related to $s_1, s_2$ and $s_3$. Figure 14a shows the PDFs of the most extensive and compressive strain rates ($s_1$ and $s_3$) and the strain rate tensor norm ($|s_N|$) in Case A3D at $t = 0.9\ \hbox {ms}$. As expected, $s_1$ and $s_3$ are positive and negative respectively, characterizing the extensive and compressive strain rates. The peaks of strain rate tensor norm lies within 100–$600\ \hbox {s}^{-1}$, with a decreasing magnitude at higher strain rates. Figure 14b shows the PDFs of the angle $\theta _1$ between the most extensive strain rate eigenvectors and the flame normal unit vectors at the flame front for both Case A3D and Case B3D at the same time, $t = 0.9\ \hbox {ms}$. As can be seen, the PDFs of the alignment have a large peak at cos($\theta _1$)$\simeq 1$ for both cases, which indicates that the extensive strain rate eigenvectors are preferentially aligned with the flame normal, as also found in Swaminathan and Grout (2006). Compared to Case A3D, the preferential alignment (PDF near $\hbox {cos}(\theta _1) = 1$) is somewhat reduced in Case B3D. Since Case B3D has stronger turbulent fluctuations and lower Damköhler number, this confirms that the preferential alignment is reduced when the Damköhler number is decreased (Chakraborty and Swaminathan 2007; Hamlington et al. 2011).

Fig. 14

a PDFs of the most extensive and most compressive strain rates ($s_1$ and $s_3$) and strain rate tensor norm ($|s_N|$) in Case A3D at $t = 0.9\ \hbox {ms}$; b PDFs of the extensive strain rate eigenvector alignment with the flame normal unit vector at the flame front in Case A3D and Case B3D at $t = 0.9\ \hbox {ms}$

4 Conclusions and Perspectives

The transient ignition process in a pre-chamber/main chamber system has been investigated by DNS. Four phases have been identified controlling the ignition process in the system: (1) Spark ignition and stable flame development in the pre-chamber; (2) Hot jet flow propagating through the orifice and igniting the main-chamber mixtures; (3) Radical quenching within the orifice; (4) Back-propagation from the main chamber to the pre-chamber. This last step depends strongly on the volumes of pre-chamber and main chamber, and is therefore not universal; it is also less relevant for the present study, since it takes place after ignition. The pre-chamber jet flow effects on the ignition of the main-chamber mixtures have been analyzed. The characteristic time-scales of the hot jet are important to successfully initiate ignition in the main chamber. Radical quenching in Phase 3 is mainly due to (1) lack of radical supply from the pre-chamber, and (2) quenching of the elementary reactions in the orifice due to excessive wall heat loss. Finally, it is found that the transient ignition process is composed of (1) NOLI event; (2) flame development supported by the jet flow, and (3) flame propagation independently from the hot jet (global ignition). Turbulence effects have also been checked. It appears that turbulence enhances the chemical and enrichment effect at local spots in the main chamber, leading to easier local ignition. On the other hand, local ignition spots are more easily dissipated away by a higher turbulence intensity, thus resulting in a longer global ignition delay. 3D DNS have also been carried out, confirming the transient ignition process and the turbulence effect on this process. The present findings support the concept of a critical Damköhler number to delineate between ignition and misfire, but not as a standalone parameter.