Effects of Hydrogen-Enrichment on Flame-Holding of Natural Gas Jet Flames in Crossflow at Elevated Temperature and Pressure

Abstract

The effect of hydrogen ($\mathrm {H}_{\mathrm {2}}$) enrichment on the flame-holding characteristics of two natural gas jet flames in crossflow is investigated here, experimentally. The flame and flowfield measurements are analyzed using simultaneously acquired high-speed (10 kHz) stereoscopic particle image velocimetry, planar laser-induced fluorescence of the hydroxyl radical, and OH* chemiluminescence. The flames, enriched with 20% and 40% $\mathrm {H}_{\mathrm {2}}$, by volume, are studied at conditions typical of the mixing duct of a modern gas turbine engine; specifically in confinement, at 10 bars, and with a crossflow preheat of 530 K. Consistent with previous findings, the 40% $\mathrm {H}_{\mathrm {2}}$ flame was found to be stabilized on the windward and leeward side of the jet, while the 20% $\mathrm {H}_{\mathrm {2}}$ flame was stabilized only on the leeward side. Analysis of mean and instantaneous velocity fields showed no major differences in the trajectories and principal compressive strain fields of the two flames. The presence of the windward stabilized flame in the 40% $\mathrm {H}_{\mathrm {2}}$ case was, however, found to decrease the centerline velocity decay and greatly reduce or eliminate large scale vortices along the windward shear layer. The difference in the flame-holding here was attributed to the difference in the extinction strain rate from the addition of hydrogen, which would impact the local and global extinction of the flame along the high shear windward region of the flame.

1 Introduction

With the increasing utilization of wind and solar energy for power generation, there is a growing interest in the use of hydrogen ($\mathrm {H}_{\mathrm {2}}$) as a means by which to store and recover energy generated during off-peak demand periods. One strategy for recovering energy stored as hydrogen is through its combustion in a gas turbine powerplant. As large scale gas turbine powerplants are now generally designed around the combustion of natural gas, which has significantly different combustion dynamics, it is more feasible to deliver hydrogen to the combustor via admixture with natural gas than in its pure form. Despite this, the delivery of a hydrogen-enriched fuel to a combustor designed around pure natural gas poses significant technical challenges. Key among these is the possibility of a flashback event leading to the stabilization of a flame at or near the wall of the fuel-air premixing channel. Whereas a flashback event is certainly undesirable in gas turbine combustor, if it leads to flame-holding at or near the fuel-injector, the results can be catastrophic. The use of hydrogen-enriched fuels, which tend to have higher flame speeds and greater resistance to strain-induced extinction, requires a deep, fundamental understanding of the effect of hydrogen on the flame-holding characteristics of a natural gas fuel jet in the narrow flow-channel of a gas turbine premixer.

In modern gas turbine combustors, natural gas is typically injected as a jet issuing perpendicular to a crossflowing stream of air. The so-called “jet in crossflow” (JICF) injector configuration is so widely used, it is considered a canonical flow configuration and has been extensively studied. Its flowfield is characterized by a set of four strongly interacting vortex systems: a counter rotating vortex pair (CVP), shear-layer vortices, horseshoe vortices, and wake vortices (Margason 1993; Mahesh 2013; Schlüter and Schönfeld 2000; Kelso et al. 1996; Fric and Roshko 1994; Smith and Mungal 1998). The CVP, which forms in the core of the jet, dominates the far-field of the JICF. The shear layer vortices form as a result of the Kelvin-Helmholtz instability induced by the shear-layer between the jet and the crossflow. The horseshoe vortices form in the upstream region of a JICF that is injected flush from a wall and are in line with the crossflow, and the wake vortices originate from the boundary layer of the wall and form downstream of the jet exit orifice (Karagozian 2010).

The trajectory of a JICF scales with the jet exit diameter (d) and the square root of the jet-to-crossflow momentum flux ratio (r), defined below (Karagozian 2010).

$$\begin{aligned} r = \sqrt{\frac{\rho _j u_j^2}{\rho _{cf} u_{cf}^2}} \end{aligned}$$

(1)

In the above equation, $u_j$ and $\rho _j$ are the jet velocity and density, respectively, and $u_{cf}$ and $\rho _{cf}$ are the crossflow velocity and density, respectively. The streamlines of jet centerline trajectories are often calculated from the loci of the max velocity. Their scaling typically follows the power law shown in Eq. 2, where the stream-wise and transverse coordinates (x and y, respectively) are non-dimensionalized by the momentum flux ratio and jet exit diameter (d) (Karagozian 2010).

$$\begin{aligned} \frac{y}{rd} = A \left( \frac{x}{rd}\right) ^B \end{aligned}$$

(2)

In the above equation, the coefficient A is related to the crossflow fluid entrainment and B can be thought of as a shape constant (Hasselbrink and Mungal 2001a). From experimental studies of non-reacting JICF, the constants A and B have been found to lie in the ranges of $1.2<A<2.6$ and $0.28<B<0.34$, for $r<25$ (Hasselbrink and Mungal 2001a).

The equations above have been extensively validated for conditions wherein the jet issues into a crossflow significantly larger than the diameter of the jet, i.e. where the JICF may be considered “unconfined”. JICF fuel injectors, however, typically issue into a premixing channel with a much closer confinement. With closer confinement of the JICF, the effect of flow blockage by the jet, boundary layers on all four confinement walls, and heat-loss/quenching there may all affect its flame-holding characteristics compared to an unconfined JICF with similar diameter and momentum flux ratio. To understand and model the effect of hydrogen-enrichment on the physics of flame-holding by a JICF type fuel injector, it is essential to replicate the confinement effects it would experience in a gas turbine premixing duct.

While the macroscopic features of a JICF have been shown in the scientific literature to scale with jet-to-crossflow momentum flux ratio, flame-holding is driven by local mixing and strain characteristics in the shear-layer at the low-velocity periphery of the jet. In a gas turbine combustor, air is subject compression heating as it passes through the multi-stage compressor. This preheating of the air changes its density, which may affect the stability of the shear-layer between the (unheated) jet and the crossflow and thereby further alter its mixing, entrainment and flame-holding characteristics. The addition of hydrogen to natural gas will similarly reduce the jet-density, further affecting the mixing and flame-holding characteristics.

The stabilization mechanism responsible for flame-holding in JICF type gas turbine fuel injectors has been the focus of significant numerical simulation and modelling efforts in recent years. These efforts (Chen 2011; Grout et al. 2011, 2012; Kolla et al. 2012; Chan et al. 2014), led by the Combustion Research Facility of Sandia National Laboratories, applied direct numerical simulation (DNS) to study a jet of nitrogen-diluted hydrogen issuing into a high temperature crossflow of air at atmospheric pressure. The jet consisted of 70% $\mathrm {H}_{\mathrm {2}}$ and 30% ${\mathrm {N}}_2$ (by volume) and issued into the cross-flow via a round, 1 mm diameter hole flush with the wall. The crossflow temperature was 750 K, to mimic the expected compression heating of a gas turbine combustor in the 200–400 MW range. The fuel jet temperature was set to 450 K.

These studies showed a flame that stabilized, on average, at 1.5–2 jet widths downstream and 3-5 jet heights from the jet exit, in a region of low mean flow velocity where the average mixture fraction is near stoichiometric. This region corresponds to the leeward side of the JICF, near where the two main lobes of the CVP meet. This suggests that the stabilization mechanism was driven by partially-premixed flame propagation in a region of low convective velocity. These findings are consistent with an experimental study completed at similar flow conditions by Steinberg et al. (2013), which also concluded strong heat-release on the leeward side of the JICF is critical to flame stabilization. It should be noted, however, that both the numerical and the experimental studies neglected the effect of elevated chamber pressure on the fluid dynamics and combustion chemistry.

Both increasing chamber pressure and hydrogen addition affect the chemical timescales of a jet flame in crossflow (JFICF) (albeit in opposite directions) and, therefore its propensity for stabilization or flame-holding near the injector. Whereas increasing chamber pressure tends to decrease the laminar flame speed of hydrogen-enriched natural gas, increasing reactant preheat and hydrogen-enrichment tends to increase it. Both are expected to affect the flame-holding characteristics of the injector.

Given the many competing parameters, i.e. pressure, reactant temperature, hydrogen-enrichment level and confinement effects, it is exceedingly difficult to accurately predict from first principles the flame-holding characteristics of a turbulent, JFICF of hydrogen-enriched natural gas. In our previous paper on $\mathrm {H}_{\mathrm {2}}$ enriched natural gas jet flames (Saini et al. 2020) at elevated pressure, we observed that two JFICF with similar momentum flux ratio, jet-exit Reynolds number, and thermal load showed very different flame-holding characteristics with increasing hydrogen-enrichment levels. At 40% $\mathrm {H}_{\mathrm {2}}$ enrichment, the flame was stabilized on the windward side of the jet while at 20% $\mathrm {H}_{\mathrm {2}}$ enrichment, it was stabilized on the leeward side of the jet. That study determined that this change in flame-holding behavior was independent of chamber pressure over a wide range.

The goal of this paper is to more fully explore the effect of hydrogen-enrichment on the flame-holding characteristics of a turbulent JICF of natural gas in close-confinement at a pressure and temperature representative of the premixing channel of a gas turbine. We accomplish this by performing high-speed stereoscopic particle image velocimetry (SPIV), planar laser induced fluorescence of the hydroxyl radical (OH-PLIF), and OH* chemiluminescence (OH* CL) imaging. Two JICF are studied here at 10 bars pressure, and 530 K preheat temperature, and have similar momentum flux ratio, jet-exit Reynolds number, and thermal load. We examine both the mechanism responsible for the difference in flame-holding characteristics and the effect of this on flow and flame dynamics of the JICF.

2 Experimental Setup

2.1 Test Facility

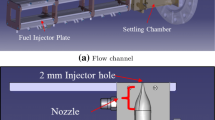
The experiments described in this paper were performed in the same test facility as our previous study (Saini et al. 2020). This test facility consisted of a flow channel and fuel injector (Fig. 1) housed in a high pressure, optically accessible combustion vessel. The flow channel was modular in design, with each of the three modules having a rectangular cross-section (measuring 40 $\times$ 60 mm). The fuel injector was mounted in the third (i.e. the most downstream) of these modules. The purpose of having two modules of the flow channel upstream of the injector was to ensure a well-developed turbulent boundary layer formed along the plate upstream of the jet-exit. Upstream of the first module was a settling chamber with a flow conditioning screen and an inlet for the injection of air seeded with tracer particles (necessary for the SPIV measurements).

Fig. 1

Sketch of the flow channel and the cross-section of the injector plate that were used to study the JFICF

The non-premixed fuel jet issued from a 2 mm diameter circular orifice mounted flush with the lower (40 mm wide) wall of the flow channel. Beneath the orifice was a nozzle designed to produce a uniform, top-hat velocity profile at the jet-exit. This was accomplished through the use of a smooth, contoured nozzle upstream of the orifice with a fifth order polynomial profile design, as described in Megerian et al. (2007). A flow conditioning screen was also mounted at the base of the injector nozzle to ensure a stable, symmetric flow throughout. The nozzle block was water-cooled to ensure a constant fuel temperature at high crossflow temperatures.

2.2 Diagnostics

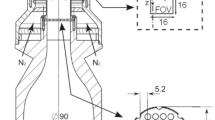
Three high bandwidth, kilohertz (kHz) acquisition-rate diagnostic systems were implemented here: stereoscopic particle image velocimetry, OH* chemiluminescence, and planar laser-induced fluorescence of the hydroxyl radical. This setup (shown in Fig. 2) was the same as the one used by Saini et al. (2020). Although this diagnostic system has been described in detail in that paper, for completeness, a brief review is included below.

Fig. 2

Sketch of the setup for the three diagnostics used here (adapted from Slabaugh et al. 2016)

2.2.1 SPIV

The SPIV system consisted of a dual-cavity, diode-pumped, solid-state, frequency-doubled Nd:YAG laser (Edgewave, IS200-2-LD) and a pair of high-speed CMOS cameras (Phantom V1212), all synchronized to run at a cyclic repetition rate of 10 kHz. The laser emitted pairs of pulses, with energies of up to 9 mJ ea., that were used to illuminate $\mathrm {TiO}_{\mathrm {2}}$ particles ($\sim$1 $\upmu \mathrm { m}$ in size) seeded into the jet and crossflow. The laser sheet measured approximately 40 mm (wide) $\times$ 1 mm (thick) at the measurement region.

The CMOS cameras were equipped with 200-mm focal-length, f/4 macro objective lenses (Nikon AF-Micro Nikkor) and 532-nm-bandpass interference filters to suppress background flame luminosity. Off-axis imaging blurs were mitigated by mounting the objective lenses on scheimpflug adapters that were aligned to the focal plane with the laser sheet. The cameras were operated in dual-frame mode with an image resolution of 640 $\times$ 800 pixels, which resulted in a field of view of 48 mm $\times$ 60 mm (in the axial and transverse directions, respectively).

Velocity vectors were calculated using a multi-pass adaptive window offset cross-correlation function via a commercially available software package (LaVision Davis 8.4.0). The final interrogation window size and overlap were 16 $\times$ 16 pixels and 50%, respectively. This yielded a spatial resolution of 1.2 mm/vector and vector spacing of 0.6 mm. To account for intensity fluctuations in the background, such as ones from reflections, spatially sliding background intensity subtraction and local particle intensity correction were applied on the particle images before vector processing.

2.2.2 OH-PLIF

The OH-PLIF system consisted of an intensified CMOS camera system, a frequency-doubled, Q-switched, diode-pumped solid state Nd:YAG laser (Edgewave IS400-2-L supplying 110 W at 532 nm), and a frequency-doubled dye laser that was pumped by the aforementioned YAG laser. The dye laser system (Sirah Credo) produced 5 W at 283.9 nm and had a pulse-repetition frequency of 10 kHz. This laser was tuned to excite the (closely spaced) Q1(9) and Q2(8) lines within the $A^2 \varSigma ^+-X^2 \varPi$ $(v'=1,v'=0)$ band. The wavelength was monitored by directing a reference leg of the laser to a system composed of a laminar reference flame, a photomultiplier tube, and a digital oscilloscope. The OH-PLIF laser sheet was approximately 40 mm (tall) $\times$ 0.2 mm (thick), and it was overlapped onto the SPIV sheet by passing the SPIV sheet through the final OH-PLIF turning mirror.

Fluorescence was acquired with a CMOS camera (LaVision HSS8), an external two-stage lens-coupled intensifier (LaVision HS-IRO), and a 64-mm focal length, f/2 UV lens (Halle Nachfl.). Elastic scattering (at 283 nm from the SPIV seed particles) was blocked with the use of a high-transmission (> 80% at 310 nm) bandpass filter while background flame emission was further limited with a 100-ns intensifier gate. The acquired images were corrected for spatial variations in the imaging system sensitivity, via normalization with an ensemble-average image of a uniformly illuminated white screen (Kaiser-Slimlite). Spatial non-uniformity of the laser sheet was normalized using the average of the fluorescence signal from acetone vapour seeded into the measurement plane.

2.2.3 OH* CL

A second intensified camera was employed to record OH* chemiluminescence (CL), a robust (line-of-sight integrated) marker for combustion heat release (Gollahalli et al. 1975). The camera for OH* CL detection was a high-speed CMOS imaging system (LaVision HSS8) equipped with an external, two-stage, lens-coupled intensifier (LaVision HS-IRO) and was fitted with a 45 mm focal length, f/1.8 objective (Cerco) and a high-transmission, band-pass interference filter. The integration time for the OH*-CL signal was 25 $\upmu \mathrm {s}$. The images here were also corrected for spatial variations in imaging system sensitivity.

2.3 Test Conditions

Two non-premixed JFICF were studied in this project. The fluid-dynamic and chemical parameters for each case are summarized in Table 1. These cases correspond to natural gas jet flames enriched by 40% and 20% $\mathrm {H}_{\mathrm {2}}$, by volume. In order to isolate the effect of $\mathrm {H}_{\mathrm {2}}$ on flame dynamics, we attempted to hold constant key parameters of the JFICF for the two cases, while varying the $\mathrm {H}_{\mathrm {2}}$ levels. The parameters held constant were the crossflow temperature and velocity (530 K and 1.47 m/s), chamber pressure (10 bars), and the jet to crossflow momentum flux ratio (defined in Eq. 1). The crossflow temperature was set so as to mimic the temperature of air undergoing adiabatic compression (e.g. through the compressor of a gas turbine engine) from 1 bar (atmospheric) to 10 bars pressure. The natural gas used in this study consisted of approximately 94% CH4, 4% C2H6 and 2% other gases (N2, CO2, CO and higher hydrocarbons), by volume. The density of the fuel mixtures was calculated using a mole-weighted sum of the densities of the constituent gases of the mixtures. The viscosity of the fuel mixtures (used to calculate the Reynolds numbers) was computed in Cantera. The fuel was not preheated.

Table 1 Test parameters for the two JFICF

Shown in Table 2 are the laminar flame speeds ($S_L$) and the extinction strain rates of the two cases, computed using a Chemkin-based opposed-jet code using the FFCM-1.0 model (Ji et al. 2010, 2011; Movaghar et al. 2020; Movaghar and Egolfopoulos 2020). These quantities were calculated at stoichiometric conditions, and the extinction strain rates were calculated in back-to-back configuration. Although we have no measure of the local stoichiometry, as JFICF are non-premixed, it is reasonable to assume the flame stabilizes at the stoichiometric contour.

Table 2 Laminar flame speed and extinction strain rate estimates for the two JFICF

3 Results and Discussion

3.1 Instantaneous and Mean Fields

The effects of $\mathrm {H}_{\mathrm {2}}$ enrichment on the flame-holding of the JFICF are investigated first qualitatively, through simultaneously presented instantaneous images of all three diagnostics. Shown in Fig. 3 are the instantaneous plots of OH* CL, OH-PLIF, and velocity magnitude (|V|) fields (all simultaneously acquired) for the 40% $\mathrm {H}_{\mathrm {2}}$ flame at 10 bar. For these images, and all other images presented henceforth, the crossflow flows from left to right, and the jet exit orifice has been set as the origin of the coordinate system. The stream-wise and transverse axes are represented by x and y, respectively, and their corresponding velocities are u and v, respectively. The OH-PLIF measurements were also binarized to better help visualize the flame contours. Details of the procedure for this binarization can be found in the “Appendix”. The |V| fields in the figure have the contours of these binarized OH-PLIF images overlaid on top in black.

Fig. 3

Instantaneous OH* CL, OH-PLIF, and |V| fields for the 40% $\mathrm {H}_{\mathrm {2}}$ flame. The |V| fields have overlaid on top the contours of the corresponding binarized OH-PLIF images in black. The diagnostics are synchronized temporally, with an interval of 0.5 ms between the images

The OH* CL and OH-PLIF fields in Fig. 3 show the JFICF with a flame sheet that is largely intact and continuous along the windward side interface between the jet and the crossflow. The flame appears to follow the growth of the shear layer on this side. These findings are consistent with previously studied $\mathrm {H}_{\mathrm {2}}$ enriched natural gas JFICF at similar enrichment levels, but lower crossflow temperature (Saini et al. 2020). The presence of high signal levels on leeward side indicates more active flame zones there. The contours of the binarized OH-PLIF fields on top of the |V| fields show that the flame for the 40% $\mathrm {H}_{\mathrm {2}}$ case resides on the periphery of the jet. The gaps in the velocity fields (white background) are a result of the masking of regions with high levels of soot. This soot mask, used and described in greater detail in a previous work, was applied to make sure no vectors were calculated from the soot particles (Saini et al. 2020).

Shown in Fig. 4 are instantaneous plots of OH* CL, OH-PLIF, and velocity magnitude (|V|) fields (all simultaneously acquired) for the 20% $\mathrm {H}_{\mathrm {2}}$ case. Unlike the 40% $\mathrm {H}_{\mathrm {2}}$ case, the OH* CL and OH-PLIF fields for this case show the flame is extinguished on the windward side. This flame appears to stabilize more in the downstream region in the wake of the jet. The binarized OH-PLIF contours on the |V| fields illustrate this well. Sooting levels were much lower for this flame, and so there was no need for the use of a soot mask. Like the 40% $\mathrm {H}_{\mathrm {2}}$ case, these findings are consistent with previously studied $\mathrm {H}_{\mathrm {2}}$ enriched natural gas jet flames at the same enrichment levels but at lower crossflow temperatures (Saini et al. 2020).

Fig. 4

Instantaneous OH* CL, OH-PLIF, and |V| fields for the 20% $\mathrm {H}_{\mathrm {2}}$ flame. The |V| fields have overlaid on top the contours of the corresponding binarized OH-PLIF images in black. The diagnostics are synchronized temporally, with an interval of 0.5 ms between the images

The mean OH* CL, OH-PLIF, and |V| fields, shown in Fig. 5, show more clearly the differences between the two cases. The contours of mean binarized OH-PLIF fields have been overlaid on top of |V| fields. Additionally, the jet centerline trajectories (defined in the next section) are overlaid on the |V| fields as a white dashed line. Regions with fewer than 25% vectors over time have been masked out (in white). The windward stabilization of 40% $\mathrm {H}_{\mathrm {2}}$ case, and lack thereof in the 20% $\mathrm {H}_{\mathrm {2}}$ case, is quite evident from these mean fields.

Fig. 5

Mean OH* CL, OH-PLIF, and |V| fields for both flames (40% and 20% $\mathrm {H}_{\mathrm {2}}$, respectively). Overlaid on the |V| fields are the contours of mean binarized OH-PLIF images (in black) and the jet centerline (dashed white line)

In the OH* CL fields, there is a region of heat release on the windward side of the jet exit orifice ($y/d<2$) for the 20% $\mathrm {H}_{\mathrm {2}}$ case, which is interesting given that otherwise this flame is windward extinguished. This region could be caused by the presence of a stagnation point or from boundary layer separation there. The mean OH-PLIF contours for the 40% $\mathrm {H}_{\mathrm {2}}$ case shows how the flame envelops the jet.

One observes more flame present on the leeward side of the 40% $\mathrm {H}_{\mathrm {2}}$ case than in the 20% $\mathrm {H}_{\mathrm {2}}$ case. The lack of a continuous flame along the windward side of the jet in the 20% $\mathrm {H}_{\mathrm {2}}$ case is a likely explanation for this difference. The intact flame on the windward side of the 40% $\mathrm {H}_{\mathrm {2}}$ case would act to both relaminarize flow in the shear layer (Takagi et al. 1980, 1981) and provide preheat and combustion radicals to stabilize the flame on the leeward side of the jet. This, together with the lower flame speed and extinction strain rate of the fuel in the 20% $\mathrm {H}_{\mathrm {2}}$ case, would make it much more difficult for the flame to counterpropagate against the crossflow at the jet periphery.

3.2 Quantitative Mean Flowfield Analysis

The |V| fields in Fig. 5 show mean flowfields that are very similar for both the 20% and 40% $\mathrm {H}_{\mathrm {2}}$ cases, qualitatively. This is consistent our current understanding of JICF, inasmuch as the jet-to-crossflow momentum flux ratio and jet-exit diameter are constant for the two cases. To build on this further, presented in this section is a more quantitative analysis of the mean flowfield, specifically in the context of understanding its effects on the flame-holding of the two JFICF, and vice-versa.

The centerline trajectories for each case are plotted in Fig. 6. As the jet initially has no momentum in the axial direction, the jet centerline trajectory serves as a proxy for macroscopic entrainment and mixing of crossflow fluid by the jet. A difference in crossflow entrainment resulting from the presence of a flame at the jet periphery may be expected to affect the centerline trajectory Hasselbrink and Mungal (2001b). In this work, the trajectories were determined from the loci of the maximum velocity magnitude (|V|) of the jets, in the same manner as what was done in Saini et al. (2020). The trajectories here were calculated in the nearfield ($x/d < 1.5$). These trajectories follow the power law scaling (Eq. 2) quite well, with the constant A being 1.54 and 1.57 for the 40% and 20% $\mathrm {H}_{\mathrm {2}}$ cases, respectively, and the constant B being 0.26 and 0.27 for the 40% and 20% $\mathrm {H}_{\mathrm {2}}$ cases, respectively.

Fig. 6

Jet velocity magnitude centerline trajectories for the two JFICF

Qualitatively and quantitatively, the centerline trajectories overlap quite well. Since the momentum flux ratio was maintained between the two flames, this finding is consistent with existing theories (Karagozian 2010). It was shown by Hasselbrink and Mungal (2001b) that the heat release from the flame in JFICF can result in greater penetration when compared to non-reacting JICF. However, the presence of a windward stabilized flame for the 40% $\mathrm {H}_{\mathrm {2}}$ case here does not seem to affect its penetration. This is consistent with the findings of Saini et al. (2020), who studied similarly confined JICF with the same $\mathrm {H}_{\mathrm {2}}$ enrichment, but at lower crossflow temperatures.

It should be noted that while the momentum flux ratios are similar for both the cases, there is a significant difference in the jet-to-crossflow density ratios of these two cases (see Table 1). This could be expected to affect the shear-layer stability, and therefore reactant mixing in the periphery of the jet (where the flame sits) (Karagozian 2010). So while the centerline trajectory, a macroscopic characteristic, remains similar between the cases, the local characteristics may be affected by the $\mathrm {H}_{\mathrm {2}}$ enrichment despite the constant jet-to-crossflow momentum flux ratio.

Using the maximum velocity centerline trajectories from Fig. 6, the decay of the mean velocity along the jet can be calculated. The centerline velocity decay is useful in assessing the impact of the windward stabilization of the flames studied here, as it has been shown to be influenced by the presence or lack of a flame (Han and Mungal 2001). Shown in Fig. 7 are the mean velocity magnitude (|V|) and transverse velocity (v) along the jet centerlines from Fig. 6. The centerline velocity magnitude plot (Fig. 7a) shows a slight difference in this velocity’s decay for the two flames, with the 20% $\mathrm {H}_{\mathrm {2}}$ case having a greater velocity decay. This discrepancy is consistent with the observations of Han and Mungal (2001), who found that the presence of heat release from a flame results in a reduction of centerline velocity decay when compared to a non-reacting JICF. Saini et al. (2020) also found that the centerline |V| for a windward stabilized flame have less decay than for a windward extinguished flame. It is possible that the temperature increase caused by the flame for the 40% $\mathrm {H}_{\mathrm {2}}$ case results in volumetric expansion and greater acceleration of the jet fluid. The 20% $\mathrm {H}_{\mathrm {2}}$ case’s flame resides, for the most part, on the leeward side of the jet, as shown in Fig. 5c, and so the flame is less likely to contribute to a temperature increase of the fluid around the jet centerline.

Fig. 7

Mean velocities for the two JFICF along their jet centerlines, normalized by their corresponding jet exit velocities

Unlike the |V| decay, the centerline v decay (Fig. 7b) for both cases qualitatively does not show a significant difference, despite the lack of a flame on the windward side of the 20% $\mathrm {H}_{\mathrm {2}}$ case’s jet. This is consistent with the observations of Hasselbrink and Mungal (2001b) for a similar range of x/(rd). The v centerline velocities here fit well with the power scaling law defined in Eq. 3 (Hasselbrink and Mungal 2001b):

$$\begin{aligned} \frac{r v}{|V_j|} = C \left( \frac{x}{rd}\right) ^D \end{aligned}$$

(3)

The constants for the 40% and 20% $\mathrm {H}_{\mathrm {2}}$ cases were 1.19 and 1.13, respectively, for C, and − 0.58 and − 0.59, respectively, for D. These values are similar to the constants determined by Hasselbrink and Mungal (2001b) (C and D of 1.0 and -0.5, respectively) for their jet flames over a similar range of x/(rd). It should be noted that Hasselbrink and Mungal (2001b) had a much larger area flow channel than that used in this experiment, which would result in less strict confinement of the JICF. In addition, the jet in that study issued from a tube extending into the crossflow, rather than from an orifice flush with the channel wall.

Shown in Fig. 8 are mean velocity magnitude profiles taken perpendicular to the jet centerline trajectories (from Fig. 6) at three axial locations. Negative values in the horizontal axis in these plots correspond to the windward side of the centerline, while positive values correspond to the leeward side. As a reference point, the location of the contour of the mean windward flame edge (calculation shown in the “Appendix”) for each flame is also overlaid on the plots as circles. From these plots, once can see the spread is similar for both cases initially. As x/d increases, both jets have the same decay in their velocities on the windward side of the profile. The leeward side, however, begins to show a greater spread for the 40% $\mathrm {H}_{\mathrm {2}}$ case. The similarity in mean velocity profile on the windward side of the jet trajectory suggests the presence of a flame there does not significantly impact the global entrainment and mixing characteristics of the flow at these conditions. This is consistent with the previous observation of the two cases having very similar jet centerline trajectories. The difference in profiles of mean velocity on the leeward side of the centerline, however, suggest the flame does have an effect on the wake. As noted previously, the 40% $\mathrm {H}_{\mathrm {2}}$ flame shows a considerably more heat-release on the leeward side of the jet than does the 20% $\mathrm {H}_{\mathrm {2}}$ case. This may arise from the higher adiabatic flame temperature of the fuel mixture, or more complete combustion of the fuel resulting from the preheating of the reactant flow by the intact flame sheet on the windward side of the jet. Whichever mechanism is responsible though, the effect would be the same: increased volumetric expansion of the jet in that region and a corresponding increase in mean velocity.

Fig. 8

Crosscuts, along the jet centerline, of the mean |V| fields (normalized by the jet exit velocity $|V_j|$). The circles represent the location of the contour of the windward flame edge, determined from the mean of the binarized OH-PLIF fields

Figure 9 shows profiles of root mean square (RMS) velocity fluctuations taken perpendicular to the jet centerline at the axial locations. Each profile shows a sharp rise and peak to the windward wide of the jet centerline and a more gradual decrease on the leeward side. Given the similarity of the RMS profiles for both the 20% and 40% $\mathrm {H}_{\mathrm {2}}$ case, it appears the presence of a flame on the windward side has limited effect on local fluid mechanics there. This is consistent with the earlier observations based on mean velocity profile and centerline trajectory. The more gradual decay of RMS velocity fluctuations the leeward side of the trajectories, however, suggests the flame does affect the flowfield there.

Fig. 9

Profiles of RMS velocity fluctuations taken perpendicular to the jet centerline at axial locations $x/d = [2, 3, 4]$. The circles represent the location of the mean windward flame contour, determined from the mean of the binarized OH-PLIF fields (see “Appendix”). Triangles represent the location of maximum vorticity

Although it is not immediately clear what mechanism is responsible for the increased leeward-side fluctuations in the 40% $\mathrm {H}_{\mathrm {2}}$ case, the increased heat-release observed in the same region appears a likely explanation. Comparing again the OH-PLIF contours in Figs. 3 and 4, one observes significantly more large scale structure in the leeward side flame in the 40% $\mathrm {H}_{\mathrm {2}}$ case than in the 20% $\mathrm {H}_{\mathrm {2}}$ case. This would lead to significantly greater local heat-release and, by extension, greater RMS velocity fluctuations there.

Figure 10 shows profiles of the ensemble-average of principle normal strain rate taken over a line perpendicular to the jet centerline at axial location near $x/d = 0.3$ (which corresponds to transverse location of roughly $y/d = 5$). Consistent with profiles of mean and RMS velocity, one observes strong similarity in both shape and magnitude for each case. This again suggests the presence of a flame on the windward side shear layer has limited effect on the underlying fluid mechanics. The effect of fluid dynamic strain on the flame at the leading edge, however, is clear.

Fig. 10

Profiles of mean (ensemble-average) principal compressive strain taken perpendicular to the jet centerline trajectory at the axial location ($x/d = 0.3$). The horizontal lines represent the extinction strain rates calculated for each corresponding condition and the circles represent the location of the mean windward flame contour, determined from the mean of the binarized OH-PLIF fields (see “Appendix”)

It is well known that the high diffusivity of hydrogen gives it a higher extinction strain rate than methane or natural gas (Pellet 1998). In Fig. 10, the extinction strain rate for the 20% $\mathrm {H}_{\mathrm {2}}$ and 40% $\mathrm {H}_{\mathrm {2}}$ cases are shown as a dashed- and a solid-line, respectively. It is clear from Fig. 10 that the local principal compressive strain rate on the windward side exceeds the extinction strain rate for the 20% $\mathrm {H}_{\mathrm {2}}$ case. On the other hand, the ensemble-average principal compressive strain rate in the 40% $\mathrm {H}_{\mathrm {2}}$ case is well below the computed extinction strain rate for that condition.

The mean flame location for the 40% $\mathrm {H}_{\mathrm {2}}$ case is shown on the profile as a filled dot at approximately 2.3 mm to the windward side of the jet centerline. Although there may be some variation between ensemble-average of principal compressive strain rate at the mean- and the instantaneous flame location, the mean OH-PLIF image shown in Fig. 5b shows there is very little axial movement of the flame at this location, and so this effect should be minimal. The mean principal compressive strain rate at the windward side flame edge is approximately − 1100 $s^{-1}$ for the 40% $\mathrm {H}_{\mathrm {2}}$ case. This is well below the extinction strain rate computed for that case. The mean flame location (on the leeward side) for the 20% $\mathrm {H}_{\mathrm {2}}$ case, shown by a white circle on the profile in Fig. 10, also lies in a region of the flame with low mean principal compressive strain rate.

Given the similarity in mean and RMS velocity and strain rate fields for the two cases and the fact that the flame is observed to reside in relatively low strain regions of the flow, it appears the primary reason for an intact flame sheet on the windward side of the 40% $\mathrm {H}_{\mathrm {2}}$ case is the effect of $\mathrm {H}_{\mathrm {2}}$-enrichment on the extinction strain rate, rather than its effect on jet density or Reynolds number.

3.3 Analysis Along the Windward Flame Edge

The preceding analysis indicates the presence of a continuous flame along the windward side of the jet does not have a major effect on the mean centerline trajectory or shear-layer. Events such as local extinction, however, are driven by high-shear events occurring in the tails of the probability density function (PDF). It is therefore instructive to compare the PDFs of instantaneous velocity and principle compressive strain along the flame contour.

Figure 11 shows the mean velocity fields measured for each case, overlaid with contours of binarized OH-PLIF signal. As the 40% $\mathrm {H}_{\mathrm {2}}$ case has a continuous flame along the windward edge and the 20% $\mathrm {H}_{\mathrm {2}}$ case does not, we are unable to make a one-to-one comparison of PDFs along the instantaneous flame contour. Rather, we shall compare the PDFS taken at several points along the mean windward flame contour measured in the 40% $\mathrm {H}_{\mathrm {2}}$ case, shown as the dashed red lines in Fig. 11, to those acquired at the same spatial locations in the 20% $\mathrm {H}_{\mathrm {2}}$ case. A description of how the mean flame contour was computed is provided in the “Appendix”.

Fig. 11

Location of mean windward flame edge from the 40% $\mathrm {H}_{\mathrm {2}}$ flame (dashed red line) overlaid on mean |V| fields for each of the two flames. Additionally, the contours of the mean of the binarized PLIF images have been overlaid on top in black

Figure 12 shows PDFs of u and v (normalized by the laminar flame speed) at select axial locations along the windward flame edge shown in Fig. 11. The trends identifiable in the PDFs are revealing. The PDFs for axial location $x/d = -1$, i.e. just upstream of the jet-exit, peak at approximately the laminar flame speed in the axial direction for the 40% $\mathrm {H}_{\mathrm {2}}$ case, with a measurable portion PDF tail extending to the left of zero. A similar profile, albeit peaking at approximately 2${\mathrm {S}}_{{\mathrm {L}}}$ is apparent in the profile of the 20% $\mathrm {H}_{\mathrm {2}}$ case. One also observes considerable flow in the negative transverse direction there. The combination of low-to-negative velocity flow in both the axial and the transverse direction for both cases are consistent with a stagnation point flow near the wall upstream of the jet and would possibly explain small region of flame observed there in Figs. 4 and 5. Given the challenge of obtaining highly accurate, spatially-resolved SPIV measurements near a highly reflective metal wall, however, it is impossible to say conclusively whether this stagnation point flow is associated with boundary layer separation there.

Fig. 12

PDFs of the axial and transverse velocity components (normalized by the laminar flame speed ${\mathrm {S}}_{\mathrm {L}}$) of the two flames along the 40% $\mathrm {H}_{\mathrm {2}}$ flame’s mean windward edge (dashed red line in Fig. 11), at a select few axial locations

The PDFs for axial locations along the mean flame contour downstream of the jet-exit show relatively little variation in shape (peak and full-width at half maximum) and are dominated by the transverse component of velocity. The PDFs of axial velocity peak at progressively higher values with downstream distance, consistent with the entrainment of crossflow fluid by the jet. In both cases, the PDFs peak at 2–4 $S_L$ over the range of axial locations measured. We note of course, that the PDFs account for neither the orientation of the flamelet with respect to the fluid velocity, or the local propagation velocity of the flame. Nonetheless, these quantities are useful for quantitative comparison of the cases with one another and with numerical simulations of the flames.

When considering the local fluid velocity along the mean windward side flame edge, a key quantity of interest is the so-called “stoichiometric velocity”, or $U_S$. The concept of stoichiometric velocity was developed by Donbar et al. (2001) and Han and Mungal (2003a). It is defined as the conditional mean axial velocity at the stoichiometric contour of a non-premixed fuel jet issuing into a co-flowing oxidizer. Stoichiometric velocity is defined as:

$$\begin{aligned} U_S = Z_S U_0 + (1 - Z_S) U_{cf} \end{aligned}$$

(4)

(where $Z_S$ is the stoichiometric mixture fraction, $U_0$ is the momentum-averaged jet velocity and $U_{cf}$ is the coflow velocity), based on the assumptions that (1) all diffusion coefficients are equal, (2) pressure gradients are small, and (3) boundary conditions for the mixture fraction and the normalized jet velocity are identical. Han and Mungal (2003b) expanded this concept to cover jets deflected by an angle $\theta$, via the equation:

$$\begin{aligned} U_S = Z_S U_0 + (1 - Z_S) U_{cf} \sin \theta \end{aligned}$$

(5)

The stoichiometric velocities for the 40% and 20% $\mathrm {H}_{\mathrm {2}}$ fuels in this study are 0.94 and 0.87 m/s, respectively. Normalizing these with respect to the computed laminar flame speeds for each fuel gives $U_S/\mathrm {S}_{\mathrm {L}}$ = 1.7 and 1.94 for the 40% and 20% $\mathrm {H}_{\mathrm {2}}$ cases, respectively.

The $U_S/\mathrm {S}_{\mathrm {L}}$ computed for each condition are shown as the vertical lines plotted in Fig. 12. In contrast to the observations of Donbar et al. (2001), Han and Mungal (2003a), and Han and Mungal (2003b), the PDF of transverse velocity peaks in both cases to left of the computed stoichiometric velocity for each mixture. Nonetheless, there is reason to believe our measurements are consistent with those of previous studies. First, we note that whereas the mean windward side flame edge is defined in this study based on the OH-PLIF images, those in the previous studies were based on CH-PLIF images. It is well-established (Donbar et al. 2000) that in non-premixed jet flames, the CH contour is found on the fuel-side of the reaction interface, where fluid velocity must necessarily be higher. This would result in a slight biasing of the result toward the lower velocity crossflow. This effect is exacerbated by the thickness of the OH layer, compared to the CH. In addition, the Donbar et al. (2001), Han and Mungal (2003a), and Han and Mungal (2003b) studies used fuels with much higher stoichiometric mixture fraction $Z_S$ than those in the present study. This would have the effect of drawing the reaction zone into a significantly higher velocity region of the shear-layer, where fuel-air mixing is more dominated by shear-driven turbulent mixing. Finally, we note that the simple relation derived by Donbar et al. (2000) is based on the assumption of equal diffusivity of reactants, a condition clearly not satisfied by a hydrogen-enriched natural gas fuel.

Given the limitations noted above, the fact that transverse velocity peaks only slightly to the lower velocity side of the value computed for stoichiometric velocity suggests that flame holding in this study is driven by a similar mechanism to that proposed by Donbar et al. (2001), Han and Mungal (2003a), and Han and Mungal (2003b). In this study however, the lower stoichiometric mixture fraction and higher diffusivity of hydrogen appears to drive the flame to stabilize in a slightly lower velocity region of the shear-layer than the previous studies.

Figure 13 shows the PDFs of principal compressive strain rate for both cases, taken along the mean windward flame edge shown in Fig. 11. Consistent with Fig. 12, the PDFs of principal compressive strain show considerable similarity in shape and magnitude for both cases. At axial locations $x/d = [1, 3, 5]$, the PDF of principal compressive strain peaks at approximately -300 $s^{-1}$, which is well below the extinction strain rate (computed at stoichiometric conditions for this temperature and pressure) of either fuel.

Fig. 13

PDFs of the compressive principal strain rate of the two flames along the 40% $\mathrm {H}_{\mathrm {2}}$ flame’s mean windward edge (dashed red line in Fig. 11), at a select few axial locations (top row). The bottom row shows the same PDFs, but without the $x/d=-1$ curve (for better horizontal axis scaling)

The PDF of principal compressive strain at $x/d = -1$, however, shows that a significant fraction of the PDF in the 20% $\mathrm {H}_{\mathrm {2}}$ case lies beyond the extinction strain rate. It is well known that flames may exceed their extinction strain-rate briefly without inducing a local (or global) extinction of the flame (Rehm and Clemens 1998). The longer a flame resides in a region of high strain, however, the more likely it is to fully extinguish. It is clear from Fig. 13 that the 20% $\mathrm {H}_{\mathrm {2}}$ case exceeds its extinction strain rate considerably more frequently than does the 40% $\mathrm {H}_{\mathrm {2}}$ case. This is clearly supported by the observation that whereas the 40% $\mathrm {H}_{\mathrm {2}}$ case has an intact flame on windward side, the 20% $\mathrm {H}_{\mathrm {2}}$ case is extinguished there.

3.4 Impact of Flame-Holding on Dynamics

While Figs. 13 and 12 show the PDFs of velocity and principal compressive strain are similar for the two cases, they do not show the effect of the flame on the large scale (temporal) dynamics of the shear layer. It is well established that shear-layer vortices are dominant flow structure in the JICF (Kelso et al. 1996). The tendency of a flame to relaminarize the shear-layer of a jet, however, will certainly affect both the formation and development of these vortices and thereby affect large-scale mixing and entrainment. (Muniz and Mungal 2001; Takagi et al. 1980; Han and Mungal 2001)

Figure 14 shows the power spectra of u taken at three downstream points ($x/d \ge 7$) along the 40% $\mathrm {H}_{\mathrm {2}}$ case’s mean windward flame edge location (shown in Fig. 11). The limited spatial resolution of the SPIV measurements compared to the width of the shear-layer rendered power spectra at $x/d < 7$ unfeasible. To increase the signal to noise ratio, for each time series, spectra were calculated for 1000 image sequences every 500 images, and then averaged into a single spectrum. In these spectra, we observe a peak at 160 Hz (shown by vertical dashed red lines) in the 20% $\mathrm {H}_{\mathrm {2}}$ case. This peak is not seen in the spectra of the 40% $\mathrm {H}_{\mathrm {2}}$ case at the same location (dashed red line). That this frequency spike is visible at several downstream locations and appears more prominent with downstream distance are consistent with it being representative of a large scale coherent structure in the flow. Based on prior knowledge of the flow topology of the jet in crossflow, this peak is likely associated with shear-layer vortices propagating along the periphery of the jet.

Fig. 14

Power spectra of the axial velocity component at three axial locations along the 40% $\mathrm {H}_{\mathrm {2}}$ flame’s windward edge. The top and bottom rows contain spectra for the 40% $\mathrm {H}_{\mathrm {2}}$ and 20% $\mathrm {H}_{\mathrm {2}}$ flames, respectively. The red dashed lines show the location of 160 Hz on the horizontal axis

Given the similarity between the mean velocity and principal compressive strain of each case, it seems clear that the explanation for the difference in frequency content in the shear layer is associated with the presence of a flame in the 40% $\mathrm {H}_{\mathrm {2}}$ case. The volumetric expansion of the flow caused by heat release from the windward flame in that area appears to have sufficiently relaminarized the flow in the shear layer to inhibit the development of large scale shear-layer vortices.

To better characterize the fluid-dynamic phenomena responsible for the 160 Hz peak in the power spectra shown in Fig. 14, we performed a proper orthogonal decomposition (POD) on the SPIV data. POD is a well-established technique in the field of fluid mechanics (Berkooz et al. 1993). The result of the POD is a set of orthogonal eigenmodes ordered by their contribution to the turbulent kinetic energy. For each eigenmode, temporal mode coefficients can be obtained by taking the scalar products of the instantaneous flow-fields with the eigenmode. The POD was calculated using the method of snapshots (Sirovich 1987), using all 10,000 consecutive frames of SPIV acquired in each measurement run.

Based on the temporal mode coefficients of the first four eigenmodes (and the known temporal separation between frames), the corresponding power spectra were determined for each case. These spectra are presented in Fig. 15. As in Fig. 14, to increase the signal to noise ratio, we split the time-series of temporal coefficients into blocks of 1000 consecutive points, with 50% overlap between each block, and averaged the resulting spectra. Consistent with the power spectra of axial velocity shown in Fig. 14, the spectra of eigenmodes 3 and 4 in the 20% $\mathrm {H}_{\mathrm {2}}$ case show a peak at 160 Hz. A similar 160 Hz peak is not observed in the corresponding spectra of temporal mode coefficients in the 40% $\mathrm {H}_{\mathrm {2}}$ case. Indeed, no clear peak at any frequency is observed in the spectra of temporal mode coefficients computed for the 40% $\mathrm {H}_{\mathrm {2}}$ case.

Fig. 15

Power spectra of the temporal coefficients of the first four modes from the POD of the velocity fields of both the cases. The red dashed lines show the location of 160 Hz on the horizontal axis

Figure 16 shows the vorticity fields computed from the first four spatial eigenmodes of velocity for each case. The vorticity is shown here rather than the velocity magnitude as it better shows the vortex dynamics of the flow. For the 40% $\mathrm {H}_{\mathrm {2}}$ case, the energies of these modes, as a percentage of the total energy, are 6.23%, 2.36%, 1.98%, and 1.64%, respectively. For the 20% $\mathrm {H}_{\mathrm {2}}$ case, the energies are 2.46%, 1.26%, 1.17%, and 1.16%, respectively. Although the field of view of the SPIV measurements is limited to the near field of the JICF, the eigenmodes yield important insight into the global flow-field structure. The color contours in these plots represent vorticity, computed based on the vectors calculated for each mode. It is clear from these plots that the dominant flow structure in the near field, i.e. the structure associated with the first two eigenmodes, is the jet and its windward side shear-layer.

Fig. 16

Vorticity fields calculated from the first four spatial modes from the POD of the velocity fields for both cases. Overlaid on top of these fields is the velocity centerline trajectory of the jet (dashed black line)

In modes 3 and 4 of the 20% $\mathrm {H}_{\mathrm {2}}$ case, we observe what appear to a series of vortices along the shear-layer on the windward side of the jet centerline trajectory. We note that spatial eigenmodes do not necessarily correspond to fluid dynamic structures. The similarity in size, shape and spatial location, however, strongly suggest that in this particular case they do in fact result from vortices propagating downstream through the shear-layer. The spatial eigenmodes computed for the 40% $\mathrm {H}_{\mathrm {2}}$ case do not show a similar chain of vortex-like structures along the shear layer on the windward side of the jet. This indicates that the presence of a flame in windward-side shear layer for the 40% $\mathrm {H}_{\mathrm {2}}$ case results in significant damping, or outright elimination, of shear-layer vortices for that condition.

4 Conclusion

In this study, we have explored the effect of hydrogen addition on the flame-holding characteristics of a jet-in-crossflow type fuel injector at conditions similar to what one would find in the mixing duct of a modern gas turbine combustor. The fuel jet issued from a small (2 mm diameter) circular orifice located flush with the surface of a mixing channel with relatively small (40 $\times$ 60 mm) cross sectional area designed to mimic the close confinement of a generic gas turbine mixing duct. The injector was operated at 10 bars pressure, with 530 K preheat, and $r = 10$, where r is the square root of the jet-to-crossflow momentum flux ratio. The flame-holding characteristics of two JICF with 20% and 40% $\mathrm {H}_{\mathrm {2}}$ admixture (by volume) were studied using highspeed laser imaging diagnostics (kHz SPIV, OH-PLIF and OH* chemiluminescence imaging).

Consistent with Saini et al. (2020), the two JICF showed considerably different flame-holding behavior in the mixing duct. Whereas the JICF with 40% $\mathrm {H}_{\mathrm {2}}$ enrichment anchored at the jet-exit and had an intact flame sheet along the windward and leeward side of the jet, the case with 20% $\mathrm {H}_{\mathrm {2}}$ enrichment was largely extinguished along the windward edge and stabilized mostly on the leeward side. A small region of flame however, possibly linked to boundary layer separation at injector, was observed to persist at the wall in this case.

Comparison of instantaneous-, mean-, and fluctuating velocity fields indicate the trajectories and the principal compressive strain-rate fields were largely unchanged by the hydrogen-content of the fuel jet. Consistent with existing theory for the JICF, jet-to-crossflow momentum flux ratio appears to be the dominant parameter driving macroscopic characteristics such as centerline trajectory and penetration. The difference in flame-holding, therefore, must result from hydrogen raising the extinction strain rate of the fuel and thereby preventing local- or global extinction of the jet along the (high-shear) windward interface between the jet and the crossflow.

The presence of an intact flame along the windward side of the jet was observed to significantly affect the fluid-dynamics and heat-release of the JICF. The JICF with 40% $\mathrm {H}_{\mathrm {2}}$ enrichment, despite having a similar centerline trajectory, showed a slower decay in centerline velocity. This is consistent with significantly increased heat-release and volumetric expansion of the flow in the near-field region of the jet. In addition, the presence of a flame along the windward edge was observed to reduce or eliminate the formation of large-scale shear-layer vortices in this highly confined JICF.

Taken together, the data, analysis and observations presented in this study represent an interesting and unique test case for understanding and modeling the effect of hydrogen on the flame-holding characteristics of a fuel injector designed for use with natural gas at gas turbine conditions.

Appendix

1.1 Binarization of PLIF Images

As noted in Sect. 3.1, reaction zones in the JFICF were identified through binarization of the OH-PLIF images. Prior to binarization, the images were pre-processed. First, the raw images were converted from integer to floating point variable, to avoid rounding error in subsequent processing steps. Spatial non-uniformity of the OH-PLIF excitation sheet was then normalized using an ensemble-average image of fluorescence from acetone vapor seeded flow channel. Spatial variation in camera and intensifier sensitivity was normalized using an ensemble-average image of a uniformly illuminated screen (Kaiser–Slimlite). The images were then binned (2 $\times$ 2 pixels) to improve SNR and smoothed with a Gaussian filter (7 $\times$ 7). A sliding background filter was then applied to attenuate diffuse background noise and the images were binarized about a threshold value ($\gamma$). Finally, a median filter (7 $\times$ 7 pixel) was applied to the binarized images to remove speckle noise that remained after binarization. Figure 17 shows a sample OH-PLIF raw- and pre-processed image.

Fig. 17

Sample OH-PLIF image at different stages of the binarization

To ensure the binarized images accurately captured the flame location, we tested the sensitivity of the results for a range of binarization threshholds ($\gamma \pm 20\%$). Figure 18 shows that for $\gamma \pm 20\%$, the contour of the flame leading edge (taken in this test to be the 15% contour in ensemble-average of binarized PLIF images) varies by no more than 0.28 mm. As this is significantly lower than the SPIV spatial resolution (1.2 mm/vector) against which the results are compared, we conclude the binarization threshold is sufficiently robust for the purposes of this study.

Fig. 18

Location of the 15% contours on the windward side of the 40% $\mathrm {H}_{\mathrm {2}}$ case, calculated at different axial locations (x/d) and for three different binarization threshold values. The numbers on the scatter plot represent the difference in the contour locations for the highest and lowest binarization threshold values ($0.8 \gamma$ and $1.2 \gamma$, respectively), at a given x/d

1.2 Calculation of Mean Windward Flame Edge Location

The binarization of the OH-PLIF images provides a clearer view of the windward flame, especially once the images have been ensemble averaged. However, in order to analyze the velocity field data at the mean flame edge (as was done in Sect. 3.3), a single contour representing this flame edge would be necessary. To calculate such a contour, an additional threshold cutoff ($\alpha$) would need to be applied to the ensemble averaged binarized images. Similar to the binarization threshold value from before, the cutoff value here would need to be chosen such that any variations in it would not change the resulting contour’s position more than the SPIV spatial resolution.

To determine the threshold used to define the mean flame leading edge contour, we first applied a range of cutoff values about a chosen threshold value $\alpha$ (i.e. $\alpha \pm 0.05$) to the ensemble-average image of the binarized PLIF measurements. This resulted in several contours of the windward flame edge for this particular $\alpha$. At a given axial location (x/d), the upper and lower bound of the transverse location (y/d) of the aforementioned range of contours can be determined. The difference between the two can be viewed as the thickness of the envelope of the windward flame edge contours when a threshold of $\alpha \pm 0.05$ is applied. This contour envelope thickness was averaged over all the axial locations in $x/d=[0,7]$. This process was repeated for $0.03 \le \alpha \ge 0.35$ and the results have been plotted in Fig. 19. It was found that the smallest envelope thickness was at $\alpha = 14.5\%$, and this value (0.85 mm) was less than the SPIV spatial resolution (1.2 mm). Therefore, this was determined to be the most robust identifier for the mean flame location.

Fig. 19

Envelope thickness of the contour representing the mean windward edge of the 40% $\mathrm {H}_{\mathrm {2}}$ flame for varying cutoff values ($\alpha$). The dot on the plot represents the location of the minimum (14.5%)