Modelling Heat Loss Effects in the Large Eddy Simulation of a Lean Swirl-Stabilised Flame

Abstract

The flame in a gas turbine model combustor close to blow-off is studied using large eddy simulation with the objective of investigating the sensitivity of including different heat loss effects within the modelling. A presumed joint probability density function approach based on the mixture fraction and progress variable with unstrained flamelets is used. The normalised enthalpy is included in the probability density function to account for heat loss within the flame. Two simulations are presented that use fixed temperature boundary conditions, and use adiabatic and non-adiabatic formulations of the combustion model. The results are compared against the previous fully adiabatic case and experimental data. The statistics for the simulations are similar to the results obtained from the fully adiabatic case. Improved statistics are obtained for the temperature in the near-wall regions. The non-adiabatic flamelet case shows the average reaction rate values at the flame root are approximately 50% smaller in comparison to the adiabatic flamelet cases. This causes the lift-off height to be overestimated. The time series of the lift-off height and the volume integrated heat release rate show that including non-adiabatic flamelets causes the flame to be highly unstable. A higher enthalpy deficit is seen in the near-field regions when the flame root is not present and experiencing some lift-off, suggesting that the flame is more dynamic when including heat loss.

1 Introduction

Lean combustion is utilised in modern gas turbine combustors in order to reduce the production of pollutants. The stability of lean flames is enhanced through the use of swirling flow, since an Inner Recirculation Zone (IRZ) is formed by the flow field, and hot combustion products and radical species are continuously supplied to the flame root to aid flame stabilisation (Syred 2006). However, it is well known that lean combustion is highly unstable and such flames are susceptible to local extinction and flame blow-off. The mechanisms leading to blow-off are not well understood and under such conditions, the flame heat release becomes weaker. Therefore, heat loss effects can influence the stabilisation of the flame. There have been a number of recent modelling studies on flame blow-off (Zhang and Mastorakos 2016; Ma et al. 2019), but heat loss effects are seldom considered. Thus, it is of interest from a modelling perspective to observe how heat loss effects can influence the flame behaviour close to lean blow-off conditions.

Large Eddy Simulation (LES) has proven to be successful at modelling heat loss effects in simulations of turbulent flames. One approach for including heat loss effects is to account for heat transfer from the walls of the combustion chamber, which can lead to achieving an improved accuracy. A simple approach is by imposing wall temperature boundary conditions (Tay Wo Chong et al. 2010; Palies et al. 2011; Mercier et al. 2014; Benard et al. 2019) by following experimental measurements obtained on the combustion chamber surfaces (Brübach et al. 2013). Alternative methods include a conjugate heat transfer approach (Bauerheim et al. 2015), or using a fully coupled LES/heat conduction approach, where an additional solver is used to compute the temperature distribution for the solid structure of the combustion chamber (Shahi et al. 2015; Ghani et al. 2016; Miguel-Brebion et al. 2016; Kraus et al. 2018).

Alternatively, heat loss effects can be modelled by considering heat loss in flamelet calculations. An early approach considered an enthalpy defect approach in the flamelets (Bray and Peters 1994; Marracino and Lentini 1997; Hossain et al. 2002), which is achieved by considering the heat loss through radiation. A burner-stabilised flame method for building the flamelet library for tabulated chemistry models has been proposed in the studies by van Oijen and de Goey (2000), and Fiorina et al. (2003). The non-adiabatic effects are obtained by submitting a heat flux to the wall of the burner to decrease the enthalpy in that region (Cecere et al. 2011; Donini et al. 2017). Other approaches have more recently been proposed for non-adiabatic flamelet approaches, which include a wall heat transfer model (Ma et al. 2018) and a Perfectly Stirred Reactor (PSR) approach for Moderate or Intense Low-oxygen Dilution (MILD) combustion (Chen et al. 2018a). A final approach is to add a heat sink term on to the heat release term in the one-dimensional energy equation to mimic the heat loss effects across the flame, as proposed by Proch and Kempf (2015).

The gas turbine model combustor developed by the German Aerospace Centre (DLR) is a partially premixed system containing two swirl generators (Meier et al. 2006; Weigand et al. 2006). Extensive measurements using laser diagnostics for three operating conditions have been obtained for flames under thermo-acoustically stable and unstable conditions, and for a flame close to blow-off. The third case is of interest for this study and this flame showed sudden lift-off with partial extinction and re-ignition, leading to re-anchoring of the flame to the stabilisation point (Stöhr et al. 2011). Understanding the mechanisms leading to blow-off is challenging, owing to the complex interactions between turbulence, the heat release from combustion and molecular transport (Shanbhogue et al. 2009). In addition, the study by Palies et al. (2011) suggested the use of adiabatic walls can cause significant changes to the shape of the flame and hence, the flame to be studied here may be sensitive to changes when including heat loss effects in the modelling approach. Furthermore, the role of heat loss on the blow-off behaviour of the flame is not clear.

The aim of this work is to investigate the influences of heat loss on the stabilisation of a flame close to blow-off in a gas turbine model combustor. The objectives are to compare two simulations using non-adiabatic wall conditions, where one will also use a non-adiabatic flamelet approach. These results will be compared to the fully adiabatic case that has been studied by Massey et al. (2019a). The remainder of this paper is organised as follows. A description of the numerical modelling strategy is outlined in Sect. 2, followed by a description of the gas turbine model combustor experiment to be simulated in Sect. 3. The results and observations are presented in Sect. 4 and the key findings of the study are summarised in Sect. 5.

2 Large Eddy Simulation Methodology

The numerical modelling methodology that is used for this study is based on the previous LES study by Chen et al. (2017). This modelling approach is a tabulated chemistry approach, which is based on unstrained premixed flamelets. A non-premixed mode contribution to the sub-grid reaction rate source term is also included, since partially premixed flames are considered. This approach has been tested throughly for partially premixed flames where local extinction and failed ignition are present (Langella et al. 2018; Chen et al. 2019a, 2020; Massey et al. 2019a). The filtered conservation equations for mass and momentum are solved, along with the total enthalpy (sum of the sensible and chemical enthalpies) under the low Mach number assumption. Four additional scalars are required for partially premixed combustion modelling. Their transport equations with their closure models are presented next.

2.1 Combustion Modelling

The filtered means and variances of the mixture fraction $\xi$ and the normalised reaction progress variable c are used to describe partially premixed flames. The mixture fraction is calculated using the definition proposed by Bilger (1988). The progress variable is defined as ${ c = \psi / { \psi }^{ \mathrm { eq } } }$, where $\psi = {Y}_{\mathrm{CO}}+{Y}_{{\mathrm{CO}}_{2}}$ and the superscript ‘eq’ denotes the equilibrium value for a given mixture fraction. Transporting the progress variable requires care, since unclosed terms arise when deriving the progress variable transport equation from first principles (Bray et al. 2005). Scaled and unscaled progress variable approaches have been tested in the study by Chen et al. (2020). It is observed that the scaled progress variable approach performs better in capturing local extinction and this approach is used here. The transport equations for the scalars used to describe partially premixed flames are given as

$$\begin{aligned} {\overline{\rho }} \frac{ \mathrm { D } {\widetilde{\xi }} }{ \mathrm { D } t }\simeq \varvec{ \nabla } \cdot \bigg [ \bigg ( \overline{ \rho {\mathscr {D}} } + {\overline{\rho }} \frac{ { \nu }_{ T } }{ { \mathrm {Sc}}\!_{ T } } \bigg ) \varvec{ \nabla } {\widetilde{\xi }} \, \bigg ] \, , \end{aligned}$$

(1)

$$\begin{aligned} {\overline{\rho }} \frac{ \mathrm { D } { \sigma }_{ \xi , \mathrm { sgs } }^{ 2 } }{ \mathrm { D } t }&\simeq \varvec{ \nabla } \cdot \bigg [ \bigg ( \overline{ \rho {\mathscr {D}} } + \overline{ \rho } \frac{ { \nu }_{ T } }{ { \mathrm {Sc}}\!_{ T } } \bigg ) \varvec{ \nabla } { \sigma }_{ \xi , \mathrm { sgs } }^{ 2 } \bigg ] - 2 \, {\overline{\rho }} { {\widetilde{\chi }} }_{ \xi , \mathrm { sgs } } + 2 \, {\overline{\rho }} \frac{ { \nu }_{ T } }{ { \mathrm {Sc}}\!_{ T } } \, { \big |\varvec{ \nabla } {\widetilde{\xi }} \, \big |}^{ 2 } \, , \end{aligned}$$

(2)

$$\begin{aligned} {\overline{\rho }} \frac{ \mathrm { D } {\widetilde{c}} }{ \mathrm { D } t }&\simeq \varvec{ \nabla } \cdot \bigg [ \bigg ( \overline{ \rho {\mathscr {D}} } + {\overline{\rho }} \frac{ { \nu }_{ T } }{ { \mathrm {Sc}}\!_{ T } } \bigg ) \varvec{ \nabla } {\widetilde{c}} \, \bigg ] + \overline{ { \dot{ \omega } }^{ * } } \, , \end{aligned}$$

(3)

$$\begin{aligned} {\overline{\rho }} \frac{ \mathrm { D } { \sigma }_{ c , \mathrm { sgs } }^{ 2 } }{ \mathrm { D } t }&\simeq \varvec{ \nabla } \cdot \bigg [ \bigg ( \overline{ \rho {\mathscr {D}} } + {\overline{\rho }} \frac{ { \nu }_{ T } }{ { \mathrm {Sc}}\!_{T}} \bigg ) \varvec{ \nabla } { \sigma }_{ c , \mathrm { sgs } }^{ 2 } \bigg ] - 2 \, {\overline{\rho }} { {\widetilde{\chi }} }_{ c , \mathrm { sgs } }+ 2 \, {\overline{\rho }} \frac{ { \nu }_{ T } }{ { \mathrm {Sc}}\!_{T}} \, { \big |\varvec{ \nabla } {\widetilde{c}} \, \big |}^{ 2 } \\&\quad + 2 \, \big ( \overline{ c \, { \dot{ \omega } }^{ * } } - {\widetilde{c}} \, \overline{ { \dot{ \omega } }^{ * } } \big ) \, . \nonumber \end{aligned}$$

(4)

The molecular diffusion terms are taken to be the same for each species, since the Lewis numbers are close to unity for methane–air mixtures. The molecular diffusion term in Eqs. (1)–(4) is determined as $\overline{ \rho {\mathscr {D}} } = {\overline{\rho }} \widetilde{ \nu } / \mathrm { Sc }$, where $\mathrm { Sc } = 0.7$. The eddy viscosity ${ \nu }_{ T }$ is closed using the Smagorinsky model (Smagorinsky 1963) and a turbulent Schmidt number of ${ \mathrm { Sc } }_{ T } = 0.4$ is used (Pitsch and Steiner 2000). The sub-grid Scalar Dissipation Rate (SDR) terms ${ {\widetilde{\chi }} }_{ \xi , \mathrm { sgs } }$ and ${ {\widetilde{\chi }} }_{ c , \mathrm { sgs } }$ require modelling. The sub-grid SDR for $\xi$ is modelled using a linear relaxation model ${ {\widetilde{\chi }} }_{ \xi , \mathrm { sgs } } = { C }_{ \xi } ( { \nu }_{ T } / { \varDelta }^{ 2 } ) { \sigma }_{ \xi , \mathrm { sgs } }^{ 2 }$ (Pitsch 2006). The sub-grid SDR for c is modelled using the algebraic expression proposed by Dunstan et al. (2013), which has also been used in previous studies (Chen et al. 2019b, c; Massey et al. 2019a, b).

The Favre-filtered temperature ${\widetilde{T}}$ is obtained using the filtered enthalpy transport equation and is calculated using the mixture-averaged enthalpy of formation ${ \widetilde{ \varDelta h } }_{ f }^{ 0 }$ and specific heat capacity ${{\widetilde{c}} }_{ p }$ through the approximation ${\widetilde{T}} = { T }_{ 0 } + ( {\widetilde{h}} - { \widetilde{ \varDelta h } }_{ f }^{ 0 } ) / { {\widetilde{c}} }_{ p }$, where ${ { T }_{ 0 } = 298.15 \, \mathrm { K } }$. The mixture density is computed using the state equation ${ {\overline{\rho }} = {\overline{p}} {\widetilde{M}} / { \mathfrak {R}}^{ 0 } {\widetilde{T}} }$, where ${\widetilde{M}}$ represents the Favre-filtered molecular mass of the mixture and ${ \mathfrak {R}}^{ 0 }$ is the universal gas constant.

The filtered reaction rate for partially premixed combustion $\overline{ { \dot{ \omega } }^{ * } }$ requires closure, which also appears as a source term in Eq. (4). This is determined by treating it as a combination of the instantaneous burning modes. In the study by Domingo et al. (2002), the instantaneous form of Eq. (3) is derived and it is shown that the source term ${ \dot{ \omega } }^{ * }$ includes contributions from different burning modes. The filtered form of this source term is written as (Domingo et al. 2002; Bray et al. 2005)

$$\begin{aligned} \overline{ { \dot{ \omega } }^{ * } } = \underbrace{ \frac{ { \overline{ \dot{ \omega } } }_{ \psi } }{ { \psi }\!^{ \mathrm { eq } } } }_{ \text {Premixed } { \overline{ \dot{ \omega } } }_{ \mathrm { fp } } } \; + \; \; \; \underbrace{ \overline{ \rho { \chi }_{ \xi } \frac{ c }{ { \psi }\!^{ \mathrm { eq } } } \frac{ { \mathrm { d } }\!^{ 2 } { \psi }\!^{ \mathrm { eq } } }{ \mathrm { d }\! { \xi }^{ 2 } } } }_{ \text {Non-premixed } { \overline{ \dot{ \omega } } }_{ \mathrm { np } } } \; \; \; + \underbrace{ \overline{ 2\,\! \rho { \chi }_{ \xi c } \frac{ 1 }{ { \psi }\!^{ \mathrm { eq } } } \frac{ \mathrm { d }\! { \psi }\!^{ \mathrm { eq } } }{ \mathrm { d }\! \xi } } }_{ \text {Cross dissipation term } { \overline{ \dot{ \omega } } }_{ \mathrm { cdr } } } \, . \end{aligned}$$

(5)

The three terms on the right-hand side of Eq. (5) represent the contributions from premixed and non-premixed combustion modes, and their interactions resulting from the cross dissipation rate; these are denoted as ${ \overline{ \dot{ \omega } } }_{ \mathrm { fp } }$, ${ \overline{ \dot{ \omega } } }_{ \mathrm { np } }$ and ${ \overline{ \dot{ \omega } } }_{ \mathrm { cdr } }$ respectively. The cross dissipation term is neglected following previous studies (Bray et al. 2005; Ruan et al. 2014).

The first term of Eq. (5) is the premixed contribution, where the unscaled reaction rate is ${ { \dot{ \omega } }_{ \psi } = { \dot{ \omega } }_{ \mathrm { CO } } + { \dot{ \omega } }_{ { \mathrm { CO } }_{ 2 } } }$ to be consistent with the definition of c. A presumed sub-grid joint PDF approach is used for ${ \overline{ \dot{ \omega } } }_{ \mathrm { fp } }$, which is parameterised by the mixture fraction and progress variable. The expression for ${ \overline{ \dot{ \omega } } }_{ \mathrm { fp } }$ written as (Ruan et al. 2014)

$$\begin{aligned} { \overline{ \dot{ \omega } } }_{ \mathrm { fp } } = \overline{ \rho } \int _{ 0 }^{ 1 } \int _{ 0 }^{ 1 } \frac{ { \dot{ \omega } }_{ \mathrm { fp } } ( \eta , \zeta ) }{ \rho ( \eta , \zeta ) } \, {\widetilde{P}} ( \eta , \zeta ) \; \mathrm { d } \eta \, \mathrm { d } \zeta \, , \end{aligned}$$

(6)

where ${ \dot{ \omega } }_{ \mathrm { fp } } ( \eta , \zeta )$ and $\rho ( \eta , \zeta )$ are the flamelet reaction rate and density respectively, which are obtained through one-dimensional unstrained planar laminar premixed flame calculations over the flammability range in mixture fraction space. The joint PDF contains the sample space variables $\eta$ and $\zeta$ for the first two moments of the mixture fraction and progress variable respectively. The density-weighted joint PDF is approximated as ${ {\widetilde{P}} ( \eta , \zeta ) \approx { {\widetilde{P}} }_{ \beta }( \eta \, ; \, {\widetilde{\xi }} , { \sigma }_{ \xi , \mathrm { sgs } }^{ 2 } ) \times { {\widetilde{P}} }_{ \beta } ( \zeta \, ; \, {\widetilde{c}} , { \sigma }_{ c , \mathrm { sgs } }^{ 2 } ) }$ and the shape of the two PDFs are assigned using beta functions. There are indeed fluctuations of $\xi$ and c that influence each other and this correlation is significant in RANS modelling, as the fluctuations are entirely modelled. This correlation is included within the joint PDF through the copula method (Darbyshire and Swaminathan 2012; Ruan et al. 2014). The DNS study by Chen et al. (2018b) demonstrated that the sub-grid correlation is relatively less influential on the time-averaged statistics because the contribution related to the large-scale fluctuations is resolved in LES. It is also seen in the previous numerical study by Massey et al. (2019a) that the normalised filter width within the reaction region is of the order of the laminar flame thickness of a stoichiometric laminar premixed methane–air flame. Therefore, the sub-grid correlation is not considered and the statistical independence assumption for the two beta PDFs is made for simplicity.

The non-premixed contribution ${ \overline{ \dot{ \omega } } }_{ \mathrm { np } }$ is modelled using the expression (Ruan et al. 2014)

$$\begin{aligned} { \overline{ \dot{ \omega } } }_{ \mathrm { np } } = \overline{ \rho } \, {\widetilde{c}} \, { {\widetilde{\chi }} }_{ \xi } \int _{ 0 }^{ 1 } \frac{ 1 }{ { \psi }^{ \mathrm { eq } } \left( \eta \right) } \frac{ { \mathrm { d } }^{ 2 } { \psi }^{ \mathrm { eq } } \left( \eta \right) }{ \mathrm { d } { \eta }^{ 2 } } {\widetilde{P}} \left( \eta \right) \, \mathrm { d } \eta \, . \end{aligned}$$

(7)

The non-premixed contribution does not come from counterflow diffusion flamelets and is instead a correction term for the premixed contribution term. This term contains the filtered mixture fraction scalar dissipation rate, which is the sum of the resolved and SGS contributions and is expressed as ${ { {\widetilde{\chi }} }_{ \xi } = \widetilde{ {\mathscr {D}} } ( \varvec{ \nabla } {\widetilde{\xi }} \cdot \varvec{ \nabla } {\widetilde{\xi }} ) + { {\widetilde{\chi }} }_{ \xi , \mathrm { sgs } } }$. The non-premixed contribution is typically only significant in the stoichiometric regions, since ${ { \mathrm { d } }^{ 2 } { \psi }^{ \mathrm { eq } } / \mathrm { d } { \eta }^{ 2 } }$ is zero elsewhere (Ruan et al. 2014).

The final term that requires closure is the reaction related source term in Eq. (4) and is written as ${ ( \overline{ c \, { \dot{ \omega } }^{ * } } - {\widetilde{c}} \, \overline{ { \dot{ \omega } }^{ * } } ) = ( \overline{ c \, { \dot{ \omega } }_{ \mathrm { fp } } } - \widetilde{ c } \, { \overline{ \dot{ \omega } } }_{ \mathrm { fp } } ) + ( \overline{ c \, { \dot{ \omega } }_{ \mathrm { np } } } - \widetilde{ c } \, { \overline{ \dot{ \omega } } }_{ \mathrm { np } } ) }$, where ${ ( \overline{ c \, { \dot{ \omega } }_{ \mathrm { np } } } - {\widetilde{c}} \, { \overline{ \dot{ \omega } } }_{ \mathrm { np } } ) = 0 }$ following Eq. (7). The term $\overline{ c \, { \dot{ \omega } }_{ \mathrm { fp } } }$ is evaluated in a similar manner to Eq. (6) (Ruan et al. 2014).

2.2 Non-adiabatic Flamelet Formulation

The original studies by van Oijen and de Goey (2000) and Fiorina et al. (2003) for the FGM and FPI approaches respectively suggested that freely propagating premixed flames or burner-stabilised flames can be used to build the flame library for adiabatic conditions. However, only the burner-stabilised flame method is used for the non-adiabatic flame calculations. The study by Proch and Kempf (2015) proposed a method for undertaking non-adiabatic calculations of freely propagating premixed flames. The heat loss is introduced by scaling the source term due to chemical reaction in the one-dimensional energy equation. The method is referred to as the heat release damping method. This approach has also been applied to non-premixed flames by introducing the same scaling on to the chemical reaction source term in the counterflow diffusion flame equation, as well as to the energy equation (Wollny et al. 2018).

The heat release damping approach is applied in this work to build a non-adiabatic flamelet library, since the adiabatic library is constructed using one-dimensional freely propagating premixed flames (Chen et al. 2017). The non-adiabatic effects at the flamelet level are included in the premixed contribution of the filtered reaction rate by following the approach outlined by Proch and Kempf (2015) that is proposed for premixed flames. This approach is adopted here by undertaking the calculations in mixture fraction space at different heat loss levels. The flamelet calculations are undertaken using Cantera (Goodwin et al. 2017) with the GRI–Mech 3.0 chemical mechanism for methane–air combustion. The heat loss is introduced in the one-dimensional freely propagating premixed laminar flame calculations by altering the chemical reaction source term in the energy equation. The one-dimensional energy equation is written as

$$\begin{aligned} \rho U { c }_{ p } \frac{ \mathrm { d } T }{ \mathrm { d } x } = \frac{ \mathrm { d } }{ \mathrm { d } x } \left( \lambda \frac{ \mathrm { d } T }{ \mathrm { d } x } \right) + \rho \frac{ \mathrm { d } T }{ \mathrm { d } x } \Bigg ( \sum _{ \alpha = 1 }^{ N } { c }_{ p , \alpha } { {\mathscr {D}} }_{ \alpha } \frac{ \mathrm { d } { Y }_{ \alpha } }{ \mathrm { d } x } \Bigg ) - ( 1 - \kappa )\sum _{ \alpha = 1 }^{ N } { h }_{ \alpha } { \dot{ \omega } }_{ \alpha } \, , \end{aligned}$$

(8)

where $\kappa$ is the introduced heat loss factor. For a given equivalence ratio, laminar flame calculations are performed for a number of heat loss factor values ranging from $\kappa = 0$ (adiabatic conditions) to $\kappa = 0.4$ with increments of 0.04 to give 11 flamelet solutions for each equivalence ratio. These calculations are then repeated for 20 different equivalence ratios covering the flammability range. Beyond $\kappa = 0.4$, no flame solution could be obtained for the case closest to the lean flammability limit. This produces ${ \mathrm { N } }_{ { h }^{ * } }$ two-dimensional laminar flame matrices ${ {\mathbf {L}} }^{ \varvec{ \varphi } }$ of size ${ \mathrm { N } }_{ \xi } \times { \mathrm { N } }_{ c }$. A schematic of the laminar non-adiabatic flamelet calculations procedure is shown in Fig. 1. As shown in Fig. 2, the flame speed decreases and the flame thickness increases when the heat loss factor is increased. For the highest heat loss case with $\kappa =0.4$, the value of ${ s }_{ L }^{ 0 }$ is less than $8 \, \%$ of the adiabatic value for all equivalence ratios. Therefore, the flame is considered to be quenched for higher heat losses.

Fig. 1

Schematic of generating the flamelet solutions with the heat release damping approach

Fig. 2

Flamelets generated using the heat release damping approach (Proch and Kempf 2015; Wollny et al. 2018). The flame speed (a) and flame thickness (b) are plotted against $\phi$ for different values of $\kappa$ in the range $0 \le \kappa \le 0.4$

It is possible in the LES that the heat loss (enthalpy defect) is higher than that for $\kappa =0.4$ at a given local equivalence ratio. To cover this in the flamelet table, four more heat loss levels are included and these solutions are obtained by progressively lowering the gas temperature to $300 \, \mathrm { K }$ for each solution point in the one-dimensional laminar flame at the last heat loss factor $\kappa =0.4$. As a result, only the temperature related quantities (T, ${ c }_{ p }$, $\rho$ and h) are different in these four additional solutions, whereas the mixture composition remains the same as that for the solution produced with $\kappa =0.4$. In total, there are 15 (heat loss levels) $\times$ 20 (equivalence ratios) computed laminar flame solutions and subsequently, these one-dimensional solutions are interpolated into three-dimensional space and are parameterised by the mixture fraction, progress variable and enthalpy.

For the non-adiabatic flamelets, the progress variable definition is rewritten as

$$c = \frac{{Y_{{{\text{CO}}}} + Y_{{{\text{CO}}_{2} }} }}{{Y_{{{\text{CO}}}}^{{{\text{eq}}}} (\xi ,h^{*} ) + Y_{{{\text{CO}}_{2} }}^{{{\text{eq}}}} (\xi ,h^{*} )}},$$

(9)

and the normalised enthalpy is given by

$$\begin{aligned} { h }^{ * } = \frac{ h - { h }_{ \mathrm { min } } ( \xi , c ) }{ { h }_{ \mathrm { ad } } ( \xi , c ) - { h }_{ \mathrm { min } } ( \xi , c ) } \, . \end{aligned}$$

(10)

The subscripts ‘min’ and ‘ad’ denote the minimum and adiabatic mixture enthalpies respectively at a given mixture fraction and progress variable. The values of ${ h }_{ \mathrm { min } }$ and ${ h }_{ \mathrm { max } }$ are tabulated as functions of $\xi$ and c for the normalisation of the filtered enthalpy in the LES. Figures 3 and 4 respectively show the temperature and reaction rate fields obtained from the flamelet calculations in c and ${ h }^{ * }$ space for three representative $\xi$ values. It can be seen that the reaction rate is zero when ${ h }^{ * } < 0.6$ for all three mixture fractions, whereas the temperature smoothly decreases to $300 \, \mathrm { K }$ as ${ h }^{ * }$ approaches zero. This is physically consistent with the heat loss process when the flame is quenched by the wall and reaction rate decreases to zero, but the temperature decreases gradually through heat conduction.

Fig. 3

Contour plots of the flamelet temperature over progress variable and normalised enthalpy space

Fig. 4

Contour plots of the flamelet reaction rate over progress variable and normalised enthalpy space

These laminar flame solutions are then used for the integration of filtered quantities required in the LES. Following the previous study by Chen et al. (2018a), the filtered premixed reaction rate source term is modelled as

$$\begin{aligned} { \overline{ \dot{ \omega } } }_{ \mathrm { fp } } = \overline{ \rho } \int _{ 0 }^{ 1 } \int _{ 0 }^{ 1 } \int _{ 0 }^{ 1 } \frac{ { \dot{ \omega } } _{ \mathrm { fp } } ( \eta , \zeta , {\mathscr {H}} ) }{ \rho ( \eta , \zeta , {\mathscr {H}} ) } \, {\widetilde{P}} ( \eta , \zeta , {\mathscr {H}} ) \; \mathrm { d } \eta \, \mathrm { d } \zeta \, \mathrm { d } {\mathscr {H}} \, , \end{aligned}$$

(11)

where ${ {\widetilde{P}} ( \eta , \zeta , {\mathscr {H}} ) \approx { {\widetilde{P}} }_{ \beta } ( \eta \, ; \, {\widetilde{\xi }} , { \sigma }_{ \xi , \mathrm { sgs } }^{ 2 } ) \times { {\widetilde{P}} }_{ \beta } ( \zeta \, ; \, {\widetilde{c}} , { \sigma }_{ c , \mathrm { sgs } }^{ 2 } ) \times \delta ( {\mathscr {H}} - { {\widetilde{h}} }^{ * } ) }$ is the joint PDF of the mixture fraction, progress variable and normalised enthalpy and $\mathscr { H }$ denotes the sample space variable for the normalised enthalpy. The presumed beta PDF distribution is again used for $\xi$ and c, while a Dirac delta function is used for ${ h }^{ * }$. The look-up table for the LES now has five dimensions of size ${ \varvec{ {\mathbf {M}} } }^{ \varvec{ {\widetilde{\varphi }} } }$ with dimensions ${ { \mathrm { N } }_{ {\widetilde{\xi }} } \times { \mathrm { N } }_{ {\widetilde{c}} } \times { \mathrm { N } }_{ { {\widetilde{g}} }_{ \xi } } \times { \mathrm { N } }_{ { \widetilde{ g } }_{ c } } \times { \mathrm { N } }_{ { {\widetilde{h}} }^{ * } } }$. The number of points in the look-up table are 44, 51, 15, 31 and 15 in ${\widetilde{\xi }}$, ${\widetilde{c}}$, ${ \sigma }_{ \xi , \mathrm { sgs } }^{ 2 }$, ${ \sigma }_{ c , \mathrm { sgs } }^{ 2 }$ and ${ {\widetilde{h}} }^{ * }$ directions respectively. The resolution is improved near ${\widetilde{c}} = 0.7$ and for near-stoichiometric mixtures, where high reaction rates are expected. Linear interpolation is used in each of the five dimensions and the error with a high reaction rate is estimated to be approximately $1 \, \%$ (Ruan et al. 2014).

The non-premixed contribution ${ \overline{ \dot{ \omega } } }_{ \mathrm { np } }$ is significant only in the vicinity of the stoichiometric mixture fraction. Such mixtures are located far from the combustion chamber walls, as observed in the experiments (Weigand et al. 2006). Thus, this term is taken to be unaffected by the wall heat losses.

3 Gas Turbine Model Combustor

3.1 Experimental Case

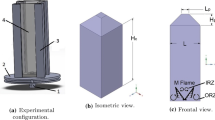
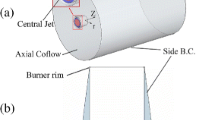
A schematic of the DLR combustor is shown in Fig. 5 and a full description of the measurement techniques is available in the corresponding experimental studies (Meier et al. 2006; Weigand et al. 2006; Stöhr et al. 2011). The combustion chamber had a square cross-section of internal area of $85 \times 85 \, { \mathrm { mm } }^{ 2 }$ and a length of $114 \, \mathrm { mm }$. Dry air at atmospheric pressure and room temperature entered a single plenum and then passed through two radial swirlers. The two co-swirling flows entered the combustion chamber through a central nozzle of diameter $15 \, \mathrm { mm }$ and an annular nozzle with inner and outer diameters of $17 \, \mathrm { mm }$ and $25 \, \mathrm { mm }$ respectively. Methane was fed through a non-swirling nozzle ring that had 72 channels ($0.5 \times 0.5 \, { \mathrm { mm } }^{ 2 }$) located between the two air nozzles. The exit planes of the central air and methane nozzles are $4.5 \, \mathrm { mm }$ below the exit of the annular air nozzle and the entrance to the combustion chamber, which is positioned at $x = 0$, as shown by the co-ordinate axes in Fig. 5. The air and methane flow rates for the flame close to blow-off, referred to as flame C, are listed in Table 1 along with the thermal power and global equivalence ratio. Under these operating conditions, the flame root was positioned at an average height of approximately $6 \, \mathrm { mm }$ above the fuel nozzle. The flame was observed to be highly unstable with random sudden lift-off events and the flame base returning to the location $x = 1.5 \, \mathrm { mm }$. These lift-off events typically lasted 0.1–$0.15 \, \mathrm { s }$ and occurred 1–2 times per second. The stabilised flame and its lift-off events were shown by Stöhr et al. (2011) using the time sequences of the combined high-speed ($5 \, \mathrm { kHz }$) PIV and OH-PLIF images.

Fig. 5

Schematic drawing of the gas turbine model combustor (Meier et al. 2006; Weigand et al. 2006)

Table 1 Operating conditions for flame C (Meier et al. 2006; Weigand et al. 2006)

3.2 Computational Model

The computational domain is the same as used in the previous study by Massey et al. (2019a) and this grid consists of $20 \, \mathrm { million }$ unstructured tetrahedral cells. The model includes an air feed pipe, the plenum, both swirlers, the combustion chamber and a large cylindrical atmospheric far-field downstream of the combustion chamber exit, in order to prevent acoustic wave reflection. All of the walls have no-slip conditions imposed, apart from the walls in the streamwise direction of the extended far-field domain, which have slip conditions imposed. The outlet is specified to have zero streamwise gradients for all the variables. The air feed pipe and fuel injector have constant mass flow rate boundary conditions imposed using the values in Table 1 along with a top-hat velocity profile. All 72 fuel injectors are included in the mesh to provide an improved accuracy for the fuel–air mixing field. A uniform grid around the fuel nozzle region with a spacing of $0.1 \, \mathrm { mm }$, which corresponds to 5 mesh points. There is also refinement along the outer contoured wall of the outer nozzle to ensure that the flow separation is captured correctly. At least two cells adjacent to the wall are within ${ { y }^{ + } < 5 }$, in order to ensure that the velocity field in those regions is insensitive to the use of a wall model. The minimum cell sizes around the fuel nozzle, swirlers and shear layers are 0.1, 0.3 and $0.5 \, \mathrm { mm }$ respectively.

In this study, heat loss through the chamber walls is considered to be more influential on the flame behaviour under the near blow-off condition (${ \phi }_{ \mathrm { glob } } = 0.55$) with a small thermal power of $7.6 \, \mathrm { kW }$. Thus, non-adiabatic effects are accounted for at both the LES (through isothermal wall boundary condition) and flamelet levels. The individual effects at these two different levels are examined in this study through comparisons with the previous LES results obtained from the fully adiabatic simulation (Massey et al. 2019a). The bottom plane of the combustion chamber uses an isothermal boundary condition of $700 \, \mathrm { K }$ and the side walls of the combustion chamber have a linear profile up to $40 \, \mathrm { mm }$ that increases from 700 to $1000 \, \mathrm { K }$; beyond $40 \, \mathrm { mm }$, an isothermal temperature of $1000 \, \mathrm { K }$ is used.¹ These wall boundary conditions are illustrated in Fig. 6.

Fig. 6

Temperature boundary conditions for the non-adiabatic simulations (NAW and NAF)

The computational set-up that is used for the three simulations is listed in Table 2. Case AD is the adiabatic case that is analysed in the study by Massey et al. (2019a) and cases NAW and NAF both use non-adiabatic wall conditions. Case NAF is the only case to use the non-adiabatic flamelet approach that is described in Sect. 2.2. The adiabatic framework that is described in previous numerical studies (Chen et al. 2017; Massey et al. 2019a) is used for cases AD and NAW. For case NAW, the wall heat loss effects on the temperature field are included when solving for $\widetilde{ h }$ through the wall boundary condition in the LES. In addition, the heat loss effects at the flamelet level are considered in the NAF case, where the normalised enthalpy is included in the table as an additional dimension to integrate the flamelet solutions under a range of heat loss conditions.

Table 2 Details of the heat loss effects considered in the simulated cases

The simulations are performed using OpenFOAM 2.3.0 and the PIMPLE algorithm is used for pressure-velocity coupling. Second-order central difference schemes are used for the velocity, where no blending factors are used. The use of blending factors causes the opening angle to be under predicted and this severely affects the structure of the IRZ (Chen et al. 2019b, c). Achieving numerical stability with purely second-order central difference schemes is difficult, owing to the presence of very small tetrahedral cells that are present near the exit of the fuel nozzle, since all 72 fuel injectors are included in the grid and the local velocity magnitudes are high. However, these cells are also not near the flame and this issue does not affect the flame’s structure, since the mixing field close to the fuel nozzle is resolved (Massey et al. 2019a). To ensure numerical stability, an implicit Euler scheme is used for time marching, but with a small time step of $\varDelta t = 0.15 \, \upmu {\mathrm {s}}$. This ensures the CFL number remains below 0.4 across the whole domain and ensures suitable accuracy for the time derivatives by avoiding numerical diffusion. The simulations were ran on ARCHER, a national high performance computing facility in the United Kingdom. The cases AD, NAW and NAF require around 80, 100, 60 respectively of physical time to allow initial transients to pass out of the domain. The time-averaged statistics are computed using samples collected over $24 \, \mathrm { ms }$ after the initial transient periods. This $24 \, \mathrm { ms }$ sample corresponds to approximately 6 flow through times.

4 Results

4.1 General Comparisons

Figure 7 shows typical time-averaged statistics comparisons between the three simulations and measurements for the Favre-filtered axial velocity and mixture fraction at different heights from the exit of the annular nozzle. The axial velocity and mixture fraction profiles are shown in Figs. 7a and 7b respectively. It is seen in Fig. 7a that all three simulations show the same variation in the near-field, with some under prediction in the peak axial velocity at $x = 5 \, \mathrm { mm }$ and $10 \, \mathrm { mm }$. Further downstream, cases AD and NAW show the same trend, whereas there is a small shift of the peaks away from the centreline for case NAF. This suggests that when the heat loss effects are included in the canonical model, i.e. premixed flamelets, the opening angle of the swirl flame becomes slightly larger due to weakened reaction rates in the inner shear layer, which is shown later in this section. The results at $x = 20 \, \mathrm { mm }$ and $30 \, \mathrm { mm }$ suggest that the width of the IRZ at this location is over predicted for all three cases. However, the velocity variation is captured well at $x = 60 \, \mathrm { mm }$ in the LES showing good agreement with the measurements. For the mixture fraction fields, all three simulations give similar predictions at all axial positions in Fig. 7b, suggesting that the overall mixing field is captured well in the LES regardless of the heat loss modelling. All three cases marginally over predict the mixture fraction at all streamwise locations. On the whole, the change in the modelling conditions for the three cases does not affect the axial velocity and mixture fraction fields.

Fig. 7

Comparisons of the time-averaged (a) axial velocity and (b) mixture fraction between the measurements (Meier et al. 2006; Weigand et al. 2006) (symbols) and the computations (lines), where the latter results are azimuthally averaged. The computations are cases AD (black curve), NAW (blue curve) and NAF (red curve)

The computed and measured temperature profiles are compared in Fig. 8a, b for the mean and resolved r.m.s. values respectively. For the near-field positions $x = 5 \, \mathrm { mm }$ and $10 \, \mathrm { mm }$ in Fig. 8a, the mean temperature is over predicted by $20 \, \%$ to $30 \, \%$ in case AD for large radial positions ($\vert y \vert > 20 \, \mathrm { mm }$) when approaching the wall, as adiabatic wall boundary conditions are imposed. The over predictions of the near-wall temperature for case AD are also seen in the r.m.s. temperature profiles in Fig. 8b. By contrast, the predictions given by NAW and NAF improve significantly in this region showing good agreement with the experimental data. This suggests that the temperature profiles specified on the combustion chamber dump plane and side walls are satisfactory. The temperature at $x = 5 \, \mathrm { mm }$ and $10 \, \mathrm { mm }$ along the centreline is under predicted by $13 \, \%$ and $4 \, \%$ respectively for case AD. However, significant decreases are seen in the centreline temperature at these two locations for cases NAW and NAF, due to the presence of non-adiabatic effects. This can also be seen in the r.m.s. profiles for cases NAW and NAF, as shown in Fig. 8b. This under prediction of the centreline temperature in the non-adiabatic cases NAW and NAF indicates an over predicted flame lift-off height. The lift-off height is based on the minimum height from the fuel injector exit where ${\widetilde{T}} = 1500 \, \mathrm { K }$ within a radius of $\vert y \vert < 10\; \mathrm { mm }$. In addition, the temperature in the jet regions in the near-field at $x = 5 \, \mathrm { mm }$ is under predicted for all three cases. Therefore, the inclusion of non-adiabatic conditions severely affects the flame root and its position, which dictates the overall stability and eventual blow-off behaviours of this flame (Stöhr et al. 2011). In the regions further downstream from $x = 20 \, \mathrm { mm }$, the profiles for all three cases are similar and hence, the non-adiabatic modelling only significantly affects the flame in the near-field around the flame root region.

Fig. 8

Comparisons of the time-averaged (a) mean and (b) r.m.s. temperature between the measurements (Meier et al. 2006; Weigand et al. 2006) (symbols) and the computations (lines), where the latter results are azimuthally averaged. The computations are cases AD (black curve), NAW (blue curve) and NAF (red curve)

Instantaneous snapshots of the filtered reaction rate of the progress variable for the three LES cases are shown in Fig. 9. It is shown in Fig. 9a that the flame appears to be thinner and more stable for case AD, whereas the reactions are distributed over a larger region for case NAW in Fig. 9b. In addition, the flames for these two cases have an established flame root with high values of the filtered reaction rate. Both of these observations are seen in the time-averaged fields in Fig. 10. The reaction rate values are higher in case NAW in comparison to case AD because the local mixture fractions for case NAW are slightly higher and closer to stoichiometry, specifically in the regions further away from the centreline at $\vert y \vert \approx 20 \, \mathrm { mm }$ (see Fig. 7b). However, the averaged field for case NAW shows that the flame stabilises on the wall of the annular air nozzle ($2 \, \mathrm { mm }$ below $x = 0$ in Fig. 10) and a different flame (‘M’ shape) is observed in comparison to the other two cases. This behaviour must be avoided because it provides an additional unphysical anchoring point for the flame, since the flame has a ‘V’ shape, as seen in the CH-PLIF image at the top of Fig. 10. Thus, the conditions used in the modelling approach for case NAW cannot be used for further investigation on flame blow-off behaviours, despite the improvements obtained for the temperature in the near-wall regions. The angles of the ‘V’ flame in the three cases are seen to be larger in comparison to the CH-PLIF image, as seen in Fig. 10. The angle of the flame that is marked in the CH-PLIF image is $\theta = { 44 }^{ \circ }$ and the angles are seen to be larger by $\varDelta \theta$ for the three simulations, as seen in the time-averaged fields in Fig. 10. For case AD, the angle increase is within ${ { 9.5 }^{ \circ }< \varDelta \theta < { 11 }^{ \circ } }$. The angle increase for case NAW is within ${ { 13.5 }^{ \circ }< \varDelta \theta < { 15 }^{ \circ } }$ and the increase for case NAF is within ${ { 17 }^{ \circ }< \varDelta \theta < { 20 }^{ \circ } }$. Thus, the inclusion of heat loss is seen to increase the opening angle of the flame. The upper and lower bounds of $\varDelta \theta$ change depending on the lower and upper bounds used for $\langle \overline{ { \dot{ \omega } }^{ * } } \rangle$. Care must be taken with such comparisons between the LES results and the CH-PLIF measurements, especially since the mixture fraction distribution also changes, as the concentration of CH for a given value of the reaction rate will vary. The instantaneous and time-averaged filtered reaction rates for case NAF, as seen in Figs. 9c and 10c respectively, show that there is a significant decrease in the local values of the reaction rate. This is caused by including the heat loss effects in the flamelet reaction rate in the canonical model, as shown earlier in Figs. 3 and 4 . The average reaction rate values at the flame root for this case are approximately $50 \, \%$ smaller than the values for the adiabatic flamelet cases, as well as along the inner shear layer. The time-averaged contour also shows that the flame root is at a higher position in comparison to cases AD and NAW.

Fig. 9

Filtered reaction rate fields for cases (a) AD, (b) NAW and (c) NAF in the x–y mid-plane

Fig. 10

Time- and azimuthally-averaged filtered reaction rate fields for cases (a) AD, (b) NAW and (c) NAF in the x–y mid-plane. The image above is the averaged CH-PLIF image (Weigand et al. 2006)

Scatter plots of the temperature against the mixture fraction are shown in Fig. 11 to observe the influence of heat loss in case NAF. The adiabatic equilibrium temperature ${ T }_{ \mathrm { ad } }^{ \mathrm { eq } }$ in mixture fraction space is also shown in each scatter plot. It should be noted that the results from the simulations, shown in Fig. 11a, b, are filtered and density weighted. The measurements, shown in Fig. 11c, are instantaneous and include the sub-grid contributions. This causes the peak computed values to be lower and are distributed over a broader mixture fraction range. The comparisons presented in Fig. 11 are at $x = 5 \mathrm { mm }$, which is close to the flame root region and where significant variations in the temperature and mixture fraction are seen, as shown in Figs. 7b and 8. The mixture fraction varies between 0 and 0.2, which suggests the methane–air mixtures are partially premixed. Three regions are considered, which are the IRZ ($0 \le \vert y \vert \le 2 \, \mathrm { mm }$), the inner shear layer ($4 \le \vert y \vert \le 6 \, \mathrm { mm }$) and the Outer Recirculation Zone (ORZ) region ($27 \le \vert y \vert \le 30 \, \mathrm { mm }$). The outer recirculation zone is considered, since this is the closest region to the wall where measurements are available.

Fig. 11

Scatter plots of the temperature against the mixture fraction at $x = 5\, \mathrm { mm }$. The filtered values for (a) case AD and (b) case NAF, and (c) the instantaneous Raman measurements (Meier et al. 2006) are all shown with the adiabatic equilibrium temperature ${ T }_{ \mathrm { ad } }^{ \mathrm { eq } }$

For the IRZ region, the temperatures are under predicted in both simulations in comparison to the measurements. This is due to strong sub-grid temperature fluctuations near the fuel injectors, which cannot be resolved by the LES grid. The temperatures are also under predicted for both simulations, since the reactant mixtures in the experiment are subjected to some preheating by the walls (Meier et al. 2006). There is some heat loss present with case NAF, as the peak temperature is approximately $1200 \, \mathrm { K }$, which is lower than the peak temperature of approximately $1550 \, \mathrm { K }$ in case AD. Within the inner shear layer, the peak temperature in case NAF is approximately $1300 \, \mathrm { K }$, which is lower than the peak temperature of approximately $1650 \, \mathrm { K }$. However, the temperature distributions with the mixture fraction are significantly different. The high temperature mixtures are predominantly fuel-rich in case AD, whereas the mixture fraction range in case NAF is not as broad and is similar to the experimental measurements in Fig. 11c. The ORZ region contains mixtures that are around the global mixture fraction of 0.031, which corresponds to ${ \phi }_{ \mathrm { glob } }$. It is shown for case AD that the temperatures of the methane–air mixtures follow the adiabatic equilibrium temperature curve. Case NAF shows there is some heat loss as the temperature is lower for mixtures around the global value, which is also seen in the measurements.

4.2 Lift-Off Height and Heat Release Rate

Case NAF is analysed and compared in more detail with case AD, in order to gain insights into the role of including heat loss on the stabilisation of the flame. The lift-off height variation over a period of $45 \, \mathrm { ms }$ is shown in Fig. 12 for cases AD and NAF. It is demonstrated that the lift-off height varies considerably across the sample, but only short lift-off events ($< 5 \, \mathrm { ms }$) can be seen in Fig. 12 for case NAF. A time series of the lift-off height in case AD is directly compared with case NAF. The average lift-off height in Fig. 12 is approximately $8.3 \, \mathrm { mm }$ for case NAF, which is $2.3 \, \mathrm { mm }$ higher than the experimentally observed value (Weigand et al. 2006). The mean lift-off height is significantly higher, since it is shown in Fig. 12 that the lift-off height reaches larger values beyond $10 \, \mathrm { mm }$ at least once every $5 \, \mathrm { ms }$. The histograms of the lift-off heights for the two cases in Fig. 12 are shown in Fig. 13a, b for cases AD and NAF respectively. It is shown that the lift-off height for case AD varies between 3–14 mm, whereas it ranges between 2.5–17 mm for case NAF. Moreover, it is seen in Fig. 13b that the bins in the range of 6–$11 \, \mathrm { mm }$ have a high number of counts, whereas the bins for the lift-off height in the range of 5–$9 \, \mathrm { mm }$ have a high number of counts for case AD. Therefore, the flame is more unstable when non-adiabatic effects are included, as the flame root position varies more across the time series in Fig. 12. This movement and frequent disappearance of the flame root is reported in the study by Stöhr et al. (2011).

Fig. 12

Time series of the lift-off height for cases AD (black curve) and NAF (red curve), where ${ t }_{ 0 } = 359 \, \mathrm { ms }$ and $84 \, \mathrm { ms }$ are respectively for cases AD and NAF

Fig. 13

Histograms of the lift-off height for the time series shown in Fig. 12 for cases (a) AD and (b) NAF

The variation of the volume integrated heat release rate is shown in Fig. 14 for cases AD and NAF. The heat release rate time series is seen to be periodic for both cases, as the heat release rate is coupled to the rotation of the PVC (Zhang and Mastorakos 2019). It is demonstrated in Fig. 12 that the lift-off height approaches high values between 10–15 and 25–$30 \, \mathrm { ms }$ for case NAF. In both of these intervals, the heat release rate decreases by approximately $4 \, \mathrm { kW }$. A similar decrease in case AD is not seen in Fig. 14. As with the lift-off height time series, the heat release rate varies considerably more for case NAF. This is also seen in the histograms, which are shown in Fig. 15. The histogram for case NAF in Fig. 15b shows that the volume integrated heat release rate is between 3.1–$8.4 \, \mathrm { kW }$, whereas the volume integrated heat release rate for case AD is between 5.4–$8.8 \, \mathrm { kW }$, as seen in Fig. 15a. There are also a large number of counts between 7–$7.4 \, \mathrm { kW }$ for case AD, which is close to the thermal power of $7.6 \, \mathrm { kW }$ that is stated by Weigand et al. (2006). The mean value for case NAF is approximately $5.5 \, \mathrm { kW }$, which is due to the reduced reaction rates that are seen in Figs. 9 and 10 that are within the flamelet table and therefore, this causes the thermal power to be reduced. It is of interest to determine how the heat loss through the enthalpy deficit in the look-up table varies when the structure of the flame changes. This is analysed next for when the flame has an established flame root and when it is as its maximum lift-off height in Fig. 12.

Fig. 14

Time series of the volume integrated heat release rate for cases AD (black curve) and NAF (red curve), where ${ t }_{ 0 } = 359 \, \mathrm { ms }$ and $84 \, \mathrm { ms }$ are respectively for cases AD and NAF

Fig. 15

Histograms of the volume integrated heat release rate for the time series shown in Fig. 14 for cases (a) AD and (b) NAF

4.3 Enthalpy Deficit Within the Flame

The instantaneous snapshot of the filtered reaction rate is shown in Fig. 16a, which is the same as the contour shown in Fig. 9c, where the flame has an established flame root. The normalised filtered enthalpy deficit $\varDelta { {\widetilde{h}} }^{ * }$ for the same instantaneous snapshot is shown in Fig. 16b. This is defined as

$$\begin{aligned} \varDelta { {\widetilde{h}} }^{ * } = {\widetilde{h}}^{ * } - 1 = \frac{ h - { h }_{ \mathrm { min } } ( \xi , c ) }{ { h }_{ \mathrm { ad } } ( \xi , c ) - { h }_{ \mathrm { min } } ( \xi , c ) } - 1 \, , \end{aligned}$$

(12)

where values of $\varDelta { {\widetilde{h}} }^{ * } = -1$ and $\varDelta { {\widetilde{h}} }^{ * } = 0$ signify maximum heat loss and adiabatic conditions respectively. It is shown that the enthalpy deficit is approximately $10 \, \%$ near the flame root, which corresponds to an approximate $25 \, \%$ decrease in the reaction rate and is due to the reduced heat release. Further downstream in the region of $y = -15 \, \mathrm { mm }$, it is seen in Fig. 16a that the reaction rate is small within a large coherent structure. Within this region, the enthalpy deficit is approximately $40 \, \%$, as seen in Fig. 16b. This suggests that the reaction that takes place within the vortex centres that are convected downstream along the shear layer are susceptible to heat loss. Significant enthalpy deficit regions ($30 \, \% \le \varDelta { {\widetilde{h}} }^{ * } \le 60 \, \%$) are also within the ORZ and near the walls, due to the lower temperature boundary conditions applied to the walls. At $x > 20 \, \mathrm { mm }$ and $y > 20 \, \mathrm { mm }$, higher reaction rate regions are present with enthalpy deficits of less than $10 \, \%$, as seen in Fig. 16.

Fig. 16

Instantaneous snapshots of the (a) filtered reaction rate (the same as Fig. 9c) and (b) normalised enthalpy deficit at an arbitrarily chosen time when the flame has an established flame root

The shape of the flame with an established flame root is compared to the flame when it is as its maximum observed lift-off height in Fig. 12. The instantaneous snapshots for the filtered reaction rate and enthalpy deficit are shown in Fig. 17a, b respectively. The filtered reaction rate values are significantly smaller in Fig. 17a than in Fig. 16a. It is shown that the enthalpy deficit is higher around the flame in Fig. 17b, where the highest value is approximately $60 \, \%$. Furthermore, it is seen that the leading edge of the high enthalpy deficit region at $x = 10 \, \mathrm { mm}$ on the left-hand side of Fig. 17b is within the flame. At this region, the reaction rate values in Fig. 17a are close to zero and therefore, the non-adiabatic flamelet model may account for some local extinction within the flame due to heat loss.

Fig. 17

Instantaneous snapshots of the (a) filtered reaction rate and (b) normalised enthalpy deficit when the lift-off height in Fig. 12 is at its maximum at $t = { t }_{ 0 } + 26.925 \, \mathrm { ms }$

Based on the observations in Figs. 16 and 17, it is suggested that the enthalpy deficit within the flame increases when the flame does not have an established flame root and when its lift-off height increases. Only the results in the x–y mid-plane are shown in Figs. 16 and 17 and therefore, the results are missing the full three-dimensional features of the flame. The histograms of the enthalpy deficit on planes normal to the streamwise direction are shown in Figs. 18 and 19 for the locations $x = 5 \, \mathrm { mm }$, $10 \, \mathrm { mm }$ and $20 \, \mathrm { mm }$, which correspond to Figs. 16 and 17 respectively. To ensure that the enthalpy deficit in the flame is investigated, only the enthalpy deficit in the regions with $\overline{ { \dot{ \omega } }^{ * } } > 5 \, \mathrm {kg/m}^{3}\,\hbox{s}$ is used to construct the histograms. When the flame has an established flame root, it is shown for all three locations in Fig. 18 that the enthalpy deficit is predominantly within $5 \, \%< \varDelta { {\widetilde{h}} }^{ * } < 10 \, \%$. However in the event when the lift-off height is high, the enthalpy deficit in the near-field region of $x = 5 \, \mathrm { mm }$ is within the range $15 \, \%< \varDelta { {\widetilde{h}} }^{ * } < 30 \, \%$, as seen in Fig. 19a. At $x = 10 \, \mathrm { mm }$, the enthalpy deficit decreases and is within the range $10 \, \%< \varDelta { {\widetilde{h}} }^{ * } < 20 \, \%$, as seen in Fig. 19b. This suggests that the flame is vulnerable to a high heat loss near where the flame root is expected to be when the flame experiences some lift-off. Further downstream at $x = 20 \, \mathrm { mm }$, the histogram in Fig. 19c is very similar to when then flame has a stable root, as seen in Fig. 18c, and the heat loss is less significant. Therefore, this analysis does comply with the initial observations made in Figs. 16 and 17 . Further analysis needs to be undertaken with a longer time sample and of a case where the complete blow-off of the flame is captured, in order to determine the role of heat loss with flame blow-off.

Fig. 18

Histograms of the normalised enthalpy deficit within the flame ($\overline{ { \dot{ \omega } }^{ * } } > 5 \, \mathrm {kg/m}^3\,\hbox {s}$) for the same time as Fig. 16 on planes normal to the streamwise direction at (a) $x = 5 \, \mathrm { mm }$, (b) $10 \, \mathrm { mm }$ and (c) $20 \, \mathrm { mm }$

Fig. 19

Histograms of the normalised enthalpy deficit within the flame ($\overline{ { \dot{ \omega } }^{ * } } > 5 \, \mathrm {kg/m}^3\,\hbox {s}$) for the same time as Fig. 17 on planes normal to the streamwise direction at (a) $x = 5 \, \mathrm { mm }$, (b) $10 \, \mathrm { mm }$ and (c) $20 \, \mathrm { mm }$

5 Conclusions

Two simulations of a flame that is close to lean blow-off with non-adiabatic modelling are studied, which are referred to as cases NAW and NAF. Both simulations use fixed wall temperature boundary conditions, but case NAF also includes non-adiabatic flamelets within the sub-grid combustion modelling. The combustion closure is based on unstrained flamelets with a presumed joint PDF approach based on the mixture fraction, progress variable and the normalised enthalpy, where the latter is included in the PDF to introduce the heat loss effects. The simulations are compared to the adiabatic simulation that is previously studied by Massey et al. (2019a), referred to as case AD, and the experimental data. The axial velocity and mixture fraction statistics are unaffected by the inclusion of heat loss, but some differences are seen in the temperature statistics comparisons. Cases NAW and NAF give improvements with the temperature in the near-wall regions, as case AD over predicts the temperature, due to the use of adiabatic walls. However, a change in flame shape is seen for case NAW, as the flame has an ‘M’ shape and differs from the observed ‘V’ shape flame in the experiment. In addition, cases NAW and NAF show under predictions in the average centreline temperature at the near-field and indicate that the flame root height is over predicted. It is also suggested that the heat loss effects are influential on the stabilisation of the flame by analysing the lift-off height and the volume integrated heat release rate time series in case NAF. The time series of the lift-off height and the volume integrated heat release rate show that the flame in case NAF is more dynamic in comparison to case AD. It is also suggested that the inclusion of non-adiabatic flamelets does affect the stabilisation of the flame. A higher enthalpy deficit is seen in the near-field regions when the flame root is not present and experiencing some lift-off, suggesting that the flame is more dynamic when including heat loss. Further investigation needs to be undertaken on the role of heat loss modelling in flames experiencing complete flame blow-off.