1 Introduction

The images to be fused may suffer from degradation factors such as noise and poor illumination [1,2,3,4]. There exist various fusion methods like pixel averaging, maximum value selection, weighted average, region energy, region variance, and so on [3,4,5,6,7,8,9]. The use of fractional calculus in fusion allows for more flexibility in optimizing fusion quality. In the form of fractional order derivatives, the theory of fractional calculus has been widely applied in different science and engineering disciplines [5,6,7,8,9,10,11,12]. Local feature representation and intermediate time-frequency representation capabilities were used in [13, 14] with a combination of Fractional Fourier transform (FRFT) and non-subsampled contourlet transforms (NSCT). The structural information of an image may be recovered and transferred into the fused image by minimizing the energy function [15]. Mathematically, the wavelet operation can execute a Fourier transform of the input function before multiplying it with different scaled Fourier transforms of the wavelet mother function [16].

In most fractional differentials, initial conditions are generally required in terms of fractional-order derivatives. This can be solved theoretically easily, but these real-time solutions are useless because there is no clear physical interpretation of such initial conditions in the fractional domain. On the other hand, the Caputo fractional derivative involves standard initial conditions regarding integer-order derivatives. These initial conditions are significant in real-time due to the integer order involved. In addition, Caputo fractional derivatives also needs nth order derivatives of the functions, and almost all functions fulfill this requirement. Therefore, Caputo fractional derivatives find are of great significance in real-time applications such as image processing.

In many situations, image processing requires both high spatial and high spectral information in a single image. As a result, researchers are required to improve the spatial and spectral content of images. This cannot be achieved using a single image. Therefore, fusion must be employed to integrate spatial and spectral information from different images. Imaging instruments may not be capable of providing such information either through design limitations or because of observational constraints. One possible solution for this is to use mathematical approaches to extract observational constraints in image fusion. In a visual sensor network (VSN), sensors are cameras that record images and video sequences. In such applications, a camera may not give a perfect rendition that includes all the necessary details of the scene at a time. This may be because of poor lighting during the night (underexposed image), exposure to sunlight (overexposed image), and/or limited depth of focus of the optical lenses of the cameras (multi-focus image). Image fusion techniques therefore gather all the important information from multiple images and incorporates them into a single image. In this paper, we have performed a fusion of overexposed and underexposed images.

Our technique involves incorporating discrete wavelets and fractional differential models to create the image fusion that is required to increase final image resolution. To preserve the edges of the enhanced fused image, a fractional differential-based intensification operator is used in the proposed method. The advantage of using the fractional differential is that it preserves low illumination features efficiently in smooth areas. The fractional differential also preserves high-illumination marginal features where grey levels evidently change. The fractional differential also improves texture details in places where the grey levels remain constant.

The work sequence and benefits are as follows: (i) The horizontal and vertical sub-bands of overexposed and underexposed images are separately enhanced using Caputo Differential Operator (CDO); image fusion is performed by taking the average of the transformed horizontal and vertical fractional derivatives. (ii) The input histogram is modified to reduce the extreme slopes in the transformation function. The large histogram values have been reduced using partial fractional derivatives corresponding to the uniform histogram regions. (iii) The initial conditions need not to be defined when the differential equations are solved using Caputo’s definition and can be easily defined for multiple spaces (i.e., one dimensional or two dimensional). (iv) The main emphasis has been placed upon the contrast intensification operator that is used to calculate the transformations. This is the major advantage of our proposed method over other methods. (v) We have employed two-dimensional fractional derivative-based transformation, which is not reported in the literature so far, and it is an efficient way to restore textural information. (vi) A favorable comparative evaluation with recent state-of-the-art methods and our proposed method is presented.

The remainder of the paper is laid out as follows: Section 2 lists the background and technical details of approaches like Discrete Wavelet Transform (DWT), Histogram Equalization (HE), and fractional order differential-based enhancement that we have employed.Our proposed technique is described in Section 3. Various performance measures are described in Section 4. The results and discussions are presented in Section 5. We present our conclusions in Section 6.

2 Background

Szeliski [17] developed a method to compute the histogram of an image generated from a set of multi-exposure images. By applying the Szeliski’s histogram equalization process, the average intensity of the image did not change, and DWT-based fusion was used [18]. DWT with histogram equalization is explained clearly in [19]. Histogram equalization is a process that increases image contrast and also compensates for the loss in contrast during intensity averaging. From the application perspective, image enhancement and smoothing also play an important role in the fuzzy frameworks [20,21,22].

2.1 Discrete wavelet transform (DWT)

Wavelets can be introduced in at least two different ways: the continuous wavelet transform and multiresolution analysis. In this study, the design strategy for the realistically applicable discrete wavelet transformations was multiscale approximation (DWT). Multiscale analysis can be thought of as a series of distinct coefficient approximations of a given function. More sub-signals and specific information at bigger sizes would also arise as the decomposition level rose. More data might help the model perform better, but it might also make the model less stable and less efficient at computation. As a result, choosing an appropriate decomposition level in DWT based on multiscale approximation is crucial. In this study, we select level 4 decomposition (\( \mathcal{j} \) denotes the decomposition level). The approximation level will be equal to the maximum level of decomposition for any level of wavelet decomposition. On the other hand, each level’s details coefficients must be taken into account, so in a level-n decomposition we will only use levels n approximation and each level’s details will be taken into account. Evidently, higher level decomposition is accountable for higher frequencies since it increases the amplitude of the signal in proportion to the level of decomposition.

In DWT the basic function are sets of scaling function and wavelet function [23]. We consider image Iij of size m × n such that i = 1, 2, 3…m and j = 1, 2, 3…n. The scaling function (L(x)) and wavelet function (W(x)) is represented as

$$ L(x)={2}^{\frac{\mathcal{j}}{2}}.L\left({2}^{\mathcal{j}}x-k\right), $$
(1)
$$ W(x)={2}^{\frac{\mathcal{j}}{2}}.W\left({2}^{\mathcal{j}}x-k\right). $$
(2)

\( \mathrm{where}\ \mathcal{j} \) is the scale and \( \mathcal{k} \) is used to shift the wavelet for the scaling factor. DWT decomposes a function f(x) into a coefficient with the scale \( \mathcal{j} \) and the shift \( \mathcal{k} \) such that the approximate coefficient is

$$ {A}_L\left(j,k\right)=\frac{1}{mn}{\sum}_{i=1}^m{\sum}_{j=1}^n{I}_{ij}L(x). $$
(3)

The detail coefficient is

$$ {D}_W\left(j,k\right)=\frac{1}{mn}{\sum}_{i=1}^m{\sum}_{j=1}^n{I}_{ij}W(x). $$
(4)

The IDWT is written as

$$ {I}_{ij}=\frac{1}{\sqrt{mn}}\sum {A}_L\left(j,k\right)L(x)+\frac{1}{\sqrt{mn}}\sum {D}_W\left(j,k\right)W(x). $$
(5)

The images are decomposed into wavelet coefficients using DWT. The fusion rule is used, resulting in the fusion of the coefficient sets. In order to improve the quality of the fused image in the spatial domain, the fused sets of coefficients are then subjected to inverse DWT (IDWT) to recover the image.

2.2 Histogram equalization based image enhancement

Histogram equalization is the most used technique to enhance low-contrast images. In histogram equalization, we first calculate the histogram of pixel contrasts [19]. Histogram values are represented by a column vector H. The probability function with contrast value k is given as \( p(k)=\frac{n(k)}{H} \). Here, n(k) is the number of pixels with contrast value k = 0, 1, 2…(L − 1). The cumulative distribution function (CDF) of the intensity probability function is given as \( c(k)={\sum}_{k=0}^Lp(k). \)Here, L is the maximum intensity value. When c(k) = 1 then the output fused image Sij is given by \( {S}_{ij}=\left(L-1\right){\sum}_{k=0}^Lp(k) \). Sij maps the contrast from input image to output image. In histogram equalization this mapping is obtained by multiplying the function c(k) with the maximum contrast value (L − 1) [24] such that the histogram value (h(k)) (becomes)

$$ h(k)=\left[\left(L-1\right)c(k)+0.5\right], $$
(6)
$$ h(k)-h\left(k-1\right)=\left(L-1\right)p(k),1\le k\le L-1. $$
(7)

The value of (L − 1) is 255.The HE method has various drawbacks. The first drawback is that when a histogram bin has a large value, then the mapping function exhibits an extreme slope. From Eq. (6), we observe that when h(k) has a large value then there are sharp transitions in Sij which degrades the quality of output image in terms of overstretching or introducing contour artifacts. The second problem with histogram equalization is that when the input image is dark, then HE transforms the low intensity level to a bright intensity level, which increases the noise component.

2.3 Fractional order derivatives

Fractional order derivatives have been proven to reduce noise in image fusion applications by restoring the detail and texture of images well [25]. In images, the gray level value of the pixels in neighbourhood are self-similar and correlated. A fractional order differential of any constant is a non-zero value. Thus, fractional order differentials intrinsically express texture and edge details well.

In [26] the authors proposed a novel variational model for image fusion. A bidirectional filter was used to preserve the edges of fused image. In order to overcome the visually ill effects of the super-resolution fusion model, the fractional order total variation (FOTV) regularization term is used to preserve the low-frequency contour features in the smooth areas so as to enhance texture details in the areas where gray-level doesn’t change significantly. In order to better control the variation model for image processing, gradient information had been used to fully exploit the fractional order total variation model. By foreseeing the advantage of the gradient information, we have used the gradient information in two folds i.e., in the form of the horizontal and vertical fields of a differential vector.

In [27], we propose a novel fractional-order based method by integrating spatial and spectral–spatial priors. The spatial fractional-order gradient feature (SFOG) maintains consistency between two fused images to efficiently transfer the information of the images to be fused. This paper does not seek to cover advanced image-feature representations, but the proposed method incorporates both fractional derivative-based edge and feature enhancement.

In [28], the difference between the resolutions of the fused images is calculated and fractional-order differentiation (FOD) is used to inject the spatial details into any one low resolution image. This means that only one of the fused images is enhanced with spatial details and that in such cases, if some details are missing, then the image may not be visually pleasing. In our proposed method we have used a resolution enhancement operator along with the CDO for both the overexposed and underexposed images to obtain a resolution enhanced image.

In [29] authors have proposed a fractional differential-based method to improve the visual effects in images. In this paper the high resolution and multi-spectral images are fused in such a way that fractional-order differential operators (FODO) and guided filters limit the spectral distortion and spatial information loss. But, under some evaluation conditions this method cannot obtain the best results due to deficiency in some of the medium-scale details. This can be improved by using multiscale analysis. Therefore, we propose a method which uses horizontal and vertical spaces for both overexposed and underexposed image.

In [30] authors have used the Savitzky-Golay differentiator (SGD) for image enhancement. In [31] authors have used a fractional order-based gradient (FG) for edge enhancement. In [32] authors have used sigmoid functions and fractional order differentials (SFFO) for edge information-based fusion only. The performance of differential order derivatives has significantly improved as compared to the conventional integer-based methods due to their capacity to induce non-linear enhancement of texture and edge details. These existing methods have several inherited problems for instance, the issue of over illumination arises for overexposed images and the limitation of enhancing only low contrast images or high contrast images. The calculation time for such algorithms is also too costly to implement; so far neither edge nor texture-based fusion using fractional order differential has been reported in the literature.

3 The proposed methodology

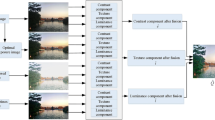
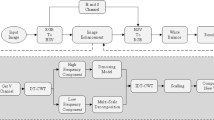
The act of combining the required information from two or more images into a single high-resolution fused image is known as image fusion. Images taken under improper or sub-optimal illumination conditions, may have their contrast enhanced using a contrast intensification operator (k). The illumination conditions may vary for the images to be fused [33]. Images recorded with inadequate lighting are referred as underexposed, whereas images captured with too much lighting are referred as overexposed. The proposed algorithm uses an intensification-based enhancement method to fuse the overexposed and underexposed images. The block diagram for the proposed algorithm is presented in Fig. 1.

Fig. 1
figure 1

Block diagram of the proposed method

Full size image

The underexposed and overexposed images are first decomposed using DWT, resulting in horizontal and vertical sub-bands within this proposed technique. Since these sub-bands contain ample structural information for the input images, the sub-bands are first enhanced using the CDO function and then fused using the average based fusion rule. Once the fused image is obtained after the CDO operation the overexposed and underexposed images, along with the fused image, are subjected to further resolution enhancement operations and a high-resolution image is obtained. We then employ texture enhancement to modify high and low intensity values in the resolution enhanced image, which yields the final image after these smoothing operations.

3.1 Caputo fractional order derivative for image fusion

Let Gij be a grey scale image, where i = 1, 2, …. m and j = 1, 2, …. n. The image Gij can be written as \( {G}_{ij}={\sum}_{k=1}^i{\sum}_{l=1}^j{G}_{kl} \). We can define its two finite operators for row and column gradients from the definition of the integral images [14,15,16]. The differential of the image with respect to two image planes, one horizontal (h) and other vertical (v) for image G is given as \( \frac{\partial^2G}{\partial h\partial v} \) which is obtained using DWT. Here, Gij is represented as a matrix [6, 7] such that

$$ \left[\begin{array}{cccc}{G}_{11}& {G}_{12}={G}_{11}+{G}_{12}& \dots & {G}_{1n}={\sum}_{j=1}^n{G}_{1j}\\ {}{G}_{21}={G}_{11}+{G}_{21}& {G}_{22}={\sum}_{i=1}^2{\sum}_{j=1}^2{G}_{ij}& \dots & {G}_{2n}={\sum}_{i=1}^2{\sum}_{j=1}^n{G}_{ij}\\ {}\dots & \dots & \dots & \dots \\ {}\dots & \dots & \dots & \dots \\ {}{G}_{m1}={\sum}_{i=1}^{\mathrm{m}}{G}_{i1}& {G}_{m2}={\sum}_{i=1}^m{\sum}_{j=1}^2{G}_{ij}& \dots & {G}_{mn}={\sum}_{i=1}^m{\sum}_{j=1}^n{G}_{ij}\end{array}\right]. $$
(8)

Now, the transformation of the partial derivatives is applied. We consider the gradient ∆G(h, v) in the vector field. In order to derive the fractional derivative and its transformation, the fractional derivatives w.r.t horizontal space and vertical space of image G is represented as \( {D}_h^{\alpha }G\left(h,v\right)\ and\ {D}_v^{\alpha }G\left(h,v\right), \) respectively [34]. Here, α is the order of the fractional derivative. The partial derivative of ∆G(h, v) is written as \( \Delta G\left(h,v\right)=\frac{\partial }{\partial h}G\left(h,v\right)+\frac{\partial }{\partial v}G\left(h,v\right). \)We consider G(h, v) as a function which can be expanded using the Taylor series such that \( \left(h,v\right)=\sum \limits_{n,m}{c}_{n,m}\frac{h^n{v}^m}{m!n!} \), where \( {c}_{n,m}=\frac{\partial^n{\partial}^mG\left(0,0\right)}{\partial {h}^n\partial {v}^m} \). Using Caputo Differential Operator (CDO), calculate the fractional derivative for image G. The CDO for the function f is defined in the dimensional space x (as)

$$ {D}_x^{\alpha }f(x)=\frac{1}{\Gamma \left(n-\alpha \right)}{\int}_0^x{x}^{n-\alpha -1}\frac{\partial^nf(x)}{\partial {x}^n} dx,\left(n-1\right)<\alpha <n, $$
(9a)
$$ {D}_x^{\alpha }f(x)=\frac{\partial^nf(x)}{\partial {x}^n},\alpha =n, $$
(9b)

where Γ(.) is the gamma function.

Algorithm 1 presents the steps of proposed algorithm for computing fractional derivatives and fused image Sij.

Lemma

The CDO based fractional derivative\( \left({D}_x^{\alpha }{x}^p\right) \) of a polynomial function xp is expressed as

$$ {D}_x^{\alpha }{x}^p={\displaystyle \begin{array}{c}\frac{\Gamma \left(p+1\right)}{\Gamma \left(p-\alpha +1\right)}{x}^{p-\alpha },0<\alpha <1,p>0\\ {}0,0<\alpha <1,p=0\end{array}} $$
(10)

The value of polynomial function is zero when the degree is zero i.e., p = 0.

The input image has two spaces, h and v. So, we can derive the two-dimensional CDO based fractional derivative as

$$ {D}_h^{\alpha }G\left(h,v\right)={\sum}_{n,m}{c}_{n,m}\frac{h^{n-\alpha }{v}^m}{n!m!}.\frac{\Gamma \left(n+1\right)}{\Gamma \left(n-\alpha +1\right)} $$
(11a)
$$ {D}_{\mathrm{v}}^{\alpha }G\left(h,v\right)={\sum}_{n,m}{c}_{n,m}\frac{h^{n-\alpha }}{m!}.\frac{v^m}{\Gamma \left(n-\alpha +1\right)}. $$
(11b)

Using the contrast operator (k), the transformed horizontal space (h′) and vertical space (v′) can be written as h′ = h + ∂kv and v′ = v − ∂kh, such that G′(h′, v′)maps to G(h, v). This operator is useful to keep the edge information intact. The transformed fractional order\( \left({\alpha}_{n,m}^{\prime}\right) \) is given as, \( {\alpha}_{n,m}^{\prime }={c}_{n,m}+\partial k\left[n{c}_{n-1,m+1}-m{c}_{n+1,m-1}\right]\forall n,m \) [6, 7]. The transformed partial derivatives are written as

$$ \frac{\partial }{\partial {h}^{\prime }}{G}^{\prime \left({h}^{\prime },{v}^{\prime}\right)}=\frac{\partial }{\partial h}G\left(h,v\right)+\partial k\frac{\partial }{\partial v}G\left(h,v\right), $$
(12a)
$$ \frac{\partial }{\partial {v}^{\prime }}{G}^{\prime}\left({h}^{\prime },{v}^{\prime}\right)=\frac{\partial }{\partial v}G\left(h,v\right)-\partial k\frac{\partial }{\partial h}G\left(h,v\right). $$
(12b)

By using Binomial expansion, the transformed horizontal space (h′(n − α)) and vertical space (v′m) can be written as

$$ {h^{\prime}}^{\left(n-\alpha \right)}={\left(h+\partial kv\right)}^{n-\alpha}\approx {h}^{n-\alpha }+\left(n-\alpha \right)\partial k{h}^{n-\alpha -1}v, $$
(13a)
$$ {v^{\prime}}^m={\left(v-\partial kh\right)}^m\approx {v}^m-m\ \partial kh{v}^{m-1}. $$
(13b)

Therefore, transformed partial derivative for \( G\ \left({D}_{h^{\prime}}^{\alpha }{G}^{\prime \left({h}^{\prime },{v}^{\prime}\right)}\right) \) is written as

$$ {D}_{h^{\prime}}^{\alpha }{G}^{\prime \left({h}^{\prime },{v}^{\prime}\right)}={\sum}_{n\ge 1,m}{c}_{n,m}^{\prime}\frac{{h^{\prime}}^{n-\alpha }}{m!}.\frac{{v^{\prime}}^m}{\Gamma \left(n-\alpha +1\right)}. $$
(14)

Substituting Eqs. (13a) and (13b) into Eq. 14, we have

$$ {D}_{h^{\prime}}^{\alpha }G\left({h}^{\prime },{v}^{\prime}\right)={\sum}_{n\ge 1,m}\frac{1}{m!\Gamma \left(\mathrm{n}-\alpha +1\right)}\left[{c}_{n,m}+\partial kn{c}_{n-1,m+1}-\partial km{c}_{n+1,m-1}\right].\left[{h}^{n-\alpha }{v}^m+\left(n-\alpha \right)\partial k{h}^{n-\alpha -1}{v}^{m+1}-m\ \partial k{h}^{n-\alpha +1}{v}^{m-1}\right]. $$
(15)

After simplifying Eq. (15), we have

$$ {D}_{h^{\prime}}^{\alpha }G\left({h}^{\prime },{v}^{\prime}\right)={D}_h^{\alpha }G\left(h,v\right)+\alpha \partial k{\sum}_{n,m}\frac{1}{m!\Gamma \left(n-\alpha +1\right)}{c}_{n-1,m+1}{h}^{n-\alpha }{v}^m. $$
(16)

The last term of Eq. (16) is written as \( {D}_v^{\prime }G\left(h,v\right)\frac{\partial G\left(h,v\right)}{\partial v},{Z}_h^{\prime }G\left(h,v\right)={\int}_0^hG\left(h,v\right) dh \).

Now, Eq. (16) can be rewritten as

$$ {D}_{h^{\prime}}^{\alpha }{G}^{\prime \left({h}^{\prime },{v}^{\prime}\right)}={D}_h^{\alpha }G\left(h,v\right)+v\partial k{D}_h^{\alpha }{Z}_h^{\prime }{D}_v^{\prime }G\left(h,v\right), $$
(17a)
$$ {D}_{v^{\prime}}^{\alpha }{G}^{\prime \left({h}^{\prime },{v}^{\prime}\right)}={D}_v^{\alpha }G\left(h,v\right)-v\partial k{D}_v^{\alpha }{Z}_v^{\prime }{D}_h^{\prime }G\left(h,v\right). $$
(17b)

Now fuse two images X and Y, where X = [Xij] and Y = [Yij]. We have assumed image X to be the overexposed image and Y to be the underexposed image. Firstly, we calculate their transformed horizontal and vertical fractional derivatives as, \( {D}_{h\prime}^{\alpha }{X}^{\prime}\left({h}^{\prime },{v}^{\prime}\right),{D}_{v\prime}^{\alpha }{X}^{\prime}\left({h}^{\prime },{v}^{\prime}\right) \) and \( {D}_{h\prime}^{\alpha }{Y}^{\prime}\left({h}^{\prime },{v}^{\prime}\right),{D}_{v\prime}^{\alpha }{Y}^{\prime}\left({h}^{\prime },{v}^{\prime}\right) \) respectively. We fuse X and Y to produce final fused image S using average based fusion rule as

$$ {D}_{h\prime}^{\alpha }S\left({h}^{\prime },{v}^{\prime}\right)=\frac{D_{h\prime}^{\alpha }{X}^{\prime}\left({h}^{\prime },{v}^{\prime}\right)+{D}_{h\prime}^{\alpha }{Y}^{\prime}\left({h}^{\prime },{v}^{\prime}\right)}{2}, $$
(18a)
$$ {D}_{v\prime}^{\alpha }S\left({h}^{\prime },{v}^{\prime}\right)=\frac{D_{v\prime}^{\alpha }{X}^{\prime}\left({h}^{\prime },{v}^{\prime}\right)+{D}_{v\prime}^{\alpha }{Y}^{\prime}\left({h}^{\prime },{v}^{\prime}\right)}{2}. $$
(18b)

Now, the inverse DWT operation is performed, and the final fused image Sij is computed as

$$ {S}_{ij}={\sum}_{k=1}^i{\sum}_{l=1}^j\left[{D}_{h\prime}^{\alpha }{S}_{kl}\left({h}^{\prime },{v}^{\prime}\right)+{D}_{v\prime}^{\alpha }{S}_{kl}\left({h}^{\prime },{v}^{\prime}\right)\right]. $$
(19)

We have presented the qualitative results for Caputo enhanced overexposed, Caputo enhanced underexposed image and the fused image (Sij) in later sections. Below the example is presented for Algorithm 1.

Algorithm 1
figure i

Proposed algorithm for computing fractional derivatives and fused image

Full size image

3.1.1 Example for transformed partial derivate (underexposed image)

3.1.2 Example for transformed partial derivate (overexposed image)

3.1.3 Example for final fused image

(Average based fusion of Transformed partial derivate (underexposed image)

and transformed partial derivate (underexposed image)).

3.2 Resolution enhancement

In order to remove the edge and saturation-based artifacts in horizontal and vertical sub-band regions we incorporated resolution-based enhancement. The image is decomposed into horizontal and vertical levels using CDO with multiple brightness levels to which we apply resolution level-based transformation. For the low frequency component, we estimate the dominant brightness level in the corresponding sub-band [35, 36]. The high frequency components are dominant in the bright regions. The overexposed and underexposed images have varying intensity distributions. We have chosen a tuning parameter for overexposed and underexposed images. This resolution level-based enhancement is applied to these two images. Algorithm 2 details the steps we take to effect the resolution enhancement process.

Generally, pixel resolution is computed using image size and dividing by 1 million. For example: we have taken four image sizes i.e., 128, 256, 512, 1024. We can compute the resolution level control parameter as follows. Let us say image dimension is 128 × 128. Its pixel resolution is computed as 128 * 128 = 16,384 bytes. Dividing it by 1 million = 0.016384 M pixel (approximately), which can be considered as μh(i, j). Consider a gray scale image to have a total 0 to 255 Gy levels. We obtain value of μ by solving the equation below from Section 3.2. Let us consider that, for the overexposed image,

$$ {\displaystyle \begin{array}{c}{\mu}_X\left(i,j\right)=\exp \left(\frac{1}{N}\sum \limits_{\forall i,j}\left\{\log \left({\mu}_h\left(i,j\right)-k\left({\mu}_h\left(i,j\right)-{m}_h\right)\right)+\varepsilon \right\}\right)\\ {}{\mu}_X\left(i,j\right)=\exp \left(|\frac{1}{255}\sum \limits_{\forall \mathrm{255,255}}\left\{\log \left(0.016-0.5\left(0.016-0.016\right)\right)\right\}|\right)\\ {}{\mu}_X\left(i,j\right)=\mathit{\exp}\left(|-1.78|\right)=5.92\end{array}} $$

Thus, we have chosen the optimum value of μ to be 5 for our experiments.

The resolution level at every pixel space (μX(i, j)) for the overexposed image is computed as \( {\mu}_X\left(i,j\right)=\exp \left(\frac{1}{N}\sum \limits_{\forall i,j}\left\{\log \left({\mu}_h\left(i,j\right)-k\left({\mu}_h\left(i,j\right)-{m}_h\right)\right)+\varepsilon \right\}\right) \). μh(i, j) is the high resolution level value, k is the contrast parameter and mh is the mean high resolution value. The resolution level for the underexposed image at every pixel space (μY(i, j)) is computed as \( {\mu}_Y\left(i,j\right)=\exp \left(\frac{1}{N}\sum \limits_{\forall i,j}\left\{\log \left({\mu}_l\left(i,j\right)-k\left({\mu}_l\left(i,j\right)-{m}_l\right)\right)+\varepsilon \right\}\right) \). μl(i, j) is the low resolution level value, k is the contrast parameter and ml is the mean low resolution value. μl(i, j) and μh(i, j) indicate the resolution level control parameters. Based on the value of maximum decomposition level from \( {2}^{\mathcal{j}} \), we used \( \mathcal{j}=4 \). Therefore \( {2}^{\mathcal{j}}=16 \). So have chosen this resolution level control parameter between 0 to 15. The need of lower value of resolution control parameter indicates that the inbuild resolution of image is better (i.e. over exposed images). The need of higher value of resolution control parameter indicates that the inbuild resolution of image is poor (i.e. underexposed images). However, we can use different values for resolution control based on decomposition level and intensity of image pixels. The values are chosen as 10 ≥ μh(i, j) > 0 and 15 ≥ μl(i, j) > 10. N is the total number of pixels in the image. ε is a small constant that prevents the log function from attaining values approaching infinity. The μl(i, j) and μh(i, j) elements give the low and high bounds of intensity levels. The resolution enhanced image \( \left({S}_{ij}^{\mu}\right) \) (becomes)

$$ {S}_{ij}^{\mu }={\sum}_{k=1}^i{\sum}_{l=1}^j{\left({\left[{\mu}_X\left(k,l\right)\right]}^T\left[{\mu}_X\left(k,l\right)\right]\right)}^{-1}\times {\sum}_{k=1}^i{\sum}_{l=1}^j\left({\left[{\mu}_X\left(k,l\right)\right]}^T\left[{\mu}_Y\left(k,l\right)\right].{S}_{ij}\right). $$
(20)
Algorithm 2
figure j

Proposed algorithm for resolution enhancement

Full size image

3.3 Smoothing (texture enhancement)

In order to preserve the image details in low and high frequency layers we perform texture enhancement as well. Algorithm 3 details the steps for proposed texture enhancement. The texture enhancement function is based on the gamma function [37, 38] and is specified as \( T(L)={\left(\frac{L}{M_k}\right)}^{\frac{1}{\lambda }}+1 \), k = {l, h}. M is the size of each section of intensity range. Ml is the low intensity value and Mh is the high intensity value. L is the intensity value and λ is the texture adjustment component. λ is adjusted to preserve the image texture. As λ increases the resultant image becomes more saturated. The maximum value of λ is selected by computing the maximum value of the T(L) function. The range is given as {0 ≤ L ≤ Ml} and {Ml ≤ L ≤ Mh}. Thus, we have two transformed layers which are fused together to generate an enhanced image. We use a minimizing function for gradients and variations in intensity levels in corresponding horizontal and vertical details. The smoothing function ψ is represented in the form of a Lagrange multiplier and gradient (∇) (as)

$$ \psi =\int \left|\nabla \right|+{\lambda}^{-1}{\left\Vert G\right\Vert}_{L^1}d\Omega . $$
(21)

Here Ω is image domain. \( {\left\Vert .\right\Vert}_{L^1} \) is L1 norm. λ is the Lagrange multiplier [39]. The final image after smoothing is written as ψij in the form of horizontal and vertical components as

$$ {\psi}_{ij}=\left|{\nabla}_h+{\nabla}_v\right|+{\lambda}^{-1}{\left\Vert {S}_{ij}^{\mu}\left(h,v\right)-h-v\right\Vert}_{L^1}. $$
(22)

The solution of Eq. (22) is found by the Euler Lagrange operation as

$$ {\psi}_{ij}=\int \int {S}_{ij}^{\mu } dhdv. $$
(23a)

ψij is written in the form of the following variation

$$ {\psi}_{ij}=\frac{\delta \psi}{\delta v}+\frac{\delta \psi}{\delta h}-\frac{\delta }{\delta v}\frac{\delta \psi}{\delta h}-\frac{\delta }{\delta h}\frac{\delta \psi}{\delta v}. $$
(23b)

In terms of partial derivatives, the first order Hamilton-Jacobi equation [39] is solved using the steepest gradient as

$$ {\nabla}_h=\frac{\delta \psi}{\delta h}=\frac{\delta }{\delta h}\left(\frac{k{S}_{ij}^{\mu}\left(h,v\right)}{{\left(X{\left(h,v\right)}^2+Y{\left(h,v\right)}^2\right)}^{\frac{1}{2}}}\right)+\frac{\delta }{\delta h}\left(\frac{k{S}_{ij}^{\mu}\left(h,v\right)}{{\left(X{\left(h,v\right)}^2+Y{\left(h,v\right)}^2\right)}^{\frac{1}{2}}}\right).\lambda \frac{S_{ij}^{\mu }-\psi }{\left|{S}_{ij}^{\mu }-\psi \right|}, $$
(24a)
$$ {\nabla}_v=\frac{\delta \psi}{\delta v}=\frac{\delta }{\delta v}\left(\frac{kX\left(h,v\right)}{S_{ij}^{\mu}\left(h,v\right)}\right)+\frac{\delta }{\delta v}\left(\frac{kY\left(h,v\right)}{S_{ij}^{\mu}\left(h,v\right)}\right).\lambda \frac{S_{ij}^{\mu }-\psi }{\left|{S}_{ij}^{\mu }-\psi \right|}. $$
(24b)

Here, λ is the Lagrange multiplier which is inversely proportional to the intensity of the smoothing process. In our experiments, we have used λ = [0, 1] which is defined by heterogeneous local distribution. We intend to identify the extreme intensity values and low intensity values with neighborhood.

Algorithm 3
figure k

Proposed algorithm for texture enhancement

Full size image

3.4 Computation of histogram values

We use a logarithmic function that reduces large values effectively whilst preserving the image details. The histogram value h(k) is transformed to a modified histogram value as m(k) using the logarithmic function. Mathematically,

\( m(k)=\frac{\log \left(h(k).{h}_{max}(k).{10}^{-\mu }+1\right)}{\log \left({h}_{max}^2(k).{10}^{-\mu }+1\right)}. \)Here, h(k) is a histogram value at contrast k. hmax(k) is the maximum value of the histogram bin. μ is the resolution level control parameter for the histogram. As the value of μ increases then the value h(k). hmax(k). 10−μ decreases, which makes m(k) linearly proportional to hk. When μ decreases, the value hmax(k). 10−μ becomes dominant and can be written as

$$ \log \left(h(k).{h}_{max}(k).{10}^{-\mu }+1\right)\approx \log \left(h(k)\right)+\log \left({h}_{max}(k).{10}^{-\mu}\right)\approx \log \left({h}_{max}(k).{10}^{-\mu}\right). $$

When μ = 5, the output image has fewer artifacts on the image as observed by an objective assessment of the quantitative results.

4 Performance measures

Various quantitative measures such as entropy, standard deviation, fusion factor, fusion symmetry, peak signal to noise ratio, and luminance distortion are used for objective assessment of different methods of image enhancement [40,41,42]. Entropy is a performance metric that calculates the information content of an image, and is mathematically defined for the output fused image S (as)

$$ E(S)={\sum}_{i=0}^{L-1}{p}_S(i){\mathit{\log}}_2{p}_S(i), $$
(25)

where L is the number of grey levels, pS(i) = nL/i, is the ratio between the number of pixels with grey values (nL), and the total number of pixels (i). The term pS(i) is the probability of pixel intensity computed for an output fused image. Mathematically, an image with a high entropy holds a vast amount of information. The standard deviation (SD) of such an image is defined as

$$ SD={\left\{\frac{1}{m\times n}{\sum}_{i=1}^m{\sum}_{j=1}^n{\left({S}_{ij}-\mathcal{m}\right)}^2\right\}}^{\frac{1}{2}}, $$
(26)

where \( \mathcal{m} \)represents the mean value of the image. The standard deviation value is high for a high-quality fused image.

The amount of edge information transmitted from the input picture to the fused image is measured by edge strength (ES). Mathematically,

$$ ES=\frac{\sum_{i=1}^m{\sum}_{j=1}^n\left[{D}_{h^{\prime}}^{\alpha }{S}_{ij}{h^{\prime}}^{\left(n-\alpha \right)}+{D}_{v^{\prime}}^{\alpha }{S}_{ij}{v^{\prime}}^m\right]}{\sum_{i=1}^m{\sum}_{j=1}^n\left[{h}^{\prime}\left(i,j\right)+{v}^{\prime}\left(i,j\right)\right]}, $$
(27)

where h′(n − α) and v′m are the horizontal and vertical space weights assigned to Xij and Yij (respectively)

Fusion Factor (FF) is a performance measure that calculates the amount of mutual information between the input image and the fused image. Mathematically,

$$ FF={MI}_{u,S}+{MI}_{o,S}, $$
(28)

where MIu, Srepresents mutual information between the underexposed image and the fused image, and MIo, S represents mutual information between the overexposed image and the fused image.

$$ {MI}_{o,S}=E(u)+E(S)-E\left(u,S\right), $$
(29a)
$$ {MI}_{o,F}=E(o)+E(S)-E\left(o,S\right). $$
(29b)

Here, E(u), E(o) represent the entropy of underexposed and overexposed images, respectively, E(S) is the entropy of the fused image, and E(u, S), E(o, S) is the joint entropy of the underexposed and overexposed images w.r.t. the fused image.

Fusion Symmetry (FS) represents the symmetrical balance of the fusion process and compares the underexposed and overexposed images. Mathematically,

$$ FS=\left|\frac{MI_{u,S}-{MI}_{o,S}}{2\left({MI}_{u,S}+{MI}_{o,S}\right)}\right|.\kern0.5em $$
(30)

Peak signal to noise ratio is calculated for the overexposed images (PSNRover) and underexposed images (PSNRunder) with respect to the output fused image as

$$ PSN{R}_{over}=20{\mathit{\log}}_{10}\left(\frac{L^2}{\frac{1}{mn}{\sum}_{i=1}^m{\sum}_{j=1}^{\mathrm{n}}{\left({X}_{ij}-{S}_{ij}\right)}^2}\right), $$
(31a)
$$ PSN{R}_{under}=20{\mathit{\log}}_{10}\left(\frac{L^2}{\frac{1}{mn}{\sum}_{i=1}^m{\sum}_{j=1}^n{\left({Y}_{ij}-{S}_{ij}\right)}^2}\right), $$
(31b)

Overall PSNR is calculated as,

$$ PSNR=\frac{PSN{R}_{over}+ PSN{R}_{under}}{2} $$
(32)

When the fused and reference images are similar then the PSNR value will be high. A higher value of PSNR implies better fusion.

Luminance distortion \( \left(\mathcal{L}\right) \) measures the closeness between the mean luminance of overexposed and underexposed images [43]. It is used to evaluate the mean brightness in an image that has been introduced by the enhancement method. It is expressed as

$$ \mathcal{L}=\frac{2{\mu}_o{\mu}_u}{\mu_o^2+{\mu}_u^2}. $$
(33)

where μo and μu are the mean luminance values of the overexposed and underexposed images, respectively and \( \mathcal{L} \) is in the range [0, 1]. When \( \mathcal{L}\to 1, \) then images have the same luminance, which indicates that the change in mean image brightness becomes small.

Measurement of enhancement (ME) measures overall enhancement in the fused image [44]. Since images have spatially varying intensity distributions, we estimate the optimal brightness range using minimum and maximum histogram bin values. Mathematically

$$ ME=\frac{1}{mn}{\sum}_{j=1}^n{\sum}_{i=1}^m{S}_{ij}\frac{h_{max}(k)}{h_{min}(k)+\mathcal{a}}\ln \frac{h_{max}(k)}{h_{min}(k)+\mathcal{a}}. $$
(34)

Here,\( \mathcal{a} \) is a small non-zero positive constant to avoid division by 0. We have assumed that \( \mathcal{a}=0.0001 \) [44].

The contrast feature value is computed by using the joint probability of an occurrence matrix [43] for an image. Mathematically

$$ \mathcal{C}={\sum}_{i=1}^m{\sum}_{j=1}^n{\left(i-j\right)}^2{F}_{norm}^{\prime}\left(i,j\right). $$
(35)

The joint probability of occurrence differs between pixels with a gray value around n and those with gray values around m. The normalized invariant co-occurrence function is written as

$$ {F}_{norm}^{\prime}\left(i,j\right)=\mathit{\max}\left(0,\mathit{\max}\left(0,1-\frac{\left|I\left(x,y\right)-m\right|}{5}\right)-\frac{\left|\left(I\left(x,y\right)\pm 5\right)-n\right|}{5}\right). $$
(36)

5 Numerical results and discussions

This paper uses images as the basis for our experiments which are drawn on the gray image datasets available at https://ccia.ugr.es/cvg/CG/base.htm and https://sipi.usc.edu/database/database.php?volume=misc&image=26 (Weblink: https://ccia.ugr.es/cvg/CG/base.htm), (Weblink: https://sipi.usc.edu/database/database.php?volume=misc&image=26).

We have compared our proposed method with other methods i.e., FOTV [26], SFOG [27], FOD [28], FODO [29], SGD [30], FG [31], and SFFO [32]. The performance of our proposed method was analyzed in terms of its subjective and objective results. Figures 2 and 3 show the underexposed and overexposed input images, respectively. Figure 4 shows the qualitative result using the proposed method for the selected pixel space shown in the red box in the horizontal and vertical direction for input images. Figure 4 also tabulates the corresponding histogram plots for input images using the proposed method (μ = 5, λ = 0.2, c(k) = 0.5) i.e., Caputo enhanced underexposed image; Caputo enhanced underexposed image; Caputo enhanced fused image (Sij); Resolution enhanced image (\( {S}_{ij}^{\mu}\Big) \); Texture enhanced image, and Final image (ψij). The corresponding histograms show that the intermediate stages of the proposed method support visual enhancement of the final image.

Fig. 2
figure 2

Underexposed image sets for input

Full size image
Fig. 3
figure 3

Overexposed image sets for input

Full size image
Fig. 4
figure 4figure 4figure 4figure 4

Qualitative comparison and corresponding histogram plots using proposed method (μ = 5, λ = 0.2, c(k) = 0.5) [Caputo enhanced underexposed image , Caputo enhanced underexposed image, Caputo enhanced fused image (Sij), Resolution enhanced image (\( {S}_{ij}^{\mu}\Big) \), Texture enhanced image, and Final image (ψij)]

Full size image

The quantitative numerical results analyze the performance of the proposed method as compared to other state of the art methods i.e., FOTV [26], SFOG [27], FOD [28], FODO [29], SGD [30], FG [31], and SFFO [32]. The visual quality of the fused image is better, and it contains clearer details. We chose DWT as the first step in the proposed technique because it improves perceived image quality by increasing directional information while introducing no blocking artifacts. Table 1 compares various stages of the proposed algorithm in terms of histogram values with respect to μ, λ. The most balanced values of the histogram are obtained at μ = 5. Using m(k) validated that for values of μ < 5 or μ > 5 the image has more effects towards reducing the artifacts. It was observed that as λ increases, the strength index of the texture decreases. It was observed from Table 1 that the optimum value of μ = 5 and λ = 0.2 was selected to achieve the most visually pleasing results. Table 2 Presents a comparison between the various methods in terms of histogram values for various fractional orders i.e., α = 0.3, 0.5, 0.9,and 1. We observed from Table 2 that at α = 0.5 the proposed method gives more useful results compared to other methods. Therefore, we chose μ = 5, λ = 0.2,and α = 0.5 as input parameter settings for the proposed method in Tables 3, 4 and 5.

Table 1 Comparison among various stages of proposed algorithm in terms of histogram values
Full size table
Table 2 Comparison among various methods in terms of histogram values for various fractional orders
Full size table
Table 3 Comparison among various methods for different performance measures at c(k) = 0.3 in proposed method
Full size table
Table 4 Comparison among various methods for different performance measures at c(k) = 0.5 in proposed method
Full size table
Table 5 Comparison among various methods for different performance measures at c(k) = 0.9 in proposed method
Full size table

Tables 3, 4, and 5 show a comparison among various methods for different performance measures (average values), such as Entropy (Eq. 25), Standard Deviation (Eq. 26), Edge Strength (Eq. 27), Fusion Factor (Eq. 28) Fusion Symmetry (Eq. 30), PSNR (Eq. 32), Luminance Distortion (Eq. 33) and Computational Time at c(k) = 0.3,0.5, and 0.9 (for proposed method only) respectively.

The average information in an image is measured using entropy. When the grey levels of the image have the same frequency, the value of entropy is maximal. In other words, when the grey levels have the same frequency, the entropy value is higher. The performance results demonstrate that the proposed algorithm produces higher entropy levels than the other methods. The standard deviation of the contrast in the fused image is compared (SD). The SD is more efficient in the absence of noise since the standard deviation is larger when the image has high contrast. The proposed method’s edge strength (ES) is greater than existing approaches, resulting in better image quality. If the image’s information content is higher, the FF value will be higher. The symmetry of the fused image as related to the input image is referred to as fusion symmetry. The value of fusion symmetry (FS) should be as low as feasible for a better-quality fused image. Using our proposed technique, the PSNR value is also enhanced. The suggested approach decreases luminance distortion. Although the proposed method takes longer to compute than other state-of-the-art methods, it outperforms those other state-of-the-art methods on significant performance measures.

Figure 5 plots values for the computed enhancement measurements (Eq. 34) for various fractional orders. Figure 6 plots the contrast feature values (Eq. 35) for different fractional orders. We observe that when the fractional-order α = 0.5, the enhancement value is optimal, and the same is true for contrast feature values. We have computed the contrast feature value at different image sizes i.e., m, n = 128,256,512,and 1024. The best feature contrast is obtained for larger values of m and n. Therefore, by choosing the optimum value of fractional order, the image quality can be considerably improved. From the plotted values of various performance measures, we concluded that the proposed algorithm produces significantly superior fusion results when compared to the other methods.

Fig. 5
figure 5

Computed values for the enhancement measurements for various fractional orders using proposed method

Full size image
Fig. 6
figure 6

Computed value of contrast feature for different fractional orders using proposed method

Full size image

6 Conclusion

Overexposed or underexposed images require different analytical techniques to mine their informational potential value. Therefore, images captured in various lighting conditions require enhancement, which we present in the proposed method. The experimental findings demonstrate that employing the proposed image fusion approach enhances image fusion quality. This proposed method uses a CDO, intensifying the contrast and edge strength of the overexposed and underexposed images. The proposed method also employs resolution and texture enhancement, demonstrating that the final image has improved salient visual information and has significantly improved texture and contrast components. Compared to existing state-of-the-art approaches, the quality of the final image created by the suggested method is aesthetically superior. The proposed method also outperforms the other methods of objective image quality metrics. In addition, the way in which our method uses a CD operator to preserve the edge and texture details of an image makes it highly effective as a denoising technique, which could be explored in medical image processing applications. The presence of noise makes the images unclear to identify and analyze. Hence, denoising of medical images is an essential pre-processing technique for further medical image processing stages.