Abstract
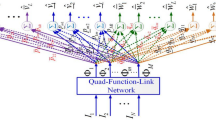
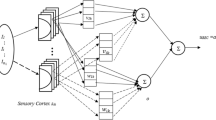
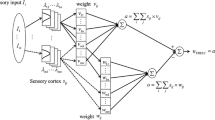
This study aims to propose a more efficient hybrid algorithm to achieve favorable control performance for uncertain nonlinear systems. The proposed algorithm comprises a dual function-link network-based multilayer wavelet fuzzy brain emotional controller and a sign(.) functional compensator. The proposed algorithm estimates the judgment and emotion of a brain that includes two fuzzy inference systems for the amygdala network and the prefrontal cortex network via using a dual-function-link network and three sub-structures. Three sub-structures are a dual-function-link network, an amygdala network, and a prefrontal cortex network. Particularly, the dual-function-link network is used to adjust the amygdala and orbitofrontal weights separately so that the proposed algorithm can efficiently reduce the tracking error, follow the reference signal well, and achieve good performance. A Lyapunov stability function is used to determine the adaptive laws, which are used to efficiently tune the system parameters online. Simulation and experimental studies for an antilock braking system and a magnetic levitation system are presented to verify the effectiveness and advantage of the proposed algorithm.


















Similar content being viewed by others
References
Yang W, Jhang ST, Shi SG, Xu ZS, Ma ZM (2020) A novel additive consistency for intuitionistic fuzzy preference relations in group decision making. Appl Intell 50(12):4342–4356
Tak N, Evren AA, Tez M, Egrioglu E (2018) Recurrent type-1 fuzzy functions approach for time series forecasting. Appl Intell 48(1):68–77
Huynh T-T, Le T-L, Lin C-M (2020) A TOPSIS multi-criteria decision method-based intelligent recurrent wavelet CMAC control system design for MIMO uncertain nonlinear systems. Neural Comput & Applic 32(8):4025–4043
Huynh T-T, Lin C-M, Le T-L, Zhong Z A (2020) mixed gaussian membership function fuzzy cmac for a three-link robot. In: 2020 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE),. IEEE, pp 1–7
Qiao J, Wang L (2021) Nonlinear system modeling and application based on restricted Boltzmann machine and improved BP neural network. Appl Intell 51(1):37–50
Huynh T-T, Le T-L, Lin C-M (2018) Self-organizing recurrent wavelet fuzzy neural network-based control system design for mimo uncertain nonlinear systems using topsis method. Int J Fuzzy Syst 21(2):468–487
Lucas C, Shahmirzadi D, Sheikholeslami N (2004) Introducing BELBIC: brain emotional learning based intelligent controller. Intell Automation Soft Computing 10(1):11–21
Huynh T-T, Lin C-M, Le T-L, Le N-Q-K VV-P, Chao F (2020) Self-organizing double function-link fuzzy brain emotional control system design for uncertain nonlinear systems. IEEE Trans Syst, Man, Cybernetics: Syst:1–17. https://doi.org/10.1109/TSMC.2020.3036404
Sun Y, Xu J, Qiang H, Lin G (2019) Adaptive neural-fuzzy robust position control scheme for maglev train systems with experimental verification. IEEE Trans Ind Electron 66(11):8589–8599
Lin Q, Chen S, Lin C (2018) Parametric fault diagnosis based on fuzzy cerebellar model neural networks. IEEE Trans Indust Electr 66(10):8104–8115
Nighot M, Ghatol A, Thakare V (2018) Self-organized hybrid wireless sensor network for finding randomly moving target in unknown environment. Int J Interact Mult Artif Intell 5(1):16–28
LeDoux J (1991) Emotion and the limbic system concept. Concepts Neurosci 2:169–199
Rouhani H, Jalili M, Araabi BN, Eppler W, Lucas C (2007) Brain emotional learning based intelligent controller applied to neurofuzzy model of micro-heat exchanger. Expert Syst Appl 32(3):911–918
Hsu C-F, Su C-T, Lee T-T Chaos synchronization using brain-emotional-learning-based fuzzy control. In: 2016 Joint 8th International Conference on Soft Computing and Intelligent Systems (SCIS) and 17th International Symposium on Advanced Intelligent Systems (ISIS), 2016. IEEE, pp 811–816
Zhao J, Lin C-M, Chao F (2018) Wavelet fuzzy brain emotional learning control system design for mimo uncertain nonlinear systems. Front Neurosci 12
Lin C-M, Chung C-C (2015) Fuzzy brain emotional learning control system design for nonlinear systems. International Journal of Fuzzy Systems 17(2):117–128
Ayachi R, Bouhani H, Amor NB (2018) An evolutionary approach for learning opponent's deadline and reserve points in multi-issue negotiation. Int J Inter Multimedia Artif Intell 5(3):131–140
Milad HS, Farooq U, El-Hawary ME, Asad MU (2016) Neo-fuzzy integrated adaptive decayed brain emotional learning network for online time series prediction. IEEE Access 5:1037–1049
Hsu C-F, Lee T-T (2017) Emotional fuzzy sliding-mode control for unknown nonlinear systems. Int J Fuzzy Syst 19(3):942–953
Le T-L, Lin C-M, Huynh T-T (2018) Self-evolving type-2 fuzzy brain emotional learning control design for chaotic systems using PSO. Appl Soft Comput 73:418–433
Le T-L, Huynh T-T, Lin C-M (2020) Adaptive filter design for active noise cancellation using recurrent type-2 fuzzy brain emotional learning neural network. Neural Comput & Applic 32(12):8725–8734
Huynh T-T, Lin C-M, Le T-L, Nguyen NP, Hong S-K, Chao F (2020) Wavelet interval type-2 fuzzy quad-function-link brain emotional control algorithm for the synchronization of 3d nonlinear chaotic systems. Int J Fuzzy Syst 22(8):2546–2564
Lin C-M, Hsu C-F (2003) Neural-network hybrid control for antilock braking systems. IEEE Trans Neural Netw 14(2):351–359
Wang W-Y, Li I-H, Chen M-C, Su S-F, Hsu S-B (2009) Dynamic slip-ratio estimation and control of antilock braking systems using an observer-based direct adaptive fuzzy–neural controller. IEEE Trans Ind Electron 56(5):1746–1756
Lin C-M, Li H-Y (2013) Intelligent hybrid control system design for antilock braking systems using self-organizing function-link fuzzy cerebellar model articulation controller. IEEE Trans Fuzzy Syst 21(6):1044–1055
Hsu C-F, Kuo T-C (2014) Adaptive exponential-reaching sliding-mode control for antilock braking systems. Nonlinear Dyn 77(3):993–1010
Hsu C-F (2016) Intelligent exponential sliding-mode control with uncertainty estimator for antilock braking systems. Neural Comput & Applic 27(6):1463–1475
Lin C-M, Le T-L (2017) PSO-self-organizing interval type-2 fuzzy neural network for antilock braking systems. Int J Fuzzy Syst 19(5):1362–1374
Sun W, Zhang J, Liu Z (2019) Two-time-scale redesign for antilock braking systems of ground vehicles. IEEE Trans Ind Electron 66(6):4577–4586
Zhai M, Long Z, Li X (2019) Fault-tolerant control of magnetic levitation system based on state observer in high speed maglev train. IEEE Access 7:31624–31633
Safaeian R, Heydari H (2019) Optimal design of a compact passive magnetic bearing based on dynamic modelling. IET Electr Power Appl 13(6):720–729
Beijen MA, Heertjes MF, Butler H, Steinbuch M (2019) Mixed feedback and feedforward control design for multi-axis vibration isolation systems. Mechatronics 61:106–116
Wu Z, Wang X, Jiao Y, Zhu Y, Zhou J (2019) Guidance performance evaluation method for infrared imaging guided missile based on extended object-oriented petri net. Optik 185:88–96
Zhang Y, Xian B, Ma S (2015) Continuous robust tracking control for magnetic levitation system with unidirectional input constraint. IEEE Trans Ind Electron 62(9):5971–5980
de Jesús RJ, Zhang L, Lughofer E, Cruz P, Alsaedi A, Hayat T (2017) Modeling and control with neural networks for a magnetic levitation system. Neurocomputing 227:113–121
Sadek U, Sarjaš A, Chowdhury A, Svečko R (2017) Improved adaptive fuzzy backstepping control of a magnetic levitation system based on symbiotic organism search. Appl Soft Comput 56:19–33
Lin C-M, Huynh T-T (2019) Dynamic TOPSIS fuzzy cerebellar model articulation controller for magnetic levitation system. J Intell Fuzzy Syst 36(3):2465–2480
Ali OAM, Ali AY, Sumait BS (2015) Comparison between the effects of different types of membership functions on fuzzy logic controller performance. Int J 76:76–83
Bigand A, Colot O (2016) Membership function construction for interval-valued fuzzy sets with application to Gaussian noise reduction. Fuzzy Sets Syst 286:66–85
Rong N, Wang Z, Ding S, Zhang H (2018) Interval type-2 regional switching T–S fuzzy control for time-delay systems via membership function dependent approach. Fuzzy Sets Syst 374:152–169
Gardner MW, Dorling S (1998) Artificial neural networks (the multilayer perceptron)—a review of applications in the atmospheric sciences. Atmos Environ 32(14–15):2627–2636
Svozil D, Kvasnicka V, Pospichal J (1997) Introduction to multi-layer feed-forward neural networks. Chemom Intell Lab Syst 39(1):43–62
Patra JC, Pal RN (1995) A functional link artificial neural network for adaptive channel equalization. Signal Process 43(2):181–195
Zhou Q, Chao F, Lin C-M (2018) A functional-link-based fuzzy brain emotional learning network for breast tumor classification and chaotic system synchronization. Int J Fuzzy Syst 20(2):349–365
Lin C-M, Huynh T-T (2018) Function-link fuzzy cerebellar model articulation controller design for nonlinear chaotic systems using topsis multiple attribute decision-making method. Int J Fuzzy Syst 20(6):1839–1856
Huynh TT, Lin CM Wavelet dual function-link fuzzy brain emotional learning system design for system identification and trajectory tracking of nonlinear systems. In: 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), 6–9 Oct. 2019 2019. pp 1653–1657
Lin C-M, Li H-Y (2012) TSK fuzzy CMAC-based robust adaptive backstepping control for uncertain nonlinear systems. IEEE Trans Fuzzy Syst 20(6):1147–1154
Le T-L (2019) Intelligent fuzzy controller design for antilock braking systems. J Intell Fuzzy Syst 36(4):3303–3315
Huynh TT, Lin CM, Le TL, Cho H, Pham TTT, Le NQK, Chao F (2020) A new self-organizing fuzzy cerebellar model articulation controller for uncertain nonlinear systems using overlapped gaussian membership functions. IEEE Trans Ind Electron 67(11):9671–9682
Slotine JJE, Li W (1991) Applied nonlinear control. Prentice-Hall, Englewood Cliffs
Sharkawy AB (2010) Genetic fuzzy self-tuning PID controllers for antilock braking systems. Eng Appl Artif Intell 23(7):1041–1052
Acknowledgments
This research was supported by the Ministry of Science and Technology of Taiwan under grant MOST 109-2811-E-155-504-MY3.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof for Theorem 1
Proof: A Lyapunov function is determined as:
Next, taking the derivative of (65), then using (49), gives:
-
Remark 1
\( {\boldsymbol{p}}^{\ast },{\boldsymbol{q}}^{\ast },{{\boldsymbol{z}}_k^a}^{\ast },{{\boldsymbol{z}}_k^o}^{\ast },{\boldsymbol{m}}^{\ast },\mathrm{and}\ {\boldsymbol{\sigma}}^{\ast } \)are constants; hence,
-
Remark 2
Using (66)–(68), (65) becomes
Via the adaptive laws in (50)–(53) and the robust controller in (54), then (69) becomes
If the error bound for \( \dot{\hat{\Delta}} \) is chosen as
then (60) is rewritten as
As \( \dot{V}(t)\le 0 \), it indicates that \( \tilde{\Delta} \) and s(t) are bounded. Set \( \Psi (t)\equiv \left(\Delta -\left|\boldsymbol{\varTheta} \right|\right)\boldsymbol{s}(t)\le \left(\Delta -\left|\boldsymbol{\varTheta} \right|\right)\left|\boldsymbol{s}(t)\right|\le -\dot{V}(t) \), then integrate Ψ(t) with respect to time, gives
\( \dot{V}(0) \) is bounded and \( \dot{V}(t) \) does not increase, obtains:
Furthermore, \( \dot{\Psi}(t) \) is bounded via Barbalat’s Lemma, then \( \underset{t\to \infty }{\lim}\Psi (t)\to 0 \). That means s → 0 when t→∞ [50]. Consequently, the WDFLFBEC is asymptotically stable. Hence, the control system is stable.
Rights and permissions
About this article
Cite this article
Huynh, TT., Lin, CM., Le, NQK. et al. Intelligent wavelet fuzzy brain emotional controller using dual function-link network for uncertain nonlinear control systems. Appl Intell 52, 2720–2744 (2022). https://doi.org/10.1007/s10489-021-02482-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-021-02482-4