Skip to main content
SpringerLink
Log in

Vibration of fluid-conveying pipe with nonlinear supports at both ends

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

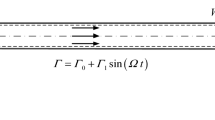
The axial fluid-induced vibration of pipes is very widespread in engineering applications. The nonlinear forced vibration of a viscoelastic fluid-conveying pipe with nonlinear supports at both ends is investigated. The multi-scale method combined with the modal revision method is formulated for the fluid-conveying pipe system with nonlinear boundary conditions. The governing equations and the nonlinear boundary conditions are rescaled simultaneously as linear inhomogeneous equations and linear inhomogeneous boundary conditions on different time-scales. The modal revision method is used to transform the linear inhomogeneous boundary problem into a linear homogeneous boundary problem. The differential quadrature element method (DQEM) is used to verify the approximate analytical results. The results show good agreement between these two methods. A detailed analysis of the boundary nonlinearity is also presented. The obtained results demonstrate that the boundary nonlinearities have a significant effect on the dynamic characteristics of the fluid-conveying pipe, and can lead to significant differences in the dynamic responses of the pipe system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. ZHANG, W. G., LIN, G. M., SHANG, M., and ZHOU, F. Fracture analysis of hydraulic pipe of airplane. Advanced Materials Research, 971–973, 485–488 (2014)

    Google Scholar 

  2. TATSUSHI, A., MIZUKAMI, R., and KITAMURA, R. Buckling of rectangular composite pipes under torsion. Applied Sciences, 11, 1342–1353 (2021)

    Article  Google Scholar 

  3. PARK, J. H., CHO, Y. K., KIM, S. H., and LEE, J. H. Estimation of leak rate through circumferential cracks in pipes in nuclear power plants. Nuclear Engineering and Technology, 47, 332–339 (2015)

    Article  Google Scholar 

  4. PARK, J. H., LEE, J. H., and OH, Y. J. Estimation of leak rate through cracks in bimaterial pipes in nuclear power plants. Nuclear Engineering and Technology, 48, 1264–1272 (2016)

    Article  Google Scholar 

  5. ANDREIKIV, O. E., IVANYTS’KYI, Y. L., TERLETS’KA, Z. O., and KIT, M. B. Evaluation of the durability of a pipe of oil pipeline with surface crack under biaxial block loading. Materials Science, 40, 103–108 (2004)

    Google Scholar 

  6. ANDREIKIV, O. E., NYKYFORCHYN, H. M., SHTOIKO, I. P., and LYSYK, A. R. Evaluation of the residual life of a pipe of oil pipeline with an external surface stress-corrosion crack for a laminar flow of oil with repeated hydraulic shocks. Materials Science, 53, 216–225 (2017)

    Article  Google Scholar 

  7. BULLERI, B., GENONI, M., GALLONE, G., and MARCHETTI, A. Multi-layer pipes for hydrocarbons conveyance. Macromolecular Symposia, 218, 363–371 (2004)

    Google Scholar 

  8. KAEWUNRUEN, S., CHIRAVATCHRADEJ, J., and CHUCHEEPSAKUL, S. Nonlinear free vibrations of marine risers/pipes transporting fluid. Ocean Engineering, 32, 417–440 (2005)

    Article  Google Scholar 

  9. YAZDCHI, M. and CRISFIELD, M. A. Non-linear dynamic behaviour of flexible marine pipes and risers. International Journal for Numerical Methods in Engineering, 54, 1265–1308 (2002)

    Article  MATH  Google Scholar 

  10. ASHLEY, H. and HAVILAND, G. Bending vibrations of a pipe line containing flowing fluid. Journal of Applied Mechanics, 17, 229–232 (1950)

    Article  MathSciNet  Google Scholar 

  11. JIANG, T., DAI, H. L., ZHOU, K., and WANG, L. Nonplanar post-buckling analysis of simply supported pipes conveying fluid with an axially sliding downstream end. Applied Mathematics and Mechanics (English Edition), 41(1), 15–32 (2020) https://doi.org/10.1007/s10483-020-2557-9

    Article  MathSciNet  MATH  Google Scholar 

  12. PANDA, L. N. and KAR, R. C. Nonlinear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances. Nonlinear Dynamics, 49, 9–30 (2007)

    Article  MATH  Google Scholar 

  13. WANG, L. A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid. International Journal of Non-Linear Mechanics, 44, 115–121 (2009)

    Article  Google Scholar 

  14. MOHAMMADI, J. and NIKKHAH-BAHRAMI, M. Stability analyses of articulated rigid pipes conveying fluid with harmonic velocity using the method of multiple time scales. Journal of Mechanical Science and Technology, 34, 965–976 (2020)

    Article  Google Scholar 

  15. WANG, L., JIANG, T. L., and DAI, H. L. Three-dimensional dynamics of supported pipes conveying fluid. Acta Mechanica Sinica, 33, 1065–1074 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  16. XIE, W. D., GAO, X. F., and XU, W. H. Stability and nonlinear vibrations of a flexible pipe parametrically excited by an internal varying flow density. Acta Mechanica Sinica, 36, 206–219 (2019)

    Article  MathSciNet  Google Scholar 

  17. LIANG, F., YANG, X. D., ZHANG, W., QIAN, Y. J., and MELNIK, R. V. N. Parametric vibration analysis of pipes conveying fluid by nonlinear normal modes and a numerical iterative approach. Advances in Applied Mathematics and Mechanics, 11, 38–52 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  18. WANG, Y. J., ZHANG, Q. C., WANG, W., and YANG, T. Z. In-plane dynamics of a fluid-conveying corrugated pipe supported at both ends. Applied Mathematics and Mechanics (English Edition), 40(8), 1119–1134 (2019) https://doi.org/10.1007/s10483-019-2511-6

    Article  MathSciNet  Google Scholar 

  19. LONG, R. H. Experimental and theoretical study of transverse vibration of a tube containing flowing fluid. Journal of Applied Mechanics, 22, 65–68 (1955)

    Article  Google Scholar 

  20. PAÏDOUSSIS, M. P. and ISSID, N. T. Dynamic stability of pipes conveying fluid. Journal of Sound and Vibration, 33, 267–294 (1974)

    Article  Google Scholar 

  21. GHAYESH, M. H., PAÏDOUSSIS, M. P., and AMABILI, M. Nonlinear dynamics of cantilevered extensible pipes conveying fluid. Journal of Sound and Vibration, 332, 6405–6418 (2013)

    Article  Google Scholar 

  22. CHEN, L. Q., ZHANG, Y. L., ZHANG, G. C., and DING, H. Evolution of the double-jumping in pipes conveying fluid flowing at the supercritical speed. International Journal of Non-Linear Mechanics, 58, 11–21 (2014)

    Article  Google Scholar 

  23. CHANG, G. H. and MODARRES-SADEGHI, Y. Flow-induced oscillations of a cantilevered pipe conveying fluid with base excitation. Journal of Sound and Vibration, 333, 4265–4280 (2014)

    Article  Google Scholar 

  24. ADEGOKE, A. S., ADEWUMI, O., FASHANU, A., and OYEDIRAN, A. Analysis of nonlinear axial vibrations of a cantilevered pipe conveying pulsating two-phase flow. Journal of Computational Applied Mechanics, 51, 311–322 (2020)

    Google Scholar 

  25. GIACOBBI, D. B., SEMLER, C., and PAÏDOUSSIS, M. P. Dynamics of pipes conveying fluid of axially varying density. Journal of Sound and Vibration, 473, 115202 (2020)

    Article  Google Scholar 

  26. CHEHREGHANI, M., ABDELBAKI, A. R., MISRA, A. K., and PAÏDOUSSIS, M. P. Experiments on the dynamics of a cantilevered pipe conveying fluid and subjected to reverse annular flow. Journal of Sound and Vibration, 515, 116480 (2021)

    Article  Google Scholar 

  27. ZHOU, K., NI, Q., WANG, L., and DAI, H. L. Planar and non-planar vibrations of a fluid-conveying cantilevered pipe subjected to axial base excitation. Nonlinear Dynamics, 99, 2527–2549 (2020)

    Article  Google Scholar 

  28. WANG, Y. K., WANG, L., NI, Q., DAI, H. L., YAN, H., and LUO, Y. Y. Non-planar responses of cantilevered pipes conveying fluid with intermediate motion constraints. Nonlinear Dynamics, 93, 505–524 (2018)

    Article  Google Scholar 

  29. ABBASBANDY, S. and SHIVANIAN, E. Prediction of multiplicity of solutions of nonlinear boundary value problems: novel application of homotopy analysis method. Communications in Nonlinear Science and Numerical Simulation, 15, 3830–3846 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  30. HASAN, Y. Q. and ZHU, L. M. Solving singular boundary value problems of higher-order ordinary differential equations by modified Adomian decomposition method. Communications in Nonlinear Science and Numerical Simulation, 14, 2592–2596 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  31. LIU, X. J., ZHOU, Y. H., WANG, X. M., and WANG, J. Z. A wavelet method for solving a class of nonlinear boundary value problems. Communications in Nonlinear Science and Numerical Simulation, 18, 1939–1948 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  32. MATTEO, A. D. and PIRROTTA, A. Generalized differential transform method for nonlinear boundary value problem of fractional order. Communications in Nonlinear Science and Numerical Simulation, 29, 88–101 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  33. NAYFEH, A. H. and ASFAR, K. R. Response of a bar constrained by a non-linear spring to a harmonic excitation. Journal of Sound and Vibration, 105, 1–15 (1986)

    Article  MATH  Google Scholar 

  34. WANG, Y. R. and FANG, Z. W. Vibrations in an elastic beam with nonlinear supports at both ends. Journal of Applied Mechanics and Technical Physics, 56, 337–346 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  35. QIAN, Q., WANG, L., and NI, Q. Nonlinear responses of a fluid-conveying pipe embedded in nonlinear elastic foundations. Acta Mechanica Solida Sinica, 21, 170–176 (2008)

    Article  Google Scholar 

  36. NI, Q., TANG, M., LUO, Y. Y., WANG, Y. K., and WANG, L. Internal-external resonance of a curved pipe conveying fluid resting on a nonlinear elastic foundation. Nonlinear Dynamics, 76, 867–886 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  37. NI, Q., WANG, L., and QIAN, Q. Bifurcations and chaotic motions of a curved pipe conveying fluid with nonlinear constraints. Computers and Structures, 84, 708–717 (2006)

    Article  Google Scholar 

  38. ÖZHAN, B. B. and PAKDEMIRLI, M. Principal parametric resonances of a general continuous system with cubic nonlinearities. Applied Mathematics and Computation, 219, 2412–2423 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  39. DING, H., JI, J. C., and CHEN, L. Q. Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mechanical Systems and Signal Processing, 121, 675–688 (2019)

    Article  Google Scholar 

  40. MAO, X. Y., DING, H., and CHEN, L. Q. Vibration of flexible structures under nonlinear boundary conditions. Journal of Applied Mechanics, 84, 111006 (2017)

    Article  Google Scholar 

  41. WANG, X. W. and WANG, Y. L. Free vibration analysis of multiple-stepped beams by the differential quadrature element method. Applied Mathematics and Computation, 219, 5802–5810 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  42. WANG, Y. L., WANG, X. W., and ZHOU, Y. Static and free vibration analyses of rectangular plates by the new version of the differential quadrature element method. International Journal for Numerical Methods in Engineering, 59, 1207–1226 (2004)

    Article  MATH  Google Scholar 

  43. MALIK, M. and BERT, C. W. Implementing multiple boundary conditions in the DQ solution of higher-order PDE’s: application to free vibration of plates. International Journal for Numerical Methods in Engineering, 39, 1237–1258 (1996)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai Key Laboratory of Mechanics in Energy Engineering, School of Mechanics and Engineering Science, Shanghai University, Shanghai, 200072, China

    Sha Wei, Xiong Yan, Xiaoye Mao, Hu Ding & Liqun Chen

  2. School of Engineering Science, University of Science and Technology of China, Hefei, 230026, China

    Xin Fan

Authors
  1. Sha Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiong Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xin Fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaoye Mao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hu Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Liqun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liqun Chen.

Additional information

Citation: WEI, S., YAN, X., FAN, X., MAO, X. Y., DING, H., and CHEN, L. Q. Vibration of fluid-conveying pipe with nonlinear supports at both ends. Applied Mathematics and Mechanics (English Edition), 43(6), 845–862 (2022) https://doi.org/10.1007/s10483-022-2857-6

Project supported by the National Natural Science Foundation of China (Nos. 12072181 and 12121002) and the State Key Laboratory of Mechanical System and Vibration of China (No. MSV202105)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wei, S., Yan, X., Fan, X. et al. Vibration of fluid-conveying pipe with nonlinear supports at both ends. Appl. Math. Mech.-Engl. Ed. 43, 845–862 (2022). https://doi.org/10.1007/s10483-022-2857-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-022-2857-6

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation