Skip to main content
SpringerLink
Log in

A screw dislocation near one open inhomogeneity and another closed inhomogeneity both permitting constant interior stresses

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

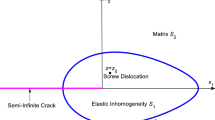
We prove that the interior stresses within both a non-parabolic open in-homogeneity and another interacting non-elliptical closed inhomogeneity can still remain constant when the matrix is simultaneously under the action of a screw dislocation and uniform remote anti-plane stresses. The constancy of interior stresses is realized through the construction of a conformal mapping function for the doubly connected domain occupied by the surrounding matrix. The mapping function is endowed with the information describing the screw dislocation via the incorporation of two specifically defined logarithmic terms. The constant interior stress fields are observed to be independent of the specific open and closed shapes of the two inhomogeneities and the existence of the screw dislocation. In contrast, the existence of the neighboring screw dislocation significantly affects the open and closed shapes of the two inhomogeneities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. LIU, L. P. Solution to the Eshelby conjectures. Proceedings of the Royal Society of London A, 464, 573–594 (2008)

    MathSciNet  MATH  Google Scholar 

  2. KANG, H., KIM, E., and MILTON, G. W. Inclusion pairs satisfying Eshelby’s uniformity property. SIAM Journal on Applied Mathematics, 69, 577–595 (2008)

    Article  MathSciNet  Google Scholar 

  3. WANG, X. Uniform fields inside two non-elliptical inclusions. Mathematics and Mechanics of Solids, 17, 736–761 (2012)

    Article  MathSciNet  Google Scholar 

  4. WANG, X. and SCHIAVONE, P. Two inhomogeneities of irregular shape with internal uniform stress fields interacting with a screw dislocation. Comptes Rendus Mecanique, 344, 532–538 (2016)

    Article  Google Scholar 

  5. DAI, M., GAO, C. F., and RU, C. Q. Uniform stress fields inside multiple inclusions in an elastic infinite plane under plane deformation. Proceedings of the Royal Society of London A, 471(2177), 20140933 (2015)

    Google Scholar 

  6. DAI, M., RU, C. Q., and GAO, C. F. Uniform strain fields inside multiple inclusions in an elastic infinite plane under anti-plane shear. Mathematics and Mechanics of Solids, 22, 114–128 (2017)

    Article  MathSciNet  Google Scholar 

  7. ANTIPOV, Y. A. Method of Riemann surfaces for an inverse antiplane problem in an n-connected domain. Complex Variables and Elliptic Equations, 65, 455–480 (2020)

    Article  MathSciNet  Google Scholar 

  8. WANG, X., YANG, P., and SCHIAVONE, P. Uniform fields inside two interacting non-parabolic and non-elliptical inhomogeneities. Zeitschrift für angewandte Mathematik und Physik, 71(1), 25 (2020)

    Article  MathSciNet  Google Scholar 

  9. MURA, T. Continuous distribution of dislocations and the mathematical theory of plasticity. Physica Status Solidi B, 10, 447–453 (1965)

    Article  Google Scholar 

  10. MURA, T. Continuum theory of plasticity and dislocations. International Journal of Engineering Science, 5, 341–351 (1967)

    Article  Google Scholar 

  11. ZAISER, M. and AIFANTIS, E. C. Randomness and slip avalanches in gradient plasticity. International Journal of Plasticity, 22, 1432–1455 (2006)

    Article  Google Scholar 

  12. VINOGRADOV, V. and WILLIS, J. R. The pair distribution function for an array of screw dislocations. International Journal of Solids and Structures, 45, 3726–3738 (2008)

    Article  Google Scholar 

  13. MORIN, L., BRENNER, R., and SUQUET, P. Numerical simulation of model problems in plasticity based on field dislocation mechanics. Modelling and Simulation in Materials Science and Engineering, 27(8), 085012 (2019)

    Article  Google Scholar 

  14. WANG, X. and SCHIAVONE, P. A screw dislocation near a non-parabolic open inhomogeneity with internal uniform stresses. Comptes Rendus Mecanique, 347(12), 967–972 (2019)

    Article  Google Scholar 

  15. TING, T. C. T. Anisotropic Elasticity—Theory and Applications, Oxford University Press, New York (1996)

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai, 200237, China

    Xu Wang & Ping Yang

  2. Department of Mechanical Engineering, University of Alberta, Donadeo, 10-203, Canada

    P. Schiavone

  3. Innovation Centre for Engineering, Alberta, T6G 1H9, Canada

    P. Schiavone

Authors
  1. Xu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ping Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. P. Schiavone
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Xu Wang or P. Schiavone.

Additional information

Project supported by the National Natural Science Foundation of China (No. 11272121) and the Natural Sciences and Engineering Research Council of Canada (No. RGPIN-2017-03716115112)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Yang, P. & Schiavone, P. A screw dislocation near one open inhomogeneity and another closed inhomogeneity both permitting constant interior stresses. Appl. Math. Mech.-Engl. Ed. 42, 173–182 (2021). https://doi.org/10.1007/s10483-021-2702-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-021-2702-8

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation