Skip to main content

Advertisement

SpringerLink
Log in

Vibration reduction evaluation of a linear system with a nonlinear energy sink under a harmonic and random excitation

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

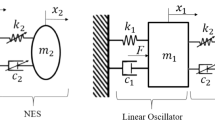
The nonlinear behaviors and vibration reduction of a linear system with nonlinear energy sink (NES) are investigated. The linear system is excited by a harmonic and random base excitation, consisting of a mass block, a linear spring, and a linear viscous damper. The NES is composed of a mass block, a linear viscous damper, and a spring with ideal cubic nonlinear stiffness. Based on the generalized harmonic function method, the steady-state Fokker-Planck-Kolmogorov equation is presented to reveal the response of the system. The path integral method based on the Gauss-Legendre polynomial is used to achieve the numerical solutions. The performance of vibration reduction is evaluated by the displacement and velocity transition probability densities, the transmissibility transition probability density, and the percentage of the energy absorption transition probability density of the linear oscillator. The sensitivity of the parameters is analyzed for varying the nonlinear stiffness coefficient and the damper ratio. The investigation illustrates that a linear system with NES can also realize great vibration reduction under harmonic and random base excitations and random bifurcation may appear under different parameters, which will affect the stability of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. MALATKAR, P. and NAYFEH, A. F. Steady-state dynamics of a linear structure weakly coupled to an essentially nonlinear oscillator. Nonlinear Dynamics, 47, 167–179 (2006)

    Article  Google Scholar 

  2. LEE, Y. S., VAKAKIS, A. F., and BERGMAN, L. A. Passive non-linear targeted energy transfer and its application to vibration absorption: a review. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 222, 77–134 (2008)

    Article  Google Scholar 

  3. VAKAKIS, A. F., GENDELMAN, O. V., BERGMAN, L. A., MCFARLAND, D. M., KERSCHEN, G., and LEE, Y. S. Nonlinear targeted energy transfer in mechanics and structural systems. Solid Mechanics and Its Application, 156, 88–159 (2009)

    MATH  Google Scholar 

  4. JIANG, X., MCFARLAND, D. M., and BERGMAN, L. A. Steady state passive nonlinear energy pumping in coupled oscillators: theoretical and experimental results. Nonlinear Dynamics, 33, 87–102 (2003)

    Article  Google Scholar 

  5. SAVADKOOHI, A. T., MANEVITCH, L. I., and LAMARQUE, C. H. Analysis of the transient behavior in a two-degree-of-freedom nonlinear system. Chaos Solution and Fractals, 44, 450–463 (2011) Vibration reduction evaluation of a linear system with a nonlinear energy sink 13

    Article  Google Scholar 

  6. SAVADKOOHI, A. T., LAMARQUE, C. H., and DIMITRIJEVIC, Z. Vibratory energy exchange between a linear and a non-smooth system in the presence of the gravity. Nonlinear Dynamics, 70, 1473–1483 (2012)

    Article  MathSciNet  Google Scholar 

  7. WEISS, M., CHENIA, M., and SAVADKOOHI, A. T. Multi-scale energy exchanges between an elasto-plastic oscillator and a light non-smooth system with external pre-stress. Nonlinear Dynamics, 83, 109–135 (2016)

    Article  MathSciNet  Google Scholar 

  8. LAMARQU, C. H., SAVADKOOHI, A. T., and CHARLEMAGNE, S. Nonlinear vibratory interactions between a linear and a non-smooth forced oscillator in the gravitational field. Mechanical System and Signal Processing, 89, 131–148 (2017)

    Article  Google Scholar 

  9. YANG, K., ZHANG, Y. W., and DING, H. Nonlinear energy sink for whole-spacecraft vibration reduction. Journal of Vibration and Acoustics, 139, 021011 (2017)

    Article  Google Scholar 

  10. ZANG, J. and CHEN, L. Q. Complex dynamics of a harmonically excited structure coupled with a nonlinear energy sink. Acta Mechanics Sinica, 33, 801–822 (2017)

    Article  MathSciNet  Google Scholar 

  11. GENDELMAN, O. V., STAROSVETSKY, Y., and FELDMAN, M. Attractors of harmonically forced linear oscillator with attached nonlinear energy sink I: description of response regimes. Nonlinear Dynamics, 51, 31–46 (2007)

    Article  Google Scholar 

  12. STAROSVETSKY, Y. and GENDELMAN, O. V. Attractors of harmonically forced linear oscillator with attached nonlinear energy sink II: optimization of a nonlinear vibration absorber. Nonlinear Dynamics, 51, 47–57 (2007)

    Article  Google Scholar 

  13. STAROSVETSKY, Y. and GENDELMAN, O. V. Response regimes of linear oscillator coupled to nonlinear energy sink with harmonic forcing and frequency detuning. Journal of Sound and Vibration, 315, 746–765 (2008)

    Article  Google Scholar 

  14. STAROSVETSKY, Y. and GENDELMAN, O. V. DOF oscillatory system with essential mass and potential asymmetry. Physical D: Nonlinear Phenomena, 237, 1719–1733 (2008)

    Article  Google Scholar 

  15. BELLIZZI, S., COTE, R., and PACHEBAT, M. Response of a two-degree-of-freedom system coupled to a nonlinear damper under multi-forcing frequencies. Journal of Sound and Vibration, 332, 1639–1653 (2013)

    Article  Google Scholar 

  16. PARSEH, M., DARDEL, M., and GHASEMI, M. H. Performance comparison of nonlinear energy sink and linear tuned mass damper in steady-state dynamics of a linear beam. Nonlinear Dynamics, 81, 1981–2002 (2015)

    Article  MathSciNet  Google Scholar 

  17. TAGHIPOUR, J. and DARDEL, M. Steady-state dynamics and robustness of a harmonically excited essentially nonlinear oscillator coupled with a two-DOF nonlinear energy sink. Mechanical Systems and Signal Processing, 62-63, 164–182 (2015)

    Article  Google Scholar 

  18. YE, S. Q., MAO, X. Y., DING, H., JI, J. C., and CHEN, L. Q. Nonlinear vibrations of a slightly curved beam with nonlinear boundary conditions. International Journal of Mechanical Sciences, 168, 105294 (2020)

    Article  Google Scholar 

  19. MALATKAR, P. and NAYFEH, A. H. Steady-state dynamics of a linear structure weakly coupled to an essentially nonlinear oscillator. Nonlinear Dynamics, 47, 167–179 (2006)

    Article  Google Scholar 

  20. LI, X., ZHANG, Y. W., and DING, H. Integration of a nonlinear energy sink and a piezoelectric energy harvester. Applied Mathematics and Mechanics (English Edition), 38(7), 1019–1030 (2017) https://doi.org/10.1007/s10483-017-2220-6

    Article  MathSciNet  Google Scholar 

  21. LUONGO, A. and ZULLI, D. Dynamic analysis of externally excited NES-controlled systems via a mixed multiple scale harmonic balance algorithm. Nonlinear Dynamics, 70, 2049–2061 (2012)

    Article  MathSciNet  Google Scholar 

  22. GUO, H. L., CHEN, Y. S., and YANG, T. Z. Limit cycle oscillation suppression of 2-DOF airfoil using nonlinear energy sink. Applied Mathematics and Mechanics (English Edition), 34(10), 1277–1290 (2013) https://doi.org/10.1007/s10483-013-1744-7

    Google Scholar 

  23. GENDELMAN, O. V., GORLOV, D. V., and MANEVITCH, L. I. Dynamics of coupled linear and essentially nonlinear oscillators with substantially different masses. Journal of Sound and Vibration, 286, 1–19 (2005) 14 Jiren XUE, Yewei ZHANG, Hu DING, and Liqun CHEN

    Article  Google Scholar 

  24. KERSCHEN, G., KOWTKO, J. J., and MCFARLAND, D. M. Theoretical and experimental study of multimodal targeted transfer in a system of coupled oscillators. Nonlinear Dynamics, 47, 285–309 (2006)

    Article  MathSciNet  Google Scholar 

  25. KERSCHEN, G., MCFARLAND, D. M., and KOWTKO, J. J. Experimental demonstration of transient resonance capture in a system of two coupled oscillators with essential stiffness nonlinearity. Journal of Sound and Vibration, 195, 822–838 (2007)

    Article  Google Scholar 

  26. TSAKIRTZI, S., KERSCHEN, G., and PANAGOPOULOS, P. N. Multi-frequency nonlinear energy transfer from linear oscillators to mode essentially nonlinear attachments. Journal of Sound and Vibration, 285, 483–490 (2005)

    Article  Google Scholar 

  27. SHIROKY, I. B. and GENDELMAN, O. V. Essentially nonlinear vibration absorber in a parametrically excited system. Zeitschrift für Angewandte Mathematik und Mechanik, 88, 573–596 (2008)

    Article  MathSciNet  Google Scholar 

  28. STAROSVETSKY, Y. and GENDELMAN, O. V. Response regimes in forced system with nonlinear energy sink: quasi-periodic and random forcing. Nonlinear Dynamics, 64, 177–195 (2011)

    Article  MathSciNet  Google Scholar 

  29. XIONG, H., KONG, X. R., YANG, Z. G., and LIU, Y. Response regimes of narrow-band stochastic excited linear oscillator coupled to nonlinear energy sink. Chinese Journal of Aeronautics, 28, 55–101 (2015)

    Article  Google Scholar 

  30. HUANG, Z. L., ZHU, W. Q., and SUZUKI, Y. Stochastic averaging of strongly non-linear oscillators under combined harmonic and white noise excitations. Journal of Sound and Vibration, 238, 233–256 (2000)

    Article  MathSciNet  Google Scholar 

  31. DING, H., ZHU, M. H., and CHEN, L. Q. Dynamic stiffness method for free vibration of an axially moving beam with generalized boundary conditions. Applied Mathematics and Mechanics (English Edition), 40(7), 911–924 (2019) hhttps://doi.org/10.1007/s10483-019-2493-8

    Article  MathSciNet  Google Scholar 

  32. ZHAO, Y., ZHANG, Y. H., and LIN, J. H. Summary on the pseudo-excitation method for vehicle random vibration PSD analysis (in Chinese). Applied Mathematics and Mechanics, 34, 34–55 (2013)

    Article  Google Scholar 

  33. SU, C., ZHONG, C. Y., and ZHOU, L. C. Random vibration analysis of coupled vehicle-bridge systems with the explicit time-domain method (in Chinese). Applied Mathematics and Mechanics, 38, 107–158 (2017)

    Google Scholar 

  34. WOJTKIEWICZ, S. F., BERGMAN, L. A., and SPENCER JR, B. F. Robust Numerical Solution of the Fokker-Planck-Kolmogorov Equation for Two Dimensional Stochastic Dynamical Systems, Technical Report AAE 94-08, Department of Aeronautical and Astronautica Engineering, University of Illinois at Urbana-Champaign, Urbana-Champaign (1994)

    Google Scholar 

  35. LANGLEY, R. S. A finite element method for the statistics of non-linear random vibration. Journal of Sound and Vibration, 101, 41–54 (1985)

    Article  Google Scholar 

  36. KUMAR, P. and NARAYANAN, S. Solution of Fokker-Planck equation by finite element and finite difference methods for nonlinear system. SADHANA, 31, 455–473 (2006)

    MathSciNet  MATH  Google Scholar 

  37. KUMAR, M., CHAKRAVORTY, S., and JOHN, J. L. Computational nonlinear stochastic control based on the Fokker-Planck-Kolmogorov equation. American Institute of Aeronautics and Astronautics, 25, 1–15 (2008)

    Google Scholar 

  38. SUN, J. Q. and HSU, C. S. The generalized cell mapping method in nonlinear random vibration based on short-time Gaussian approximation. Journal of Applied Mechanics, 57, 1018–1025 (1990)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai Key Laboratory of Mechanics in Energy Engineering, School of Mechanics and Engineering Science, Shanghai University, Shanghai, 200072, China

    Jiren Xue, Yewei Zhang, Hu Ding & Liqun Chen

  2. Faculty of Aerospace Engineering, Shenyang Aerospace University, Shenyang, 110136, China

    Yewei Zhang

Authors
  1. Jiren Xue
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yewei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hu Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liqun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yewei Zhang.

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 11772205 and 11572182) and the Liaoning Revitalization Talents Program of China (No.XLYC1807172)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xue, J., Zhang, Y., Ding, H. et al. Vibration reduction evaluation of a linear system with a nonlinear energy sink under a harmonic and random excitation. Appl. Math. Mech.-Engl. Ed. 41, 1–14 (2020). https://doi.org/10.1007/s10483-020-2560-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-020-2560-6

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation