Meeting economic and social viability goals in regional airline schemes through hub-and-spoke network connectivity

Abstract

We examine the viability of regional connectivity schemes by considering both social and economic objectives. In India the scheme is called UDAN (loosely translated affordable air travel) which is designed to include economically backward communities in India into the air travel grid. Using secondary data sources from the airline sector in India, and qualitative interviews of knowledgeable personnel in the airline industry, we demonstrate the importance of hub-and-spoke network design in comparison to point-to-point connectivity for regional connectivity networks. Specifically, we develop Viable Hub Location Problem for Regional Connectivity (VHLPRC) for resilience and sustainability through bilevel optimization with single leader and two independent followers. We test our proposed approach using datasets from USA and India. Our analyses suggest strategically choosing primary hubs and re-routing traffic through regional hubs for long-term commercial viability or survivability of regional connectivity schemes. The introduction of regional hubs had mixed effects. On the positive side, it improved reach, albeit at considerable (hidden) costs. On the negative side, several sub-programs had to be abandoned for a variety of reasons, including lack of demand traffic. The lessons learned from this study inform policy makers, academics, and practicing managers on how to remain viable and sustain operations in regional connectivity schemes. With the introduction of social variables, commercial viability has been shown to face specific real-life challenges. An attempt to help solve these problems is also presented in this paper through risk reduction, capacity augmentation, and by continuing fare subsidies.

1 Introduction

Enhancing connectivity in airline networks enhances economic growth, and also ensures equity of access across various members of a community (Barnhart et al., 2012; Jacquillat & Vaze, 2018). In the U.S., post-deregulation free market competition in the aviation sector largely addressed economic growth (Flynn & Ratick, 1988). Deregulation stimulated growth in air passenger traffic that attracted many low-cost private airlines, thereby improving network connectivity through addition of routes and also encouraging frequent flying (Pels et al., 2009). Deregulation also prompted design of hub-and-spoke networks that was deployed to improve airline efficiency and promote economies of scale and scope (Adler, 2005). However, airline efficiency was adversely affected due to regional imbalance stemming from lack of growth for routes and airports that had low demand (Das et al., 2020). Free market-based competition implicitly discouraged development of transport connectivity to economically weak (remote) routes due to high fixed costs of operations. Achieving economies of scale or scope by plying in these remote areas became difficult (Fageda et al., 2018).

Due to a lack of market-driven growth and commercial non-viability of low-traffic routes, public sector intervention was needed to connect remote regions or communities to the mainstream air traffic grid. Governments in major economies realized this and introduced subsidies to enhance connectivity within isolated and remote routes (Bråthen & Halpern, 2012). Public welfare schemes like the Essential Air Services (EAS) scheme in the USA (introduced in 1978), Remote Air Services Subsidy Scheme (RASS) in Australia (introduced in 1983), Public Service Obligations (PSO) in the European Union (introduced in 1992), Rural Air Services (RAS) scheme in Malaysia (introduced in 2007), and UDAN Regional Connectivity Scheme (RCS) in India (introduced in 2016) are the many examples around the world with similar social objectives of enhancing reach. Other countries like Canada, Brazil, Russia, China, Peru, and Chile have also pursued similar schemes, but with less documented policies (Fageda et al., 2018). Policy implementation largely focused on connecting regional routes to the national air transport system, promoting territorial cohesion, guaranteeing essential services like healthcare and education, and reducing alienation of remotely situated communities (Das et al., 2022). On a practical front, these countries were finding it hard to sustain remote connectivity (Fageda et al., 2018). Risks like vulnerability associated with economic and equitable growth in airline network connectivity are deserving of research attention. This is one of the research objectives in this article – to understand the viability of air traffic networks with a social objective (of maximizing reach) over and above an economic objective (of financial soundness).

Operational risks, market demand risks, financial risks and network design risks are all examples of risks that threaten long-term viability of air travel services in regional connectivity schemes (Iyer & Thomas, 2021). With respect to operational and market demand risks, there are pressures of rising costs and declining returns of investments for airlines (Baker et al., 2015). In response, airline operators use low-capacity aircraft for regional routes to be profitable. Low-capacity aircraft had sub-optimal utilization and low load factors. Also, lack of pilots and staff further reduced efficiency levels. Due to capacity constraints at existing hubs, there was deterioration of accessibility for regional routes (Dixit et al., 2023). Financially, the lack of incentives and subsidies to help promote regional connectivity for airline carriers deters airports from supporting such schemes for long term sustainability (Iyer & Thomas, 2021). With respect to network risks, the overall network performance is dependent on individual node and link performance. For example, the busiest airports in India, namely Delhi, Mumbai, Bengaluru, Chennai, and Kolkata, are not only national hubs but are also international hubs. Similarly, Beijing Capital, Shanghai Pudong, and Guangzhou Baiyun are much more connected internationally than to other regional Chinese airports (Zhang et al., 2017). Nevertheless, hub-and-spoke network design generates higher demand for many routes as compared to the point-to-point connectivity. As examples of the failure of point-to-point connectivity schemes in India, are the bankruptcy of regional airlines like Air Odisha and Air Deccan (Das et al., 2020). To a large extent, these failures are attributable to lack of demand and under-utilized capacity. Also, the dynamic nature of landing slots availability and resulting congestion added to network design risks (Das et al., 2020). Details of UDAN regional connectivity scheme together with the challenges are addressed in Appendix A.

We focus on hub-and-spoke network design to address commercial viability that can alleviate connectivity issues in remote regions (Alumur et al., 2021). Ivanov and Dolgui (2020) proposed viability theory for supply chains and defined it as ‘the ability of the system to meet demands of surviving in a changing environment’. Recent reports suggests that long term unpredictability due to shifts in market conditions, pandemic disruption scenarios, and economic downturns has resulted in viability concerns for regional air travel connectivity schemes.¹ Survivability in the context of commercial viability can be fostered through joint consideration of agility, resilience and sustainability responses (Ivanov, 2022; Ivanov et al., 2023). The effectiveness and efficiency of various reconfigurations of networks can also be useful to improve commercial viability (Brusset et al., 2023; Dolgui et al., 2023; Sardesai & Klingebiel, 2023). Hence, we consider resilience, sustainability, and efficiency as objectives to enhance viability in regional air travel connectivity schemes.

Survivability models in the hub location literature have focused on economic and facility protection (against potential disruption) issues (An et al., 2015; Barahimi & Vergara, 2020; Ivanov, 2023; Kim, 2012). While hub protection models have included survivability issues (by considering backup routes), its application to regional air travel connectivity schemes are still under-explored. Further, there is a hierarchical decision-making process between the regulator (leader) and national and regional airline operators (two followers) who tend to have different objectives. Bilevel optimization is a useful methodology to tackle this problem (Bracken & McGill, 1974; Moore & Bard, 1990). We formulate viable hub location problem for regional air travel connectivity schemes as a multi-objective bilevel program with a single leader and two independent followers. While the economic objective of cost minimization is crucial for operational viability of operators, other objectives like resilience and social sustainability (enhancing reach) may be needed by regulator to address long-term viability. We apply the hub protection model approach for regional air travel connectivity schemes by considering the primary and regional hub locations as a strategy to improve resilience for viability. Thus, all the traffic flows through primary hubs to improve operational efficiency of the network during normal times. However, during congestion and disruption, rerouting all the demand through regional hubs minimizes traffic loss and also improving social sustainability (Pourmohammadi et al., 2023). Over and above the objective of resilience, an maximizing social utility is considered as a societal goal and is just as important for viability (Ivanov & Keskin, 2023). Thus, we include responsibility (of maximizing reach) as an objective for viability because it creates sustainable economic and social goals (like employment growth) under the triple (people, profits, and planet) bottom line framework (Sodhi, 2015; Tang, 2018). To summarize, the research questions used in this paper is formulated as follows:

• How can regional air travel connectivity schemes remain viable and sustain operations?

• How can resilience and social objectives of sustainability (like enhancing reach) improve viability in hub location problems that include regional connectivity?

• How can viable hub location analysis enhance the operational routes for regional connectivity scheme in a hierarchical decision-making environment involving government agency and airline operators?

This paper is structured as follows. Section 2 focuses on the literature review on resilient and sustainable hub location models for viable operations. Section 3 highlights the fundamental concepts for multi-objective single leader and multi follower bilevel optimization, and the proposed formulation for the regional connectivity. Section 4 presents the solution approaches for the model. Section 5 presents the computational results and the application of our proposed approach to the empirical data sets of UDAN scheme in India and standard Civil Aeronautics Board (CAB) dataset in USA. Section 6 presents the managerial and policy implications. Section 7 concludes the paper with limitations, and suggestions for future research.

2 Overview of related literature

We examine past research in the hub location literature that focus on commercial viability to identify opportunities to improve remote connectivity. Since the seminal work by O’Kelly (1986), hub location problems have continued to provide a plethora of opportunities to improve transportation and telecommunications systems (Alumur et al., 2021; Campbell, 1994; Kim & O’Kelly, 2009). A hub acts as a trans-shipment, consolidation, or sorting center for several connected nodes by exploiting economies of scale associated to the flows routed through each pair of hub nodes (Campbell, 1994; Contreras et al., 2011; Ernst & Krishnamoorthy, 1998). To improve the viability of aviation regional connectivity, a hub network needs to be designed to tackle operational and disruption risks along with meeting social responsibility aspects of sustainability. We augment the extant research in hub-and-spoke models by incorporating resilience and sustainability in networks and summarize the findings in Table 1.

Table 1 Addressing related hub-and-spoke literature

The hub location literature has addressed resilience as a recovery strategy against operational and disruption risks (Zhalechian et al., 2018). O’Kelly (2015) specified that hub networks require strengthened defences to address vulnerability of hub interconnection points. Zhalechian et al. (2018) identified multiple fortification avenues to build proactive capability, and business continuity using measures like reactive capability and design quality characteristics that could help improve resiliency in hub networks. Similarly, Kim (2012) developed hub protection models to specifically incorporate survivability in network designs to overcome possible disruption situations and used backup routing schemes as proactive capability measures to enhance network resilience. Masoumzadeh et al. (2016) built on the work of Kim (2012) by maximizing flows through node pairs with poorest potential flow given budget restrictions. Rahimi et al. (2019)’s hub protection model demonstrated the fact that capacity levels and transportation modes influences transportation cost and time. An et al. (2015) illustrated the use of backup hubs and alternate routes to proactively handle hub disruptions and found that failure of hubs and reactive disruption management could face higher recovery costs. In contrast, Yildiz and Karasan (2015) pointed that pursuing survivability comes with a high price including making drastic changes to the network design. Two interesting studies by Azizi et al. (2016) and Mokhtar et al. (2019) also proposed solutions to the problem of high transportation costs. Azizi et al. (2016) demonstrated that if hub unavailability is considered at the design stage, there could be considerable reduction in expected transportation costs associated with disruptions. Mokhtar et al. (2019) proposed that allocating exactly two hubs to a non-hub node can help the network survive against link failures. Overall, we infer that multiple allocation models with backup facilities help improve resilience of the network. Accordingly, we seek to identify primary and regional hubs for regional connectivity in order to improve viability.

Hub location models addressing network disruptions have been modelled as bilevel problems. Bilevel optimization helps solve two-person non-cooperative games wherein players move in sequence as leader and follower respectively. For example, Parvaresh et al. (2013) using this approach reported that disruptions at hubs could severely affect network's performance. Multi-objective multiple allocation hub median problems under intentional disruptions have also been addressed using the bilevel model (Parvaresh et al., 2014). In this research study, reliability is accomplished by identifying worst-case and normal transportation costs. In the extant literature, interdiction and fortification problems have also been formulated using bilevel and trilevel optimization approaches respectively (Lei, 2013; Ramamoorthy et al., 2018). Specifically, fortification strategy strengthens the network against intentional disruptions (Ghaffarinasab & Atayi, 2018; Ramamoorthy et al., 2018). The usefulness of bilevel optimization approach for regional air travel connectivity is based on expert judgement and past seminal references in the extant literature. To the best of our knowledge, bilevel optimization with single leader with two independent followers in hub location literature is still unexplored.

The hub location literature have also addressed sustainability aspects like social responsibility and environment. Zhalechian et al. (2017) considered economical, responsiveness, and social responsibility while designing the hub-and-spoke network. They identified social responsibility as key goals for regions of high unemployment and less economic growth. Interestingly, Pourmohammadi et al. (2023) discovered that as number of hubs increased, job opportunities and regional development also increased. However, in tandem, fixed costs and routing costs also increased. Mohammadi et al. (2014) explored economic and environmental decisions simultaneously and identified the optimal vehicle speed to reduce air and noise pollution. Niknamfar and Niaki (2016) proposed a bi-objective hub location model with centralized carrier collaboration between holding companies and carriers and pointed out that taxes and number of vehicles influenced fuel consumption and profit. Dukkanci et al. (2019) modelled the green hub location problem and identified that emissions behaved as a convex function to the number of hubs. While green investments can be explored (Adnan et al., 2023), we focus on social responsibility aspect of sustainability to improve reach in regional air travel connectivity schemes. There is an increasing interest among researchers to explore social sustainability aspects of business during disruptions (Bag et al., 2022).

Government policies that influence air connectivity to remote regions are classified under four categories, namely, route-based policies, passenger-based policies, airline-based policies, and airport-based policies (Fageda et al., 2018). The route-based policy is suitable in deregulated airline markets like USA, European Union, Australia, Malaysia, and India, because it provides subsidy to an airline for plying a commercially unviable/untested route (Wittman et al., 2016). The passenger-based policy provides discounts to passengers in remote regions on domestic flights that cater to key travel needs such as medical care. Ecuador, Scotland, Spain, and Portugal provide this type of policy (Fageda et al., 2017). The airline-based policy is suitable where state-owned airlines support air services in remote regions which may otherwise be unprofitable. Canada, Malaysia, Colombia, India, and Ecuador follow this policy (Fageda et al., 2018). Finally, the airport-based policy provides subsidies to airport operators to expand or improve the capacity of available infrastructure to enhance regional connectivity. Canada, European Union, Brazil, Australia, and USA have airport programs to support this policy (Smyth et al., 2012). Specifically, the UDAN scheme focuses on expanding the aviation footprint in India as well as connecting to remote areas (Das et al., 2022). Accordingly, we incorporate social objectives such as fare subsidies to improve regional connectivity and maximize reach to enhance connectivity. The affordability of such routes is ensured by limiting the fare on a maximum of half of available seats to fares set by the operator (Iyer & Thomas, 2021). Similarly, in the EAS scheme, a community is eligible for funds if it is beyond 70 highway miles from the nearest Federal Aviation Administration (FAA) medium hub or large hub. While nearly 64% of the US population lives within 70 miles of medium or large sized hub, consolidation of traffic occurs at larger airports resulting in airport leakage (Grubesic & Matisziw, 2011). Overall, we speculate that EAS, PSO, and UDAN schemes differ in terms of degree of attainment of social objectives based on the research findings summarized in Table 2.

Table 2 Key studies that addressed regional airline connectivity

As can be observed from the above review, resilience and sustainability has attracted attention in the hub location problems in independent research silos. Building regional connectivity as a specific research objective has been understudied in the past literature. Our hunch is that by considering resilience and responsibility elements of sustainability together in hub-and-spoke networks, a better understanding between economic (cost) and social goals (reach) can be facilitated within regional air travel connectivity schemes in order to remain viable in the future.

3 Problem description and model formulation

We study a setting in which the regulator is the leader or system planner. Since only non-congested primary hubs (used for international and domestic travel) needed to be chosen by the regulator, additional regional hubs are opened. Thus, the leader moves first by choosing a subset of r primary hubs from the existing set H of p well served airports and opening q regional hubs. The objective of the regulator is to minimize the traffic loss of followers’ optimal route based on minimization of transportation unreliability through r primary hubs and q regional hubs. Similarly, over and above the economic objective of cost minimization (or profit maximization), maximizing social utility is an important objective. Thus, the regulator maximizes responsibility based on employment and economic development measures for the q regional hubs. On the contrary, the national and regional airline operators, who are the independent followers, focus on reducing transportation costs. Specifically, we formulate a multi objective bilevel program with the role of regulator at the upper level and independent national and regional airline operators at the lower level in decision-making.

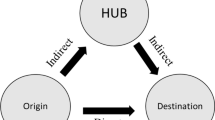
The multi-objective bilevel optimization problems are hierarchical leader–follower Stackelberg games comprising several subsystems with conflicting goals (Parvaresh et al., 2014). These problems are non-linear and find many practical applications, especially in engineering design organizations (Sinha et al., 2018). The mathematical equations can be simplified if the problems optimize multiple conflicting goals at the upper level with independent objective functions at the lower level (Calvete & Galé, 2007). The regulator’s decisions to choose only a subset of well-served hubs for efficient regional connectivity adversely impacts (cannibalizes) the overall performance of the existing hub network. Further, increasing the number of hubs in regional cities could further deteriorate the profits of national and regional airline operators. Our bilevel model provides an opportunity to the regulator to improve resilience and responsibility by including those regional hubs which increases reach of the network potentially enhancing social objectives. Also, rerouting through regional hubs by airline operators improves protection of remaining hubs against disruptions. Since, we have independent followers, the route disruption of national airline operator does not impact regional airline operator. We created a Viable Hub Location Problem for Regional Connectivity (VHLRC) model based on the proposed configuration (Fig. 1) and subsequent formulation.

Fig. 1

Bilevel Hub location problem with regulator and two independent operators

In VHLRC, the regulator focuses on airport-based policies according to the operators’ decisions of route allocation. We introduce the following notation in Table 3.

Table 3 Bilevel model index, parameters and decision variables

Based on these notations, the multi-objective bilevel program is presented as follows:

$$ \begin{aligned}\mathop {\min }\limits_{z,zb} F_{1} \left( {X,Y,z,zb} \right) = &\,\mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} (L_{ijkm} X_{ijkm} + \mathop \sum \limits_{n} \overline{L}_{ijkm} LB_{ijn} X_{ijkm} Y_{ijn} )\\ & + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \Gamma_{ij} (PL_{ijkm} X_{ijkm} \\ &+ \mathop \sum \limits_{n} \overline{PL}_{ijkm} PLB_{ijn} X_{ijkm} Y_{ijn} )\end{aligned} $$

(1)

$$ \mathop {\max }\limits_{z,zb} F_{2} \left( {X,Y,z,zb} \right) = Wen\mathop \sum \limits_{{n \in N/\left\{ I \right\}}} (FJ_{n} + VJ_{n} )ur_{n} zb_{n} + Wed\mathop \sum \limits_{{n \in N/\left\{ I \right\}}} EV_{n} \left( {1 - rd_{n} } \right)zb_{n} - Wen*v*\mathop \sum \limits_{k \in H} (FJ_{k} + VJ_{k} )ur_{k} \left( {1 - z_{k} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} U_{ij} T_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} U_{ij} T_{ijn} Y_{ijn} $$

(2)

subject to

$$ \mathop \sum \limits_{k\varepsilon H} z_{k} = r $$

(3)

$$ \mathop \sum \limits_{{n \in N/\left\{ I \right\}}} zb_{n} = q $$

(4)

$$ z_{k} + zb_{k} \le 1 \quad \forall k \in H $$

(5)

$$ d_{kn} \ge d^{man} - M\left( {2 - z_{k} - zb_{n} } \right)\quad \forall k \in H,n \in N $$

(6)

$$ z_{k} \in \left\{ {0,1} \right\}\quad \forall k \in H $$

(7)

$$ zb_{n} \in \left\{ {0,1} \right\} \quad \forall n \in N $$

(8)

where national airline operator solves X through

$$ \mathop {{\text{min}}}\limits_{X} f\left( {X,z} \right) = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij}^{na} d_{ijkm} X_{ijkm} $$

(9)

subject to

$$ \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} X_{ijkm} = 1\quad \forall i,j \in N $$

(10)

$$ \mathop \sum \limits_{m \in H} X_{ijkm} + \mathop \sum \limits_{{m \in H/\left\{ k \right\}}} X_{ijmk} \le z_{k} \quad \forall i,j \in N, k \in H $$

(11)

$$ X_{ijkm} \ge 0\quad \forall i,j \in N, k,m \in H $$

(12)

and regional airline operator solves Y through

$$ \mathop {{\text{min}}}\limits_{Y} f\left( {Y,zb} \right) = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij}^{ra} d_{ijn} Y_{ijn} $$

(13)

subject to

$$ \mathop \sum \limits_{n \in N} Y_{ijn} = 1\quad \forall i,j \in N $$

(14)

$$ Y_{ijn} \le zb_{n} \quad \forall i,j,n \in N $$

(15)

$$ Y_{ijn} \ge 0\quad \forall i,j,n \in N $$

(16)

In VHLRC, objective (1) comprises of disruption risk and operational risk. The disruption risk (resilience loss) according to the routing scheme through primary and regional routes, is calculated similar to p-hub protection model with primary and secondary routes (PROPS), as addressed by Kim (2012). Secondly, operational risk is revenue loss due to underutilization of the aircraft. This is addressed using the passenger load factor. The overall traffic loss (disruption + operational risk) for the network is calculated based on the reliability for individual routes using Boolean logic. For example, considering inter-hub reliability factor ${\alpha }_{r}=0$ and intra-hub reliability factor ${\gamma }_{n}=1$, the disruption risk is addressed in Fig. 2. Similarly, we calculated the operational risk.

Fig. 2

Computation of disruption risk through primary and regional hubs

The objective (2) related to social responsibility includes employment opportunities and economic growth from the regional hubs (Zhalechian et al., 2017) and fare subsidies. The employment opportunities include fixed-job opportunities (managerial positions) and variable job opportunities (workers). The objective for responsibility also included the potential job loss due to lesser primary hubs for regional connectivity. Since primary hubs are already developed, we do not include a measure of economic growth for the primary hubs. Further, the objective includes the revenue generated from the fraction of RCS seats sold in RCS flights at a subsidized fare.

The constraint (3) ensures that r primary hubs remain open, while constraint (4) indicates the opening of q regional hubs. Constraint (5) restricts the co-location of primary and regional hubs. Constraint (6) is the mandatory dispersion constraint which ensures that the primary and regional hubs are not located closer than $d^{man}$. Here $M$ is a large number greater than $\mathop {\max }\limits_{k,n} d_{kn}$. Constraint (7)-(8) imposes integrality on the primary and regional hub facilities.

The national airline operator at the lower level has the objective (9) to minimize the transportation cost of opening primary hubs pre-congestion or disruption. Constraint (10) restricts the flow between source i and destination j via primary hubs k and m. Constraint (11) is the facet defining constraint ensuring that flow be sent through open primary hubs only (Hamacher et al., 2004). The regional airline operator at the lower level has the objective (13) to minimize the transportation cost of opening regional hubs post-congestion or disruption. Constraint (14) selects one regional hub n for each Origin–Destination (O-D) pair $\left( {i,j} \right)$, and Constraint (15) ensures that flow is sent only through open regional hubs. Finally, Constraints (12) and (16) are the non-negativity constraints on fractional flows. To address survivability, we assume that the national and regional airline operator fulfill the same demand to mitigate disruption, i.e., $W_{ij}^{na} = W_{ij}^{ra} = W_{ij}$.

• Capacity constraints of primary hub

The capacitated version of the problem includes the restriction of flow from primary hub by the national airline operator. Constraint (17) models the capacity constraints.

$$ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} W_{ij} X_{ijkm} \le \tau_{k} z_{k} \quad \forall k \in H $$

(17)

We have independent followers with separate decision variables in the bilevel formulation for both uncapacitated and capacitated problems. We can convert the bilevel problem with single follower by adding the objectives of the followers and using all lower-level constraints (Calvete & Galé, 2007). Thus, the objective function of the follower converts to:

$$ \mathop {{\text{min}}}\limits_{X,Y} f\left( {X,Y,z,zb} \right) = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} $$

(18)

4 Solution approach

4.1 Closest assignment constraints for uncapacitated problem

The uncapacitated version of the problem can be reduced to a bi-objective single-level optimization problem by exploiting the structure of the lower-level problem. The airline operator reallocates demand nodes to surviving hubs to fulfill allocation at minimum possible cost. This allocation can be possible through Closest Assignment Constraint (CAC) formulation which allocate the node to the closest open hub since the network satisfies triangular inequality and identical economies of scale on inter-hub links. Espejo et al. (2012) gave a summary of CACs applicable to the discrete location problems in literature. We model CACs for our problem using a similar approach.

We start with Wagner and Falkson (1975) (WF) CAC, also proposed by Ramamoorthy et al. (2018) for hub interdiction problems. Additional constraints are added, which forbids the assignment of flows between any O-D pair to a path costlier than path $i \to k \to m \to j$ till hubs k and m are open, and path $i \to n \to j$ till hub n is open.

$$ \mathop \sum \limits_{{\left( {q,s} \right) \in E_{ijkm} }} X_{ijqs} \le 2 - z_{k} - z_{m}\quad \forall\, i,j \in N, k,m \in H $$

(CAC1a)

where $E_{ijkm} = \left\{ {\left( {q,s} \right)\left| {d_{ijqs} } \right\rangle d_{ijkm} } \right\}$

$$ \mathop \sum \limits_{{\left( a \right) \in A_{ijn} }} Y_{ija} \le 1 - zb_{n} \quad \forall \,i,j,n \in N $$

(CAC1b)

where $A_{ijn} = \left\{ {\left( a \right)\left| {d_{ija} } \right\rangle d_{ijn} } \right\}$.

Second, we use the CAC proposed by Church and Cohon (1976) (CC) applicable to energy facility siting and construct for our problem.

$$ \mathop \sum \limits_{{\left( {q,s} \right) \in C_{ijkm} }} X_{ijqs} + X_{ijkm} \ge z_{k} + z_{m} - 1 \quad \forall i,j \in N, k,m \in H $$

(CAC2a)

where $C_{ijkm} = \left\{ {\left( {q,s} \right)|d_{ijqs} < d_{ijkm} or \left( {d_{ijqs} = d_{ijkm} and \left( {q \ne k or \left( {q = k and s \ne m} \right)} \right)} \right)} \right\}$

$$ \mathop \sum \limits_{{\left( a \right) \in C_{ijn} }} Y_{ija} + Y_{ijn} \ge zb_{n} \quad \forall i,j,n \in N $$

(CAC2b)

where $C_{ijn} = \left\{ {\left( a \right)|d_{ija} < d_{ijn} or \left( {d_{ija} = d_{ijn} and a \ne n} \right)} \right\}$.

Third, we use the CAC proposed by Dobson and Karmarkar (1987) (DK) applicable to competitive location and construct the same for our problem.

$$ X_{ijkm} \le 2 - z_{q} - z_{s} \quad \forall i,j \in N, k,m \in H,\;\{ \left( {q,s} \right)|d_{ijqs} < d_{ijkm} \} $$

(CAC3a)

$$ Y_{ijn} \le 1 - zb_{a} \quad \forall i,j,n \in N, \{ \left( a \right)|d_{ija} < d_{ijn} \} $$

(CAC3b)

Fourth, we utilize the CAC by Rojeski and ReVelle (1970) (RR) in the context of budget constrained median problem for the backup route. RR ensures that if a regional hub is located at $n$, and there is no other regional hub closer to O-D pair $\left( {i,j} \right)$ ($zb_{a} : a \in C_{ijn} )$, then $\left( {i,j} \right)$ must be assigned to hub $n$.

$$ X_{ijkm} + \mathop \sum \limits_{{\left( {q,s} \right) \in C_{ijkm} }} z_{qs} \ge z_{k} + z_{m} - 1 \quad \forall i,j \in N, k,m \in H $$

(CAC4a)

$$ Y_{ijn} + \mathop \sum \limits_{{a \in C_{ijn} }} zb_{a} \ge zb_{n} \quad \forall i,j,n \in N $$

(CAC4b)

where, $z_{km} = 1$ when both the hubs k and m are open. Thus, $z_{km}$ is defined as the product as $z_{km} = z_{k} z_{m}$. The following constraints are added to linearize this equality.

$$ z_{km} \ge z_{k} + z_{m} - 1\quad \forall k,m \in H $$

(CAC4c)

$$ z_{km} \le z_{k} \quad \forall k,m \in H $$

(CAC4d)

$$ z_{km} \le z_{m} \quad \forall k,m \in H $$

(CAC4e)

• Reduced formulation of CACs

The refinement to primary route CACs is based on the dominance principles that leads to fewer constraints(Ramamoorthy et al., 2018). For a given O-D pair $\left( {i,j} \right)$ and hubs k and m $\left( {m \ne k} \right)$, $CAC_{ijkm}$ dominates $CAC_{ijmk}$ when $d_{ijkm} < d_{ijmk}$. For a given set $H_{ij}{\prime} = \left\{ {H_{ijkm}^{^{\prime\prime}} {|}k,m \in H,k \le m} \right\}$ for an O-D pair $\left( {i,j} \right)$, where,

$$ H_{ijkm}^{^{\prime\prime}} = \left\{ {\begin{array}{*{20}c} {\left( {k,m} \right) \quad if\quad d_{ijkm} \le d_{ijmk} } \\ {\left( {m,k} \right)\quad if\quad d_{ijkm} > d_{ijmk} } \\ \end{array} } \right. $$

For example, the CAC1a can be re-written as follows:

$$ \mathop \sum \limits_{{\left( {q,s} \right) \in E_{ijkm} }} X_{ijqs} \le 2 - z_{k} - z_{m} \quad \forall i,j \in N;\left( {k,m} \right) \in H_{ij}{\prime} $$

Similarly, we re-write the other primary route CACs as well by replacing $\left( {k,m} \right) \in N$ with $\left( {k,m} \right) \in H_{ij}{\prime}$. This reduced CAC constraint set has $\left| N \right|^{2} \left( {\frac{{p^{2} + p}}{2}} \right)$ constraints compared to $\left| N \right|^{2} p^{2}$ constraints.

4.2 Strong duality conditions

The lower-level problem for the airline operator in VHLRC is a linear program with continuous variables. We use strong duality conditions to reduce the uncapacitated problem to the single level. While KKT conditions can also be explored, finding an appropriate big-$M$ in KKT reformulation is as hard as solving the original bilevel problem since the value may cut off the optimal point of the lower level dual problem (Kleinert et al., 2020). Therefore, we apply the valid primal–dual inequalities by exploiting the strong duality condition as addressed by Kleinert et al. (2021).

For the given upper-level variables $z_{k}^{*}$ and $zb_{n}^{*}$, we use $\varnothing_{ij}$,$\delta_{ij}$, $\lambda_{ijk}$ and $\varphi_{ijn}$ as the dual variables to get Lagrangian relaxation $LR$ as follows:

$$ LR = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} \left( {\mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} X_{ijkm} - 1} \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} \left( {\mathop \sum \limits_{n \in N} Y_{ijn} - 1} \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \lambda_{ijk} (\mathop \sum \limits_{m \in H} X_{ijkm} + \mathop \sum \limits_{{m \in H/\left\{ k \right\}}} X_{ijmk} - z_{k}^{*} ) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \varphi_{ijn} \left( {Y_{ijn} - zb_{n}^{*} } \right) $$

Differentiate with respect to ${X}_{ijkm}$, we get

$$ \emptyset_{ij} + \lambda_{ijk} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k = m $$

$$ \emptyset_{ij} + \lambda_{ijk} + \lambda_{ijm} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k \ne m $$

$$ \lambda_{ijk} \le 0, \emptyset_{ij} \in {\mathbb{R}}\quad \forall i,j \in N, k \in H $$

Differentiate with respect to $Y_{ijn}$, we get

$$ \delta_{ij} + \varphi_{ijn} \le W_{ij} d_{ijn} \quad \forall i,j,n \in N $$

$$ \varphi_{ijn} \le 0, \delta_{ij} \in {\mathbb{R}}\quad \forall i,j,n \in N $$

Unlike the CAC formulation, the capacitated version of the problem can also be reduced using the strong duality conditions. For the given upper-level variables $z_{k}^{*}$ and $zb_{n}^{*}$, we use $\phi_{ij}$,$\delta_{ij}$, $\lambda_{ijk}$, $\varphi_{ijn}$, and $\omega_{k}$ as the dual variables to get Lagrangian relaxation $LR$ as follows:

$$ LR = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} \left( {\mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} X_{ijkm} - 1} \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} \left( {\mathop \sum \limits_{n \in N} Y_{ijn} - 1} \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \lambda_{ijk} (\mathop \sum \limits_{m \in H} X_{ijkm} + \mathop \sum \limits_{{m \in H/\left\{ k \right\}}} X_{ijmk} - z_{k}^{*} ) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \varphi_{ijn} \left( {Y_{ijn} - zb_{n}^{*} } \right) + \mathop \sum \limits_{k \in H} \omega_{k} \left( {\mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} W_{ij} X_{ijkm} - {\uptau }_{k} z_{k}^{*} } \right) $$

Differentiate with respect to $X_{ijkm}$, we get

$$ \emptyset_{ij} + \lambda_{ijk} + W_{ij} \omega_{k} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k = m $$

$$ \emptyset_{ij} + \lambda_{ijk} + \lambda_{ijm} + W_{ij} \omega_{k} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k \ne m $$

$$ \lambda_{ijk} \le 0, \omega_{k} \le 0,\emptyset_{ij} \in {\mathbb{R}}\quad \forall i,j \in N, k \in H $$

Differentiate with respect to $Y_{ijn}$, we get

$$ \delta_{ij} + \varphi_{ijn} \le W_{ij} d_{ijn} \quad \forall i,j,n \in N $$

$$ \varphi_{ijn} \le 0, \delta_{ij} \in {\mathbb{R}}\quad \forall i,j,n \in N $$

The single-level multi-objective uncapacitated problem with strong duality conditions can be written as:

$$ \mathop {\min }\limits_{X,Y,z,zb} F1 = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} (L_{ijkm} X_{ijkm} + \mathop \sum \limits_{n} \overline{L}_{ijkm} LB_{ijn} X_{ijkm} Y_{ijn} ) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \Gamma_{ij} \left( {PL_{ijkm} X_{ijkm} + \mathop \sum \limits_{n} \overline{PL}_{ijkm} PLB_{ijn} Y_{ijkmn} } \right) $$

(19)

$$ \mathop {\max }\limits_{X,Y,z,zb} F2 = Wen\mathop \sum \limits_{{n \in N/\left\{ I \right\}}} (FJ_{n} + VJ_{n} )ur_{n} zb_{n} + Wed\mathop \sum \limits_{{n \in N/\left\{ I \right\}}} EV_{n} \left( {1 - rd_{n} } \right)zb_{n} - Wen*v*\mathop \sum \limits_{k \in H} (FJ_{k} + VJ_{k} )ur_{k} \left( {1 - z_{k} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} U_{ij} T_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} U_{ij} T_{ijn} Y_{ijkmn} $$

(20)

subject to.

(3)-(8), (10)-(12), (14)-(16)

$$ \emptyset_{ij} + \lambda_{ijk} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k = m $$

(21)

$$ \emptyset_{ij} + \lambda_{ijk} + \lambda_{ijm} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k \ne m $$

(22)

$$ \delta_{ij} + \varphi_{ijn} \le W_{ij} d_{ijn} \quad \forall i,j,n \in N $$

(23)

$$ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \lambda_{ijk} z_{k} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \varphi_{ijn} zb_{n} $$

(24)

$$ \lambda_{ijk} ,\varphi_{ijn} \le 0, \emptyset_{ij} , \delta_{ij} \in {\mathbb{R}}\quad \forall i,j,n \in N, k,m \in H $$

(25)

The bilinear terms in (24) are replaced as $\sum_{i\in N}\sum_{j\in N}{\lambda }_{ijk}{z}_{k}= {V}_{k}$ and $\sum_{i\in N}\sum_{j\in N}{\varphi }_{ijn}{zb}_{n}={B}_{n}$. We replace (24) with constraints (26) and linearization (27)-(31) referred as LI1.

$$ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} + \mathop \sum \limits_{k \in H} V_{k} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} + \mathop \sum \limits_{n \in N} B_{n} $$

(26)

$$ V_{k} \ge - M_{k}^{a} z_{k} \quad \forall k \in H $$

(27)

$$ V_{k} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \lambda_{ijk} + M_{k}^{c} \left( {1 - z_{k} } \right)\quad \forall k \in H $$

(28)

$$ B_{n} \ge - M_{n}^{a} zb_{n} \quad \forall k \in H $$

(29)

$$ V_{k} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \varphi_{ijn} + M_{n}^{a} \left( {1 - zb_{n} } \right)\quad \forall k \in H $$

(30)

$$ V_{k} ,B_{n} \le 0\quad \forall k \in H, n \in N $$

(31)

where $M_{k}^{a} = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} W_{ij} \left( {\mathop {\max }\limits_{k,m} d_{ijkm} } \right) - \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} W_{ij} \left( {\mathop {\min }\limits_{m} d_{ijkm} } \right), \quad \forall k \in H$ and $M_{n}^{a} = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} W_{ij} \left( {\mathop {\max }\limits_{n} d_{ijn} } \right), \quad \forall n \in N$ are found from the shadow prices $\left( {\lambda_{ijk} ,\varphi_{ijn} } \right)$ of the constraint (11) and (15) respectively.

Similarly, single-level multi-objective capacitated problem with strong duality conditions can be written as:

Objectives (19), (20)

subject to.

(3)–(8), (10)–(12), (14)–(17), (23), (25), LI1,

$$ \emptyset_{ij} + \lambda_{ijk} + W_{ij} \omega_{k} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k = m $$

(32)

$$ \emptyset_{ij} + \lambda_{ijk} + \lambda_{ijm} + W_{ij} \omega_{k} \le W_{ij} d_{ijkm} \quad \forall i,j \in N, k,m \in H, k \ne m $$

(33)

$$ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} + \mathop \sum \limits_{k \in H} V_{k} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} + \mathop \sum \limits_{n \in N} B_{n} + \mathop \sum \limits_{k \in H} \vartheta_{k} \tau_{k} $$

(34)

$$ \vartheta_{k} \le \omega_{k} + M_{k}^{b} \left( {1 - z_{k} } \right)\quad \forall k \in H $$

(35)

$$ \vartheta_{k} \ge \omega_{k} \quad \forall k \in H $$

(36)

$$ \vartheta_{k} \ge - M_{k}^{b} \left( {z_{k} } \right)\quad \forall k \in H $$

(37)

$$ \vartheta_{k} ,\omega_{k} \le 0 \quad \forall k \in H $$

(38)

Linearization (35)–(38) are referred as LI2 where ${M}_{k}^{b}=\underset{i,j\in N, m\in H}{{\text{max}}}{d}_{ijkm}$ is the shadow price for constraint (17).

Alternatively, in place of facet defining constraint (11), constraints (39)–(40) help generate the alternate set of valid inequality (41):

$$ \mathop \sum \limits_{m \in H} X_{ijkm} \le z_{k} \quad \forall i,j \in N, k \in H $$

(39)

$$ \mathop \sum \limits_{k \in H} X_{ijkm} \le z_{m} \quad \forall i,j \in N, m \in H $$

(40)

$$ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \lambda_{ijk} z_{k} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} \lambda_{ijm} z_{m} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \varphi_{ijn} zb_{n} $$

(41)

Bilinear constraint (41) is linearized using the standard approach of McCormick envelopes. Thus, we replace (41) with (42) and linearization (43)–(52), which is referred as LI3:

$$ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \propto_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} \beta_{ijm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \varsigma_{ijn} $$

(42)

$$ \propto_{ijk} \le \lambda_{ijk} + M_{ij}^{a} \left( {1 - z_{k} } \right)\quad \forall i,j \in N, k \in H $$

(43)

$$ \propto_{ijk} \ge \lambda_{ijk} \quad \forall i,j \in N, k \in H $$

(44)

$$ \propto_{ijk} \ge - M_{ij}^{a} z_{k} \quad \forall i,j \in N, k \in H $$

(45)

$$ \beta_{ijm} \le \lambda_{ijm} + M_{ij}^{a} \left( {1 - z_{m} } \right)\quad \forall i,j \in N, m \in H $$

(46)

$$ \beta_{ijm} \ge \lambda_{ijm} \quad \forall i,j \in N, m \in H $$

(47)

$$ \beta_{ijm} \ge - M_{ij}^{a} z_{m} \quad \forall i,j \in N, m \in H $$

(48)

$$ \varsigma_{ijn} \le \varphi_{ijn} + M_{ij}^{a} \left( {1 - zb_{n} } \right)\quad \forall i,j,n \in N $$

(49)

$$ \varsigma_{ijn} \ge \varphi_{ijn} \quad \forall i,j,n \in N $$

(50)

$$ \varsigma_{ijn} \ge - M_{ij}^{a} zb_{n} \quad \forall i,j,n \in N $$

(51)

$$ \propto_{ijk} , \beta_{ijm} ,\varsigma_{ijn} \le 0\quad \forall i,j,n \in N, k,m \in H $$

(52)

where $M_{ij}^{a} = \mathop {\max }\limits_{k,m \in H} W_{ij} d_{ijkm}$ are valid values for big-M for $i,j \in N$.

For the capacitated problem, constraint (42) is replaced with (53) and LI1 with LI3 in SD1:

$$ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} d_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} W_{ij} d_{ijn} Y_{ijn} \le \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \emptyset_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \propto_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} \beta_{ijm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \delta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \varsigma_{ijn} + \mathop \sum \limits_{k \in H} \vartheta_{k} {\uptau }_{k} $$

(53)

4.3 Linearized reformulation

Overall, the bilevel multi-objective problems are converted to single-level multi-objective problems. However, the traffic loss objective (19) is still bilinear. The linearization strategy, as applied by An et al. (2015), is used to create the compact reformulation for the objective function. The number of variable changes is minor, and constraints change only linearly. We replace (19) with (54) for uncapacitated and capacitated problems:

$$ \mathop {\min }\limits_{X,Y,z,zb,\Omega ,s} F1 = \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} L_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \Gamma_{ij} PL_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \left( {\Omega_{ijn} - \sigma_{ij} Y_{ijn} } \right) $$

(54)

Constraints (55)–(56) are added to achieve the linearization:

$$ \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} \overline{L}_{ijkm} LB_{ijn} X_{ijkm} + \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} X_{ijkm} - s_{ijn} + \sigma_{ij} = \Omega_{ijn} \quad \forall i,j,n \in N $$

(55)

$$ s_{ijn} \le \left( {\mu_{ij} + \sigma_{ij} } \right)\left( {1 - Y_{ijn} } \right)\quad \forall i,j,n \in N $$

(56)

$\mu_{ij} = W_{ij} \mathop {\max }\limits_{k,m \in H, n \in N} (L_{ijkm} + \overline{L}_{ijkm} LB_{ijn} ) + \Gamma_{ij} \mathop {\max }\limits_{k,m \in H, n \in N} (PL_{ijkm} + \overline{PL}_{ijkm} PLB_{ijn} )\break$ and $\sigma_{ij} = 0$ are the predetermined coefficients similar to An et al. (2015). We add new variables ${\Omega }_{ijn} , {\text{s}}_{ijn}$ to linearize the quadratic term $\mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \mathop \sum \limits_{n \in N} W_{ij} \overline{L}_{ijkm}\break LB_{ijn} X_{ijkm} Y_{ijn} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \mathop \sum \limits_{n} \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} X_{ijkm} Y_{ijn}$ in the objective and add constraints (55), (56). The number of variables and constraints introduced are $O\left( {\left| {\text{N}} \right|^{3} } \right)$, thus not exceeding model’s complexity significantly.

4.4 Multi objective optimization

The linearized single-level reformulation, as depicted is still having multiple objectives of the regulator. Hence, two solution approaches, namely, fuzzy goal programming (Zimmerman, 1983) and fair optimization (Sawik, 2015), are proposed in this work to solve the multi-objective optimization problem as depicted in Appendix B. We compare the approaches to generate trade-offs.

4.5 Benders decomposition

We apply Benders decomposition as depicted in Appendix C to the fastest linearization for traffic loss objective for the uncapacitated and capacitated versions. The traditional Benders decomposition algorithm progressively solves a more information-rich master problem in each iteration since we keep improving the integer solution vectors and Benders cuts respectively. We tune the parameters, namely MIPFocus and VarBranch, and add Lazy Benders cuts in Gurobi solver to accelerate the convergence, which has shown positive results in our experiments.

5 Computational results

We perform the computational experiments to the USA and India datasets respectively. All computational outcomes are performed using Python 3.9 with Gurobi version 10.0.0 on a server with Intel(R) Core i5-1135G7 CPU @2.4 GHz and 16 GB of RAM. We first perform a comparative study of the computational efficiencies of the formulated CACs for the uncapacitated version of the problem. We tested our approach for the USA’s CAB dataset initially and utilized the findings for the UDAN dataset. The performance profiles for alternate CACs shows the probability that CPU time of formulation $a$ is ${2}^{\tau }$ the CPU time for the most efficient formulation. ${\rho }_{a}(\tau )$ is the probability that $a$ is the most efficient formulation at $\tau =0$. The WF CAC performs better as compared to the other CACs in 84% of the instances as shown in Fig. 3. The relative performance of CC, DK and RR deteriorates in that order. Hence, we consider only WF CAC for the rest of the computational experiments.

Fig. 3

Performance profiles for various CACs

In order to calculate the intra-hub reliability for CAB dataset, we apply the method for calculating the disruption probability for the nodes as proposed by Sawik (2016). The disruption probability of node i is ${\pi }_{i}={p}^{*}+\left(1-{p}^{*}\right){p}^{r}+\left(1-{p}^{*}\right)(1-{p}^{r}){p}_{i}$, where ${p}^{*}$ is the global disruption probability with all nodes being simultaneously disrupted, ${p}^{r}$ is the regional disruption probability for geographic region r, and ${p}_{i}$ is the local disruption probability for node i. The intra-hub reliability for node i is ${\gamma }_{i}=(1-{\pi }_{i})$. We assume three regions for CAB dataset. The global disruption probability is assumed to be 10%. The coastal nodes are assumed to have 10% regional disruption probability, while the inland nodes have 5% regional disruption probability. Thus ${p}^{*}=0.1$ and ${p}^{r}=\{\mathrm{0.05,0.1}\}$. The local disruption ${p}_{i}$ is similar to An et al. (2015). The intra-hub reliability is assumed to be 0.8 for UDAN dataset due to lack of data related to disruption probability.

Distance-based measurement of disruption mitigation is vital for regional connectivity. We map the reliability for each route based on ${d}_{ij}$, the distance between nodes i and j. The route reliability is identified as ${r}_{ij}=\{1-\frac{{d}_{ij}}{\underset{i,\mathit{j\epsilon N}}{{\text{max}}}{d}_{ij}}\}$ similar to Korani and Eydi (2021). Hence, lower-capacity aircraft can be utilized for shorter routes. However, since the regional hubs should serve in geographically different areas, the mandatory separation between primary and regional hubs is assumed to be 500 miles for the CAB dataset and 500 km for UDAN dataset. Thus, new hubs will be located far apart from the identified primary hubs.

The weights for employment and economic growth parameters are taken as $U(\mathrm{5,10})$ and $U\left(\mathrm{10,15}\right)$ respectively, similar to Zhalechian et al. (2017). The probability of job loss if the well-served hub is not chosen for regional connectivity is taken as 0.2.

5.1 Validation of model on CAB dataset

The launch of the RCS scheme provides a good opportunity to implement the aforementioned multi-objective bilevel model given the strategic nature of hub location decision. While the EAS scheme in USA started in 1978 is based on the hub-and-spoke design, the CAB dataset of 1970 provides the opportunity to test the approach at the design stage itself (Fig. 4). The CAB dataset is used for $\left| N \right| = 25$, $p\varepsilon \left\{ {5,7} \right\}$, $r\varepsilon \left\{ {2,p - 2} \right\}$ and $q\varepsilon \left\{ {2, \ldots ,r} \right\}$ for the formulation. The p well served airports are found by solving the p-hub median problem for $\alpha ,$ = 0.2 and $\alpha_{r}$ is also assumed to be 0.2. The first five well served airports are assumed to be international hubs. However, the dataset only provides the cost/distance and the demand matrix. We ignore the passenger load factor in objective (1), and the revenue generated for regional route in objective (2) during the design stage.

Fig. 4

Commercial airports in USA in 2011 with details of 25 airports from CAB dataset

5.1.1 Model performance for the uncapacitated problem

The uncapacitated problem is first relaxed for the responsibility objective and checked for traffic loss objective. The numerical experiments generate different scenarios using different primary hubs and regional hubs as summarized in Tables 4, 5. Once the primary hubs are identified, the regional hubs are selected so that the dispersion from the remaining hubs is high, as shown in Fig. 5. Hence, this would help reduce the ripple effect in case of disruptions. With the same number of regional hubs, reducing the number of primary hubs reduces network's resilient performance. Similarly, the responsibility level also reduces as the number of primary hubs reduces. As the number of regional hubs in the network increase, the potential traffic loss reduces. Hence, the level of resilience of the network increase, and the alternate regional routes mitigates the impact of lesser number of primary hubs. Further, additional regional hubs also increase the level of responsibility.

Table 4 Results for uncapacitated problem corresponding to CAB dataset

Table 5 Results for capacitated problem corresponding to CAB dataset

Fig. 5

Primary and regional hubs for various configurations of uncapacitated problem

Hubs in Los Angeles (12), Dallas-Fort (7) and New York (17) are preferred primary hubs since these are highly dispersed across the geography, and they are open in 10, 9 and 7 out of 13 experimented instances respectively. When there are 7 primary hubs, San Francisco (22), a coastal hub, is not selected in 9 out of 10 instances. Denver (8) is the most preferred regional hub and is selected in all the experimented instances, followed by Cincinnati (5), selected in precisely 7 out of 13 instances. Next, Atlanta (1) and Boston (3) are selected in precisely 6 out of 13 instances. Computationally, SD1 is more efficient than SD2 for small-sized problems and reverse is true for large-sized problems. However, the CAC reformulation can solve all the instances much quicker. Benders decomposition further improved the solve time for some instances.

The model is then relaxed for the traffic loss objective and checked for responsibility objective. Chicago (4) and San Francisco (22) are preferred primary hubs in the experimented instances, followed by Los Angeles (12) and New York (17). New Orleans (16) and Tampa (24) are the most preferred regional hubs, followed by Atlanta (1). As the number of regional hubs increase, there is a significant increase in the responsibility levels. However, the traffic loss also increases with the number of regional hubs. All the instances are solved using SD and CAC formulations easily.

5.1.1.1 Model performance for the capacitated problem

The capacity constraints impact Dallas-Fort (7), New York (17) and San Francisco (22) more than other hubs. The results for traffic loss objective are like the uncapacitated problem for 10 out of 13 instances. Surprisingly, in two of the instances, Dallas-Fort (7) is preferred as compared to Los Angeles (12) even though it has more capacity since the mandatory separation distance needs to be maintained. Also, regional hub, Minneapolis (15) is more preferred as compared to Kansas (11) for better intra-hub reliability. For the responsibility objective, New York is least preferred primary hub due to capacity constraints and Detroit (9) and Tampa (24) are preferred as regional hubs due to less economic value and high unemployment rate respectively. The CPU time is higher for SD2 as compared to SD1 reformulation. However, the time reduces for the Benders decomposition.

5.1.2 Fuzzy goal programming and fair optimization results

In Table 6, we illustrate the results of fuzzy goal programming and fair optimization for uncapacitated problem based on the CAC reformulation, where the absolute deviations of the objective function values from their desired values are minimized. The values of λ in fuzzy goal programming show that the desired values for both the goals are satisfied is above 0.65 in all the instances. Similarly, ordered weighted averaging in fair optimization show that both the objectives are equitably efficient, and we get a fair solution. The choice of primary and regional hubs in all the instances for both approaches shows that the traffic loss and responsibility objectives are equally satisfied.

Table 6 Fuzzy goal programming and fair optimization results for uncapacitated CAB dataset

In 9 out of 13 instances, fuzzy goal programming and fair optimization results reveal a similar primary hub and regional hub location strategy. In 4 instances, {(7,3,2), (7,3,3), (7,4,2), (7,5,3)}, the results differ. For traffic loss objective, fair optimization performs better than fuzzy goal programming in the case of {(7,3,2), (7,3,3)}, while the fuzzy goal programming performs better for other instances (Fig. 6). The results are reversed for the two approaches when responsibility is the objective. We get similar insights for the capacitated problem.

Fig. 6

Comparison of fuzzy goal programming and fair optimization

5.2 UDAN datasets

Since the multi-objective bilevel optimization problem is validated for the CAB dataset, we can now test the approach for the UDAN-RCS. The data for passenger demand, flow capacity, seat capacity, seat prices, passenger load factor, and hub capacity are collected from Directorate General of Civil Aviation (DGCA). The unemployment rate, economic growth, fixed and variable job opportunities, and regional development data are collected from National Sample Survey Office of India (NSSO). The rest of the parameters for social responsibility are similar to the CAB dataset.

5.2.1 Phase wise analysis

The regional aviation scheme in India had 27 well served and 31 underserved or unserved (total 58) functional airports against the targeted 70 airports at the end of 2018 in phase I of UDAN scheme (Fig. 7). We use the demand and city locations data for these 58 airports to check the efficacy of the scheme across three phases of the scheme. We calculate the Haversine distances between the city pairs. Due to computational burden, our analysis has five, six, or seven well served airports: Delhi (1), Mumbai (2), Chennai (3), Kolkata (4), Bengaluru (5), Hyderabad (6), and Ahmedabad (7). Out of these, airports (1) to (5) are also international hubs. In phase II, 70 airports were functional. However, out of initial 58 airports, only 49 airports were operational for regional connectivity and 21 new airports were added. The regional aviation scheme in India had 96 functional airports and 11 helipads (total 107) by June 2022 after the third phase of the scheme. Ultimately, in phase III, out of the initial 58 airports, 54 airports were operational.

Fig. 7

Geographical locations of nodes and zones for UDAN-RCS dataset

Due to computational complexity, we solve the uncapacitated problem with CAC formulation and Bender’s decomposition. The results for the two objectives individually are presented in Table 7. At the design stage in phase I, we ignore the passenger load factor term in objective (1), and the revenue generated for regional route in objective (2) like the CAB dataset. We witness from Fig. 7 that Hyderabad (6), Kolkata (4), and Mumbai (2) hubs are opened in all the instances for both objectives since the locations are geographically superior to other primary hubs. Kolkata is geographically far from other unserved and underserved airports. Further, there are more jobs opportunities in the location. Hence, opening this hub will result in increased social responsibility. Being India's financial capital, Mumbai provides more employment and economic growth. Similarly, the Hyderabad hub is more centrally located and more suitable for maintaining the mandatory dispersion constraints. As for the regional hubs, Indore (19) is the preferred choice in four out of six instances for the two objectives. This is again due to the requirements of mandatory separation. Vishakhapatnam (26) is a preferred choice to reduce the traffic loss objective. Dimapur (14) and Imphal (16) are preferred choices to reduce the social alienation of north-east India and thus improve social responsibility.

Table 7 Overall results for the uncapacitated model using phase wise data from UDAN scheme

In phase II and phase III, we consider overall objectives with passenger load factor and revenue generated through regional routes. Bengaluru and Kolkata are not much preferred primary hubs if we consider the traffic loss objective. Similarly, Chennai (3) and Mumbai are also less preferred as compared to Delhi (1) and Hyderabad in a few instances. Jharsuguda (39), Mysore (45), and Kandla (36) are preferred as regional hubs due to either geographical proximity or higher demand generated through these nodes. If we consider the responsibility objective, Delhi (1) and Mumbai are less preferred choices to open in phase II, while Bengaluru and Mumbai are the least preferred choices in phase III even though there is high demand through these hubs. Interestingly, Jaisalmer (34) is the preferred choice for regional hub followed by Gwalior (50) in phase-II, and Imphal (16) in phase-III respectively. Shillong (51) and Jamnagar (53) are other preferred choices in phase-III. We find that these regional hubs were underserved or unserved airports at the start of the scheme except for Imphal. Thus, the social objective is fulfilled which further promotes viability of the scheme through the selection of these hubs. Even, Imphal, which lies in the north-east India, helps to promote social cohesion, and improves national airline connectivity. Interestingly, Hyderabad (6) is opened in all phase for both the objectives. This gives the policymakers a fair idea regarding the hub’s viability for regional connectivity. Overall, {6,3,3} followed by {7,3,3} configurations provide the best results in terms of both traffic loss and responsibility objectives (Fig. 8). Interestingly, with the same number of well served airports, traffic loss may increase or decrease with a decrease in primary hubs based on location of regional hubs. Surprisingly, traffic loss reduces even with reduced primary hubs when there are 6 or 7 well served airports. Thus, there is an incentive to open only less congested hubs due to the superiority of decentralized network as compared to a centralized network. With an increase in regional hubs, there is a reduction of traffic loss in all the instances. Further, responsibility gain tends to increase as the number of primary hubs increases.

Fig. 8

Changes in different objectives across phases

Table 8 show the results for the capacitated problem. While there were no limitations of capacity during the phase I as per the data, capacity constraints impacted the scheme in further phases. In phase II, Bengaluru and Kolkata are less preferred choice for opening as compared to Delhi and Mumbai for traffic loss objective. Jharsuguda and Mysore are again identified as preferrable regional hubs as in the uncapacitated problem for both phase II and phase III to address the demands of east and south zones respectively. In case of the responsibility objective, Delhi is the least preferred hub for opening followed by Bengaluru. Jaisalmer, Nasik (40) (underserved airports), and Gwalior (unserved airport before phase I) are the preferred regional hubs for most instances. However, in phase III, while Bengaluru is preferred for opening for traffic loss objective like the uncapacitated problem, Kolkata is not preferred for opening in few instances. This may be due to increased traffic intensity of Bengaluru as compared to Chennai in south India as the scheme progresses. Shillong is again preferred as the regional hub for responsibility gain specifically in phase III. Interestingly, SD2 performs better than SD1 in most instances. Benders decomposition reduce considerable burden as shown in the results.

Table 8 Overall results for the capacitated model using Phase wise data from UDAN scheme

Tables 9 and 10 show the fuzzy goal programming results and fair optimization results for the uncapacitated and capacitated problems respectively showcase similar trade-offs while decision making. For the uncapacitated problem in phase I, Ahmedabad is not open for all the instances. Further, Imphal and Indore are selected as regional hubs since both the traffic loss and responsibility objectives need to be satisfied. Computationally, all the instances are significantly challenging to solve even with CAC reformulation. In phase II, Bengaluru is the most least preferred primary hub followed by Kolkata and Chennai in that order. Jharsuguda, Shillong, and Jaisalmer are some of the preferred regional hubs. These results provide useful insights related to the upcoming demand centers to focus on long term growth of the scheme. However, for the capacitated problem, we find that some of the solutions are infeasible, which suggests that both the objectives cannot be simultaneously optimized. Thus, the decision-maker need to focus on individual objective and change course as per the macro-economic requirements. In phase III, we identify that while Kolkata and Bangalore are least preferred primary hubs in uncapacitated problem, for the capacitated problem, Chennai is less preferred as compared to Bangalore. Jharsuguda, Nasik, and Shillong are mostly considered as regional hubs in both the problems.

Table 9 Fuzzy goal programming and fair optimization results for uncapacitated problem

Table 10 Fuzzy goal programming and fair optimization results for capacitated problem

5.2.2 Zone wise analysis

We identify six zones, namely North (N), South (S), West (W), East (E), Central (C), and Northeast (NE) in Fig. 7. The North, South, and West zones are already doing well in terms of aviation regional connectivity as compared to East, Central, and North East zones. For the uncapacitated problem, the traffic loss objective with {6,3,3} configuration included one hub in north, two hubs in south, two hubs in west, and one hub in east. There are three regional underserved hubs. Social responsibility includes one hub in north, two hubs in south, one hub in east, one hub in central, and one hub in northeast. Out of the regional hubs, one was unserved at the start of phase-I while one improves territorial cohesion to the northeast. Thus, we see the importance of individual objectives based on the need of the market. An extra primary hub in West in the {7,3,3} configuration can improve reach for the west zone as well. For the capacitated problem, we find similar results with the exception that Ahmedabad is preferred over Mumbai in {6,3,3} configuration to tackle capacity limitations. The multi objective approach identifies a bouquet of regional hubs (Jharsuguda, Shillong, Jaisalmer, Nasik, Mysore, Imphal, Indore, Dimapur) equitably and efficiently distributed in various zones to improve viability. The overall insights from the results for stakeholders and network design experts are summarized in Table 11.

Table 11 Insights for stakeholders and network design experts

6 Discussion

We answer the research questions as addressed in the introduction section and offer relevant managerial and policy implications. For the first research question relating to regional connectivity schemes remaining viable and sustaining operations, we check the feasibility of our approach with the USA and India datasets. We addressed the viability of the operations by considering the flow of traffic, passenger load factor, and percent of RCS seats for a particular route. We found that viability analysis and disruption mitigation for regional connectivity requires a more resilient network with regional backup hubs as well as flexibility of operations. Supported by qualitative interviews and consistent with the work carried out in Das et al. (2020), we methodically proposed the identification of primary hubs and opening of regional hubs based on overall survivability of the network to maintain commercial viability. Major decisions relating to viability can be taken by upper-level managers while re-routing decisions can be taken by airline operators.

In contrast to work done by Kim (2012) and Azizi et al. (2016), our results indicate that identifying as many regional or backup routes through regional hubs can be a useful technique to improve resilience and thereby viability, especially for schemes like UDAN. Policy insights relating to location of regional hubs and flexibility of operations in terms of different objectives can promote the development of other such regional connectivity schemes. Also, the regulator’s objective of improving social responsibility for sustainability provides useful configurations that focus on improving employment opportunities and regional development. Thus, the regulator has a choice to decide the location of hubs based on traffic loss objective, social objective or both objectives. Further, there can be improved policy making for future phases by promoting territorial cohesion as well as by remaining efficient and viable for the business.

For the second research question relating to resilience and responsibility objectives for improving viability in hub location problems, we have proposed a unified modelling framework for the regional connectivity. Specifically, our results indicate that the two objectives may/may not be in harmony given the current demand and social requirements of various communities. The ambiguity attached to decision making under uncertainty with different objectives is tackled using the fuzzy goal programming and fair optimization approaches. Overall, our methodology adds novelty to hub location literature by addressing various aspects like traffic loss, passenger load factor, revenue generated, and mandatory separation distance of small sized aircrafts from larger aircrafts. Further, we incorporate hub capacity constraints to address the importance of congestion in line with the future scope from Pourmohammadi et al. (2023).

For the third research question relating to government agency and airline operators, we present the bilevel model and zone wise analysis for better decision making. Firstly, we have analyzed a bilevel model with a regulator and two independent operators based on the allocation of various responsibilities. The risk reduction in the regional airline network is illustrated through minimizing traffic loss due to operational risks and disruption risks. Our results reveal that point-to-point connectivity approach for the RCS may prove to be slow in terms of merging with the existing airline network. In contrast to the work done by Matisziw et al. (2012) where a community is assigned to a set of hubs, we show that the hub-and-spoke network can be re-aligned through regional routes and incentivizing these nodes also fulfil key social objectives. Further, we propose the advantages of choosing some primary hubs and building regional hubs in Tier-II and Tier-III cities for a decentralized reconfiguration. Overall, reconfiguration based on different zones provides managers empirical evidence about the location of regional hubs as short-term and long-term survivability options. While we can adopt the old network based on generated demand, new networks will improve efficiency and promote network cohesion. Policy makers can further propose regional routes that are more efficient than the existing network.

We do concede that policy making leading to market expansion by enhancing social reach is a long-term goal while subsidization could be construed as a near-term intervention (Grubesic et al., 2012). We propose that the lack of incentives for regional connectivity schemes for airport and airline managers can be nullified through proper implementation of policy consistent with the recommendations that stem from our modeling results. More airlines will be willing to traverse through regional hubs since the market dynamics requires congestion-free primary hubs and development of alternate routes. Hence, further steps can be taken for business continuity similar to the ones expressed in Zhalechian et al. (2018) and applied to regional connectivity schemes.

7 Conclusions

In this paper, we formulate a multi-objective bilevel hub location problem with single leader and two independent followers. The leader identifies primary and regional hubs while the followers identify the primary and regional routes to improve the viability of the regional connectivity scheme. We propose that resilience and responsibility aspects of sustainability are crucial for commercial viability and addressing the consequences of disruptions in hub networks. We consider two objectives at the upper level and two separate objectives for two followers at the lower level. The first objective at the upper level is related to the multiple assignment p-hub protection model with regional hubs. The second objective is related to the social responsibility of opening regional hubs in the network. The lower-level objectives are concerned with minimizing the total routing cost in the hub network. The model is linearized using novel CAC formulations, strong duality and valid primal–dual inequality. We also contribute to multi-objective methodology by comparing fuzzy goal programming and fair optimization techniques while balancing the two conflicting objectives of the linearized model.

As far as the academic contribution is concerned, we illustrated the bilevel nature of the problem with two independent operators, where the operator is the follower who tries to minimize the transportation cost given the capacity limitations of hubs. Secondly, we have incorporated the passenger load factor and distance-based reliability to improve the commercial viability and aid in disruption mitigation. To prevent global disruption propagations to the regional and local level, we identify regional hubs which are geographically dispersed from the original primary hubs. We improve the responsibility objective from the literature by including job losses that may happen due to lesser well served airports and revenue generated through fare subsidies for regional connectivity. Moreover, we identify that an improved economic and employment growth is crucial for enhancing the reach. Due to the complexity of the formulation, our study is limited to the standard CAB dataset and UDAN case study. However, we did derive novel insights based on the generated results. Specifically, we reflect the implications for stakeholders and network design experts. Fostering and analysing viability through a decentralized network during design stage and operations stage can help in mitigating the impact of disruption and operational risks.

There are several directions for future research. Computational results demonstrated that using exact algorithms for solving viable network design problems with resiliency results in excess CPU time and there is a need to develop efficient heuristics and metaheuristics. Secondly, the model can incorporate more goals of the leader like improving environmental sustainability and service level of the network. Overall, our contribution will benefit future research in hub network design for regional connectivity for these requirements.

Appendices

Appendix A: Background of regional connectivity scheme in India

As the investment in aviation infrastructure and aviation ecosystem was growing in prevalence across the western developed nations for the past three decades, the regional imbalance and inequity in developing economy like India hampered the growth of aviation infrastructure. The aviation economic growth in India was spurred by free market competition, better quality of service, additional passenger and cargo traffic, and lower fares of airline carriers. As the Air corporation act repealed the nationalization of civil aviation in 1994, the deregulation and privatization spurred the growth of the aviation industry. Further, the Route Dispersal Guidelines (RDGs) in March, 1994 promoted the growth of airline traffic in remote and underserved regions. The RDGs divided the domestic routes based on three categories. The Category I routes catered to 12 domestic trunk routes. The category II routes catered to routes connecting north-east, Jammu and Kashmir, Andaman and Nicobar Islands, and Lakshwadeep. The Category III routes included other than Category I and Category II routes.

In 2016, the RDG guidelines were amended to include 20 domestic major direct trunk routes. The Category II routes were divided between Category II (flights connecting stations in North-East, J&K, Himachal Pradesh, Uttarakhand, Andaman and Nicobar Islands, and Lakshwadeep) and Category IIA (flights originating and terminating amongst stations in Category II) routes. Category III included other than Category I and Category II routes. According to the RDG 2016, 10% of the airline capacity on Category I routes must be deployed to Category II routes, and 1% of the Category I capacity on Category IIA routes. Airlines must operate 35% of the capacity of Category I routes on Category III routes. The capacity is judged based on available seat kilometers calculated by multiplying seats available by distance flown.

The five largest low-cost private airlines were very efficient as they captured around 79% of the passenger traffic in 2016 while the national carrier, Air India, only captured 15% of the market. Most of the routes were commercially unviable and required a policy driven support for sustainability. The commercial unviability of the regional routes resulted in alienation of certain communities, especially the North Eastern states of India. Taking a cue from the global subsidy schemes in aviation sector, the Government of India launched the UDAN regional connectivity scheme in 2016. The UDAN scheme focus on not just improved the connectivity of regional locations, but also promoting lifeline services across difficult terrains. Viability gap funding is awarded to airlines to compensate for revenue loss due to fare capping and low demand traffic patterns. Cross subsidization through the regional connectivity fund, is financed by the levy on domestic departures on Category I and Category III routes.

There were numerous challenges to the UDAN scheme. First, regional airports lacked the basic infrastructure that is needed for commercial operations. For example, several airports lacked state of the art instrumental landing systems, adequate runway areas and radar systems. Thus, the aircraft operations were restricted based on visual flight rules, restricting slot availability to day time traffic only (Das et al., 2020). Second, fluctuating weather conditions also led to massive cancellations of flights, and at times to permanent closure of some routes. The pandemic disruption further exacerbated this problem. Third, the problem of slot unavailability at busy metro airports led to congestion (Dixit et al., 2023). Because smaller aircrafts that were used for regional connectivity were slow in speed, the already constrained runway capacity (in part due to heavy separation requirements between aircrafts) and slower runway exits caused operational challenges almost daily. Fourth, capacity augmentation of aircrafts for regional connectivity is difficult due to unpredictability of revenues from point-to-point network routes (Das et al., 2020). Airlines do not tend to aggressively bid for these routes which indicates a lack of co-operation between regulator (government) and airline operator in a hierarchical environment. A similar pattern of overall under-utilization of many subsidized routes was observed in the EAS scheme in USA as well (Grubesic et al., 2012). While commercial networks in the USA are topologically designed as hub-and-spoke systems to promote efficiency, the EAS program lacked in terms of operational efficiency (high load factor) and spatial efficiency (shortfall in potential demand coverage) (Grubesic et al., 2016). Overall, the underserved and unserved airports for both schemes (UDAN in India and EAS in USA) continue to be under-studied to date.

Appendix B: Multi objective optimization

2.1 Fuzzy goal programming

The fuzzy goal programming approach is a multi-criteria decision-making approach to consider several objectives together. It extends the goal programming approach and incorporates ambiguity, uncertainty, and complexity of the parameters used for real-world problems. Zadeh (1965) introduced the fuzzy set theory and proposed the membership function. The general formulation and specific formulation for minimization and maximization of objectives for the membership function is given as follows:

$$ \mu_{i} \left( x \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {if \quad f_{i} \left( x \right) \le b_{i} } \hfill \\ {1 - \frac{{f_{i} \left( x \right) - b_{i} }}{{\Delta_{i} }}} \hfill &\quad {if \quad b_{i} < f_{i} \left( x \right) \le b_{i} + \Delta_{i} } \hfill \\ {0 } \hfill &\quad {if \quad f_{i} \left( x \right) > b_{i} + \Delta_{i} } \hfill \\ \end{array} } \right. $$

(B.1)

For minimization:

$$ \mu_{i} \left( x \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {if \quad f_{i} \left( x \right) \le b_{i} } \hfill \\ {\frac{{U_{i} - f_{i} \left( x \right)}}{{U_{i} - b_{i} }}} \hfill &\quad {if\quad b_{i} \le f_{i} \left( x \right) \le U_{i} } \hfill \\ {0 } \hfill &\quad {if\quad f_{i} \left( x \right) \ge b_{i} } \hfill \\ \end{array} } \right. $$

(B.2)

For maximization:

$$ \mu_{i} \left( x \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {if \quad f_{i} \left( x \right) \ge b_{i} } \hfill \\ {\frac{{f_{i} \left( x \right) - L_{i} }}{{b_{i} - L_{i} }}} \hfill &\quad {if\quad L_{i} \le f_{i} \left( x \right) \le b_{i} } \hfill \\ {0 } \hfill & \quad{if\quad f_{i} \left( x \right) \le b_{i} } \hfill \\ \end{array} } \right. $$

(B.3)

where $\mu_{i} \left( x \right)$ is the membership function, $b_{i}$ is the aspired level for the fuzzy goal i, and $\Delta_{i}$ is the maximum tolerable level associated with objective $f_{i} \left( x \right)$. Thus, $L_{i}$ and $U_{i}$ are the lower and upper bounds of $i$ th goal $b_{i}$. The fuzzy goal programming approach proposed by Zimmerman (1983) for the multiple conflicting objectives is identified as $\max \left\{ {\lambda : x\varepsilon X, \lambda \le 1 - \frac{{f_{i} \left( x \right) - b_{i} }}{{\Delta_{i} }}, \lambda \ge 0;i = 1, \ldots ,n} \right\}$. The approach is used to evaluate the trade-offs between conflicting goals. The first goal concerns minimizing traffic loss between O-D pairs in the proposed linearized formulation. The goal can be written in fuzzy systems as $\mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} W_{ij} L_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \Gamma_{ij} PL_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n} \left( {\Omega_{ijn} - \sigma_{ij} Y_{ijn} } \right)\tilde{ \le } F1$. Similarly, the second goal that maximizes responsibility can be written as $Wen\mathop \sum \limits_{n \in N} (FJ_{n} + VJ_{n} )ur_{n} zb_{n} + Wed\mathop \sum \limits_{n \in N} EV_{n} \left( {1 - rd_{n} } \right)zb_{n} - Wen*v*\mathop \sum \limits_{k \in H} (FJ_{k} + VJ_{k} )ur_{k} (1 - z_{k} ) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} U_{ij} T_{ijkm} X_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} U_{ij} T_{ijn} Y_{ijn} \tilde{ \ge }F2$. The fuzzy goal programming approach can be summarized as follows:

$$ Max Z = \lambda $$

(B.4)

subject to

$$ \lambda \le \frac{{U_{1} - \left( {\begin{array}{*{20}c} {\mathop \sum \nolimits_{i \in N} \mathop \sum \nolimits_{j \in N} \mathop \sum \nolimits_{k \in H} \mathop \sum \nolimits_{m \in H} W_{ij} L_{ijkm} X_{ijkm} + \mathop \sum \nolimits_{i \in N} \mathop \sum \nolimits_{j \in N} \mathop \sum \nolimits_{k \in H} \mathop \sum \nolimits_{m \in H} \Gamma_{ij} PL_{ijkm} X_{ijkm} } \\ { + \mathop \sum \nolimits_{i \in N} \mathop \sum \nolimits_{j \in N} \mathop \sum \nolimits_{n} \left( {\Omega_{ijn} - \sigma_{ij} Y_{ijn} } \right)} \\ \end{array} } \right) }}{{U_{1} - b_{1} }} $$

(B.5)

$$ \lambda \le \frac{{\begin{array}{*{20}c} {Wen\mathop \sum \nolimits_{n \in N} (FJ_{n} + VJ_{n} )ur_{n} zb_{n} + Wed\mathop \sum \nolimits_{n \in N} EV_{n} \left( {1 - rd_{n} } \right)zb_{n} - Wen*v*\mathop \sum \nolimits_{k \in H} (FJ_{k} + VJ_{k} )ur_{k} \left( {1 - z_{k} } \right)} \\ { + \mathop \sum \nolimits_{i \in N} \mathop \sum \nolimits_{j \in N} \mathop \sum \nolimits_{k \in H} \mathop \sum \nolimits_{m \in H} U_{ij} T_{ijkm} X_{ijkm} + \mathop \sum \nolimits_{i \in N} \mathop \sum \nolimits_{j \in N} \mathop \sum \nolimits_{n \in N} U_{ij} T_{ijn} Y_{ijn} - b_{2} } \\ \end{array} }}{{b_{2} - L_{2} }} $$

(B.6)

$$ \lambda \ge 0 $$

(B.7)

and rest of the constraints. Here ${b}_{i}$ is the aspiration level of ith objective function.

2.2 Fair optimization

A multi-objective optimization problem with m objective functions, $f_{k} \left( x \right), k = 1, \ldots ,m$, to be minimized can be formulated as $\min \left\{ {f_{k} \left( x \right):x \in Q} \right\}$. In fair optimization, the objective functions are equally important, where normalized objective functions are much close to each other (Kostreva et al., 2004). The normalizations in the interval [0,1] remove dimensional inconsistency among various objectives. The non-increasing ordering of m objective functions is depicted as $\Theta \left( y \right) = \left( {\theta_{1} \left( y \right),\theta_{2} \left( y \right), \ldots \theta_{m} \left( y \right)} \right)$, where $\theta_{1} \left( y \right) \ge \theta_{2} \left( y \right) \ge \ldots \ge \theta_{m} \left( y \right)$. The cumulative ordering of m objectives is depicted as $\overline{\Theta }\left( y \right) = \left( {\overline{\theta }_{1} \left( y \right),\overline{\theta }_{2} \left( y \right), \ldots \overline{\theta }_{m} \left( y \right)} \right)$, where $\overline{\theta }_{l} \left( y \right) = \mathop \sum \limits_{k = 1}^{l} \theta_{k} \left( y \right);l = 1,2, \ldots m$ is the total number of l largest outcomes. Thus, $\overline{\theta }_{1} \left( y \right)$ is the largest outcome, $\overline{\theta }_{2} \left( y \right)$ is the total of two largest outcomes. Similarly, $\overline{\theta }_{m} \left( y \right)$ is the total of m outcomes. The fair or equitably efficient solution is a Pareto solution of the multi-objective problem with objectives $\overline{\Theta }\left( {f\left( x \right)} \right)$ and depicted as $\min \left\{ {\left( {\overline{\theta }_{1} \left( {f\left( x \right)} \right),\overline{\theta }_{2} \left( {f\left( x \right)} \right), \ldots \overline{\theta }_{m} \left( {f\left( x \right)} \right)} \right):x\varepsilon Q} \right\}$. The minimization of the last objective minimizes the sum of outcomes. The lexicographic minimax problem $lex\min \left\{ {\left( {\overline{\theta }_{1} \left( {f\left( x \right)} \right),\overline{\theta }_{2} \left( {f\left( x \right)} \right), \ldots \overline{\theta }_{m} \left( {f\left( x \right)} \right)} \right):x \in Q} \right\}$ is solved to find a fair solution. The problem minimizes the worst objective value first, then the second-worst objective (provided that the worst one is as small as possible), and so on.

The integer program for finding l largest outcomes, $\overline{\theta }_{l} \left( y \right)$ for a given outcome vector $y = \left( {y_{1} , \ldots ,y_{m} } \right)$ is given by $\overline{\theta }_{l} \left( y \right) = {\text{max}}\{ \left( {\mathop \sum \limits_{k \in m} y_{k} z_{kl} } \right): \mathop \sum \limits_{k \in m} z_{kl} = l,z_{kl} \in \left\{ {0,1} \right\}; k = 1, \ldots ,m$}. We relax the binary variables $z_{kl}$ to find the dual linear program $\overline{\theta }_{l} \left( y \right) = \min \left\{ {\left( {l\lambda_{l} + \mathop \sum \limits_{k \in m} \delta_{kl} } \right): \lambda_{l} + \delta_{kl} \ge y_{k} , \delta_{kl} \ge 0;k = 1, \ldots ,m} \right\}$, where $\lambda_{l}$ is unrestricted variable and $\delta_{kl}$ upside deviation of $y_{k}$ from the value of $\lambda_{l}$. This dual linear program is formulated to replace the multi-objective optimization problem $\min \left\{ {\left( {\overline{\theta }_{1} \left( {f\left( x \right)} \right),\overline{\theta }_{2} \left( {f\left( x \right)} \right), \ldots \overline{\theta }_{m} \left( {f\left( x \right)} \right)} \right):x\varepsilon Q} \right\}$. The problem is replaced as ${\text{min}}\left\{ {\left( {\lambda_{1} + \mathop \sum \limits_{k \in m} \delta_{kl} , 2\lambda_{2} + \mathop \sum \limits_{k \in m} \delta_{kl} , \ldots , m\lambda_{m} + \mathop \sum \limits_{k \in m} \delta_{kl} } \right):x \in Q, \lambda_{l} + \delta_{kl} \ge f_{k} \left( x \right), \delta_{kl} \ge 0;k,l = 1,..m} \right\}$. The ordered weighted averaging (OWA) aggregation for the multi-objective minimization problem can be replaced as minimization of the fairly aggregated objective function $\mathop \sum \limits_{k \in m} v_{k} \overline{\theta }_{k} \left( y \right)$, where positive weights $v_{k}$ are assigned to ordered values rather than specific criteria (used in weighted sum aggregation). Thus, with equal weights $v_{l} = 1$, the OWA problem is formulated as $\min \left\{ {\mathop \sum \limits_{l} \left( {l\lambda_{l} + \mathop \sum \limits_{k \in m} \delta_{kl} } \right): x\varepsilon Q, \lambda_{l} + \delta_{kl} \ge f_{k} \left( x \right), \delta_{kl} \ge 0;k,l = 1, \ldots ,m} \right\}$. If $x^{*} \varepsilon Q$ is the optimal solution of the OWA problem, it is also the fair and Pareto optimal solution of the multi-objective problem $\min \left\{ {f_{1} \left( x \right),f_{2} \left( x \right), \ldots f_{m} \left( x \right):x \in Q} \right\}$ (Sawik, 2015). We find the minimum and maximum value of potential traffic loss and the maximum and minimum value of responsibility. We formulate the OWA problem with equal weights for both objectives to find the equitably efficient solution.

Appendix C: Benders decomposition

3.1 Uncapacitated version

We use the WF-CAC based reformulation to generate the master problem and sub-problem for the traffic loss objective. The dual of primal sub-problem for the uncapacitated version of VHLRC is stated as:

$$ \begin{aligned} & \mathop {{\text{max}}}\limits_{\theta ,\phi ,\partial ,\varrho ,A,B,h,\eta } \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} A_{ijn} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k}^{*} \partial_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n}^{*} \varrho_{ijn} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{{\left( {k,m} \right) \in H_{ij}{\prime} }} \left( {2 - z_{k}^{*} - z_{m}^{*} } \right)h_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \left( {1 - zb_{n}^{*} } \right)\eta_{ijn} \\ \end{aligned} $$

(C.1)

subject to

$$ \begin{aligned} & \theta_{ij} + \partial_{ijk} + A_{ijn} \left( {W_{ij} \overline{L}_{ijkm} LB_{ijn} + \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} } \right) + \mathop \sum \limits_{{\left( {q,s} \right)|d_{ijqs} < d_{ijkm} }} h_{ijqs} \le W_{ij} L_{ijkm} \\ & \quad + \Gamma_{ij} PL_{ijkm} \quad \forall i,j,n \in N, k,m \in H, k = m \\ \end{aligned} $$

(C.2)

$$ \begin{aligned} & \theta_{ij} + \partial_{ijk} + \partial_{ijm} + A_{ijn} \left( {W_{ij} \overline{L}_{ijkm} LB_{ijn} + \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} } \right) + \mathop \sum \limits_{{\left( {q,s} \right)|d_{ijqs} < d_{ijkm} }} h_{ijqs} \\ & \quad \le W_{ij} L_{ijkm} + \Gamma_{ij} PL_{ijkm} \quad \forall i,j,n \in N, k,m \in H, k \ne m \\ \end{aligned} $$

(C.3)

$$ B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) + \phi_{ij} + \varrho_{ijn} + \mathop \sum \limits_{{\left( a \right)|d_{ija} < d_{ijn} }} \eta_{ijn} \le - \sigma_{ij} \quad \forall i,j,n \in N $$

(C.4)

$$ - A_{ijn} + B_{ijn} \le 0\quad \forall i,j,n \in N $$

(C.5)

$$ h_{ijkm} \ge 0\quad \forall i,j \in N,\left( {k,m} \right) \in H_{ij}{\prime} $$

(C.6)

$$ \theta_{ij} ,\phi_{ij} {\text{unbounded}}; \partial_{ijk} ,\varrho_{ijn} ,A_{ijn} ,B_{ijn} ,\eta_{ijn} \ge 0\quad \forall i,j,n \in N, k,m \in H $$

(C.7)

The problem is bound with a solution $\theta^{*} ,\phi^{*} , \partial^{*} , \varrho^{*} , A^{*} ,B^{*} ,h^{*} ,\eta^{*}$, since variables $\partial_{ijk} ,\varrho_{ijn} , A_{ijn} ,B_{ijn} ,h_{ijkm} ,\eta_{ijn}$ are positive and $\theta_{ij}$, $\phi_{ij}$ has finite bound from constraints (C.2)–(C.4). We add the following optimality cut to the master problem:

$$ \begin{aligned} & \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} A_{ijn} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k} \partial_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n} \varrho_{ijn} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{{\left( {k,m} \right) \in H_{ij}{\prime} }} \left( {2 - z_{k} - z_{m} } \right)h_{ijkm} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \left( {1 - zb_{n} } \right)\eta_{ijn} \le \xi \\ \end{aligned} $$

(C.8)

Master Problem: Let $S_{O}$ be the set of solutions $\left( {\theta^{*} ,\phi^{*} , \partial^{*} , \varrho^{*} , A^{*} ,B^{*} ,h^{*} ,\eta^{*} } \right)$ of optimality cuts. In each iteration, a cut is added based on the solution of sub-problem. The corresponding master problem is defined as follows:

Min $\xi$.

subject to.

(3)–(8)

$$ \begin{aligned} \xi & \ge \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} A_{ijn}^{*} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn}^{*} \left( {\mu_{ij} + \sigma_{ij} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij}^{*} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k} \partial_{ijk}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n} \varrho_{ijn}^{*} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{{\left( {k,m} \right) \in H_{ij}{\prime} }} \left( {2 - z_{k} - z_{m} } \right)h_{ijkm}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \left( {1 - zb_{n} } \right)\eta_{ijn}^{*} \\ & \quad \forall \left( {\theta^{*} ,\phi^{*} , \partial^{*} , \varrho^{*} , A^{*} ,B^{*} ,h^{*} ,\eta^{*} } \right) \in S_{O} \\ \end{aligned} $$

(C.9)

$$ \xi \ge 0 $$

(C.10)

3.2 Capacitated version

The capacitated version of VHLRC is solved using strong duality reformulations. We use primal sub-problem of SD-1, and show the corresponding dual of primal sub-problem:

$$ \begin{aligned} & \mathop {\max }\limits_{A,B,\theta ,\phi ,\partial ,ϱ ,\varpi ,\zeta ,\gamma ,\iota ,\psi ,\kappa ,\rho } \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n\in N} A_{ijn} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) \\ & \quad \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k}^{*} \partial_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n}^{*} \varrho_{ijn} \\ & \quad + \mathop \sum \limits_{k \in H} \varpi_{k} \tau_{k} z_{k}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \left( {\gamma_{ijkm}^{1} + \gamma_{ijkm}^{2} } \right)W_{ij} d_{ijkm} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \iota_{ijn} W_{ij} d_{ijn} + \mathop \sum \limits_{k \in H} (M_{k}^{a} z_{k}^{*} \psi_{k}^{1} + M_{k}^{a} \left( {1 - z_{k}^{*} } \right)\psi_{k}^{2} ) \\ & \quad + \mathop \sum \limits_{n \in N} \left( {M_{n}^{a} zb_{n}^{*} \kappa_{n}^{1} + M_{n}^{a} \left( {1 - zb_{n}^{*} } \right)\kappa_{n}^{2} } \right) + \mathop \sum \limits_{k \in H} \left( {M_{k}^{b} \left( {1 - z_{k}^{*} } \right)\rho_{k}^{1} + M_{k}^{b} z_{k}^{*} \rho_{k}^{3} } \right) \\ \end{aligned} $$

(C.11)

subject to

$$ \theta_{ij} + \partial_{ijk} + A_{ijn} \left( {W_{ij} \overline{L}_{ijkm} LB_{ijn} + \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} } \right) + \zeta W_{ij} d_{ijkm} + \varpi_{k} W_{ij} \le W_{ij} L_{ijkm} + \Gamma_{ij} PL_{ijkm} \quad \forall i,j \in N, k,m \in H, k = m $$

(C.12)

$$ \theta_{ij} + \partial_{ijk} + \partial_{ijm} + A_{ijn} \left( {W_{ij} \overline{L}_{ijkm} LB_{ijn} + \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} } \right) + \zeta W_{ij} d_{ijkm} + \varpi_{k} W_{ij} \le W_{ij} L_{ijkm} + \Gamma_{ij} PL_{ijkm} \quad \forall i,j \in N, k,m \in H, k \ne m $$

(C.13)

$$ B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) + \phi_{ij} + \varrho_{ijn} + \zeta W_{ij} d_{ijn} \le - \sigma_{ij} \quad \forall i,j,n \in N $$

(C.14)

$$ - \zeta + \gamma_{ijkm}^{1} + \gamma_{ijkm}^{2} \le 0 \quad \forall i,j \in N, k,m \in H $$

(C.15)

$$ - \zeta + \iota_{ijn} \le 0 \quad \forall i,j,n \in N $$

(C.16)

$$ \gamma_{ijkk}^{1} + \gamma_{ijkm}^{2} - \psi_{k}^{2} \le 0\quad \forall i,j \in N, k,m \in H $$

(C.17)

$$ - \zeta - \psi_{k}^{1} + \psi_{k}^{2} \le 0\quad \forall k \in H $$

(C.18)

$$ \iota_{ijn} - \kappa_{n}^{2} \le 0\quad \forall i,j,n \in N $$

(C.19)

$$ \gamma_{ijkm}^{1} W_{ij} + \gamma_{ijkm}^{2} W_{ij} - \rho_{k}^{1} + \rho_{k}^{2} \le 0 \quad \forall i,j \in N, k,m \in H $$

(C.20)

$$ - \zeta - \kappa_{n}^{1} + \kappa_{n}^{2} \le 0\quad \forall n \in N $$

(C.21)

$$ - \zeta + \rho_{k}^{1} - \rho_{k}^{2} - \rho_{k}^{3} \le 0\quad \forall k \in H $$

(C.22)

$$ \theta_{ij} , \phi_{ij} {\text{unbounded}};\partial_{ijk} ,\varrho_{ijn} ,\varpi_{k} ,A_{ijn} ,B_{ijn} ,\zeta ,\gamma_{ijkm} ,\iota_{ijn} , \psi_{k} ,\kappa_{n} ,\rho_{k} \ge 0\quad \forall i,j,n \in N, k,m \in H $$

(C.23)

The problem is bound with a solution $\theta^{*} ,\phi^{*} , \partial^{*} ,\varrho^{*} ,\varpi^{*} A^{*} ,B^{*} , \zeta^{*} , \gamma^{*} ,\iota^{*} ,\psi^{*} ,\kappa^{*} , \rho^{*}$, since variables $\partial_{ijk} ,\varrho_{ijn} ,\varpi_{k} ,A_{ijn} ,B_{ijn} ,\zeta ,\gamma_{ijkm} ,\iota_{ijn} , \psi_{k} , \kappa_{n} ,\rho_{k}$ are positive and $\theta_{ij} , \phi_{ij}$ has finite bound from constraints (C.12)–(C.14). We add following optimality cut to the master problem:

$$ \begin{aligned} & \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n\in N} A_{ijn} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij} \\ & \quad \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k} \partial_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n} \varrho_{ijn} + \mathop \sum \limits_{k \in H} \varpi_{k} \tau_{k} z_{k} \\ & \quad \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \left( {\gamma_{ijkm}^{1} + \gamma_{ijkm}^{2} } \right)W_{ij} d_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \iota_{ijn} W_{ij} d_{ijn} \\ & \quad \mathop \sum \limits_{k \in H} \left( {M_{k}^{a} z_{k} \psi_{k}^{1} + M_{k}^{a} \left( {1 - z_{k} } \right)\psi_{k}^{2} } \right) + \mathop \sum \limits_{n \in N} (M_{n}^{a} zb_{n} \kappa_{n}^{1} + M_{n}^{a} \left( {1 - zb_{n} } \right)\kappa_{n}^{2} ) \\ & \quad + \mathop \sum \limits_{k \in H} \left( {M_{k}^{b} \left( {1 - z_{k} } \right)\rho_{k}^{1} + M_{k}^{b} z_{k} \rho_{k}^{3} } \right) \le \xi \\ \end{aligned} $$

(C.24)

Let $S_{O}$ be the set of solutions $\left( {\theta^{*} ,\phi^{*} , \partial^{*} ,\varrho^{*} ,\varpi^{*} ,A^{*} ,B^{*} , \zeta^{*} , \gamma^{*} ,\iota^{*} ,\psi^{*} ,\kappa^{*} , \rho^{*} } \right)$ of optimality cuts. The corresponding master problem is defined as follows:

Min $\xi$

subject to.

$\left( 3 \right) - \left( 8 \right)$,

$$ \begin{aligned} \xi & \ge \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n\in N} A_{ijn}^{*} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn}^{*} \left( {\mu_{ij} + \sigma_{ij} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij}^{*} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k} \partial_{ijk}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n} \varrho_{ijn}^{*} + \mathop \sum \limits_{k \in H} \varpi_{k}^{*} \tau_{k} z_{k} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \left( {\gamma_{ijkm}^{1*} + \gamma_{ijkm}^{2*} } \right)W_{ij} d_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} l_{ijn}^{*} W_{ij} d_{ijn} \\ & \quad + \sum\limits_{k \in H} {\left( {M_{k}^{a} z_{k} \psi_{k}^{1*} + M_{k}^{a} \left( {1 - z_{k} } \right)\psi_{k}^{2*} } \right) + \mathop \sum \limits_{n \in N} (M_{n}^{a} zb_{n} \kappa_{n}^{1*} + M_{n}^{a} \left( {1 - zb_{n} } \right)\kappa_{n}^{2*} )} \\ & \quad + \mathop \sum \limits_{k \in H} \quad \left( {M_{k}^{b} \left( {1 - z_{k} } \right)\rho_{k}^{1*} + M_{k}^{b} z_{k} \rho_{k}^{3*} } \right)\\ &\qquad\qquad \quad \forall \left( {\theta^{*} ,\phi^{*} , \partial^{*} ,\rangle^{*} ,\varpi^{*} ,A^{*} ,B^{*} , \zeta^{*} , \gamma^{*} ,l^{*} ,\psi^{*} ,\kappa^{*} , \rho^{*} } \right) \in S_{O} \\ \end{aligned} $$

(C.25)

$$ \xi \ge 0 $$

Alternatively, dual of primal sub-problem for SD2 is as follows:

$$ \begin{aligned} & \mathop {\max }\limits_{A,B,\theta ,\phi ,\partial ,\varrho ,\varpi ,\zeta ,\gamma ,\iota ,\psi ,\eta ,\kappa ,\rho } \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n\in N} A_{ijn} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k}^{*} \partial_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n}^{*} \varrho_{ijn} \\ & \quad + \mathop \sum \limits_{k \in H} \varpi_{k} \tau_{k} z_{k}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \left( {\gamma_{ijkm}^{1} + \gamma_{ijkm}^{2} } \right)W_{ij} d_{ijkm} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \iota_{ijn} W_{ij} d_{ijn} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \left( {M_{ij}^{a} \left( {1 - z_{k}^{*} } \right)\psi_{ijk}^{1} + M_{ij}^{a} z_{k}^{*} \psi_{ijk}^{3} } \right) \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} (M_{ij}^{a} \left( {1 - z_{m}^{*} } \right)\eta_{ijm}^{1} + M_{ij}^{a} z_{m}^{*} \eta_{ijm}^{3} )\\ &\quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} M_{ij}^{a} \left( {1 - zb_{n}^{*} } \right)\kappa_{ijn}^{1} + M_{ij}^{a} zb_{n}^{*} \kappa_{ijn}^{3} \\ & \quad + \mathop \sum \limits_{k \in H} \left( {M_{k}^{b} \left( {1 - z_{k}^{*} } \right)\rho_{k}^{1} + M_{k}^{b} z_{k}^{*} \rho_{k}^{3} } \right) \\ \end{aligned} $$

(C.26)

subject to

$$ \theta_{ij} + \partial_{ijk} + A_{ijn} \left( {W_{ij} \overline{L}_{ijkm} LB_{ijn} + \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} } \right) + \zeta W_{ij} d_{ijkm} + \varpi_{k} W_{ij} \le W_{ij} L_{ijkm} + \Gamma_{ij} PL_{ijkm} \quad \forall i,j \in N, k,m \in H, k = m $$

(C.27)

$$ \theta_{ij} + \partial_{ijk} + \partial_{ijm} + A_{ijn} \left( {W_{ij} \overline{L}_{ijkm} LB_{ijn} + \Gamma_{ij} \overline{PL}_{ijkm} PLB_{ijn} } \right) + \zeta W_{ij} d_{ijkm} + \varpi_{k} W_{ij} \le W_{ij} L_{ijkm} + \Gamma_{ij} PL_{ijkm} \quad \forall i,j \in N, k,m \in H, k \ne m $$

(C.28)

$$ B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) + \phi_{ij} + \varrho_{ijn} + \zeta W_{ij} d_{ijn} \le - \sigma_{ij} \quad \forall i,j,n \in N $$

(C.29)

$$ - \zeta + \gamma_{ijkm}^{1} + \gamma_{ijkm}^{2} \le 0 \quad \forall i,j \in N, k,m \in H $$

(C.30)

$$ - \zeta + \iota_{ijn} \le 0 \quad \forall i,j,n \in N $$

(C.31)

$$ \gamma_{ijkm}^{1} + \gamma_{ijkm}^{2} - \psi_{ijk}^{1} + \psi_{ijk}^{2} \le 0 \quad \forall i,j \in N, k,m \in H $$

(C.32)

$$ \gamma_{ijkm}^{2} - \eta_{ijm}^{1} + \eta_{ijm}^{2} \le 0 \quad \forall i,j \in N, k,m \in H $$

(C.33)

$$ \iota_{ijn} - \kappa_{ijn}^{1} + \kappa_{ijn}^{2} \le 0\quad \forall i,j,n \in N $$

(C.34)

$$ \gamma_{ijkm}^{1} W_{ij} + \gamma_{ijkm}^{2} W_{ij} - \rho_{k}^{1} + \rho_{k}^{2} \le 0\quad \forall i,j \in N, k,m \in H $$

(C.35)

$$ - \zeta + \psi_{ijk}^{1} - \psi_{ijk}^{2} - \psi_{ijk}^{3} \le 0 \quad \forall i,j \in N, k \in H $$

(C.36)

$$ - \zeta + \eta_{ijm}^{1} - \eta_{ijm}^{2} - \eta_{ijm}^{3} \le 0\quad \forall i,j \in N, m \in H $$

(C.37)

$$ - \zeta + \kappa_{ijn}^{1} - \kappa_{ijn}^{2} - \kappa_{ijn}^{3} \le 0\quad \forall i,j,n \in N $$

(C.38)

$$ - \zeta + \rho_{k}^{1} - \rho_{k}^{2} - \rho_{k}^{3} \le 0 \quad \forall k \in H $$

(C.39)

$$ \theta_{ij} , \phi_{ij} {\text{unbounded}};\partial_{ijk} ,\varrho_{ijn} ,\varpi_{k} ,A_{ijn} ,B_{ijn} ,\zeta ,\gamma_{ijkm} ,\iota_{ijn} , \psi_{ijk} , \eta_{ijm} ,\kappa_{ijn} ,\rho_{k} \ge 0\quad \forall i,j,n \in N, k,m \in H $$

(C.40)

The problem is bound with a solution $\theta^{*} ,\phi^{*} , \partial^{*} ,\varrho^{*} ,\varpi^{*} A^{*} ,B^{*} , \zeta^{*} , \gamma^{*} ,\iota^{*} ,\psi^{*} ,\eta^{*} ,\kappa^{*} , \rho^{*}$, since variables $\partial_{ijk} ,\varrho_{ijn} ,\varpi_{k} ,A_{ijn} ,B_{ijn} ,\zeta ,\gamma_{ijkm} ,\iota_{ijn} , \psi_{ijk} , \eta_{ijm} ,\kappa_{ijn} ,\rho_{k}$ are positive and $\theta_{ij} , \phi_{ij}$ has finite bound from constraints (C.27)–(C.29). We add the following optimality cut to the master problem:

$$ \begin{aligned} & \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n\in N} A_{ijn} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn} \left( {\mu_{ij} + \sigma_{ij} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k} \partial_{ijk} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n} \varrho_{ijn} + \mathop \sum \limits_{k \in H} \varpi_{k} \tau_{k} z_{k} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \left( {\gamma_{ijkm}^{1} + \gamma_{ijkm}^{2} } \right)W_{ij} d_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \iota_{ijn} W_{ij} d_{ijn} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \left( {M_{ij}^{a} \left( {1 - z_{k} } \right)\psi_{ijk}^{1} + M_{ij}^{a} z_{k} \psi_{ijk}^{3} } \right)\\ &\quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} (M_{ij}^{a} \left( {1 - z_{m} } \right)\eta_{ijm}^{1} + M_{ij}^{a} z_{m} \eta_{ijm}^{3} ) \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} M_{ij}^{a} \left( {1 - zb_{n} } \right)\kappa_{ijn}^{1} + M_{ij}^{a} zb_{n} \kappa_{ijn}^{3*} + \mathop \sum \limits_{k \in H} \left( {M_{k}^{b} \left( {1 - z_{k} } \right)\rho_{k}^{1} + M_{k}^{b} z_{k} \rho_{k}^{3} } \right) \le \xi \\ \end{aligned} $$

(C.41)

Let $S_{O}$ be the set of solutions $\left( {\theta^{*} ,\phi^{*} , \partial^{*} ,\varrho^{*} ,\varpi^{*} ,A^{*} ,B^{*} , \zeta^{*} , \gamma^{*} ,\iota^{*} ,\psi^{*} ,\eta^{*} ,\kappa^{*} , \rho^{*} } \right)$ of optimality cuts. The corresponding master problem is defined as follows:

Min $\xi$.

subject to.

(3)–(8)

$$ \begin{aligned} \xi & \ge \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n\smallint N} A_{ijn}^{*} \sigma_{ij} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} B_{ijn}^{*} \left( {\mu_{ij} + \sigma_{ij} } \right) + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \theta_{ij}^{*} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \phi_{ij}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} z_{k} \partial_{ijk}^{*} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} zb_{n} \varrho_{ijn}^{*} + \mathop \sum \limits_{k \in H} \varpi_{k}^{*} \tau_{k} z_{k} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \mathop \sum \limits_{m \in H} \left( {\gamma_{ijkm}^{1*} + \gamma_{ijkm}^{2*} } \right)W_{ij} d_{ijkm} + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} \iota_{ijn}^{*} W_{ij} d_{ijn} \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{k \in H} \left( {M_{ij}^{a} \left( {1 - z_{k} } \right)\psi_{ijk}^{1*} + M_{ij}^{a} z_{k} \psi_{ijk}^{3*} } \right) \\ &\quad+ \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{m \in H} (M_{ij}^{a} \left( {1 - z_{m} } \right)\eta_{ijm}^{1*} + M_{ij}^{a} z_{m} \eta_{ijm}^{3*} ) \\ & \quad + \mathop \sum \limits_{i \in N} \mathop \sum \limits_{j \in N} \mathop \sum \limits_{n \in N} M_{ij}^{a} \left( {1 - zb_{n} } \right)\kappa_{ijn}^{1*} + M_{ij}^{c} zb_{n} \kappa_{ijn}^{3*} + \mathop \sum \limits_{k \in H} \left( {M_{k}^{b} \left( {1 - z_{k} } \right)\rho_{k}^{1*} + M_{k}^{b} z_{k} \rho_{k}^{3*} } \right) \\ & \quad \forall \left( {\theta^{*} ,\phi^{*} , \partial^{*} ,\varrho^{*} ,\varpi^{*} ,A^{*} ,B^{*} , \zeta^{*} , \gamma^{*} ,\iota^{*} ,\psi^{*} ,\eta^{*} ,\kappa^{*} , \rho^{*} } \right) \in S_{O} \\ \end{aligned} $$

(C.42)

$$ \xi \ge 0 $$