1 Introduction

There has been a significant increase in the volume of world trade with an average annual growth of 3.8% until 2018. The growth rate has dropped to 1.1% in the following year due to the COVID-19 pandemic and after that it recovered to pre-pandemic levels in 2022. Containerized transportation is one of the main engines of global trade since containers are widely used to transport any means of commodity, particularly, 80% of global trade by volume or 70% by value was carried by sea and handled by ports (Unctad, 2020). In 2020, 785 million twenty-foot equivalent units (TEUs) of containers were handled in container ports worldwide Unctad (2020, p. 14). The increasing demand has driven the shipping industry to operate larger ships, e.g. ships with more than 23,000 TEU capacity.

The increasing transport demand has also triggered fierce competition between container liner shipping companies which in return urges companies to maximize revenues and utilize the vessels as efficiently as possible in each service. In this scope, maximizing cargo income in a shipping service consistently is paramount for economic sustainability as each container type has a specific income. The pool of containers available at different ports may not be suitable for the full utilization of the vessel. Stowage coordinators of a liner shipping company decide cargo composition, i.e. the number and specifications of containers to be loaded from each port from a pool of containers accumulated at the port, and generate a ship stowage plan ensuring that the vessel is utilized to its best with respect to capacity obeying a set of seaworthiness constraints (Pacino et al., 2011). Cargo composition, also referred as cargo mix in some studies, impacts the ship berthing times at each port. Cargoes are (un)loaded by quay cranes at each port. A cargo composition plan aiming to minimize the idle time of cranes at each port would directly reduce port emissions, and contribute to environmental sustainability as well.

Due to increasing transportation demand, supply chain disruptions (e.g., port congestions, blocking of Suez canal by a ship, typhoons at ports, COVID-19 restrictions’ impact at ports and lack- and then over-supply of empty containers worldwide), and trading imbalance between regions, export containers accumulate at ports around the world and wait to be transported (Lee and Song, 2017). In this study, we propose a Decision Support System (DSS) for sustainable cargo composition (cargo mix) for liner companies to maximize shipping revenue by selecting the most appropriate set of containers to be loaded on the ship at each port and generating a seaworthy stowage plan in collaboration with each port en-route aiming to minimize the over-stowage and the port crane idle times (and emissions consequently).

Containerships are designed to transport containers in bays which are the crosswise areas that divide the vessels into sections from bow to stern. A bay is composed of slots in which containers are stowed. The basic layout of a container vessel is shown in Fig. 1. The figure shows how containers are arranged in storage areas called bays along the entire length of the vessel.

Fig. 1
figure 1

Layout of container vessel (source: Christensen and Pacino (2017))

Full size image

The allocation of ship slot booking requests is mostly based on the first come first served (FCFS) strategy or determined by an empirical judgment of the value of the customer. However, the severe imbalance between supply and demand in the container shipping market which has deepened during the COVID-19 pandemic encourages large container liner shipping companies to seek suitable capacity management models to improve their revenue, especially on long-haul services. Normally, a container liner shipping company has a wide variety of customers that can be divided into contractual customers and spot customers. A contractual customer signs a long-term container shipping contract with the company for a number of slots. Spot customers are small-scale customers that generally have small container shipping demand. They include small and medium-sized enterprises, small international traders and freight forwarders. The shipping company has more leverage on spot customers in cargo composition decisions. Since both high-profit (e.g. long haul and reefer containers) and low-profit containers are carried on the same ship, these two types of containers compete for the ship capacity. Therefore, the shipping company determines the cargo composition in each service considering container types’ revenue, ship stowage properties and en-route port attributes. Different freight rates are applied to containers depending on their destination ports, sizes, and types. The liner companies usually receive higher returns from long-distance containers. Rates also change depending on the size, such as 20, 40 and 45-ft.

Selecting high-profit containers, however, does not necessarily provide a feasibile service, higher income or a more sustainable service. The destination, type and size compositions of containers should enable planners to produce a stowage plan that is seaworthy while shortening ship berthing duration at ports as much as possible. Two major factors affect the ship duration at port: Crane operations and over-stowage. When ships get alongside the jetty, the cranes immediately start unloading and loading operations. The port operator determines the number of assigned cranes by considering the number of containers to be loaded/unloaded and the size of the ship. Each crane works at particular bays of the ship. The significant criterion here is that the work cycle of all cranes should be in synchronization. Each crane’s starting and finishing time should be close enough not to leave any crane idle for a long time. Not complying with this criterion results in longer waiting times for ships at the port, and consequently higher port emissions. Therefore, planners should create a reliable and sustainable stowage plan in which the containers to be handled at that port are homogeneously distributed along the ship enabling all cranes work in similar durations. Meanwhile, if a container must be removed from a stack to retrieve a container underneath it, the container being removed is said to be overstowing the container being retrieved. The process of removing an overstowing container to retrieve a container beneath it is called shifting. One of the goals of stowage planning is to minimize shifting or, equivalently, to minimize overstowage since it extends the waiting time at a port.

The main contribution of this paper is of both practical and methodological importance for a real-life problem that liner companies face. We attempt to incorporate collaborative features to create a realistic DSS for sustainable cargo composition for liner companies. In particular, our modeling framework encompasses: (1) Economical return of all containers by considering ports in a service, (2) Ship stability parameters stemmed from (un)loading of selected containers, (3) All types of over-stow, and (4) Crane and vessel utility maximization, and emission reduction, at each port in the service.

For this purpose, we first develop a mixed integer non-linear programming (MINLP) formulation and a two-stage solution approach which decomposes the original problem into two mixed integer linear programming (MILP) formulations. In the first stage, we maximize the total revenue by determining the containers to be transported with minimal over-stow while ensuring a balanced workload among the cranes in the ports. In this stage, we determine the containers that should be allocated to each bay. In the second stage, we generate a detailed slot-assignment plan which minimizes the overall trim-moment of the ship. The trim of a ship can be defined by the angle by which the ship tilts in a container loading condition relative to its baseline and calculated by the difference between its aft and fore drafts. The trimming moment is the moment required to change the trim of the ship by one cm.

Next, we compare our two-stage solution methodology with the heuristic approaches implemented by most liner companies for filtering out the containers with respect to their revenue. The two data-filtering heuristics used by these companies basically aim at decreasing the size of the planning problem by sorting and choosing the containers to be loaded at ship at each port with respect to the net revenue gain. Our numerical results show that our proposed two-stage solution approach is capable of delivering high-quality solutions within reasonable times. We also show that our method outperforms the commonly-used data filtering heuristics with respect to solution quality.

The remainder of this paper is organized as follows: in Sect. 2 we provide a literature review on studies related to capacity management and cargo composition in shipping, stowage planning, and ship operations at ports. The proposed DSS framework for sustainable cargo composition is described in Sect. 3. In Sect. 4 we provide basic assumptions and preliminaries related to the problem of interest. We present the mathematical model in Sect. 5. In Sect. 6 we discuss the two-stage solution approach as well as the two container filtering-based data pre-processing algorithms. Numerical experiments to assess the performance of the proposed approach is reported in Sect. 7. Conclusions and recommendations for further research are outlined in Sect. 8.

2 Literature review

Cargo composition problem can be viewed as an integration of capacity management, slot allocation, cargo selection and stowage planning for a ship in a cyclic shipping service in collaboration with en-route ports. Therefore, we review studies for each of these components.

2.1 Capacity management and revenue management in shipping

The purpose of shipping revenue management is to maximize revenue growth for a company by optimizing capacity/service availability and prices based on micro-level forecasting of customer behavior. In our work, the capacity and service availability component of revenue management (RM) are addressed. Therefore, the focus is given on capacity management and cargo selection in shipping services considering revenues. Meng et al. (2019) has provided a comprehensive survey on RM in liner shipping services. They reviewed the RM studies for container liner shipping services and identified valuable future research directions in container shipping RM. A nested booking limit algorithm for this situation is proposed in Zurheide and Fischer (2012). In Zurheide and Fischer (2011), a network slot allocation model is proposed to determine booking limits for a liner shipping network considering different paths in the network, transshipments between services and service segments. Later, Zurheide and Fischer (2015) discussed three different booking acceptance strategies for liner shipping, namely booking limits, nested booking limits (NBL) and a newly developed bid-price (BP) strategy and evaluated their performance in a simulation study reporting that for higher levels of demand, the NBL and BP strategies outperform a FCFS strategy. Ang et al. (2007) focused on RM through booking acceptance under shipping capacity but without considering ship technicalities and stability. Wang et al. (2015) proposed an algorithm for solving the tactical seasonal liner revenue management problem for a given weekly multi-type shipment demand pattern in a particular season. The objective is to maximize the container shipping profit (see e.g. Brouer et al. (2018), Wong et al. (2022) for alternative objectives) for a fixed multi-type of container demand over a shipping network in a particular season. In their study, Chen et al. (2016) considered the empty container relocation in revenue management to find an optimal pricing strategy.

Lee and Song (2017) reviewed the relevant studies and has demonstrated in their study that pricing is closely related to competition issue, whereas contracting is related to cooperation issue. Moussawi-Haidar (2014) investigated a single-leg cargo revenue management problem, in which a two-dimensional cargo capacity is sold through allotment contracts and in the spot market. In another study Wang and Meng (2021) investigated how to determine the optimal freight rate of spot containers for each origin and destination (OD) pairs of a shipping network to maximize the total profit by considering uncertainties of demand volume and remaining ship capacity (see exemplar OD pairs from tramp shipping in Fagerholt et al. (2013)). Zhao et al. (2022) studied the assignment of container slots to specific demand types to maximize the revenue in a shipping network. Similarly, Chen et al.. (2022) focused on container slot exchange with revenue considerations in a shipping alliance.

2.2 Stowage planning and port operations

Ship operations addressing the efficiency of stowage plans, ship stability and port operations related topics have attracted many researchers over the last three decades. Recent stowage planning related studies were reviewed in Twiller et al. (2023) with a focus on ship operations and in Iris and Pacino (2015) with a focus on container port operations. Bilican et al. (2020) proposed a two-stage mathematical model and a heuristic algorithm for efficient multi-port bay planning along with stability parameters such as trim and stress factors. Christensen and Pacino (2017) proposed a matheuristic algorithm for the cargo composition problem with block stowage. It also accounts for the draft restrictions at the visited ports and a block stowage strategy which is the logical partitioning of the vessel into blocks. Each block is then allowed to host only containers that have the same discharge port. This alternative way of stowing containers is aimed at improving operations at ports. In a more recent study Christensen et al. (2019) studied stochastic cargo composition problem with uncertain demand. They analyzed the cargo composition needed for a liner vessel to maximize its revenue on a given service and presented a rolling horizon matheuristic. These studies do not consider the impact of port operations (e.g. crane operations) on stowage planning and cargo composition unlike our study.

To integrate port relevant factors, Pacino (2018) presented a mathematical model that addressed crane utilization along with block stowage strategies. Azevedo et al. (2018) proposed a model which integrates the 3D Stowage Planning (3DSP), crane allocation and crane scheduling problems. To solve large scale problems, they proposed a combined solution methodology which incorporates mathematical programming and simulation optimization methodologies with a genetic algorithm. These stowage planning studies do not consider the cargo selection decisions unlike our study. Sun et al. (2021) addressed vessel stability constraints in the quay crane scheduling problem (QCSP) which is essential to improve quay crane operations in container terminals (Iris et al., 2015). In a more recent study Lee and Low (2022) presented a constraint programming-based model for the capacity planning of containerships, considering several operational factors and limitations. The proposed model seeks to minimize the number of empty TEU slots, the number of re-stows, and the number of TEUs located in bays that are not covered by cranes.

In some studies, stowage planning is studied solely as a single-port operational problem. Iris et al. (2018) presented the flexible containership loading problem for a single seaport container terminal. They integrated the assignment and scheduling of yard vehicles and container load sequencing with the assignment of specific containers to the vessel positions as for operative stowage planning (slot planning). They assume liner shipping company delivers a class-based stowage plan to the port operator and the port conducts the detailed stowage plan in a collaborative way. They presented mathematical model and a heuristic algorithm to solve the problem. There are also other studies about designing frameworks for collaboration between supply chain members (see e.g. Liu et al. (2023)).

This study combines multi-port cargo selection, ship slot allocation and stowage planning into a cargo composition DSS framework. To the best of our knowledge, there is no such study that encompasses cargo composition planning, taking into account factors such as cargo revenues, over-stowage, port crane utilization and ship stability considerations (e.g., trim, stress factors, and GM) for a shipping route in collaboration with en-route ports. Therefore, the proposed algorithms and DSS will facilitate the planning and fill a gap in this area.

3 Decision support system general framework

The proposed DSS consists of a two-stage structure in which two MILP formulations are employed sequentially. In the first level of two-stage programming, the model generates an initial cargo composition with bay plan by allocating a container to each bay on the ship from a large pool of containers available at each port by maximizing revenue (from selected containers’ transportation), minimizing the number of over-stowage and providing even distribution of containers for better crane utilization (and reduced emissions) at each port. Depending on the number of available cranes in each port, the first-stage model also attempts to distribute the containers throughout the bays in such a way that the workload of each crane is considerably close to each other in each port. This minimizes the idleness of cranes, and consequently port emissions, since each crane loads/unloads similar number of containers, thereby shortening ships duration at port. The first stage of the DSS is solved using all available container as an input. Next, the DSS employs the second level and generates the final cargo composition with stowage plan by re-assigning containers within their allocated bays such that the desired ship stability and seaworthiness is ensured. Figure 2 illustrates the data inputs, decisions, objectives and information flow in the DSS environment.

Fig. 2
figure 2

General structure of the DSS

Full size image

The developed DSS is designed to run in a cloud environment. The algorithm starts with the generation of transportation matrix where all available containers of different properties can be grouped based on their origin and destination ports, type (dry or reefer), size (20-ft, 40-ft) and their revenue. Transportation matrix includes all the container data currently available at each port at the time of the model implementation.

4 Assumptions and preliminaries

We now provide key assumptions and preliminaries on concepts related to our problem description.

4.1 Key assumptions

The problem in this paper seeks to determine the containers to be chosen based on capacity of the ship. A containership’s cargo space is divided into sections called bays, and each bay is divided into an on deck and a below deck part by a number of hatch-covers, which are flat, leak-proof structures. Each sub-section of a bay consists of a row of container stacks divided into slots that can hold a 20 feet container. A containership transports its cargo between several ports denoted by i, j  \(\in \)  I. Assuming that a ship starts its service from port 1, all containers bound for the next ports are loaded. At the second port, it discharges all containers bound for the second port and loads containers to be transported to subsequent ports. This study can easily address out-of-region demands (e.g. from Asia to Europe), where discharge is dominant mode in the destination region. Shortly after the ship‘s arrival to the port, a specific number of cranes that were determined before, are assigned to the ship depending on the length of the ship and the total number of containers to be loaded and unloaded at the designated port. Therefore, it is highly likely that there might be different number of cranes available at each port. In our model, we respect this flexibility and assume that the number of cranes at each port may vary.

Considering crane utilization modeling for ports in service, bays are assumed to be distributed evenly among cranes. In other words, each crane is assigned to a specific part of the ship such that they work independently on the bays within their segment. In our modeling framework, one of the objectives is to end up with a balanced workload among the cranes by assigning an approximately equal number of containers to be loaded and unloaded.

4.2 Preliminaries on container operations and ship characteristics

4.2.1 Trim

The trim occurs when the bow or the aft of the ship is submerged deeper into the water. In other words, trim is the angle by which the vessel tilts, fore and aft, relative to its baseline. It can be expressed as the difference between a ship’s aft and fore drafts resulting from the variation of stern and bow moments. These moments occur at the longitudinal center of gravity (LCG). Figure 3 illustrates the trim and trimming moment concepts on a ship with two containers of weights \(W_1\) and \(W_2\) located above points B and C, respectively (Bilican et al., 2020).

Fig. 3
figure 3

The trim and trimming moment concepts (source: Bilican et al. (2020))

Full size image

Considering Fig. 3, the bow moment and the aft moment are calculated as \(M_b=W_1d_{AB}\) and \(M_s=W_2d_{AC}\), respectively, where \(d_{AB}\) and \(d_{AC}\) are the distances of containers to the LCG point denoted by A. Therefore, the resulting trimming moment will simply be \(M_d=W_2d_{AC}-W_1d_{AB}\). The sign of \(M_d\) indicates the side by which the ship is trimmed.

4.2.2 Container properties

Containers come in 3 different sizes, i.e., 20, 40 and 45 feet long. Their weights range from 5 to 32 tons. Among several types of containers, dry and reefer containers are the most common ones. In this study, we consider 20 and 40 feet dry and reefer containers. We further assume that six weight groups, i.e., 5, 10, 15, 20, 25 and 30 tons, exist and each of these containers is assigned to one of these groups.

4.2.3 Stack weight

Stack weight is the maximum weight of containers that a stack can hold in a vertical pile on the ship. There might be several stacks in a bay. The sum of the weight limits of all these stacks yields to bay weight limit in our model.

4.2.4 Shear force and bending moments

Ships are made up of frames that span transversal from bow to stern. These frames support the hull and give the ship its shape and strength. The structural integrity of a ship is tested by some external powers exerted by the load (lightship weight and cargo weight) downwards and the buoyancy force that the water acts upwards. These two factors form the Shear Force (SF) and Bending Moment (BM) on the ship, thereby creating stress on its structure, specifically at the frames. When these two external parallel forces are exerted in opposite directions on a structure to break it apart, the resulting forces are named as “shear force” which is measured in tons.

BM, on the other hand, is the amount of bending caused by SF. Consequently, BM and SF are decisive in the junction of frames. Each frame has limitations in terms of BM and SF by design, and SF and BM must be kept within these limits at each frame. The easiest way to remove excessive SF and BM is to evenly distribute the cargo throughout the ship storage areas, i.e., bays.

In this study, frames and their allowable limits are taken into consideration for BM and SF calculations. For additional information on the concept of SF and BM, the reader can refer to Bilican et al. (2020)

4.2.5 Metacentric height

The metacentric height (GM) is a measurement of the initial static stability of a floating body. Its value is crucial for ship safety to navigate. For each type of ship, specific GM values are set at the design phase. GM is calculated as the distance between the center of gravity of a ship and its metacenter. A larger metacentric height implies greater initial stability against overturning. The transversal stability is portrayed in Fig. 4.

Fig. 4
figure 4

Transversal stability and metacentric height (Adapted from Christensen and Pacino (2017))

Full size image

The metacentre point is determined at the initial design phase of a ship and its exact position is obtained from ship stability books. In Fig. 4, K represents the keel of the ship. Therefore, the distance from K to M, KM, can simply be obtained from the ship stability book. The only variable point that we can control is the center of gravity denoted by G. The center of gravity changes according to the cargo distribution scheme and requires detailed calculation. As long as the exact position of G is determined, the GM distance can be easily calculated as: \(GM=KM-KG\).

5 Problem formulation

In this section, we provide the MINLP model developed for the above-mentioned problem. Below we first list the notation for all sets, indices, parameters, and decision variables used in the formulation.

5.1 General notation

\(b \in B\):

Set of bays

\(f \in F\):

Set of frames

\(i,i',i'',j \in I\):

Set of ports

\(k \in K\):

Set of container weight groups

\(c \in C\):

Set of container groups (with respect to type, length and revenue), i.e. 1: Dry 20-ft container, 2: Dry 40-ft container, 3: Reefer 20-ft container, 4: Reefer 40-ft container)

\(n, n' \in N\):

Set of cranes

\(b' \in B_f\):

Set of bays up to the frame f, \(B_f \subseteq B\)

Parameters

\(R_c\):

Revenue value of containers of category c [$]

\(C^{os}\):

Cost of stowing a container [$]

\(C^{cr}\):

Cost of a single crane movement [$]

\(C^{tm}\):

Additional fuel cost per mile resulting from ship stability maintenance [$/(ton meter \(\times \) nm)]. This cost is associated with the change in the draft. If all containers are loaded evenly, that is with 0 trimming moment, then a mean draft value occurs in the center. However, if the distribution is not even, fore and/or aft drafts can be beyond allowable ranges due to large trimming moment values. In such cases, engineers fill the ballast tanks to keep the drafts within limits and ensure stability. This implies that the ship takes extra load and attains a higher draft value. This increased draft actually results in higher fuel consumption.

\(s_{ij}\):

Distance between ports i and j [nm]

\(Q_D^b\):

Dry container capacity of bay b [unit]

\(Q_R^b\):

Reefer container capacity of bay b [unit]

\(Q^b\):

Total container capacity of bay b [unit], i.e., \(Q^b=Q_D^b+Q_R^b\)

\(T_{ijck}\):

Number of available containers transported from port i to j in weight group k and category c (for simplicity, containers transported from port i to j are called as \(i-j\) containers) [unit]

\(n_j\):

Number of available cranes at port j [unit]

\(w_k\):

Weight of a container in group k [ton]

\(d_b\):

Distance of bay b to the LCG point of the ship [meter]

\(S_b\):

Stack weight limit of bay b [ton]

\(M^{fore}\):

The maximum moment that ballast tanks at the fore of the LCG can create [ton meter]

\(M^{aft}\):

The maximum moment that ballast tanks at the aft of the LCG can create [ton meter]

\(SF_f^{max}\):

Allowable SF at frame f [ton]

\(H_f^L\):

The light weight of the ship up to frame f [ton]

\(d_f^L\):

The distance from frame f to the longitudinal center of gravity of the lightweight ship [meters]

\(d_f^C\):

The distance from frame f to the longitudinal center of gravity of cargo up to frame f [meters]

\(d_{fi}^B\):

The distance from frame f to the longitudinal center of buoyancy of the hull in port i [meters]

\(\Delta _{fi}\):

The displacement (or buoyancy) force up to frame f from the bow of the ship in port i [ton]

\(\beta _{fi}\):

The difference between moments created by buoyancy force and lightship up to frame f. That is, \(\beta _{fi}=\Delta _{fi}d_{fi}^B-H_f^Ld_f^L, \forall {f} \in F, i \in I\)

\(BM_f^{max}\):

Allowable BM at frame f [ton meter]

\(d_{keel}^{lower}\):

The distance from CG (center of gravity) of lower bays (under-deck) to the keel [meters]

\(d_{keel}^{upper}\):

The distance from CG (center of gravity) of upper bays (upper-deck) to the keel [meters]

\(KG^L\):

KG distance of light ship [meter]

KM:

The distance from keel to metacenter point [meter]

\(GM^{Lower}\):

Allowable minimum GM height [meter]

\(GM^{Upper}\):

Allowable maximum GM height [meter]

\(\Delta \):

Displacement of the ship [ton]

\(\Delta ^L\):

Displacement of the light ship [ton]

D:

Number of bays at the fore of LCG point [unit]

U:

Number of upper-deck or under-deck bays [unit] (we assume that there are the same number of lower-deck and upper-deck bays)

Decision Variables

\(x_{ijck}^b\):

Integer, number of \(i-j\) containers in weight group k and in category c assigned to bay b [unit]

\(\phi _i^b\):

Integer, number of over-stows that might occur on a single bay b (either on deck or under deck bays) at port i [unit]

\(\lambda _i^b\):

Integer, number of over-stows that might occur between on deck and under deck bay b at port i [unit]

\(\rho _i^b\):

Integer, number of replicating over-stows that might occur between on deck and under deck bay b at port i [unit]

\(\gamma _i\):

Integer, the difference between the number of processed containers by one crane and the average number of processed containers per crane at port i [unit]

\(Z_j^n\):

Integer, number of containers processed by crane n at port j [unit]

\(V_i\):

Continuous, total weight of containers loaded at port i [ton]

\(V_i^b\):

Continuous, total weight of containers loaded on bay b at port i [ton]

\(M_i\):

Continuous, actual trimming moment that occurs at port i [ton meter]

\(Y_{ij}^b\):

Binary, 1 if there is any container in bay b being transported from port i to j

\(H_{fi}^C\):

Continuous, the cargo weight of the ship up to frame f at port i [ton]

\(KG_i^C\):

Continuous, KG distance of the cargo on board at port i [meter]

\(KG_i^{Final}\):

Continuous, final KG distance of the ship at port i [meter]

\(GM_i\):

Continuous, GM value at port i [meters]

5.2 MINLP formulation

$$\begin{aligned} \max z= & {} \sum \limits _{i\in I}^{{}}{\sum \limits _{j\in I}^{{}}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{\sum \limits _{b\in B}^{{}}{{{R}_{c}}x_{ijck}^{b}}}}}}-\sum \limits _{i\in I}^{{}}{\sum \limits _{b\in B}^{{}}{{{C}^{os}}(\pi _{i}^{b}+\lambda _{i}^{b}+\rho _{i}^{b})}}-\sum \limits _{i\in I}^{{}}{{{C}^{cr}}{{\gamma }_{i}}} \nonumber \\{} & {} - \sum \limits _{i=1}^{\left| I \right| -1}{\sum \limits _{j=i+1}^{{}}{{{s}_{ij}}{{C}^{tm}}{{{{M}}}_{i}}}} \end{aligned}$$
(1)

subject to

$$\begin{aligned}{} & {} \sum \limits _{{i}'=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j1k}^{b}}}}+2\sum \limits _{{i}'=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j2k}^{b}}}}\le Q_{D}^{b}\text { }, \forall i\in I,b\in B \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j3k}^{b}}}}+2\sum \limits _{{{i}^{'}}=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j4k}^{b}}}}\le Q_{R}^{b}\text { }, \forall i\in I,b\in B \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \sum \limits _{b\in B}^{{}}{x_{ijck}^{b}}\le {{T}_{ijck}}\text { }, \forall i\in I,j\in I,c\in C,k\in K \end{aligned}$$
(4)
$$\begin{aligned}{} & {} Z_{j}^{n}=\sum \limits _{i=1}^{j-1}{\sum \limits _{b\in {{B}_{in}}}^{{}}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{ijck}^{b}}}+}}\sum \limits _{i=j+1}^{\left| I \right| }{\sum \limits _{b\in {{B}_{in}}}^{{}}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{jick}^{b}}}}}\text { }\forall j\in I,n\in {{N}_{j}} \end{aligned}$$
(5)
$$\begin{aligned}{} & {} {{\gamma }_{j}}\ge \left| Z_{j}^{n'}-\left[ (\sum \limits _{n=1}^{{{n}_{j}}}{Z_{j}^{n}})/{{n}_{j}} \right] \right| \text { }, \forall j\in I, n'\in {{N}_{j}} \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=i+1}^{j-1}{\sum \limits _{{i}''=j+1}^{\left| I \right| -1}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{{i}'{i}''ck}^{b}}}}}+(Y_{ij}^{b}-1){{Q}^{b}}\le \pi _{j}^{b}, \forall b\in B,\{i,j\in I\left| i <j\} \right. \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=i+1}^{j-1}{\sum \limits _{{i}''=j+1}^{\left| I \right| -1}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{{i}'{i}''ck}^{b+U}}}}}+(Y_{ij}^{b}-1){{Q}^{b+U}}\le \lambda _{j}^{b+U}, \forall b\in B,\{i,j\in I\left| i <j\} \right. \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{ijck}^{b+U}}}+(Y_{ij}^{b}-1){{Q}^{b+U}}\le \rho _{j}^{b+U}\text { }, \forall b\in B(where\text { }b\le U)\{i,j\in I\left| i <j\} \right. \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{ijck}^{b}}}\le Y_{ij}^{b}{{Q}^{b}}, \forall b\in B,\{i,j\in I\left| i <j\} \right. ,c\in C \end{aligned}$$
(10)
$$\begin{aligned}{} & {} {{V}_{i}}=\sum \limits _{{i}'=1}^{i}{\sum \limits _{k\in K}^{{}}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{c\in C}^{{}}{\sum \limits _{b\in B}^{{}}{{{w}_{k}}x_{{i}'jck}^{b}}}}}}\le \Delta \text { }, \forall i\in I \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=0}^{i}{\sum \limits _{k=1}^{\left| K \right| }{\sum \limits _{j=i+1}^{\left| I \right| -1}{\sum \limits _{c\in C}^{{}}{{{w}_{k}}x_{{i}'jck}^{b}}=V_{i}^{b}}}}, \forall b\in B,i\in I \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \sum \limits _{b=D+ 1}^{\left| B \right| }{V_{i}^{b}{{d}_{b}}\text { }-}\text { }\sum \limits _{b=1}^{D}{V_{i}^{b}{{d}_{b}}={{M}_{i}}}, \forall i\in I \end{aligned}$$
(13)
$$\begin{aligned}{} & {} V_{i}^{b}\le {{S}_{b}}, \forall b\in B,i\in I \end{aligned}$$
(14)
$$\begin{aligned}{} & {} {{M}_{i}}\le {{M}^{fore}}, \forall i\in I \end{aligned}$$
(15)
$$\begin{aligned}{} & {} -{{M}_{i}}\le {{M}^{aft}}, \forall i\in I \end{aligned}$$
(16)
$$\begin{aligned}{} & {} {{\Delta }_{fi}}-H_{f}^{L}-H_{fi}^{C}\le SF_{f}^{\max }, \forall f\in F,i\in I \end{aligned}$$
(17)
$$\begin{aligned}{} & {} H_{fi}^{C}=\sum \limits _{b\in B_f}^{}{V_{i}^{b}}, \forall f\in F,i\in I \end{aligned}$$
(18)
$$\begin{aligned}{} & {} {{\beta }_{fi}}-H_{fi}^{C}d_{f}^{C}\le BM_{f}^{\max }, \forall f\in F,i\in I \end{aligned}$$
(19)
$$\begin{aligned}{} & {} KG_{i}^{C}=\left[ \frac{\sum \limits _{b=1}^{U}{V_{i}^{b}d_{keel}^{lower}+\sum \limits _{b=U+1}^{2U}{V_{i}^{b}d_{keel}^{upper}}}}{{{{{V}}}_{i}}} \right] \text { }, \forall i\in I \end{aligned}$$
(20)
$$\begin{aligned}{} & {} KG_{i}^{Final}=\left[ \frac{\sum \limits _{b=1}^{2U}{V_{i}^{b}KG_{i}^{C}+{{\Delta }^{L}}K{{G}^{L}}}}{{{V}_{i}}+{{\Delta }^{L}}} \right] \text { }, \forall i\in I \end{aligned}$$
(21)
$$\begin{aligned}{} & {} G{{M}_{i}}=KM-KG_{i}^{Final}\text { }, \forall i\in I \end{aligned}$$
(22)
$$\begin{aligned}{} & {} G{{M}^{lower}}\le G{{M}_{i}}\le G{{M}^{upper}}\text { }, \forall i\in I \end{aligned}$$
(23)
$$\begin{aligned}{} & {} x_{ijck}^{b}\in \{0,1,2,...\}, \forall b\in B,i,j\in I, k\in K,c\in C \end{aligned}$$
(24)
$$\begin{aligned}{} & {} Y_{ij}^{b}\in \{0,1\}, \forall b\in B,i,j\in I \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \pi _{i}^{b},\text { }\lambda _{i}^{b},\text { }\rho _{i}^{b},V_{i}^{b}\ge 0, \forall b\in B,i\in I \end{aligned}$$
(26)
$$\begin{aligned}{} & {} {{\gamma }_{i}}\in \{0,1,2,...\}, \forall i\in I \end{aligned}$$
(27)
$$\begin{aligned}{} & {} {{M}_{i}},{{V}_{i}},K{{G}_{i}^{C}},G{{M}_{i}},KG_{i}^{Final}\ge 0, \forall i\in I \end{aligned}$$
(28)
$$\begin{aligned}{} & {} H_{fi}^{c}\ge 0, \forall f\in F,i\in I \end{aligned}$$
(29)

The objective function (1) has four terms. Each container category has its own value associated with its profit returns. The first term seeks to maximize the revenue by determining the containers to be transported through a selection process based on containers’ revenue. The second part of the objective aims to minimize the overall cost linked to the occurrence of over-stows. We assume that the cost of stowing a container, represented by \(C^{os}\), remains constant and is already known. For a better understanding of how the decision variables \(\pi \), \(\lambda \), and \(\rho \) influence various types of over-stows, please refer to the example illustrated in Fig. 5.

In this particular scenario, each figure corresponds to an individual bay denoted as b, and the containers being transported from port 1 to 4 (referred to as 1–4 containers) have already been successfully loaded. However, if we attempt to load containers 2–5, 2–6, 3–5, and 3–6 on top of the existing 1–4 containers within the same bay, over-stows will inevitably occur (see Fig. 5a).

The decision variable \({{\pi }{^b_i}}\) corresponds to instances of over-stows in bay \(b\in B\) at port \(i\in I\). These instances can occur in either an upper deck or under deck bay, where the hatch cover does not need to be lifted, as illustrated in Fig. 5a. On the other hand, Fig. 5b displays two overlaid bays, namely the upper and under deck bays, separated by a hatch cover. In this case, the \(1-4\) containers are placed on the under-deck bay. Stowing the 1–5, 1–6, 2–5, 2–6, 3–5, and 3–6 containers on the upper deck bays creates inter-bay over-stows, denoted by \({{\lambda }{^b_i}}\), for all \(b\in B\) and \(i\in I\).

Finally, in Fig. 5c, the 1–4 containers are positioned on the upper deck bays. Stowing the 2–3, 2–4, 2–5, 2–6, 3–4, 3–5, and 3–6 containers on under deck bays leads to replicating over-stows, where the over-stow is duplicated at ports 2 and 3. These replicating over-stows are represented by the decision variable \({\rho _i^b}\), for all \(b\in B\) and \(i\in I\).

The third objective is to minimize disparities in the number of containers loaded/unloaded by each crane, thereby maximizing crane utility. The cost of a single crane movement is denoted by \(C^{cr}\). The integer variable \(\gamma \) represents the difference between the number of processed containers by a specific crane and the average number of processed containers per crane at port i [unit]. This equation aims to reduce the gap between the actual and average processed containers at each port, encouraging cranes to handle a similar or closely matched number of containers. By achieving this objective, the model not only helps minimize the duration of the ship’s visit but also reduces idle periods for all cranes.

In the fourth component of the objective function, our goal is to minimize the total additional fuel cost resulting from ship instability during a tour. We can determine the total weight of containers to be loaded at port i. When containers are evenly distributed, meaning there is no trimming moment, this weight leads to an unavoidable increase in the draft. The draft represents the final and optimal depth at which the ship should sail. Therefore, the operating cost associated with this draft is inevitable for the agencies. However, if the containers are not evenly distributed, a certain amount of trimming moment occurs. To rebalance the ship, engineers perform ballasting operations. This ballast operation adds extra weight to the ship, resulting in an increase in the existing draft. The model aims to minimize the cost associated with this increment in the draft value. This cost is calculated for each port prior to departure. It is important to note that the fixed and known cost associated with the trimming moment is denoted as \({{C}^{tm}}\). Additionally, \({{{M}}_i}\) represents the actual trimming moment that occurs at port i.

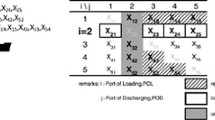
Constraints (2) and (3) ensure that the total usage of any bay does not exceed its capacity in terms of dry and reefer containers respectively. The first part of the constraint focuses on 20 ft. containers, while the latter part considers 40 ft. containers assigned to bay b collectively. Consequently, this constraint takes into account all containers assigned to bay \(b\in B\) at each port and guarantees that the total number of containers does not surpass the capacity of the corresponding bay. To illustrate, let’s consider a scenario where a container ship visits 6 ports and is currently at port 2. For a specific bay b, the number of containers loaded at previous ports (i.e. port 1) and the current port (i.e., port 2) cannot exceed the bay’s capacity. In other words, the total number of containers loaded at previous ports (e.g., containers 1–3, 1–4, 1–5, 1–6) and the current port (e.g., containers 2–3, 2–4, 2–5, 2–6) must be less than or equal to the capacity of bay b.

Constraint set (4) ensures that the total number of selected containers does not exceed the number of total available containers in a given port.

Constraint sets (5) and (6) pertain to the crane utility aspect. In constraint (5), the model computes the total number of containers assigned to the operational segment of each crane at every port. Once the total number of containers processed by each crane at each port is determined, constraint set (6) obtains the deviation of the number of container handled by a specific crane from the average number of containers processed by a crane in that port.

Constraint set (7) establishes the upper limit for the maximum number of first type over-stows that can occur on a single bay \(b\in B\) at port \(j\in I\). It defines the upper bound for the decision variable \({{\pi }^b_{j}}\). Similarly, constraint set (8) determines the maximum number of over-stows that can happen between the upper and under deck bays, separated by a hatch-cover. It sets the upper limit for the second type of over-stow. In this constraint set, each bay is examined in conjunction with its upper neighbor deck bay. Therefore, the reference to \(b\text { }+\text { }U\) in the constraint set signifies the upper neighbor bay of bay \(b\in B\).

Constraint set (9) addresses the replicating over-stows depicted in Fig. 5c. It states that if an upper deck has an available \(i-j\) container, loading a container to the under deck at ports between \(i+1\) and \(j-1\) will result in over-stows equal to the number of \(i-j\) containers. Furthermore, this over-stow scenario can replicate itself up to \(j-(i+1)\) times based on the presence of \((i+1)-(j-1)\) containers.

Constraint set (10) establishes the relationship between \(x_{ijck}^{b}\) variables (for 20-ft and 40-ft) and the binary variable \({{Y}_{ij}^{b}}\). Additionally, this constraint set, in conjunction with constraint sets (7)–(9), determine the maximum number of over-stows that can occur on a bay \(b\in B\). More details of these constraints are available in Bilican et al. (2020).

Constraint set (11)computes the cumulative weight of containers onboard the ship. The weight-carrying capacity of a ship is determined by its displacement. Hence, this constraint guarantees that the combined weight of containers remains within the limits of the ship’s displacement.

Constraint set (12) evaluates the weight of each bay following the completion of the loading and unloading operations, just before the ship departs from the port. Meanwhile, constraint set (13) computes the trimming moments based on the longitudinal center of gravity (LCG) of the ship. The distance of each bay to the LCG is provided as a parameter.

Each bay comprises multiple stacks or tiers, with each stack having a distinct weight capacity that determines the maximum number of containers of varying weights it can accommodate. If the total weight of containers assigned to bay \(b\in B\) exceeds the combined weight capacity of all stacks in that bay, the slot planning (Parreño et al., 2016) process may become infeasible. To prevent such a scenario, we calculate the weight capacity of the bay by aggregating the weight capacities of all stacks within that bay, considering their upper or under deck positions. In this regard, constraint set (14) guarantees that the assigned containers do not surpass these bay capacities.

In the event of trim on a containership, it becomes necessary for planners to utilize ballast tanks in order to restore stability. However, for the ballast condition to be effective, the moment produced by the ballast tanks must surpass the existing trimming moment. Hence, constraint sets (15) and (16) ensure that the trimming moments stay within acceptable limits, facilitating their counterbalancing with fore and aft ballast tanks, respectively.

Constraint sets (17)–(19) are dedicated to addressing stress-related considerations. Constraint sets (17) and (19) ensure that the shear force and bending moment at each frame do not exceed their allowable thresholds, promoting a uniform weight distribution along the length of the ship and maintaining stress factors within design levels. Constraint set (18) calculates the total weight of containers loaded onto the bays up to frame f, while constraint set (19) calculates the displacement (or buoyancy) force from the bow of the ship up to frame f at port i, which serves as an input for shear force calculations.

Constraint sets (20)–(23) are implemented to maintain the GM (metacentric height) within the permissible limits. However, the computation of the GM value introduces non-linearity in equations (20) and (21) due to the denominator variable, which represents the total weight of containers loaded at port i. Lastly, constraint sets (24)–(29) define the domains of the decision variables.

Fig. 5
figure 5

Over-stow instances with a rear view of the ship (Source Bilican et al. (2020))

Full size image

6 Solution approach

In this section we explain the two-stage formulation approach used in our decision support system framework. The first stage formulation aims at maximizing the revenue without accounting for the stability parameters of the containership. This formulation basically assigns containers to bays such that the total revenue is maximized by maximizing revenue of transported containers and crane utilities while minimizing the number of over-stows. The solution obtained from the first stage model is fed into the second stage model as an input and the second stage formulation seeks to improve the stability of the ship by minimizing the trimming moment value for each port. In this stage, the model performs inter-bay container exchanges without deteriorating the optimal objective function value obtained in the first stage. In other words, it ensures that the revenue obtained in the first stage does not change while the stability of the ship is improved.

6.1 First stage formulation

$$\begin{aligned}&\max {{z}_{S1}} =&\, \sum \limits _{i\in I}^{{}}{\sum \limits _{j\in I}^{{}}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{\sum \limits _{b\in B}^{{}}{{{R}_{c}}x_{ijck}^{b}}}}}}-\sum \limits _{i\in I}^{{}}{\sum \limits _{b\in B}^{{}}{{{C}^{os}}(\pi _{i}^{b}+\lambda _{i}^{b}+\rho _{i}^{b})}}-\sum \limits _{i\in I}^{{}}{{{C}^{cr}}{{\gamma }_{i}}} \end{aligned}$$
(30)

subject to

$$\begin{aligned}{} & {} \sum \limits _{{i}'=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j1k}^{b}}}}+2\sum \limits _{{i}'=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j2k}^{b}}}}\le Q_{D}^{b}\text {, }\forall i\in I,b\in B \end{aligned}$$
(31)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j3k}^{b}}}}+2\sum \limits _{{{i}^{'}}=1}^{i}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{k\in K}^{{}}{x_{{i}'j4k}^{b}}}}\le Q_{R}^{b}\text {, }\forall i\in I,b\in B \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \sum \limits _{b\in B}^{{}}{x_{ijck}^{b}}\le {{T}_{ijck}}\text {, }\forall i\in I,j\in I,c\in C,k\in K \end{aligned}$$
(33)
$$\begin{aligned}{} & {} Z_{j}^{n}=\sum \limits _{i=1}^{j-1}{\sum \limits _{b\in {{B}_{in}}}^{{}}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{ijck}^{b}}}+}}\sum \limits _{i=j+1}^{\left| I \right| }{\sum \limits _{b\in {{B}_{in}}}^{{}}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{jick}^{b}}}}}\text { }, \forall j\in I,n\in {{N}_{j}} \end{aligned}$$
(34)
$$\begin{aligned}{} & {} {{\gamma }_{j}}\ge Z_{j}^{n'}-\left[ (\sum \limits _{n=1}^{{{n}_{j}}}{Z_{j}^{n}})/{{n}_{j}} \right] , \forall j\in I, n'\in {{N}_{j}} \end{aligned}$$
(35)
$$\begin{aligned}{} & {} {{\gamma }_{j}}\ge -Z_{j}^{n'}+\left[ (\sum \limits _{n=1}^{{{n}_{j}}}{Z_{j}^{n}})/{{n}_{j}} \right] , \forall j\in I,n'\in {{N}_{j}} \end{aligned}$$
(36)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=i+1}^{j-1}{\sum \limits _{{i}''=j+1}^{\left| I \right| -1}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{{i}'{i}''ck}^{b}}}}}+(Y_{ij}^{b}-1){{Q}^{b}}\le \pi _{j}^{b}, \forall b\in B,\{i,j\in I\left| i <j\} \right. \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=i+1}^{j-1}{\sum \limits _{{i}''=j+1}^{\left| I \right| -1}{\sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{{i}'{i}''ck}^{b+U}}}}}+(Y_{ij}^{b}-1){{Q}^{b+U}}\le \lambda _{j}^{b+U}, \forall b\in B,\{i,j\in I\left| i <j\} \right. \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{ijck}^{b+U}}}+(Y_{ij}^{b}-1){{Q}^{b+U}}\le \rho _{j}^{b+U}\text { }, \forall b\in B,\{i,j\in I\left| i <j\} \right. \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \sum \limits _{c\in C}^{{}}{\sum \limits _{k\in K}^{{}}{x_{ijck}^{b}}}\le Y_{ij}^{b}{{Q}^{b}}, \forall b\in B,\{i,j\in I\left| i <j\} \right. ,c\in C \end{aligned}$$
(40)
$$\begin{aligned}{} & {} {{V}_{i}}=\sum \limits _{{i}'=1}^{i}{\sum \limits _{k\in K}^{{}}{\sum \limits _{j=i+1}^{\left| I \right| }{\sum \limits _{c\in C}^{{}}{\sum \limits _{b\in B}^{{}}{{{w}_{k}}x_{{i}'jck}^{b}}}}}}\le \Delta \text { }, \forall i\in I \end{aligned}$$
(41)
$$\begin{aligned}{} & {} x_{ijck}^{b}\in \{0,1,2,...\}, \forall b\in B,i,j\in I, k\in K,c\in C \end{aligned}$$
(42)
$$\begin{aligned}{} & {} Y_{ij}^{b}\in \{0,1\}, \forall b\in B,i,j\in I \end{aligned}$$
(43)
$$\begin{aligned}{} & {} \pi _{i}^{b},\text { }\lambda _{i}^{b},\text { }\rho _{i}^{b}\ge 0, \forall b\in B,i\in I \end{aligned}$$
(44)
$$\begin{aligned}{} & {} {{\gamma }_{i}}\in \{0,1,2,...\}, \forall i\in I \end{aligned}$$
(45)
$$\begin{aligned}{} & {} {{V}_{i}}\ge 0, \forall i\in I \end{aligned}$$
(46)

The objective function (30) has now the first three terms of the objective function (1) and excludes the term which addressed the trimming moment of the ship. As discussed previously, the first term seeks to maximize revenue by determining the containers to be transported to and from each port. The second term minimizes the cost related to the over-stow instances. The third term minimizes the cost associated with the differences on the number of containers loaded/unloaded by each crane. Constraint sets ((31) and (32)) guarantee that the total usage of any bay is less than or equal to the capacity of that bay for reefer and dry containers separately. Constraint set (33) ensures that the total number of selected containers does not exceed the number of total available containers in a given port. Constraint sets (34), (35) and (36) address the crane utilization. We note that constraint sets (35) and (36) are the linearized version of the constraint (7). Constraint sets (37)–(40) are over-stow constraints as explained in Bilican et al. (2020). All types of over stowage are considered in this work. Constraint set (41) ensures that the total weight of containers does not exceed the displacement of the ship. Finally, constraint sets (42)–(46) declare variable domains.

6.2 Second stage formulation

Below we define the additional parameters and decision variables used in the second stage of our model. Recall that the output of the first stage in terms of the number of \(i-j\) containers in category c assigned to bay b is taken as an input to Stage 2. Therefore, we use the value of related decision variables of Stage 1 as parameters in Stage 2.

Additional parameters

\(\bar{x}_{ijc}^{b}\):

= Number of \(i-j\) containers (from origin to destination) of category c assigned to bay b [unit] (obtained from Stage 1)

\({{\bar{V}}_{i}}\):

= Total weight of containers loaded at port i [ton] (obtained from Stage 1)

Additional decision variables

\(y_{ijck}^{b}\):

= integer, Number of \(i-j\) containers (from origin to destination) in weight group k and in category c assigned to bay b [unit]

Model

$$\begin{aligned}&\min {{z}_{S2}} =&\, \sum \limits _{i=1}^{\left| I \right| -1}{{{{M}}_{i}}} \end{aligned}$$
(47)
$$\begin{aligned} \text{ subject } \text{ to }{} & {} \sum \limits _{k=1}^{6}{y_{ijck}^{b}}=\bar{x}_{ijc}^{b}\text { }, \forall i\in I,j\in I,c\in C,b\in B \end{aligned}$$
(48)
$$\begin{aligned}{} & {} \sum \limits _{{i}'=0}^{i}{\sum \limits _{k=1}^{\left| K \right| }{\sum \limits _{j=i+1}^{\left| I \right| -1}{\sum \limits _{c\in C}^{{}}{{{w}_{k}}y _{{i}'jck}^{b}}=V_{i}^{b}}}}, \forall b\in B,i\in I \end{aligned}$$
(49)
$$\begin{aligned}{} & {} \sum \limits _{b=D+ 1}^{\left| B \right| }{V_{i}^{b}{{d}_{b}}\text { }-}\text { }\sum \limits _{b=1}^{D}{V_{i}^{b}{{d}_{b}}={{M}_{i}}}, \forall i\in I \end{aligned}$$
(50)
$$\begin{aligned}{} & {} V_{i}^{b}\le {{S}_{b}}, \forall b\in B,i\in I \end{aligned}$$
(51)
$$\begin{aligned}{} & {} {{M}_{i}}\le {{M}^{fore}}, \forall i\in I \end{aligned}$$
(52)
$$\begin{aligned}{} & {} -{{M}_{i}}\le {{M}^{aft}}, \forall i\in I \end{aligned}$$
(53)
$$\begin{aligned}{} & {} {{\Delta }_{fi}}-H_{f}^{L}-H_{fi}^{C}\le SF_{f}^{\max }, \forall f\in F,i\in I \end{aligned}$$
(54)
$$\begin{aligned}{} & {} {{\beta }_{fi}}-H_{fi}^{C}d_{f}^{C}\le BM_{f}^{\max }, \forall f\in F,i\in I \end{aligned}$$
(55)
$$\begin{aligned}{} & {} H_{fi}^{C}=\sum \limits _{b\in B_f}^{}{V_{i}^{b}}, \forall f\in F,i\in I \end{aligned}$$
(56)
$$\begin{aligned}{} & {} KG_{i}^{C}=\left[ \frac{\sum \limits _{b=1}^{U}{V_{i}^{b}d_{keel}^{lower}+\sum \limits _{b=U+1}^{2U}{V_{i}^{b}d_{keel}^{upper}}}}{{{{\bar{V}}}_{i}}} \right] \text { }, \forall i\in I \end{aligned}$$
(57)
$$\begin{aligned}{} & {} KG_{i}^{Final}=\left[ \frac{\sum \limits _{b=1}^{2U}{V_{i}^{b}KG_{i}^{C}+{{\Delta }^{L}}K{{G}^{L}}}}{{\bar{V}_{i}}+{{\Delta }^{L}}} \right] \text { }, \forall i\in I \end{aligned}$$
(58)
$$\begin{aligned}{} & {} G{{M}_{i}}=KM-KG_{i}^{Final}\text { }, \forall i\in I \end{aligned}$$
(59)
$$\begin{aligned}{} & {} G{{M}^{lower}}\le G{{M}_{i}}\le G{{M}^{upper}}\text { }, \forall i\in I \end{aligned}$$
(60)
$$\begin{aligned}{} & {} y_{ijck}^{b}\in \left\{ 0,1,2,... \right\} , \forall i\in I,j\in I,c\in C,k\in K,b\in B \end{aligned}$$
(61)
$$\begin{aligned}{} & {} V_{i}^{b}\ge 0, \forall i\in I,b\in B \end{aligned}$$
(62)
$$\begin{aligned}{} & {} G{{M}_{i}},{{M}_{i}},KG_{i}^{Final}\ge 0, \forall i\in I \end{aligned}$$
(63)
$$\begin{aligned}{} & {} H_{fi}^{C}\ge 0, \forall f\in F,i\in I \end{aligned}$$
(64)
$$\begin{aligned}{} & {} KG_{i}^{C}\ge 0, \forall i\in I \end{aligned}$$
(65)

The objective function (47) minimizes the trimming moment value for each port to avoid trimmed ship. Constraint set (48) ensures that the optimality obtained in the first level is maintained. Number of \(i-j\) containers in category c assigned to bay b which is obtained from phase-1 is used as a parameter in this equation. Constraint set (49) calculates the weight of each bay after loading and unloading operations, prior to leaving the port while (50) calculates trimming moments according to the longitudinal center of gravity of the ship. The stack weight limits are considered in (51). Constraint sets (52) and (53) guarantee that the resultant trimming moment is within the limit that can be corrected by ballast tanks. Constraint sets (54)–(56) address the stress factors. Constraint sets (57)–(60) ensure that the GM value is within allowable limits. In these equations, the we overcome non-linearity that appeared in combined model by simply introducing (Total weight of containers loaded at port i [ton]) as a parameter, obtained from phase 1. Constraint sets (61)–(65) declare variable domains.

6.3 Myopic greedy approaches: data pre-processing algorithms

We now describe two myopic but practical algorithms for the cargo composition problem used by liner shipping companies. A shipping company might try to prioritize containers with highest revenue. Therefore, these two algorithms select a subset of available containers based on revenue and run second stage model with the selected containers. For the sake of fair analysis, we compare our DSS framework with these myopic approaches.

6.3.1 Heuristic-1: Greedy algorithm for sequence of port visits

The first heuristic algorithm basically prioritizes containers with respect to their revenue at each port considering the port sequence of the shipping service. The revenue from a container mainly depends on the distance travelled, length, weight, and type of the container. Starting from the first port, the algorithm selects the best containers (with highest revenue) to fill the ship capacity. After each selection of a container, the algorithm checks the total weight of all selected containers to ensure that they do not exceed the deadweight ship capacity, if deadweight is exceeded, the container is dropped from selection list. Once the first port is completed, the algorithm moves to the second port and unload all containers destined for this port. Then, the algorithm fills the idle ship capacity from the available containers at second port one by one following the weight constraints. The algorithm continues in this fashion until the last port and display the final list of containers to be loaded. The final list is the input data set for mathematical model. The pseudocode for the algorithm is presented in Algorithm 1.

Algorithm 1
figure a

Greedy algorithm for the given sequence of port visits.

Full size image

6.3.2 Heuristic-2: Greedy algorithm for all containers in the service

The basic difference of heuristic-2 with the heuristic-1 is that heuristic-2 filters the containers by considering all available containers instead of following the port sequence. The algorithm sorts all containers with respect to their revenue and chooses containers starting from the one with the highest revenue. Selected containers are then added to the container list of corresponding departure ports. After each addition, the algorithm checks the available ship capacity and deadweight limitations for each port list. If any of the capacity and weight constraints are violated, the container is simply removed from the list. The pseudocode for this algorithm is presented in Algorithm 2.

Algorithm 2
figure b

Greedy algorithm for all containers in the service.

Full size image

7 Numerical results

7.1 Examplary solution

Prior to discussing the details of our numerical experiments and test problem designs, we find it useful to present a basic illustrative CSP and its corresponding solution achieved through MILP.

In this example, we analyze a vessel equipped with 9 bays, each accommodating 20 containers, resulting in a total capacity of 180 containers. Three cranes are assigned to work on these bays. Each crane is assigned to work on 3 successive bays. The vessel makes stops at 6 different ports. The availability of containers is specified in Table 1. The first column of the table indicates the originating port (indexed by i), while the second column represents the destination port (indexed by j). The third column denotes the container type, dry or reefer and 20-ft or 40-ft (index c). For simplicity, we assume that all containers in this example are of the 20-ft dry container type. The fourth column provides information about the weight groups of the containers, which is crucial for considerations related to deadweight and stability (index k). The fifth column presents the corresponding revenue associated with each container type, and the final column indicates the quantity of available containers for each type.

In the example problem we assume that there exist 1032 containers readily available at all ports for transportation to subsequent ports. Furthermore, a deadweight tonnage of 2700 tons is considered. The ship is initially assumed to be empty. In Table 1, many containers are loaded (i) either at port 1 or port 2 (first/early ports) and unloaded (j) at ports 4, 5 or 6 (later ports) as destinations. These features ensure a realistic problem setting.

Table 1 Example problem data
Full size table

For illustrative purposes, we only employed the Heuristic-1 algorithm to solve the problem. The heuristic algorithm selected 207 containers for transportation to subsequent ports based on their revenue. The detailed list of containers, along with their respective properties, is reported in Table 2.

Table 2 Heuristic-1 filtered data
Full size table

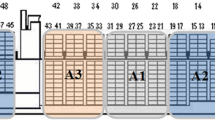
We applied our stage 1 and stage 2 models to this filtered data. In stage 1, our model produced a bay plan with 0 over-stow instances and $844,293 revenue. The results also showed that all cranes handled the same amount of containers leading to no idle time and full efficiency. The outcome of stage 1 is used as input for stage 2 for further stability calculations. In the second stage, the trimming moment was minimized. The bay plan generated by our model for port 1 after loading \(1-j\) containers is depicted in Fig. 6. A summary of all results is provided in Table 3.

Fig. 6
figure 6

Bay plan at port 1 after loading \(1-j\) containers

Full size image
Table 3 Solution characteristics
Full size table

7.2 Experiment design

In this section we compare the performance of our two-stage solution methodology with the two heuristic approaches that rely on container filtering used by many liner companies as discussed before. Below we first present the details of our test instances and numerical results. Next, we discuss our findings.

In order to assess the performance of our DSS that adopts the two-stage formulation, we have generated 30 test instances (10 instances for each solution approach) with different ship capacities as 12,000 TEU, 14,000 TEU, 16,000 TEU, 18,000 TEU, and 20,000 TEU. In order to conduct more extensive trials, we have generated randomized transportation matrix, all consisting of 112,800 containers. Then, the average of all these results is reflected in the corresponding tables. We also assumed that the container ship travels through 6 ports and is expected to load and unload a group of containers at each port by using 3 cranes for 12,000 TEU, 14,000 TEU, 16,000 TEU size instances and 4 cranes for 18,000 TEU, and 20,000 TEU size instances.

The following parameters are fixed for all cases. \(C^{os}\) (cost of stowing a container) and \(C^{cr}\) (cost of a single crane movement) are assumed fixed as 1500 and 150, respectively. \(C^{tm}\), the additional fuel cost per mile resulting from ship stability maintenance, is assumed to be 100 $/(ton meter \(\times \) nm). The distances between ports i and j are determined random uniformly between 100 and 2000 nautical miles. The other parameters that vary in accordance with the problem size are reported in Table 4.

Table 4 Parameters used for each problem size
Full size table

We assume that 75–80% of the ship capacity is on spot sale. The spot capacity is divided into 2 different groups to stow reefer and dry containers. Based on literature, 8–10% of the ship capacity is reserved for reefer containers. This general rule is followed to generate instances in this study. We divide the ship capacities into two different customer requests, contractual and spot. 20% of the ship’s capacity is assumed to be contractual and this capacity is excluded from our calculations. The rest of the ship capacity is reserved for spot customers and is taken into consideration in our experiments.

In our numerical study, all experiments are run by a Microsoft Windows 10 64-Bit operated PC with Intel Core i7 6500U CPU @2.50 GHz with 8 GB RAM. The MILP models are implemented in IBM ILOG CPLEX environment and solved with CPLEX 20.1.0 The proposed heuristic algorithms are coded in Python 3.6 (PyCharm Community 2017.3). For all models, we use the default optimality gap setting as 0.01% and set the maximum computational time as 1 h as the termination criterion.

We solved the problem by using three approaches as: (1) filtering the containers using the Filtering Heurisc-1 and solved the problem for remaining containers using the two-stage formulation, (2) filtering the containers using the Filtering Heuristic-2 and solved the problem for remaining containers using the two-stage formulation, (3) solving the problem for all containers using the two-stage formulation. We shortly refer these three approaches as FH1+2SMILP, FH2+2SMILP, and 2SMILP, respectively.

7.3 Results

Before solving the problem using the two-stage MILP, we first applied the two filtering heuristics to decrease the number of containers that can be assigned to the containership. In particular for each TEU size we considered a total of 112,800 containers. The number of containers after using the two filtering approaches have decreased by more than 90% on average. The total number of containers and the number of containers obtained after filtering them with the heuristics are given in Table5. For instance, the number of containers taken into account for the largest problem instance (i.e., 20,000 TEU capacity) reduces to the number of container between 14,000 and 17,000 for the first and 14,500 and 17,500 for the second filtering heuristic, respectively.

In our numerical experiments, we compare the performance of the two-stage formulation and the proposed heuristic algorithms in terms of computational time (CPU Time), solution quality (% optimality gap) and objective function value as depicted in Table 6. For each approach Table 6 reports the detailed comparison results for each size problem and solution approach. The results reveal that in terms of CPU time solutions with the filtered data set can be obtained within a minute for FH1+2SMILP and FH2+2SMILP on average. For the 2SMILP, on the other hand, the CPU times vary between 500 and 4200 s and tend to increase with the problem size. This is an expected result since the 2SMILP uses all container data as an input which increases the size of the problem drastically. In terms of optimality gaps, the table reveals that all solutions can be obtained almost with zero gap. Since we use the defaults optimality gap setting for CPLEX, in some instances it returns a solution within the 0.01% gap in less than 1 h.

The last group of columns in Table 6 shows the differences in terms of objective function value of each approach. In particular, the revenue obtained with the filtered approaches appear to be very close to each other. In all instances, except 12,000 and 20,000 TEU capacity, FH2+2SMILP yields a very slightly (around 1%) higher revenue than that of the FH1+2SMILP. 2SMILP, on the other hand, outperforms these two data-filtering based approaches within a range of 24–38%. In particular for the 12,000 TEU capacity, it has a 38% better performance than the FH1+2SMILP and FH2+2SMILP. This ratio varies between 24% and 30% for the rest of the instances.

Table 5 Number of containers considered in each solution approach
Full size table
Table 6 Performance of solution approaches
Full size table
Table 7 Solution characteristics
Full size table
Table 8 Crane utilizations
Full size table

The results imply that it is possible to end up with relatively higher revenues with the 2SMILP approach if the decision maker is willing to spend at most 1 h for the container stowage decisions. This is because, the number of transported containers in 2SMILP is higher than those in the other data-filtered approaches. However, the higher volume of transported containers leads to longer port stays, more crane allocations and higher operating costs. In FH1+2SMILP and FH2+2SMILP, on the other hand, the number of transported containers is less than that of the 2SMILP which results in skipping some ports. The stay at ports is shorter and the operating cost might be significantly lower. In that case the liner should consider the returns and expenses separately on each model and decide accordingly.

Table 7 reports the solution characteristics obtained by each approach. In particular, we list the total number of transported containers, the number of over-stows, resulting trimming moments and GM values for each instance. The total number of transported containers are almost equal for the FH1+2SMILP and FH2+2SMILP approaches. For the 2SMILP, the number of contains transported is quite more than those of the other two approaches on average. In all instances all solution approaches yielded 0 over-stows. For the trimming moments and GM values, the results show that there is no significant difference among the solution approaches. We also observe that in all six configurations, the stability parameters (GM and trimming moment) remain within limits.

As for crane utilization, the model produces a ship stowage plan such that all cranes load/unload similar number of containers at ports. Table 8 displays the details of the crane utilization at each port.

8 Conclusion

In this study, we approached the problem of container stowage from a revenue maximization and sustainability perspective while accounting for ship stability and crane utilization. To achieve this, we first developed a MINLP formulation and then a two-stage solution approach which decomposes the problem into two MILPs. The first stage model maximizes the total revenue by determining the containers to be transported while ensuring a balanced workload among the cranes to reduce port emissions. The second stage generates a container-bay assignment plan that minimizes the overall trim-moment of the ship and ensures ship stability in sailing using first stage results.

Our numerical experiments showed that the two-stage methodology which uses all container data as an input outperforms the container filtering-based heuristic approaches used by many liner companies in terms of revenue. Although, as expected, the two-stage formulation returns feasible solutions in short computational times when combined with the filtering-based heuristics, it results in considerable losses in terms of revenue. The two-stage formulation alone, on the other hand, results in a 25–40% increased revenue at the cost of longer computing times. Considering that the time required to develop effective stowage plans is measured in hours, our proposed approach has potential to improve the profitability of liner companies while ensuring ship stability, safety, and efficient crane utilization.

Our study can also easily address cargo composition with circular economy considerations. Waste shipment in containers and empty container repositioning are two important circular economy applications in shipping (Chen et al., 2016; Debnath and Sarkar, 2023). Our problem can generate results for the scenario when containers carrying waste and empty containers are valued as much as laden containers and our results can be analyzed for policy discussions.

Finally, there are important future research directions arising from our study. Current work focuses on a single service. Future studies can tackle the cargo composition problem for several shipping routes in a combined way. That problem would give an opportunity for integrating cargo routing and ship stowage planning for a set of ships and routes. Alternatively, the cargo composition problem can be coupled with the revenue management problem to make pricing decisions in each shipping service.