The urban air mobility problem

Abstract

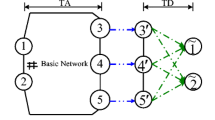
Over the next two decades, Urban Air Mobility (UAM) Systems are anticipated to revolutionize the mass transportation industry. As envisioned presently, these systems will consist of electric vertical take-off and landing aircraft (eVTOLs) that operate from specially designed ports dispersed throughout a city. We consider the network logistics associated with the operation of a UAM system in its early phases, and focus on a problem of ‘routing and scheduling eVTOLs to maximize passenger throughput’. Key challenges for providers are the temporal nature of the demand, time windows for customers, and battery management constraints of the eVTOLs. We develop a three-index, arc-based formulation, routing eVTOLs over a time-expanded network. Due to the computational limitations of the arc-based formulation, we develop an alternate path-based formulation, and design a corresponding column generation procedure, identifying charge-feasible routes by way of a resource-constrained shortest path problem. The path-based approach is computationally robust, and can be applied in a heuristic manner by (i) sparsifying the time-expanded network, (ii) limiting column generation to the root node in a branch-and-bound scheme, and (iii) applying early termination criteria in the column generation procedure. Our computational experience on a large set of test instances indicates that the path-based approach identifies high-quality solutions for large instances. We conduct a case study using Washington D.C. taxi data, to demonstrate the viability of the column generation based heuristic procedure on real-world data.

Appendices

Appendix A: Modeling extensions

The three-index formulation described in the paper can be extended to incorporate a variety of realistic modeling goals. We discuss such considerations in this section and the ways in which the model can be adapted to include them.

1.1 A.0.1. Multiple port allocation

In our paper, we assume a single customer-port allocation. That is, we assume each customer has a unique origin and destination port, when in reality there may be a choice of such ports available. For instance, if the customer’s final destination is sufficiently close to two ports, a customer may accept flights to either one. We extend our definitions in the following way. Suppose there are L possible origin–destination pairs, each with possibly different time windows. We define, for each customer, a set of origin–destination port pairs $\{(o^j_c,d^j_c)\}_{l=1}^L$ and a corresponding set of discrete time windows $\{T_c^j\}_{l=1}^L$. We extend $\mathcal {F}(c)$ to include each of the possible flight arcs for customer c. This will be the collection of arcs $(i,j) \in B$, for which there exists an $l \in \{1,\dots ,L\}$ such that $p_i = o^l_c$, $p_j = d^l_c$, and $t_i \in T_c^l$. Besides this generalization of $\mathcal {F}(c)$, nothing else needs to be changed in MIP3 to account for multiple port allocation.

1.2 A.0.2. Soft time windows

In many vehicle routing applications involving time windows, a popular extension is the inclusion of ‘soft’ time windows. The idea is to relax each time window constraint and instead penalize its violation in the objective function. This relaxation may be desirable in our setting, where a UAM provider may accept a small loss in quality of service in exchange for increased market share.

Such an extension can be achieved in the following way. For each customer $c \in C$, and for each $(i,j) \in \mathcal {F}(c)$, we define a coefficient $w_{ij}^c \in \mathbb {R}$. This coefficient reflects the value of servicing customer c by flying him along arc (i, j). The coefficients can be determined using any model desired. For instance, if $T_c = \{t_c^a,\dots ,t_c^b\}$ is the contiguous, discrete time window of customer c, one simple such definition is:

$$\begin{aligned} w_{ij}^c = \frac{t_c^b - t_i}{t_c^b - t_c^a} \qquad \forall (i, j) \in \mathcal {F}(c), \end{aligned}$$

which linearly decays from 1 to 0 the later the departure time, $t_i$. The objective function is then modified to

$$\begin{aligned} \max \sum _r \sum _{\{(i,j) \in \mathcal {F}(r)\}}w_{ij}^cy_{ij}^c. \end{aligned}$$

1.3 A.0.3. Customer groups

The three-index formulation assumes each customer is traveling individually, when, in reality, passengers may wish to travel together. Groups of customers can be included in the formulation by simply weighting the objective value of the particular customer (now customer group), c, by the number of customers in the group, $n_c$, changing the objective to

$$\begin{aligned} \text {Max } \sum _{c \in C} n_c\sum _{\{(i,j) \in \mathcal {F}(c)\}}y_{ij}^c \end{aligned}$$

and changing the passenger flow equation to

$$\begin{aligned} \sum _{\{c \mid (i,j) \in \mathcal {F}(c)\}} n_cy^c_{ij} \le \sum _k S x^k_{ij} \quad \forall (i,j) \in \mathcal {F}, \end{aligned}$$

to account for the increase in load factor.

1.4 A.0.4. Battery swaps

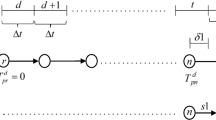
The model above assumes charge levels evolve according to $e_{ij}$, defined for each $(i,j) \in B$. Each arc $(i,j) \in B$ corresponds to a possible transition an eVTOL may make in the time expanded network. If $p_i \ne p_j$, then it must be the case that $t_i + t_{p_i,p_j} = t_j$ (that is, the time at node j must be equal to the time at node i, plus the travel time between the two nodes). We allow for eVTOLs to remain at a port by defining the artificial travel time $t_{ii} = 1$ for each $i \in N$. In the case $p_i \ne p_j$, $e_{ij} < 0$, as an eVTOL is depleting its charge level by flying from one port to another. In the case $p_i = p_j$, $e_{ij} \ge 0$, corresponding to a battery charge increase from recharging. As such arcs correspond to a single time step forward, $e_{ij}$ is specifically the charge increase possible in one time step. This can correspond to a recharging policy or a battery swap policy. In the battery swap policy, $e_{ij} = Q_+$, fully replenishing the charge level.

However, it may be the case that the battery swap process takes more than a single time step. We can account for this by adapting our network in the following way. Suppose a battery swap takes X time steps. For each $i \in M$ such that $t_i + X \in T$, add the arc (i, j) to B, where $p_j = p_i$ and $t_j = t_i + X$. These arcs correspond to remaining at a port for X time steps. Then, for each of these arcs, define $e_{ij} = Q_+$. This will allow the possibility of an eVTOL swapping its battery, with such a choice preventing take-offs during the battery swap period. One can include battery swap and recharging options simultaneously.

Appendix B: Two-index heuristic

The charge constraints significantly complicate the problem, and, therefore, limit the problem sizes that can be solved within a reasonable computation time by an MIP solver. In this section, we present an MIP-based heuristic to identify feasible solutions for large problem sizes. We use a two-index formulation of the UAMP with charge constraints relaxed, and then use the output of such a formulation to dramatically sparsify the network prior to re-solving with the three-index formulation.

The charge-relaxed two-index formulation is constructed by aggregating the eVTOL flow variables from MIP3, $x_{ij} = \sum _{k\in K} x_{ij}^k$. The integer-valued variable $x_{ij}$ thus corresponds to the number of eVTOLs traveling along arc (i, j). We have the resulting integer program (MIP2).

$$\begin{aligned}&\max \sum _{c \in C} \sum _{\{(i,j) \in \mathcal {F}(c)\}}y_{ij}^c \end{aligned}$$

(26)

$$\begin{aligned}&\text {s.t.} \,\,\,\sum _{j \in \delta ^+(i)}x_{ij}- \sum _{j \in \delta ^-(i)}x_{ji} = {\left\{ \begin{array}{ll} |K| &{} i = s \\ 0 &{} i \in M \backslash \{s,f\}\\ -|K| &{} i = f \end{array}\right. } \quad \forall i \in M\cup \{s,f\} \end{aligned}$$

(27)

$$\begin{aligned}&\sum _{\{c \mid (i,j) \in \mathcal {F}(c)\}} y^c_{ij} \le S x_{ij} \quad \forall (i,j) \in \mathcal {F}\end{aligned}$$

(28)

$$\begin{aligned}&\sum _{(i,j) \in \mathcal {F}(c)}y_{ij}^c \le 1 \quad \forall c \in C\end{aligned}$$

(29)

$$\begin{aligned}&x_{ij} \in \mathbb {Z} \quad \forall i,j \in M \end{aligned}$$

(30)

$$\begin{aligned}&y_{ij}^c \in \{0,1\} \quad \forall (i,j) \in \mathcal {F}(r), c \in C \end{aligned}$$

(31)

The objective (26) maximizes the number of customers that are served. Constraints (27) ensure continuity of flow throughout the network. Constraints (28) limit the number of customers flying along an arc by the number of eVTOLs flying along the same arc multiplied by the eVTOL capacity. Constraints (29) ensure that each customer is served at most once. Constraints (30) ensure integer-valued eVTOL variables, and (31) ensure binary-valued passenger flow variables. By both relaxing charge-constraints and aggregating eVTOL flow variables, MIP2 is extremely efficient, running within seconds on large (e.g., $1000+$ customer) problem sizes.

Let R-MIP3 denote MIP3 without the charge constraints. It is clear that any feasible solution of R-MIP3 can be converted into a feasible solution of MIP2. It is straightforward to show that any feasible solution of MIP2 can be converted into a solution of R-MIP3 by disaggregating the integer-valued flow variables $x_{ij}$. That is, we can identify $x_{ij}^k \in \{0,1\}$ for all $(i,j) \in B$ and $k \in K$ such that $\sum _k x_{ij}^k = x_{ij}$ and the flow equations hold. Thus, MIP2 provides a set of K throughput-maximizing paths through the network, which may not satisfy charge constraints.

Fig. 13

Left: Optimality gap of MIP2$\Rightarrow$3 for Problem Set A. For sizes greater than 100, where the true optimal solution is unavailable, the best known objective value is used. For all problem sizes, the gap is within 8%. Right: The run times for the exact MIP3 algorithm and the heuristic MIP2$\Rightarrow$3 algorithm are provided. The former explodes, whereas the latter is relatively constant as the number of customers increases

Fig. 14

Left: Optimality gap of MIP2$\Rightarrow$3 on Problem Set B. For all problem sizes, the optimality gap is within 8%. Right: The run times for RCG and the heuristic MIP2$\Rightarrow$3 algorithm

Our sparsification heuristic appeals to the efficiency of MIP2, as well as the throughput-maximizing quality of the arcs in a given solution. The process is as follows. We first solve MIP2, and obtain an optimal solution $x^* = \{x^*_{ij}\}_{(i,j) \in B}$. We then construct a sparsified network $B^0$. An arc $(i,j) \in B$ is included in $B^0$ if and only if $x^*_{ij} > 0$ or $p_i = p_j$ and $t_j = t_i + 1$. That is, we only keep the arcs from the solution of MIP2 as well as the arcs corresponding to remaining at a port for consecutive time steps. Keeping these latter arcs ensures charge feasibility. MIP3 can be run on this dramatically sparsified network. We refer to the process of sparsifying in this fashion, and then running MIP3 on the sparsified network as MIP2$\Rightarrow$3

This heuristic naturally can lead to suboptimal solutions, as the only customer-serving paths in the problem are those produced by MIP2, which may be charge-infeasible. This can be mitigated by, instead of running MIP2 once, running it multiple times, each time cutting off the previously obtained paths. Then, each of the arcs from all the MIP2 runs are included in B, allowing greater system flexibility. However, a balance must be sought, as the more arcs included in B, the longer the computation time.

In Fig. 13, the performance on Problem Set A of MIP2$\Rightarrow$3 is compared to that of the exact MIP3. We observe the solution quality is always within 8% of the optimal solution (or the best known solution, if the optimal solution is unavailable). Meanwhile, the run time of MIP2$\Rightarrow$3 is quite insensitive to increases in the number of customers, whereas MIP3 explodes in run time.

However, MIP2$\Rightarrow$3 falls short when compared to the path-based heuristics. In Fig. 14, MIP2$\Rightarrow$3 is compared to RCG, using Problem Set B. We see that (with one exception), RCG produces better solutions in less time, particularly as the number of customers increases.

Appendix C: Sparsification

We may prove that, with certain assumptions, the sparsification procedure does not cut off the optimal solution.

Theorem 1

Suppose $Q_+ = \infty$, the distances between ports satisfy the triangle inequality, and that the change in charge level due to recharging is convex with respect to the current charge level. Then, the optimal solution to the UAMP has the same objective value as the optimal solution to the UAMP restricted to the stay-put arcs, anticipatory arcs, and flight arcs.

Proof

Let $\textbf{r} = \{r_1, \dots , r_n\}$ be an optimal path for the UAMP, where $r_i \in M$ $\forall i \in \{1,\dots ,n\}$, and $(r_i, r_{i+1}) \in B$ $\forall i \in \{1,\dots ,n-1\}$. We shall construct a charge-feasible path $\mathbf {r'} = \{r_1', \dots , r_m'\}$, where $r_i' \in M$ $\forall i \in \{1,\dots ,n\}$, that serves the same customers as $\textbf{r}$, and is such that $(r_i', r_{i+1}') \in B'$ $\forall i \in \{1,\dots ,n-1\}$.

The construction is as follows. Initialize $\mathbf {r'} = \{r_1\}$. Starting from $i = 1$, we determine if $(r_i, r_{i+1}) \in B'$. If so, append $r_{i+1}$ to $\mathbf {r'}$. Suppose $(r_i, r_{i+1}) \notin B'$. Since $(r_i, r_{i+1}) \notin B'$, the arc is neither a flight arc, a stay put arc, nor an anticipatory arc. Since the distances between ports satisfy the triangle inequality, we may assume, without loss of generality, that there is some $k \in \mathbb {Z}^+$ such that $\{(r_{i+1}, r_{i+2}), \dots , (r_{i+k}, r_{i+k+1})\}$ is a sequence of stay put arcs, and that $\{r_{i+k}, r_{i+k+1})$ is a flight arc. Let $r_{i}^j \in M$ denote the node satisfying $p_{r_i^j} = p_{r_i}$ and $t_{r_i^j} = t_{r_i} + j$. That is, $r_i^j$ is the port-time node at the same port as $r_i$, j time steps ahead. We may observe that rather than following the sequence $\{r_i, r_{i+1}, r_{i+2}, \dots , r_{i+k-1}, r_{i+k}\}$, we may follow the sequence $\{r_i, r_i^1, r_i^2, \dots , r_i^k, r_{i+k}\}$, consisting of only stay put arcs and an anticipatory arc. Since the charge level is convex with respect to the current charge level, and since $Q_+ = \infty$, the charge level upon arrival at $r_{i+k}$ along the second sequence will be no less than along the first sequence. We therefore can append the nodes $r_i^1, \dots , r_i^k, r_{i+k}, r_{i+k+1}$ to $\mathbf {r'}$, and continue from $i = i + k + 1$. We continue this until reaching $i = n-1$, in which case $(r_{n-1}, r_n\}$ is, without loss of generality, either a stay put arc or a flight arc, and thus in $B'$, so $r_{n}$ may be appended to $\mathbf {r'}$. Since $\textbf{r}$ is charge-feasible, $\mathbf {r'}$ is charge-feasible, and furthermore, $\mathbf {r'}$ serves the same customers as the path $\textbf{r}$. $\square$

We demonstrate we need all anticipatory arcs, rather than just the ‘extreme’ anticipatory arcs, in order for the sparsified network to keep the optimal solution by means of an example instance of the UAMP, visualized in Fig. 15. In the instance, there is a single eVTOL, and three customers. Passenger 1 wishes to depart from Port 1 towards Port 2 at time 0. Passenger 2 wishes to depart from Port 3 towards Port 4 at either time 5, 6, or 7. Passenger 3 wishes to depart from Port 4 towards Port 5 at time 8. Assuming it is charge feasible, the optimal solution is to fly Passenger 1 from Port 1 to Port 2 at time 0 (arriving at time 3), then to immediately dead head from Port 2 to Port 3. From there, we immediately bring Passenger 2 from Port 3 to Port 4 (departing at time 6), and then immediately take Passenger 3 from Port 4 to Port 5. We note that this sequence is the only way to serve each of the customers, and that it requires a non-extreme anticipatory arc (the one connecting Port 2 to Port 3, departing at time 3). Thus we cannot delete such arcs from the network and guarantee that we do not cut off optimal solutions.

Fig. 15

Example instance of the UAMP demonstrating we must include all anticipatory arcs, rather than just ‘extreme’ anticipatory arcs

Appendix D: Load factor analysis

Of particular relevance to a UAM provider may be the average flight occupancy, or load factor. In particular, there may be interest in the proportion of ‘deadheads’ (flights in the solution in which there are no passengers), flights with a single customer, two customers, and so on. We selected parameters to establish a crowded scenario. In particular, the number of ports was set to four, the number of eVTOLs to three, and the number of time steps to 25. We then were able to quickly solve 500-customer problems. Furthermore, by reducing the time horizon in this fashion, we significantly increase the density of customer flight requests. There are roughly $t_{max} {|P| \atopwithdelims ()2}$ possible flight paths, corresponding to every origin–destination pair and every flight time. Thus, when we restrict the number of ports to four and the number of time steps to 25, there are at most 150 possible paths (fewer if it is infeasible to get from any one particular port to another in one time step). If customer requests are distributed uniformly across the possible requests, each with a wait time of three time steps, then varying the number of customers from 50 to 500 corresponds to an expected number of passengers requesting a particular arc varying from roughly 1 to 10.

In this setting, we observed how the load factor of the eVTOLs and the total system throughput varies as we increase the density of customer requests. In Fig. 16, we present the average load factor for four different parameter settings: setting the number of eVTOLs to 3 and 4 and setting the capacities of the eVTOLs to 5 and 6.

An important metric for a UAM provider might also be the eVTOL flight time per customer (that is, the total time spent flying divided by the number of customers served). One of the principal costs for a UAM provider might be the recharging of its fleet, and providing service might only be profitable if the flight time per customer is below a certain threshold. In Fig. 17, we plot the average flight time per customer for the four different parameter settings versus the number of customers (corresponding to customer request density). We observe a clear delineation between the different capacity levels: When the capacity is increased from 5 to 6, there is a decrease in flight time per customer. Meanwhile, increasing the fleet size increases the flight time per customer slightly, as the chances of flying at less than full load factor decrease when more eVTOLs are available.

Fig. 16

Average percent load factor for the four different parameter settings. While all parameter settings appear to have similar results in the extreme cases (highly sparse and highly dense customer requests, respectively), the lower capacity configurations climb slightly faster towards full occupancy

Fig. 17

The average flight time per customer for varying parameter settings across a varying number of customers (corresponding to customer request density). In the higher density setting, a marked improvement (a decrease in flight time per customer) emerges for the higher capacity parameter settings

Tables corresponding to computational results in main paper

Tables 5, 6, 7, 8, 9 and 10 present the detailed computational results for the various algorithms discussed in the paper.

Table 5 Run times (in s) for the various methods on Problem Set A (4 ports, 4 eVTOLs)

Table 6 Objective values for each of the algorithms, given the three hour time limit, on Problem Set A

Table 7 Run times for the better performing heuristics on the 8 port, 8 eVTOL problem (Problem Set B), given a three hour time limit

Table 8 Objective values for the better-performing heuristics on the 8 port, 8 eVTOL problem (Problem Set B), given a three hour time limit

Table 9 Run times for the better performing heuristics on the 8 port, 8 eVTOL problem (Problem Set B*), using a time step size of two minutes

Table 10 Objective values for the better-performing heuristics on the 8 port, 8 eVTOL problem (Problem Set B*), using a time step size of two minutes