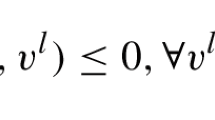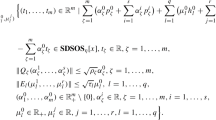Abstract
In this paper we study two-stage affinely adjustable robust multi-objective optimization problems. We show how (weak) Pareto optimal solutions of these robust multi-objective problems can be found by solving conic linear programming problems. We do this by first deriving numerically verifiable conditions that characterize (weak) Pareto optimal solutions of affinely adjustable robust multi-objective programs under a spectrahedron uncertainty set. The uncertainty set covers most of the commonly used uncertainty sets of robust optimization. We then reformulate the weighted-sum optimization problems of the multi-objective problems, derived with the aid of the optimality conditions, as equivalent conic linear programming problems, such as semidefinite programs or second-order cone programs, to find the (weak) Pareto optimal solutions. We illustrate by an example how our results can be used to find a second-stage (weak) Pareto optimal solution by solving a semidefinite program using a commonly available software.
Similar content being viewed by others
References
Ben-Tal, A., Goryashko, A., Guslitzer, E., & Nemirovski, A. (2004). Adjustable robust solutions of uncertain linear programs. Math. Program.,99(2), Ser. A, 351–376.
Ben-Tal, A., Ghaoui, L. El, & Nemirovski, A. (2009) Robust Optimization, Princeton University Press,
Bertsimas, D., Brown, D. B., & Caramanis, C. (2011). Theory and applications of robust optimization. SIAM Review, 53, 464–501.
Bertsimas, D., & de Ruiter, F. J. C. T. (2016). Duality in two-stage adaptive linear optimization: faster computation and stronger bounds. INFORMS Journal on Computing, 28(3), 500–511.
Bertsimas, D., & Goyal, V. (2013). On the approximability of adjustable robust convex optimization under uncertainty. Mathematical Methods of Operational Research, 77(3), 323–343.
Blekherman, G., Parrilo, P. A., & Thomas, R. (2012). Semidefinite Optimization and Convex Algebraic Geometry. Philadelphia: SIAM Publications.
Chen, A., & Zhang, Y. (2009). Uncertain linear programs: Extended affinely adjustable robust counterparts. Operations Research, 57(6), 1469–1482.
Chuong, T. D. (2017). Robust alternative theorem for linear inequalities with applications to robust multi-objective optimization. Operations Research Letters, 45(6), 575–580.
Chuong, T. D. (2018). Linear matrix inequality conditions and duality for a class of robust multi-objective convex polynomial programs. SIAM Journal on Optimization, 28, 2466–2488.
Chuong, T. D. (2020). Robust optimality and duality in multiobjective optimization problems under data uncertainty. SIAM Journal on Optimization, 30(2), 1501–1526.
Chuong, T. D., & Jeyakumar, V. (2020). Generalized Farkas Lemma with adjustable variables and two-stage robust linear programs. Journal of Optimization Theory and Applications, 187, 488–519.
Chuong, T. D., & Jeyakumar, V. (2017). A generalized Farkas lemma with a numerical certificate and linear semi-infinite programs with SDP duals. Linear Algebra and its Applications, 515, 38–52.
Chuong, T. D., Mak-Hau, V. H., Yearwood, J., Dazeley, R., Nguyen, M.-T., & Cao, T. (2022). Robust Pareto solutions for convex quadratic multiobjective optimization problems under data uncertainty. Annals of Operations Research. https://doi.org/10.1007/s10479-021-04461-x.
de Ruiter, F., Ben-Tal, A., Brekelmans, R., & den Hertog, D. (2017). Robust optimization of uncertain multistage inventory systems with inexact data in decision rules. Comp. Manag. Sci., 45–66.
Delage, E., & Iancu, D. A. (2015). Robust Multistage Decision Making. INFORMS TutORials in Operations Research, chap., 2, 20–46.
Denysiuk, R., Moreira, A. V., Matos, J. C., Oliveira, J.R.M., & Santos, A. (2017) Two-stage multi-objective optimization of maintenance scheduling for pavements, J. Infrastruct. Syst., 23, https://doi.org/10.1061/(ASCE)IS.1943-555X.0000355.
Ehrgott, M. (2005). Multicriteria Optimization. Berlin: Springer.
Ehrgott, M., Ide, J., & Schobel, A. (2014). Minmax robustness for multi-objective optimization problems. European Journal of Operational Research, 239(1), 17–31.
Engau, A., & Devon, S. (2020). Pareto solutions in multicriteria optimization under uncertainty, European. European Journal of Operational Research, 281, 357–368.
Fabrizio, A., Nicola, B., Claudio, D. S., Gerardo, M. M., & Giuseppe, P. V. (2016). Multi-stage and multi-objective optimization for energy retrofitting a developed hospital reference building: A new approach to assess cost-optimality. Applied Energy, 174, 37–68.
Fabrizio, A., Nicola, B., Rosa, F. D. M., Gerardo, M. M., & Giuseppe, P. V. (2017). Resilience of robust cost-optimal energy retrofit of buildings to globalwarming: A multi-stage, multi-objective approach. Energy and Buildings, 153, 150–167.
Feige, U., Jain, K., Mahdian, M., & Mirrokni, V. (2007) Robust Combinatorial Optimization with Exponential Scenarios, In: Fischetti M., Williamson D.P. (eds) Integer Programming and Combinatorial Optimization. IPCO 2007. Lecture Notes in Computer Science, vol 4513. Springer.
Fredriksson, A. (2017) Robust optimization in radiation therapy, Advances and Trends in optimization with engineering applications, SIAM Publications.
Georgiev, P. G., Luc, D. T., & Pardalos, P. M. (2013). Robust aspects of solutions in deterministic multiple objective linear programming. European Journal of Operational Research, 229(1), 29–36.
Goberna, M. A., & López, M. A. (1998). Linear Semi-Infinite Optimization. Chichester: John Wiley & Sons.
Goberna, M. A., Jeyakumar, V., Li, G., & Vicente-Perez, J. (2022). The radius of robust feasibility of uncertain mathematical programs: a survey and recent developments. European Journal of Operational Research, 296(3), 749–763.
Goberna, M. A., Jeyakumar, V., Li, G., & Vicente-Perez, J. (2018). Guaranteeing highly robust weakly efficient solutions for uncertain multi-objective convex programs, European. European Journal of Operational Research, 242, 40–50.
Goberna, M. A., Jeyakumar, V., Li, G., & Vicente-Perez, J. (2015). Robust solutions to multi-objective linear programs with uncertain data. European Journal of Operational Research, 242(3), 730–743.
Goberna, M. A., Jeyakumar, V., Li, G., & Perez, J.-V. (2014). Robust solutions of multi-objective linear semi-infinite programs under constraint data uncertainty. SIAM Journal on Optimization, 24(3), 1402–1419.
Grant, M., & Boyd, S. (2008) Graph implementations for nonsmooth convex programs. In V. Blondel, S. Boyd, and H. Kimura, editors, Recent Advances in Learning and Control, Lecture Notes in Control and Information Sciences, pages 95-110. Springer,
Huang, R.-H., Yang, C.-L., & Hsu, C.-T. (2015). Multi-objective two-stage multiprocessor flow shop scheduling-a subgroup particle swarm optimisation approach. International Journal of Systems Science, 46(16), 3010–3018.
Ide, J., & Schöbel, A. (2016). Robustness for uncertain multi-objective optimization: a survey and analysis of different concepts. OR Spectrum, 38, 235–271.
Jeyakumar, V., & Luc, D. T. (2008) Nonsmooth Vector Functions and Continuous Optimization, Springer Series in Optimization and Its Applications, Springer.
Kuhn, K., Raith, A., Schmidt, M. & Schöbel, A. (2016) Bi-objective robust optimisation,European Journal of Operational Research 252, 418–431 .
Kuroiwa, D., & Lee, G. M. (2012). On robust multi-objective optimization. Vietnam Journal of Mathematics, 40(2–3), 305–317.
La Torre, D., & Mendivil, F. (2018). Portfolio optimization under partial uncertainty and incomplete information: a probability multimeasure-based approach. Annals of Operations Research, 267(1–2), 267–279.
Lee, J. H., & Jiao, L. (2021). Finding efficient solutions in robust multiple objective optimization with SOS-convex polynomial data. Annals of Operations Research, 296, 803–820.
Lin, W., Jin, X., Mu, Y., Jia, H., Xu, X., Yu, X., & Zhao, B. (2018). A two-stage multi-objective scheduling method for integrated community energy system. Applied Energy, 216, 428–441.
Mordukhovich, B. S., & Nam, N. M. (2014). An easy path to convex analysis and applications, Synthesis Lectures on Mathematics and Statistics, 14. Williston: Morgan & Claypool Publishers.
Rockafellar, R. T. (1970). Convex Analysis. Princeton, NJ: Princeton University Press.
Sion, M. (1958). On general minimax theorems. Pacific Journal of mathematics, 8, 171–176.
Spieker, H., Hagg, A., Gaier, A., Meilinger, S., & Asteroth, A. (2017). Multi-stage evolution of single- and multi-objective MCLP: Successive placement of charging stations. Soft Computing, 21, 4859–4872.
Yanikoglu, I., Gorissen, B. L., & den Hertog, D. (2019). A survey of adjustable robust optimization. European Journal of Operational Research, 277(3), 799–813.
Wiecek, M. M., & Dranichak, G. M. (2016) Robust multi-objective optimization for decision making under uncertainty and conflict. In A. Gupta and A. Capponi (Eds.), TutORials in operations research, optimization challenges in complex, networked, and risky systems (pp. 84-114). INFORMS,
Zamani, M., Soleimani-damaneh, M., & Kabgani, A. (2015). Robustness in nonsmooth nonlinear multi-objective programming. European Journal of Operational Research, 247(2), 370–378.
Zheng, J., Wu, Q., & Jing, Z. (2017). Coordinated scheduling strategy to optimize conflicting benefits for daily operation of integrated electricity and gas networks. Applied Energy, 192, 370–81.
Acknowledgements
The authors would like to thank the referees for their constructive comments and valuable suggestions which have contributed to the final version of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research of the second author was supported by a research grant from Australian Research Council.
Appendix: Robust multi-objective linear programs and SDP reformulations
Appendix: Robust multi-objective linear programs and SDP reformulations
In this appendix, we give optimality conditions and semidefinite programming reformulations for a single-stage robust multi-objective linear optimization models that can be used to transform the previous two-stage optimization problem to a single-stage problem.
Let us consider a robust counterpart of (UP) given by

where \(f_r(x):=\max \limits _{u\in U}c_r(u)^\top x, r=1,\dots ,p\) for \( x\in {\mathbb {R}}^{n}.\)
The following lemma presents optimality conditions of the robust multi-objective program (RP) that has been employed in the proofs of the previous sections.
Lemma 4.1
(Necessary optimality for (RP)) For the problem (RP), let the cone C be closed, where
If \(\bar{x}\in {\mathbb {R}}^{n}\) is a weak Pareto solution of problem (RP), then, there exist \((\alpha _1,\ldots ,\alpha _p)\in {\mathbb {R}}^p_+\setminus \{0\}\), \(\lambda _j\ge 0, j= 1,\ldots ,q, \mu \ge 0\), \({{\bar{u}}}^r \in U, r=1,\ldots ,p\) and \( u^j\in U, j= 1,\ldots ,q,\) such that
Proof
The proof uses a classical alternative theorem (see e.g., (Rockafellar 1970, Theorem 21.1) to show that every weak Pareto solution can be determined by a convex program (RP) (cf. Ehrgott (2005)). Applying a classical minimax theorem (see e.g., ( Sion 1958, Theorem 4.2) and a strong separation theorem (see e.g., Mordukhovich & Nam 2014, Theorem 2.2) gives the desired result. We omit the details for the purpose of a shorter presentation the paper. \(\square \)
For each \(\alpha :=(\alpha _1,\ldots ,\alpha _p)\in {\mathbb {R}}^p_+\setminus \{0\},\) we consider a (scalar) robust weighted-sum optimization problem of (RP) as follows:

A semidefinite programming reformulation problem for (RP\(_{\alpha }\)) is given by

The following lemma presents an exact semidefinite programming (SDP) reformulation for (RP\(_{\alpha }\)) that has been employed in the proofs of the previous sections.
Lemma 4.2
(Exact SDP reformulation for (RP\(_{\alpha }\))) Let \(\alpha :=(\alpha _1,\ldots ,\alpha _p)\in {\mathbb {R}}^p_+\setminus \{0\}\) be such that the problem (RP\(_{\alpha }\)) admits an optimal solution and assume that \({{\bar{x}}}\in {\mathbb {R}}^{n}\) is an optimal solution of problem (RP\(_{\alpha }\)). Assume that the cone C in (5.11) is closed and there exists \({{\hat{u}}}:= ({{\hat{u}}}_1,\ldots ,{{\hat{u}}}_s)\in {\mathbb {R}}^s \) such that \(A_0+\sum _{i=1}^s{{\hat{u}}}_iA_i\succ 0\). Then, there exist \(\tilde{Z}_r\succeq 0, r=1,\ldots ,p, Z_j\succeq 0, j=1,\ldots ,q\) such that \(({{\bar{x}}},{{\tilde{Z}}}_1,\ldots ,{{\tilde{Z}}}_p,Z_1,\ldots , Z_q)\) is an optimal solution of problem (RP\(^*_{\alpha }\)) and
where val(RP\(_{\alpha }\)) and val(RP\(^*_{\alpha }\)) stand for the optimal values of problem (RP\(_{\alpha }\)) and problem (RP\(^*_{\alpha }\)), respectively.
Proof
The proof uses a strong duality in semidefinite programming (cf. Blekherman 2012, Theorem 2.15) to get the desired result. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chuong, T.D., Jeyakumar, V. Adjustable robust multiobjective linear optimization: Pareto optimal solutions via conic programming. Ann Oper Res (2022). https://doi.org/10.1007/s10479-022-05104-5
Accepted:
Published:
DOI: https://doi.org/10.1007/s10479-022-05104-5