1 Introduction

Should a firm invest in CSR (Friedman, 1970; Caroll, 1979; Jones, 1980; Wood, 1991; Campbell, 2007)? This question has been debated for decades and has been the subject of hundreds of articles focusing on the compatibility between CSR and a firm’s shareholder view (Aguinis & Glavas, 2012; Dixon-Fowler et al., 2013; Margolis et al., 2007; Wu, 2006). Although empirical evidence is mixed, most past research focusing on the relationship between corporate social performance and corporate financial performance tends to corroborate the compatibility between these two perspectives. Even recent studies have highlighted the existence of more complex relationships, such as non-linearities (Barnett & Salomon, 2012; Meier et al., 2019; Surroca et al., 2010).

More recently, new studies have focused on a second aspect of this relationship, namely, the link between CSR and corporate financial risk, understood as the risk incurred by shareholders, that is, the risk associated with stock price fluctuations (Klein & Dawar, 2004; Luo & Bhattacharya, 2009; Harjoto & Jo, 2011; Dhaliwal et al., 2011; Su et al., 2020; Shiu & Yang, 2017; Giannarakis et al., 2020). Two main theoretical perspectives were then mobilized. The first perspective, based on agency theory, posits arguments in favor of a positive relationship with the increase in CSR investments generating greater risk, mainly due to the discretionary behavior of managers, such as the instrumentalizing of CSR investments for private profits (Barnea & Rubin, 2010; Behl et al., 2021). The second perspective, developing an insurance-type argument, proposes an opposite reading, with CSR investments acting in this framework as a mechanism against reputational effects or major business risks (Godfrey et al., 2009). Recent empirical results, although partly contradictory, tend to corroborate the insurance view, with CSR investment reducing the financial risk of companies.

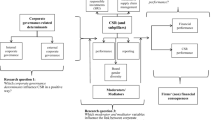
Research focusing on the relationship between CSR risks is, then, based on a conception of stock risk (systematic versus specific) and its measurement. While many studies have focused on systematic risk and its consequences for firms’ cost of capital, new research has focused on total risk and/or specific risk. Moreover, recent research questions the existence of a linear relationship between CSR and risk. By limiting abnormal behaviors, CSR could limit the consequences of extreme business events. From this perspective, new models for modeling dependence have been developed to model complex dependencies, notably through copula functions. Compared to traditional measures based on correlations, copula functions make it possible to study in depth the dependency structure between two variables without making any a priori assumptions about the nature of the relationship. The latter can also cumulate characteristics, such as non-linearity, asymmetry, or a certain level of leptokurtivity. While copula functions have already been used to model different dependence structures in finance (Patton, 2001; Rockinger & Jondeau, 2001; Scaillet, 2002; Malevergne and Sornette, 2002; Ane' & Kharoubi, 2003; Junker et al., 2006), to the best of our knowledge, no study mobilizing copula functions has been conducted to account for the structure of dependence between CSR and the financial risk of firms, even though recent theoretical arguments and empirical data point in the direction of a non-linear relationship (Farah et al., 2021; Orlitzky & Benjamin, 2001). This article aims to fill this gap and seeks to identify the extent to which copula functions can account for this dependence structure and whether the observed relationship makes it possible to envisage CSR as an active lever for managing firms’ financial risk. However, before measuring and modeling the dependence, this research aims to answer the question: Does investing in CSR help to mitigate risk within the firm?

Using a sample of 254 European firms, for which we have the full CSR ratings provided by Bloomberg for the years 2018–2020, our research aims to analyze the relationship between CSR and risk. To measure specific risk, we use well-developed specific risk measures, the realized idiosyncratic volatility (Brandt et al., 2010; Goetzmann & Kumar, 2008; Malkiel & Xu, 2006; Merton, 1987), and the expected idiosyncratic volatility derived from an EGARCH model (Karakas, 2016; Embrechts et al., 2002). We then apply the Granger test of causality between CSR and the expected idiosyncratic volatility after testing the stationarity of the series. In the second part, we apply six copula functions (Archimedean, Gumbel, Clayton, Frank, Plackett, and Ali–Mikhail–Haq) to identify which function best fits the dependence structure between CSR and risk.

Our results highlight, first, the causality effect of CSR on risk and, second, the dependence between CSR and risk. In particular, we show that the Clayton copula function best fits the dependence structure between CSR and risk. However, our results indicate that the dependence structure is not identical across all CSR ratings. Thus, the Clayton copula function best captures the relationship between the environmental rating and risk, while the Gumbel copula function is better suited for the relationship between financial risk and governance. Globally, all our results highlight the existence of asymmetry and leptokurtic relationships. This result suggests that even if the relationship is partially negative, CSR cannot be easily used as an insurance mechanism to mitigate normal risk. However, our results suggest that CSR can act as a protection mechanism against extreme business events.

The rest of the paper is organized as follows. Section 2 presents a review of the literature on CSR and risk. Section 3 outlines our sample, our measures of risk, the Granger test of causality, and the copula functions mobilized. Section 4 presents the main empirical results. Section 5 discusses these results and concludes the study.

2 Literature review

Idiosyncratic volatility is the volatility of stock returns beyond systematic risk, reflecting the unique risks of firms. Idiosyncratic risk accounts for a large proportion of firms’ total risks. Idiosyncratic risk accounts for approximately 80% of total stock risk and security price fluctuations (Bansal & Clelland, 2004; Gaspar & Massa, 2006; Goyal & Santa-Clara, 2003), and investors set a lower cost of capital for firms with a lower risk (e.g., Merton, 1987; Shin & Stulz, 2000). Goyal and Santa‐Clara (2003) stated that idiosyncratic risk explains most of the variation in average stock risk over time. Indeed, it is idiosyncratic risk that drives the forecastability of the stock market. Given the impact of idiosyncratic risk on firm value and risk, it is important for managers and investors alike to carefully manage non-systematic firm risk. Mishra and Modi (2013) documented that CSR can be a strategic option through which firms manage their idiosyncratic risk.

Several studies have examined the question of whether idiosyncratic risk can be reduced by integrating CSR into management strategies, which would increase profitability and investors’ willingness to invest. The theoretical logic behind the possible relationship between firm idiosyncratic risk and CSR was established by Godfrey (2005) and echoed by Luo and Bhattacharya (2009). Godfrey (2005) presented a theoretical framework based on business ethics, social psychology, law, microeconomics, and the strategic management literature. He proposed three assertions: (1) corporate philanthropy (a manifestation of CSR) can generate positive moral capital among communities and stakeholders, (2) moral capital can provide "insurance-like" protection for the firm, and (3) this insurance-like protection contributes to shareholder wealth. The risk management value of positive moral capital draws on risk management principles and insurance theory. Moral capital provides insurance-like protection for relational wealth because it fulfills the core function of an insurance contract: It insures firm value streams against the loss of economic value due to operational risks. The firm gains insurance-like benefits in two ways: (1) the degradation of relationship-based intangible assets will be tempered by positive moral capital (less trust is violated, reputation is not so tarnished), and (2) punishments and sanctions by stakeholders will be less severe than in the absence of positive moral capital. In the same vein, Gaspar and Massa (2006) postulated that when firms operate within a highly competitive environment, idiosyncratic risk is significantly higher. As such, Chen et al. (2018) added that in a highly competitive market, a good operating strategy, including CSR activities, can contribute to the creation of solid relationships with stakeholders, thereby lowering idiosyncratic risk. Similarly, Peloza (2006) notes that the benefit of CSR is insurance against negative events that would otherwise harm financial performance. Bansal and Clelland (2004) argue that environmentally legitimate firms incur less unsystematic stock market risk than illegitimate firms. Firms are perceived as environmentally illegitimate when their performance regarding the natural environment conforms to stakeholders’ expectations. Echoing this, Luo and Bhattacharya (2009) add that CSR activities and mainly corporate social performance protect the firm and its public image and, consequently, relieve regulatory pressure and enable the firm to insulate itself from scrutiny.

Using real options theory, Husted (2005) developed the notion of CSR as a real option and its implications for risk management. He explained that real options theory suggests that CSR projects provide a way of reducing the downside business risk of the firm and, hence, are an essential element in the risk management of the corporation. This assertion is argued for two reasons. First, real CSR options involve operating and strategic decisions made by managers that are likely to influence the business or unsystematic risk of the firm (Bowman, 1980). Second, real options provide an important way for firms to manage business risk by reducing the downside risk of future investments (Bowman & Hurry, 1993; Miller and Reuer, 1996).

Empirically, several studies have addressed the question of whether idiosyncratic risk can be reduced by integrating CSR into management strategies. Klein and Dawar (2004) examined the potential for CSR to provide insurance-like protection and found that consumer perceptions of a firm’s CSR moderated their attributions of blame in a product–harm crisis situation. They argued that, even if CSR fulfillment does not increase immediate profitability, it may be instrumental in reducing the effects of a damaging event. Similarly, Luo and Bhattacharya (2009) concluded that superior CSR over competitors helps the firm through tougher times with more stable future cash flows and less volatile firm stock prices, thus lowering firm-idiosyncratic risk. Harjoto and Jo (2011) further indicated that CSR can minimize the damage caused by bad news and the risk of falling stock prices. Dhaliwal et al. (2011) also stated that when firms interact with stakeholders via CSR activities, it can minimize the effects of asymmetric information, thereby giving stakeholders a greater understanding of the firm’s operating model and building a positive business image, which reduces uncertainties during operations and equity capital costs. Su et al. (2020) studied firms targeting emerging markets and concluded that firms engaged in CSR activities exhibited better reputations, as well as increased operating and revenue performance. In the same vein, Shiu and Yang (2017) examined whether firms engaging in CSR could benefit from insurance-like effects during negative events. They found that if a firm could engage in CSR, it would diminish the possibility of stock prices pulling back after a sudden event.

Goss and Roberts (2011) examined the relationship between CSR and bank loans and concluded that companies with better CSR performance have more chances to obtain bank loans and benefit from lower borrowing costs. Similarly, Chen et al. (2020) found that socially responsible firms have a significantly lower ex-ante cost of capital.

Marti et al. (2015) conducted research into the relationship between CSR and financial performance during financial crises. They found that, during the crisis, companies that implemented CSR strategies obtained better financial performance than those that implemented traditional management strategies. They argued that companies with higher levels of CSR engagement experienced lower operating risks and more stable performance. Ioannon and Serafeim (2015) pointed out that market analysts forecast better financial performance for firms with higher levels of CSR engagement. Later, the empirical analysis of Chen et al.’s (2018) empirical analysis suggests that firms with good CSR performance have significantly lower idiosyncratic risk. In the different market states, the results also show that the idiosyncratic risks of firms with the worst CSR performance are significantly higher, meaning that when firms cannot effectively practice CSR activities, operating uncertainties increase costs and idiosyncratic risk.

In summary, the above study results imply that in a competitive market, the integration of CSR into operational and management strategies exerts positive effects: It builds solid relationships with stakeholders, reduces the ex‐ante cost of capital, increases operating performance, and permits analysts to forecast the firm’s future more accurately. Generally, then, it reduces uncertainties in operations and lessens idiosyncratic risk. However, firms should pay the costs to implement CSR investment policies. The costs are multiple and relate to resources, financing, operations, and principal–agent conflicts. As such, there must be an optimal point at which the positive effect of CSR offsets its costs. Only below this level are the benefits of CSR higher than the costs. Hence, the relationship between CSR and idiosyncratic risk is predicted to be non-linear. Most studies on the CSR–risk nexus have focused on a linear relationship. To the best of our knowledge, only two recent papers have defended a nonlinear relationship. First, Farah et al. (2021) explained that the relationship between CSR and risk is not necessarily linear; instead, it is curvilinear. That is, because CSR has dual effects on a firm’s costs and benefits, the impact of CSR on a firm’s operating leverage and then on its systematic risk is nonlinear. In other words, CSR fulfillment should increase the firm’s beta due to the incremental operating cost. Subsequently, it would start to decrease beta when it reaches a moderately high level. Second, Li et al. (2021) show that CSR can negatively affect idiosyncratic risk; however, the relationship is U-shaped. In this paper, we innovatively show the nonlinear relationship between CSR and idiosyncratic risk using a copula approach.

3 Methodology and empirical analysis

3.1 Sample

The sample consisted of all quoted companies from European countries that are part of the Bloomberg ESG database from 2018 to 2020 and for which all ESG scores are available. Our sample is then composed of 254 firms across 15 different European countries (Denmark, Norway, Swiss, Austria, Italy, Netherlands, France, Spain, Greece, Belgium, Sweden, Austria, Finland, Luxembourg, Portugal). Stock returns are extracted weekly from Bloomberg database.

To analyze the impact of CSR dimensions on risk idiosyncratic, we consider the following criteria. ESG means using Environmental, Social and Governance factors to evaluate companies and countries on how far advanced they are with sustainability. When enough data has been acquired on these three metrics, they can be integrated into the investment process when deciding what equities or bonds to buy.

The ESG environment criteria relate to the impact of a company or country on climate change (greenhouse gas emissions, waste management, or energy efficiency). Considering the efforts to fight global warming, the reduction of emissions and decarbonization play an increasingly important role.

The ESG society criteria include human rights, working conditions in the supply chain, any exposure to illegal child labor, and occupational health and safety. The social score increases if the business is well integrated into its local community and receives its "blessing" to operate.

ESG governance criteria refer to the rules and principles that define the rights, responsibilities, and expectations of the actors responsible for running a business. A well-thought-out governance system helps to align or balance the interests of stakeholders and contributes to the long-term strategy of the company.

3.2 Idiosyncratic risk estimation

Idiosyncratic risk is caused by firm-specific characteristics and is associated with the residual risk that cannot be explained by changes in average market portfolio returns. In line with previous literature, we used the CAPM model with the quarterly excess returns, the return of STOXX Europe 600 as return of the market and the return of EONIA INDEX as risk-free return.

$${R}_{it}-{R}_{ft}={\alpha }_{i}+{\beta }_{i}\left({R}_{Mt}-{R}_{ft}\right)+{\varepsilon }_{it}$$
(1)

with

$${\varepsilon }_{i,t}\sim N(0,{\sigma }_{i,t}^{2})$$

Following Merton (1987), Malkiel and Xu (2006), Goetzmann and Kumar (2008), Fu (2009) Brandt et al (2010) and Huang et al (2010). Idiosyncratic risk is estimated by two ways: Realized Idiosyncratic Volatility and the Expected idiosyncratic volatility.

Realized idiosyncratic volatility (RIVit), for the firm i at the year t, is measured as the standard deviation of the regression residuals.

$${RIV}_{it}= \sqrt{Var({\varepsilon }_{it})}$$
(2)

Expected idiosyncratic volatility (EIVit), for the firm i at the year t. Finance theory indicates that investor decisions are based on expected rather than current measure. The EIVit, is derived as the forecasted residual volatility from a set of exponentials generalized autoregressive conditional heteroskedasticity (EGARCH) models.

To overcome some weaknesses of the GARCH model in handling financial time series, Nelson (1991) proposes the exponential GARCH (EGARCH) model. In particular, to allow asymmetric effects between positive and negative asset returns, he considers the weighted innovation. This model differs in several ways. First, it uses logged conditional variance to relax the positiveness constraint of model coefficients. Second, the use of the weighted innovation enables the model to respond asymmetrically to positive and negative lagged values.

The return-generating process follows the specification of the CAPM, resulting in the following EGARCH (p, q) model specification: The expected idiosyncratic volatility is estimated as the square root of the conditional variance, which is modeled as a function of the last p residual variances and the last q shocks (Eq. 3).

$$ ln\sigma _{{i,t}}^{2} = ~\alpha _{i} + \mathop \sum \limits_{{t = 1}}^{p} b_{{i,l}} ln\sigma _{{i,t - 1}}^{2} + ~\mathop \sum \limits_{{k = 1}}^{q} c_{{i,k}} \left\{ {\theta \left( {\frac{{\varepsilon _{{i,t - k}} }}{{\sigma _{{i,t - k}} }}} \right) + \gamma \left[ {\left| {\frac{{\varepsilon _{{i,t - k}} }}{{\sigma _{{i,t - k}} }}} \right| - \sqrt {2/\pi } } \right]} \right\} $$
(3)

Following Karakas (2016) and Embrechts et al. (2002), we use EGARCH (1,1) for estimating of the EIVit for the firm i at the year t.

3.3 Tests of Granger causality

We aim to investigate causal relations between CSR and idiosyncratic risk, proxied by the expected idiosyncratic volatility. To this end, pairwise Granger (1969) causality tests were used to explore unidirectional and bidirectional causality. The methodology employed in this study is based on Granger (1969). Granger causality is pragmatic, well defined, and has exhibited many successful applications in a variety of fields, from quantitative finance (Billio et al., 2012; Corsi et al., 2018) to transportations (Zanin et al., 2017).

The Granger tests, where y causes x, involve the estimation of the following equation:

$${x}_{t}= \sum_{k=1}^{p}{\varphi }_{k,1}{x}_{t-k}+\sum_{k=1}^{p}{\varphi }_{k,2}{y}_{t-k}+{\varepsilon }_{t}$$
(4)
$$\mathrm{With}\quad { \varepsilon }_{i,t}\sim N(0,{\sigma }_{i,t}^{2})$$

The \({\varphi }_{k,1}\) and \({\varphi }_{k,2}\) are the coefficients to estimate. Absence of directional causality is indicated if the set of parameters are statistically insignificant. We can then test if, different CSR causes idiosyncratic risk, and vice versa. Therefore, in estimating the Granger causality models, the stationarity of the series involved must be first ascertained. To this end, the Dickey- Fuller unit root test was performed for the stock and exchange series.

3.4 Copulas estimation

This research used a method of estimating dependence based on copulas, introduced by (Sklar, 1959). The copula function is a class of functions that use marginal probability density function to obtain joint distribution. It is used to model multivariate joint distribution and is suitable to apply in the study of finance analysis. There are many practical applications of copulas (Lu and al. 2014; Bruneau et al. 2020). Nelsen (1999) gave a definition of the copula with a mathematic perspective. Later applications of copulas were defined in finance by Embrechts, et al. (2002).

The copula is defined as a C: [0,1]2 → [0,1] that ensures the limiting conditions

$$C(u,0) = C(0,u) = 0 and C(u,1) = C(1,u) = u, \forall u \in [\mathrm{0,1}].$$
$$(u1,u2,v1,v2) \in [\mathrm{0,1}]4, such that u1 \le u2, v1 \le v2$$
$$C(u2,v2) - C(u2,v1) - C(u1,v2) + C(u1,v1) \ge 0.$$

Ultimately, for twice differentiable and two increasing property can be replaced by the condition

$$c\left(u,v\right)= \frac{{\partial }^{2}C(u,v)}{\partial u\partial v} \ge 0$$

where c(u,v) is the copula density. In the following, for n-uniform random U1, U2, …, Un, variables, the joint distribution function C is defined, with θ is dependence parameter.

$$C(u1, u2,\dots , un, \theta ) = P(U1 \le u1, U2 \le u2, \dots Un \le un).$$

3.4.1 Archimedean copula

Archimedean copulas are a family of a copula that play an important role because they present several desired properties. They are related to multivariate distributions generated by mixtures.

Let φ define a function ϕ: [0,1] → [0,∞] which is continuous and provides:

$$\upphi (1)=0,\upphi (0)=\infty .$$

For all t ∈ (0,1), ϕ'(t) < 0, φ is decreasing, for all t ∈ (0,1) φ′′(t) ≥ 0, φ is convex.

φ has an inverse φ−1: [0,∞] → [0,1], which has the same properties out of ϕ(−1)(0) = 1 and ϕ(−1)(∞) = 0.

The Archimedean Copula is defined by

$$C(u,v) = {\phi }^{(-1)}[\phi (u)+\phi (v)]$$
(5)

The most used Archimedean Copula are following (Nelsen, 1999, Genest and al. 2006): Gumbel copula, Clayton copula, Frank copula, Joe Copula, Plackett Copula, Ali Mikhail Haq Copula.

Gumbel Copula: This Archimedean copula is defined with a generator function \(\phi (t ) = (-lnt) \theta ,\theta \ge 1\)

$${C}_{\theta }(u,v)=exp (-[(-lnu)\theta +(-lnv)\theta ]1/\theta )$$
(6)

where ϴ is the copula parameter restricted to [1, ∞).

This copula is asymmetric, with more weight in the right tail. Beside this, it is extreme value copula.

Clayton Copula: This Archimedean copula is defined by a generator function \(\varnothing \left(t\right)= \frac{{t}^{-\theta }-1}{\theta }\)

$${C}_{\theta }(u,v)=({u}^{-\theta } +{v}^{-\theta }-1)$$
(7)

where θ is the copula parameter restricted to (0,∞). This copula is also asymmetric, but with more weight in the left tail.

Frank Copula: It is defines with the generator function; \(\varnothing \left(t\right)= -ln\frac{-{e}^{-\theta t}-1}{{e}^{-\theta }-1}\)

$${C}_{\theta }\left(u,v\right)=-\frac{1}{\theta }ln\left(1+\frac{\left({e}^{-\theta u}-1\right)\left({e}^{-\theta v}-1\right)}{\left({e}^{-\theta }-1\right)}\right)$$
(8)

where θ is the copula parameter restricted to (0,∞).

Joe Copula: It is defined with the help of generator function; \(\varphi \left(t\right)=-ln\left[1-{(1-t)}^{\theta }\right]\)

$$ C_{\theta } \left( {u,v} \right) = 1 - \left[ {\left( {1 - u} \right)^{\theta } + \left( {1 - v} \right)^{\theta } - \left( {1 - u} \right)^{\theta } \left( {1 - v} \right)^{\theta } } \right]^{{1/\theta }} $$
(9)

where θ is the copula parameter restricted to [1,∞]. This copula family is similar to the Gumbel. The right tail positive dependence is stronger more than Gumbel.

Plackett Copula: this copula function is defined as:

$$C\left(u,v\right)= \frac{1+\left(\theta -1\right)-\sqrt{{\left[1+(\theta -1)(u+v)\right]}^{2}-4\theta \left(\theta -1\right)uv}}{2(\theta -1)}$$
(10)

where θ is the copula parameter restricted to (0, ∞).

Ali Mikhail Haq Copula: This Archimedean copula is defined with the help of generator function \(\varphi \left(t\right)=ln\left[1-\theta (1-t)\right]/t\)

$${C}_{\theta }\left(u,v\right)= \frac{uv}{1-\theta (1-u)(1-v)}$$
(11)

where θ is the copula parameter restricted to [− 1,1].

4 Empirical results

The Panel A of Table 1 displays summary statistics of the Realized idiosyncratic volatility. over the sample. The RIVs range from 0.0001 to 3.1523 with a mean value equals 0.3483. The skewness level is high (3.6754). The distribution of the RIVs is then symmetric. The kurtosis level is greater than 3, attesting that the distribution is not normal.

Table 1 Realized idiosyncratic volatility
Full size table

Panel B of Table 1 shows correlation and dependencies between the different CSR scores and the RIV. Clearly, Pearson’s correlations between all CSR dimensions and RIVs are not significant. We then complete the dependence analysis by calculating Spearman’s Rho and Kendall’s Tau. This first analysis must be completed by the Grangers’ test that is better suited for time series.

Panel B of Table 1 shows that scores Esg. Soc. And Env are significantly correlated with the realized idiosyncratic risk.

Table 2 presents the gaussian or the mean and the standard deviation of all the Expected idiosyncratic volatility computed for the i firm at the t quarter, modelled by an EGARCH(1,1).

Table 2 Expected idiosyncratic volatility series marginal modeling
Full size table

Different ESG causes significantly the idiosyncratic risk. This relationship, and unidirectional causality, between these two variables is clearly demonstrated. Table 3 illustrates the disparate tests in the two directions between: SCORE ESG, SCORE SOC. SCORE ENV. SCORE GOUV. and the Expected idiosyncratic volatility. Various scores cause idiosyncratic risk. This implies that investing in ESG affects idiosyncratic risk. The relationship between ESG, idiosyncratic risk, and dependencies will be measured in the following.

Table 3 Granger’s tests of causality between ESG and Expected idiosyncratic volatility
Full size table

The stationarity of the series involved was tested using the Dickey-Fuller unit root test. The results indicated that the series have one unit root which means that they are non-stationary at their levels but are first-difference stationary.

The results related to the copula modeling are presented in Table 4. In this table, we can read the dependence structure between the different CSR scores and Expected idiosyncratic volatility. Clearly, the Clayton copula best fits the dependence between the SCORE ESG and Expected idiosyncratic volatility. The Frank copula best fits the dependence between the SCORE ESG and Expected idiosyncratic volatility. Cayton Copula fit the best the dependence between the SCORE ESG and Expected idiosyncratic volatility. The Gumbel copula best fits the dependence between the SCORE ESG and Expected idiosyncratic volatility.

Table 4 CSR SCORES and Expected idiosyncratic volatility dependence structure modeling
Full size table

Figure 1 demonstrates several probability densities with a copula between the expected idiosyncratic volatility and distinct scores: a Clayton copula with a parameter q = 0.79 for the dependence with the Score ESG and a Kendal’s coefficient: \(\tau \hspace{0.17em}\)= − 0.8245, with a p-value = 0.00032. A Frank copula with q = 0.49 for the dependence with the Score SOC and Kendal’s coefficient: \(\tau \) = − 0.8045, with a p-value = 0.00012. A Clayton copula with q = 0.65 for the ENV score, with a Kendal’s coefficient: \(\tau \) = − 0.7565 and a p-value = 0.00076. A Gumbel copula with q = 0.88 for the SCORE GOUV, with a Kendal’s coefficient: \(\tau \) = − 0.6525, and p-value = 0.00082.

Fig. 1
figure 1

Probability density with copula. These figures represent the probability distributions of the copulas. The horizontal axes contain the distribution of the probability densities of the 2 variables, while the vertical axes represent the density of the chosen copula function, obtained from the two variables

Full size image

We observed a strong asymmetry and thickness of the tail for all densities. The estimated Kendal coefficient for each copula is greater than that measured for realized idiosyncratic volatility. This coefficient is also significant for all dimensions of the ESG score. Thus, the copula approach allows a better estimate of the dependence between the variables of idiosyncratic risk and the ESG score. These results display the ESG scores. SOC Env is significantly correlated with the realized idiosyncratic risk. This result also supports the nonlinear correlation between the realized idiosyncratic risk and ESG.

5 Conclusion

In this paper, we shed new light on the CSR–firm risk relationship by applying a broad class of copula functions for modeling the dependence structure of the dimensions of CSR fulfillment and idiosyncratic risk. Using a sample of 254 European-listed firms from 2011 to 2020, we highlight two main findings. First, the correlation between CSR dimensions and idiosyncratic risk was negative. This result confirms the risk insurance hypothesis, which states that firms invest in CSR projects to control risk and that CSR can be a strategic option through which firms manage their idiosyncratic risk (Godfrey, 2005; Luo & Bhattacharya, 2009; Mishra & Modi, 2013). Second, the causality between CSR dimensions and idiosyncratic risk is significant. Third, for our innovative methodology based on various copula functions, it goes in the direction of the very recent research of Farah et al. (2021), which documents an effect on firms’ systematic risk, and Li et al. (2021), which depicts a U-shaped relationship between CSR and idiosyncratic risk.

By assessing the causality effect between CSR dimensions and firm idiosyncratic risk, our study has important implications for firms and their stakeholders, especially shareholders. The relationships explain how changes in the CSR investment level affect the rates of change in the specific risk level. Notably, our findings highlight a nonlinear correlation between realized idiosyncratic risk and the diverse dimensions of CSR activities. That is, if costs outweigh benefits when moving from low to moderate levels of the extent of CSR, but benefits outweigh costs when moving from moderate to high levels of the CSR, then increases in the CSR would produce a negative effect on idiosyncratic, only if a certain level of the CSR is reached. A CSR below a certain threshold level can only increase a firm’s idiosyncratic risk.

In summary, to manage specific risk through CSR investments, firms must actively engage in CSR practices until a certain level (the threshold) of the benefits from CSR engagement outweighs the incremental operating costs induced by that engagement. That said, some firms, especially, as Farah et al. (2021) explained, small and medium-sized enterprises may have limited resources to engage in an active CSR investment strategy. Consequently, these enterprises would fail to take advantage of this investment because the benefits of the insignificant CSR investments will not cover the costs of their implementation. Furthermore, our findings are useful for investors as they permit them to draw unambiguous or unconditional inferences about the impact of CSR on risks. Because investors seek to hedge idiosyncratic risk, they should consider the CSR level. If a firm’s CSR investment is low, its specific risk will decline with an improvement in CSR.

We recognize that our study has several important limitations. First, we focused on publicly traded European companies with ESG ratings. This choice raises the question of the replicability of our results in other contexts (the USA, Asia, etc.). Moreover, only the largest companies had ESG scores. The question of generalizing our results to smaller companies is raised. Second, our results were developed over a limited time frame. This choice was made to neutralize the possible temporal effects related to changes in the dependency structure. However, this raises the question of extending the results to other periods and opens up new avenues of research to monitor the evolution of dependency structures over time.

Finally, our work is descriptive in nature. It aims to observe the dependency structure between risk and ESG scores. While the causality tests conducted led us to go beyond simple dependence to show the existence of causality and, hence, the ability of companies to use CSR as an insurance mechanism, our results do not allow us to understand the mechanisms by which this occurs. Nor do they allow us to consider the effects of other variables on specific risk management.

Our results allow us to highlight several other new avenues of research. First, our results demonstrate that the use of copula functions allows us to consider complex dependence structures between the specific risk of a firm and its level of CSR. However, our results raise the question of the stability of these dependence structures. Future research should evaluate the degree of stability of these dependence structures and possibly consider dynamic methods to measure their deformation over time. Second, while our results are consistent with a causal link that allows us to consider CSR as an insurance mechanism against extreme risks, they raise the question of synergies among insurance levers. Indeed, investments in the various dimensions of CSR do not have a homogeneous effect. The question is raised regarding their coherence and the influence of this coherence on the overall dependency structure between risk and the overall level of CSR. Finally, it would be interesting to explore the impact of the COVID-19 crisis on the relationship between CSR and specific risks. Indeed, the COVID–19 pandemic has had unprecedented financial and economic impacts that have undoubtedly heightened attention on firms’ social and environmental engagement. It would be very interesting to extend our study by using observations after January 2020 to obtain a clean understanding of the CRS–idiosyncratic risk nexus during bad times.