A multi-objective humanitarian pickup and delivery vehicle routing problem with drones

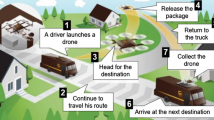
Abstract

This paper applies the truck and drone cooperative delivery model to humanitarian logistics and proposes a multi-objective humanitarian pickup and delivery vehicle routing problem with drones (m-HPDVRPD) which contains two subproblems: cooperative routing subproblem and relief supplies allocation subproblem. The m-HPDVRPD is formulated as a multi-objective mixed integer linear programming (MILP) model with two objectives, which simultaneously minimizes the maximum cooperative routing time and maximizes the minimum fulfillment rate of demand nodes. We develop a hybrid multi-objective evolutionary algorithm with specialized local search operators (HMOEAS) and a hybrid multi-objective ant colony algorithm (HACO) for the problem. A set of numerical experiments are performed to compare the performance of the two algorithms and their three variants. And the experimental results prove that HMOEAS is more effective than other methods. Taking the Corona Virus Disease 2019 (COVID-19) epidemic in Wuhan as a case, we compare the truck-drone cooperative delivery model with the truck-only delivery and the drone-only delivery models, and find that our model has advantages in the delivery efficiency of anti-epidemic materials. Moreover, based on the real-world case, a sensitivity analysis is conducted to investigate the impact of different drone parameters on the efficiency of truck-drone cooperative delivery.

Appendices

Appendix A

Suppose a solution is {1 2 6 3 8 9 5 10 0 4} according to the example in 4.1.1, which contains two routes: route1 is {0 1 2 6 3 8 9 5 10 0} and route2 is {0 4 0}. Taking the replenishment node 6 as the dividing point, route1 can be divided into segment1 {0 1 2} and segment 2 {6 3 8 9 5 10}.

There are only two truck demand nodes in segment1 where the truck with drone leaves the depot fully loaded, all the goods on the truck are distributed to demand node1 and demand node 2. According to formula (34), the average fulfillment rate of segment 1 is $r_{1} = Q_{1} /\left( {q_{1} + q_{2} } \right)$, so the actual fulfillment rate of both truck customers is $r_{1}$, and the allocation amount of the demand node 1 and demand node 2 are $q_{1} \times r_{1}$ and $q_{2} \times r_{1}$, respectively.

There are two drone tours and two truck demand nodes in segment 2. According to formula (34), the average fulfillment rate of segment 2 is $r_{2} = Q_{1} /\left( {q_{3} + q_{8} + q_{9} + q_{5} + q_{10} } \right)$. When the drone is fully loaded, the average fulfillment rate of the drone tour can reach the maximum value. According to formula (35), the maximum average fulfillment rate of drone tours1 {3 8 9} and drone tour 2 {5 10} are $r_{d1} = Q_{2} /\left( {q_{8} + q_{9} } \right)$ and $r_{d2} = Q_{2} /q_{10}$, respectively. If $r_{2} = min\left\{ { r_{2} , r_{d1} ,r_{d2} } \right\}$, the actual average fulfillment rate of all customers in segment 2 are $r_{2}$. The minimum fulfillment rate of demand nodes in segment 2 is $r_{2}$. If $r_{d1} = min\left\{ { r_{2} , r_{d1} ,r_{d2} } \right\}$ and $r_{2} \ge r_{d2}$, the actual average fulfillment rate of demand nodes in drone tour 1 is $r_{d1}$, and the actual average fulfillment rate of demand nodes in drone tour 2 is $r_{d2}$,but the actual average fulfillment rate of truck customers should be recalculated as $r_{t} = \left( {Q_{1} - 2 \times Q_{2} } \right)/\left( {q_{3} + q_{5} } \right)$. Because of $r_{t} \ge r_{2} \ge r_{d2} > r_{d1}$, the minimum fulfillment rate of demand nodes in segment 2 is $r_{d1}$. Similarly, if $r_{d2} = min\left\{ { r_{2} , r_{d1} ,r_{d2} } \right\}$ and $r_{2} \ge r_{d1}$, the minimum fulfillment rate of segment 2 is $r_{d2}$.

If $r_{d1} = min\left\{ { r_{2} , r_{d1} ,r_{d2} } \right\}$ and $r_{2} \le r_{d2}$, the actual average fulfillment rate of demand nodes in drone tour 1 is $r_{d1}$, but the remaining quantity of supplies should be redistributed by the remaining demand nodes according to the average fulfillment rate. Thus, the actual average fulfillment rate of rest demand nodes is $rv^{^{\prime}} = \left( {Q_{1} - Q_{2} } \right)/\left( {q_{3} + q_{5} + q_{10} } \right)$. Because of $rv^{^{\prime}} \ge r_{d1}$, the minimum fulfillment rate of demand nodes in segment 2 is $r_{d1}$. Similarly, if $r_{d2} = min\left\{ { r_{2} , r_{d1} ,r_{d2} } \right\}$ and $r_{2} \le r_{d1}$, the minimum fulfillment rate of segment 2 is $r_{d2}$.

Based on the above calculation results, the allocation of each demand node is equal to the product of its demand and fulfillment rate. Also, the fulfillment rate and allocation amount of each demand node in route2 are calculated in the same way.

Appendix B: The m-HPDVRPD is NP-hard

Proposition1: The m-HPDVRPD is NP-hard.

Proof. The m-HPDVRPD can be transformed into a single-objective pickup and delivery vehicle routing problem with drones (PDVRPD) through the additive weighing method (Ehrgott, 2005) or the ε-constraint method (Anderluh et al., 2019; Haimes, 1971; Mavrotas, 2009). In PDVRPD, the replenishment node may or may not be visited by trucks. If there are no replenishment nodes, the PDVRPD turns out to be VRPD. It can be said that the VRPD is a special case of the PDVRPD. In VRPD, there are multiple trucks and each truck equipped with one drone. If there is only one truck and one drone in VRPD, the VRPD becomes the TSPD. In this sense, the TSPD is a special case of the VRPD. There are two types of demand nodes: truck demand nodes and drone demand nodes. Truck demand nodes are served by the truck and drone demand nodes are served by the drone. If there are no drone demand nodes, the drone will not be activated and always ride on the truck, and the TSPD turns out to be the TSP. The TSP can be said to a special case of the TSPD.

As we all know, TSP is NP-hard (Mikosch et al., 2014; Parker & Rardin, 1983), so its extended TSPD, VRPD, PDVRPD and m-HPDVRPD are at least as difficult as TSP.

Appendix C: Parameters setting

In this section, we conduct a series of preliminary experiments to adjust the parameters used in HMOEAS and HACO. The values of each parameter are set to two levels, and three representative instances (B6, C5 D5) from Table 3 (according to the node distribution density) are selected to study the influence of these parameters on the results. The algorithm parameters are initially set to fixed values. When studying the relationship between one of the parameters and the approximate optimal solution, the other parameters remain unchanged (Hiba Bederina, 2018; Zhang et al., 2019). For each experiment, both HMOEAS and HACO produce a set of non-dominant solutions, but it is not realistic to list them all in table. We focus on the best objective value achieved by the algorithms, that is, the best solution for optimizing each objective in the set of non-dominant solutions. Next, we will call them the best fulfillment rate objective value (BFR) and the best travel time objective value (BTT) achieved by algorithms. Each experiment was run 10 times, and the BFR and BTT obtained by HMOEAS and HACO are listed in Table

Table 12 Experimental results obtained by HMOEAS under different parameter value

12 and Table

Table 13 Experimental results obtained by HACO under different parameters values

13, respectively.

3.1 (1) HMOEAS parameters setting

For the HMOEAS, each parameter value is set two levels. The initial values of population size, crossover probability, mutation probability, maximum number of generations (N), tournament size coefficient (λ) and tournament selection times (Titer) are set to 100, 0.8, 0.2, 100, 0.05, and 50, respectively. The other level values of the parameters and the results of the experiments are shown in Table 12.

As shown in Table 12, the first column represents the instances used in the experiment, the second columns represent two optimal objectives, third columns represent the experimental results obtained by HMOEAS with the initial values of parameters and the remaining columns represent the experimental results with changed parameter values. Each experiment includes six results, and the “bold” indicates better results than the initial parameter experiment. From the Table 12, we observed the following:

• (1) For the experiment with a population size of 200, only the “BTT” of D5 is better than that with population size of 100. Two results are same as the experiment with 100. And three results are worse than the fixed parameters experiment. Therefore, the performance of HMOEAS with population size of 100 is better than 200.

• (2) Except for two “BFR” results of C5 and B6, the remaining results obtained by HMOEAS with crossover rate of 0.8 are better than those obtained with 1. Therefore, the performance of HMOEAS is better when the crossover ratio is 0.8.

• (3) For the experiment with a mutation probability of 0.4, there are 3 results which are better than the experiment with 0.2, and two results which are the same as the experiment with 0.2. Although the “BFR” result of D5 obtained by experiment with 0.2 is better than that of experiment with 0.4, the 0.4 method performed better overall.

• (4) For the experiment with tournament size of 0.1, half of the results are the same as the experiment with 0.05, and the other half of the results are better than that of experiment with 0.05. Therefore, HMOEAS with tournament size of 0.1 has better performance.

• (5) Same as the (4) comparison results, half of the results of the experiment with the number of tournament selections of 100 and the experiment with the number of iterations 200 are the same as the experimental results with the fixed parameters, and the other half are better than the experimental results with the fixed parameters. Therefore, the HMOEAS with the number of tournament selections of 100 and the number of iterations 200 performs better.

Based on the above analysis, the parameters of HMOEAS are set as follows. The population size is set to 100, crossover rate is fixed 0.8, mutation rate is fixed 0.4, the coefficient for tournament size (λ) is setting equal to 0.1, the number of tournament selections (Titer) is set to 100, and the number of generations (N) is set to 200. The number of local search iterations (D) equals to the number of local search operators in an algorithm. To facilitate the comparison of algorithms performance, MOEA, HMOEA share the HMOEAS parameters' values, and the HACO share the maximum number of iterations of HMOEAS,200.

3.2 (2) HACO parameters setting

For HACO, we first set the maximum number of iterations to 200, which is the same value as HMOEAS, and then adjust the parameters through experiments. The values of $\alpha ,\beta ,\gamma$ are all set to four levels $\left\{ {1,2,3,4} \right\}$, and the values of other parameters are set to three levels (as shown in second column of Table 13). The initial values of ant size, $\alpha ,\beta ,\gamma ,q_{0} ,p_{m} ,\rho {\text{and}} Q$ are set to 35, 1, 3, 2, 0.2, 0.2, 0.3 and 100 respectively. The experiments results are shown in Table 13.

As shown in Table 13, the first row and second row represent the selected instances and the best values of two objectives, respectively. The first column and second column represent the parameters and their values, respectively. Each experiment includes six results, the “bold” and “underscore” indicate best result and worst result, respectively. Comparing the results of rows 3, 4 and 5 in Table 13, we can see that there are the largest number of best results when the ant size is 100. Therefore, HACO with an ant size of 100 is considered the best performer. From the number of “bold” and “underline” in rows 6, 7and 8, we can find that when $q_{0}$ is 0.6, there are largest number of best results and least worst results. Therefore, HACO with $q_{0}$ of 0.6 is considered the best performer. The experimental results of other parameters are also compared in the same way, and the relatively good values of these parameters are marked “bold” in the second column. Based on the above discussion, we implemented HACO with ant size = 100, $q_{0} = 0.6, p_{m} = 0.6, \rho = 0.5,Q = 200,\alpha = 2,\beta = 1, \gamma = 4$.