How retailer overconfidence affects supply chain transparency with manufacturer encroachment

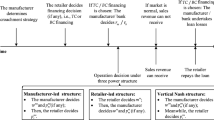
Abstract

This study analyzed how retailer overconfidence affects supply chain transparency for manufacturers who can encroach on the retail channel by paying a fixed entry cost. Both the reselling model and agent selling model were examined. The results show that an overconfident retailer has more incentive to increase the supply chain transparency in the reselling model than in the agency selling model. In detail, retailer overconfidence may lead to supply chain transparency even at a moderate channel substitution rate, and this effect can be enhanced with an increasing level of retailer overconfidence. This finding differs from conventional wisdom, which indicates that a retailer should not share any information if the channel substitution rate is not sufficiently high. The findings of this study are helpful to explain why some retailers voluntarily share information with manufacturers that have less-competitive direct selling channels. Additionally, from the perspective of entry cost, the results also indicate that an overconfident retailer can have more incentive than a normal retailer to increase the supply chain transparency in the reselling model. For the agent selling model, the results show that the above findings are reversed. Finally, whether using a wholesale or agency model, the retailer may benefit from its overconfidence bias in certain situations when it can voluntarily share information.

Appendix

1.1 Derivation of the equilibrium results of the reselling agreement

We note that the retailer observes the true demand after her information-sharing decision; thus, her overconfidence bias only affects that sharing decision. In other words, the retailer and manufacturer’s quantity decision and encroachment decision are independent of the retailer’s cognitive bias because when they make these decisions, the retailer already knows the exact demand and she is no longer overconfident. Thus, the proof structure closely follows that of Huang et al. (2018) and Zhang and Zhang (2020).

Case NN We first derive the equilibrium results when the retailer does not share information and the manufacturer does not encroach. This case is a traditional retail supply chain with asymmetric information. The retailer’s profit function is given by $\pi _r(q_1)=(a +\theta - q_1 - w) q_1$, and it is straightforward to derive the retailer’s optimal quantity $q_1(w)= \frac{a+\theta -w}{2}$. Observing only the prior distribution for the demand, the manufacturer sets the wholesale price to maximize his expected profit. We can solve the manufacturer’s problem for this Stackelberg game as $\pi _m(w)=E_\theta \{w q_1(w)\}$, thus the manufacturer’s optimal wholesale price $w^{NN}=\frac{a+d}{2}$. Substituting $w^{NN}$ into the retailer’s best response $q_1(w)$ and both firms’ profit functions, we obtain $q_1^{NN}=\frac{a-d+2 \theta }{4}$, $\pi _r^{NN}=\frac{(a-d+2 \theta )^2}{16}$ and $\pi _m^{NN}=\frac{(a+d)^2}{8}$.

Case NE Since the manufacturer encroaches, there is quantity competition between the retail channel and direct channel. This case is a traditional dual channel supply chain with asymmetric information in which the downstream privately observes the demand information. The retailer’s and manufacturer’s profit functions can be expressed as $\pi _r(q_1)=(a-b q_2+\theta -q_1-w) q_1$ and $\pi _m(q_2,w)=E_\theta \{w q_1+(a-b q_1+\theta -q_2) q_2\}-I$, respectively. It is obvious that the retailer’s best response $q_1(\ddot{q_2};w)=\frac{a-b \ddot{q_2}+\theta -w}{2}$. Similarly, the manufacturer’s best response is $q_2(\ddot{q_1};w)=\frac{a+d-b E_\theta (\ddot{q_1})}{4-b^2}$. Here, we use “$\ddot{}$” to represent the conjectured variable. When the conjecture is consistent with the actual optimal decision, the Nash equilibrium is established, so we have $q_1=\ddot{q_1}$ and $q_2=\ddot{q_2}$. Solving these two equations jointly, the optimal quantity depends on the given wholesale price w, which can be expressed as $q_1(w)=\frac{2 a (2-b)+b^2 (d-\theta )-2 b d-4 (w-\theta )}{2 \left( 4-b^2\right) }$ and $q_2(w)=\frac{a (2-b)+(2-b) d+b w}{4-b^2}$. Because the manufacturer only observes the prior distribution for the demand, he uses only that to determine the wholesale price to maximize his expected profit. Thus the manufacturer’s optimal wholesale price $w^{NE}=\frac{\left( b^3-4 b^2+8\right) (a+d)}{16-6 b^2}$. Substituting $w^{NE}$ into the retailer’s best response $q_1(w)$, the manufacturer’s best response $q_2(w)$, and both firms’ profit functions, we obtain $q_1^{NE}=\frac{4 a (1-b)-(2-b) (2+3 b)d+(8-3 b^2) \theta }{16-6 b^2}$, $q_2^{NE}=\frac{(2-b) (4+b) (a+\theta )}{16-6 b^2}$, $\pi _r^{NE}=\frac{(4 a (1-b)-(4+4 b-3 b^2) d+(8-3 b^2) \theta )^2}{4 (8-3 b^2)^2}$, and $\pi _m^{NE}=\frac{(6-b) (2-b) (a+d)^2}{4 (8-3 b^2)}-I$.

Case SN In this case, the retailer shares information and the manufacturer does not encroach. This case is a traditional retail supply chain with symmetric information. The retailer’s profit function is given by $\pi _r(q_1)=(a +\theta - q_1 - w) q_1$, and it is straightforward to derive the retailer’s optimal quantity $q_1(w)= \frac{a+\theta -w}{2}$. The manufacturer also observes the true demand, so he determines the wholesale price using the true profit function. We can solve the manufacturer’s problem for this Stackelberg game as $\pi _m(w)=w q_1(w)$, thus the manufacturer’s optimal wholesale price is $w^{SN}=\frac{a+\theta }{2}$. Substituting $w^{SN}$ into the retailer’s best response $q_1(w)$ and both firms’ profit functions, we can obtain $q_1^{SN}=\frac{a+\theta }{4}$, $\pi _r^{SN}=\frac{1}{16} (a+\theta )^2$, and $\pi _m^{SN}=\frac{1}{8} (a+\theta )^2$.

Case SE Here, the retailer shares information and the manufacturer encroaches. This case is a traditional dual channel supply chain with symmetric information, in which the upstream also observes the demand information. The retailer’s and manufacturer’s profit functions can be expressed as $\pi _r(q_1)=(a-b q_2+\theta -q_1-w) q_1$ and $\pi _m(q_2,w)=w q_1+(a-b q_1+\theta -q_2) q_2-I$, respectively. Similar to Case NE, using the first-order optimality condition and jointly finding solutions, we obtain the optimal quantity depends on the given wholesale price w, which can be expressed as $q_1(w)=\frac{(2-b) (a+\theta )-2 w}{4-b^2}$ and $q_2(w)=\frac{(2-b) (a+\theta )+b w}{4-b^2}$. The manufacturer can observe the true demand, so he determines the wholesale price to maximize his real profit function. Thus the manufacturer’s optimal wholesale price is $w^{SE}=\frac{\left( b^3-4 b^2+8\right) (a+\theta )}{16-6 b^2}$. Substituting $w^{SE}$ into the retailer’s best response $q_1(w)$, the manufacturer’s best response $q_2(w)$, and both firms’ profit functions, we can obtain $q_1^{SE}=\frac{2 (1-b) (a+\theta )}{8-3 b^2}$, $q_2^{SE}=\frac{(2-b) (4+b) (a+\theta )}{16-6 b^2}$, $\pi _r^{SE}=\frac{4 (1-b)^2 (a+\theta )^2}{(8-3 b^2)^2}$, and $\pi _m^{SE}=\frac{(6-b) (2-b) (a+\theta )^2}{4 (8-3 b^2)}-I$.

1.2 Derivation of the equilibrium results for the agency selling agreement

Case NN Similar to the previous proofs, we derive the equilibrium results under agency selling when the retailer does not share information and the manufacturer does not encroach. In this case, the manufacturer directly decides the retail price. The retailer’s and manufacturer’s profit functions can be expressed as $\pi _r=r (a+\theta -q_1) q_1$ and $\pi _m=E_\theta \{(1-r)(a+\theta -q_1) q_1\}$. Solving the first-order condition $\frac{\partial \pi _r}{\partial q_1}=0$, the optimal order quantities to maximize the manufacturer’s expected profit can be given by $q_1^{NN}=\frac{a+d}{2}$. Then, by substituting $q_1^{NN}$ into both firms’ profit functions, we can obtain $\pi _r^{NN} =\frac{r(a+d)(a-d+2 \theta )}{4}$ and $\pi _m^{NN} =\frac{(1-r)(a+d)^2}{4}$.

Case NE Since the manufacturer encroaches, then there is quantity competition between the agency selling channel and the direct channel. This case, the downstream privately observes the demand information and does not share it. The retailer’s and manufacturer’s profit functions can be expressed as $\pi _r=r(a+\theta -q_1-b q_2) q_1$ and $\pi _m=E_\theta \{(1-r) (a+\theta -q_1-b q_2) q_1+(a+\theta -q_2-b q_1) q_2\}-I$, respectively. Similar to reselling agreement case, we solve the first-order condition $\frac{\partial \pi _r}{\partial q_1}=0$ and $\frac{\partial \{E_\theta \pi _m\}}{\partial q_2}=0$, simultaneously. The optimal order quantities to maximize the manufacturer’s expected profit are given by $q_1^{NE}=\frac{(a+d) (2(1-r)-b (2-r))}{4 (1-r)-b^2 (2-r)^2}$ and $q_2^{NE}=\frac{(a+d) (2-b (2-r)) (1-r)}{4 (1-r)-b^2 (2-r)^2}$. We note that $q_1^{NE}$ must be positive, so we have $b<\frac{2(1-r)}{2-r}$. Substituting $q_1^{NE}$ and $q_2^{NE}$ into both firms’ profit functions, we can obtain $\pi _r^{NE}=\frac{((a+d) r (2 (1-r)-b (2-r)) (a (1-b) (2 (1-r)+b (2-r))-d (2 (1-r)-b r-b^2 (2-3 r+r^2))+(4 (1-r)-b^2 (2-r)^2) \theta ))}{(4 (1-r)-b^2 (2-r)^2)^2}$ and $\pi _m^{NE}=\frac{(1-b) (a+d)^2 (2-3 r+r^2)}{4 (1-r)-b^2 (2-r)^2}-I$.

Case SN The retailer shares information and the manufacturer does not encroach. This case is an agency selling supply chain with symmetric information. The retailer’s and manufacturer’s profit functions can be expressed as $\pi _r=r(a+\theta -q_1) q_1$ and $\pi _m=(1-r) (a+\theta -q_1) q_1$, respectively. Solving the first-order condition, the optimal order quantity to maximize the manufacturer’s true profit is $q_1^{SN}=\frac{a+\theta }{2}$. Then, by substituting $q_1^{SN}$ into both firms’ profit functions, we can obtain $\pi _r^{SN}=\frac{r (a+\theta )^2}{4}$ and $\pi _m^{SN}=\frac{(1-r) (a+\theta )^2}{4}$.

Case SE The retailer shares information and the manufacturer encroaches. This case is an agency selling dual channel supply chain with symmetric information, in which the upstream also observes the demand information. The retailer’s and manufacturer’s profit functions can be expressed as $\pi _r=r (a+\theta -q_1-b q_2) q_1$ and $\pi _m=(1-r) (a+\theta -q_1-b q_2) q_1+(a+\theta -q_2-b q_1) q_2-I$, respectively. The optimal order quantities to maximize the manufacturer’s true profit are $q_1^{SE}=\frac{(a+\theta ) (2 (1-r)-b (2-r)) }{4 (1-r)-b^2 (2-r)^2}$ and $q_2^{SE}=\frac{(a+\theta ) (2-b (2-r)) (1-r) }{4 (1-r)-b^2 (2-r)^2}$. Substituting $q_1^{SE}$ and $q_2^{SE}$ into both firms’ profit functions, we can obtain $\pi _r^{SE}=\frac{r (1-b) (4 (1-r)^2-b^2 (2-r)^2) (a+\theta )^2}{(4 (1-r)-b^2 (2-r)^2)^2}$ and $\pi _m^{SE}=\frac{(1-b) (2-r) (1-r) (a+\theta )^2}{4 (1-r)-b^2 (2-r)^2}-I$.

Proof of Lemma 1

If the retailer does not share the demand information with the manufacturer, the manufacturer decides whether to encroach by comparing the expected profit for cases NE and NN. That means that the manufacturer encroaches when $\frac{(12-8 b+b^2) (a+d)^2}{4 (8-3 b^2)}-I-\frac{1}{8} (a+d)^2 \ge 0$, which reduces to $I \le \frac{(16-16 b+5 b^2) (a+d)^2}{8 (8-3 b^2)}$. When the retailer shares demand information with the manufacturer, the manufacturer decides whether to encroach by comparing the profit for Cases SE and SN. Then, the manufacturer encroaches if and only if $\frac{(6-b) (2-b) (a+\theta )^2}{4 (8-3 b^2)}-I-\frac{1}{8} (a+\theta )^2\ge 0$, which is $I\le \frac{(16-16 b+5 b^2) (a+\theta )^2}{8 (8-3 b^2)}$, due to $0\le \theta \le 2d$ Therefore, $\frac{(16-16 b+5 b^2)a^2}{8 (8-3 b^2)} \le \frac{(16-16 b+5 b^2) (a+\theta )^2}{8 (8-3 b^2)}\le \frac{(16-16 b+5 b^2) (a+2d)^2}{8 (8-3 b^2)}$. Then, we conclude that if $I\le \frac{(16-16 b+5 b^2)a^2}{8 (8-3 b^2)}$, then the manufacturer always encroaches no matter what market potential is, while if the entry cost $I>\frac{(16-16 b+5 b^2) (a+2d)^2}{8 (8-3 b^2)}$, the manufacturer never encroaches. In addition, when the entry cost is moderate, the manufacturer encroaches when $I\le \frac{(16-16 b+5 b^2) (a+\theta )^2}{8 (8-3 b^2)}$, which equivalent to $\theta \ge \sqrt{\frac{8 (8-3 b^2)I}{16-16 b+5 b^2}}-a$. Moreover, because the retailer is overconfident, she makes a decision as though the demand potential were $\Theta :=\alpha d+(1-\alpha )\theta$, rather than the given true demand potential $\theta$. We define $I_0=\frac{(16-16 b+5 b^2) (a+d)^2}{8 (8-3 b^2)}$, $I_1=\frac{(16-16 b+5 b^2) (a+\alpha d )^2}{8 (8-3 b^2)}$, and $I_2=\frac{(16-16 b+5 b^2) (a+2d-\alpha d )^2}{8 (8-3 b^2)}$, and we note that $I_1<I_0<I_2$. Therefore, we can get the overconfident retailer’s expected profit before demand disclosed as the following:

$$\begin{aligned}&\pi _r^{N}(I)={\left\{ \begin{array}{ll} \frac{4 (1-b)^2(a+d)^2}{(8-3 b^2)^2} +\frac{ d^2(1-\alpha )^2}{12 } &{}\quad I \le I_0\\ \frac{(a+ d)^2}{16}+\frac{d^2 (1-\alpha )^2}{12} &{}\quad I > I_0 \end{array}\right. } \end{aligned}$$

(8)

$$\begin{aligned}&\pi _r^{S}(I)= {\left\{ \begin{array}{ll} \frac{4 (1-b)^2 (3(a +d)^2+d^2(1-\alpha )^2)}{3(8-3 b^2)^2} &{}\quad I\le I_1\\ \frac{(a+\hat{\Theta })^3-(a+\alpha d)^3}{48(2d-2\alpha d)} +\frac{4 (1-b)^2 ((a+2d-\alpha d)^3 -(a+\hat{\Theta })^3)}{3(8-3 b^2)^2(2d-2\alpha d)} &{}\quad I_1 < I\le I_2\\ \frac{3(a +d)^2+d^2 (1-\alpha )^2}{48} &{}\quad I > I_2 \end{array}\right. } \end{aligned}$$

(9)

where $\hat{\Theta }=\alpha d+(1-\alpha )(\sqrt{\frac{8 (8-3 b^2)I}{16-16 b+5 b^2}}-a)$. $\square$

Proof of Proposition 1

We examine the monotonicity of $\pi _r^{N}(I)$ and $\pi _r^{S}(I)$ with entry cost I where $I_1<I\le I_2$. We know $\frac{\partial \pi _r^{S}}{\partial \hat{\Theta }}=\frac{b (4+b) (8-3 b) (4-3 b) (a+\hat{\Theta })^2}{32 (8-3 b^2)^2 d (1-\alpha )}>0$ for $0<b<1$ and $\hat{\Theta }$ is increasing in I. Thus, $\pi _r^{S}(I)$ is increasing in I. Also, letting $\pi _r^{N}|_{I\le I_0}-\pi _r^{N}|_{I>I_0}=-(\frac{b (4+b) (8-3 b) (4-3 b)}{16(8-3 b^2)^2}) (a+d)^2<0$, we know $\pi _r^{N}(I)$ is also increasing in I. The retailer’s expected profit has a sudden upward jump at $I_0$ in the no-sharing condition. Based on the monotonicity of $\pi _r^{N}(I)$ and $\pi _r^{S}(I)$, it is essential to compare $\pi _r^{N}(I_0)$ and $\pi _r^{S}(I_0)$ to determine the retailer’s information decision when $I_1<I\le I_0$. Next, we define $g(b, \alpha )=\pi _r^{S}(I_0)-\pi _r^{N}(I_0)$ and derive $\frac{\partial g(b, \alpha )}{\partial b}=\frac{4 (1-b) (8-6 b+3 b^2) (3 a^2+3 a d (1+\alpha )-d^2 (1-5 \alpha +\alpha ^2))}{3 (8-3 b^2)^3}>0$ for $0<b<1$, $a>2d$, and $0<\alpha <1$, which represent that $g(b, \alpha )$ is increasing in b. Simultaneously, we can derive $g(0, \alpha )=-\frac{d^2 (1-\alpha )^2}{16}<0$ and $g(1, \alpha )=\frac{3 a^2+3 a d (1+\alpha )-d^2 (7-17 \alpha +7 \alpha ^2)}{96}>0$ for $0<b<1$, $a>2d$, and $0<\alpha <1$. Hence there exists a unique solution $b^{*}$ satisfying $g(b^{*}, \alpha )=0$, such that $g(b, \alpha )<0$ if $b<b^*$, and $g(b, \alpha )>0$ otherwise. If $b>b^*$, there exists a unique threshold $I^*$ satisfying $\pi _r^{N}(I^*)=\pi _r^{S}(I^*)$, such that $\pi _r^{N}(I^*)<\pi _r^{S}(I^*)$ for $I^*<I<I_0$. Furthermore, $\frac{\partial g(b, \alpha )}{\partial \alpha }=\frac{3 a b (128-112 b+9 b^3) d+d^2 (768+640 b-1136 b^2+153 b^4-(768+256 b-800 b^2+126 b^4) \alpha )}{96 (8-3 b^2)^2}$, so $\frac{\partial ^2 g(b, \alpha )}{\partial \alpha ^2}=-\frac{(384+128 b-400 b^2+63 b^4) d^2}{48 (8-3 b^2)^2}<0$ for $0<b<1$ and $d>0$. This implies that $\frac{\partial g(b, \alpha )}{\partial \alpha }$ is decreasing in $\alpha$, thus $\frac{\partial g(b, \alpha )}{\partial \alpha }>\frac{\partial g(b, \alpha )}{\partial \alpha }|_{\alpha =1}=\frac{b (128-112 b+9 b^3) d (a+d)}{32 (8-3 b^2)^2}>0$. Therefore, $g(b, \alpha )$ is strictly increasing in $\alpha$. Combined with our knowledge that $g(b, \alpha )$ is increasing in b, we see that $b^*$ is the unique solution to $g(b, \alpha )=0$, hence $b^*$ is decreasing in $\alpha$. $\square$

Proof of Proposition 2

We define $G(\hat{\Theta }^*,b,d,\alpha )=\frac{(a+\hat{\Theta }^* )^3-(a+\alpha d)^3}{48(2d-2\alpha d)}+\frac{4 (1-b)^2 ((a+2d-\alpha d)^3-(a+\hat{\Theta }^* )^3)}{3(8-3 b^2)^2(2d-2\alpha d)}-\frac{4 (1-b)^2(a+d)^2}{(8-3 b^2)^2}- \frac{d^2(1-\alpha )^2}{12}$, where $\hat{\Theta }^*=\alpha d+(1-\alpha )(\sqrt{\frac{8 (8-3 b^2)I^*}{16-16 b+5 b^2}}-a)$. It is obvious that $\frac{dI^*}{d\hat{\Theta }^*}>0$. Based on the Implicit Function Theorem, we have $\frac{\partial I^*}{\partial \alpha }=\frac{\partial I^*}{\partial \hat{\Theta }^*}\times \frac{\partial \hat{\Theta }^*}{\partial \alpha }=\frac{\partial I^*}{\partial \hat{\Theta }^*}\cdot (-\frac{\partial G}{\partial \alpha }/\frac{\partial G}{\partial \hat{\Theta }^*})$. Similarly, $\frac{\partial I^*}{\partial b}=\frac{\partial I^*}{\partial \hat{\Theta }^*}\times \frac{\partial \hat{\Theta }^*}{\partial b}=\frac{\partial I^*}{\partial \hat{\Theta }^*}\cdot (-\frac{\partial G}{\partial b}/\frac{\partial G}{\partial \hat{\Theta }^*})$. We consider the first-order derivatives of $G(\hat{\Theta }^*,b,d,\alpha )$ with respect to $\hat{\Theta }^*$ and b as follows:

$$\begin{aligned}&\frac{\partial G}{\partial \hat{\Theta }^*}=\frac{b (4+b) (8-3 b) (4-3 b)(a+\hat{\Theta }^* )^2}{32 (8-3 b^2)^2 d (1-\alpha )}>0 \\&\frac{\partial G}{\partial b}=\frac{4 (1-b) (8-6 b+3 b^2) (-3 a^2 d \alpha -3 a d^2 \alpha ^2+d^3 (-2+6 \alpha -6 \alpha ^2 +\alpha ^3)+\hat{\Theta }^*(3 a^2+3 a \hat{\Theta }^* +\hat{\Theta }^{*2}))}{3 (8-3 b^2)^3 d (1-\alpha )} \end{aligned}$$

Both of these are increasing in $\hat{\Theta }^*$, and $\alpha d<\hat{\Theta }^*<d$, so we have $\frac{\partial G}{\partial b}\ge \frac{4 (1-b) (8-6 b+3 b^2) (3 a^2+3 a d (1+\alpha )-d^2 (1-5 \alpha +\alpha ^2))}{3 (8-3 b^2)^3}>0$ for $0<b<1$ and $a>2d>0$, thus $\frac{\partial I^*}{\partial b}<0$. The first-order derivative of $G(\hat{\Theta }^*,b,d,\alpha )$ with $\alpha$ is

$$\begin{aligned} \frac{\partial G}{\partial \alpha }&=\frac{1}{96 (8-3 b^2)^2 d (1-\alpha )^2}(d^3 (768 (1-\alpha )^3+128 b (2-\alpha )^2 (1-2 \alpha )\\&\quad +9 b^4 (16-48 \alpha +45 \alpha ^2-14 \alpha ^3) \\&\quad +16 b^2 (-64+192 \alpha -171 \alpha ^2+50 \alpha ^3)) -3 a^2 b (128-112 b+9 b^3) (d-\hat{\Theta }^* )\\&\quad +b (128-112 b+9 b^3) \hat{\Theta }^{*3}\\&\quad +3 a b (128-112 b+9 b^3) (d^2 (-2+\alpha ) \alpha +\hat{\Theta }^{*2})) \end{aligned}$$

Letting $G'(\alpha )=\frac{\partial G}{\partial \alpha }$, we can derive $G''(\alpha )=-\frac{1}{48 (8-3 b^2)^2 d (1-\alpha )^3}(d^3 (384 (1-\alpha )^3+128 b (2-3 \alpha +3 \alpha ^2-\alpha ^3)+9 b^4 (8-21 \alpha +21 \alpha ^2-7 \alpha ^3)-16 b^2 (32-75 \alpha +75 \alpha ^2-25 \alpha ^3))+3 a^2 b (128-112 b+9 b^3) (d-\hat{\Theta }^* )-b (128-112 b+9 b^3) \hat{\Theta }^{*3}+3 a b (128-112 b+9 b^3) (d^2-\hat{\Theta }^{*2}))$, and $G'''(\alpha )=-\frac{b (4+b) (8-3 b) (4-3 b)(d-\hat{\Theta }^* ) (3 a^2+d^2+d \hat{\Theta }^* +\hat{\Theta }^{*2}+3 a (d+\hat{\Theta }^* ))}{16 (8-3 b^2)^2 d (1-\alpha )^4}>0$ for $0<b<1$ and $\hat{\Theta }^*<d$. Then, $G''(\alpha )\le G''(0)=-\frac{(384+128 b-400 b^2+63 b^4) d^2}{48 (8-3 b^2)^2}<0$ for $\hat{\Theta }^*=d$. Therefore, $G'(\alpha )$ is strictly decreasing in $\alpha$, and $G'(\alpha )<G'(0)<0$ for $a>2d$ and $0<b<1$. Therefore, $\frac{\partial I^*}{\partial \alpha }<0$; that is, $I^*$ is decreasing in $\alpha$. $\square$

Proof of Lemma 2

If the agency selling retailer does not share the information with the manufacturer, the manufacturer decides whether to encroach by comparing the expected profit for cases NE and NN, as was done for the reselling case. The manufacturer encroaches when $\frac{(1-b)\ (2-r) (1-r)(a+d)^2}{4 (1-r)-b^2 (2-r)^2}-I-\frac{(a+d)^2 (1-r)}{4}\ge 0$, which reduces to $I \le \tilde{I_0} =\frac{(1-r)(2-b (2-r))^2 (a+d)^2 }{4 (4 (1-r)-b^2 (2-r)^2)}$. If the agency selling retailer shares demand information with the manufacturer, the manufacturer decides whether to encroach by comparing the profit for Cases SE and SN. The manufacturer encroaches if and only if $\frac{(1-b) (2-r) (1-r) (a+\theta )^2}{4 (1-r)-b^2 (2-r)^2}-I-\frac{(1-r) (a+\theta )^2}{4} \ge 0$, which is equivalent to $I\le \frac{(1-r) (2-b (2-r))^2 (a+\theta )^2}{4 (4 (1-r)-b^2 (2-r)^2)}$, due to $0\le \theta \le 2d$. Thus, we have $\frac{(1-r) (2-b (2-r))^2 a^2}{4 (4 (1-r)-b^2 (2-r)^2)} \le \frac{(1-r) (2-b (2-r))^2 (a+\theta )^2}{4 (4 (1-r)-b^2 (2-r)^2)} \le \frac{(1-r) (2-b (2-r))^2 (a+2d )^2}{4 (4 (1-r)-b^2 (2-r)^2)}$. Then we can get that if $I\le \frac{(1-r) (2-b (2-r))^2 a^2}{4 (4 (1-r)-b^2 (2-r)^2)}$, the manufacturer always encroaches no matter what market potential is, while if the entry cost $I>\frac{(1-r) (2-b (2-r))^2 (a+2d )^2}{4 (4 (1-r)-b^2 (2-r)^2)}$, the manufacturer never encroaches. When the entry cost is moderate, the manufacturer encroaches when $I\le \frac{(1-r) (2-b (2-r))^2 (a+\theta )^2}{4 (4 (1-r)-b^2 (2-r)^2)}$, which is equivalent to $\theta \ge \sqrt{\frac{4 (4 (1-r)-b^2 (2-r)^2)I}{(1-r) (2-b (2-r))^2 }}-a$. Moreover, when the retailer is overconfident, she makes her decision as though the demand potential were $\Theta :=\alpha d+(1-\alpha )\theta$, rather than the given true demand potential $\theta$. We define $\tilde{I_1} =\frac{(1-r) (2-b (2-r))^2 a^2}{4 (4 (1-r)-b^2 (2-r)^2)}$ and $\tilde{I_2}=\frac{(1-r) (2-b (2-r))^2 (a+2d )^2}{4 (4 (1-r)-b^2 (2-r)^2)}$. Therefore, we can get the overconfident retailer’s expected profit before demand disclosed as the following:

$$\begin{aligned}&\tilde{\pi }_r^{N}(I)={\left\{ \begin{array}{ll} \frac{r(1-b) (4 (1-r)^2-b^2 (2-r)^2)(a+d)^2 }{(4 (1-r)-b^2 (2-r)^2)^2} &{}\quad I \le \tilde{I_0}\\ \frac{r(a+d)^2}{4} &{}\quad I > \tilde{I_0} \end{array}\right. } \end{aligned}$$

(10)

$$\begin{aligned}&\tilde{\pi }_r^{S}(I)= {\left\{ \begin{array}{ll} \frac{ r(1-b)(4 (1-r)^2-b^2 (2-r)^2) (3(a+d)^2+d^2(1-\alpha )^2)}{3(b^2 (2-r)^2-4 (1-r))^2} &{}\quad I\le \tilde{I_1}\\ \frac{ r ((a+\hat{\Theta })^3-(a+\alpha d)^3)}{12(2d-2 \alpha d)} +\frac{r(1-b) (4 (1-r)^2-b^2 (2-r)^2) ((a+2d-2 \alpha d)^3 -(a+\hat{\Theta })^3)}{3(b^2 (2-r)^2-4 (1-r))^2(2d-2 \alpha d)}&{}\quad \tilde{I_1} < I\le \tilde{I_2}\\ \frac{(a+d)^2 r}{4}+\frac{r d^2(1-\alpha )^2}{12} &{}\quad I > \tilde{I_2} \end{array}\right. } \end{aligned}$$

(11)

where $\tilde{\Theta }= \alpha d+(1-\alpha )(\sqrt{\frac{4 (4 (1-r)-b^2 (2-r)^2)I}{(1-r) (2-b (2-r))^2 }}-a)$. $\square$

Proof of Proposition 3

Similar to the proof of Proposition 1, we examine the monotonicity of $\tilde{\pi }_r^{N}(I)$ and $\tilde{\pi }_r^{S}(I)$ with entry cost I where $\tilde{I_1}<I\le \tilde{I_2}$. We know $\frac{\partial \pi _r^{S}}{\partial \hat{\Theta }}=\frac{b r (16 (1-r)^2-4 b^2 (2-r)^2+b^3 (2-r)^4-4 b (2-r)^2 (1-2 r)) (a+\theta )^2}{8 d (b^2 (2-r)^2-4 (1-r))^2 (1-\alpha )}>0$ for $0<b<\frac{2(1-r)}{2-r}$, and $\tilde{\Theta }$ is increasing in I obviously, thus $\tilde{\pi }_r^{S}(I)$ is increasing in I. Also, $\tilde{\pi }_r^{N}|_{I\le I_0}-\tilde{\pi }_r^{N}|_{I>I_0}<0$, so $\tilde{\pi }_r^{N}(I)$ is also increasing in I. The retailer’s expected profit has a sudden upward jump at $\tilde{I_0}$ in the no-sharing condition. Based on the monotonicity of $\tilde{\pi }_r^{N}(I)$ and $\tilde{\pi }_r^{S}(I)$, it is essential to compare $\tilde{\pi }_r^{N}(\tilde{I_0})$ and $\tilde{\pi }_r^{S}(\tilde{I_0})$ to determine the retailer’s information decision. Next, we define $f(b, \alpha )=\tilde{\pi }_r^{S}(\tilde{I_0})-\tilde{\pi }_r^{N}(\tilde{I_0})$ and derive that $f(0, \alpha )=-\frac{r(3 a^2 \alpha +3 a d (4-3 \alpha ) \alpha +d^2 (-2+18 \alpha -24 \alpha ^2+9 \alpha ^3))}{24 (1-\alpha )}>0$ for $0<b<\frac{2(1-r)}{2-r}$ and $\alpha <\tilde{\alpha }^*$. In this, $\tilde{\alpha }^*$ is the unique solution of $\frac{a(a+4d)^2}{4d^3}-2+18 \alpha -24 \alpha ^2+9 \alpha ^3=0$ for $0<\alpha <1$ and $f(\frac{2(1-r)}{2-r}, \alpha )=-\frac{r (3 a^2-3 a d (-3+\alpha )-d^2 (-5+\alpha +\alpha ^2))}{24}<0$. Simultaneously, $\frac{\partial g(b, \alpha )}{\partial b}<0$, which represents that $f(b, \alpha )$, is decreasing in b. Hence there exists a unique solution $\tilde{b}^{*}$ satisfying $f(\tilde{b}^{*}, \alpha )=0$, such that $f(b, \alpha )>0$ if $b<\tilde{b}^*$ and $f(b, \alpha )<0$ otherwise for $\alpha <\tilde{\alpha }^*$. Since $b<\tilde{b}^*$, there exists a unique threshold $\tilde{I}^*$ satisfying $\tilde{\pi }_r^{N}(I^*)=\tilde{\pi }_r^{S}(I^*)$, such that $\tilde{\pi }_r^{N}(\tilde{I}^*)<\tilde{\pi }_r^{S}(\tilde{I}^*)$ for $\tilde{I}_0<I<\tilde{I}^*$. Denoting $h(\alpha )=\frac{\partial f(b, \alpha )}{\partial \alpha }$, we can derive $h''(\alpha )=\frac{(1-b) (3 a^2+3 a d+d^2) (b^2 (2-r)^2-4 (1-r)^2) r}{(b^2 (2-r)^2-4 (1-r))^2 (1-\alpha )^4}<0$. This means that $h'(\alpha )$ decreasing in $\alpha$ and $h'(\alpha )<h'(0)<0$. Therefore, $f(b, \alpha )$ is decreasing in $\alpha$ for $0<\alpha <\tilde{\alpha }^*$. Moreover, $f(b,\alpha )$ is decreasing in b, and $\tilde{b}^*$ is the unique solution to $f(b,\alpha )=0$, thus, $\tilde{b}^*$ is decreasing in $\alpha$. $\square$

Proof of Proposition 4

The proof of the monotonicity of $\tilde{I}^*$ with $\alpha$ can be analogously analyzed when the reselling agreement is used. We define $F(\tilde{\Theta }^*,b,d,\alpha )=\frac{r((a+\tilde{\Theta }^*)^3 -(a+\alpha d)^3)}{12(2d-2 \alpha d)}+\frac{r(1-b) (4 (1-r)^2-b^2 (2-r)^2) ((a+2d-2 \alpha d)^3-(a+\tilde{\Theta }^*)^3)}{3(b^2 (2-r)^2-4 (1-r))^2(2d-2 \alpha d)}-\frac{r(a+d)^2}{4}$, where $\tilde{\Theta }^*= \alpha d+(1-\alpha )(\sqrt{\frac{4 (4 (1-r)-b^2 (2-r)^2)\tilde{I}^*}{(1-r) (2-b (2-r))^2 }}-a)$. By the Implicit Function Theorem, we have $\frac{\partial \tilde{I}^*}{\partial \alpha }=\frac{\partial \tilde{I}^*}{\partial }\times \frac{\partial \tilde{\Theta }^*}{\partial \alpha }=\frac{\partial \tilde{I}^*}{\partial \tilde{\Theta }^*}\cdot (-\frac{\partial F}{\partial \alpha }/\frac{\partial F}{\partial \tilde{\Theta }^*})$. It is obvious that $\frac{d\tilde{I}^*}{d\tilde{\Theta }^*}>0$, $\frac{\partial F}{\partial \tilde{\Theta }^*}>0$ and $\frac{\partial F}{\partial \alpha }<0$ which can be examined in a similar way for $0<\alpha <\tilde{\alpha }^*$ and $0<b<\tilde{b}^*$. This gives us $\frac{\partial \tilde{I}^*}{\partial \alpha }>0$ in this circumstance. $\square$