Abstract
We investigate the effects of ordering-timing strategies on radio-frequency identification (RFID) adoption sequences and firms’ profitability in a supply chain with a manufacturer and two retailers, both of whom suffer from misplaced inventory problems. The manufacturer is the Stackelberg leader, the two retailers engage in a quantity competition and simultaneously/sequentially make decisions on RFID adoption under two ordering-timing strategies. We derive the equilibrium strategies for RFID adoption and characterize each partner’s optimal order quantity and profit. We show that the equilibrium strategies for RFID adoption are identical regardless of the two competing retailers’ RFID adoption sequences. The retailer with a smaller misplacement rate will never adopt RFID alone. However, for the retailer with a higher misplacement rate: the more intense the competition is, the more likely he is to adopt RFID; ordering later always promotes him to adopt RFID; ordering earlier is more attractive than adopting RFID when the tagging cost is intermediate. Furthermore, as long as one or both retailers adopt RFID, ordering simultaneously can achieve Pareto improvement for both retailers. When neither retailer adopts RFID, the optimal ordering strategies depend on the misplacement rates and competition intensity.







Similar content being viewed by others
Notes
For ease of exposition, we refer to the manufacturer as “she” and the retailer as “he”.
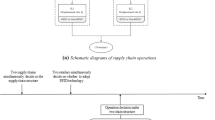
Both retailers have two ordering-timing strategies, i.e., ordering sequentially and ordering simultaneously. Ordering sequentially means that the retailer 1 (2) orders earlier (later) than the retailer 2 (1), whereas ordering simultaneously means that both retailers order at the same time. Therefore, if the retailer 1 (2) prefers ordering sequentially (simultaneously) to ordering simultaneously (sequentially), he obtains an advantage of ordering earlier.
References
Ben-Daya, M., Hassini, E., & Bahroun, Z. (2019). Internet of things and supply chain management: A literature review. International Journal of Production Research, 57(15–16), 4719–4742.
Camdercli, A., & Swaminathan, J. (2010). Misplaced inventory and radio-frequency identification (RFID) technology: Information and coordination. Production and Operations Management, 19(1), 1–18.
Cannella, S., Dominguez, R., & Framinan, J. (2017). Inventory record inaccuracy—The impact of structural complexity and lead time variability. Omega, 68, 123–138.
Chen, X., & Wang, X. (2015). Free or bundled: Channel selection decisions under different power structures. Omega, 53, 11–20.
Chen, S., Wang, H., Xie, Y., et al. (2014). Mean-risk analysis of radio frequency identification technology in supply chain with inventory misplacement: Risk-sharing and coordination. Omega, 46, 86–103.
Choi, T. M., Ma, C., Shen, B., et al. (2019). Optimal pricing in mass customization supply chains with risk-averse agents and retail competition. Omega, 88, 150–161.
Donaldson, T. (2015). Survey: More manufacturers, retailers adopt RFID for better inventory visibility. https://sourcingjournal.com/topics/retail/survey-manufacturers-retailers-adopt-rfid-better-inventory-visibility-26379/. Retrieved date February 27, 2020.
Ellis, S. C., Rao, S., Raju, D., et al. (2018). RFID tag performance: Linking the laboratory to the field through unsupervised learning. Production and Operations Management, 27(10), 1834–1848.
Fan, T., Tao, F., Deng, S., et al. (2015). Impact of RFID technology on supply chain decisions with inventory inaccuracies. International Journal of Production Economics, 159, 117–125.
Gaukler, G., Seifert, R., & Hausman, W. (2007). Item-level RFID in the retail supply chain. Production and Operations Management, 16(1), 65–76.
Golmohammadi, A., Tajbakhsh, A., Dia, M., & Takouda, P. M. (2019). Effect of timing on reliability improvement and ordering decisions in a decentralized assembly system. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03399-5.
Ha, A., Tian, Q., & Tong, S. (2017). Information sharing in competing supply chains with production cost reduction. Manufacturing & Service Operations Management, 19(2), 246–262.
Ha, A., & Tong, S. (2008). Contracting and information sharing under supply chain competition. Management Science, 54(4), 701–715.
Hardgrave, B., Aloysius, J., & Goyal, S. (2013). RFID-enabled visibility and retail inventory record inaccuracy: Experiments in the field. Production and Operations Management, 22(4), 843–856.
He, B., Li, G., & Liu, M. (2016). Impacts of decision sequences on a random yield supply chain with a service level requirement. Annals of Operations Research, 268(1–2), 469–495.
Heese, H. (2007). Inventory record inaccuracy, double, marginalization and RFID adoption. Production and Operations Management, 16(7), 221–229.
Hu, B., Hu, M., & Yang, Y. (2017). Open or closed? Technology sharing, supplier investment, and competition. Management Science, 19(1), 132–149.
Jin, Y., Hu, Q., Kim, S. W., et al. (2019). Supplier development and integration in competitive supply chains. Production and Operations Management, 28(5), 1256–1271.
Lan, Y., Yan, H., Ren, D., et al. (2019). Merger strategies in a supply chain with asymmetric capital-constrained retailers upon market power dependent trade credit. Omega, 83, 299–318.
Lee, H., & Özer, Ö. (2007). Unlocking the value of RFID. Production and Operations Management, 16(1), 40–64.
Luo, Z., Chen, X., & Kai, M. (2018). The effect of customer value and power structure on retail supply chain product choice and pricing decisions. Omega, 77, 115–126.
Matsui, K. (2017). When should a manufacturer set its direct price and wholesale price in dual-channel supply chains? European Journal of Operational Research, 258, 501–511.
Qi, Q., Wang, J., & Bai, Q. (2017). Pricing decision of a two-echelon supply chain with one supplier and two retailers under a carbon cap regulation. Journal of Cleaner Production, 151, 286–302.
Rekik, Y. (2011). Inventory inaccuracies in the wholesale supply chain. International Journal of Production Economics, 133(1), 172–181.
Rekik, Y., & Sahin, E. (2012). Exploring inventory systems sensitive to shrinkage—Analysis of a periodic review inventory under a service level constraint. International Journal of Production Research, 50(13), 3529–3546.
Rekik, Y., Sahin, E., & Dallery, Y. (2008). Analysis of the impact of the RFID technology on reducing product misplacement errors at retail stores. International Journal of Production Economics, 112(1), 264–278.
Rekik, Y., Syntetos, A., & Jemai, Z. (2015). An e-retailing supply chain subject to inventory inaccuracies. International Journal of Production Economics, 167, 139–155.
Shin, S., & Eksioglu, B. (2015). An empirical study of RFID productivity in the U.S. retail supply chain. International Journal of Production Economics, 163, 89–96.
Thiel, D., Hovelaque, V., & Hoa, V. (2010). Impact of inventory inaccuracies on service-level quality in (Q, R) continuous-review lost-sales inventory models. International Journal of Production Economics, 123(2), 301–311.
Whang, S. (2010). Timing of RFID adoption in a supply chain. Management Science, 56(2), 343–355.
Wu, X., & Zhang, F. (2014). Home or overseas? An analysis of sourcing strategies under competition. Management Science, 60(5), 1223–1240.
Xu, J., Wei, J., Feng, G., et al. (2012). Comparing improvement strategies for inventory inaccuracy in a two-echelon supply chain. European Journal of Operational Research, 221(1), 213–221.
Yan, Y., Zhao, R., & Lan, Y. (2017). Asymmetric retailers with different moving sequences: Group buying vs individual purchasing. European Journal of Operational Research, 261(3), 903–917.
Yang, H., & Chen, W. (2020). Game modes and investment cost locations in Radio-Frequency Identification (RFID) adoption. European Journal of Operational Research. https://doi.org/10.1016/j.ejor.2020.02.044.
Yang, H., Luo, J., & Wang, H. (2017). The role of revenue sharing and first-mover advantage in emission abatement with carbon tax and consumer environmental awareness. International Journal of Production Economics, 193, 691–702.
Yoon, D. H. (2016). Supplier encroachment and investment spillovers. Production and Operations Management, 25(11), 1839–1854.
Zhang, L. H., Li, T., & Fan, T. J. (2018a). Inventory misplacement and demand forecast error in the supply chain: profitable RFID strategies under wholesale and buy-back contracts. International Journal of Production Research, 56(15), 5188–5205.
Zhang, L. H., Li, T., & Fan, T. J. (2018b). Radio-frequency identification (RFID) adoption with inventory misplacement under retail competition. European Journal of Operational Research, 270(3), 1028–1043.
Zhang, L. H., Yao, J., & Xu, L. (2020). Emission reduction and market encroachment: Whether the manufacturer opens a direct channel or not? Journal of Cleaner Production. https://doi.org/10.1016/j.jclepro.2020.121932.
Zhou, W. (2009). RFID and item-level information visibility. European Journal of Operational Research, 198(1), 252–258.
Zhou, W., & Piramuthu, S. (2015). Identification shrinkage in inventory management: an RFID-based solution. Annals of Operations Research, 258(2), 285–300.
Acknowledgments
The authors sincerely thank the editor, Prof. K Manjunatha Prasad, and two anonymous reviewers for their constructive comments and suggestions that help improve the quality of the study. This work was supported by the National Natural Science Foundation of China (71971137, 71601114), the Postdoctoral Science Foundation project of China (2019T120307, 2019M651404), the Cruise Program of Science and Technology Ministry of China (2018-473).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Proposition 1
-
(a)
For Nash quantity game, we solve the problem by backward induction with \( p_{i - y}^{NN} = a - (1 - \alpha_{i} )q_{i - y}^{NN} - \gamma (1 - \alpha_{j} )q_{j - y}^{NN} \). In the second stage of the output game, both retailers decide on their order quantities \( q_{1 - n}^{NN} \) and \( q_{2 - n}^{NN} \) on the basis of the manufacturer’s wholesale price \( w_{n}^{NN} \). With \( {{\partial^{2} \pi_{i - n}^{NN} } \mathord{\left/ {\vphantom {{\partial^{2} \pi_{i - n}^{NN} } {\partial^{2} q_{i - n}^{NN} }}} \right. \kern-0pt} {\partial^{2} q_{i - n}^{NN} }} = - 2(1 - \alpha_{i} )^{2} < 0 \), we set \( {{\partial \pi_{i - n}^{NN} } \mathord{\left/ {\vphantom {{\partial \pi_{i - n}^{NN} } {\partial q_{i - n}^{NN} }}} \right. \kern-0pt} {\partial q_{i - n}^{NN} }} = 0 \) and generate the retailer \( i \)‘s order quantity \( q_{i - n}^{NN} = \frac{a}{{(2 + \gamma )(1 - \alpha_{i} )}} - \frac{{[2(1 - \alpha_{j} ) - \gamma (1 - \alpha_{i} )]w_{n}^{NN} }}{{(4 - \gamma^{2} )(1 - \alpha_{i} )^{2} (1 - \alpha_{j} )}} \). In the first stage, the manufacturer determines her wholesale price taking into account the two retailers’ order quantity decisions. With \( \frac{{\partial^{2} \pi_{m - n}^{NN} }}{{\partial^{2} w_{n}^{NN} }} = - \frac{{4(2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} ) + 4[(1 - \alpha_{1} ) - (1 - \alpha_{2} )]^{2} }}{{(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} (1 - \alpha_{2} )^{2} }} < 0 \), we set \( {{\partial \pi_{m - n}^{NN} } \mathord{\left/ {\vphantom {{\partial \pi_{m - n}^{NN} } {\partial w_{n}^{NN} }}} \right. \kern-0pt} {\partial w_{n}^{NN} }} = 0 \) and generate the optimal wholesale price \( w_{n}^{{NN^{*} }} = v_{n} a + {{c_{m} } \mathord{\left/ {\vphantom {{c_{m} } 2}} \right. \kern-0pt} 2} \).
-
(b)
For Stackelberg quantity game, we solve the problem by backward induction with \( p_{i - y}^{NN} = a - (1 - \alpha_{i} )q_{i - y}^{NN} - \gamma (1 - \alpha_{j} )q_{j - y}^{NN} \). In the third stage, the retailer 2 decides on his order quantity on the basis of the retailer 1’s order quantity. With \( {{\partial^{2} \pi_{2 - s}^{NN} } \mathord{\left/ {\vphantom {{\partial^{2} \pi_{2 - s}^{NN} } {\partial^{2} q_{2 - s}^{NN} }}} \right. \kern-0pt} {\partial^{2} q_{2 - s}^{NN} }} = - 2(1 - \alpha_{1} )^{2} < 0 \), we set \( {{\partial \pi_{2 - s}^{NN} } \mathord{\left/ {\vphantom {{\partial \pi_{2 - s}^{NN} } {\partial q_{2 - s}^{NN} }}} \right. \kern-0pt} {\partial q_{2 - s}^{NN} }} = 0 \) and generate the retailer 2’s order quantity \( q_{2 - s}^{NN} = \frac{{(1 - \alpha_{2} )[a - q_{1 - s}^{NN} \gamma (1 - \alpha_{1} )] - w_{s}^{NN} }}{{2(1 - \alpha_{2} )^{2} }} \). In the second stage, anticipating the retailer 2’s response function \( q_{2 - s}^{NN} \), the optimum \( q_{1 - s}^{NN} \) is determined by \( {{\partial \pi_{1 - s}^{NN} } \mathord{\left/ {\vphantom {{\partial \pi_{1 - s}^{NN} } {\partial q_{1 - s}^{NN} }}} \right. \kern-0pt} {\partial q_{1 - s}^{NN} }} = 0 \) because \( {{\partial^{2} \pi_{1 - s}^{NN} } \mathord{\left/ {\vphantom {{\partial^{2} \pi_{1 - s}^{NN} } {\partial^{2} q_{1 - s}^{NN} }}} \right. \kern-0pt} {\partial^{2} q_{1 - s}^{NN} }} = - (2 - \gamma^{2} )(1 - \alpha_{1} )(1 - \alpha_{2} ) < 0 \), leading to the retailer 1’s order quantity is \( q_{1 - s}^{NN} = \frac{(2 - \gamma )}{{2(1 - \alpha_{1} )(2 - \gamma^{2} )}}a + \frac{{[\gamma (1 - \alpha_{1} ) - 2(1 - \alpha_{2} )]}}{{2(1 - \alpha_{2} )(1 - \alpha_{1} )^{2} (2 - \gamma^{2} )}}w_{s}^{NN} \). In the first stage, the manufacturer determines her wholesale price taking into account the two retailers’ order quantity decisions. The optimum \( w_{s}^{NN} \) is determined by \( {{\partial \pi_{m - s}^{NN} } \mathord{\left/ {\vphantom {{\partial \pi_{m - s}^{NN} } {\partial w_{s}^{NN} }}} \right. \kern-0pt} {\partial w_{s}^{NN} }} = 0 \) because \( \frac{{\partial^{2} \pi_{m - s}^{NN} }}{{\partial^{2} w_{s}^{NN} }} = - \frac{{2(2 - \gamma )(1 - \alpha_{1} )^{2} + [2(1 - \alpha_{1} ) - \gamma (1 - \alpha_{2} )]^{2} }}{{2(2 - \gamma^{2} )(1 - \alpha_{1} )^{2} (1 - \alpha_{2} )^{2} }} < 0 \), resulting in the optimal wholesale price is \( w_{s}^{{NN^{*} }} = v_{s} a + {{c_{m} } \mathord{\left/ {\vphantom {{c_{m} } 2}} \right. \kern-0pt} 2} \).
1.1 Summary of abbreviations in Proposition 1
1.2 Summary of abbreviations in Corollary 1
Proof of Proposition 2
-
(a)
For Nash quantity game, we solve the problem by backward induction with \( p_{1 - y}^{AN} = a - q_{1 - y}^{AN} - \gamma (1 - \alpha_{2} )q_{2 - y}^{AN} \) and \( p_{2 - y}^{AN} = a - (1 - \alpha_{2} )q_{2 - y}^{AN} - \gamma q_{1 - y}^{AN} \). The two stage of the output game are similar to that of Proposition 1 and hence are omitted. We only discuss the first stage of the pricing game. The manufacturer determines the wholesale price \( w_{n}^{AN} \) and the cost-sharing coefficient \( \theta_{n}^{AN} \), with consideration of the two retailers’ order quantity decisions. We obtain the Hessian matrix \( H_{n}^{AN} = {{4c_{t}^{2} } \mathord{\left/ {\vphantom {{4c_{t}^{2} } {(4 - \gamma^{2} )(1 - \alpha_{2} )^{2} }}} \right. \kern-0pt} {(4 - \gamma^{2} )(1 - \alpha_{2} )^{2} }} > 0 \), where \( \frac{{\partial^{2} \pi_{m - n}^{AN} }}{{\partial^{2} w_{n}^{AN} }} = - \frac{{4[(2 - \gamma )(1 - \alpha_{2} ) + \alpha_{2}^{2} ]}}{{(4 - \gamma^{2} )(1 - \alpha_{2} )^{2} }} < 0 \), \( \frac{{\partial^{2} \pi_{m - n}^{AN} }}{{\partial w_{n}^{AN} \partial \theta_{n}^{AN} }} = \frac{{2(\gamma + 2\alpha_{2} - 2)c_{t} }}{{(4 - \gamma^{2} )(1 - \alpha_{2} )}} \), \( \frac{{\partial^{2} \pi_{m - n}^{AN} }}{{\partial \theta_{n}^{AN} \partial w_{n}^{AN} }} = \frac{{2(\gamma + 2\alpha_{2} - 2)c_{t} }}{{(4 - \gamma^{2} )(1 - \alpha_{2} )}} \), and \( \frac{{\partial^{2} \pi_{m - n}^{AN} }}{{\partial^{2} \theta_{n}^{AN} }} = \frac{{4c_{t}^{2} }}{{(\gamma^{2} - 4)}} \). On this basis, we know that \( H_{n}^{AN} \) is negative definite, hence the manufacturer has the maximum profit. The optimum \( w_{n}^{AN} \) and \( \theta_{n}^{AN} \) are determined by \( {{\partial \pi_{m - n}^{AN} } \mathord{\left/ {\vphantom {{\partial \pi_{m - n}^{AN} } {\partial w_{n}^{AN} }}} \right. \kern-0pt} {\partial w_{n}^{AN} }} = 0 \) and \( {{\partial \pi_{m - n}^{AN} } \mathord{\left/ {\vphantom {{\partial \pi_{m - n}^{AN} } {\partial \theta_{n}^{AN} }}} \right. \kern-0pt} {\partial \theta_{n}^{AN} }} = 0 \).
-
(b)
For Stackelberg quantity game, we solve the problem by backward induction with \( p_{1 - y}^{AN} = a - q_{1 - y}^{AN} - \gamma (1 - \alpha_{2} )q_{2 - y}^{AN} \) and \( p_{2 - y}^{AN} = a - (1 - \alpha_{2} )q_{2 - y}^{AN} - \gamma q_{1 - y}^{AN} \). The third stage and the two stage of the output game are similar to those of Proposition 1 and hence are omitted. We only discuss the first stage of the pricing game. The manufacturer determines the wholesale price \( w_{s}^{AN} \) and the cost-sharing coefficient \( \theta_{s}^{AN} \), with consideration of the two retailers’ order quantity decisions. We obtain the Hessian matrix \( H_{s}^{AN} = {{2c_{t}^{2} } \mathord{\left/ {\vphantom {{2c_{t}^{2} } {(2 - \gamma^{2} )(1 - \alpha_{2} )^{2} }}} \right. \kern-0pt} {(2 - \gamma^{2} )(1 - \alpha_{2} )^{2} }} > 0 \), where \( \frac{{\partial^{2} \pi_{m - s}^{AN} }}{{\partial^{2} w_{s}^{AN} }} = - \frac{{4(1 - \alpha_{2} )(2 - \gamma ) + 4\alpha_{2}^{2} - \gamma^{2} }}{{2(2 - \gamma^{2} )(1 - \alpha_{2} )^{2} }} < 0 \), \( \frac{{\partial^{2} \pi_{m - s}^{AN} }}{{\partial w_{s}^{AN} \partial \theta_{s}^{AN} }} = \frac{{(\gamma + 2\alpha_{2} - 2)c_{t} }}{{(2 - \gamma^{2} )(1 - \alpha_{2} )}} \), \( \frac{{\partial^{2} \pi_{m - s}^{AN} }}{{\partial \theta_{s}^{AN} \partial w_{s}^{AN} }} = \frac{{(\gamma + 2\alpha_{2} - 2)c_{t} }}{{(2 - \gamma^{2} )(1 - \alpha_{2} )}} \), and \( \frac{{\partial^{2} \pi_{m - s}^{AN} }}{{\partial^{2} \theta_{s}^{AN} }} = \frac{{2c_{t}^{2} }}{{(\gamma^{2} - 2)}} \). On this basis, we know that \( H_{s}^{AN} \) is negative definite, hence the manufacturer has the maximum profit. The optimum \( w_{s}^{AN} \) and \( \theta_{s}^{AN} \) are determined by \( {{\partial \pi_{m - s}^{AN} } \mathord{\left/ {\vphantom {{\partial \pi_{m - s}^{AN} } {\partial w_{s}^{AN} }}} \right. \kern-0pt} {\partial w_{s}^{AN} }} = 0 \) and \( {{\partial \pi_{m - s}^{AN} } \mathord{\left/ {\vphantom {{\partial \pi_{m - s}^{AN} } {\partial \theta_{s}^{AN} }}} \right. \kern-0pt} {\partial \theta_{s}^{AN} }} = 0 \). We therefore generate the Proposition 2.
1.3 Summary of abbreviations in Proposition 2
1.4 Summary of abbreviations in Corollary 2
Proof of Proposition 3
-
(a)
For Nash quantity game, the proof is similar to that of Proposition 2 and hence is omitted.
-
(b)
For Stackelberg quantity game, the proof is similar to that of Proposition 2 and hence is omitted. We only discuss the Hessian matrix. The manufacturer determines the wholesale price \( w_{s}^{NA} \) and the cost-sharing coefficient \( \theta_{s}^{NA} \), with consideration of the two retailers’ order quantity decisions. We obtain the Hessian matrix \( H_{s}^{NA} = {{2c_{t}^{2} } \mathord{\left/ {\vphantom {{2c_{t}^{2} } {(2 - \gamma^{2} )(1 - \alpha_{1} )^{2} }}} \right. \kern-0pt} {(2 - \gamma^{2} )(1 - \alpha_{1} )^{2} }} > 0 \), where \( \frac{{\partial^{2} \pi_{m - s}^{NA} }}{{\partial^{2} w_{s}^{NA} }} = \frac{{\gamma^{2} (1 - \alpha_{1} )^{2} - 4(2 - \gamma )(1 - \alpha_{1} ) - 4\alpha_{1}^{2} }}{{2(2 - \gamma^{2} )(1 - \alpha_{1} )^{2} }} < 0 \), \( \frac{{\partial^{2} \pi_{m - s}^{NA} }}{{\partial w_{s}^{NA} \partial \theta_{s}^{NA} }} = \frac{{[2\gamma - (4 - \gamma^{2} )(1 - \alpha_{1} )]c_{t} }}{{2(2 - \gamma^{2} )(1 - \alpha_{1} )}} \), \( \frac{{\partial^{2} \pi_{m - s}^{NA} }}{{\partial \theta_{s}^{NA} \partial w_{s}^{NA} }} = \frac{{[2\gamma - (4 - \gamma^{2} )(1 - \alpha_{1} )]c_{t} }}{{2(2 - \gamma^{2} )(1 - \alpha_{1} )}} \), and \( \frac{{\partial^{2} \pi_{m - s}^{NA} }}{{\partial^{2} \theta_{s}^{NA} }} = - \frac{{(4 - \gamma^{2} )c_{t}^{2} }}{{2(2 - \gamma^{2} )}} \). On this basis, we know that \( H_{s}^{NA} \) is negative definite, therefore the manufacturer has the maximum profit.
1.5 Summary of abbreviations in Proposition 3
1.6 Summary of abbreviations in Corollary 3
Proof of Proposition 4
-
(a)
For Nash quantity game, the proof is similar to that of Proposition 2 and hence is omitted. We only discuss the Hessian matrix. The manufacturer determines the wholesale price \( w_{n}^{AA} \) and the cost-sharing coefficient \( \theta_{n}^{AA} \), with consideration of the two retailers’ order quantity decisions. We obtain the Hessian matrix \( H_{n}^{AA} = 0 \), where \( \frac{{\partial^{2} \pi_{m - n}^{AA} }}{{\partial^{2} w_{n}^{AA} }} = - \frac{4}{(\gamma + 2)} \), \( \frac{{\partial^{2} \pi_{m - n}^{AA} }}{{\partial w_{n}^{AA} \partial \theta_{n}^{AA} }} = - \frac{{4c_{t} }}{(\gamma + 2)} \), \( \frac{{\partial^{2} \pi_{m - n}^{AA} }}{{\partial \theta_{n}^{AA} \partial w_{n}^{AA} }} = - \frac{{4c_{t} }}{(\gamma + 2)} \), and \( \frac{{\partial^{2} \pi_{m - n}^{AA} }}{{\partial^{2} \theta_{n}^{AA} }} = - \frac{{4c_{t}^{2} }}{(\gamma + 2)} \). The optimum \( w_{n}^{AA} \) and \( \theta_{n}^{AA} \) are determined by \( {{\partial \pi_{m - n}^{AA} } \mathord{\left/ {\vphantom {{\partial \pi_{m - n}^{AA} } {\partial w_{n}^{AA} }}} \right. \kern-0pt} {\partial w_{n}^{AA} }} = {{\partial \pi_{m - n}^{AA} } \mathord{\left/ {\vphantom {{\partial \pi_{m - n}^{AA} } {\partial \theta_{n}^{AA} }}} \right. \kern-0pt} {\partial \theta_{n}^{AA} }} = 0 \).
-
(b)
For Stackelberg quantity game, the proof is similar to that of Proposition 2 and hence is omitted. We only discuss the Hessian matrix. The manufacturer determines the wholesale price \( w_{s}^{AA} \) and the cost-sharing coefficient \( \theta_{s}^{AA} \), with consideration of the two retailers’ order quantity decisions. We obtain the Hessian matrix \( H_{s}^{AA} = 0 \), where \( \frac{{\partial^{2} \pi_{m - s}^{AA} }}{{\partial^{2} w_{s}^{AA} }} = \frac{{\gamma^{2} + 4\gamma - 8}}{{2(2 - \gamma^{2} )}} \), \( \frac{{\partial^{2} \pi_{m - s}^{AA} }}{{\partial w_{s}^{AA} \partial \theta_{s}^{AA} }} = \frac{{(\gamma^{2} + 4\gamma - 8)c_{t} }}{{2(2 - \gamma^{2} )}} \), \( \frac{{\partial^{2} \pi_{m - s}^{AA} }}{{\partial \theta_{s}^{AA} \partial w_{s}^{AA} }} = \frac{{(\gamma^{2} + 4\gamma - 8)c_{t} }}{{2(2 - \gamma^{2} )}} \), and \( \frac{{\partial^{2} \pi_{m - s}^{AA} }}{{\partial^{2} \theta_{s}^{AA} }} = \frac{{(\gamma^{2} + 4\gamma - 8)c_{t}^{2} }}{{2(2 - \gamma^{2} )}} \). The optimum \( w_{s}^{AA} \) and \( \theta_{s}^{AA} \) are determined by \( {{\partial \pi_{m - s}^{AA} } \mathord{\left/ {\vphantom {{\partial \pi_{m - s}^{AA} } {\partial w_{s}^{AA} }}} \right. \kern-0pt} {\partial w_{s}^{AA} }} = {{\partial \pi_{m - s}^{AA} } \mathord{\left/ {\vphantom {{\partial \pi_{m - s}^{AA} } {\partial \theta_{s}^{AA} }}} \right. \kern-0pt} {\partial \theta_{s}^{AA} }} = 0 \).
1.7 Summary of abbreviations in Proposition 4
Proof of proposition 5
(I) We first analyze the equilibrium strategies for RFID adoption when both retailers simultaneously make order quantity decisions.
(i) Given that two retailers’ RFID adoption sequences are simultaneously:
AA will be an equilibrium strategy if and only if \( \left\{ \begin{aligned} \pi_{1 - n}^{AA*} \ge \pi_{1 - n}^{NA*} \hfill \\ \pi_{2 - n}^{AA*} \ge \pi_{2 - n}^{AN*} \hfill \\ \end{aligned} \right. \). Thus, we derive that both retailers will adopt RFID when \( c_{t} \le \hbox{min} (c_{t1 - n}^{A} ,c_{t2 - n}^{A} ) \). We compare the relative sizes of \( c_{t1 - n}^{A} \) and \( c_{t2 - n}^{A} \), and obtain \( c_{t2 - n}^{A} - c_{t1 - n}^{A} = \frac{{(\alpha_{2} - \alpha_{1} )c_{m} }}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}} \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t2 - n}^{A} = c_{t1 - n}^{A} = \bar{c}_{t - n} \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - n} ] \); if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t2 - n}^{A} - c_{t1 - n}^{A} > 0 \), resulting in that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - n}^{A} ] \); if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - n}^{A} - c_{t1 - n}^{A} < 0 \), bringing about that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - n}^{A} ] \). Where \( c_{t1 - n}^{A} = {{\alpha_{1} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{1} c_{m} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} \), \( c_{t2 - n}^{A} = {{\alpha_{2} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{2} c_{m} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} \) and \( \overline{c}_{t - n} = {{\alpha c_{m} } \mathord{\left/ {\vphantom {{\alpha c_{m} } {(1 - \alpha )}}} \right. \kern-0pt} {(1 - \alpha )}} \).
AN will be an equilibrium strategy if \( \left\{ \begin{aligned} \pi_{1 - n}^{AN*} \ge \pi_{1 - n}^{NN*} \hfill \\ \pi_{2 - n}^{AN*} > \pi_{2 - n}^{AA*} \hfill \\ \end{aligned} \right. \). Thus, we derive that only retailer 1 will adopt RFID when \( c_{t2 - n}^{A} < c_{t} \le c_{t1 - n}^{N} \). We compare the relative sizes of \( c_{t2 - n}^{A} \) and \( c_{t1 - n}^{N} \), and then obtain \( c_{t1 - n}^{N} - c_{t2 - n}^{A} = \left( {\frac{{(2 + \gamma )(2 - \gamma )(1 - \alpha_{1} )a}}{{4\left( {(\alpha_{1} - \alpha_{2} )^{2} + (2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )} \right)}} + \frac{{c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)(\alpha_{1} - \alpha_{2} ) \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t1 - n}^{N} - c_{t2 - n}^{A} = 0 \), leading to that AN will not exist; if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t1 - n}^{N} - c_{t2 - n}^{A} < 0 \), resulting in that AN will not exist; if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t1 - n}^{N} - c_{t2 - n}^{A} > 0 \), bringing about that AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{A} ,c_{t1 - n}^{N} ] \). Where \( c_{t1 - n}^{N} = \left( {{{2v_{n} } \mathord{\left/ {\vphantom {{2v_{n} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} - {{\gamma v_{n} } \mathord{\left/ {\vphantom {{\gamma v_{n} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} - {{(2 - \gamma )} \mathord{\left/ {\vphantom {{(2 - \gamma )} 2}} \right. \kern-0pt} 2}} \right)a + {{\alpha_{1} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{1} c_{m} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} \).
NA will be an equilibrium strategy if \( \left\{ \begin{aligned} \pi_{1 - n}^{NA*} > \pi_{1 - n}^{AA*} \hfill \\ \pi_{2 - n}^{NA*} \ge \pi_{2 - n}^{NN*} \hfill \\ \end{aligned} \right. \). Thus, we derive that only retailer 2 will adopt RFID when \( c_{t1 - n}^{A} < c_{t} \le c_{t2 - n}^{N} \). We compare the relative sizes of \( c_{t1 - n}^{A} \) and \( c_{t2 - n}^{N} \), and then obtain \( c_{t2 - n}^{N} - c_{t1 - n}^{A} = \left( {\frac{{(2 + \gamma )(2 - \gamma )(1 - \alpha_{2} )a}}{{4\left( {(\alpha_{2} - \alpha_{1} )^{2} + (2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )} \right)}} + \frac{{c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)(\alpha_{2} - \alpha_{1} ) \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t2 - n}^{N} - c_{t1 - n}^{A} = 0 \), leading to that NA will not exist; if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - n}^{N} - c_{t1 - n}^{A} < 0 \), resulting in that NA will not exist; if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t2 - n}^{N} - c_{t1 - n}^{A} > 0 \), bringing about that NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{A} ,c_{t2 - n}^{N} ] \). Where \( c_{t2 - n}^{N} = \left( {{{2v_{n} } \mathord{\left/ {\vphantom {{2v_{n} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} - {{\gamma v_{n} } \mathord{\left/ {\vphantom {{\gamma v_{n} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} - {{(2 - \gamma )} \mathord{\left/ {\vphantom {{(2 - \gamma )} 2}} \right. \kern-0pt} 2}} \right)a + {{\alpha_{2} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{2} c_{m} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} \).
NN will be an equilibrium strategy if \( \left\{ \begin{aligned} \pi_{1 - n}^{NN*} > \pi_{1 - n}^{AN*} \hfill \\ \pi_{2 - n}^{NN*} > \pi_{2 - n}^{NA*} \hfill \\ \end{aligned} \right. \). Thus, we derive that both retailers will forgo RFID adoption when \( c_{t} > \hbox{max} (c_{t1 - n}^{N} ,c_{t2 - n}^{N} ) \). We compare the relative sizes of \( c_{t1 - n}^{N} \) and \( c_{t2 - n}^{N} \), and then obtain \( c_{t2 - n}^{N} - c_{t1 - n}^{N} = \frac{{(2av_{n} + av_{n} \gamma + \alpha_{2} c_{m} )(\alpha_{2} - \alpha_{1} )}}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}} \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive that \( c_{t2 - n}^{N} = c_{t1 - n}^{N} = \bar{c}_{t - n} \), leading to that NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - n} , + \infty ) \); if \( \alpha_{1} < \alpha_{2} \), we can derive \( c_{t2 - n}^{N} - c_{t1 - n}^{N} > 0 \), resulting in that NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{N} , + \infty ) \); if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - n}^{N} - c_{t1 - n}^{N} < 0 \), bringing about that NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{N} , + \infty ) \).
Consequently, we obtain the equilibrium strategies for RFID adoption when both retailers simultaneously make decisions on RFID adoption and order quantity. If \( \alpha_{1} = \alpha_{2} = \alpha \): AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - n} ] \), NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - n} , + \infty ) \); if \( \alpha_{1} < \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - n}^{A} ] \), NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{A} ,c_{t2 - n}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{N} , + \infty ) \); if \( \alpha_{1} > \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - n}^{A} ] \), AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{A} ,c_{t1 - n}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{N} , + \infty ) \). Thus, we obtain the results of proposition 5.
(ii) Given that two retailers’ RFID adoption sequences are sequentially:
If the retailer 1 has adopted RFID: AA will be an equilibrium strategy if the retailer 2 adopts RFID, AN will be an equilibrium strategy if the retailer 2 refuses to adopt RFID. We take \( \Delta_{2 - n}^{A} = \pi_{2 - n}^{AA*} - \pi_{2 - n}^{AN*} \) as the retailer 2’s profit variation between AA and AN, and obtain that the retailer 2 adopts RFID when \( c_{t} \in (0,c_{t2 - n}^{A} ] \) while forgoes RFID adoption when \( c_{t} \in (c_{t2 - n}^{A} , + \infty ) \).
If the retailer 1 has not adopted RFID: NA will be an equilibrium strategy if the retailer 2 adopts RFID, NN will be an equilibrium strategy if the retailer 2 refuses to adopt RFID. We take \( \Delta_{2 - n}^{N} = \pi_{2 - n}^{NA*} - \pi_{2 - n}^{NN*} \) as the retailer 2’s profit variation between NA and NN, and obtain that the retailer 2 adopts RFID when \( c_{t} \in (0,c_{t2 - n}^{N} ] \) while forgoes RFID adoption when \( c_{t} \in (c_{t2 - n}^{N} , + \infty ) \).
Using backward induction, we first characterize the retailer 2’s RFID adoption decisions. According to comparing the relative sizes of \( c_{t2 - n}^{A} \) and \( c_{t2 - n}^{N} \), we obtain \( c_{t2 - n}^{N} - c_{t2 - n}^{A} = \frac{{(\alpha_{2} - \alpha_{1} )(1 - \alpha_{2} )(4 - \gamma^{2} )a}}{{4\left( {(\alpha_{1} - \alpha_{2} )^{2} + (2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )} \right)}} \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t2 - n}^{N} = c_{t2 - n}^{A} = \bar{c}_{t - n} \), leading to that the retailer 2 always adopts RFID when \( c_{t} \in (0,\bar{c}_{t - n} ] \) while forgoes RFID adoption when \( c_{t} \in (\bar{c}_{t - n} , + \infty ) \), regardless of whether the retailer 1 adopts RFID; if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t2 - n}^{N} - c_{t2 - n}^{A} > 0 \), hence, the retailer 2 always adopts RFID when \( c_{t} \in (0,c_{t2 - n}^{A} ] \), the two retailers have the opposite decisions on RFID adoption when \( c_{t} \in (c_{t2 - n}^{A} ,c_{t2 - n}^{N} ] \), and the retailer 2 forgoes RFID adoption when \( c_{t} \in (c_{t2 - n}^{N} , + \infty ) \); if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - n}^{N} - c_{t2 - n}^{A} < 0 \), hence, the retailer 2 always adopts RFID when \( c_{t} \in (0,c_{t2 - n}^{N} ] \), the two retailers have the same decisions on RFID adoption when \( c_{t} \in (c_{t2 - n}^{N} ,c_{t2 - n}^{A} ] \), and the retailer 2 forgoes RFID adoption when \( c_{t} \in (c_{t2 - n}^{A} , + \infty ) \).
We turn to deal with the equilibrium RFID adoption strategies.
If \( \alpha_{1} = \alpha_{2} = \alpha \): given \( c_{t} \in (0,\bar{c}_{t - n} ] \), the retailer 2 always adopts RFID. Under such a circumstance, we take \( \Delta_{1 - n}^{A} = \pi_{1 - n}^{AA*} - \pi_{1 - n}^{NA*} \) as the retailer 1’s profit variation between AA and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,\bar{c}_{t - n} ] \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - n} ] \).
Given \( c_{t} \in (\bar{c}_{t - n} , + \infty ) \), the retailer 2 always refuses to adopt RFID. Under such a circumstance, we take \( \Delta_{1 - n}^{N} = \pi_{1 - n}^{AN*} - \pi_{1 - n}^{NN*} \) as the retailer 1’s profit variation between AN and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (\bar{c}_{t - n} , + \infty ) \), resulting in that NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - n} , + \infty ) \).
If \( \alpha_{1} < \alpha_{2} \): given \( c_{t} \in (0,c_{t2 - n}^{A} ] \), the retailer 2 always adopts RFID. Under such a circumstance, we take \( \Delta_{1 - n}^{A} = \pi_{1 - n}^{AA*} - \pi_{1 - n}^{NA*} \) as the retailer 1’s profit variation between AA and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - n}^{A} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - n}^{A} , + \infty ) \). We compare the relative sizes of \( c_{t1 - n}^{A} \) and \( c_{t2 - n}^{A} \), and then obtain \( c_{t2 - n}^{A} - c_{t1 - n}^{A} = \frac{{(\alpha_{2} - \alpha_{1} )c_{m} }}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}} > 0 \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - n}^{A} ] \) and NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{A} ,c_{t2 - n}^{A} ] \).
Given \( c_{t} \in (c_{t2 - n}^{A} ,c_{t2 - n}^{N} ] \), the two retailers have the opposite decisions on RFID adoption. Under such a circumstance, we take \( \Delta_{1 - n}^{NA} = \pi_{1 - n}^{AN*} - \pi_{1 - n}^{NA*} \) as the retailer 1’s profit variation between AN and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - n}^{NA} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - n}^{NA} , + \infty ) \). We compare the relative sizes of \( c_{t2 - n}^{A} \) and \( c_{t1 - n}^{NA} \), and then obtain \( c_{t2 - n}^{A} - c_{t1 - n}^{NA} = \frac{{2(\alpha_{2} - \alpha_{1} )c_{m} }}{{(2 + \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )}} > 0 \), resulting in that NA is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{A} ,c_{t2 - n}^{N} ] \). Where \( c_{t1 - n}^{NA} = \frac{{\alpha_{2} c_{m} }}{{(1 - \alpha_{2} )}} + \frac{{2(\alpha_{1} - \alpha_{2} )c_{m} }}{{(2 + \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )}} \).
Given \( c_{t} \in (c_{t2 - n}^{N} , + \infty ) \), the retailer 2 always refuses to adopt RFID. Under such a circumstance, we take \( \Delta_{1 - n}^{N} = \pi_{1 - n}^{AN*} - \pi_{1 - n}^{NN*} \) as the retailer 1’s profit variation between AN and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - n}^{N} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - n}^{N} , + \infty ) \). We compare the relative sizes of \( c_{t2 - n}^{N} \) and \( c_{t1 - n}^{N} \), and then obtain \( c_{t2 - n}^{N} - c_{t1 - n}^{N} = \frac{{(2av_{n} + av_{n} \gamma + \alpha_{2} c_{m} )(\alpha_{2} - \alpha_{1} )}}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}} > 0 \), bring about that NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{N} , + \infty ) \).
If \( \alpha_{1} > \alpha_{2} \): given \( c_{t} \in (0,c_{t2 - n}^{N} ] \), the retailer 2 always adopts RFID. Under such a circumstance, we take \( \Delta_{1 - n}^{A} = \pi_{1 - n}^{AA*} - \pi_{1 - n}^{NA*} \) as the retailer 1’s profit variation between AA and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - n}^{A} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - n}^{A} , + \infty ) \). We compare the relative sizes of \( c_{t2 - n}^{N} \) and \( c_{t1 - n}^{A} \), and then obtain \( c_{t2 - n}^{N} - c_{t1 - n}^{A} = \frac{{(2 - \gamma )(2 + \gamma )(1 - \alpha_{2} )(\alpha_{2} - \alpha_{1} )a}}{{4\left[ {(1 - \alpha_{1} )^{2} - \gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + (1 - \alpha_{2} )^{2} } \right]}} + \left( {\frac{{\alpha_{2} - \alpha_{1} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)c_{m} < 0 \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - n}^{N} ] \).
Given \( c_{t} \in (c_{t2 - n}^{N} ,c_{t2 - n}^{A} ] \), the two retailers have the same decisions on RFID adoption. Under such a circumstance, we take \( \Delta_{1 - n}^{AN} = \pi_{1 - n}^{AA*} - \pi_{1 - n}^{NN*} \) as the retailer 1’s profit variation between AA and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - n}^{AN} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - n}^{AN} , + \infty ) \). We compare the relative size of \( c_{t1 - n}^{AN} \) and \( c_{t2 - n}^{A} \). With \( c_{t1 - n}^{AN} - c_{t2 - n}^{A} = \left( {\frac{{2(1 - \alpha_{2} )[2v_{n} - (1 - \alpha_{1} )] - \gamma (1 - \alpha_{1} )[2v_{n} - (1 - \alpha_{2} )]}}{{(2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)a + \frac{{2(\alpha_{1} - \alpha_{2} )c_{m} }}{{(2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )}} > 0 \), we obtain that AA is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{N} ,c_{t2 - n}^{A} ] \). Where \( c_{t1 - n}^{AN} = \left( {\frac{{2(1 - \alpha_{2} )[2v_{n} - (1 - \alpha_{1} )] - \gamma (1 - \alpha_{1} )[2v_{n} - (1 - \alpha_{2} )]}}{{(2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)a + \left( {\frac{{2(1 - \alpha_{2} )\alpha_{1} - \gamma (1 - \alpha_{1} )\alpha_{2} }}{{(2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)c_{m} \).
Given \( c_{t} \in (c_{t2 - n}^{A} , + \infty ) \), the retailer 2 always refuses to adopt RFID. Under such a circumstance, we take \( \Delta_{1 - n}^{N} = \pi_{1 - n}^{AN*} - \pi_{1 - n}^{NN*} \) as the retailer 1’s profit variation between AN and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - n}^{N} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - n}^{N} , + \infty ) \). We compare the relative sizes of \( c_{t1 - n}^{N} \) and \( c_{t2 - n}^{A} \). With \( c_{t1 - n}^{N} - c_{t2 - n}^{A} = \left( {\frac{{(2 - \gamma )(2 + \gamma )(1 - \alpha_{1} )a}}{{4\left[ {(1 - \alpha_{1} )^{2} - \gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + (1 - \alpha_{2} )^{2} } \right]}} + \frac{{c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)(\alpha_{1} - \alpha_{2} ) > 0 \), we obtain that AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{A} ,c_{t1 - n}^{N} ] \) and NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{N} , + \infty ) \).
Consequently, we obtain the equilibrium strategies for RFID adoption when the two retailers sequentially make decisions on RFID adoption and simultaneously make decisions on order quantity. If \( \alpha_{1} = \alpha_{2} = \alpha \): AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - n} ] \), NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - n} , + \infty ) \); if \( \alpha_{1} < \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - n}^{A} ] \), NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{A} ,c_{t2 - n}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{N} , + \infty ) \); if \( \alpha_{1} > \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - n}^{A} ] \), AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - n}^{A} ,c_{t1 - n}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - n}^{N} , + \infty ) \). Thus, we find that when both retailers simultaneously make order quantity decisions, whether the two retailers adopt RFID simultaneously or sequentially does not affect the equilibrium strategies for RFID adoption.
(II) We then analyze the equilibrium strategies for RFID adoption when both retailers sequentially make order quantity decisions.
(i) Given that two retailers’ RFID adoption sequences are simultaneously:
AA will be an equilibrium strategy if and only if \( \left\{ \begin{aligned} \pi_{1 - s}^{AA*} \ge \pi_{1 - s}^{NA*} \hfill \\ \pi_{2 - s}^{AA*} \ge \pi_{2 - s}^{AN*} \hfill \\ \end{aligned} \right. \). Thus, we derive that both retailers will adopt RFID when \( c_{t} \le \hbox{min} (c_{t1 - s}^{A} ,c_{t2 - s}^{A} ) \). We compare the relative size of \( c_{t1 - s}^{A} \) and \( c_{t2 - s}^{A} \), and then obtain \( c_{t2 - s}^{A} - c_{t1 - s}^{A} = \frac{{(\alpha_{2} - \alpha_{1} )c_{m} }}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}} \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t2 - s}^{A} = c_{t1 - s}^{A} = \bar{c}_{t - s} \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - s} ] \); if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t2 - s}^{A} - c_{t1 - s}^{A} > 0 \), resulting in that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - s}^{A} ] \); if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - s}^{A} - c_{t1 - s}^{A} < 0 \), bringing about that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - s}^{A} ] \). Where \( c_{t1 - s}^{A} = {{\alpha_{1} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{1} c_{m} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} \), \( c_{t2 - s}^{A} = {{\alpha_{2} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{2} c_{m} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} \) and \( \bar{c}_{t - s} = {{\alpha c_{m} } \mathord{\left/ {\vphantom {{\alpha c_{m} } {(1 - \alpha )}}} \right. \kern-0pt} {(1 - \alpha )}} \).
AN will be an equilibrium strategy if \( \left\{ \begin{aligned} \pi_{1 - s}^{AN*} \ge \pi_{1 - s}^{NN*} \hfill \\ \pi_{2 - s}^{AN*} \ge \pi_{2 - s}^{AA*} \hfill \\ \end{aligned} \right. \). Thus, we derive that only retailer 1 will adopt RFID when \( c_{t2 - s}^{A} < c_{t} \le c_{t1 - s}^{N} \). We compare the relative sizes of \( c_{t2 - s}^{A} \) and \( c_{t1 - s}^{N} \), as \( c_{t1 - s}^{N} - c_{t2 - s}^{A} = \left( {\frac{{(8 - 4\gamma^{2} )(1 - \alpha_{1} )a}}{{2\left[ {(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} } \right]}} + \frac{{c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)(\alpha_{1} - \alpha_{2} ) \), Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t1 - s}^{N} - c_{t2 - s}^{A} = 0 \), leading to that AN will not exist; if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t1 - s}^{N} - c_{t2 - s}^{A} < 0 \), resulting in that AN will not exist; if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t1 - s}^{N} - c_{t2 - s}^{A} > 0 \), bringing about that AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{A} ,c_{t1 - s}^{N} ] \). Where \( c_{t1 - s}^{N} = \left( {{{2v_{s} } \mathord{\left/ {\vphantom {{2v_{s} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} - {{\gamma v_{s} } \mathord{\left/ {\vphantom {{\gamma v_{s} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} - {{(2 - \gamma )} \mathord{\left/ {\vphantom {{(2 - \gamma )} 2}} \right. \kern-0pt} 2}} \right)a + {{\alpha_{1} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{1} c_{m} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} \).
NA will be an equilibrium strategy if \( \left\{ \begin{aligned} \pi_{1 - s}^{NA*} \ge \pi_{1 - s}^{AA*} \hfill \\ \pi_{2 - s}^{NA*} \ge \pi_{2 - s}^{NN*} \hfill \\ \end{aligned} \right. \). Thus, we derive that only retailer 2 will adopt RFID when \( c_{t1 - s}^{A} < c_{t} \le c_{t2 - s}^{N} \). We compare the relative sizes of \( c_{t1 - s}^{A} \) and \( c_{t2 - s}^{N} \), as \( c_{t2 - s}^{N} - c_{t1 - s}^{A} = \left( {\frac{{(16 - 8\gamma^{2} )(1 - \alpha_{2} )a}}{{(4 - \gamma^{2} )[(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} ]}} + \frac{{c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)(\alpha_{2} - \alpha_{1} ) \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t2 - s}^{N} - c_{t1 - s}^{A} = 0 \), leading to that NA will not exist; if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - s}^{N} - c_{t1 - s}^{A} < 0 \), resulting in that NA will not exist; if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t2 - s}^{N} - c_{t1 - s}^{A} > 0 \), bringing about that NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{A} ,c_{t2 - s}^{N} ] \).
Where \( c_{t2 - s}^{N} = \left( {{{2v_{s} } \mathord{\left/ {\vphantom {{2v_{s} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} - {{4\gamma v_{s} } \mathord{\left/ {\vphantom {{4\gamma v_{s} } {(1 - \alpha_{1} )(4 - \gamma^{2} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )(4 - \gamma^{2} )}} - {{(4 - \gamma^{2} - 2\gamma )} \mathord{\left/ {\vphantom {{(4 - \gamma^{2} - 2\gamma )} {(4 - \gamma^{2} )}}} \right. \kern-0pt} {(4 - \gamma^{2} )}}} \right)a + {{\alpha_{2} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{2} c_{m} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} \).
NN will be an equilibrium strategy if \( \left\{ \begin{aligned} \pi_{1 - s}^{NN*} \ge \pi_{1 - s}^{AN*} \hfill \\ \pi_{2 - s}^{NN*} \ge \pi_{2 - s}^{NA*} \hfill \\ \end{aligned} \right. \). Thus, we derive that both retailers will forgo RFID adoption when \( c_{t} > \hbox{max} (c_{t1 - s}^{N} ,c_{t2 - s}^{N} ) \). We compare the relative sizes of \( c_{t1 - s}^{N} \) and \( c_{t2 - s}^{N} \), as \( c_{t2 - s}^{N} - c_{t1 - s}^{N} = \frac{{(4 - \gamma^{2} )\left[ {(1 - \alpha_{1} )^{2} - (1 - \alpha_{2} )^{2} } \right]a}}{{(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} }} + \frac{{(\alpha_{2} - \alpha_{1} )c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}} \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t2 - s}^{N} = c_{t1 - s}^{N} = \bar{c}_{t - s} \), leading to that NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - s} , + \infty ) \); if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t2 - s}^{N} - c_{t1 - s}^{N} > 0 \), resulting in that NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \); i f \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - s}^{N} - c_{t1 - s}^{N} < 0 \), bringing about that NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{N} , + \infty ) \).
Consequently, we obtain the equilibrium strategies for RFID adoption when both retailers simultaneously make decisions on RFID adoption and sequentially make decisions on order quantity. If \( \alpha_{1} = \alpha_{2} = \alpha \): AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - s} ] \), NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - s} , + \infty ) \); if \( \alpha_{1} < \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - s}^{A} ] \), NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{A} ,c_{t2 - s}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \); if \( \alpha_{1} > \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - s}^{A} ] \), AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{A} ,c_{t1 - s}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{N} , + \infty ) \). Thus, we obtain the results of proposition 5.
(ii) Given that two retailers’ RFID adoption sequences are sequentially:
If the retailer 1 has adopted RFID: AA will be an equilibrium strategy if the retailer 2 adopts RFID, AN will be an equilibrium strategy if the retailer 2 refuses to adopt RFID. We take \( \Delta_{2 - s}^{A} = \pi_{2 - s}^{AA*} - \pi_{2 - s}^{AN*} \) as the retailer 2’s profit variation between AA and AN, and obtain that the retailer 2 adopts RFID when \( c_{t} \in (0,c_{t2 - s}^{A} ] \) while forgoes RFID adoption when \( c_{t} \in (c_{t2 - s}^{A} , + \infty ) \).
If the retailer 1 has not adopted RFID: NA will be an equilibrium strategy if the retailer 2 adopts RFID, NN will be an equilibrium strategy if the retailer 2 refuses to adopt RFID. We take \( \Delta_{2 - s}^{N} = \pi_{2 - s}^{NA*} - \pi_{2 - s}^{NN*} \) as the retailer 2’s profit variation between NA and NN, and obtain that the retailer 2 adopts RFID when \( c_{t} \in (0,c_{t2 - s}^{N} ] \) while forgoes RFID adoption when \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \).
Using backward induction, we first characterize the retailer 2’s RFID adoption decisions. According to comparing the relative sizes of \( c_{t2 - s}^{A} \) and \( c_{t2 - s}^{N} \), we obtain \( c_{t2 - s}^{N} - c_{t2 - s}^{A} = \frac{{(16 - 8\gamma^{2} )(1 - \alpha_{2} )(\alpha_{2} - \alpha_{1} )a}}{{(4 - \gamma^{2} )[(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} ]}} \). Specifically, if \( \alpha_{1} = \alpha_{2} = \alpha \), we derive \( c_{t2 - s}^{N} = c_{t2 - s}^{A} = \bar{c}_{t - s} \), leading to that the retailer 2 always adopts RFID when \( c_{t} \in (0,\bar{c}_{t - s} ] \) while forgoes RFID adoption when \( c_{t} \in (\bar{c}_{t - s} , + \infty ) \), regardless of whether the retailer 1 adopts RFID; if \( \alpha_{1} < \alpha_{2} \), we derive \( c_{t2 - s}^{N} - c_{t2 - s}^{A} > 0 \), hence, the retailer 2 always adopts RFID when \( c_{t} \in (0,c_{t2 - s}^{A} ] \), the two retailers have the opposite decisions on RFID adoption when \( c_{t} \in (c_{t2 - s}^{A} ,c_{t2 - s}^{N} ] \), the retailer 2 forgoes RFID adoption when \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \); if \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t2 - s}^{N} - c_{t2 - s}^{A} < 0 \), hence, the retailer 2 always adopts RFID when \( c_{t} \in (0,c_{t2 - s}^{N} ] \), the two retailers have the same decisions on RFID adoption when \( c_{t} \in (c_{t2 - s}^{N} ,c_{t2 - s}^{A} ] \), and the retailer 2 forgoes RFID adoption when \( c_{t} \in (c_{t2 - s}^{A} , + \infty ) \).
We turn to deal with the equilibrium RFID adoption strategies.
If \( \alpha_{1} = \alpha_{2} = \alpha \): given \( c_{t} \in (0,\bar{c}_{t - s} ] \), the retailer 2 always adopts RFID. Under such a circumstance, we take \( \Delta_{1 - s}^{A} = \pi_{1 - s}^{AA*} - \pi_{1 - s}^{NA*} \) as the retailer 1’s profit variation between AA and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,\bar{c}_{t - s} ] \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - s} ] \).
Given \( c_{t} \in (\bar{c}_{t - s} , + \infty ) \), the retailer 2 always refuses to adopt RFID. Under such a circumstance, we take \( \Delta_{1 - s}^{N} = \pi_{1 - s}^{AN*} - \pi_{1 - s}^{NN*} \) as the retailer 1’s profit variation between AN and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (\bar{c}_{t - s} , + \infty ) \), resulting in that NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - s} , + \infty ) \).
If \( \alpha_{1} < \alpha_{2} \): given \( c_{t} \in (0,c_{t2 - s}^{A} ] \), the retailer 2 always adopts RFID. Under such a circumstance, we take \( \Delta_{1 - s}^{A} = \pi_{1 - s}^{AA*} - \pi_{1 - s}^{NA*} \) as the retailer 1’s profit variation between AA and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - s}^{A} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - s}^{A} , + \infty ) \). We compare the relative sizes of \( c_{t1 - s}^{A} \) and \( c_{t2 - s}^{A} \), and then obtain \( c_{t2 - s}^{A} - c_{t1 - s}^{A} = \frac{{(\alpha_{2} - \alpha_{1} )c_{m} }}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}} > 0 \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - s}^{A} ] \) and NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{A} ,c_{t2 - s}^{A} ] \).
Given \( c_{t} \in (c_{t2 - s}^{A} ,c_{t2 - s}^{N} ] \), the two retailers have the opposite decisions on RFID adoption. Under such a circumstance, we take \( \Delta_{1 - s}^{NA} = \pi_{1 - s}^{AN*} - \pi_{1 - s}^{NA*} \) as the retailer 1’s profit variation between AN and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - s}^{NA} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - s}^{NA} , + \infty ) \). We compare the relative sizes of \( c_{t2 - s}^{A} \) and \( c_{t1 - s}^{NA} \), and then obtain \( c_{t2 - s}^{A} - c_{t1 - s}^{NA} = \frac{{2c_{m} }}{(2 + \gamma )}\left( {\frac{{\alpha_{2} - \alpha_{1} }}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}}} \right) > 0 \), resulting in that NA is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{A} ,c_{t2 - s}^{N} ] \). Where \( c_{t1 - s}^{NA} = \frac{{c_{m} }}{(2 + \gamma )}\left( {\frac{{\gamma \alpha_{2} }}{{(1 - \alpha_{2} )}} + \frac{{2\alpha_{1} }}{{(1 - \alpha_{1} )}}} \right) \).
Given \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \), the retailer 2 always refuses to adopt RFID. Under such a circumstance, we take \( \Delta_{1 - s}^{N} = \pi_{1 - s}^{AN*} - \pi_{1 - s}^{NN*} \) as the retailer 1’s profit variation between AN and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - s}^{N} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - s}^{N} , + \infty ) \). We compare the relative sizes of \( c_{t2 - s}^{N} \) and \( c_{t1 - s}^{N} \), and then obtain \( c_{t2 - s}^{N} - c_{t1 - s}^{N} = \frac{{(4 - \gamma^{2} )\left[ {(1 - \alpha_{1} )^{2} - (1 - \alpha_{2} )^{2} } \right]a}}{{(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} }} + \frac{{(\alpha_{2} - \alpha_{1} )c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}} > 0 \), then NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \).
If \( \alpha_{1} > \alpha_{2} \): given \( c_{t} \in (0,c_{t2 - s}^{N} ] \), the retailer 2 always adopts RFID. Under such a circumstance, we take \( \Delta_{1 - s}^{A} = \pi_{1 - s}^{AA*} - \pi_{1 - s}^{NA*} \) as the retailer 1’s profit variation between AA and NA, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - s}^{A} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - s}^{A} , + \infty ) \). We compare the relative sizes of \( c_{t2 - s}^{N} \) and \( c_{t1 - s}^{A} \), as \( c_{t2 - s}^{N} - c_{t1 - s}^{A} = \left( {\frac{{(16 - 8\gamma^{2} )(1 - \alpha_{2} )a}}{{(4 - \gamma^{2} )[(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} ]}} + \frac{{c_{m} }}{{(1 - \alpha_{2} )(1 - \alpha_{1} )}}} \right)(\alpha_{2} - \alpha_{1} ) < 0 \), leading to that AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - s}^{N} ] \).
Given \( c_{t} \in (c_{t2 - s}^{N} ,c_{t2 - s}^{A} ] \), the two retailers have the same decisions on RFID adoption. Under such a circumstance, we take \( \Delta_{1 - s}^{AN} = \pi_{1 - s}^{AA*} - \pi_{1 - s}^{NN*} \) as the retailer 1’s profit variation between AA and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - s}^{AN} ] \) while forgoes RFID when \( c_{t} \in (c_{t1 - s}^{AN} , + \infty ) \). We compare the relative size of \( c_{t1 - s}^{AN} \) and \( c_{t2 - s}^{A} \), as \( c_{t1 - s}^{AN} - c_{t2 - s}^{A} = \left( {\frac{{2(4 - 2\gamma^{2} )(1 - \alpha_{1} )a}}{{(2 - \gamma )\left[ {(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} } \right]}} + \frac{{2c_{m} }}{{(2 - \gamma )(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)(\alpha_{1} - \alpha_{2} ) > 0 \), resulting in that AA is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{N} ,c_{t2 - s}^{A} ] \). Where \( c_{t1 - s}^{AN} = \left( {\frac{{4v_{s} }}{{(2 - \gamma )(1 - \alpha_{1} )}} - \frac{{2\gamma v_{s} }}{{(2 - \gamma )(1 - \alpha_{2} )}} - 1} \right)a + \left( {\frac{{2\alpha_{1} }}{{(2 - \gamma )(1 - \alpha_{1} )}} - \frac{{\gamma \alpha_{2} }}{{(2 - \gamma )(1 - \alpha_{2} )}}} \right)c_{m} \).
Given \( c_{t} \in (c_{t2 - s}^{A} , + \infty ) \), the retailer 2 always refuses to adopt RFID. Under such a circumstance, we take \( \Delta_{1 - s}^{N} = \pi_{1 - s}^{AN*} - \pi_{1 - s}^{NN*} \) as the retailer 1’s profit variation between AN and NN, and derive that the retailer 1 adopts RFID when \( c_{t} \in (0,c_{t1 - s}^{N} ] \) while refuses to adopt RFID when \( c_{t} \in (c_{t1 - s}^{N} , + \infty ) \). We compare the relative sizes of \( c_{t1 - s}^{N} \) and \( c_{t2 - s}^{A} \), as \( c_{t1 - s}^{N} - c_{t2 - s}^{A} = \left( {\frac{{(8 - 4\gamma^{2} )(1 - \alpha_{1} )a}}{{2\left[ {(4 - \gamma^{2} )(1 - \alpha_{1} )^{2} - 4\gamma (1 - \alpha_{1} )(1 - \alpha_{2} ) + 4(1 - \alpha_{2} )^{2} } \right]}} + \frac{{c_{m} }}{{(1 - \alpha_{1} )(1 - \alpha_{2} )}}} \right)(\alpha_{1} - \alpha_{2} ) > 0 \), bringing about that AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{A} ,c_{t1 - s}^{N} ] \) and NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{N} , + \infty ) \).
Consequently, we obtain the equilibrium strategies for RFID adoption when both retailers simultaneously make decisions on RFID adoption and sequentially make decisions on order quantity. If \( \alpha_{1} = \alpha_{2} = \alpha \): AA is an equilibrium strategy when \( c_{t} \in (0,\bar{c}_{t - s} ] \), NN is an equilibrium strategy when \( c_{t} \in (\bar{c}_{t - s} , + \infty ) \); if \( \alpha_{1} < \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t1 - s}^{A} ] \), NA is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{A} ,c_{t2 - s}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \); if \( \alpha_{1} > \alpha_{2} \), AA is an equilibrium strategy when \( c_{t} \in (0,c_{t2 - s}^{A} ] \), AN is an equilibrium strategy when \( c_{t} \in (c_{t2 - s}^{A} ,c_{t1 - s}^{N} ] \), NN is an equilibrium strategy when \( c_{t} \in (c_{t1 - s}^{N} , + \infty ) \). Thus, we find that when both retailers sequentially make order quantity decisions, whether the two retailers adopt RFID simultaneously or sequentially does not affect the equilibrium strategies for RFID adoption.
Proof of Lemma 1
When \( \alpha_{1} = \alpha_{2} = \alpha \), we have \( \bar{c}_{t - n} = \bar{c}_{t - s} = \bar{c}_{t} = {{\alpha c_{m} } \mathord{\left/ {\vphantom {{\alpha c_{m} } {(1 - \alpha )}}} \right. \kern-0pt} {(1 - \alpha )}} \); when \( \alpha_{1} < \alpha_{2} \), we have \( \left( {{{2v_{n} } \mathord{\left/ {\vphantom {{2v_{n} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} - {{\gamma v_{n} } \mathord{\left/ {\vphantom {{\gamma v_{n} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} - {{(2 - \gamma )} \mathord{\left/ {\vphantom {{(2 - \gamma )} 2}} \right. \kern-0pt} 2}} \right)a < 0 \) and \( \left( {{{2v_{s} } \mathord{\left/ {\vphantom {{2v_{s} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} - {{4\gamma v_{s} } \mathord{\left/ {\vphantom {{4\gamma v_{s} } {(1 - \alpha_{1} )(4 - \gamma^{2} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )(4 - \gamma^{2} )}} - {{(4 - \gamma^{2} - 2\gamma )} \mathord{\left/ {\vphantom {{(4 - \gamma^{2} - 2\gamma )} {(4 - \gamma^{2} )}}} \right. \kern-0pt} {(4 - \gamma^{2} )}}} \right)a > 0 \), hence we obtain \( c_{t2 - n}^{N} - c_{t2 - s}^{N} < 0 \); when \( \alpha_{1} > \alpha_{2} \), we derive \( c_{t1 - n}^{N} - c_{t1 - s}^{N} = (v_{n} - v_{s} )\left( {{2 \mathord{\left/ {\vphantom {2 {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} - {\gamma \mathord{\left/ {\vphantom {\gamma {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}}} \right)a > 0 \).
Proof of Proposition 6(i)
Given \( \alpha_{1} = \alpha_{2} = \alpha \), we compare with the retailer 1’s profits under different ordering-timing strategies.
When \( c_{t} \in (0,\bar{c}_{t} ] \), we obtain \( \pi_{1 - s}^{AA*} - \pi_{1 - n}^{AA*} = {{\gamma^{4} (a - c_{m} - c_{t} )^{2} } \mathord{\left/ {\vphantom {{\gamma^{4} (a - c_{m} - c_{t} )^{2} } {32(2 - \gamma^{2} )(2 + \gamma )^{2} }}} \right. \kern-0pt} {32(2 - \gamma^{2} )(2 + \gamma )^{2} }} > 0 \); when \( c_{t} \in (\bar{c}_{t} , + \infty ) \), we obtain \( \pi_{1 - s}^{NN*} - \pi_{1 - n}^{NN*} = (2 - \gamma )^{2} \left( {{1 \mathord{\left/ {\vphantom {1 {4(16 - 8\gamma^{2} )}}} \right. \kern-0pt} {4(16 - 8\gamma^{2} )}} - {1 \mathord{\left/ {\vphantom {1 {4(4 - \gamma^{2} )^{2} }}} \right. \kern-0pt} {4(4 - \gamma^{2} )^{2} }}} \right)\left( {a - {{c_{m} } \mathord{\left/ {\vphantom {{c_{m} } {(1 - \alpha )}}} \right. \kern-0pt} {(1 - \alpha )}}} \right)^{2} > 0 \). Thus, the retailer 1 prefers to order sequentially. In a similar way, we derive that the retailer 2 prefers to order simultaneously.
Proof of Proposition 6(ii)
From Proposition 6(i), we obtain that when \( c_{t} \in (0,\bar{c}_{t} ] \), the retailer 1 prefers to order sequentially; for the retailer 2, ordering simultaneously will be more beneficial than ordering sequentially. Therefore, a transfer payment should be existed to achieve a win–win situation. Taking \( \pi_{n}^{AA*} = \pi_{1 - n}^{AA*} + \pi_{2 - n}^{AA*} \) and \( \pi_{s}^{AA*} = \pi_{1 - s}^{AA*} + \pi_{2 - s}^{AA*} \) as the retailers’ total profits under ordering simultaneously and ordering sequentially, respectively. We obtain \( \pi_{n}^{AA*} - \pi_{s}^{AA*} > 0 \), hence ordering simultaneously can bring the retailers’ more total profits when \( c_{t} \in (0,\bar{c}_{t} ] \). The retailer 2 should share his profit \( F \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{AA*} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{AA*} ] \) to the retailer 1 to achieve Pareto improvement.
When \( c_{t} \in (\bar{c}_{t} , + \infty ) \), the proof is similar to the case when \( c_{t} \in (0,\bar{c}_{t} ] \). Therefore we derive when \( c_{t} \in (\bar{c}_{t} , + \infty ) \), ordering simultaneously can bring the retailers’ more total profits. The retailer 2 should share his profit \( F \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} ] \) to the retailer 1 to achieve Pareto improvement.
1.8 Summary of abbreviations in Proposition 6
Proof of Proposition 7(i)
Given \( \alpha_{1} < \alpha_{2} \), we compare with the retailer 1’s profits under different ordering-timing strategies.
When \( c_{t} \in (0,c_{t2 - n}^{N} ] \), the proof is similar to that of Proposition 6(i) and hence is omitted; when \( c_{t} \in (c_{t2 - n}^{N} ,c_{t2 - s}^{N} ] \), we obtain \( \pi_{1 - s}^{NA*} - \pi_{1 - n}^{NN*} \le 0 \) if \( \gamma \in (0,\overline{{\gamma_{1} }} ] \), while \( \pi_{1 - s}^{NA} - \pi_{1 - n}^{NN} > 0 \) otherwise; when \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \), we obtain \( \pi_{1 - s}^{NN*} - \pi_{1 - n}^{NN*} \le 0 \) if \( \gamma \in (0,\overline{{\gamma_{2} }} ] \), while \( \pi_{1 - s}^{NN} - \pi_{1 - n}^{NN} > 0 \) otherwise. In a similar way, we derive the retailer 2 always obtain higher profits by ordering simultaneously.
Proof of proposition 7(ii)
When \( c_{t} \in (0,\bar{c}_{t1}^{A} ] \), the proof is similar to that of proposition 6(ii) and hence is omitted.
When \( c_{t} \in (\bar{c}_{t1}^{A} ,c_{t2 - n}^{N} ] \), ordering simultaneously can bring the retailers’ more total profits. The retailer 2 should share his profit \( F \in [\underleftarrow F^{NA*} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NA*} ] \) to the retailer 1 to achieve Pareto improvement.
When \( c_{t} \in (c_{t2 - n}^{N} ,c_{t2 - s}^{N} ] \) and \( \gamma \in (\overline{{\gamma_{1} }} ,1] \), we obtain \( \pi_{s}^{NN*} < \pi_{n}^{NN*} \). Therefore, ordering simultaneously can bring the retailers’ more total profits when. The retailer 2 should share his profit \( F \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{N*} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{N*} ] \) to the retailer 1 to achieve Pareto improvement.
When \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \) and \( \gamma \in (\overline{{\gamma_{1} }} ,1] \): we obtain \( \pi_{s}^{NN*} \ge \pi_{n}^{NN*} \) if \( k \in (0,\overleftarrow {k} ] \). Therefore, ordering sequentially can bring the retailers’ more total profits. The retailer 1 should share his profit \( F \in [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} ] \) to the retailer 2 to achieve Pareto improvement. In addition, we obtain \( \pi_{s}^{NN*} < \pi_{n}^{NN*} \) if \( k \in (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{k} ,1) \), hence ordering simultaneously can bring the retailers’ more total profits. The retailer 2 should share his profit \( F \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} ] \) to the retailer 1 to achieve Pareto improvement. Where \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NA*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{1 - s}^{NA*} = \pi_{1 - n}^{NA*} } \right\} \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NA*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{2 - n}^{NA*} = \pi_{2 - s}^{NA*} } \right\} \), \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{N*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{1 - n}^{NN*} = \pi_{1 - s}^{NA*} } \right\} \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{N*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{2 - n}^{NN*} = \pi_{2 - s}^{NA*} } \right\} \), \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{1 - s}^{NN*} = \pi_{1 - n}^{NN*} } \right\} \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{NN*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{2 - n}^{NN*} = \pi_{2 - s}^{NN*} } \right\} \).
1.9 Summary of abbreviations in Proposition 7
\( \overline{{\gamma_{1} }} = \mathop {\arg }\limits_{\gamma } \left\{ {\pi_{1 - s}^{NA*} = \pi_{1 - n}^{NA*} } \right\} \), \( \overline{{\gamma_{2} }} = \mathop {\arg }\limits_{\gamma } \left\{ {\pi_{1 - s}^{NN*} = \pi_{1 - n}^{NN*} } \right\} \), \( \overleftarrow {k} = \mathop {\arg }\limits_{k} \{ \pi_{1 - s}^{NN*} + \pi_{2 - s}^{NN*} = \pi_{1 - n}^{NN*} + \pi_{2 - n}^{NN*} \} \).
Proof of Proposition 8(i)
Given \( \alpha_{1} > \alpha_{2} \), we compare with the retailer 1’s profits under different ordering-timing strategies, and obtain that he always obtain higher profits by ordering sequentially.
We compare with the retailer 2’s profits under different ordering-timing strategies. When \( c_{t} \in (0,c_{t1 - s}^{N} ] \), the proof is similar to that of Proposition 6(i) and hence is omitted; when \( c_{t} \in (c_{t1 - s}^{N} ,c_{t1 - n}^{N} ] \), we obtain \( \pi_{2 - n}^{AN*} - \pi_{2 - s}^{NN*} \le 0 \) if \( \gamma \in (0,\overline{{\gamma_{3} }} ] \), while \( \pi_{2 - n}^{AN*} - \pi_{2 - s}^{NN*} > 0 \) otherwise; when \( c_{t} \in (c_{t1 - n}^{N} , + \infty ) \), we obtain \( \pi_{2 - n}^{NN*} - \pi_{2 - s}^{NN*} \le 0 \) if \( \gamma \in (0,\overline{{\gamma_{4} }} ] \), while \( \pi_{2 - n}^{NN*} - \pi_{2 - s}^{NN*} > 0 \) otherwise.
Proof of Proposition 8(ii)
When \( c_{t} \in (0,\bar{c}_{t2}^{A} ] \), the proof is similar to that of proposition 6(ii) and hence is omitted.
When \( c_{t} \in (\bar{c}_{t2}^{A} ,c_{t1 - s}^{N} ] \), ordering simultaneously can bring the retailers’ more total profits. The retailer 2 should share his profit \( F \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{F}^{AN*} ,\vec{F}^{AN*} ] \) to the retailer 1 to achieve Pareto improvement.
When \( c_{t} \in (c_{t1 - s}^{N} ,c_{t1 - n}^{N} ] \) and \( \gamma \in (\overline{{\gamma_{3} }} ,1] \), we obtain \( \pi_{2 - n}^{AN*} - \pi_{2 - s}^{NN*} > 0 \). Therefore, ordering sequentially can bring the retailers’ more total profits. The retailer 1 should share his profit \( F \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\rightarrow}$}}{F}^{N*} ,\vec{F}^{N*} ] \) to the retailer 2 to achieve Pareto improvement.
When \( c_{t} \in (c_{t2 - s}^{N} , + \infty ) \) and \( \gamma \in (\overline{{\gamma_{4} }} ,1] \): we obtain \( \pi_{s}^{NN*} \le \pi_{n}^{NN*} \) if \( k \in (1,\vec{k}] \). Therefore, ordering simultaneously can bring the retailers’ more total profits. The retailer 2 should share his profit \( F \in [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\rightarrow}$}}{F}^{NN*} ,\vec{F}^{NN*} ] \) to the retailer 1 to achieve Pareto improvement. Moreover, we obtain \( \pi_{s}^{NN*} > \pi_{n}^{NN*} \) if \( k \in (\vec{k}, + \infty ) \), hence ordering sequentially can bring the retailers’ more total profits. The retailer 1 should share his profit \( F \in [\vec{F}^{NN*} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\rightarrow}$}}{F}^{NN*} ] \) to the retailer 2 to achieve Pareto improvement. Where \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\rightarrow}$}}{F}^{AN*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{1 - s}^{AN*} = \pi_{1 - n}^{AN*} } \right\} \), \( \vec{F}^{AN*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{2 - n}^{AN*} = \pi_{2 - s}^{AN*} } \right\} \), \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\rightarrow}$}}{F}^{NN*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{1 - s}^{NN*} = \pi_{1 - n}^{NN*} } \right\} \), \( \vec{F}^{NN*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{2 - n}^{NN*} = \pi_{2 - s}^{NN*} } \right\} \), \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\rightarrow}$}}{F}^{N*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{2 - n}^{AN*} = \pi_{2 - s}^{NN*} } \right\} \), \( \vec{F}^{N*} = \mathop {\arg }\limits_{F} \left\{ {\pi_{1 - n}^{AN*} = \pi_{1 - s}^{NN*} } \right\} \).
1.10 Summary of abbreviations in Proposition 8
\( \overline{{\gamma_{3} }} = \mathop {\arg }\limits_{\gamma } \left\{ {\pi_{2 - s}^{AN*} = \pi_{2 - n}^{AN*} } \right\} \), \( \overline{{\gamma_{4} }} = \mathop {\arg }\limits_{\gamma } \left\{ {\pi_{2 - n}^{NN*} = \pi_{2 - s}^{NN*} } \right\} \), \( \overrightarrow {k} = \mathop {\arg }\limits_{k} \{ \pi_{1 - s}^{NN*} + \pi_{2 - s}^{NN*} = \pi_{1 - n}^{NN*} + \pi_{2 - n}^{NN*} \} \).
Proof of Proposition 9
The proof is similar to that of Proposition 1 and hence is omitted.
Proof of Proposition 10
The proof is similar to that of Proposition 5 and hence is omitted.
1.11 Summary of abbreviations in Proposition 10
\( \tilde{c}_{t} = {{\alpha c_{m} } \mathord{\left/ {\vphantom {{\alpha c_{m} } {(1 - \alpha )}}} \right. \kern-0pt} {(1 - \alpha )}} \), \( \tilde{c}_{t1}^{A} = \tilde{c}_{t1}^{N} = {{\alpha_{1} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{1} c_{m} } {(1 - \alpha_{1} )}}} \right. \kern-0pt} {(1 - \alpha_{1} )}} \), \( \tilde{c}_{t2}^{A} = \tilde{c}_{t2}^{N} = {{\alpha_{2} c_{m} } \mathord{\left/ {\vphantom {{\alpha_{2} c_{m} } {(1 - \alpha_{2} )}}} \right. \kern-0pt} {(1 - \alpha_{2} )}} \).
Proof of Proposition 11
The proof is similar to those of Propositions 7–8 and hence is omitted.
1.12 Summary of abbreviations in Proposition 11
\( \overline{{\tilde{\gamma }_{1} }} = \mathop {\arg }\limits_{{\tilde{\gamma }}} \left\{ {\tilde{\pi }_{1 - s}^{NN*} + \tilde{\pi }_{2 - s}^{NN*} = \tilde{\pi }_{1 - n}^{NN*} + \tilde{\pi }_{2 - n}^{NN*} } \right\} \), \( \overline{{\tilde{\gamma }_{2} }} = \mathop {\arg }\limits_{{\tilde{\gamma }}} \left\{ {\tilde{\pi }_{2 - n}^{NN*} = \tilde{\pi }_{2 - s}^{NN*} } \right\} \), \( \overleftarrow {{\tilde{k}}} = \mathop {\arg }\limits_{{\tilde{k}}} \{ \tilde{\pi }_{1 - s}^{NN*} + \tilde{\pi }_{2 - s}^{NN*} = \tilde{\pi }_{1 - n}^{NN*} + \tilde{\pi }_{2 - n}^{NN*} \} \), \( \overrightarrow {{\tilde{k}}} = \mathop {\arg }\limits_{{\tilde{k}}} \left\{ {\tilde{\pi }_{1 - s}^{NN*} + \tilde{\pi }_{2 - s}^{NN*} = \tilde{\pi }_{1 - n}^{NN*} + \tilde{\pi }_{2 - n}^{NN*} } \right\} \).
Rights and permissions
About this article
Cite this article
Zhang, LH., Wang, SS. Strategic analysis of RFID adoption sequences in a supply chain with Cournot competition: effects of ordering-timing strategies. Ann Oper Res 315, 2169–2208 (2022). https://doi.org/10.1007/s10479-020-03674-w
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-020-03674-w