1 Introduction

The problem of alternative-fuel station location is a recent, but very applicable research topic within location science. The plans from European Commission (2013) have emphasized the importance of the alternative-fuel station location problem. The topic is especially timely in the light of the recent European directive that requires Member States to provide a minimum coverage of refueling points for alternative-fuels (European Commission 2014). The directive forms a regulatory framework for alternative-fuels such as hydrogen, electricity, liquefied natural gas and compressed natural gas. What makes the problem of determining locations of alternative-fuel refuelling stations different from those of petrol stations is the scarcity of the current infrastructure. Hence, making appropriate decisions in the infrastructure investment and development is critical, especially in the scenarios of unexpected station failures. In practice, station failures occur randomly and drivers do not have the information of station failures before they travel. They may thus not complete their trip because of running out of fuel. In other words, the unexpected station failures may cause a significant impact on the performance of alternative-fuel station network. To mitigate the loss caused by the station failures, we consider the integration of station failures in the alternative-fuel station network design.

Models and algorithms for the alternative-fuel station location problem without station failures have been studied for a decade. The first model is introduced by Kuby and Lim (2005), known as the flow-refuelling location model (FRLM) with the concept of vehicle range. The authors observe that origin-destination data, rather than simple traffic count on edges, is required to model this problem properly. Multiple facilities may be required to serve individual journeys. It can be shown that it is not sufficient to consider only node locations for facilities, thus making the problem harder to solve. An integer programming formulation is provided in their work. The following conclusions were taken from their experimentation: (i) the longer the vehicles’ range the fewer facilities are needed to capture all the demand, but placing facilities only at nodes (junctions) may be unable to provide total coverage; (ii) there is a lack of convexity in the trade-off curve between the number of refuelling stations opened and the volume of flow they capture; (iii) greedy solution approaches tend to give very poor results; and (iv) unlike in maximum cover location problems, alternate optima do not often occur in the FRLM.

Upchurch et al. (2009) extend the above model to the case of capacitated facilities. A 25-city case study (“Arizona”) is used to illustrate the problem. Another important case study (“Florida” with 74 cities and 302 candidate locations) is introduced by Kuby et al. (2009). Lim and Kuby (2010) design some heuristic algorithms for the FRLM. There are three heuristics but with a common subroutine to evaluate the objective function value: (i) the “greedy-adding” or “add” algorithm simply adds one more facility in each iteration so as to maximise the increase in flow capture; (ii) the “greedy-adding with substitution” or “add-swap” algorithm also attempts in each iteration to replace an existing facility with a potential facility, and each iteration thus consists of an “add” and a “swap” move; and (iii) a genetic algorithm is based on the chromosome representation of a list of open facilities. The evaluation of a given solution is not a straightforward task. For a given solution, i.e. a set of facilities, the evaluation subroutine must evaluate every origin-destination path to see whether it is refuelable—if so, its flow is added to the objective function value. We note that all the algorithms are capable of handling pre-existing facilities. The algorithms are used to evaluate a smaller instance and the large “Florida” network as well. The authors found that the greedy algorithms perform quite well, nearly as well as the genetic algorithms (except for the case of a very short vehicle range), and are significantly faster.

Lately, research has focused on obtaining more efficient formulations and algorithms to the FRLM. The motivation for this is that the original Kuby and Lim (2005) model requires a massive pre-processing effort. All facility combinations must be checked whether they can refuel each origin-destination journey and the resulting coefficients inserted as input into the integer programming model. This takes an immense amount of time, so much so, that the authors could not even generate the integer programming model for the “Florida” instance, let alone solve it. Capar and Kuby (2012) put forward a more complex model, but without the above pre-processing requirement. This new formulation is in fact as fast as the greedy heuristics of Lim and Kuby (2010). Capar et al. (2013) offer a more efficient formulation than Capar and Kuby (2012). While the previous model uses a “node-cover/path-cover” logic, the authors propose an “arc-cover/path-cover” model. MirHassani and Ebrazi (2013) develop a flexible mixed-integer linear programming model based on a single-path to a multi-path formulation. The model is able to obtain the optimal solution much faster than the previous set cover version of the FRLM, and could solve the large-size networks under the maximum cover form within a reasonable computation time. Chung and Kwon (2015) extend the FRLM to handle multi-period planning for electric car charging station location, in which a pre-specified number of charging stations are sequentially placed on a freeway network for a finite time. In this problem, time-dependent traffic flows increase with the growth of plug-in electric vehicle market. The objective is to maximise the total traffic volume covered over time. A case study with the real traffic flow data of the Korean Expressway network is used to evaluate the model. Li et al. (2016) develop a multi-period multi-path refueling location model, formulated as a mixed-integer linear program, to expand public electric vehicle charging network to serve growing intercity trips. The model captures the dynamics in the topological structure of the network with the emerging public electric vehicle market and obtains the cost-effective station roll-out scheme on both spatial and temporal dimensions. A heuristic based on genetic algorithm is constructed to solve the large-size instances. The efficiency of the model and algorithm is demonstrated on a real-world case study based on the geographic settings of South Carolina. Ghamami et al. (2016) propose a general corridor model, formulated as a mixed-integer program with nonlinear constraint, to optimally configure plug-in electric vehicle charging infrastructure for supporting long-distance intercity travel. The model aims to minimise a total system cost inclusive of infrastructure investment, battery cost and user cost. A specialized metaheuristic algorithm based on Simulated Annealing is developed to solve the large-size problem in a reasonable computation time. Tran et al. (2017a) develop an efficient heuristic algorithm for the FRLM. This algorithm is built based on solving the sequence of sub-problems that are restricted on a set of promising station candidates, and fixing a number of the best promising station locations. In addition, the authors integrate a parallel computing strategy into solving the set of sub-problems simultaneously. Comparison results show that the algorithm can achieve the optimal solutions for the tested instances with less computation time than CPLEX, and outperforms genetic algorithm and greedy algorithm in the literature.

Although models and algorithms for the various types of FRLM have been comprehensively explored, there are a few efforts in considering the impact of uncertainty to the FRLM. Mak et al. (2013) investigate demand uncertainty in a flow-interception location model. Robust optimisation models are developed to support the planning process for deploying battery swapping infrastructure. Jung et al. (2014) consider itinerary interception (instead of flow-interception), stochastic demand (known as dynamic service requests) and queuing delay for electric car recharging facility location problem in South Korea. Their model and solution method are constructed on a bi-level, simulation-optimisation framework that combines an upper level multiple-server allocation model with queuing delay and a lower level dispatch simulation. Tan and Lin (2014) study the problem of siting electric vehicle charging stations in a transportation network with demand uncertainty. A stochastic model of the flow capturing location and allocation problem is extended to solve this problem. The results show that the stochastic model is more realistic and captures the actual coverage of the demand. Bhatti et al. (2015) introduce the two-stage alternative-fuel service location model in the presence of endogenous demand learning time for the alternative-fuel charging service. In the model, charging service stations are sequentially deployed over two stages. The rate of service demand, considered to be uncertain, is fully learned at the end of the first stage. The demand learning time (or the length of the first stage) is determined by a service provider’s deployment action. The service provider then has the option to locate additional stations in the second stage. This model can deliver a service provider’s approximated expected profit within an error rate given by a network designer. Hosseini and MirHassani (2015) build a two-stage stochastic mixed-integer programming model for refueling station location problem (including uncapacitated and capacitated) under uncertainty of traffic flows. In this model, the first stage locates permanent stations and the second stage locates portable stations. A two-step heuristic algorithm is developed for solving efficiently the stochastic model. In particular, in the first step, two core sets, that are defined by the obtained solution of relaxed capacitated model, are used to reduce the size of problem. In the second step, the station locations are determined by a greedy iterative method on the restricted problem. The model and algorithm are evaluated on an intercity network for Arizona, the United States. The results show that the proposed algorithm performs extremely well in the capacitated problem and produces good quality solutions within a reasonable computation time. Recently, Wang et al. (2017) have developed a continuum approximation model for solving a dynamic facility location problem in a large-scale growing market. The model can produce the optimal facility location and the deployment time such that total cost for facility construction and customer service in a planning horizon is minimised.

In the literature of location science, reliable models have received considerable attention. For example, they are developed for the maximum covering problem (Daskin 1983; Camm et al. 2002), the p-median problem (Drezner 1987; Berman et al. 2007), the fixed-charge location problem (Snyder and Daskin 2005; Cui et al. 2010), and various supply chain systems (Qi et al. 2010; Peng et al. 2011). As for the aspect of failure assumption, there are two approaches for the assumption of facility failure probabilities, i.e., equal probabilities (Drezner 1987; Snyder and Daskin 2005) and unequal probabilities (Berman et al. 2007; Cui et al. 2010; O’Hanley et al. 2013). Reliable models for the unequal failure probabilities are more sophisticated than others. Lim et al. (2013) investigate the impact of misestimating the failure probabilities on facility location problem with random disruptions. As for the modelling aspect, in general, there are three typical approaches for the reliable problems, such as backup-and-fortification model (see Li et al. 2013), “level-r” assignment model (see Cui et al. 2010) and probability chains model (see O’Hanley et al. 2013). The former two approaches cannot be easily applied for the reliable FRLM problem, while the last approach can be extended to deal with the reliable network design. A comprehensive review of other facility location problems under uncertainty is available in Snyder (2006).

From the literature, it can be seen that the FRLM under the impact of station failures has not received an appropriate attention although the failures are always existing in practice and have a significant impact on the optimal station location of the FRLM. In this paper, we propose a mixed-integer non-linear programming (MINLP) model to optimally locate the alternative-fuel stations whose failure probability are given initially. In the model, total expected traffic volume is maximised such that all the constraints of the FRLM are satisfied. Based on the linearisation techniques, known as probability chains (O’Hanley et al. 2013; Tran et al. 2017b) in the reliable facility location model and piecewise-linear functions, we linearise the compound probability terms in the non-linear model to develop a linear version for solving the problem. In addition, the model is extended to deal with the reliable multi-period alternative-fuel station location problem. An efficient Tabu search algorithm is also constructed to solve the large-size instances. The efficacy of the linear model and the algorithm is tested on several benchmark instances of the FRLM, and a sensitivity analysis of failure probability is investigated as well.

The remainder of this paper is organized as follows. In Sect. 2, we present an MINLP model for the FRLM under impact of station failures, and an extension of this model for the reliable multi-period alternative-fuel station network design. Then, Sect. 3 describes the linearisation techniques used to build a linear version of the non-linear model. Next, Sect. 4 presents an efficient Tabu Search algorithm for solving the large-size instances. Section 5 shows our numerical experiments for the model and algorithm on the well-known benchmark instances, along with a sensitivity analysis of failure probability. Finally, some findings from our study and some future works are provided in Sect. 6.

2 The FRLM under impact of station failures

2.1 Formulation of the standard FRLM

In this section, we first present all notations of indices, sets, parameters and decision variables that have been used in the formulation of Capar et al. (2013) for the standard FRLM without station failures. Next, the assumptions for constructing the FRLM are provided. Finally, the formulation is described in detail.

Indices and sets:

i, j, k

Indices for nodes (i.e., station locations)

q

Index for paths (i.e., origin-destination pairs)

N

Set of nodes

Q

Set of paths

(j, k)

Directed arc starting from node j and ending at node k

\({A_{q}}\)

Set of directed arcs on path q, sorted from origin to destination and back to origin

\(K_{q}^{jk}\)

Set of candidate nodes that can refuel the directed arc \((j,k)\in {A}_{q}\)

Parameters:

R

Range of vehicles

\(f_{q}\)

Volume of traffic flow on path q

p

Number of stations to be located

Decision variables:

\(x_{i}=\left\{ \begin{array}{ll} 1 &{} \text {if station is located at node i,}\\ 0 &{} \text {otherwise.} \end{array}\right. \)

\(y_{q}=\left\{ \begin{array}{ll} 1 &{} \text {if the flow on path } q \text { is refuelled,}\\ 0 &{} \text {otherwise}. \end{array}\right. \)

The assumptions used to formulate the FRLM consist of the following

  • The traffic flow between an origin-destination pair is only through a single path (i.e., shortest path) and its volume is given.

  • Drivers have full knowledge of refuelling station locations along their path and know when to refuel in order to complete their trip without running out of fuel.

  • All vehicles have the same vehicle range R.

  • Only nodes in the network are considered to be refuelling station locations.

  • Refuelling stations are uncapacitated.

  • Fuel consumption is proportional to traveling distance.

Based on these assumptions, Capar et al. (2013) develop an arc-cover-path-cover formulation for the FRLM without station failures. The authors replace the usage of combination pre-generation in Kuby and Lim (2005) by the concept of that a path can be refuelled if all directed arcs on the round-trip path are served. For example, we consider a refuelling station location network on a path q (from A to D), \(G=(N_{q},A_{q})\) where \(N_{q}=\{\text {A,B,C,D}\}\) is a set of nodes on the path and \(A_{q}=\{\text {(A,B),(B,C),(C,D)}\}\) is a set of arcs on the path. The distances between nodes are shown in Fig. 1. A corresponding network of Capar et al. (2013) is presented by \(\overrightarrow{G}=(N_{q},\overrightarrow{A}_{q})\) where \(\overrightarrow{A}_{q}=\{\text {(A,B),(B,C),(C,D)},\text {(D,C),(C,B),(B,A)}\}\) is a set of directed arcs. Then, path q can be refuelled only if the traffic volumes in all the directed arcs are served. For each directed arc (j, k) on path q, a set of candidate sites \(K_{q}^{jk}\) which can refuel the arc has to be determined based on the vehicle range R. Assuming that \(R=100\), the set of candidate sites for directed arc (C, D) is {B, C}, since only if refuelling at station B or C we can drive to D without running out of fuel.

Fig. 1
figure 1

An example of the single-path based network of Capar et al. (2013)

Full size image

The arc-cover-path-cover mathematical model can be formulated as follows:

[FRLM]

$$\begin{aligned}&\text {max}\;\;{\textstyle {\displaystyle \sum _{{\displaystyle {\textstyle {\displaystyle {\scriptstyle q\in Q}}}}}f_{q}y_{q}}} \end{aligned}$$
(1)
$$\begin{aligned}&\text {s.t. }\,\sum _{i\in K_{q}^{jk}}x_{i}\ge y_{q},\,\,\,\forall q\in Q,\,(j,k)\in {A}_{q}, \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{{\displaystyle {\scriptstyle i}}\in N}x_{i}=p, \end{aligned}$$
(3)
$$\begin{aligned}&x_{i},y_{q}\in \left\{ 0,1\right\} ,\,\,\,\forall i\in N,q\in Q. \end{aligned}$$
(4)

The objective function (1) is to maximise the total traffic volume which can be refuelled. Constraints (2) assure that path q is refuelable if and only if every directed arc along the path is travelable after refuelling at one of the facilities built. Constraint (3) makes sure that only p facilities are located, while constraints (4) are to define binary variables.

In the literature review, there are four formulations for the FRLM without station failures [for example, Kuby and Lim (2005), Capar and Kuby (2012), MirHassani and Ebrazi (2013) and Capar et al. (2013)]. The model developed by Capar et al. (2013) is known as the most efficient formulation for the FRLM so far, since the number of variables (i.e., binary and continuous) and the number of constraints in this model are smaller than others (Tran et al. 2017a). Based on the formulation of Capar et al. (2013), we develop an MINLP model for the FRLM with station failures in the next section.

2.2 An MINLP model for the FRLM under impact of station failures

The design of alternative-fuel station network under impact of station failures is to optimally locate unreliable stations in order to maximise the total expected traffic volume served. Herein, we refer to the problem formally as UFRLM. In the problem, we consider failures due to random events (e.g., technical malfunctions, natural disasters, etc.) rather than the presence of an intelligent attacker (e.g., saboteur or terrorist). We assume that multiple stations with given failure probability can simultaneously fail and disrupted traffic flows can be served through remaining operational stations. A reliable estimation of the station failure probabilities may be based on the document of equipment’s potential failures in building the alternative-fuel stations, and/or the historical observation of operating station’s failure data in other networks. In this study, we assume that the estimation of station failure probabilities is perfectly accurate, and exogenously provided by users. Since stations have distantly geographical locations, a station failure may not affect to other station’s failure. We thus assume that the failure probabilities are only dependent on station location, and they are independent each other. The assumption of unexpected failures with station-dependent probabilities is commonly used for such reliable location models [for example, Cui et al. (2010), O’Hanley et al. (2013), Tran et al. (2017b), etc.]. In addition, although drivers have full knowledge of refuelling station locations along their path and know when to refuel in order to complete their trip without running out of fuel, they do not have information of station failures (due to randomly unexpected failures in practice). Hence, driver’s behaviour is presumed not to change under any scenario of station failure. To formulate the UFRLM, some additional notations are modified as follows.

Parameters:

\(\delta _{i}\)

Failure probability of station i

\(\bar{\delta _{i}}\)

Operational probability of station i (i.e., \(\bar{\delta }_{i}=1-\delta _{i}\))

\(K_{q}^{\ell }\)

Set of stations that can fuel the \(\ell \)th arc in \({A}_{q}\) on path q

\(n_{q}\)

The number of directed arcs on path q (i.e., \(n_{q}=|{A}_{q}|\))

Decision variables:

\(y_{q}^{\ell }\)

Operational probability of the \(\ell \)th arc belonging to path q

Then, an MINLP model for the FRLM under impact of station failures is formulated by:

[UFRLM-NLP]

$$\begin{aligned}&\text {max}\,{\textstyle {\displaystyle \sum _{{\displaystyle {\textstyle {\displaystyle {\scriptstyle q\in Q}}}}}f_{q}\left( \prod _{\ell =1}^{n_{q}}y_{q}^{\ell }\right) }} \end{aligned}$$
(5)
$$\begin{aligned}&\text {s.t. }\,1-\prod _{i\in K_{q}^{\ell }}(1-\bar{\delta }_{i}x_{i})\ge y_{q}^{\ell }\,\,\,\forall q\in Q,\,\ell =1,\ldots ,n_{q}, \end{aligned}$$
(6)
$$\begin{aligned}&\sum _{{\displaystyle {\scriptstyle i}}\in N}x_{i}=p, \end{aligned}$$
(7)
$$\begin{aligned}&x_{i}\in \left\{ 0,1\right\} \,\,\,\forall i\in N, \end{aligned}$$
(8)
$$\begin{aligned}&y_{q}^{\ell }\in [0,1]\,\,\,\forall q\in Q,\ \ell =1,\ldots ,n_{q}. \end{aligned}$$
(9)

The objective function (5) is the maximisation of total expected traffic volume, where non-linear element (i.e.,\({\displaystyle {\textstyle \prod _{\ell =1}^{n_{q}}}}y_{q}^{\ell }\)) represents successfully operational probability of path q. In particular, the probability is the product of operational probability of arcs belonging to the path. Constraints (6) determine the operational probability of the arcs along the path q (i.e., \(y_{q}^{\ell }\)) which depends on the operational probability of fuel stations that can fuel the arc. For each the \(\ell \)th arc on path q, the product \({\displaystyle {\textstyle \prod _{i\in K_{q}^{\ell }}}}(1-\bar{\delta }_{i}x_{i})\) determines the probability that the \(\ell \)th arc cannot be fuelled by any fuel station from the set of possible stations \(K_{q}^{\ell }\). Each expression \((1-\bar{\delta }_{i}x_{i})\) in the product equates to 1 if a fuel station is not located at site i\((x_{i}=0)\), or \(\delta _{i}\) if a fuel station is located at site i\((x_{i}=1)\). Therefore, the term \(1-{\displaystyle {\textstyle \prod _{i\in K_{q}^{\ell }}}}(1-\bar{\delta }_{i}x_{i})\) is the correct operational probability of path q. Constraint (7) is the same with (3) that only p facilities are located. Constraints (8) are to define binary location variables, while constraints (9) define operational probability variables for arcs along paths.

2.3 Reliable multi-period alternative-fuel station network design

The above-mentioned model is referred to as the single-period alternative-fuel station network design. In this section, we present a framework to deal with the reliable multi-period alternative-fuel station network design problem. Assume that there are T periods of network development \((t=1,\ldots ,T)\), the framework is implemented as follows. In the early period \((t=1)\) of alternative-fuel station network design, the UFRLM with the small number of station \(p_{1}\) and a low range of vehicles \(R_{1}\) is solved to find the optimal station locations. In the next period \((t=2)\) of alternative-fuel station network development, we keep \(p_{1}\) the optimal station locations obtained in the early period, and solve the UFRLM with the number of additional stations and a range of vehicles \(R_{2}\) (where \(R_{2}\) may be unequal to \(R_{1}\)). The procedure is continued until the maximum number of stations \(p_{max}\) is located. In other words, the final period \((t=T)\) of alternative-fuel station network design and development is completed.

The UFRLM in the early period of reliable multi-period alternative-fuel station network design is similar to the UFRLM-NLP. In the next periods, however, constraint (7) is replaced by two following constraints:

$$\begin{aligned}&\sum _{{\displaystyle {\scriptstyle i}}\in N\backslash N^{*}}x_{i}=\Delta p_{t}, \end{aligned}$$
(10)
$$\begin{aligned}&x_{i}=1\,\forall i\in N^{*}, \end{aligned}$$
(11)

where \(\Delta p_{t}\) is the number of additional stations at period t, and \(N^{*}\) represents a set of the optimal station locations located in the previous periods.

3 A linearised model for the UFRLM

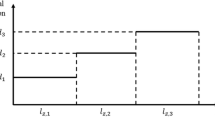
To solve the UFRLM-NLP, we need to handle the non-linear terms in the objective function (5) and the constraints (6). Firstly, for the non-linear terms of the objective function we let \(z_{q}={\displaystyle {\textstyle \prod _{\ell =1}^{n_{q}}}}y_{q}^{\ell },\forall q\in Q\) and take the logarithm of both sides: \(\text {ln}(z_{q})={\displaystyle {\textstyle \sum _{\ell =1}^{n_{q}}}}\text {ln}(y_{q}^{\ell }),\forall q\in Q.\) We then approximate the logarithmic functions by the piecewise-linear functions (see Fig. 2). Denote \(a_{k},\,k=0,1,\ldots ,m\) (\(a_{0}<a_{1}<\cdots <a_{m})\) as the break points of \(f(x)=\text {ln}(x)\), we obtain the piecewise-linear function for each logarithmic function by

$$\begin{aligned}&\lambda _{k}a_{k}+(1-\lambda _{k})a_{0}\le x\le \lambda _{k}a_{k+1}+(1-\lambda _{k})a_{m},\ k=0,1,\ldots ,m-1, \end{aligned}$$
(12)
$$\begin{aligned}&f(a_{k})+s_{k}(x-a_{k})-\text {M}(1-\lambda _{k})\le f(x)\le f(a_{k})+s_{k}(x-a_{k})\nonumber \\&\quad +\,\text {M}(1-\lambda _{k}),\ k=0,1,\ldots ,m-1, \end{aligned}$$
(13)
$$\begin{aligned}&{\displaystyle {\sum _{k=0}^{m-1}}}\lambda _{k}=1, \end{aligned}$$
(14)
$$\begin{aligned}&\lambda _{k}\in \{0,1\},\ k=0,1,\ldots ,m-1, \end{aligned}$$
(15)

where M is a large positive number, and \(s_{k}=\frac{f(a_{k+1})-f(a_{k})}{a_{k+1}-a_{k}}\) is the slope of function f(x) in range \([a_{k},a_{k+1}]\).

Fig. 2
figure 2

Piecewise linearisation for logarithmic function \(\text {ln}(x)\)

Full size image

We solve the set of constraints to find appropriate values \(\lambda _{k}\) for the approximation. Then, we can determine values \(\text {ln}(y_{q}^{\ell })\) (or \(\text {ln}(z_{q}))\) from \(y_{q}^{\ell }\) (or \(z_{q}\)); and contrariwise, \(y_{q}^{\ell }\) (or \(z_{q}\)) can be obtained from \(\text {ln}(y_{q}^{\ell })\) (or \(\text {ln}(z_{q}))\). In particular, with a given value \(y_{q}^{\ell }\) (or \(z_{q}\)), constraints (12) and (14)–(15) support to identify index k (i.e., \(\lambda _{k}=1\)) in which the corresponding value \(\text {ln}(y_{q}^{\ell })\) (or \(\text {ln}(z_{q}))\) can be obtained by constraints (13).

For example, we would like to approximate \(\text {ln}(x)\) at \(x=0.3\). If we consider \(m=2\) and \(a_{0}=0.01,a_{1}=0.5,a_{2}=1\) are the break points of \(\text {ln}(x)\), the set of constraints (12)–(15) becomes

$$\begin{aligned}&\lambda _{0}a_{0}+(1-\lambda _{0})a_{0}\le x\le \lambda _{0}a_{1}+(1-\lambda _{0})a_{2}, \end{aligned}$$
(16)
$$\begin{aligned}&\lambda _{1}a_{1}+(1-\lambda _{1})a_{0}\le x\le \lambda _{1}a_{2}+(1-\lambda _{1})a_{2}, \end{aligned}$$
(17)
$$\begin{aligned}&\text {ln}(a_{0})+s_{0}(x-a_{0})-\text {M}(1-\lambda _{0})\le \text {ln}(x)\le \text {ln}(a_{0})+s_{0}(x-a_{0})+\text {M}(1-\lambda _{0}), \end{aligned}$$
(18)
$$\begin{aligned}&\text {ln}(a_{1})+s_{1}(x-a_{1})-\text {M}(1-\lambda _{1})\le \text {ln}(x)\le \text {ln}(a_{1})+s_{1}(x-a_{1})+\text {M}(1-\lambda _{1}), \end{aligned}$$
(19)
$$\begin{aligned}&\lambda _{0}+\lambda _{1}=1, \end{aligned}$$
(20)
$$\begin{aligned}&\lambda _{0},\lambda _{1}\in \{0,1\}. \end{aligned}$$
(21)

By solving the set of constraints, we obtain the only solution as follows: \(\lambda _{0}=1\) and \(\lambda _{1}=0\). Obviously, constraints (16)–(17): \(a_{0}\le x\le a_{1},a_{0}\le x\le a_{2}\) are satisfied with \(a_{0}=0.01,a_{1}=0.5,a_{2}=1\) and \(x=0.3\); and constraint (19): \(-\,\text {M}\le \text {ln}(x)\le \text {M}\) is certainly satisfied. Then, constraint (18) computes the approximate value of \(\text {ln}(x)=\text {ln}(a_{0})+s_{0}(x-a_{0})=-\,2.29\). There is a gap between this approximate value and its actual value (i.e., \(\text {ln}(0.3)= -\,1.20\)). The gap can be reduced as increasing the number of break points m.

Next, we apply the probability chains technique, introduced by O’Hanley et al. (2013) and developed by Tran et al. (2017b), to linearise the non-linear terms of the constraints (6). The technique is based on the use of a specialized flow network to evaluate compound probability terms. We denote \(n_{q\ell }\) to be the number of stations in \(K_{q}^{\ell }\), \(i_{k}\) to be the kth site in \(K_{q}^{\ell }\) and introduce the following auxiliary variables:

\(u_{qk}^{\ell }=\) probability that the \(\ell \)th arc on path \(q\) can be refuelled by a fuel station located at the \(k\)th site in \(K_{q}^{\ell }\) (if no fuel station is located at \(i_{k}\), then \(u_{qk}^{\ell }=0\)),

\(v_{qk}^{\ell }=\) probability that the \(\ell \)th arc on path \(q\) cannot be refuelled by fuel stations located among the first \(k\) sites in \(K_{q}^{\ell }\) (if no fuel station is located at any site \(i_{h}\), \(h\le k\), then \(v_{qk}^{\ell }=1\)).

Fig. 3
figure 3

Graph representation of probability chain for hypothetical arc \(\ell \) on path q

Full size image

Then, the constraints (6) can be transformed into:

$$\begin{aligned}&1-v_{qn_{q\ell }}^{\ell }\ge y_{q}^{\ell }\,\,\,\forall q\in Q,\,\ell =1,\ldots ,n_{q}, \end{aligned}$$
(22)
$$\begin{aligned}&u_{q1}^{\ell }+v_{q1}^{\ell }=1\ \ \ \forall q\in Q,\ \ell =1,\ldots ,n_{q}, \end{aligned}$$
(23)
$$\begin{aligned}&u_{qk}^{\ell }+v_{qk}^{\ell }=v_{q(k-1)}^{\ell }\ \ \ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ k=2,\ldots ,n_{q\ell }, \end{aligned}$$
(24)
$$\begin{aligned}&u_{qk}^{\ell }\le \bar{\delta }_{i_{k}}x_{i_{k}}\ \ \ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ k=1,\ldots ,n_{q\ell }, \end{aligned}$$
(25)
$$\begin{aligned}&u_{qk}^{\ell }\le \bar{\delta }_{i_{k}}v_{q(k-1)}^{\ell }\ \ \ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ k=2,\ldots ,n_{q\ell }, \end{aligned}$$
(26)
$$\begin{aligned}&u_{qk}^{\ell },v_{qk}^{\ell }\ge 0\,\,\,\forall q\in Q,\ \ell =1,\ldots ,n_{q},k=1,\ldots ,n_{q\ell }. \end{aligned}$$
(27)

The model is to maximise the total expected traffic volume. In other words, it aims to maximise the operational probability of paths, which leads to maximise the operational probability of corresponding arcs on the paths (i.e., \(y_{q}^{\ell }\)). To do this, we minimise the failure probability of the arcs (i.e., \(v_{qn_{q\ell }}^{\ell }\)). Based on the technique of probability chains, we can compute correctly the failure probabilities. Figure 3 describes a general graph representation of probability chains for this problem. To understand the operational scheme of the probability chains we illustrate by an following example. Assume that sites 2, 1 and 3 can fuel the \(\ell \)th arc on path q, then \(K_{q}^{\ell }=\{2;1;3\}\), \(n_{q\ell }=3\), and \(i_{1}=2,i_{2}=1,i_{3}=3\). In addition, we assume that fuel stations are only located at sites 2 and 3, then \(x_{i_{1}}=1,x_{i_{2}}=0,x_{i_{3}}=1\). To compute the failure probability of the \(\ell \)th arc on path q, we would like to minimise the last term of the probability chains (i.e., \(v_{q3}^{\ell }\)). It means that we need to maximise possible values \(u_{q1}^{\ell }\),\(u_{q2}^{\ell }\) and \(u_{q3}^{\ell }\). Constraints (23)–(26) specify for \(x_{i_{1}}=1\) that \(u_{q1}^{\ell }=\bar{\delta _{2}}\) is the possible maximum value and then \(v_{q1}^{\ell }=\delta _{2}\) [due to constraints (24)]. Next, for \(x_{i_{2}}=0\) we obtain the possible maximum value \(u_{q2}^{\ell }=0\) and then \(v_{q2}^{\ell }=\delta _{2}\) [due to constraints (24)]. Finally, for \(x_{i_{3}}=1\) we obtain the possible maximum value \(u_{q3}^{\ell }=\delta _{2}\bar{\delta }_{3}\) and then \(v_{q3}^{\ell }=\delta _{2}\delta _{3}\) [due to constraints (24)]. This is also the correct failure probability of the \(\ell \)th arc on path q in this example (Fig. 4).

Fig. 4
figure 4

An illustrative example of probability chain

Full size image

Finally, let \(\alpha _{q}=\text {ln}(z_{q})\) and \(\beta _{q}^{\ell }=\text {ln}(y_{q}^{\ell })\), a linear version of the UFRLM-NLP is then derived as follows:

[UFRLM-LP]

$$\begin{aligned}&\text {max}\,{\textstyle {\displaystyle \sum _{{\displaystyle {\textstyle {\displaystyle {\scriptstyle q\in Q}}}}}f_{q}z_{q}}} \end{aligned}$$
(28)
$$\begin{aligned}&\text {s.t. }\,\alpha _{q}=\sum _{\ell =1}^{n_{q}}\beta _{q}^{\ell },\ \forall q\in Q, \end{aligned}$$
(29)
$$\begin{aligned}&\lambda _{k_{q}}a_{k_{q}}+(1-\lambda _{k_{q}})a_{0}\le z_{q}\le \lambda _{k_{q}}a_{k_{q}+1}+(1-\lambda _{k_{q}})a_{m},\ \forall q\in Q,\ k_{q}=0,1,\ldots ,m-1, \end{aligned}$$
(30)
$$\begin{aligned}&\text {ln}(a_{k_{q}})+s_{k_{q}}(z_{q}-a_{k_{q}})-\text {M}(1-\lambda _{k_{q}})\le \alpha _{q}\le \text {ln}(a_{k_{q}})+s_{k_{q}}(z_{q}-a_{k_{q}})+\text {M}(1-\lambda _{k_{q}}),\nonumber \\&\quad \forall q\in Q,\ k_{q}=0,1,\ldots ,m-1, \end{aligned}$$
(31)
$$\begin{aligned}&s_{k_{q}}=\frac{\text {ln}(a_{k_{q}+1})-\text {ln}(a_{k_{q}})}{a_{k_{q}+1}-a_{k_{q}}},\ \forall q\in Q,\ k_{q}=0,1,\ldots ,m-1, \end{aligned}$$
(32)
$$\begin{aligned}&{\displaystyle \sum _{k_{q}=0}^{m-1}}\lambda _{k_{q}}=1,\ \forall q\in Q, \end{aligned}$$
(33)
$$\begin{aligned}&\lambda _{h_{q\ell }}a_{h_{q\ell }}+(1-\lambda _{h_{q\ell }})a_{0}\le y_{q}^{\ell }\le \lambda _{h_{q\ell }}a_{h_{q\ell }+1}+(1-\lambda _{h_{q\ell }})a_{m},\ \forall q\in Q,\nonumber \\&\quad \ell =1,\ldots ,n_{q},\ h_{q\ell }=0,1,\ldots ,m-1, \end{aligned}$$
(34)
$$\begin{aligned}&\text {ln}(a_{h_{q\ell }})+s_{h_{q\ell }}(y_{q}^{\ell }-a_{h_{q\ell }})-\text {M}(1-\lambda _{h_{q\ell }})\le \beta _{q}^{\ell }\le \text {ln}(a_{h_{q\ell }})+s_{h_{q\ell }}(y_{q}^{\ell }-a_{h_{q\ell }})+\text {M}(1-\lambda _{h_{q\ell }}),\nonumber \\&\quad \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ h_{q\ell }=0,1,\ldots ,m-1, \end{aligned}$$
(35)
$$\begin{aligned}&s_{h_{q\ell }}=\frac{\text {ln}(a_{h_{q\ell }+1})-\text {ln}(a_{h_{q\ell }})}{a_{h_{q\ell }+1}-a_{h_{q\ell }}},\ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ h_{q\ell }=0,1,\ldots ,m-1, \end{aligned}$$
(36)
$$\begin{aligned}&{\displaystyle \sum _{h_{q\ell }=0}^{m-1}}\lambda _{h_{q\ell }}=1,\ \forall q\in Q,\ \ell =1,\ldots ,n_{q}, \end{aligned}$$
(37)
$$\begin{aligned}&1-v_{qn_{q\ell }}^{\ell }\ge y_{q}^{\ell },\,\forall q\in Q,\,\ell =1,\ldots ,n_{q}, \end{aligned}$$
(38)
$$\begin{aligned}&u_{q1}^{\ell }+v_{q1}^{\ell }=1,\ \forall q\in Q,\ \ell =1,\ldots ,n_{q}, \end{aligned}$$
(39)
$$\begin{aligned}&u_{qk}^{\ell }+v_{qk}^{\ell }=v_{q(k-1)}^{\ell },\ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ k=2,\ldots ,n_{q\ell }, \end{aligned}$$
(40)
$$\begin{aligned}&u_{qk}^{\ell }\le \bar{\delta }_{i_{k}}x_{i_{k}},\ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ k=1,\ldots ,n_{q\ell }, \end{aligned}$$
(41)
$$\begin{aligned}&u_{qk}^{\ell }\le \bar{\delta }_{i_{k}}v_{q(k-1)}^{\ell },\ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ k=2,\ldots ,n_{q\ell }, \end{aligned}$$
(42)
$$\begin{aligned}&\sum _{{\displaystyle {\scriptstyle i}}\in N}x_{i}=p, \end{aligned}$$
(43)
$$\begin{aligned}&x_{i}\in \left\{ 0,1\right\} ,\,\forall i\in N, \end{aligned}$$
(44)
$$\begin{aligned}&y_{q}^{\ell },z_{q}\in [0,1],\,\forall q\in Q,\ \ell =1,\ldots ,n_{q}, \end{aligned}$$
(45)
$$\begin{aligned}&\lambda _{k_{q}}\in \{0,1\},\ \forall q\in Q,\ k_{q}=0,1,\ldots ,m-1, \end{aligned}$$
(46)
$$\begin{aligned}&\lambda _{h_{q\ell }}\in \{0,1\},\ \forall q\in Q,\ \ell =1,\ldots ,n_{q},\ h_{q\ell }=0,1,\ldots ,m-1, \end{aligned}$$
(47)
$$\begin{aligned}&u_{qk}^{\ell },v_{qk}^{\ell }\ge 0,\,\forall q\in Q,\ \ell =1,\ldots ,n_{q},\ k=1,\ldots ,n_{q\ell }, \end{aligned}$$
(48)
$$\begin{aligned}&\alpha _{q},\beta _{q}^{\ell }\in [0,1],\,\forall q\in Q,\ \ell =1,\ldots ,n_{q}. \end{aligned}$$
(49)

In this linear model, the objective function (28) is still the maximisation of total expected traffic volume in the network. Constraints (29) represent the relationship of \(\alpha _{q}=\text {ln}(z_{q})\) and \(\beta _{q}^{\ell }=\text {ln}(y_{q}^{\ell })\). Constraints (30)–(33) are used to approximate values \(\text {ln}(z_{q})\) and \(z_{q}\), while constraints (34)–(37) are used to approximate values \(\text {ln}(y_{q}^{\ell })\) and \(y_{q}^{\ell }\). Constraints (38)–(42) determine the maximum operational probability of the arcs along path q (i.e., \(y_{q}^{\ell }\)) by probability chains. Constraint (43) allows only p facilities to be located. Constraints (44)–(49) are to define binary location variables, operational probability variables, and auxiliary variables for the approximation and linearisation.

The UFRLM-NLP model consists of a non-linear objective function, a set of \({\displaystyle {\textstyle {\displaystyle {\textstyle \sum _{q=1}^{Q}}}n_{q}}}\) non-linear constraints, a linear constraint, N binary variables and \({\displaystyle {\textstyle {\displaystyle {\textstyle \sum _{q=1}^{Q}}}n_{q}}}\) continuous variables. After performing the linearisation, the size of our model significantly increases up to \({\textstyle N+\left( Q+{\textstyle {\displaystyle {\textstyle {\displaystyle {\textstyle \sum _{_{q=1}}^{Q}}}}n_{q}}}\right) m}\) binary variables, \(2\left( Q+{\displaystyle {\textstyle {\displaystyle {\textstyle \sum _{_{q=1}}^{Q}}}}n_{q}}+\sum _{q=1}^{Q}\sum _{\ell =1}^{n_{q}}n_{q\ell }\right) \) continuous variables and \(Q\left( 3m+2\right) +3{\displaystyle {\textstyle {\displaystyle {\textstyle \sum _{_{q=1}}^{Q}}}}n_{q}}\left( m+1\right) +3\sum _{q=1}^{Q}\sum _{\ell =1}^{n_{q}}n_{q\ell }\) + 1 linear constraints. Therefore, it may not efficiently solve the large-size instances with a large range of vehicles by commercial mixed-integer linear programming solvers.

4 Tabu search for the UFRLM

Since the above-mentioned linearised model may not efficiently solve the large-size instances of the UFRLM due to increasing the significant number of auxiliary variables and constraints for the approximation and linearisation, we develop Tabu search for the large-size instances. Tabu search, introduced by Glover (1989), is a local search method that has been used to solve successfully a variety of optimization problems.

Fig. 5
figure 5

A solution representation of Tabu search algorithm for the UFRLM

Full size image

The first step of Tabu search design is to construct a solution representation for the UFRLM. In this paper, we use a \(1\times p\) row vector \(\text {X}=[\pi _{[1]},\pi _{[2]},\ldots ,\pi _{[i]},\ldots ,\pi _{[p]}]\) of located stations, where \(\pi _{[i]}\) is station located at the ith position, to represent the solution. Figure 5 presents an example of the solution representation.

In the next step, the k-opt neighborhood structure is used to generate the set of neighboring solutions for the search process. In particular, k stations in the set of the located stations are exchanged with the set of the non-located stations to construct a neighboring solution (see Fig. 6 for an example of 2-opt neighborhood structure). In the search process, the best improvement strategy is used. It means that the algorithm searches the whole set of generated neighboring solutions and determines the best solution. If the objective of the best solution is improved as compared with that of the current solution, the overall best solution is updated. Otherwise, it is chosen to become the incumbent solution for search process in next iteration. Following a move, the best solution in the neighboring solutions is added to a tabu list. The tabu list prohibits recent combinations of moves from being chosen in an attempt to prevent the search from cycling back to previously visited solutions. The length of this tabu list is determined by a preliminary testing.

Fig. 6
figure 6

An illustration of the 2-opt based neighborhood structure

Full size image

We propose an procedure to construct an initial good-quality solution for Tabu search. The procedure selects p the best potential stations based on their score that are calculated on three criteria: (i) station’s operational probability, (ii) total traffic volume travelling through station, and (iii) the number of arcs that station can refuel. Particularly, the score of station i (denoted by \(\omega _{i}\)) can be computed as follows.

$$\begin{aligned} \omega _{i}=\bar{\delta }_{i}\times \left( \sum _{j\in Q_{i}}f_{j}\right) \times \Omega _{i}, \end{aligned}$$
(50)

where \(Q_{i}\) is the set of paths that contain station i, and \(\Omega _{i}\) is the number of arcs that station i can refuel.

In Tabu search, computing the objective values of neighboring solutions at an iteration is usually time-consuming, especially in the large-size instances. Therefore, we implement an intelligent computation strategy to save on the computational effort of this operation. In the strategy, we only recalculate the \(y_{q}^{\ell }\) probabilities affected by the change. Specifically, assume that we exchange station i in the set of located stations and station j in the set of non-located stations. Let \(L_{q}^{i}\) and \(L_{q}^{j}\) be the sets of arcs on path q that stations i and j can refuel, respectively. Then, the probabilities affected by station i (i.e., \(y_{q}^{\ell },\;\forall q\in Q_{i},\;\ell \in L_{q}^{i}\)) are removed from the operational probability of path p (denoted by \(Y_{q}\)) in the objective value, while the probabilities affected by station j (i.e., \(y_{q}^{\ell },\;\forall q\in Q_{j},\;\ell \in L_{q}^{j}\)) are added into \(Y_{q}\) in the objective value. Let \(\widetilde{y}_{q}^{\ell }\) and \(\widetilde{Y}_{q}\) be the changed operational probability of arc \(\ell \) on path q, and that of path q, respectively. We denote the sets of removed-stations and added-stations via the exchanging process by \(\varPhi \) and \(\varPsi \), respectively. The intelligent computation procedure can then be described in Fig. 7.

In addition, we integrate a parallel computing strategy for evaluating the objective values of the set of neighboring solutions. We divide the solution set into H regions that are assigned into H cores of the CPU to perform parallel computing. The computation time of Tabu search with the parallel computing strategy (\(H=4\) cores) can be improved about 2.5 times. A flow chart of the proposed algorithm is presented in Fig. 8. In the algorithm, termination conditions include a maximum number of iterations, a number of iterations that the best solution found is not improved, and a time limit.

Fig. 7
figure 7

An intelligent computation procedure for re-evaluate the objective value

Full size image
Fig. 8
figure 8

A flow chart of Tabu search with parallel computing strategy for the UFRLM

Full size image

5 Numerical experiments

In this section, we investigate the efficacy of solving the UFRLM by the proposed solution methods. We evaluate the efficacy on three well-known benchmark datasets in which the failure probabilities of stations are uniformly generated in the range 0.01 to 0.20. Next, our solution approach for the multi-period alternative-fuel station network design is discussed. Finally, we do a sensitivity analysis of failure probabilities to study how variability in the probability of station failure affects solution robustness.

Our models and algorithm were implemented in Visual C++ in which the UFRLM-LP was solved by the IBM ILOG CPLEX version 12.4 callable library. To evaluate the solution quality of the models and algorithm, we modelled the UFRLM-NLP in AIMMS version 4.40 and used its outer approximation algorithm (Hunting 2011) for solving this non-linear problem. However, this algorithm does not ensure to obtain the global optimal solution as well. Hence, we used the enumeration method to support the evaluation of solution quality although it is applicable for the small-size instances. The computational experiments were run on the Microsoft Windows 7 Enterprise PC with an Intel Core i3-6100U processor (2.30 GHz per chip) and 8 GB of RAM.

5.1 Benchmark datasets

The experiments were carried out on three benchmark datasets of the FRLM, taken from the literature.

  • Hodgson dataset (Hodgson 1990): it is a 25-node alternative-fuel station location network. In the network, flow volumes are estimated using a gravity model, and then assigned to their shortest paths. The network has 25 candidate sites and 300 origin-destination pairs.

  • Florida dataset (Kuby et al. 2009): a Florida state highway network consists of 302 nodes (i.e., junctions) and 495 arcs. Each node serves as a candidate site. Of the 302 candidate sites, we consider 74 origin-destination nodes for trips. Due to the assumption of refuelable return trips, the network of 74 origin-destination nodes only requires 2701 unique origin-destination pairs. The network includes all inter-state, toll, U.S. highways and other important state highways. Florida’s inter-city volumes are based on a spatial interaction model, but short intra-zonal flows are excluded.

  • California dataset (Arslan et al. 2014): a California state road network consists of 339 nodes and 617 arcs. We consider all 1167 possible origin-destination pairs of the urban population centers in California, in which their population is more than 50,000 and their distance is not closer than 30 km. Flow volume on each pair is calculated using the gravity model of Hodgson (1990).

In the experiments of solving the UFRLM, a set of scenarios are generated by changing the range of vehicles R and the number of stations to be located p. The range of vehicles \(R=\) 4, 8, and 12 are applied for Hodgson network; 60, 100, and 200 miles are applied for Florida network; and 100, 150 and 200 km are applied for California network. For Hodgson network, two sets of various stations \(p=[1-10]\) and \(p=\{5;10;15;20;25\}\) are used to validate the accuracy of the proposed solution methods as compared with the enumeration method and AIMMS, respectively. For Florida and California networks, we use a set of stations \(p=\{10;20;30;40;50;60;70;80;90;100;150;200;250;300\}\) to evaluate the performance of our model and algorithm.

A design of experiment was applied to determine the best values for the parameters of the linearised model and Tabu search algorithm for solving the UFRLM. In particular, we solved the Hodgson (e.g., \(R=4,\ p=10,20\)), Florida (e.g., \(R=60,\ p=50,100,150\)) and California (e.g., \(R=100,\ p=50,100,150\)) instances by the proposed model and algorithm with the various values of parameters. For the linearised model, the number of break points (e.g., \(m=10,20,30\)) for the logarithmic function’s approximation was tested; while the maximum number of iterations (e.g., 15, 25, 35 for Hodgson instances, and 100, 200, 300 for other instances), the time limit (e.g., 5, 10, 15 min for Hodgson instances, and 30, 60, 90 min for other instances), the length of tabu list (e.g., 5, 10, 15) and the number of iterations that the best solution has no improvement (e.g., 5, 10, 15) are tested for Tabu search algorithm. From the preliminary experiment, for the UFRLM-LP we used the number of break points \(m=10\) for approximating the logarithmic functions in Hodgson instances, and \(m=20\) for both Florida and California instances. When applying Tabu search algorithm for Hodgson instances, we set the maximum number of iterations, the time limit and the length of tabu list to be 25, 5 min and 5, respectively. For Florida and California instances, the maximum number of iterations was set to 100 and 200 for the number of stations \(p\le 50\) and \(p>50\), respectively. For both the instances, the time limit was set to 1 h and the length of tabu list was set to 10. In addition, Tabu search algorithm terminates if there is no improvement on the best solution found during 10 iterations. The number of cores (\(H=4\)) was implemented for solving all the instances by this algorithm with parallel computing strategy. Due to the huge size of neighboring solution set, we only applied 1-opt neighborhood structure for these instances.

5.2 Computational results

According to our best knowledge, there is no model or algorithm for solving the UFRLM from the literature. To validate the accuracy of our solution method, we compare it with the enumeration method and the solution obtained by AIMMS’s outer approximation algorithm (Hunting 2011). The enumeration method cannot solve the large-size instances within a reasonable computation time, we thus make the comparison on Hodgson instances with the small number of stations \(p=[1-10]\). The AIMMS’s outer approximation algorithm can solve Hodgson instances with the larger number of stations \(p=\{5,10,15, 20,25\}\), but also fails to solve Florida and California instances (even with \(p=5\)) within the 8-h limit.

Table 1 Results for the enumeration method, AIMMS, UFRLM-LP and FRLM on Hodgson instances with the small number of station candidates
Full size table

Table 1 shows the comparison results of our model (UFRLM-LP), the enumeration method and AIMMS in terms of the solution quality and the computation time in seconds. We denote total normal traffic volume of a solution for the FRLM by “Normal”, and total expected traffic volume of a solution for the UFRLM by “Expect” (herein these values are measured by trips %). It can be seen that our model and AIMMS can obtain the optimal solutions (solved by the enumeration method) for these Hodgson instances. However, the average computation time of our model (0.84 s) is much smaller than that of the enumeration method (4642.44 s) and of AIMMS (87.13 s).

In this table, we also present the comparison of the located stations between the UFRLM-LP and the standard FRLM under the scenario of station failures. This comparison aims to investigate the loss of the optimal solutions obtained by the standard FRLM under the impact of station failures, which demonstrates the efficiency of our model’s solutions. The results show that the UFRLM-LP gives up a little on total “normal” traffic volume (1.62% lower on average), but improves on total “expected” traffic volume (2.53% higher). The impact of station failures on the solution, obtained by the standard FRLM, is proportional to the range of vehicles since increasing the range of vehicles implies the higher number of station candidates located in paths. For example, our model improves on total “expected” traffic volume 1.02%, 2.58% and 3.98% on average for \(R=4\), 8 and 12, respectively. The results demonstrate that our model produces more reliable solutions than the standard FRLM under the impact of station failures.

In addition, we compute the difference of total “normal” traffic volume (obtained by the standard FRLM) and total “expected” traffic volume (obtained by our model or algorithm), denoted by \(\triangle \). This value represents the minimum impact of station failures in the design of alternative-fuel station network. Table 1 shows that increasing the range of vehicles R and the number of station candidates p can cause more loss in total traffic volume (e.g., the average losses are 6.71, 11.27 and 12.24 for \(R=4,8\) and 12, respectively). The overall average loss is 10.07 for these instances.

Table 2 Comparison of AIMMS, Tabu search, UFRLM-LP and FRLM on Hodgson instances
Full size table

Next, Table 2 presents the results of solving Hodgson instances with the larger number of station candidates \(p=\{5,10,15,20,25\}\). It can be seen that the impact of station failures becomes greater as increasing the number of station candidates. The overall average loss for these instances increases up to 12.06. In this table, we make a comparison among our model and algorithm with AIMMS. Our model and algorithm outperform AIMMS on these instances, in terms of the solution quality (the average total expected traffic volume 65.79, 65.72 vs. 65.24) and the average computation time (1.13, 0.47 vs. 162.01 s). Tabu search algorithm can find the same solution as our model for almost the tested instances (except for the instance \(R=4\), \(p=15\)) within a faster average computation time. The results also show that our model (algorithm) reduces total “normal” traffic volume by 1.51% (0.93%) with an 2.97% (2.82%) increase in total “expected” traffic volume on average. Once again, this demonstrates the efficiency of our model and algorithm in producing reliable solutions for the UFRLM.

Table 3 Comparison of Tabu search, UFRLM-LP and FRLM on Florida instances
Full size table
Table 4 Comparison of Tabu search, UFRLM-LP and FRLM on California instances
Full size table

To evaluate the efficacy of our model and algorithm for solving the large-size instances, we solve Florida and California instances with the large number of station candidates. The obtained solutions are still compared with those of the standard FRLM to demonstrate the impact of station failures on the large-size instances. From Tables 3 and 4, our model can improve on total “expected” traffic volume (12.93% and 22.64% for Florida and California instances, respectively) with a decrease in total “normal” traffic volume (1.67% and 2.14% for Florida and California instances, respectively) on average; while our algorithm can improve on total “expected” traffic volume (17.44% and 30.85% for Florida and California instances, respectively) with a decrease in total “normal” traffic volume (2.39% and 2.82% for Florida and California instances, respectively) on average. These show that impact of station failures on the performance of network design significantly increases for the large-size networks. It can be seen that the larger network size causes the larger loss for the UFRLM with the small number of station candidates (see values \(\Delta \)). The overall average loss are 4.93 and 4.95 for Florida and California instances, respectively.

In addition, the size of network affects to the computation time of our model. For example, the average computation time increases from 1.13 s for solving Hodgson instances up to 13,295.83 and 7100.69 s for solving Florida and California instances, respectively. Although increasing the number of stations does not change the size of linearised model, it significantly affects to the computation time. For Florida and California instances, the peak computation time is on \(p=100\) and \(p=40\), respectively. When we increase more the number of stations, the computation time starts to reduce. A similar trend is also applied for the Tabu search algorithm, but its peak computation time is on \(p=100\) or 150 for both the instances.

As compared with the Tabu search algorithm, it can be seen that our UFRLM-LP is outperformed in almost all tested instances, except for the instances with the largest number of stations (e.g., 250 and 300) in which our model can find the same solution within a less average computation time. For Florida instances, the average total “expected” traffic volumes obtained by the Tabu search algorithm and the UFRLM-LP are 92.77 and 89.35, respectively; while these values are 93.20 and 89.65 respectively for California instances. In summary, the results show that the Tabu search algorithm is better than the UFRLM-LP in terms of the solution quality and the computation time. Therefore, when solving the large-size instances of the UFRLM, we suggest to apply the Tabu search algorithm.

5.3 Discussion on multi-period alternative-fuel station network design

In this section, we evaluate the performance of the framework described in Sect. 2.3 for reliable multi-period alternative-fuel station network development on Hodgson instance. Assume that the development of the reliable station network includes three periods, i.e., the early period (\(t=1\)), the extension period (\(t=2\)) and the completed period (\(t=3\)). Due to the budget limit of building stations, the planner would like to locate 4 stations in the early period, 2 stations in the extension period, and 4 stations in the completed period. A range of vehicle \(R=4\) is applied in the early period, and \(R=8\) is used for both the remaining periods. At each period, we assume that the planner would like to maximise the percentage of total expected traffic flow which is independent from the network development in next periods.

Fig. 9
figure 9

An illustration of the reliable three-period station network design on Hodgson instance. a Hodgson network. b Hodgson network in the early period (\(t=1, R_1=4, p_1=4\)). c Hodgson network in the extension period (\(t=2, R_2=8, \triangle p_2=2\)). d Hodgson network in the completed period (\(t=3, R_3=8, \triangle p_3=4\))

Full size image

We then applied the proposed framework to locate alternative-fuel stations in three periods for Hodgson instance. Figure 9 shows the result of three-period station network development. It can be seen that the optimal station locations in the early period are the same with those of solving the UFRLM-LP with \(R=4\) and \(p=4\). However, in the next two periods (i.e., the extension period and the completed period) the optimal station locations are not the same with those of the single-period network design (i.e., solving the UFRLM-LP with \(R=8\) and \(p=6\), and the one with \(R=8\) and \(p=10\), respectively). Obviously, this is because we keep the number of optimal station locations obtained in the early-period network design for next periods (which may not belong the set of the optimal station locations as solving the UFRLM-LP any more). The percentages of total expected traffic volume obtained in the following two periods of reliable Hodgson network design (e.g., 46.95% and 62.70%) are smaller than the corresponding values of the single-period network design (e.g., 51.47% and 64.42%, respectively). Figure 10 illustrates the optimal station locations of the single-period Hodgson network design.

In summary, the framework described in Sect. 2.3 is an useful tool to deal with the reliable alternative-fuel station network design in the case that the future network development is unknown or implicit. Then, we try to maximise the percentage of total expected traffic volume in each development period. Otherwise, if the future network development is known, we can apply the single-period network design where the number of station locations at each period is built based on the optimal locations of the UFRLM-LP. For example, in above-mentioned Hodgson network design, we locate stations 14, 17, 19 and 20 (in the early period), stations 2 and 23 (in the extension period), and stations 4, 8, 9 and 10 (in the completed period).

Fig. 10
figure 10

An illustration of the optimal station locations for reliable Hodgson network design

Full size image

5.4 Sensitivity analysis of failure probabilities

In this section, we analyze the robustness of the UFRLM-LP solutions to variations in the failure probabilities and evaluate the possible impacts on solution quality of using inaccurate probability values. For example, the analysis is carried out on Hodgson instances with \(R=\{4,8,12\}\) and \(p=\{2,4,6,8,10\}\), with equal station failure probabilities \(\delta \) in the range \([0.0,0.05,\dots ,0.3]\).

Let \(X_{A}^{*}\) (\(X_{T}^{*}\)) be the optimal station locations obtained by the UFRLM-LP with an assumed (true) failure probability \(\delta _{A}\) (\(\delta _{T}\)). We denote by \(g(\cdot )\) the objective function value for a particular solution given that the true failure probability is \(\delta _{T}\). We define the relative percentage error in objective value when the assumed probability is \(\delta _{A}\) and the true probability is \(\delta _{T}\) as follows:

$$\begin{aligned} Error=\frac{g(X_{A}^{*})-g(X_{T}^{*})}{g(X_{T}^{*})}\times 100. \end{aligned}$$
(51)

Computational results of the robustness of the UFRLM-LP solutions are presented in Tables 5, 6 and 7 for each combination of assumed and true station failure probabilities. In the tables, the UFRLM-LP solution is robust to variations in failure probabilities if its corresponding error values are zero. We can see the robustness on two instances, i.e., \(R=4\), \(p=4\) and \(R=8\), \(p=2\), where all error values are zero. The robustness of the UFRLM-LP solutions reduces when increasing the range of vehicle R and/or the number of stations p. In particular, the number of zero-error values decreases significantly from \(R=4\) to \(R=12\), and especially at the maximum value of \(p=10\) there are only two zero-error values.

In Tables 5, 6 and 7, the last two columns report the average and maximum percentage error for each assumed probability value. The results recommend that in the case of small vehicle range (\(R=4\)) it is better to assume a small probability of failure for small values of p, and a large probability of failure for large values of p. That is because we have little room for recourse when resources are limited (small p). In this case, the best solution is to plan for normal operational conditions. On the other hand, there is more room to accommodate for potential failure when resources are greater (large p). The suggestion is not applied in the case of larger vehicle range (\(R=8\) or 12) where a clear trend is not found.

The maximum percentage error (31.11%) is found for \(R=12\), \(p=8\) as the failure probability is assumed to be zero (\(\delta _{A}=0\)) but in reality a high failure occurs (\(\delta _{T}=0.3)\). Percentage error is often quite significant for large vehicle range R and values of p when we design alternative-fuel station network assuming a low failure probability (\(\delta _{A}\le 0.1\)) but failures actually occur with high probability (\(\delta _{T}\ge 0.25\)). This finding is also applied for the case of assuming a high failure probability (\(\delta _{A}\ge 0.25\)) but failures actually occur with low probability (\(\delta _{T}\le 0.1\)).

Table 5 Solution robustness of the UFRLM-LP on Hodgson instances with \(R=4\)
Full size table
Table 6 Solution robustness of the UFRLM-LP on Hodgson instances with \(R=8\)
Full size table
Table 7 Solution robustness of the UFRLM-LP on Hodgson instances with \(R=12\)
Full size table

6 Conclusions and future work

Under the impact of station failures, the design of reliable alternative-fuel station network becomes more difficult and challenging. However, this issue has not received an appropriate attention by researchers. In the paper, we propose for the first time an MINLP model to support the design of such the alternative-fuel station network. This model optimally locates the unreliable refuelling stations to maximise the total expected traffic volume served, assuming that multiple stations can simultaneously fail and that disrupted traffic flows can then be served through remaining operational stations. We apply the linearisation techniques, i.e., probability chains and piecewise-linear functions, to linearise the compound probability terms in the MINLP model to solve this problem efficiently. We also propose a Tabu search algorithm, integrated with a parallel computing strategy and an intelligent procedure for saving computation time of re-evaluating the objective function values, in order to solve the large-size instances. In addition, an extension of the MINLP model is developed to deal with reliable multi-period alternative-fuel station network design where the future network development is unknown or implicit. Computational results show the efficiency and effectiveness of the proposed models and algorithm for solving the large-size instances. Our model can produce more reliable alternative-fuel station network under risk of station failures than the standard location model. Moreover, a sensitivity analysis was carried out to achieve a preliminary understanding of how variability in the probability of station failures affects solution robustness.

In this study, we focus on the impact of station failures on alternative-fuel station network design under the assumption that driver’s behaviour is presumed not to change under scenarios of station failure. Hence, a study for investigating the impact of arc failures (i.e., road failures) and/or modelling driver’s behaviours on this network design may be an interesting future work. In addition, it is important to determine a theoretical bound for the optimal solution of the alternative-fuel station location problem under impact of station failures so that the evaluation of solution quality obtained by the linearised model and Tabu search algorithm is more appropriate. From the successful results obtained, possible future works are to develop the similar models for solving the variants of the alternative-fuel station location problem under impact of station failures, for example, the capacitated FRLM (Upchurch et al. 2009), the FRLM with deviation(Kim and Kuby 2012, 2013), and the budget-constrained FRLM (Badri-Koohi and Tavakkoli-Moghaddam 2012; MirHassani and Ebrazi 2013). We could extend the model to solve the multi-objective FRLM (Wang and Wang 2010) with station failure probabilities as well.