An asymptotic expansion for the normalizing constant of the Conway–Maxwell–Poisson distribution

Abstract

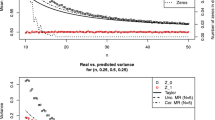
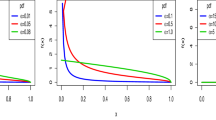
The Conway–Maxwell–Poisson distribution is a two-parameter generalization of the Poisson distribution that can be used to model data that are under- or over-dispersed relative to the Poisson distribution. The normalizing constant $Z(\lambda ,\nu )$ is given by an infinite series that in general has no closed form, although several papers have derived approximations for this sum. In this work, we start by using probabilistic argument to obtain the leading term in the asymptotic expansion of $Z(\lambda ,\nu )$ in the limit $\lambda \rightarrow \infty$ that holds for all $\nu >0$. We then use an integral representation to obtain the entire asymptotic series and give explicit formulas for the first eight coefficients. We apply this asymptotic series to obtain approximations for the mean, variance, cumulants, skewness, excess kurtosis and raw moments of CMP random variables. Numerical results confirm that these correction terms yield more accurate estimates than those obtained using just the leading-order term.

Further proofs

1.1 Proof of Theorem 1

The generalized hypergeometric function is defined by

$$\begin{aligned} {}_pF_q\left( \begin{array}{c} a_1,\ldots ,a_p \\ b_1,\ldots ,b_q \end{array};z\right) =\sum _{k=0}^\infty \frac{(a_1)_n\cdots (a_p)_n}{(b_1)_n\cdots (b_q)_n}\frac{z^n}{n!}, \end{aligned}$$

provided none of the $b_j$ are nonpositive integers, where the Pochhammer symbol is $(a)_0=1$ and $(a)_n=a(a+1)(a+2)\cdots (a+n-1)$, $n\ge 1$. In the case that $p\le q$ the infinite series converges for all finite values of z and defines an entire function. For more details see §16.2 in the NIST Library (2016). As noted by Nadarajah (2009), $Z(\lambda ,\nu )=_0F_{\nu -1}(;1,\ldots ,1;\lambda )$ for integer $\nu$. Thus, we can exploit the well-developed theory for asymptotics of the generalized hypergeometric function to obtained an asymptotic expansion for $Z(\lambda ,\nu )$ when $\nu$ is an integer. Indeed, 16.11.9 in the NIST Library (2016) can be used to write down the entire expansion for integer $\nu$. However, this expansion is only valid for integer $\nu$, and, since $b_1=\cdots =b_{\nu -1}=1$, the coefficients of the lower-order terms in the expansion must be obtained via a tedious limiting procedure. We can, however, make use of a recent work on the asymptotics of the generalized hypergeometric function to prove Theorem 1.

Proof of Theorem 1

We obtain the expansion (4) by appealing to results from the recent work of Lin and Wong (2017), in which the large z asymptotics of the generalized hypergeometric function ${}_pF_q\left( \begin{array}{c} a_1,\cdots ,a_p\\ b_1,\cdots ,b_q \end{array};z\right)$ are discussed. Here we will have $p=0$, all the $b_k=1$ and $q=\nu -1$. In the proof of Lemma 4.3 in Lin and Wong (2009) it is not essential that q is a nonnegative integer and below we copy the main steps.

Lin and Wong (2017) used as their starting point the integral representation 16.5.1 in the NIST Library (2016) of the generalized hypergeometric function. As mentioned in the introduction, the integral representation (3) is just a simple generalization of 16.5.1 in the NIST Library (2016). We rewrite it as

$$\begin{aligned} Z(\lambda ,\nu )=\frac{1}{2\pi i}\int _L\frac{\Gamma (t+1)\Gamma (-t)\left( -\lambda \right) ^t}{\left( \Gamma (t+1)\right) ^\nu }\, \mathrm{d}t, \end{aligned}$$

(29)

and use the inverse factorial expansion (again, see Lin and Wong (2017), or §2.2.2 in Paris and Kaminski (2001), and for more information about factorial series see Weniger (2010))

$$\begin{aligned} \left( \Gamma (t+1)\right) ^{-\nu }=\frac{\nu ^{\nu (t+1/2)}}{\left( 2\pi \right) ^{(\nu -1)/2}}\sum _{j=0}^\infty \frac{c_j}{\Gamma (\nu t+(1+\nu )/2+j)}, \end{aligned}$$

(30)

in the integral in (29) and combine this with the proof of Lemma 4.3 in Lin and Wong (2017). The result is asymptotic expansion (4).

To compute the $c_j$ we substitute the Stirling approximation

$$\begin{aligned} \Gamma (x)\sim \mathrm{e}^{-x}x^x\bigg (\frac{2\pi }{x}\bigg )^{1/2}\sum _{k=0}^\infty \frac{g_k}{x^k}, \quad x\rightarrow \infty , \end{aligned}$$

(see 5.11.3 in the NIST Library (2016) into both sides of (30). Here $g_0=1$, $g_1=\frac{1}{12}$, $g_2=\frac{1}{288}$, and further values are given in 5.11.4 – 5.11.6 in the NIST Library (2016). In this way we obtain large t asymptotic expansions for both sides of (30) and we can compare the coefficients to find the $c_j$. Computer algebra is very useful for this process; we used Maple to obtain the first eight coefficients. The result is:

$$\begin{aligned} c_0&=1,\quad c_1=\frac{\nu ^2-1}{24}, \quad c_2=\frac{\nu ^2-1}{1152}\left( \nu ^2+23\right) ,\nonumber \\ c_3&=\frac{\nu ^2-1}{414720}\left( 5\nu ^4-298\nu ^2+11237\right) ,\nonumber \\ c_4&=\frac{\nu ^2-1}{39813120}\left( 5\nu ^6-1887\nu ^4-241041\nu ^2+2482411\right) ,\nonumber \\ c_5&=\frac{\nu ^2-1}{6688604160}\left( 7\nu ^8-7420\nu ^6+1451274\nu ^4-220083004\nu ^2+1363929895\right) ,\nonumber \\ c_6&=\frac{\nu ^2-1}{4815794995200}\left( 35\nu ^{10}-78295\nu ^8+76299326\nu ^6+25171388146\nu ^4\right. \nonumber \\&\quad \left. -915974552561\nu ^2+4175309343349\right) ,\nonumber \\ c_7&=\frac{\nu ^2-1}{115579079884800}\left( 5\nu ^{12}-20190\nu ^{10}+45700491\nu ^8-19956117988\nu ^6\right. \nonumber \\&\quad \left. +7134232164555\nu ^4-142838662997982\nu ^2+525035501918789\right) . \end{aligned}$$

(31)

$\square$

1.2 Proof of Lemma 2

Let us first note two results that were derived using Stein’s method. Theorem 6 is proved in Stein (1986), whilst Theorem 7 is a special (and slightly simplified) case of the general bound of Theorem 3.5 of Gaunt (2015). The simplified bound is, however, sufficiently tight for the purpose of proving part (ii) of Lemma 2.

Theorem 6

Stein (1986). Let $X_1,\ldots ,X_n$ be i.i.d. random variables with ${\mathbb {E}}X_1=0$, ${\mathbb {E}}X_1^2=1$ and ${\mathbb {E}}|X_1|^3<\infty$. Set $W=\frac{1}{\sqrt{n}}\sum _{i=1}^nX_i$ and let $Z\sim N(0,1)$. Suppose $h:{\mathbb {R}}\rightarrow {\mathbb {R}}$ has a bounded first derivative on ${\mathbb {R}}$. Then

$$\begin{aligned} |{\mathbb {E}}[h(W)]-{\mathbb {E}}[h(Z)]|\le \frac{\Vert h'\Vert _\infty }{\sqrt{n}}\big (2+{\mathbb {E}}|X_1|^3\big ), \end{aligned}$$

where $\Vert h'\Vert _\infty =\sup _{x\in {\mathbb {R}}}|h'(x)|$.

Theorem 7

Gaunt (2015). Let $X_1,\ldots ,X_n$ and W be defined as in Theorem 6, but with the additional assumption that ${\mathbb {E}}|X_1|^6<\infty$. Suppose $h:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is an even function and is twice differentiable with first and second derivative bounded on ${\mathbb {R}}$. Then there exists a constant C independent of n such that

$$\begin{aligned} |{\mathbb {E}}[h(W)]-{\mathbb {E}}[h(Z)]|\le \frac{C}{n}\big (\Vert h'\Vert _\infty +\Vert h''\Vert _\infty )\big (1+|{\mathbb {E}}X_1^3|\big ){\mathbb {E}}|X_1|^6. \end{aligned}$$

Proof of Lemma 2

Let $X_\alpha \sim {\mathrm {Po}}(\alpha )$ and set $\tilde{X_\alpha }=\frac{X_\alpha -\alpha }{\sqrt{\alpha }}$. We shall suppose $\alpha \ge 1$ (later we shall let $\alpha \rightarrow \infty$). Also, let $Y_1,\ldots ,Y_{\lfloor \alpha \rfloor }$ be i.i.d. random variables following the ${\mathrm {Po}}\Big (\frac{\alpha }{\lfloor \alpha \rfloor }\Big )$ distribution, where the floor function $\lfloor x\rfloor$ is the greatest integer less than or equal to x. Then, by a standard result, $\sum _{i=1}^{\lfloor \alpha \rfloor }Y_i\sim {\mathrm {Po}}(\alpha )$, and so is equal in distribution to $X_\alpha$. Therefore $\tilde{X_\alpha }{\mathop {=}\limits ^{\mathcal {D}}}\frac{1}{\sqrt{\alpha }}\big (\sum _{i=1}^{\lfloor \alpha \rfloor }Y_i-\alpha \big )$. In order to apply Theorems 6 and 7, we note that

$$\begin{aligned} \tilde{X_\alpha }{\mathop {=}\limits ^{\mathcal {D}}}\frac{1}{\sqrt{\lfloor \alpha \rfloor }}\sum _{i=1}^{\lfloor \alpha \rfloor }\tilde{Y}_i, \end{aligned}$$

where

$$\begin{aligned} \tilde{Y_i}=\sqrt{\frac{\lfloor \alpha \rfloor }{\alpha }}\bigg (Y_i-\frac{\alpha }{\lfloor \alpha \rfloor }\bigg ), \quad i=1,\ldots ,\lfloor \alpha \rfloor . \end{aligned}$$

The random variables $\tilde{Y}_1,\ldots ,\tilde{Y}_n$ are i.i.d. with ${\mathbb {E}}\tilde{Y}_1=0$ and ${\mathbb {E}}\tilde{Y}_1^2=1$. The absolute moments of $\tilde{Y}_1$ up to sixth order are also finite and are ${\mathcal {O}}(1)$ as $\alpha \rightarrow \infty$. Parts (i) and (ii) of the lemma (for which different assumptions are made on the function h) now follow from applying Theorems 6 and 7 to bound the quantity $|{\mathbb {E}}[h(\tilde{X_\alpha })]-{\mathbb {E}}[h(Z)]|$ and noticing that the resulting bounds are of order ${\mathcal {O}}(\alpha ^{-1/2})$ and ${\mathcal {O}}(\alpha ^{-1})$, respectively, as $\alpha \rightarrow \infty$. $\square$