Abstract
Sustainable third-party reverse logistics has gradually risen to prominence as a component of contemporary commercial development as a result of the acceleration of global economic integration and the prominent growth of information technology in the logistics industry. In the procedure of sustainable third-party reverse logistics providers (S3PRLPs) selection, indeterminacy and conflict information bring great challenges to decision experts. In view of the significant superiority of q-rung orthopair fuzzy (q-ROF) set in expressing uncertain and vague assessment information, this essay designs a comprehensive assessment framework through merging the best and worst method (BWM), Multiplicative Multi-objective Optimization by Ratio Analysis with Full Multiplicative Form (MULTIMOORA) and weighted aggregated sum product assessment (WASPAS) method to address the S3PRLPs selection issue with entirely unknown weight information under q-ROF setting. Firstly, we present a novel score function for comparing q-ROF numbers after analyzing the inadequacies of previous works. Secondly, the q-ROF Frank interactive weighted average (q-ROFFIWA) and q-ROF Frank interactive weighted geometric (q-ROFFIWG) operators are advanced based on the constructed operations to take into consideration the interactive impact of information fusion procedure. Thirdly, the q-ROF-MULTIMOORA-WASPAS decision framework is built based on novel score function and the developed operators, in which the synthetic weights of the criterion are determined by the modified BWM and entropy weight method to reflect both the subjectivity of the decision expert and the objectivity of the decision information. Ultimately, an empirical example was used to evaluate S3PRLPs to demonstrate the applicability and feasibility of the developed methodology, and a comparative analysis was conducted with other existing methods to highlight its advantages in dealing with complex decision problems. The discussion from the research indicates that the developed methodology can be used to evaluate S3PRLPs and further improve the quality of logistics services for organizations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
People’s demand and standards for products gradually rise as a result of the mushroom growth development of global economic integration, the profound adjustment of world economic pattern, the continuous development of the current development pattern of mutual promotion of domestic and international double circular economic system, and the excellent development of artificial intelligence (Obasaju et al. 2021; Arato et al. 2017). These factors make the market competition in all walks of life more and more fierce. In such a situation, enterprises must optimize and adjust their industrial chains, focus on core competitiveness, and adjust non-core or non-good businesses to maintain their competitive advantage and continuously improve their core competitiveness. Since the logistics business is not the dominant business of each enterprise, building a professional logistics team and researching related logistics industry model will occupy most of the resources of the enterprise. Therefore, enterprises must optimize non-core industries and businesses, and contract some businesses to professional third-party logistics enterprises which play an irreplaceable role in the process of enterprise development and improving enterprise comprehensive competitiveness (Senthil et al. 2014). In addition, with the impact of global warming and the deteriorating ecological environment on the economy, adhering to the concept of sustainable development and realizing the unified strategy of coordination between human and socio-economic, ecological environment and social development plays a vital role in improving enterprise development and economic construction. Enterprises should not only actively respond to the call of the state and adhere to the road of sustainable development, but also gradually improve their core competitiveness in the increasingly fierce market competition, they must contract non-core business to professional third-party logistics suppliers. Third party logistics can reasonably coordinate the coordinated development of all links of enterprises, which can not only help enterprises improve their core competitiveness, but also reduce the cost of social transactions and improve the economic benefits of enterprises. Therefore, enterprises need to select appropriate suppliers under the background of sustainable construction, not only to enhance the core competitiveness of enterprises, but also to adhere to the concept of sustainable development, so as to maximize the multiple benefits of enterprises (Centobelli et al. 2017; Singh et al. 2018).
Because the issues that require decision-making in modern society involve a wide range of information and countless complicated influencing factors, traditional multi-attribute group decision-making (MADM) decision technologies are difficult to make high-quality decisions based on the information mastered by individuals. Therefore, multi-attribute group decision-making (MAGDM) makes up for the shortcomings of insufficient knowledge, experience and information of a single expert by inviting a group of experts to evaluate the existing alternatives based on experts’ cognitive capability. The selection of S3PRLPs is a classical MAGDM problem involving an expert assessment committee and numerous quantitative and qualitative criteria. Because of the inherent complexity and uncertainty of criterions, the traditional information representation models such as real number and fuzzy number are difficult for experts to portray the accurate evaluation information of S3PRLPs with respect to the assessment criteria. In comparison, as a strong and powerful uncertain information representation model, q-ROF set (Yager 2017) makes experts more universal and flexible in expressing evaluation viewpoints in the form of membership and nonmembership grades. Experts can freely give preference views according to their professional knowledge and experience. The q-ROF set can set the optimal parameters according to the evaluation information, and then flexibly solve the decision-making problem. Therefore, the q-ROF set provides an effective information representation model for decision experts to solve uncertain decision problems. Furthermore, the MULTIMOORA method is a famous decision technique by integrating the ration analysis and full multiplicative form and has been applied to deal with various actual assessment problems. The MULTIMOORA approach comprehensively ponders the merits of ration system, reference point and full multiplicative form to acquire a more rational, credibly and robust decision outcomes compared with other decision methods. The MULTIMOORA approach has been employed to construct a large number of decision algorithms in a diverse uncertainty setting, in view of its strength, but the dominance theory in the typical MULTIMOORA approach leads to irrational decision outcomes when the problem has a large number of alternatives. In view of the above-mentioned analysis and investigations, the key motivations of this research can be outlined as below:
- \(\spadesuit\):
-
The most operations of q-ROF number generated by algebraic norms and fails to take into consideration the interactive relation of membership and nonmembership degree. In addition, previous operations based on algebra and Einstein operations lack flexibility and robustness and cannot ponder the different preferences of decision experts.
- \(\spadesuit\):
-
As an effective technique to compute an exact value of q-ROF number, the score function has received more attention by scholars. However, the extant score functions ignore the hesitancy degree information, which shall lead to information loss during the process of information transformation.
- \(\spadesuit\):
-
The criteria weight plays a significant role in the course of developing decision analysis and determining the optimal option. The existing q-ROF decision methods only consider the weight of criteria in the aspect of single angle. The consideration of synthesizing the weighting criteria from both objective and subjective perspectives will make the decision analysis procedure more rational.
- \(\spadesuit\):
-
The investigation of group decision approaches under q-ROF setting is rare for settling decision issues. Additionally, the final ranking method in q-ROF-MULTIMOORA method is based upon the dominance theory. When complex decision problems have a large number of alternatives and criterions, dominance theory can pose a challenge to experts and produce irrational decision outcomes. At the same time, the three models in MULTIMOORA are deemed to have equal importance, in which case irrational decision outcomes will be obtained.
Motivated and inspired by the above, we will construct an integrated q-ROF group decision approach to select the most potential A-S3PRLP with improved score functions and operations. Correspondingly, the contributions of this study can be shown in the following:
-
We propound an innovative score function of q-ROF set and explore several properties of it and expound its superiority in the course of comparison;
-
Based upon the Frank t-norm and t-conorm, we build the q-ROF Frank interactive operational rules and further proffer several q-ROF Frank interactive aggregation operators;
-
A combination weight-determination is propounded based on the BWM and entropy weight method to estimate the importance grade of the S3PRLPs assessment criteria??
-
An integrated q-ROF-MULTIMOORA-WASPAS decision framework based on the proposed score function and operators is constructed to support the evaluation of sustainable third-party reverse logistic providers;
-
A demonstrative example concerning the assessment of S3PRLPs is applied to confirm the applicability of the q-ROF-MULTIMOORA-WASPAS decision framework, as well as the comparison investigations are also implemented to highlight the significance of the designed framework.
The remainder of this essay is constructed as follows. Section 2 gives an overview of the relevant literature in this study. Section 3 looks back on several basic notions involving q-ROF set, Frank operations and MULTIMOORA method. Section 4 propounds an innovative score function of q-ROF number and explored several properties of it. The q-ROF Frank interactive operations, related operators and desirable properties are discussed in Sect. 5. Section 6 built up an integrated q-ROF MULTIMOORA-WASPAS decision framework based on the proposed score function and operator to evaluation S3PRLPs. In Sect. 7, a case concerning the assessment of S3PRLPs is employed to further validate the practicability of the propounded decision framework, and the comparisons are implemented to highlight the effectiveness, applicability and superiority of the decision framework. Several concluding remarks and research perspectives are discussed in Sect. 8.
2 Literature overview
2.1 Evaluation of S3PRLPs
The selection of S3PRLPs can not only accelerate society’s sustainable development, but also enhance the core competitiveness of enterprise. Consequently, a multitude of investigations on these issues have been done by numerous researchers and scholars. Aguezzoul (2014) developed a literature on the problem of third-party logistics provider selection by summarizing 67 articles and divided these articles into five groups to analyse it. Prakash and Barua (2016) also introduced a fuzzy 3PRLP partner method on the basis of fuzzy TOPSIS algorithm. After that, to further fulfil the requirements of economic and business, Sen et al. (2017) pioneered a novel decision support algorithm by synthesizing the grey se theory and dominance measure for the evaluation of 3PRLP. Mavi et al. (2017) proposed a hybrid fuzzy decision algorithm based on the SWARA technique and MOORA method to obtain the order relation of S3PRLPs. Because of the complexity of third-party reverse logistics provider choice issue and the difference of decision criteria, Li et al. (2018) put forward a hybrid-MCDM assessment methodology through incorporating cumulation prospect theory and SAW method, wherein the assessment information can be signified by various ways such as interval number, linguistic term and so forth. Tavana et al. (2018) introduce a decision approach based upon analytic network process and superiority and inferiority method under intuitionistic fuzzy setting to attain the priority of S3PRLP. Zarbakhshnia et al. (2018) propounded a fuzzy SWARA-COPRAS method to select the best S3PRLP by considering the risk factor of the automotive industry. Govindan et al. (2019) introduced a combinative approach by the ELECTRE I and stochastic multi-criteria acceptability analysis to evaluate S3PRLPs. Furthermore, by considering the complicated decision data, Bai and Sarkis (2019) firstly combined the neighborhood rough set notion with TOPSIS and VIKOR method to rank S3PRLPs. Liu et al. (2019) brought forward a novel S3PRLP selection approach based on the extended BWM method and deviation model under interval-valued pythagorean hesitant fuzzy context. Rostamzadeh et al. (2020) generalized the ARAS method to fuzzy setting for assessing 3PRLPs by utilizing trapezoidal fuzzy number and 37 assessment criteria. In order to address the case which the evaluation value portrayed by different kinds of information representation model, Zhang and Su (2020) proffered an innovative heterogeneous decision algorithm based on dominance degree and hesitant fuzzy linguistic and probabilistic linguistic models. Baidya et al. (2021) presented a new logistics supplier selection model by combining CRITIC-MULTIMOORA method and Archimedean power integration operators under Bipolar fuzzy environment. Chen et al. (2021a) selected the best 3PRLP based upon entropy weight method and interval-valued intuitionistic fuzzy projection model under the situation in which the weights of criterion are completely unknown. Chen et al. (2021b) built a multiple perspective MADM framework to provide decision support for enterprise wherein the assessment portrayed in the form of generalized comparative linguistic expressions. To make experts possess more freedom to express assessment viewpoint, Mishra et al. (2021) constructed the CRITIC-EDAS approach for sorting S3PRLPs which the judgements of experts are provided in the form of Fermatean fuzzy value. To the best knowledge, there is no research based on MULTIMOORA-WASPAS method with combinative weight method for selecting S3PRLPs under q-ROF context.
2.2 q-ROF set
The complexity, randomness, and uncertainty of real-world decision-making problems make it difficult for decision-makers to accurately evaluate things within their cognitive range. In order to more accurately reflect the cognitive information provided by decision-makers, Zadeh (1965) first proposed fuzzy sets and used membership degrees to describe fuzzy information, thereby reducing information distortion. Afterwards, Atanassov (1989) proposed intuitionistic fuzzy sets by adding the concept of non membership. Furthermore, in order to overcome the limitations of expert subjective cognition, Yager (2013) proposed the Pythagorean fuzzy set by extending the constraint that the sum of membership and non membership in the intuitionistic fuzzy set is less than or equal to 1, to a sum of squares less than or equal to 1. However, decision-makers still face certain limitations when providing preference information, making it difficult to provide ideal evaluations or judgments. Therefore, the theory of q-ROF set is established through extending Pythagorean fuzzy set and further provides more spaces for evaluators to portray their assessment opinions. Because of its power in expressing ambiguity information, lots of achievements of q-ROF set have been accomplished in the aspect of decision analysis and the construction of assessment framework. At present, the research on q-ROF set mainly involves two aspects, including the theory investigations and the establishment and application of decision-making methods. For the basic theoretical research, the theoretical research framework of q-ROF set has been basically established and some achievements have been made for supporting the decision approaches construction by investigators (Peng and Huang 2020; Li et al. 2020; Zhu et al. 2021; Liu et al. 2022; Akram and Sitara 2022; Akram et al. 2021; Akram and Shumaiza 2021). In the aspect of basic theoretical research, Liu and Wang (2018a) established the basic operations of q-ROF set and introduced the basic weighted operators, which laid a theoretical foundation for the later study of the integration operator theory and group decision-making method of q-ROF set. Afterwards, based on different Archimedean operations and special functions, several functional operators which take into different information fusion characteristics are propounded to build up q-ROF decision algorithms (Liu and Wang 2018b; Jana et al. 2019; Darko and Liang 2020). However, the interactive and flexibility of the q-ROF set operational laws fail to ponder in most operators. The ranking methods of the q-ROF set play a crucial role during the procedure of decision analysis. Liu and Wang (2018a) first defined the score and accuracy functions of the q-ROF set, and gave the ranking rules of two q-ROF numbers. Since then, several improved functions have been proposed to overcome the defects and acquire a more rational comparison outcome (Wei et al. 2018; Peng et al. 2018a; Peng and Dai 2019; Xing et al. 2020).
In the aspect of decision-making method establishment and application, scholars have proposed different types of decision methods based upon diverse integration operators (Peng et al. 2016; Tian et al. 2019; Liu et al. 2021). However, the decision methods based on integration operator only considers and sorts the comprehensive evaluation values of schemes from the perspective of information fusion, ignoring the changes of internal characteristics of decision-making problems. Therefore, diverse extensions of classical decision approaches under q-ROF context are propounded for enriching the q-ROF decision methodology. Ye et al. (2021) established q-ROF TOPSIS group decision model to assess the information service quality of online health community based upon a novel distance measure. Yang et al. (2021) q-ROF-VIKOR group decision approach through combining CRITIC method to provide decision support for sustainable supply chain management. Furthermore, to ponder the psychological behavior of evaluators, Arya and Kumar (2021) developed the TODIM-VIKOR decision approach based on the presented entropy and Jensen-Tsalli divergence measure to select the optimal medical product suppliers. Liao et al. (2020) established an optimization model for determining attributes and expert weights based on the innovative q-ROF distance, combined with the classical gain and lost dominion score methods an investment evaluation model with completely unknown weight information is constructed. Although the above decision-making methods are effectively applied to deal with practical decision problems, there are still some phenomena of information distortion and counter intuition, which increases the difficulty of practical decision-making. Furthermore, there is no achievement regarding the evaluation of S3PRLPs under the q-ROF environment.
2.3 Frank t-norm and t-conorm
Frank propounded a universal expansion of the probabilistic and Lukasiewicz t-norms and t-conorms and named as Frank t-norm and t-conorm in 1979, which are general and flexible family of continuous triangular norms (Frank 1979). Since Frank t-norm and t-conorm possess a flexible parameter to control the power of the input values, it has been recognized as an efficient and workable tool in the procedure of data integration and information fusion (Xia et al. 2012; Qin et al. 2016; Peng et al. 2018a, b; Jiang and Ma 2018). Tang et al. (2018) built new MAGDM algorithm based on the propounded Frank aggregation operators with dual hesitant fuzzy information. Xing (2021) defined the frank operations on q-ROF numbers and combined the power and point operators to proposed some q-ROF power point operators. Xu et al. (2021) presented the single-valued neutrosophic 2-tuple linguistic Frank operators and then developed an improved MABACA method for tackling MAGDM problems. Yahya et al. (2021) constructed a probabilistic hesitant fuzzy MADM model based on the defined Frank aggregation operators. Sarkar et al. (2023) defined the dual hesitant q-rung orthopair fuzzy Frank operations and developed some novel power partitioned Heronian mean operators to assess the sustainable urban transport alternatives. The previous works show that Frank t-norm and t-conorm are extended to define the q-ROF Frank operations (Liu and Wang 2018b; Xing 2021). Nevertheless, the extant q-ROF Frank operations fails to think over the interactive impact during the process of information fusion. Accordingly, we shall define novel Frank operations via ponder the interactive action under q-ROF circumstance.
2.4 MULTIMOOR method
As an important branch of modern decision science, the essence of MADM is to select the optimal scheme from the set of schemes according to the considered criterions. Because the uncertainty, complexity and conflict widely exist in practical decision-making problems practical decision-making problems, a multitude of decision approaches are propounded by taking into consideration different characteristics and influences to cope with the actual decision problems based on their distinct superiorities. The MULTIMOOR method was presented by adding the full multiplicative form (FMF) on the basis of extended MOORA method, which has been acknowledged as a famous decision technique to acquire a more rational, credibly and robust decision outcomes through comprehensively pondering the merits of ration system (RS), reference point (RP) and FMF (Brauers and Zavadskas 2010). In light of the significant superiorities of the MULTIMOOR algorithm, it is extended to different fuzzy settings and uncertain information representation models to build various decision algorithms (Deliktas and Ustun 2017; Luo et al. 2019; Hafezalkotob et al. 2020; Akram et al. 2022). Aiming at the complex qualitative decision problems, Liao et al. (2019) constructed unbalanced hesitant fuzzy linguistic MULTIMOORA method based on a novel score function and utilized the presented method to deal with the shared bicycles investment problem. Wu et al. (2018) built up probabilistic linguistic MULTIMOORA decision algorithms the basis of expectation function and improved the final ranking method of MULTIMOORA based on border rule. The results show that the novel rank manner can obtain more robust decision results than dominance theory. To further accurately express complex linguistic assessment words, Gou et al. (2017) propounded the information representation model called double hierarchy hesitant fuzzy linguistic term set and constructed corresponding MULTIMOORA method to assess haze controlling measures situations. In order to take into account the psychological preferences of experts, the prospect theory MULTIMOORA approach based on the presented dependent weighted average operator is developed under probabilistic linguistic context (Liu and Li 2019). Considering that the correlation in complex decision problems, the Choquet integral and extended Bonferroni mean are extended to build up innovative MULTIMOORA method to address the risk assessment and heterogenous decision problems respectively (Wang et al. 2018; Liang et al. 2019). Lin et al. (2020) put forward the picture fuzzy MULTIMOORA model based upon the knowledge measure and novel score function to select a proper car-sharing station. For the group decision issues with unknown weight of criterion, the BWM and SWARA method severally combines with MULTIMOORA to establish group decision algorithms under three-way decision model and interval-valued Pythagorean fuzzy setting (Wang et al. 2020; He et al. 2021). The more research of MULTIMOORA model in fuzzy decision can refer to Rani and Mishra (2021), Rahimi et al. (2020) and Omrani et al. (2020). However, most extensions of the MULTIMOOR method assume that the weights of RS, RP and FMF are equal, which may cause unreasonable aggregation outcome. Accordingly, we build an integrated MULTIMOOR-WASPAS method on the basis of BWM and entropy weight algorithm.
3 Preliminaries
This section introduces several background knowledge including q-ROF set, Frank operations and the classical MULTIMOORA method, which will serve as a precursor to further research
3.1 q-ROFS
Definition 1
(Yager 2017) Assume that Y is a domain of discourse, a q-ROF set \(\mathcal {Q}\) on Y is represented via the following mathematical representation and given as below:
wherein \(\phi _{\mathcal {Q}}\left( y\right)\) and \(\varphi _{\mathcal {Q}}\left( y\right)\) respectively signify the membership grade and non-membership grade of an element \(y \in Y\), meeting the limitation condition \(0\le \left( \phi _{\mathcal {Q}}\left( y\right) \right) ^{q}+\left( \varphi _{\mathcal {Q}}\left( y\right) \right) ^{q}\le 1\). In addition, the hesitancy grade \(\pi _{\mathcal {Q}}(y)\) is depicted as \(\pi _{\mathcal {Q}}(y)=\left( 1-\left( \left( \phi _{\mathcal {Q}}\left( y\right) \right) ^{q}+\left( \varphi _{\mathcal {Q}}\left( y\right) \right) ^{q}\right) \right) ^{\frac{1}{q}}\). What’s more, the notion of q-ROF number is defined by Liu and Wang (2018a), represented as \(\mathcal {Q}=(\phi , \varphi )\) where \(\phi , \varphi \in [0, 1]\) and \(0 \le \phi ^{q}+ \varphi ^{q} \le 1\).
Definition 2
(Liu and Wang 2018a) For two arbitrary q-ROF numbers \(\mathcal {Q}_{1}=\left( \phi _{1}, \varphi _{1} \right)\) and \(\mathcal {Q}_{2}=\left( \phi _{2}, \varphi _{2} \right)\), the basic operational laws are defined as below:
3.2 Frank T-norm and S-norm
The triangle-norm T and triangle-conorm S are the intersection and union operations which are usually utilized to generate diverse information aggregation operations (Frank 1979). Based on the definition of triangle-norm T and triangle-conorm S, we can produce \(T\left( a, b\right) =f^{-1}\left( f\left( a\right) +f\left( b\right) \right)\) and \(S\left( a, b\right) =g^{-1}\left( g\left( a\right) +g\left( b\right) \right)\), wherein \(f\left( a\right)\) be a monotonically decreasing function and satisfies the following condition: \(f\left( a\right) : (0, 1]\rightarrow R^{+}\), \(f^{-1}\left( a\right) : R^{+}\rightarrow (0, 1]\) and \(\lim _{a\rightarrow \infty }f^{-1}\left( a\right) =0\), \(f^{-1}\left( 0\right) =1\), \(g\left( a\right)\) be a monotonically increasing function and satisfies the following condition: \(g\left( a\right) : (0, 1]\rightarrow R^{+}\), \(g^{-1}\left( a\right) : R^{+}\rightarrow (0, 1]\) and \(\lim _{a\rightarrow \infty }g^{-1}\left( a\right) =1\), \(f^{-1}\left( 0\right) =0\). In addition, the relation of generation function f and g can be obtained as \(g\left( a\right) =f\left( 1-a\right)\). When we set the generation function \(f(a)=-\ln \left( \frac{\zeta -1}{\zeta ^{a}-1} \right)\) and \(g(a)=-\ln \left( \frac{\zeta -1}{\zeta ^{1-a}-1}\right)\) with \(\zeta \ne 1\), we can further acquire the Frank T-norm and S-norm by \(T\left( a, b\right)\) and \(S\left( a, b\right)\), respectively, which be defined as below:
3.3 MULTIMOORA method
As an excellent decision technique, the MULTIMOORA method is proffered by Brauers and Zavadskas (2010) on the foundation of MOORA method through adding the addition of multiplicative manner. The MULTIMOORA technique attains the subordinate sorts through fusing the ratio system, reference point and full multiplicative form, and deduce the ultimate rankings through the dominance theory. The MULTIMOORA method has been shown to be more stable and effective in decision analysis since it was introduced. Considering a classical MCDM issue possesses m alternative with n criterion, the decision matrix is denoted as \(\tilde{X}=\left( \dot{x}_{ij}\right) _{m\times n}\) where \(\dot{x}_{ij} (i=1(1)m, j=1(1)n)\) is the assessment information of alternative \(\dot{a}_{i}\) under criterion \(\dot{c}_{j}\). Let d and \(n-d\) be the number of benefits and cost criterion, respectively. Before we utilize the MULTIMOORA method to develop decision analysis, the preference values should be standardized using the formulation \(\ddot{x}_{ij}=\dot{x}\big /\sqrt{\sum _{i=1}^{m}\left( \dot{x}\right) ^{2}}\). Next, we expound the algorithm of the above models:
-
(1)
The sorting values \(\tilde{y}_{1}\left( \dot{a}_{i}\right) ((i=1(1)m)\) is derived by utilizing the ratio system algorithm. The purport of ratio system algorithm is to make the the sorting values of alternatives under benefit criterion maximization and make the the sorting values of alternatives under cost criterion minimization. Then the sorting values \(\tilde{y}_{1}\left( \dot{a}_{i}\right)\) of \(\dot{a}_{i}\) is computed by the formulation \(\tilde{y}_{1}\left( \dot{a}_{i}\right) =\sum _{j=1}^{d}\ddot{x}_{ij}-\sum _{j=d+1}^{n}\ddot{x}_{ij}\). The alternative are sorted as descending order based on the values of \(\tilde{y}_{1}\left( \dot{a}_{i}\right)\).
-
(2)
The sorting values \(\tilde{y}_{2}\left( \dot{a}_{i}\right) ((i=1(1)m)\) is deduced by utilizing the reference point algorithm. The ideal of reference point algorithm considers the distance measure between the preference values with the maximum preference value over the same criterion. Then the sorting values \(\tilde{y}_{2}\left( \dot{a}_{i}\right)\) of \(\dot{a}_{i}\) is computed by \(\tilde{y}_{2}\left( \dot{a}_{i}\right) =\max \limits _{j}\left| r_{j}-\ddot{x}_{ij}\right|\), wherein \(r_{j}=\max \limits _{i}\ddot{x}_{ij}\). The alternative are sorted as ascending order based on the values of \(\tilde{y}_{1}\left( \dot{a}_{i}\right)\).
-
(3)
The sorting values \(\tilde{y}_{3}\left( \dot{a}_{i}\right) ((i=1(1)m)\) is attained by utilizing the full multiplicative form algorithm. The full multiplicative form algorithm aims to make the the sorting values of alternatives under benefit criterion maximization and make the the sorting values of alternatives under cost criterion minimization. It is different from the ratio system algorithm, the full multiplicative form algorithm employs the multiplicative manner to calculated the sorting values \(\tilde{y}_{3}\left( \dot{a}_{i}\right)\) of alternative \(\dot{a}_{i}\), namely, \(\tilde{y}_{3}\left( \dot{a}_{i}\right) =\prod _{j=1}^{d}\ddot{x}_{ij} \bigg /\prod _{j=d+1}^{n}\ddot{x}_{ij}\). The alternative are sorted as descending order based on the values of \(\tilde{y}_{1}\left( \dot{a}_{i}\right)\).
As a consequence, the final utility value of alternative \(\dot{a}_{i}\) is acquired through integrating the three sorting outcomes with the aid of the dominance theory.
4 A novel score function for comparing q-ROF numbers
This part first studies the previous score functions and discusses the deficiencies of them, and then developed a innovative score function to overcome the mentioned shortfalls.
4.1 The extant score functions
To acquire the order relation of a group q-ROF numbers, Liu and Wang (2018a) firstly given the definition of score function of q-ROF number described as \(\mathbb {S}_{1}\left( \mathcal {Q}\right) =\phi ^{q}-\varphi ^{q},\; \mathbb {S}\left( \mathcal {Q}\right) \in [-1, 1]\), where \(\mathcal {Q}=\left( \phi _, \varphi \right)\) is a q-ROF number. Afterwards, to make up the defect of score function when the membership and nonmembership grade is equal, the accuracy function is further defined as \(\mathbb {H}_{1}\left( \mathcal {Q}\right) =\phi ^{q}+\varphi ^{q},\; \mathbb {H}\left( \mathcal {Q}\right) \in [0, 1].\) Although the score function \(\mathbb {S}_{1}\left( \mathcal {Q}\right)\) can valid sort the q-ROFN numbers, it still has several limitations such as ignoring the hesitancy of q-ROF numbers. Accordingly, scholars have successively presented several diverse score functions to compare diverse q-ROF numbers, which are summarized in Table 1, in which \(\mathcal {Q}=\left( \phi , \varphi \right)\) be a q-ROF number.
4.2 An innovative score function
Under this subsection, an innovative score function of q-ROF number is propounded to conquer the above limitation and ponder the nondeterminacy grade when differentiates the q-ROF numbers.
Definition 3
Given a q-ROFN \(\mathcal {T}=\left( \phi , \varphi \right)\), a novel score function is stated as below:
Definition 4
For two arbitrary q-ROF numbers \(\mathcal {Q}_{1}=\left( \phi _{1}, \varphi _{1} \right)\) and \(\mathcal {Q}_{2}=\left( \phi _{2}, \varphi _{2} \right)\) and \(q\ge 1\). Then,
-
(1)
If \(\mathbb {S}(\mathcal {Q}_1) < \mathbb {S}(\mathcal {Q}_2)\), then \(\mathcal {Q}_1 \prec \mathcal {Q}_2\);
-
(2)
If \(\mathbb {S}(\mathcal {Q}_1) = \mathbb {S}(\mathcal {Q}_2)\), then,
-
If \(\mathbb {H}_{1}(\mathcal {Q}_1) > \mathbb {H}_{1}(\mathcal {Q}_2)\), then \(\mathcal {Q}_1 \succ \mathcal {Q}_2\);
-
If \(\mathbb {H}_{1}(\mathcal {Q}_1) = \mathbb {H}_{1}(\mathcal {Q}_2)\), then \(\mathcal {Q}_1 \sim \mathcal {Q}_2\).
-
The following desirable properties of the propounded score function are investigated in the following.
Theorem 1
Given a q-ROF number \(\mathcal {Q}=\left( \phi , \varphi \right)\), then \(\mathbb {S}(\mathcal {Q})\) is monotonous increasing in term of \(\phi\) and monotonous decreasing in term of \(\varphi\).
Proof
In view of the definition 3, we compute the partial derivation of \(\mathbb {S}(\mathcal {Q})\) withe respect to \(\phi\) and \(\varphi\),
Accordingly, we can derive that \(\mathbb {S}(\mathcal {Q})\) is monotonous increasing in term of \(\phi\) and monotonous decreasing in term of \(\varphi\) hold. \(\square\)
Theorem 2
Given a q-ROF number \(\mathcal {Q}=\left( \phi , \varphi \right)\), the score \(\mathbb {S}(\mathcal {Q})\) of \(\mathcal {Q}\) meets the follows properties:
-
(1)
\(\mathbb {S}(\mathcal {Q})=-1 \Leftrightarrow \mathbb {S}(\mathcal {Q})=\left( 1, 0 \right) ;\) \(\mathbb {S}(\mathcal {Q})=1 \Leftrightarrow \mathbb {S}(\mathcal {Q})=\left( 0, 1 \right) ;\)
-
(2)
\(-1 \le \mathbb {S}(\mathcal {Q}) \le 1.\)
Proof
(1) On the basis of the Theorem 1, it is easily to obtain that function \(\mathbb {S}\left( \mathcal {Q}\right)\) possesses the maximum value when \(\mathcal {Q}=\left( 1, 0 \right)\) and the minimum value when \(\mathcal {Q}=\left( 0, 1\right)\), namely, \(\mathbb {S} \left( \mathcal {Q}\right) _{max}=-1\) and \(\mathbb {S}\left( \mathcal {Q}\right) _{min}=-1\).
(2) Based upon (1), thus, \(-1 \le \mathbb {S} (\mathcal {Q}) \le 1\) holds. \(\square\)
Theorem 3
For two arbitrary q-ROF numbers \(\mathcal {Q}_{1}=\left( \phi _{1}, \varphi _{1} \right)\) and \(\mathcal {Q}_{2}=\left( \phi _{2}, \varphi _{2} \right)\), if \(\phi _{1}> \phi _{2}\) and \(\varphi _{1}<\varphi _{2}\), then \(\mathbb {S}(\mathcal {Q}_1) \succ \mathbb {S}(\mathcal {Q}_2)\),
Proof
With the assistance of Theorem 1, the propounded function \(\mathbb {S}(\mathcal {Q})\) is monotonous increasing in term of \(\phi\) and monotonous decreasing in term of \(\varphi\). Consequently, if \(\phi _{1}> \phi _{2}\) and \(\varphi _{1}<\varphi _{2}\), then \(\mathbb {S}(\mathcal {Q}_1) \succ \mathbb {S}(\mathcal {Q}_2)\) keeps.\(\square\)
To demonstrate the rationality and validity of the presented score function at ranking q-ROF numbers. We conduct a comparative study for comparing different forms q-ROFNs between the created function \(\mathbb {S}(\mathcal {Q})\) and the extent works involving \(\mathbb {S}_{1}\left( \mathcal {Q}\right)\) presented by Liu and Wang (2018a), \(\mathbb {S}_{2}\left( \mathcal {Q}\right)\) proposed by Wei et al. (2018), \(\mathbb {S}_{3}\left( \mathcal {Q}\right)\) developed by Peng et al. (2018a), \(\mathbb {S}_{4}\left( \mathcal {Q}\right) (\lambda =0)\) propounded by Peng and Dai (2019). The detailed comparison outcomes are displayed in Table 2, where the sort with single underline and sort with double underline signify the irrational outcomes and counterintuitive outcomes, respectively.
With the help of Table 2, it is obviously that the designed score function \(\mathbb {S}\left( \mathcal {Q}\right)\) can conquer the aforementioned deficiencies produced from \(\mathbb {S}_{1}\left( \mathcal {Q}\right)\), \(\mathbb {S}_{2}\left( \mathcal {Q}\right)\), \(\mathbb {S}_{3}\left( \mathcal {Q}\right)\) and \(\mathbb {S}_{4}\left( \mathcal {Q}\right) (\lambda =0)\). It means that the designed function can result in comparing differentiate q-ROF numbers when the extant score functions are invalid for comparing q-ROF numbers. In addition, for the irrational outcomes and counterintuitive situation, if we go on utilizing the accuracy function to finish the comparison, the ultimate comparative outcomes are coincident with our outcomes, which implies that the proffered score function is efficacious and straight-forward.
5 q-ROF Frank interactive aggregation operators
In this part, we first propose the q-ROF Frank interactive operations based on Frank T-norm and S-norm and further analyse the merits of the presented operations. Afterwards, we develop several new q-ROF Frank interactive operators and explore some properties of these operators.
5.1 q-ROF Frank interactive operations
The foundation of aggregation operators is operational laws which are generated with the help of T-norm and S-norm. Since the q-ROF set was introduced, researchers have proffered several operations based on diverse T-norm, such as Archimedean operations, Dombi operations and so forth. However, these operations have some disadvantages, such as lack of flexibility or lack of consideration of interaction effects. Inspired by the academic idea of He et al. (2014), we propose a novel interactive operations of q-ROF numbers on the basis of Frank T-norm and S-norm.
Definition 5
For two arbitrary q-ROF numbers \(\mathcal {Q}_{1}=\left( \phi _{1}, \varphi _{1} \right)\) and \(\mathcal {Q}_{2}=\left( \phi _{2}, \varphi _{2} \right)\) with \(q\ge 1, \lambda >0\), then the interactive operations of q-ROF numbers obtained are depicted as:
where S and g respectively denote the Frank S-norm and the generation function of S-norm defined in Sect. 3.2.
In the next, we defined the Frank interactive operations of q-ROF numbers based on Frank operations.
Definition 6
For two arbitrary q-ROF numbers \(\mathcal {Q}_{1}=\left( \phi _{1}, \varphi _{1} \right)\) and \(\mathcal {Q}_{2}=\left( \phi _{2}, \varphi _{2} \right)\), the Frank interactive operations of q-ROF numbers are stated as follows:
Then, we can confirm that the Frank interactive operations of q-ROF numbers possess the following properties.
Theorem 4
Suppose that \(\mathcal {Q}_{1}=\left( \phi _{1}, \varphi _{1} \right)\) and \(\mathcal {Q}_{2}=\left( \phi _{2}, \varphi _{2} \right)\) ba any two q-ROF numbers with \(\lambda , \lambda _{1}, \lambda _{2}>0\)
-
(1)
$$\begin{aligned} \mathcal {Q}_{1}\oplus _{F} \mathcal {Q}_{2}=\mathcal {Q}_{2}\oplus _{F} \mathcal {Q}_{1}; \end{aligned}$$(18)
-
(2)
$$\begin{aligned} \mathcal {Q}_{1}\otimes _{F} \mathcal {Q}_{2}=\mathcal {Q}_{2}\otimes _{F} \mathcal {Q}_{1};\end{aligned}$$(19)
-
(3)
$$\begin{aligned} \lambda \cdot _{F} \left( \mathcal {Q}_{1}\oplus _{F} \mathcal {Q}_{2}\right) =\lambda \cdot _{F} \mathcal {Q}_{1}\oplus _{F} \lambda \mathcal {Q}_{2};\end{aligned}$$(20)
-
(4)
$$\begin{aligned} \lambda _{1} \cdot _{F} \mathcal {Q}_{1}\oplus _{F} \lambda _{2} \cdot _{F} \mathcal {Q}_{1}= \left( \lambda _{1}+\lambda _{2}\right) \cdot _{F} \mathcal {Q}_{1} ;\end{aligned}$$(21)
-
(5)
$$\begin{aligned} \left( \mathcal {Q}_{1}\otimes _{F} \mathcal {Q}_{2}\right) ^{\wedge _{F} \lambda }=\mathcal {Q}_{1}^{\wedge _{F} \lambda }\otimes _{F} \mathcal {Q}_{2}^{\wedge _{F} \lambda } ;\end{aligned}$$(22)
-
(6)
$$\begin{aligned} \mathcal {Q}_{1}^{\wedge _{F} \lambda _1}\otimes _{F} \mathcal {Q}_{2}^{\wedge _{F} \lambda _2}= \mathcal {Q}_{1}^{\wedge _{F} \left( \lambda _1+\lambda _2\right) }. \end{aligned}$$(23)
.
Next, we shall conduct a comparison between the extant operations with the Frank interactive operations under q-ROF setting, the comparison results based on diverse operations are displayed in Table 3.
From Table 3, we can see that algebraic, Hamacher and Dombi operations will lead an unreasonable computational outcome when the nonmembership garde of q-ROF number is equal to zero. These operations shall further produce counter-intuitive phenomenon in the course of information fusion. What’s more, the algebraic and Algebraic interactive operations fail to ponder the flexibility of information procedure. However, q-ROF Frank interactive operations can efficiently conquer the aforementioned deficiencies of existent operations. Accordingly, the presented operations in this manuscript are more availability and rationally for integrating uncertain information.
5.2 q-ROF Frank interactive weight average operators
In the present section, we advance several q-ROF averaging operators based on Frank interactive operations. Unless otherwise specified, \(\Theta\) stands for the set of all q-ROF numbers in this chapter.
Definition 7
Suppose \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\) be "n" q-ROF numbers. \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n}\varpi _{\nu }=1\). The q-ROFFIWA operator is a n dimension mapping signified \(q-ROFFIWA: \Theta ^{n}\rightarrow \Theta\), and
In light of the Frank interactive operation of q-ROF number defined in Definition 6, the q-ROFFIWA operator possesses the following worthwhile properties.
Theorem 5
Given group q-ROF numbers signified as \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\). The fusion outcome of "n" q-ROF numbers is still a q-ROF number and can be attained through utilizing q-ROFFIWA operator, namely,
where \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n}\varpi _{\nu }=1\).
Proof
The proof can be found in Appendix. \(\square\)
Property 1
(Idempotency) Suppose \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1 (1) n\right)\) be "n" q-ROF numbers. If \(\mathcal {Q}_{\nu }=\mathcal {Q}=\left( \phi , \varphi \right) =\). Then
Proof
The proof can be found in Appendix. \(\square\)
Property 2
(Monotonicity) Suppose that \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right)\) and \(\tilde{\mathcal {Q}}_{\nu }=\left( \tilde{\phi }_{\nu }, \tilde{\varphi }_{\nu }\right) \left( \nu =1(1)n\right)\) be two families of q-ROF numbers. If \(\phi _{\nu }\ge \tilde{\phi }_{\nu }\) and \(\left( \phi _{\nu }\right) ^{q}+\left( \varphi _{\nu } \right) ^{q}\le \left( \tilde{\phi }_{\nu }\right) ^{q} + \left( \tilde{\varphi }_{\nu }\right) ^{q}\). Then
Proof
The proof can be found in Appendix. \(\square\)
Property 3
(Boundedness) Let \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right)\) be a families of q-ROF numbers.
then
Proof
The proof can be found in Appendix. \(\square\)
Property 4
Suppose that \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right)\) and \(\tilde{\mathcal {Q}}_{\nu }=\left( \tilde{\phi }_{\nu }, \tilde{\varphi }_{\nu }\right) \left( \nu =1(1)n\right)\) be two set of q-ROF numbers and \(\mathcal {Q}=\left( \phi , \varphi \right)\) be a q-ROF number. Then
The theorem can be proved easily with the aid of the q-ROFFIWA operator and Frank interactive operations of q-ROF numbers, so we omitted it.
Definition 8
Suppose \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\) be "n" q-ROF numbers. \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n}\varpi _{\nu }=1\). The q-ROFFIOWA operator is a n dimension mapping signified \(q-ROFFIOWA: \Theta ^{n}\rightarrow \Theta\), and
wherein \(\left( \varrho (1), \varrho (2), \ldots , \varrho (n) \right)\) is a permutation of \(\left( 1, 2, \ldots , n \right)\) within \(\mathcal {Q}_{\varrho (j-1)}> \mathcal {Q}_{\varrho (j)}\) for \(j=2,3, \ldots , n\).
In light of the Frank interactive operation of q-ROF number defined mentioned, the q-ROFFIWA operator possesses the following worthwhile properties.
Theorem 6
Given a group q-ROF numbers denoted as \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\). The fusion outcome of "n" q-ROF numbers is still a q-ROF number and can be attained through utilizing q-ROFFIOWA operator, namely,
where \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n}\varpi _{\nu }=1\).
5.3 q-ROF Frank interactive geometric operators
In the current subsection, we advance several q-ROF geometric operators based on Frank interactive operations. Unless otherwise specified, \(\Theta\) stands for the set of all q-ROF numbers in this chapter.
Definition 9
Suppose \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\) be "n" q-ROF numbers. \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n} \varpi _{\nu }=1\). The q-ROFFIWG operator is a n dimension mapping signified \(q-ROFFIWG: \Theta ^{n}\rightarrow \Theta\), and
In light of the Frank interactive operation of q-ROF number defined mentioned, the q-ROFFIWG operator possesses the following worthwhile properties.
Theorem 7
Considering a set of q-ROF numbers indicated as \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\). The fusion outcome of "n" q-ROF numbers is still a q-ROF number and can be attained through utilizing q-ROFFIWG operator, namely,
where \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n} \varpi _{\nu }=1\).
Property 5
(Idempotency) Suppose \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\) be "n" q-ROF numbers. If \(\mathcal {Q}_{\nu }=\mathcal {Q}=\left( \phi , \varphi \right) =\). Then
Property 6
(Monotonicity) Suppose that \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right)\) and \(\tilde{\mathcal {Q}}_{\nu }=\left( \tilde{\phi }_{\nu }, \tilde{\varphi }_{\nu }\right) \left( \nu =1(1)n\right)\) be two families of q-ROF numbers. If \(\phi _{\nu }\ge \tilde{\phi }_{\nu }\) and \(\left( \phi _{\nu }\right) ^{q}+\left( \varphi _{\nu } \right) ^{q}\le \left( \tilde{\phi }_{\nu }\right) ^{q} + \left( \tilde{\varphi }_{\nu }\right) ^{q}\). Then
Property 7
(Boundedness) Let \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right)\) be a families of q-ROF numbers.
then
Definition 10
Suppose \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\) be "n" q-ROF numbers. \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n} \varpi _{\nu }=1\). The q-ROFFIOWG operator is a n dimension mapping signified \(q-ROFFIOWG: \Theta ^{n}\rightarrow \Theta\), and
wherein \(\left( \varrho (1), \varrho (2), \ldots , \varrho (n) \right)\) is a permutation of \(\left( 1, 2, \ldots , n \right)\) within \(\mathcal {Q}_{\varrho (j-1)}> \mathcal {Q}_{\varrho (j)}\) for \(j=2,3, \ldots , n\).
Theorem 8
Ponder \(\mathcal {Q}_{\nu }=\left( \phi _{\nu }, \varphi _{\nu }\right) \left( \nu =1(1)n\right)\) be "n" q-ROF numbers. The fusion outcome of "n" q-ROF numbers is still a q-ROF number and can be attained through utilizing q-ROFFIOWG operator, namely,
where \(\varpi _{\nu }\) is the importance degree of \(\mathcal {Q}_{\nu }\) meeting \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n}\varpi _{\nu }=1\).
6 q-ROF MULTIMOORA-WASPAS method
In the section, we design an innovative methodology named q-ROF-MULTIMOORA-WASPAS, which synthesizes the combination weight, MULTIMOORA, WASPAS and the improved theory of q-ROF set to tackle the MEMCDM assessment problems. Firstly, a generalization description of the q-ROF MEMCDM decision issue is stated. Then, based upon the relatively entropy principle and improved score function of q-ROF number, the synthesis weights of assessment criterion are ascertained by united the improved BWM method and entropy weight approach. Subsequently, the decision framework of q-ROF-MULTIMOORA-WASPAS approach is designed on the basis of q-ROFFIWA operator, q-ROFFIWG operator and the novel score function to resolve the q-ROF group decision issues.
6.1 Issues statement
Aiming at a q-ROF MEMCDM decision problem, an assessment expert \(AE^{l} (l=1, 2, \ldots , L)\) provide his(her) preferences or judgements for evaluation alternatives under different criterions can be collected as a decision matrices \(G^{l}=\left( \mathcal {Q}_{\mu \nu }^{l}\right) _{m\times n}\) shown as:
wherein \(\Upsilon =\{\Upsilon _1, \Upsilon _2, \ldots , \Upsilon _{\mu } \ldots \Upsilon _m \}\) is a collection of alternatives. \(C=\{\mathcal {C}_1, \mathcal {C}_2, \ldots , \mathcal {C}_{\nu }, \ldots \mathcal {C}_n\}\) is a set of criteria with the weight vector being \(\varpi =(\varpi _1, \varpi _2, \ldots , \varpi _n)^{T}\) with \(\varpi _{\nu } \in [0, 1]\) and \(\sum _{\nu =1}^{n}\varpi _{\nu }=1\). Suppose that \(AE=\{AE_{1}, AE_{2}, \ldots , AE_{l}, \ldots , AE_{L}\}\) is a group of evaluators possessing the weight information \(\theta =\{\theta _{1}, \theta _{2}, \ldots , \theta _{L}\}^{T}\) and \(\theta \in [0, 1], \sum _{l=1}^{L}\theta _{l}=1\). The evaluators \(AE_{l}\) provide their preference(judgement) for alternative \(\Upsilon _{\mu }\) under the criteria \(\mathcal {C}_{\nu }\) by the form of q-ROF number \(\mathcal {Q}_{\mu \nu }^{l}=\left( \phi _{\mu \nu }^{l}, \varphi _{\mu \nu }^{l}\right)\), where \(\phi _{\mu \nu }^{l}, \varphi _{\mu \nu }^{l} \in [0, 1]\) and \(0 \le \left( \phi _{\mu \nu }^{l}\right) ^{q}+\left( \varphi _{\mu \nu }^{l}\right) ^{q}\le 1\).
For a classical MAGDM issue, we will build an expert committee and invite them to provide their preference standpoint for alternatives with respect to the chosen criteria. Considering the cognitive psychology and expression habits of experts, the linguistic terms are employed to describe cognitive preference information.
6.2 The procedural steps of the designed q-ROF decision framework
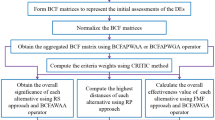
In this part, a three stages decision framework for assessing the S3PRLPs is built up, displayed in Fig. 1, the procedural steps of the q-ROF-MULTIMOORA-WASPAS approach are illustrated as below:
Stage I: Preparatory stage.
Step 1: Construct the q-ROF expert decision matrices.
Because of the vagueness and indeterminacy of experts’ cognition ability, a mapping from linguistic to q-ROF numbers displayed in Table 4 is provided for experts to help them to evaluate the decision alternatives and further provide their assessment information more accurate.
Step 2: Calculate the weight of assessment expert.
Then weight of expert stands for the important grade of experts in the course of MAGDM, which is an significant index for experts information fusion stage. In the model, a mapping from linguistic to q-ROF numbers displayed in Table 5 is utilized to portray the weight information of experts. Assume that \(\mathcal {Q}_{l}=\left( \phi _{l}, \varphi _{l}\right)\) is a q-ROF number, the weight \(\theta _{l}\) of expert \(AE_{l}\) is computed as:
Stage II: Fusion and criteria weight identification.
Step 3: Attaining the fused assessment matrix.
In this stage, we employ the q-ROFFIWA operator to fuse experts’ evaluation matrices and further obtain the synthesize evaluation matrix \(G=\left( \mathcal {Q}_{\mu \nu }\right) _{m\times n}\), where \(\mathcal {Q}_{\mu \nu }=\left( \phi _{\mu \nu }, \varphi _{\mu \nu }\right) , \mu =1(1)m, \nu =1(1)n\) be the comprehensive judgement information, wherein
Step 4: Compute the synthesis weights of evaluation criteria.
Step 4-I: Acquire the subjective weight of criteria using BWM method.
The BWM method (Rezaei 2015) is developed to further improve AHP method and obtain more reasonable weight information. BWM only needs multiple pairwise comparisons to obtain weights, which further improves the consistency of pairwise comparisons and saves computing time. The outstanding feature of BWM is to determine the best and worst attributes before pairwise comparison, and then obtain the preference of the best criteria to other attributes and the preference of other attributes to the worst criteria. Finally, the attribute weight is obtained by solving the optimization model. This step builds enhanced BWM method based on the proposed score function.
(1) Decision-making experts determine the best attribute and the worst criteria according to their cognitive ability;
(2) To perform pairwise comparison and obtain the q-ROF comparison vector (Q-BO) from the best criteria to other attributes and the q-ROF comparison vector (Q-OW) from other criteria to the worst attribute:
(3) Convert Q-BO and Q-OW vectors into score vectors according to the score function of q-ROF number shown in Definition 9;
(4) Move the score value to the range of by the following formula:
(5) The weight vector is determined by the following optimization model
For simplicity, model 1 can be converted to the following linear model:
(6) Calculate the consistency ratio. The consistency ratio (CR) of BWM is denoted as \(\zeta ^{*}\) and the associated consistency index (CI) is calculated with the aid of formulation \(CR=\frac{\zeta ^{*}}{CI}\), where the CI for BWM method can be attained in Rezaei (2015). The small the value of CR, the high the consistency.
With the assistance of LINGO software, the subjective weight vector \(\varpi _{\nu }^{s}=\left( \varpi _{1}^{s}, \varpi _{2}^{s}, \ldots , \varpi _{n}^{s}\right) ^{T}\) of criteria can be determined.
Step 4-II: Acquire the objective weight of criteria using entropy weigh method based on the score function.
Entropy, as an important measurement tool for measuring the uncertainty in information theory, is utilized to measure the degree of disorder for an information system. The smaller the information entropy of the criterion is, the greater the amount of information provided by the criterion, and the greater the role of the criterion in the overall evaluation. Thus, we can employ entropy to compute criteria weight objectively. The detailed steps can be outlined as below:
(1) Compute the score matrix of the aggregation matrix. \(G=\left( \mathcal {Q}_{\mu \nu }\right) _{m\times n}\) through the following formulation:
(2) We first utilize the linear ratio-based normalization formulation to shift the scores value and make it satisfy \(\mathbb {S}\left( \mathcal {Q}_{\mu \nu }\right) \in [0, 1]\). Then we work out the information entropy of each criterion \(\mathcal {C}_{\nu }\) based upon the shifted score matrix with the following formulation:
(3) Afterwards, the subject weight \(\varpi _{\nu }^{o}\) of criterion \(\mathcal {C}_{\nu } (\nu =1, 2, \ldots , n)\) is calculated as
By utilizing the entropy weight method, the objective weight vector \(\varpi _{\nu }^{o}=\left( \varpi _{1}^{o}, \varpi _{2}^{o}, \ldots , \varpi _{n}^{o}\right) ^{T}\) of criteria can be determined.
Step 4-III: Getting the synthesis weights of criteria utilizing the relative entropy principle.
To use the Lagrange multiplier constructor:
To calculate the partial derivative:
Set the partial derivative to zero to solve the model;
By solving the model mentioned in step 4-3, the ultimate synthetic weights of criterions \(\varpi _{\nu }^{*}=\left( \varpi _{1}^{*}, \varpi _{2}^{*}, \ldots , \varpi _{\nu }^{o}\right) ^{T}\) can be acquired.
Stage III: Sort and select the optimal S3PRLP.
After attaining the group comprehension evaluation and weight vectors of assessment criteria, we shall utilize the propounded theories to put forward the q-ROF-MULTIMOORA-WASPAS method for acquiring the order relation of assessment alternatives. In the next, the concrete steps of the MULTIMOORA-WASPAS method can be depicted as follows.
Step 5: Ascertaining the significance of the assessment alternatives on the basis of RS model.
The detailed process of the q-ROF RS model is articulated by the following sub-steps:
Step 5-I: Ascertaining the synthesize preference of diverse alternatives with respect to the benefit and cost criteria using the q-ROFFIWA operator, as below:
wherein \(\varpi _{\nu }^{*}\) is the combination weight of criterion \(\mathcal {C}_{\nu }\), g is the number of benefit criterion and \(n-g\) stands for the number of non-benefit criterion, \(U_{\mu }^{+}\) and \(U_{\mu }^{-}\) are q-ROF numbers and signified the importance of alternative \(\Upsilon _{\mu }\).
Step 5-II:Attaining the score values of \(U_{\mu }^{+}\) and \(U_{\mu }^{-}\) with the aid of the novel score function \(\mathbb {S}\), as below:
Step 5-III: Estimating the overall ranking value \(u_{\mu }\) of alternative \(\Upsilon _{\mu }\) through the following formulation:
Step 5-IV: The maximum utility value \(mu_{\mu } \in [0, 1]\) is attained based on the following formulation:
The preference order of all alternatives can be ascertained based on the value of \(mu_{\mu }\) and the alternatives are sorted in the form of the descending order displayed as \(\Phi _{1}=\left\{ \Phi _{1}\left( \Upsilon _{1}\right) , \Phi _{1}\left( \Upsilon _{2}\right) , \ldots , \Phi _{1}\left( \Upsilon _{n}\right) \right\}\).
Step 6: Determining the importance of the assessment alternatives Based upon the RP model.
The concrete procedure of the q-ROF RP model is articulated by the following sub-steps:
Step 6-I: Ascertaining the reference point. The reference point \(\sigma ^{*}=\left\{ \sigma _{1}^{*}, \sigma _{2}^{*}, \ldots , \sigma _{n}^{*}\right\}\) of each criterion \(\mathcal {C}_{\nu }\) be a q-ROF number and its valued can be achieved by the following formulation:
Step 6-II: Calculating the distance of assessment value to all reference points with the aid of the following formulation:
where \(d\left( \mathcal {Q}_{\mu \nu }, \sigma ^{*}\right)\) denoted the distance from criteria value \(\mathcal {Q}_{\mu \nu }\) to reference point \(\sigma ^{*}\) computing by the q-ROF Hamming distance \(d(\mathcal {Q}_{1}, \mathcal {Q}_{2})=\frac{1}{2}\left( \left| \left( \phi _{1}\right) ^{q}-\left( \phi _{2}\right) ^{q}\right| +\left| \left( \varphi _{1}\right) ^{q}-\left( \varphi _{2}\right) ^{q}\right| +\left| \left( \pi _{1}\right) ^{q}-\left( \pi _{2}\right) ^{q}\right| \right)\) (Liu and Wang 2018a).
Step 6-III: Computing the maximum distance of each alternative \(\Upsilon _{\mu }\), as below:
Step 6-IV: The maximum utility value \(\overline{mu}_{\mu }\in [0, 1]\) is attained based on the following formulation:
The preference order of all alternatives can be obtained by the value of \(\overline{mu}_{\mu }\) and the alternatives are sorted in the form of the ascending order displayed as \(\Phi _{2}=\left\{ \Phi _{2}\left( \Upsilon _{1}\right) , \Phi _{2}\left( \Upsilon _{2}\right) , \ldots , \Phi _{2}\left( \Upsilon _{n}\right) \right\}\).
Step 7: Attaining the significance of the assessment alternatives based upon FMF model.
The detailed process of the q-ROF FMF model is articulated by the following sub-steps:
Step 7-I: Ascertaining the synthesize preference of diverse alternatives with respect to criteria using the q-ROFFIWG operator, as below:
wherein \(\varpi _{\nu }^{*}\) is the combination weight of criteria \(\mathcal {C}_{\nu }\), g is the number of benefit criterion and \(n-g\) stands for the number of non-benefit criterion, \(H_{\mu }^{+}\) and \(H_{\mu }^{-}\) are q-ROFNs and signified the importance of alternative \(\Upsilon _{\mu }\).
Step 7-II: Attaining the score values of \(H_{\mu }^{+}\) and \(H_{\mu }^{-}\) with the aid of the novel score function \(\mathbb {S}\), as below:
Step 7-III: Estimating the overall ranking value \(\varsigma _{\mu }\) of alternative \(\Upsilon _{\mu }\) through the following formulation:
Step 7-IV: The maximum utility value \(\overline{\overline{mu}}_{\mu } \in [0, 1]\) is attained based on the following formulation:
The preference order of all alternatives can be ascertained based on the value of \(\overline{\overline{mu}}_{\mu }\) and the alternatives are sorted in the form of the descending order displayed as \(\Phi _{1}=\left\{ \Phi _{1}\left( \Upsilon _{1}\right) , \Phi _{1}\left( \Upsilon _{2}\right) , \ldots , \Phi _{1}\left( \Upsilon _{n}\right) \right\}\).
Step 7-V: The preference order of all alternatives can be ascertained based on the value of \(\tilde{\tilde{u}}_{\mu }\left( \Upsilon _{\mu }\right)\) and the alternatives are sorted in the form of the descending order displayed as \(\Phi _{3}=\left\{ \Phi _{3}\left( \Upsilon _{1}\right) , \Phi _{3}\left( \Upsilon _{2}\right) , \ldots , \Phi _{3}\left( \Upsilon _{n}\right) \right\}\).
In light of the aforementioned three stages, we can obtain the ranking values by addressing the RS, RP and FMF models and further acquire the final priority of alternatives. The original MULTIMOORA method utilizes the dominance theory to evaluate the ultimate ranking of assessment alternatives. However, the dominance theory possesses several deficiencies when it fuse the three parts to get the final order of alternatives, especially when dealing with the complex decision issues with large amounts of data. Accordingly, this essay aims to settle these defects through utilizing the WASPAS method to aggregate the values of these three parts of original MULTIMOORA. For the ranking values acquired from the three models, we will build up a new decision matrix and use the WASPAS method to evaluate the alternatives. The novel decision matrix is constructed as \(\mathcal {K}=\left( \upsilon _{\mu \jmath }\right) _{m \times 3}\), where \(\Upsilon =\{\Upsilon _{\mu }|\mu =1(1)m\}\) be a set of alternatives, the RS model, RP model and FMF model can be viewed as three criterions denoted as \(\tau =\left\{ \tau _{\jmath }|\jmath =1, 2, 3 \right\}\), \(\upsilon _{\mu \jmath }\) signifies the ranking values of each alternatives attained from the three models.
Step 8: Computing the weight \(\left\{ \chi _{1}, \chi _{2}, \chi _{3}\right\}\) of the three criteria with the help of the entropy weight approach:
Step 9: Calculate the weighted sum method (WSM) \(\Re _{\mu }^{(1)}\) and weighted prod method (WPM) \(\Re _{i}^{(2)}\) of every alternative \(\Upsilon _{\mu }\), respectively, that is
Step 10: Evaluate the best choose among the alternatives with the help of WASPAS model, which is
in which \(\iota\) is a adjustable parameter in decision strategy and \(\iota \in [0,1]\). Moreove, the WSM and WPM can be obtained through assigning the value to \(\iota =1\) and \(\iota =0\), respectively.
Step 11: End.
7 Case study: S3PRLP selection
In order to validate the feasibility and applicability of the designed q-ROF MULTIMOORA-WASPAS decision framework, we employ the decision framework to choose a desirable S3PRLP and further to improve the efficiency during the procedure of logistics transportation. Then, the sensitivity analysis of the q-ROF MULTIMOORA-WASPAS method in solving complicated decision issues is analysed in detail. Afterwards, we further analyse and discuss the superiority of the propounded q-ROF MULTIMOORA-WASPAS decision framework in the aspect of decision analysis with the aid of contrastive investigation.
7.1 Decision analysis procedure
In order to verify the practicability of the method proposed in this paper, a case of an automobile company selecting a third-party reverse logistics supplier is used to illustrate the practical application ability of the established decision-making framework. The rapid development of economic globalization provides more convenient conditions for enterprises to sell their products all over the world. While improving the competitive advantage of products, enterprises also gradually realize the importance of reverse logistics for improving product sales. Efficient reverse logistics can increase the satisfaction degree of customs and enhance the competitiveness of enterprises. In view of the complexity of reverse logistics, reverse logistics needs more professional equipment and technicians to ensure the safe development of logistics work. However, in order to improve the core competitiveness of enterprises, many enterprises focus on product R & D and sales. At the same time, due to the lack of professional logistics equipment technicians, enterprises do not pay enough attention to product logistics. Therefore, enterprises outsource reverse logistics to third-party professional logistics enterprises to improve product logistics efficiency and obtain higher customer satisfaction.
To improve the competitiveness of enterprise comprehensively, the automobile company BR will select a satisfied three-party reverse logistics supplier to undertake all logistics serve works of the BR company. Therefore, the enterprise management department builds a assessment committee through inviting four experts (denoted as \(AE_{1}, AE_{2}, AE_{3}, AE_{4}\))who possess ample professional knowledge and experiences in the aspect of professional knowledge logistic management, enterprise management. The enterprise management department selects six qualified logistics suppliers (denoted as \(\Upsilon _{\mu }(\mu =1, 2, \ldots , 6)\)) through a series of processes such as bidding and qualification examination, and the evaluation committee makes the final evaluation. By analysing the characteristics of the enterprise products and consulting the extent research literatures, the assessment committee ascertains the decision criteria in the procedure of evaluation through taking into account four main elements including economic, environmental, risk and society, the 11 criteria (denoted as \(\mathcal {C}_{\nu }(\nu =1, 2, \ldots , 11)\)) displayed in Table 6 that are ultimately considered to evaluate the six logistics suppliers and select a desirable option, whereas the assessment frame diagram is presented in Fig. 2. The Fig. 2 shows the hierarchy of the six logistics providers selected based on the selected evaluation criteria. In what follows, the propounded approach will be utilized to identify the order relation of the logistics providers.
In what follows, we shall employ the presented q-ROF MULTIMOORA-WASPAS decision framework to deal with the S3PRLP assessment and selection issue.
Step 1: In light of the fuzziness of assessment experts’ cognition, a mapping from the linguistic terms to the corresponding q-ROF number is provided to assist experts to provide their preference (evaluation) information for logistics suppliers with respect to different criteria. The assessment information for logistic suppliers through linguistic terms displayed in Table 4 are listed in Table 7, where the quadruple form (VL, ML, BL, M) signified the preference of four experts, respectively. Then we further obtain the q-ROF linguistic assessment matrix denoted as Table 7. With the aid of the table, we further attain the q-ROF numbers assessment matrix displayed in Table 8.
Step 2-3: Determining the importance degree of decision experts and the fused assessment matrix, respectively.
Because of the vagueness of experts’ cognition thought, the weights of experts are provided in the form linguistic terms \(\left\{ VHI, AMI, MI, HI\right\}\) and are further converted as \(\{AE_{1}=(0.85, 0.25), AE_{2}=(0.65, 0.45), AE_{3}=(0.55, 0.55), AE_{4}=(0.75, 0.35)\}\), therefore, expert weight information is computed by utilizing Eq. (42) (\(q=4\)) and denoted as \(\{\theta _{1}=0.3044, \theta _{2}=0.2494, \theta _{3}=0.1534, \theta _{4}=0.2928\}\). To acquire the comprehensive assessment of S3PRLPs given by all assessment committee, we achieve the aggregation procedure through utilizing the q-ROFFIWA operator displayed in Eq. (43) and attaining the fused assessment information listed in Table 9.
Step 4: Computing the combinative weight of evaluation criteria.
Step 4-I: Acquire the subjective weight of criteria using BWM method.
(1) The criterion \(\mathcal {C}_{6}\) and \(\mathcal {C}_{11}\) are respectively identified as the best and worst criteria after consultation with the assessment committee.
(2)-(4) To conduct pairwise comparison and attain the q-rung-orthopair fuzzy comparison vector Q-BO and Q-OW. Then the score values of fuzzy comparison vectors are computed by Eq. (44)–Eq. (47) and then converted into interval [1/9, 9] by Eq. (48), these results are displayed in Tables 10 and 11.
(5) Base on the optimization model of BWM in Eq. (49)–Eq. (50), we have
By utilizing the LINGO software, we can attain the subjective weight of criteria denoted as \(\varpi _{1}^{s}=0.0826, \varpi _{2}^{s}=0.1043, \varpi _{3}^{s}=0.0653, \varpi _{4}^{s}=0.0671, \varpi _{5}^{s}=0.1248, \varpi _{6}^{s}=0.1292, \varpi _{7}^{s}=0.0948, \varpi _{8}^{s}=0.1043, \varpi _{9}^{s}=0.0957, \varpi _{10}^{s}=0.0938, \varpi _{11}^{s}=0.0380\).
Step 4-II: Acquire the objective weight of criteria using entropy weigh method based on the score function.
The objective weight vector \(\varpi _{\nu }^{o}\) of criteria can be determined on the basis of entropy weight method through employing Eq. (51)–Eq. (53)., denoted as \(\varpi _{1}^{o}=0.0985, \varpi _{2}^{o}=0.0656, \varpi _{3}^{o}=0.0431, \varpi _{4}^{o}=0.1362, \varpi _{5}^{o}=0.0777, \varpi _{6}^{o}=0.1616, \varpi _{7}^{o}=0.1042, \varpi _{8}^{o}=0.0280, \varpi _{9}^{o}=0.0744, \varpi _{10}^{o}=0.1136, \varpi _{11}^{o}=0.0973\).
Step 4-III: Getting the synthesis weights of criteria through employing Eq. (55), denoted as \(\varpi _{1 }^{*}=0.0934, \varpi _{2}^{*}=0.0856, \varpi _{3}^{*}=0.0549, \varpi _{4}^{*}=0.0990, \varpi _{5}^{*}=0.1019, \varpi _{6}^{*}=0.1495, \varpi _{7}^{*}=0.1028, \varpi _{8}^{*}=0.0559, \varpi _{9}^{*}=0.0873, \varpi _{10}^{*}=0.1068 , \varpi _{11}^{*}=0.0629\).
Furthermore, the distribution situation of criteria weight is portrayed to clearly observe the importance degree of different kinds weights, which is displayed in Fig. 3.
Step 5: Achieving the decision outcomes on the basis of RS model by utilizing Eqs. (56–60), which are shown in Table 12.
Step 6: Attaining the decision resultants based on RP model by utilizing Eqs. (61–64), which are shown in Table 13. The reference point is obtained according to Eq.(61) denoted as:
Step 7: Acquiring the decision resultant based upon FMF algorithm through using Eqs. (65–69), which are shown in Table 14. Based on the decision outcomes obtained by the three algorithms of MULTIMOORA, we rebuild a new decision matrix, which is composed of m S3PRLPs and three criteria (RS, RP, FMF).
Step 8: The importance degrees of RS, RP and FMF are computed as \(\chi _{1}=0.3332, \chi _{2}=0.4441, \chi _{3}=0.2227\).
Step 9-10: The final decision results and ranks of alternative are acquired Based on the Eqs. (70)-(72), the corresponding outcomes are displayed in Table 15.
Based on the proposed MULTIMOORA-WASPAS decision framework, the decision results and final order relation of S3PRLPs are displayed in Table 15. According to the outcomes, the priority of S3PRLPs is \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{1}\). Therefore, the most desirable S3PRLP is the third option \(\Upsilon _{3}\).
7.2 Sensitivity analysis
This research builds a comprehensive group MULTIMOORA-WASPAS assessment framework to select a suitable S3PRLP under q-ROF context. The assessment information provided by experts using linguistic terms is employed for decision analysis and data fusion. During the procedure of fusion and analysis, parameter setting and weight allocation will produce different influences on the final decision outcomes and ranking of S3PRLPs. Thus, an exploration for the impact of parameter and weight is implemented in this subsection to further validate the stability of the propounded assessment framework.
To begin with, we discuss the effect of parameter \(\iota\) on the final ranking values and decision outcomes. In such a situation, we set the values of \(q=4\) and \(\zeta =3\) to analyze the influence of parameter fluctuations on the final utility value and ranks of S3PRLPs. The sorting values and final order relation of S3RLPs obtained through assigning different values of \(\iota\) are displayed in Table 16 and Fig. 4. From it, we obtain the final utility values of the selected S3PRLPs based on the values of \(\iota\) from 0.1 to 1. It is seen that the utility values of every S3PRLP increase gradually with the increase of the values of \(\iota\). Thus, the parameter \(\iota\) can be regarded as a preference index of decision expert to reasonably select the synthesize integration information through utilizing WSM and WPM. Although the utility values of S3PRLPs are diverse, the final order relation of S3PRLPs are all \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{1}\), which expounds that the developed multiple stage decision framework is stable for parameter \(\iota\). Especially, when \(\iota =1\), the final utility value of S3PRLP is computed by the MULTIMOORA-WSM method and when \(\iota =0\), the final utility value of S3PRLP is computed by the MULTIMOORA-WPM approach.
Secondly, we discuss the influence of different weight combinations on the final decision result in the presented decision framework. The criteria weight in q-ROF-MULTIMOORA-WASPAS decision framework is ascertained by combinative weight method. Thus, we shall analyse the decision result acquired by different weight spectacles. The corresponding weights and decision outcomes are displayed in Table 17. Based on it, it is obvious that the ranks based on subjective weight are different from the other three situations, which indicates that the weight possesses impact on the ranking. Accordingly, a reasonable criteria weight is the basic to acquire more rational and robust decision outcomes.
7.3 Validity test of the proposed approach
The decision results obtained by the presented q-ROF-MULTIMOORA-WASPAS decision framework shows that the rank of S3PRLPs is \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{1}\), namely, the \(\Upsilon _{3}\) and \(\Upsilon _{1}\) is the optimal and worst options, respectively. In order to validate the reliability and efficiency of the designed group decision framework, the following three standards proposed by Wang and triantaphyllou (Wang and Triantaphyllou 2008) are utilized to conduct test analysis:
Standard 1: When the assessment value of non-optimal scheme is replaced by another worse assessment value, the valid decision method will not change the optimal option because of the change of assessment information.
Standard 2: An effective decision method should follow the principle of transitivity.
Standard 3: When the original decision problem is decomposed into several decision subproblem, we employ the decision method to resolve the mentioned sub-problems and synthesize their ultimate ranking results. The comprehensive ranking outcome will maintain the consistency with the ranking results obtained from the original problem, which shows that this method is effective for coping with decision problems.
In the next, we conduct the validity analysis on the basis of the aforementioned standards. We get the final order relation of alternatives shown as \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{1}\) based upon the original information, the best and worst options are \(\Upsilon _{3}\) and \(\Upsilon _{1}\), respectively. With respect to Standard 1, we transform the assessment information of \(\Upsilon _{2}\) under different criteria in Table 9 into its complement form, which is displayed in Table 18. Based on the revised assessment information, we utilize the proposed decision framework to recompute this case and obtain the decision outcomes displayed in Table 19, the final ranks of S3PRLPs denoted as \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{1}\), namely, the optimal option is \(\Upsilon _{3}\). In light of the outcome, we find that the optimal options do not change after replacing the suboptimal alternative by another inferior options, which further validates the effectiveness of the proposed decision framework.
With respect to the standard 2 and standard 3, we divide the original into four sub-problems shown as \(\{\Upsilon _{1}, \Upsilon _{2}, \Upsilon _{3}, \Upsilon _{4}, \Upsilon _{5}\}\), \(\{\Upsilon _{1}, \Upsilon _{2}, \Upsilon _{3}, \Upsilon _{4}, \Upsilon _{6}\}\), \(\{\Upsilon _{1}, \Upsilon _{3}, \Upsilon _{4}, \Upsilon _{5}, \Upsilon _{6}\}\) and \(\{\Upsilon _{2}, \Upsilon _{3}, \Upsilon _{4}, \Upsilon _{5}, \Upsilon _{6}\}\). Then we use the proposed framework to compute the above four sun-problems and obtain the corresponding orders of S3PRLPs displayed as \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{1}\), \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{6} \succ \Upsilon _{1}\), \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{1}\) and \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{6}\) and further attain an integrated ranks of S3PRLPs as \(\Upsilon _{3} \succ \Upsilon _{4} \succ \Upsilon _{2} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{1}\). It is obviously that the integrated ranks of S3PRLPs is consistent with the original ranks. Accordingly, the decision approach meets the Standard 2 and Standard 3.
7.4 Contrastive analysis
In this subsection, we will execute a detailed comparison analysing between the designed method with the extant decision methodologies to validate the availability and the superiority of the designed innovative approach.
7.4.1 Numerical comparison
In order to confirm the efficiency and superiority of the developed q-ROF MULTIMOORA-WASPAS decision framework, we will execute the validity experiments and contrastive investigations between the previous q-ROF decision approaches and the presented method in this manuscript. The core of this essay is to build a more reasonable q-ROF decision method by merging MULTIMOORA and WASPAS method to resolve the issue with unknown criteria weight. Thus, we utilize the criteria weight determined in this article and several anterior approaches including q-ROF TOPSIS method (Ye et al. 2021), q-ROF-VIKOR model (Yang et al. 2021) and q-ROF CoCoSo method (Peng and Huang 2020) to settle the above-mentioned S3PRLP selection issue. The final decision results and ranks of S3PRLPs acquired through the aforementioned approach are displayed in Table 20. From Table 20, we can attain that although the ranks obtained from other extant methods, the optimal S3PRLP is always \(\Upsilon _{3}\), which indicates that the presented decision framework is rational and valid.
7.4.2 Further comparison
In this part, we ulteriorly expound the superiority of the presented decision framework with the aid of the comparisons in information fusion, criteria and expert weights determination, and ranking method. The significant merits of the extant approaches and the advanced decision framework are summarized in Table 21.
\(\clubsuit\) Compared with the q-ROF-TOPSIS approach proposed by Ye et al. (2021). The q-ROF-TOPSIS group decision method is presented based on the principal component analysis and entropy measure to evaluate the information service quality. This method uses entropy measure to determine the objective weight of the criteria, but ignores the subjective preference of experts for the criteria. Moreover, the q-ROF-TOPSIS determines the order of alternatives based on the closeness degree considering the positive and negative ideal solutions comprehensively, the ideal solutions obtained by utilizing the score function proposed in Liu and Wang (2018a), which may lead to several unreasonable results when the membership degree is equal to the nonmembership. By comparison, the propounded decision algorithm makes up the first deficiency with the aid of BWM method to ponder the subjective weights of criteria. Furthermore, the MULTIMOORA-WASPAS method not only synthetically takes into account the reference point method and other two integration models to acquire more robust decision results, but also avoids the unreasonable results caused by the dominance theory in the classical MULTIMOORA method. Correspondingly, the advanced MULTIMOORA-WASPAS approach is more robust in dealing with real decision problems, and the decision outcomes will be more rational and accurate.
\(\clubsuit\) Compared with the q-ROF-VIKOR approach proposed byYang et al. (2021). The q-ROF-VIKOR decision framework is constructed based on the CRITIC method to evaluate the internet of things challenges in the domain of sustainable supply chain management. It obtains the final ranks of internet of things challenges based on the comprise strategy consisting of two integration measures. However, the q-ROF-VIKOR assessment framework is built up based on the ideal solutions. Hence, it has the same defects with the TOPSIS method in which the ideal solution may not be unique in a decision problem. More importantly, the q-ROF-VIKOR decision framework determines the objective weight of the criteria via the CRITIC method, but ignores the subjective preferences of the experts. In comparison, the advanced MULTIMOORA-WASPAS approach considers the comprehensive weight of criteria by improved entropy and BWM method, which shall acquire a more reasonable and universal decision outcomes. Furthermore, the MULTIMOORA-WASPAS approach conquers the deficiency caused by the dominance theory in typical MULTIMOORA method and utilizes the WASPAS method to determine the final ranks of alternatives.
\(\clubsuit\) Compared with the q-ROF-CoCoSo approach proposed by Peng and Huang (2020). The q-ROF-CoCoSo decision algorithm is presented based on an improved score function and CRITIC method to resolve the multiple criteria decision problem with unknown criteria weight information. However, it also has the following three defects: (1) it fails to take into consideration the subjectivity preference of experts in the procedure of determining the criteria weight information. (2) although the CoCoSo method can rank the schemes based on a comprise solution consisting of three integration strategies, it ignores the impact of the reference point ideal in final sorting. In contrast, the proposed q-ROF-MULTIMOORA-WASPAS decision framework makes up the aforementioned deficiencies validly during the decision analysis procedure. Combined weights based on BWM and entropy weighting methods take into account the expert’s preferences in terms of objectivity and subjectivity; the MULTIMOORA-WASPAS approach integrating RS, RP, and FMF models is constructed to determine the integration utility value of alternatives from multiple aspects and obtain the orders of alternative by WASPAS method. Based on the comparisons, it is clear that the presented q-ROF-MULTIMOORA-WASPAS approach is more universal and flexible than q-ROF-CoCoSo decision algorithm to resolve the complex group decision issues.
\(\clubsuit\) Furthermore, we separately used the WASPAS method and the MULTIMOORA method to address this S3PRLPs selection problem to demonstrate the advantages of the proposed MULTIMOORA-WASPAS method. Based on the obtained group decision matrix and weight of criteria, we use the traditional MULTIMOORA method to obtain the final ranking of S3PRLPs as \(\Upsilon _{4} \succ \Upsilon _{3} \succ \Upsilon _{5} \succ \Upsilon _{6} \succ \Upsilon _{2} \succ \Upsilon _{1}\). We found that the ranking obtained is inconsistent with the ranking obtained by the method proposed in this article. This is because the classic MULTIMOORA method usually uses the dominance theory method to obtain the ranking results of the alternatives. However, the dominance theory is more complex and may lead to circular reasoning in pairwise comparisons, especially when the number of alternatives and criteria is large, which may lead to different alternatives obtaining the same ranking level. In addition, when applying the WASPAS method to solve this case, the final ranking of S3PRLPs is \(\Upsilon _{6} \succ \Upsilon _{3} \succ \Upsilon _{1} \succ \Upsilon _{2} \succ \Upsilon _{4} \succ \Upsilon _{5}\). We found that the ranking obtained is inconsistent with the ranking obtained by the method proposed in this article, because the WASPAS method only measures the score values of the scheme from the perspectives of WSM and WPM, and the aggregation operators used in both measures fail to consider the interactive impact between evaluation information. Overall, the method proposed in this article not only compensates for the shortcomings of the MULTIMOORA method in using dominance theory to obtain alternatives ranking, but also uses Frank interactive operators to calculate the scores of alternatives under ratio system, reference point and full-multiplicative form, which further improves the reliability, rationality, and robustness of decision results.
7.4.3 Merits analysis
Based upon the above comparison investigation with the extant literature mentioned, the significant merits and highlights of the advanced q-ROF MULTIMOORA-WASPAS decision framework are outlined as follows:
\(\checkmark\) The proposed q-ROF MULTIMOORA-WASPAS decision framework on the basis of novel score function, q-ROFFIWA operator and q-ROFFIWG operator has stronger flexibility and universality in dealing with uncertain decision problems. On the one hand, the novel score function enhances the consistency in the course of comparing q-ROF numbers through taking into consideration the hesitant degree, on the other hand, the q-ROFFIWA operator and q-ROFFIWG operator ponder the flexibility and reciprocal effect of membership and nonmembership grade, which can avoid the information loss and distorting phenomenon during the information fusion procedure.
\(\checkmark\) The weight determination of criteria and experts is momentous for managers to construct group decision framework. In the proposed method, the weights of experts are allowed to be given in the form of q-ROF numbers to express the fuzziness of expert subjective opinions; the weight of criteria is ascertained by combinative weight approach which entropy weight method portrays the objectivity of decision information and BWM characterizes the subjectivity of decision experts. It is evident that the propounded approach based upon comprehensive weights possesses stronger capability and universality in tackling practical decision issues.
\(\checkmark\) The ranking approach in this decision framework is built based on the improvement of the classical MULTIMOORA method. The final ranking determination method in most MULTIMOORA methods may bring about the irrational sorting results in the situation which involves large scale decision alternatives. Based on this, we built up a combinative decision method called MULTIMOORA-WASPAS to acquire a more reasonable sorting by using the WASPAS method to rank the three models of typical MULTIMOORA method. Accordingly, the proposed approach provides a more generalized extension of MULTIMOORA method for managers to resolve more complex decision issues.
8 Conclusion
How to effectively select and evaluate a suitable sustainable third-party logistics provider to enhance the overall competitiveness of enterprise is a significant and complex decision problem. In this essay, we design a comprehensive assessment framework through merging BWM, MULTIMOORA and WASPAS method to address the S3PRLPs selection issue with fully unknown weight information under q-ROF setting. Firstly, a novel scoring function is proposed to enhance the tractability of the process in comparing q-ROF numbers. Secondly, the q-ROFFIWA and q-ROFFIWG operators are advanced based on the constructed q-ROF Frank operations to ponder the interactive impact of information fusion procedure. Thirdly, we construct the q-ROF-MULTIMOORA-WASPAS decision framework based on the q-ROFIWA operator, the q-ROFFIWG operator, and the novel score function, where the synthetic weights of the criteria are determined by the modified BWM and entropy weight methods to account for both subjectivity and objectivity. Consequently, we utilize a practical example of the S3PRLPs selection issue to test the feasibility and practicability of the designed decision framework, and the comparative analysis is conducted with other existing methods to highlight its merits in dealing with complicated decision problems. However, when there are many criteria and they are relevant, the proposed framework will lead some deviation for the final ranks of providers. In this situation, some novel operators which consider the correlation among the criteria maybe reduce this deviation to attain more reasonable outcomes.
This study also has several limitations when dealing with the logistics provider selection problem. (1) The assessment criteria in this study are ascertained from single aspect of literature overview, thus a more comprehensive assessment criteria system by expert investigations and consultations can be constructed by taking into other perspectives such as policy and low-carbon. (2) The consensus reaching process which can improve the consistency of expert assessment fails to be pondered in our study, which may cause the deviation of the group assessment information. Therefore, further work will focus on constructing group decision models in this direction.
In the future, we will generalize the proposed decision model to others uncertain context utilize the proposed decision framework to cope with other complex assessment and selection issues such as offshore wind farm site selection (Rong and Yu 2023), emergency scheme selection (Rong et al. 2020, 2021), digitalization of transportation system evaluation (Akram et al. 2023), water supply optimal management (Akram et al. 2023), cold chain logistics distribution center selection (Rong et al. 2022), and so forth. In addition, the rise of big data and artificial intelligence brings countless challenges to resolving complex group decision problems. Accordingly, the research of large-scale group decision algorithms based upon data driven and its applications will become a hot-topic in the age of big data (Liu et al. 2019; Zhang et al. 2021).
References
Aguezzoul A (2014) Third-party logistics selection problem: a literature review on criteria and methods. Omega-Int J Manag Sci 49:69–78. https://doi.org/10.1016/j.omega.2014.05.009
Akram M, Shumaiza S (2021) Multi-criteria decision making based on q-rung orthopair fuzzy promethee approach. Iran J Fuzzy Syst 18(5):107–127. https://doi.org/10.22111/IJFS.2021.6258
Akram M, Sitara M (2022) Decision-making with q-rung orthopair fuzzy graph structures. Granul Comput 7(7):505–526. https://doi.org/10.1007/s41066-021-00281-3
Akram M, Naz S, Edalatpanah SA, Mehreen R (2021) Group decision-making framework under linguistic q-rung orthopair fuzzy Einstein models. Soft Comput 25:10309-C10334. https://doi.org/10.1007/s00500-021-05771-9
Akram M, Khan A, Ahmad U (2022) Extended multimoora method based on 2-tuple linguistic pythagorean fuzzy sets for multi-attribute group decision-making. Granul Comput 8(2):311–332. https://doi.org/10.1007/s41066-022-00330-5
Akram M, Zahid K, Kahraman C (2023) Integrated outranking techniques based on spherical fuzzy information for the digitalization of transportation system. Appl Soft Comput. https://doi.org/10.1016/j.asoc.2023.109992
Akram M, Zahid K, Deveci M (2023) Multi-criteria group decision-making for optimal management of water supply with fuzzy ELECTRE-based outranking method. Appl Soft Comput. https://doi.org/10.1016/j.asoc.2023.110403
Arato M, Speelman S, Dessein J, van Huylenbroeck G (2017) Assessment of socio-economic configuration of value chains: a proposed analysis framework to facilitate integration of small rural producers with global agribusiness. Int Food Agribus Manag Rev 20(1):25–43. https://doi.org/10.22434/IFAMR2015.0060
Arya V, Kumar S (2021) Extended TODIM method based on VIKOR for q-rung orthopair fuzzy information measures and their application in MAGDM problem of medical consumption products. Int J Intell Syst 36(11):6837–6870. https://doi.org/10.1002/int.22571
Atanassov KT (1989) More on intuitionistic fuzzy sets. Fuzzy Sets Syst 33:37C46
Bai C, Sarkis J (2019) Integrating and extending data and decision tools for sustainable third-party reverse logistics provider selection. Comput Oper Res 110:188–207. https://doi.org/10.1016/j.cor.2018.06.005
Baidya J, Garg H, Saha A, Mishra AR, Rani P, Dutta D (2021) Selection of third party reverses logistic providers: an approach of BCF-CRITIC-MULTIMOORA using Archimedean power aggregation operators. Complex Intell Syst 1:1. https://doi.org/10.1007/s40747-021-00413-x
Brauers WKM, Zavadskas EK (2010) Project management by MULTIMOORA as an instrument for transition economies. Technol Econ Dev Econ 16(1):5–24. https://doi.org/10.3846/tede.2010.01
Centobelli P, Cerchione R, Esposito E (2017) Developing the WH2 framework for environmental sustainability in logistics service providers: a taxonomy of green initiatives. J Clean Prod 165:1063–1077. https://doi.org/10.1016/j.jclepro.2017.07.150
Chen L, Duan D, Mishra AR, Alrasheedi M (2021) Sustainable third-party reverse logistics provider selection to promote circular economy using new uncertain interval-valued intuitionistic fuzzy-projection model. J Enterp Inf Manag. https://doi.org/10.1108/jeim-02-2021-0066
Chen Z, Zhang X, Govindan K, Wang X, Chin KS (2021) Third-party reverse logistics provider selection: a computational semantic analysis-based multi-perspective multi-attribute decision-making approach. Exp Syst Appl. https://doi.org/10.1016/j.eswa.2020.114051
Darko AP, Liang D (2020) Some q-rung orthopair fuzzy Hamacher aggregation operators and their application to multiple attribute group decision making with modified EDAS method. Eng Appl Artif Intell. https://doi.org/10.1016/j.engappai.2019.103259
Deliktas D, Ustun O (2017) Student selection and assignment methodology based on fuzzy MULTIMOORA and multichoice goal programming. Int Trans Oper Res 24(5):1173–1195. https://doi.org/10.1111/itor.12185
Frank MJ (1979) On the simultaneous associativity of f ( x, y ) and x + y f ( x, y ). Aequationes mathematicae 19(1):194–226. https://doi.org/10.1007/BF02189866
Gou X, Liao H, Xu Z, Herrera F (2017) Double hierarchy hesitant fuzzy linguistic term set and MULTIMOORA method: A case of study to evaluate the implementation status of haze controlling measures. Inf Fusion 38:22–34. https://doi.org/10.1016/j.inffus.2017.02.008
Govindan K, Kadzinski M, Ehling R, Miebs G (2019) Selection of a sustainable third-party reverse logistics provider based on the robustness analysis of an outranking graph kernel conducted with ELECTRE I and SMAA. Omega-Int J Manag Sci 85:1–15. https://doi.org/10.1016/j.omega.2018.05.007
Hafezalkotob A, Hafezalkotob A, Liao H, Herrera F (2020) Interval MULTIMOORA method integrating interval Borda rule and interval best-worst-method-based weighting model: case study on hybrid vehicle engine selection. IEEE Trans Cybern 50(3):1157–1169. https://doi.org/10.1109/tcyb.2018.2889730
He Y, Chen H, Zhou L, Liu J, Tao Z (2014) Intuitionistic fuzzy geometric interaction averaging operators and their application to multi-criteria decision making. Inf Sci 259:142–159. https://doi.org/10.1016/j.ins.2013.08.018
He J, Huang Z, Mishra AR, Alrasheedi M (2021) Developing a new framework for conceptualizing the emerging sustainable community-based tourism using an extended interval-valued Pythagorean fuzzy SWARA-MULTIMOORA. Technol Forecast Soc Change. https://doi.org/10.1016/j.techfore.2021.120955
Jana C, Muhiuddin G, Pal M (2019) Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making. Int J Intell Syst 34(12):3220–3240. https://doi.org/10.1002/int.22191
Jiang F, Ma Q (2018) Multi-attribute group decision making under probabilistic hesitant fuzzy environment with application to evaluate the transformation efficiency. Appl Intell 48(4):953–965. https://doi.org/10.1007/s10489-017-1041-x
Li Y, Ying C, Chin K, Yang H, Xu J (2018) Third-party reverse logistics provider selection approach based on hybrid-information MCDM and cumulative prospect theory. J Clean Prod 195:573–584. https://doi.org/10.1016/j.jclepro.2018.05.213
Li Z, Wei G, Wang R, Wu J, Wei C, Wei Y (2020) EDAS method for multiple attribute group decision making under q-rung orthopair fuzzy environment. Technol Econ Dev Econ 26(1):86–102. https://doi.org/10.3846/tede.2019.11333
Liang D, Darko AP, Xu Z, Wang M (2019) Aggregation of dual hesitant fuzzy heterogenous related information with extended Bonferroni mean and its application to MULTIMOORA. Comput Ind Eng 135:156–176. https://doi.org/10.1016/j.cie.2019.05.029
Liao H, Qin R, Gao C, Wu X, Hafezalkotob A, Herrera F (2019) Score-HeDLiSF: A score function of hesitant fuzzy linguistic term set based on hesitant degrees and linguistic scale functions: An application to unbalanced hesitant fuzzy linguistic MULTIMOORA. Inf Fusion 48:39–54. https://doi.org/10.1016/j.inffus.2018.08.006
Liao H, Zhang H, Zhang C, Wu X, Mardani A, Al-Barakat A (2020) A Q-Rung orthopair fuzzy GLDS method for investment evaluation of be angel capital in China. Technol Econ Dev Econ 26(1):103–134. https://doi.org/10.3846/tede.2020.11260
Lin M, Huang C, Xu Z (2020) MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustain Cities Soc. https://doi.org/10.1016/j.scs.2019.101873
Liu P, Li Y (2019) An extended MULTIMOORA method for probabilistic linguistic multi-criteria group decision-making based on prospect theory. Comput Ind Eng 136:528–545. https://doi.org/10.1016/j.cie.2019.07.052
Liu P, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33(2):259–280. https://doi.org/10.1002/int.21927
Liu P, Wang P (2018) Multiple-attribute decision-making based on Archimedean Bonferroni Operators of q-rung orthopair fuzzy numbers. IEEE Trans Fuzzy syst 27(5):834–848. https://doi.org/10.1109/tfuzz.2018.2826452
Liu A, Ji X, Lu H, Liu H (2019) The selection of 3PRLs on self-service mobile recycling machine: Interval-valued pythagorean hesitant fuzzy best-worst multi-criteria group decision-making. J Clean Prod 230:734–750. https://doi.org/10.1016/j.jclepro.2019.04.257
Liu BS, Zhou Q, Ding RX, Palomares I, Herrera F (2019) Large-scale group decision making model based on social network analysis: trust relationship-based conflict detection and elimination. Eur J Oper Res 275(2):737–754. https://doi.org/10.1016/j.ejor.2018.11.075
Liu Y, Wei G, Abdullah S, Liu J, Xu L, Liu H (2021) Banzhaf-Choquet-copula-based aggregation operators for managing q-rung orthopair fuzzy information. Soft Comput 25(10):6891–6914
Liu P, Naz S, Akram M, Muzammal M (2022) Group decision-making analysis based on linguistic q-rung orthopair fuzzy generalized point weighted aggregation operators. Int J Mach Learn Cybern 13(4):883–906. https://doi.org/10.1007/s13042-021-01425-2
Luo L, Zhang C, Liao H (2019) Distance-based intuitionistic multiplicative MULTIMOORA method integrating a novel weight-determining method for multiple criteria group decision making. Comput Ind Eng 131:82–98. https://doi.org/10.1016/j.cie.2019.03.038
Mavi RK, Goh M, Zarbakhshnia N (2017) Sustainable third-party reverse logistic provider selection with fuzzy SWARA and fuzzy MOORA in plastic industry. Int J Adv Manuf Technol 91(5–8):2401–2418. https://doi.org/10.1007/s00170-016-9880-x
Mishra AR, Rani P, Pandey K (2021) Fermatean fuzzy CRITIC-EDAS approach for the selection of sustainable third-party reverse logistics providers using improved generalized score function. J Ambient Intell Humanized Comput. https://doi.org/10.1007/s12652-021-02902-w
Obasaju BO, Olayiwola WK, Okodua H, Adediran OS, Lawal AI (2021) Regional economic integration and economic upgrading in global value chains: selected cases in Africa. Heliyon. https://doi.org/10.1016/j.heliyon.2021.e06112
Omrani H, Alizadeh A, Amini M (2020) A new approach based on BWM and MULTIMOORA methods for calculating semi-human development index: an application for provinces of Iran. Socio-Econ Plan Sci. https://doi.org/10.1016/j.seps.2019.02.004
Peng X, Dai J (2019) Research on the assessment of classroom teaching quality with q-rung orthopair fuzzy information based on multiparametric similarity measure and combinative distance-based assessment. Int J Intell Syst 34(7):1588–1630. https://doi.org/10.1002/int.22109
Peng X, Huang H (2020) Fuzzy decision making method based on COCOSO with CRITIC for financial risk evaluation. Technol Econ Dev Econ 26(4):695–724. https://doi.org/10.3846/tede.2020.11920
Peng JJ, Wang JQ, Wang J, Zhang HY, Chen XH (2016) Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int J Syst Sci 47(9–12):2342–2358
Peng X, Dai J, Garg H (2018a) Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. Int J Intell Syst 33(11):2255–2282. https://doi.org/10.1002/int.22028
Peng X, Dai J, Liu L (2018b) Interval-valued dual hesitant fuzzy information aggregation and its application in multiple attribute decision making. Int J Uncertain Quantif 8(4):361–382. https://doi.org/10.1615/Int.J.UncertaintyQuantification.2018021197
Prakash C, Barua MK (2016) An analysis of integrated robust hybrid model for third-party reverse logistics partner selection under fuzzy environment. Resour Conserv Recycl 108:63–81. https://doi.org/10.1016/j.resconrec.2015.12.011
Qin J, Liu X, Pedrycz W (2016) Frank aggregation operators and their application to hesitant fuzzy multiple attribute decision making. Appl Soft Comput 41:428–452. https://doi.org/10.1016/j.asoc.2015.12.030
Rahimi S, Hafezalkotob A, Monavari SM, Hafezalkotob A, Rahimi R (2020) Sustainable landfill site selection for municipal solid waste based on a hybrid decision-making approach: fuzzy group BWM-MULTIMOORA-GIS. J Clean Prod 248:1. https://doi.org/10.1016/j.jclepro.2019.119186
Rani P, Mishra AR (2021) Fermatean fuzzy Einstein aggregation operators-based MULTIMOORA method for electric vehicle charging station selection. Exp Syst Appl. https://doi.org/10.1016/j.eswa.2021.115267
Rezaei J (2015) Best-worst multi-criteria decision-making method. Omega 53:49–57. https://doi.org/10.1016/j.omega.2014.11.009
Rong Y, Yu L (2023) Decision support system for prioritization of offshore wind farm site by utilizing picture fuzzy combined compromise solution group decision method. Entropy 25(7):1081. https://doi.org/10.3390/e25071081
Rong Y, Liu Y, Pei Z (2020) Complex q-rung orthopair fuzzy 2-tuple linguistic Maclaurin symmetric mean operators and its application to emergency program selection. Int J Intell Syst 35(11):1749–1790. https://doi.org/10.1002/int.22271
Rong Y, Liu Y, Pei Z (2021) A novel multiple attribute decision-making approach for evaluation of emergency management schemes under picture fuzzy environment. Int J Mach Learn Cybern. https://doi.org/10.1007/s13042-021-01280-1
Rong Y, Yu L, Niu W, Liu Y, Senapati T, Mishra AR (2022) MARCOS approach based upon cubic Fermatean fuzzy set and its application in evaluation and selecting cold chain logistics distribution center. Eng Appl Artif Intell. https://doi.org/10.1016/j.engappai.2022.105401
Rostamzadeh R, Esmaeili A, Sivilevicius H, Nobard HBK (2020) A fuzzy decision-making approach for evaluation and selection of third party reverse logistics provider using fuzzy Aras. Transport 35(6):635–657. https://doi.org/10.3846/transport.2020.14226
Sarkar A, Moslem S, Esztergar-Kiss D, Akram M, Jin L, Senapati T (2023) A hybrid approach based on dual hesitant q-rung orthopair fuzzy Frank power partitioned Heronian mean aggregation operators for estimating sustainable urban transport solutions. Eng Appl Artif Intell. https://doi.org/10.1016/j.engappai.2023.106505
Sen DK, Datta S, Mahapatra SS (2017) Decision support framework for selection of 3PL service providers: dominance-based approach in combination with grey set theory. Int J Inf Technol Decis Mak 16(1):25–57. https://doi.org/10.1142/s0219622016500474
Senthil S, Srirangacharyulu B, Ramesh A (2014) A robust hybrid multi-criteria decision making methodology for contractor evaluation and selection in third-party reverse logistics. Exp Syst Appl 41(1):50–58. https://doi.org/10.1016/j.eswa.2013.07.010
Singh RK, Gunasekaran A, Kumar P (2018) Third party logistics (3PL) selection for cold chain management: a fuzzy AHP and fuzzy TOPSIS approach. Ann Oper Res 267(1–2):531–553. https://doi.org/10.1007/s10479-017-2591-3
Tang X, Yang S, Pedrycz W (2018) Multiple attribute decision-making approach based on dual hesitant fuzzy Frank aggregation operators. Appl Soft Comput 68:525–547. https://doi.org/10.1016/j.asoc.2018.03.055
Tavana M, Zareinejad M, Santos-Arteaga FJ (2018) An intuitionistic fuzzy-grey superiority and inferiority ranking method for third-party reverse logistics provider selection. Int J Syst Sci-Oper Logist 5(2):175–194. https://doi.org/10.1080/23302674.2016.1256448
Tian C, Peng JJ, Zhang S, Zhang WY, Wang JQ (2019) Weighted picture fuzzy aggregation operators and their applications to multi-criteria decision-making problems. Comput Ind Eng. https://doi.org/10.1016/j.cie.2019.106037
Wang X, Triantaphyllou E (2008) Ranking irregularities when evaluating alternatives by using some ELECTRE methods. Omega 36(1):45–63. https://doi.org/10.1016/j.omega.2005.12.003
Wang W, Liu X, Qin Y (2018) A fuzzy Fine-Kinney-based risk evaluation approach with extended MULTIMOORA method based on Choquet integral. Comput Ind Eng 125:111–123. https://doi.org/10.1016/j.cie.2018.08.019
Wang Y, Sun B, Zhang X, Wang Q (2020) BWM and MULTIMOORA-based multigranulation sequential three-way decision model for multi-attribute group decision-making problem. Int J Approx Reason 125:169–186. https://doi.org/10.1016/j.ijar.2020.07.003
Wei G, Gao H, Wei Y (2018) Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making. Int J Intell Syst 33(7):1426–1458. https://doi.org/10.1002/int.21985
Wu X, Liao H, Xu Z, Hafezalkotob A, Herrera F (2018) Probabilistic Linguistic MULTIMOORA: A Multicriteria Decision Making Method Based on the Probabilistic Linguistic Expectation Function and the Improved Borda Rule. IEEE Trans Fuzzy Syst 26(6):3688–3702. https://doi.org/10.1109/tfuzz.2018.2843330
Xia M, Xu Z, Zhu B (2012) Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm. Knowl-Based Syst 31:78–88. https://doi.org/10.1016/j.knosys.2012.02.004
Xing Y (2021) q-Rung orthopair fuzzy frank power point aggregation operators with new multi-parametric distance measures. J Intell Fuzzy Syst 41(6):7275–7297. https://doi.org/10.3233/jifs-211152
Xing Y, Zhang R, Wang J, Bai K, Xue J (2020) A new multi-criteria group decision-making approach based on q-rung orthopair fuzzy interaction Hamy mean operators. Neural Comput Appl 32(11):7465–7488. https://doi.org/10.1007/s00521-019-04269-8
Xu L, Liu Y, Liu F (2021) Improved MABAC method based on single-valued neutrosophic 2-tuple linguistic sets and Frank aggregation operators for MAGDM. Comput Appl Math. https://doi.org/10.1007/s40314-021-01656-7
Yager RR (2013) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965. https://doi.org/10.1109/TFUZZ.2013.2278989
Yager RR (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230. https://doi.org/10.1109/tfuzz.2016.2604005
Yahya M, Abdullah S, Chinram R, Al-Otaibi YD, Naeem M (2021) Frank aggregation operators and their application to probabilistic hesitant fuzzy multiple attribute decision-making. Int J Fuzzy Syst 23(1):194–215. https://doi.org/10.1007/s40815-020-00970-2
Yang K, Duan T, Feng J, Mishra AR (2021) Internet of things challenges of sustainable supply chain management in the manufacturing sector using an integrated q-Rung Orthopair Fuzzy-CRITIC-VIKOR method. J Enterp Inf Manag. https://doi.org/10.1108/jeim-06-2021-0261
Ye A, Zhang R, Wu P, Xing Y (2021) q-Rung orthopair fuzzy TOPSIS method and the application to information service quality evaluation in online health community. J Intell Fuzzy Syst 41(2):3697–3714. https://doi.org/10.3233/jifs-211123
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353
Zarbakhshnia N, Soleimani H, Ghaderi H (2018) Sustainable third-party reverse logistics provider evaluation and selection using fuzzy SWARA and developed fuzzy COPRAS in the presence of risk criteria. Appl Soft Comput 65:307–319. https://doi.org/10.1016/j.asoc.2018.01.023
Zhang X, Su T (2020) The dominance degree-based heterogeneous linguistic decision-making technique for sustainable 3PRLP selection. Complexity. https://doi.org/10.1155/2020/6102036
Zhang Y, Chen X, Gao L, Dong Y, Pedryczc W (2021) Consensus reaching with trust evolution in social network group decision making. Exp Syst Appl. https://doi.org/10.1016/j.eswa.2021.116022
Zhu H, Zhao J, Li H (2021) q-ROF-SIR methods and their applications to multiple attribute decision making. Int J Mach Learn Cybern. https://doi.org/10.1007/s13042-020-01267-4
Acknowledgements
The research was funded by the Ministry of Education Humanities and Social Sciences Research Planning Fund Project (23YJA630122).
Author information
Authors and Affiliations
Contributions
Yuan Rong and Liying Yu wrote the main manuscript text and finished the figures and Tables of the manuscript.Yuan Rong, Liying Yu and Yi Liu designed the methodology framework of the manuscript.Yuan Rong, Liying Yu, Yi Liu, Xingdong Peng and Harish Garg finished the conceptualization of the manuscript.All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical statement
Articles do not rely on clinical trials.
Human and animal participants
All submitted manuscripts containing research which does not involve human participants and/or animal experimentation.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The explanation of the abbreviations in this manuscript are displayed in Table 22.
Proof of Theorem 5
In what follows, we shall prove that the Eq. (25) is valid by using mathematical induction. It is apparent that Eq. (25) hold for \(n=1\). Assume that Eq. (25) is keeps for \(n=z\), then
Afterwards, when \(n=z+1\), one has
Hence, Eq.(25) is valid for \(n=z+1\). \(\square\)
Proof of Property 1
Therefore, property 1 is true. \(\square\)
Proof of Property 2
Since \(\phi _{\nu }\ge \tilde{\phi }_{\nu }\) and \(\left( \phi _{\nu }\right) ^{q}+\left( \varphi _{\nu } \right) ^{q}\le \left( \tilde{\phi }_{\nu }\right) ^{q} + \left( \tilde{\varphi }_{\nu }\right) ^{q}\), one has
Furthermore,
Based upon the score function of q-ROF numbers, we have
Accordingly, \(q-ROFFIWA\left( \mathcal {Q}_{1}, \mathcal {Q}_{2} \ldots , \mathcal {Q}_{n}\right) \ge q-ROFFIWA\left( \tilde{\mathcal {Q}}, \tilde{\mathcal {Q}} \ldots , \tilde{\mathcal {Q}}_{n}\right)\) holds, which achieves the proof of Property 2. \(\square\)
Proof of Property 3
Since \(\min \limits _{1\le \nu \le n} \left( \phi _{\nu }\right) ^{q} \le \left( \phi _{\nu }\right) ^{q} \le \max \limits _{1\le \nu \le n} \left( \phi _{\nu }\right) ^{q}\), based on the idempotency and monotonicity of q-ROFFIWA operator, one has
Furthermore,
In addition, based on the definition of q-ROF numbers, we have
With the aid of the comparison laws of q-ROF numbers, we can attain \(\mathcal {Q}^{-} \le q-ROFFIWA\left( \mathcal {Q}_{1}, \mathcal {Q}_{2} \ldots , \mathcal {Q}_{n}\right) \le \mathcal {Q}^{+}\), which achieves the proof of Property 3. \(\square\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rong, Y., Yu, L., Liu, Y. et al. An integrated group decision-making framework for assessing S3PRLPs based on MULTIMOORA-WASPAS with q-rung orthopair fuzzy information. Artif Intell Rev 57, 163 (2024). https://doi.org/10.1007/s10462-024-10782-7
Accepted:
Published:
DOI: https://doi.org/10.1007/s10462-024-10782-7