Combining quantitative and qualitative reasoning in concurrent multi-player games

Abstract

We propose a general framework for modelling and formal reasoning about multi-agent systems and, in particular, multi-stage games where both quantitative and qualitative objectives and constraints are involved. Our models enrich concurrent game models with payoffs and guards on actions associated with each state of the model and propose a quantitative extension of the logic ${\textsf {ATL}}^{*}$ that enables the combination of quantitative and qualitative reasoning. We illustrate the framework with some detailed examples. Finally, we consider the model-checking problems arising in our framework and establish some general undecidability and decidability results for them.

1 Introduction

Quantitative and qualitative reasoning about agents and multi-agent systems is pervasive in many areas of AI and game theory, including multi-agent planning and intelligent robotics. In particular, the studies of cooperative and non-cooperative multi-player games deal with both aspects of strategic abilities of agents, but usually separately. Quantitative reasoning studies the abilities of agents to achieve quantitative objectives, such as optimizing payoffs (e.g., maximizing rewards or minimizing cost) or, more generally, preferences on outcomes. This tradition comes from game theory and economics and usually studies one-shot normal form games, their (finitely or infinitely) repeated versions, and extensive form games. On the other hand, qualitative reasoning, coming mainly from logic and computer science, is about strategic abilities of players for achieving qualitative objectives: reaching or maintaining states with desired properties, e.g., winning states or safe states, etc.

Put as a slogan, quantitative reasoning is concerned with how players can become maximally rich, or how to pay as little cost as possible, while qualitative reasoning is about how players can achieve a state of ‘happiness’, e.g. winning, or how to avoid reaching a state of ‘unhappiness’ (losing) in the game.

The most essential technical difference between qualitative and quantitative objectives is that the former are typically expressed by temporal patterns over Boolean properties of game states on a given play in a finite state space and their verification requires limited memory, whereas the satisfaction of the latter depends on numerical data associated with the history of the play (accumulated utilities) or even with the whole play (average payoffs and their limit, or discounted accumulated utilities) and therefore generally requires larger, or even unbounded memory. It is thus generally computationally more demanding and costly to design or verify strategies satisfying quantitative objectives than qualitative ones. More generally, decision theory and game theory study rational behaviour of players aiming at optimising their performance in accordance with their preferences between outcomes. Preferences can be regarded as both qualitative and quantitative objectives and, if equipped with a suitable mechanism for preference aggregation over a series of outcomes accumulated in the course of the play, then our work presented here – based on quantitative payoffs in naturally ordered numerical domains – can be suitably generalised to that setting.

Often both types of reasoning about multi-agent systems are essential and must be explored interactively. For instance, in multi-agent planning and robotics it is important to achieve the agents’ qualitative goals while satisfying various quantitative constraints on time and resource consumption. This motivates the need for developing a modelling framework for combining qualitative and quantitative reasoning, which is the main objective of the present paper.

Our contribution Here we introduce a general framework for combined qualitative and quantitative reasoning, by enriching the arguably most studied models in the qualitative reasoning tradition, viz. concurrent game models, cf.  [6, 50], with a quantitative dimension as follows. The concurrent game models are multi-agent transition systems where transitions are determined by simultaneous collective actions taken by all players. States are labelled with various atomic propositions describing their important features (e.g., winning state, safe state, etc.) and enabling qualitative reasoning in the system. In the enriched models proposed here agents are associated with accumulating utilities (e.g., resources) and the state transitions determine utility payoffs to each player according to payoff tables for the one-shot normal form games associated with all possible tuples of actions that can be applied at the states. Thus, combination of quantitative game-theoretic reasoning with the qualitative logical reasoning is enabled. The resulting models can also be regarded as multi-stage games, see [35], with additional qualitative objectives. Again, put as a slogan, our framework allows, for instance, reasoning about whether and how a player can reach or maintain a state of ‘happiness’ while becoming or remaining as rich as desired, or paying an explicitly limited price on the way.

We illustrate the framework with two detailed running examples. The first one is of a more abstract, game-theoretic nature, where two players play an infinite-round combination of 3 well-known normal form games (Prisoners Dilemma, Battle of the Sexes, and Coordination Game) associated with the 3 states of the model, and the transitions between these games are determined by the action profiles applied at each round, while the players accumulate utilities in the process of the plays. The second example is of a more concrete nature, illustrating resource-bounded reasoning by modelling a scenario where a team of 3 robots has to accomplish a certain mission determined by a qualitative objective while satisfying some quantitative resource constraints (maintaining energy levels required for the execution of the required actions) throughout the operation.

To enable combined qualitative and quantitative logical reasoning we introduce a quantitative extension of the logic ${\textsf {ATL}}^{*}$, introduced in  [6], provide formal semantics for it in concurrent game models enriched with payoffs and guards, and show how it can be used for specifying properties of the running examples combining qualitative and quantitative objectives. We then study the model checking problems arising in our framework and establish some general undecidability and decidability results.

Structure of the paper In the preliminary Sect. 2 we present in detail the purely qualitative concurrent game models and the associated logic for strategic abilities ${\textsf {ATL}}^{*}$, as well as basic concepts needed to introduce quantitative constraints in the models and the logical language. In Sect. 3 we present the new modelling framework based on concurrent game models with payoffs and guards and provide detailed examples. In Sect. 4 we introduce multi-agent a quantitative extension $\textsf {QATL}^{*}$ of the logic ${\textsf {ATL}}^{*}$ provide semantics for it in concurrent game models with payoffs and guards. In Sect. 5 we establish some general decidability and undecidability results for the model-checking problems in fragments of $\textsf {QATL}^{*}$. We end with a concluding Sect. 6 discussing perspectives for further study, followed by a short technical appendix.

Related work As mentioned above, the two traditions—of quantitative and qualitative reasoning—have followed rather separate developments with generally quite different agendas, methods and results. Still, some ideas, approaches and techniques can converge to enable the study of multi-agent systems and games combining features from both. A non-exhaustive overview with inevitably incomplete list of references on the main research developments in the area are listed below. Our framework shares various common or similar conceptual and technical features with some of these works, yet, there are essential differences with each of them, justifying the originality of our framework, which are briefly discussed here.

• Purely qualitative logics of games and multi-agent systems, such as the Coalition logic CL [50], the Alternating time temporal logic ${\textsf {ATL}}^{*}$ [6], and some extensions and variations of it, incl. [21, 42, 43, 56] etc., formalizing and studying qualitative reasoning in concurrent game models. This is the closest conceptually and technically logic-based framework on which ours builds, by expanding with the quantitative features, based on payoffs and guards.

• Resource-bounded models and logics [1,2,3,4,5, 7, 8, 19, 46, 48], endowing concurrent game models with some quantitative aspects by considering cost of agents’ actions and reasoning about what players with bounded resources can achieve. These are both technically quite close and conceptually related to the present work, so we provide further more detailed parallels between them and our framework.

• Extensions of qualitative reasoning (e.g., reachability and Büchi objectives) in multi-player concurrent games with some quantitative aspects by considering a preference preorder on the set of qualitative objectives, see e.g., [14, 15], thereby adding payoff-maximizing objectives and thus creating a setting where traditional game-theoretic issues such as game value problems and Nash equilibria become relevant.

  
  

  Our framework is technically related, though richer in its quantitative features and the logical language, and more widely applicable than these.

• Essentially related in spirit to our work are also stochastic games introduced by Shapley in 1953 (see [47, 54]) and, in particular, stochastic games with quantitative objectives, such as energy games and discounted and mean-payoff games, see e.g. [51], and in particular the more recent works [58] (on multi-mean-payoff and multi-energy games) and [16] (on average-energy games). Technically, our models build on deterministic analogues of stochastic games and extend them with the qualitative aspects and the associated logical language.

• Deterministic or stochastic infinite games on graphs, with qualitative objectives: typically, reachability, and more generally, parity objectives or $\omega$-regular objectives see e.g. [25, 28,29,30]. Our framework is again technically related, but richer in its multi-agent aspects, quantitative features, and the logical language, and with wider modelling scope and potential applications.

• Purely quantitative repeated games, much studied in game theory (see e.g., [35, 49]), which can be naturally regarded as a quite special case of our framework, viz. one-state concurrent game models with accumulating payoffs paid to each player after every round.

• Conceptually different, but technically quite relevant to the purely operational models which our framework generates are studies of counter automata, Petri nets, vector addition systems (VAS, introduced in  [44]) also VAS extended with states (VASS) [11, 12, 38, 41], etc. – essentially a study of the purely quantitative single-agent case of concurrent game models (see e.g. [11, 32]), where only accumulated utilities but no qualitative objectives are taken into account and a typical problem is to decide reachability from a given initial payoff configuration of payoff configurations satisfying formally specified arithmetic constraints. More recently, two-player games (between controller and environment) on VAS and VASS have been studied, e.g. in [9, 17].

• There have also been several recent threads of research on combinations of qualitative and quantitative game analysis, coming closer in spirit to the present work, such as [59], which considers infinite 2-player turn-based games where every move is associated with a ‘reward’ (e.g., priority in parity games) after every move and eventually the payoffs are determined by the resulting infinite sequence of rewards. Also, there is an active research on mean-payoff and energy parity games, including [23, 24, 26, 27], and [13] combining parity objectives with quantitative requirements on mean payoffs or maintaining non-negative energy. Our framework is again technically related, but richer in its multi-agent aspects, quantitative features, and the logical language, and modelling scope.

• Other relevant references discussing the interaction between qualitative and quantitative reasoning in multi-player games include [52], and [37].

As noted above, resource-bounded models and logics are more closely related, both technically and conceptually, to our framework than most of the other discussed research areas, so we provide here a more detailed comparison¹ with these. First, we note that resource-bounded models and logics are more restricted in scope, as they focus only on the resource-based interpretation of the payoffs. That is an essential conceptual difference with our framework, which models a much more general scenario, where individual agents stand to gain or lose (value or resources) as a result of their collective actions, which also have the qualitative effect of determining the subsequent ‘games’ to play. Thus, the payoffs in our framework can be regarded not only as resource consumption and generation, but also as gains, incentives, rewards, etc. That, in particular, leads also to some technical differences between the above mentioned works and ours, also reflected in the logical language, formal semantics, and model-checking problems and procedures. More specifically, many of these frameworks assume only consumption of resources in the transitions, and a typical model-checking problem asks whether the proponent coalition has a resource-bounded strategy to achieve its objective with a given initial resource budget. Some of the frameworks mentioned above also consider increase of resources within a fixed total amount (e.g., money), which also has a similar technical effect of enabling decidability of the model checking, at the price of limiting the applicability. Yet others, incl. [1, 2], also allow production of resources but impose various limitations, e.g. on the number of resource units, or on the possible range of the resources [2, 7, 8], etc. More importantly, however, the consumption and production of resources in these works typically depends only on the individual agents’ actions or on the joint actions of the proponent coalition. While this makes very good sense in various real scenarios, and also often results in decidable (and sometimes even tractable) model checking, it does not cover many situations – for instance, related to multi-agent teams – where agents not only consume, but also generate resources in a way which is determined by the actions of all agents, not only those in the proponent coalition, as enabled in our framework and exemplified here in Example 2. Furthermore, our framework essentially involves the use of guards which determine the available actions to the individual agents depending on their current accumulated payoff, resp. resource availability. These make substantial technical differences and, as shown in the paper, can easily (and not surprisingly) lead to undecidable model checking, thus making the problem for constructing desirable strategies for the agents quite more challenging.

In summary, the framework presented in this work shares and combines features of several previous developments in a way that we believe to be conceptually natural, simple, elegant and uniform, while technically very rich and with a wide range of potential applications. In particular, we emphasise that the design of this framework was not driven by aiming at ensuring decidability results, but by its naturalness and intended scope of applicability.

2 Preliminaries

Concurrent game models ([6, 50]) can be regarded as multi-stage combinations of normal form games as they incorporate a whole family of such games, each associated with a state of a given transition system. However, in the concurrent game models the outcomes of a normal form game associated with a given state are simply the possible successor states with their associated games, etc. whereas no payoffs, or even preferences on outcomes, are assigned. Thus, a play in a concurrent game model consists of a sequence of – generally different – one-shot normal form games played in succession. All that is taken into account in the purely logical framework are the properties—expressed by formulae of a logical language—of the states occurring in the play. Concurrent game models can also be viewed as generalisation of (possibly infinite) extensive form games where cycles and simultaneous moves of different players are allowed, but no payoffs are assigned.

Here is the precise technical definition. A concurrent game model (CGM) is a tuple

$$\begin{aligned} \mathcal {S} = (\textsf {Ag}, \textsf {St}, \{\textsf {Act} _\textsf {a} \}_{\textsf {a} \in \textsf {Ag}}, \{\textsf {act} _{\textsf {a}}\}_{\textsf {a} \in \textsf {Ag}}, \textsf {out},\textsf {Prop},\textsf {L}) \end{aligned}$$

comprising:

• a non-empty, fixed set of players (agents) $\textsf {Ag} =\{1,\dots , k\}$ and a set of actions $\textsf {Act} _{\textsf {a}}\ne \emptyset$ for each $\textsf {a} \in \textsf {Ag}$.

  For any $A\subseteq \textsf {Ag}$ we will denote $\textsf {Act} _A{:}{=}\prod _{\textsf {a} \in A}\textsf {Act} _{\textsf {a}}$ and will use $\mathbf {\alpha }_{A}$ to denote a tuple from $\textsf {Act} _A$. In particular, $\textsf {Act} _\textsf {Ag}$ is the set of all possible action profiles in $\mathcal {S}$.

• a non-empty set of game states $\textsf {St}$.

• for each $\textsf {a} \in \textsf {Ag}$, a map $\textsf {act} _{\textsf {a}} : \textsf {St} \rightarrow \mathcal {P}({\textsf {Act} _{\textsf {a}}})$ setting for each state s the actions available to $\textsf {a}$ at s.

• a transition function $\textsf {out}: \textsf {St} \times \textsf {Act} _\textsf {Ag} \, \rightarrow \textsf {St}$ that assigns to every state q and action profile $\mathbf {\alpha }_{\textsf {Ag}} = \langle \alpha _{\textsf {1}}, \dots , \alpha _{\textsf {k}}\rangle$, such that $\alpha _{\textsf {a}} \in \textsf {act} _{\textsf {a}}(q)$ for every $\textsf {a} \in \textsf {Ag}$ (i.e., every $\alpha _{\textsf {a}}$ that can be executed by player $\textsf {a}$ in state q), the (deterministic) successor (outcome) state $\textsf {out} (q,\mathbf {\alpha }_{\textsf {Ag}})$.

• a set of atomic propositions $\textsf {Prop}$ and a labelling function $\textsf {L}:\textsf {St} \rightarrow \mathcal {P}({\textsf {Prop}})$.

Thus, all players in a CGM execute their actions synchronously and the combination of these actions, together with the current state, determines the transition to a (unique) successor state in the CGM. A play in a CGM $\mathcal {M}$ is an infinite sequence of such subsequent states. For further technical details refer to [6, 21, 31, Ch.9],

The logic of strategic abilities ${\textsf {ATL}}^{*}$, first introduced and studied in [6] (see also [21] and [31, Ch.9] for technical details and further references), is a logical system suitable for specifying and verifying qualitative objectives of players and coalitions in concurrent game models. The main syntactic construct of ${\textsf {ATL}}^{*}$ is a formula of type $\langle \!\langle {C}\rangle \!\rangle _{_{\! }} \gamma$, intuitively meaning: “The coalition C has a collective strategy to guarantee the satisfaction of the objective $\gamma$ on every play enabled by that strategy.” Formally, ${\textsf {ATL}}^{*}$ is a multi-agent extension of the branching time logic $\textsf {CTL}^{*}$, i.e., a multimodal logic extending the linear-time temporal logic $\textsf {LTL}$–comprising the temporal operators $\mathord {\mathbf {X}}$ (“at the next state”), $\mathord {\mathbf {G}}$ (“always from now on”) and $\, \mathbf {U} \,$ (“until”)–with strategic path quantifiers $\langle \!\langle {C}\rangle \!\rangle _{_{\! }}$ indexed with coalitions C of players. There are two types of formulae of ${\textsf {ATL}}^{*}$, state formulae, which constitute the logic and that are evaluated at game states, and path formulae, that are evaluated on game plays. These are defined by mutual recursion with the following grammars, where $C\subseteq \textsf {Ag}$, $\textsf {p} \in \textsf {Prop}$:

• state formulae are defined by $\varphi {:}{:}{=} \textsf {p} \mid \lnot \varphi \mid (\varphi \wedge \varphi ) \mid \langle \!\langle {C}\rangle \!\rangle _{_{\! }}\gamma$,

• and path formulae by $\gamma {:}{:}{=}\varphi \mid \lnot \gamma \mid (\gamma \wedge \gamma ) \mid \mathord {\mathbf {X}}\gamma \mid \mathord {\mathbf {G}}\gamma \mid \gamma \, \mathbf {U} \, \gamma$.

${\textsf {ATL}}^{*}$ is very expressive and that comes at a high computational price: both model checking and satisfiability are $\mathrm {2ExpTime}$-complete ([6, 53]). A computationally better behaved fragment is the logic $\textsf {ATL}$, which is the multi-agent analogue of $\textsf {CTL}$, only involving state formulae defined by the following grammar, for $C\subseteq \textsf {Ag}$, $\textsf {p} \in \textsf {Prop}$:

$$\begin{aligned} \varphi {:}{:}{=} \textsf {p} \mid \lnot \varphi \mid \varphi \wedge \varphi \mid \langle \!\langle {C}\rangle \!\rangle _{_{\! }} \mathord {\mathbf {X}}\varphi \mid \langle \!\langle {C}\rangle \!\rangle _{_{\! }} \mathord {\mathbf {G}}\varphi \mid \langle \!\langle {C}\rangle \!\rangle _{_{\! }}(\varphi \, \mathbf {U} \, \varphi ). \end{aligned}$$

For this logic model checking and satisfiability are $\mathrm {P}$-complete and $\mathrm {ExpTime}$-complete, respectively ([6, 36]). We will, however, build our extended logical formalism on ${\textsf {ATL}}^{*}$ and will essentially use its path-based semantics; the reduction to $\textsf {ATL}$-based versions is straightforward.

Payoffs Payoffs usually have numerical values. The essential divide is between integer values and arbitrary real values, because every finite game model with rational payoffs can be scaled up to one with integer payoffs. Logical reasoning and computation with real payoffs is more involved, as it crucially depends on the representation of the real values and the commensurability of the payoffs. For the sake of generality, we define all basic components of our framework in terms of an abstract numerical domain of payoffs $\mathbb {D}$, (possibly, closed under some basic arithmetical operations). More generally, that domain can be assumed to be any ordered divisible Abelian group. However, for the purposes of the present work it will suffice to assume that $\mathbb {D}$ is the set of integers $\mathbb {Z}$, possibly extended later, for technical purposes, by adding ‘infinity’ $\omega$ to obtain $\mathbb {Z}_\omega$. Thus, hereafter we only work with integer payoffs and hence integer accumulated utilities,

Arithmetic constraints We define a language of arithmetic constraints to express conditions about the payoffs and accumulated utilities of players in a given play. More precisely, the use of arithmetic constraints in our framework will be two-fold: for specifying players’ objectives (e.g. reaching or maintaining a desired level of accumulated utility) and for defining action guards, where an action guard for a given player is a mapping from states and values of the accumulated utility of that player to sets of actions that the guard declares available for the player at the current configuration. Formally, the arithmetic constraints are built on a fixed set of constants symbols X, used to name special values in the domain $\mathbb {D}$, and a set $V_{\textsf {Ag}}=\{v_{\textsf {a}}\mid \textsf {a} \in \textsf {Ag} \}$ of special variables used to refer to the accumulated utilities of the players at the current state. For any $A\subseteq \textsf {Ag}$, we denote by $V_A$ the restriction of $V_{\textsf {Ag}}$ to A.

Definition 1

(Arithmetic Constraints) Given sets $X\subseteq \mathbb {D}$ and $A\subseteq \textsf {Ag}$, we define the following:

• The elements of $T_{0}(X,A) = X\cup V_A$ are called basic terms over X and A. Terms over X and A are built from basic terms by applying addition ($+$). The set of these terms is denoted by T(X, A).

• A arithmetic constraint over X and A is any expression of the form $t_1 * t_2$ where $* \in \{<, \le , =, \ge , >\} \cup \{ \equiv _{n} \mid n \in \mathbb {N}\}$ and $t_1,t_2\in T(X,A)$. The set of these arithmetic constraints is denoted by $\textsf {AC} (X,A)$. The arithmetic constraints in $\textsf {AC} (X,A)$ which only involve relations from $\{<, \le , =, \ge , >\}$ are called simple arithmetic constraints over X and A. The set of simple arithmetic constraints is denoted by $\textsf {AC} _{s}(X,A)$. The constraints in $\textsf {AC} _{s}(X,A)$ that only involve basic terms (without addition) will be called basic arithmetic constraints over X and A. The set of basic arithmetic constraints is denoted by $\textsf {AC} _{b}(X,A)$.

• An arithmetic constraint formula (over X and A) is any Boolean combination of arithmetic constraints from $\textsf {AC} (X,A)$, i.e. defined by the following grammar: $\alpha {:}{:}{=} c \mid \lnot \alpha \mid \alpha \wedge \alpha$, where $c\in \textsf {AC} (X,A)$. The set of these arithmetic constraint formulas is denoted $\textsf {ACF} (X,A)$. We also assume to have constant arithmetic constraints $\top$ and $\bot$ either as primitives or defined as $\top =(c=c)$ and $\bot = \lnot \top$, where $c \in X$ is arbitrarily fixed. Boolean combinations of simple (respectively, basic) arithmetic constraints are called simple (resp., basic) arithmetic constraint formulae, denoted by $\textsf {ACF} _{s}(X,A)$ (respectively, $\textsf {ACF} _{b}(X,A)$). Note that, in the case when $A = \{a\}$, every formula $\alpha$ in $\textsf {ACF} _s(X,\{a\})$ can be transformed to an equivalent basic formula $\alpha '$ in $\textsf {ACF} _b(X',\{a\})$ by simplifying the occurring terms and possibly slightly extending the set of constant parameters X to $X'$ (depending both on X and $\alpha$). Note that a finite set of constraints from $\alpha$ in $\textsf {ACF} _s(X,\{a\})$ would only require a finite extension of X to $X'$ and in the case when $\mathbb {D}= \mathbb {Z}$, after suitable re-scaling of X, we can assume that $X'$ consists of integers, too.

The inclusion of the set of constant parameters X in the definitions above is only needed when basic terms and constraints over them are considered, but we keep it in the general case for the sake of uniformity. However, when X contains a name for every value in $\mathbb {D}$, or X and A are clear from context or arbitrary, we simply write $\textsf {AC},\textsf {ACF}$ etc.

Arithmetic constraint formulae have a standard interpretation in $(\mathbb {D}, \le )$ once the elements of $X\cup V_{A}$ are evaluated there. Note that the full language $\textsf {ACF} (X,A)$ is expressively equivalent on the domains of natural numbers or integers to the Presburger arithmetic PrA (after quantifiers elimination). Without essential loss of generality, for the purpose of this paper we restrict our framework to the case of simple arithmetic constraints, as defined above, which is equivalent to the strictly weaker quantifier-free fragment of PrA, not involving congruences but only = and < between terms.

3 Concurrent game models with payoffs and guards

The extended concurrent game models that we are going to introduce here can be viewed both as multi-agent transition systems and as multi-stage games, where at every stage the result of the simultaneous collective action of all players is two-fold: first, players receive individual payoffs, just like in the normal form games and repeated games traditionally studied in Game theory, and second, a transition is effected to (possibly) another state, where (possibly) another such game is played, etc., infinitely. The combination of these two fundamental features makes the analysis of such games and the identification of optimal strategies quite challenging. An important class of games closely related to those studied here is stochastic games [47, 54], where the players’ strategies and the environment deciding the transitions are stochastic. In particular, a long-standing open question there is classifying the optimal strategies in games (introduced by Gillette, 1957) of the type of ’Big Match’ [10], cf. the recent work [39] and references therein.

3.1 Definition and examples

Definition 2

(Guards) Let $\textsf {a} \in \textsf {Ag}$. An (individual) a-guard is an arithmetic constraint formula $\textsf {ac}\in \textsf {ACF} (X,\{\textsf {a} \})$.

We now extend concurrent game models with utility payoffs for every action profile applied at every state. Thus, every action profile applied at a given state has now two effects:

• (i) it assigns a payoff to each player, and

• (ii) determines a transition to a new state, where the game associated with it is played at the next round of the play.

Besides, we also add individual guards that determine which actions are available to a player at a given configuration consisting of a state and the vector of current accumulated utilities for each player, i.e. the current sum of all payoffs the player has received in the course of the current play of the game.

Definition 3

(Guarded CGM with payoffs)

A guarded CGM with payoffs (GCGMP) is a tuple

$$\begin{aligned} \mathcal {M}=(\mathcal {S}, \textsf {payoff}, \textsf {grd}) \end{aligned}$$

consisting of:

• a CGM $\mathcal {S} = (\textsf {Ag}, \textsf {St}, \{\textsf {Act} _\textsf {a} \}_{\textsf {a} \in \textsf {Ag}}, \{\textsf {act} _{\textsf {a}}\}_{\textsf {a} \in \textsf {Ag}}, \textsf {out},\textsf {Prop},\textsf {L})$,

• a payoff function, $\textsf {payoff}:\textsf {Ag} \times \textsf {St} \times \textsf {Act} _\textsf {Ag} \rightarrow \mathbb {D}$ assigning for every agent $\textsf {a}$, state s, and action profile $\alpha$ applied at s a payoff to that agent. We will also write $\textsf {payoff}_{\textsf {a}}(s,\mathbf {\alpha })$ for $\textsf {payoff}(\textsf {a},s,\mathbf {\alpha })$.

• a guard function $\textsf {grd}: \textsf {Ag} \times \textsf {St} \times \textsf {Act} _\textsf {Ag} \rightarrow \textsf {ACF} (X,\textsf {Ag})$, such that for each $\textsf {a} \in \textsf {Ag}$, state $s \in \textsf {St}$ and action $\alpha$, the guard $\textsf {grd}(\textsf {a},s,\alpha )$ is an arithmetic constraint formula in $\textsf {ACF} (X,\{\textsf {a} \})$ that determines whether $\alpha$ is enabled for $\textsf {a}$ at the state s given the value of $\textsf {a}$’s current utility in the play. To keep $\textsf {grd}$ a total function, we can assume that $\textsf {grd}(\textsf {a},s,\alpha ) = (v_\textsf {a} \ne v_\textsf {a})$ (i.e. a falsum), whenever $\alpha \notin \textsf {Act} _{\textsf {a}}$. We will also write $\textsf {grd}_{\textsf {a}}(s,\alpha )$ for $\textsf {grd}(\textsf {a},s,\alpha )$ and define the guard for $\textsf {a}$ to be the restriction $\textsf {grd}_{\textsf {a}}:\textsf {St} \times \textsf {Act} _{\textsf {a}}\rightarrow \textsf {ACF} (X,\{\textsf {a} \})$.

Every guard $\textsf {grd}_{\textsf {a}}$ must satisfy consistency conditions that enable at least one action for $\textsf {a}$ at s. Formally, for each $s\in \textsf {St}$, the arithmetic constraint formula $\bigvee _{\alpha \in \textsf {Act} _{\textsf {a}}} \textsf {grd}_{\textsf {a}}(s,\alpha )$ must be valid.

A guard $\textsf {grd}_{\textsf {a}}$ is called state-based if $\textsf {grd}_{\textsf {a}}(s,\alpha )\in \{\top ,\bot \}$ for each $s\in \textsf {St}$ and $\alpha \in \textsf {Act} _{\textsf {a}}$.

Some comments:

• The guards $\textsf {grd}_{\textsf {a}}$ refine the functions $\textsf {act} _{\textsf {a}}$ from the definition of a CGM, which can be regarded as state-based guard functions. To avoid duplicating the role of $\textsf {grd}_{\textsf {a}}$ and $\textsf {act} _{\textsf {a}}$ we hereafter assume that $\textsf {act} _{\textsf {a}}(s) = \textsf {Act} _{\textsf {a}}$.

• In our definition, the guards assigned by $\textsf {grd}_{\textsf {a}}$ only depend on the current state and the current payoff of $\textsf {a}$. The idea is that when the payoffs are interpreted as costs, or – more generally – consumption of resources, the possible actions of a player would depend on her current availability of utility/resources. In a more general framework the guards may also take into account other players’ current payoffs, e.g., when these players are supposed to act as a team (coalition). We leave this more general case to future work, as it changes the operational model substantially and raises further questions about how the communication and cooperation between agents are regulated, which need more detailed treatment.

• Note that, for completeness, the transition function $\textsf {out}$ is defined for all action profiles, not only for those which are enabled at the given state by the respective guards applied to the current payoffs.

In what follows we will use the notation $\mathbf {u}_\textsf {a}$ to refer to the component corresponding to $\textsf {a}$ in the vector $\mathbf {u}$. In particular, if $\mathbf {u}=(u_1,\ldots ,u_n)$ then $\mathbf {u}_i=u_i$.

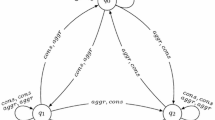
Example 1

Consider the GCGMP shown in Fig. 1 with 2 players, I and II, and 3 states, where in every state each player has 2 possible actions, C (‘cooperate’) and D (‘defect’). The transition function is depicted in the figure.

Fig. 1

A simple GCGMP combining 3 games

The normal form games associated with the states are respectively versions of the Prisoners Dilemma at state $s_{1}$, Battle of the Sexes at state $s_{2}$ and Coordination Game at state $s_{3}$.

The guards for each player $\textsf {a} \in \{ I, II\}$ are defined at each state as follows, where $u_{\textsf {a}}$ is $\textsf {a}$’s current accumulated utility. $\textsf {a}$ can apply: any action if $u_{\textsf {a}}>0$; may only apply action C if $u_{\textsf {a}}=0$; and must play an action maximizing her minimal possible payoff in the current game if $u_{\textsf {a}}<0$. Formally, for each $\textsf {a} \in \{ I, II\}$:

• $\textsf {grd}_{\textsf {a}}(s_{1},C) = (v_{\textsf {a}} \ge 0)$, $\textsf {grd}_{\textsf {a}}(s_{1},D) = (v_{\textsf {a}} \ne 0)$;

• $\textsf {grd}_{I}(s_{2},C) = \top$, $\textsf {grd}_{I}(s_{2},D) = (v_{\textsf {a}} > 0)$;

• $\textsf {grd}_{II}(s_{2},C) = (v_{\textsf {a}} \ge 0)$, $\textsf {grd}_{II}(s_{2},D) = \top$;

• $\textsf {grd}_{\textsf {a}}(s_{3},C) = \top$, $\textsf {grd}_{\textsf {a}}(s_{3},D) = (v_{\textsf {a}} \ne 0)$.

Example 2

The GCGMP shown in Fig. 2 describes the following scenario.

Fig. 2

A GCGMP for a team of robots on a mission

A team of 3 robots is on a mission. The team must accomplish a certain task, formalized as ‘reaching the state goal’. The robots work on batteries which need to be recharged in order to provide the robots with sufficient energy to be able to function. For simplicity, we measure the energy level of robots with non-negative integers. Every action of a robot consumes some of its energy. Collective actions of all robots may, additionally, increase or decrease the energy level of each of them. Thus, every collective action is associated with an ‘energy consumption/payoff table’ which represents the net change – increase or decrease – of the energy level after that collective action is performed at the given state. The system is so designed that the energy level of a robot may never go below 0 (which can be verified). Here is the detailed description of the components of the model.

Agents The 3 robots: $\textsf {a}, \textsf {b}, \textsf {c}$.

States The model contains 2 states: the base station state, ‘base’, and the target state, ‘goal’.

Actions The possible actions are:

R: ‘recharge’; N: ‘do nothing’; G: ‘reach for goal’; and B: ‘return to base’.

All robots have the same functionalities and abilities to perform actions, and their actions have the same effect.

Actions availability Each robot has the following actions possibly executable at the different states (for all other actions, the guards are set to false at the respective states): $\{R,N,G \}$ at state base and $\{N,B \}$ at state goal.

Transitions The transition function is specified in the tables in Fig. 3. Note that, since the robots abilities are assumed symmetric, it suffices to specify the action profiles as multisets, not as tuples.

Payoff tables Respectively, the payoffs are given in Fig. 3 as vectors with components that correspond to the order of the actions in the triple, not to the order of the agents which have performed them.

Fig. 3

The transition function for the team of robots example

Here are some motivating explanations of the so defined transitions and payoffs:

• The team has one recharging device which can recharge at most 2 batteries at a time and produces a total of 2 energy units in one recharge step. So if 1 or 2 robots recharge at the same time they receive a pro rata energy increase, but if all 3 robots try to recharge at the same time, the device blocks and does not charge any of them.

• The transition from one state to the other consumes a total of 3 energy units. If all 3 robots take the action which is needed for that transition (G for transition from base to goal, and B for transition from goal to base), then the energy cost of the transition is distributed equally amongst them. If only 2 of them take that action, then each consumes 2 units and the extra unit is transferred to the 3rd robot (e.g., to enable providing help, when needed).

• An attempt by a single robot to reach the other state fails and costs that robot 1 energy unit.

Fig. 4

The guard functions for the team of robots example

Guards The guards are the same for each robot, specified in Table 4, where v is the variable representing the current accumulated utility of the respective robot. Some explanations:

• As noted earlier, action B is disabled at state base and actions R and G are disabled at state goal.

• The ’do nothing’ action N does not have requirements to be enabled.

• A recharge can only be attempted if the current energy level of the robot is at most 2.

• For a robot to attempt a transition to the other state, that robot must have a minimal energy level 2.

Note that any set of two robots can ensure transition from one state to the other, but no single robot can do that.

3.2 Configurations, plays, and histories

Let $\mathcal {M}$ be a fixed GCGMP. A configuration (in $\mathcal {M}$) is a pair $(s,\mathbf {u})$ consisting of a state s and a vector $\mathbf {u}=(u_1,\dots ,u_k)$ of currently accumulated utilities, one for each agent, at that state. We define the set of possible configurations as $\textsf {Con}_{\mathcal {M}}=\textsf {St} \times \mathbb {D}^{|\textsf {Ag} |}$. An initialized GCGMP (iGCGMP) is a pair $(\mathcal {M},\textsf {init})$ where $\mathcal {M}$ is a GCGMP and $\textsf {init} =(s_{0},\mathbf {u_{0}})$ is an initial configuration, with $s_{0} \in \textsf {St}$ an initial state and $\mathbf {u_{0}} = (u^{0}_1,\dots ,u^{0}_k)$ the vector of initial utilities of all players. The (partial) configuration transition function is defined as

$$\begin{aligned} {\widehat{\textsf {out}}}: \textsf {Con}_{\mathcal {M}} \times \textsf {Act} _\textsf {Ag} \rightarrow \textsf {Con}_{\mathcal {M}}, \end{aligned}$$

such that ${\widehat{\textsf {out}}} ((s,\mathbf {u}),\mathbf {\alpha })=(s',\mathbf {u'})$ iff:

• (i) $\textsf {out} (s,\mathbf {\alpha })=s'$ (the state $s'$ is the successor of s when $\mathbf {\alpha }$ is executed).

• (ii) for each $\textsf {a} \in \textsf {Ag}$, the current utility $\mathbf {u}_\textsf {a}$ satisfies the guard $\textsf {grd}_{\textsf {a}}(s,\alpha _\textsf {a})$ for the action $\alpha _\textsf {a}$ at the current state s.

• (iii) for each $\textsf {a} \in \textsf {Ag}$, $\mathbf {u}'_{\textsf {a}}=\mathbf {u}_{\textsf {a}}+ \textsf {payoff}_{\textsf {a}}(s,\mathbf {\alpha })$.

An initialized GCGMP with a designated initial configuration $(s_{0},\mathbf {u_0})$ gives rise to a configuration graph on $\mathcal {M}$ consisting of all configurations in $\mathcal {M}$ reachable from $(s_{0},\mathbf {u_0})$ by ${\widehat{\textsf {out}}}$.

A play in a GCGMP $\mathcal {M}$ is an infinite sequence $\pi =c_0 \mathbf {\alpha }_0,c_1 \mathbf {\alpha }_1,\dots$ from $(\textsf {Con}_{\mathcal {M}}\times \textsf {Act} _\textsf {Ag})^\omega$ such that $c_{n}= \widehat{\textsf {out}}(c_{n-1}, \mathbf {\alpha }_{n-1})$ for all $n>0$. The set of all plays in $\mathcal {M}$ is denoted by $\textsf {Plays} _{\mathcal {M}}$. For each $i\ge 0$ we write $\pi [i]$ to refer to the ith pair $(c_i,\mathbf {\alpha }_i)$ on $\pi$ and $\pi [i,\infty ]=c_{i}\alpha _{i},c_{i+1}\alpha _{i+1},\dots$ to denote the sub-play of $\pi$ starting from position i. A history is any finite initial sequence $h=c_0 \mathbf {\alpha }_0,c_{1}\mathbf {\alpha }_1, \dots , c_n\in (\textsf {Con}_{\mathcal {M}}\times \textsf {Act} _\textsf {Ag})^*\textsf {Con}_{\mathcal {M}}$ of a play in $\textsf {Plays} _{\mathcal {M}}$. Note that a history ends in a configuration, but sometimes, for technical reasons, we also assume that $\mathbf {\alpha }_n$ is added (as a placeholder) and equals $\epsilon$. The set of all histories is denoted by $\textsf {Hist} _{\mathcal {M}}$. Like for plays, we use the notation h[i] and h[i, j], $i\le j$, $i<|h|$, to refer to the sub-history $h[i]\dots h[min(j,|h|-1)]$. We also allow $j=\infty$ and note that $h[ last ]$ refers to the last pair $(c_n,\epsilon )$.

For a given set Z, let $Z^{\le \omega }{:}{=} Z^{\omega } \cup Z^{*}$ denote the set of finite or infinite sequences of elements of Z and let $\textsf {Paths} _{\mathcal {M}} {:}{=} \textsf {Plays} _{\mathcal {M}} \cup \textsf {Hist} _{\mathcal {M}}$.

Finally, we introduce functions $\cdot ^c$, $\cdot ^a$, $\cdot ^u$ and $\cdot ^s$, where

$$\begin{aligned} \cdot ^c&:&\textsf {Paths} _{\mathcal {M}} \rightarrow \textsf {Con}^{\le \omega }_{\mathcal {M}} \quad \text {(removing the action components from plays)}\\ \cdot ^a&:&\textsf {Paths} _{\mathcal {M}} \rightarrow \textsf {Act} _\textsf {Ag} ^{\le \omega } \quad \text {(removing the configuration components from plays)}\\ \cdot ^u&:&\textsf {Paths} _{\mathcal {M}} \rightarrow (\mathbb {D}^\textsf {Ag})^{\le \omega } \quad \text {(removing the state and action components from plays)}\\ \cdot ^s&:&\textsf {Paths} _{\mathcal {M}} \rightarrow \textsf {St} ^{\le \omega } \quad \text {(removing the utillity and action component from plays)} \end{aligned}$$

Formally, these denote the projections of a given play or history respectively to the sequences of its configurations, action profiles, current utility vectors, and states. For illustration, consider the play $\pi =c_0 \mathbf {\alpha }_0,c_1 \mathbf {\alpha }_1,\dots$. Then:

$\pi ^c[i]=c_i$; $\pi ^a[i]=\mathbf {\alpha }_i$; $\pi ^u[i]=\mathbf {u_i}$; and $\pi ^s[i]=s_i$, where $c_i=(s_i,\mathbf {u_i})$.

Next, for each player $\textsf {a}$ and configuration $c = (s,\mathbf {u})$, we define its local projection or local (view of the) configuration for $\textsf {a}$ to be $c^\textsf {a} {:}{=} (s,\mathbf {u}_\textsf {a})$. We then define local histories and local plays for $\textsf {a}$ to be the projections of histories and plays to the respective sequences of local configurations for $\textsf {a}$ and denote the respective sets by $\textsf {Plays} ^\textsf {a} _{\mathcal {M}}$ and $\textsf {Hist} ^\textsf {a} _{\mathcal {M}}$.

Example 3

Some possible plays in Example 1, starting from the initial configuration $(s_{1}, (0,0))$, are given below. Note that, according to the guards, the first action of any agent from this configuration must be C.

(1) Players cooperate forever: $(s_{1}, 0,0) (C,C), (s_{1}, 2,2) (C,C), (s_{1}, 4,4) (C,C), \ldots$

(2) After the first round both players defect and the play moves to $s_{2}$, where player I chooses to defect whereas II cooperates. Then I must cooperate while II must defect, but at the next rounds II can choose any action, so a possible play is:

$(s_{1}, 0,0) (C,C), (s_{1}, 2,2) (D,D), (s_{2}, 1,1) (D,C), (s_{2}, 0,-1) (C,D), (s_{2}, 0,1) (C,D), (s_{2}, 0,3) (C,D), (s_{2},0,5), \ldots$

(3) After the first round player I defects while II cooperates and the play moves to $s_{3}$, where they can get stuck indefinitely, until (if ever) they happen to coordinate, so a possible play is:

$(s_{1}, 0,0) (C,C), (s_{1}, 2,2) (D,C), (s_{3}, 5,-2) (D,C), (s_{3}, 4,-3) (C,D), \ldots , (s_{3}, 0,-7) (D,C), (s_{3}, -1,-8), \ldots$.

Note, however, that once player I reaches accumulated utility 0 he may only play C at that round, so if player II has enough memory or can observe the current accumulated utility of I, then she can use the opportunity to coordinate with I at that round by playing C, thus escaping the trap at $s_{3}$ and making a sure transition to $s_{2}$. This illustrates the use of memory based strategies and also brings up the issue of the possible effects of the observation abilities assumed for the agents.

Example 4

Here are some possible plays in Example 2 starting from the initial configuration $(\textit{base}, (0,0,0))$

(1) The robots do not coordinate and keep trying to recharge forever. The mission fails, with the following play:

$(\textit{base}; 0,0,0) (RRR), (\textit{base}; 0,0,0) (RRR), (\textit{base}; 0,0,0) (RRR), \ldots$

(2) Suppose now the robots coordinate on recharging, 2 at a time, until they each reach energy levels at least 3. Then they all can take action G so the team reaches state goal, and then succeeds to return to base:

$(\textit{base}, 0,0,0) (RRN), (\textit{base}, 1,1,0) (NRR), (\textit{base}, 1,2,1) (RNR), (\textit{base}, 2,2,2) (RRN), (\textit{base}, 3,3,2) (NNR), (\textit{base}, 3,3,4) (GGG) (\textit{goal}, 2,2,3) (BBB), (\textit{base}, 1,1,2) \ldots$

(3) Suppose again the robots coordinate on recharging, but after the first recharge Robot $\textsf {a}$ goes out of order and thereafter $\textsf {a}$ does nothing (i.e., only applies the action N) while the other two robots try to accomplish the mission by recharging in parallel as much as possible each and then both taking action G. Then the team reaches state goal but cannot return to base and remains stuck at state goal forever, for one of the two functioning robots does not have enough energy to apply action B:

$(\textit{base}, 0,0,0) (RRN), (\textit{base}, 1,1,0) (NRR), (\textit{base}, 1,2,1) (NRR), (\textit{base}, 1,3,2) (NRR), (\textit{base}, 1,4,3) (NGG), (\textit{goal}, 2,2,1) (NNB), (\textit{goal}, 2,1,1) (NNN), \ldots$

(4) As above, but now $\textsf {b}$ and $\textsf {c}$ apply a cleverer plan and succeed together to reach goal and then return to base:

$(\textit{base}, 0,0,0) (RRN), (\textit{base}, 1,1,0) (NRR), (\textit{base}, 1,2,1) (NRR), (\textit{base}, 1,3,2) (NGR), (\textit{base}, 1,2,4) (NRN), (\textit{base}, 1,4,4) (NGG), (\textit{goal}, 2,2,2) (NBB), (\textit{base}, 3,0,0) \ldots$

3.3 Strategies

Intuitively, a strategy of a player is a complete conditional plan which prescribes what action the player should take in every possible “situation”. Strategies of players depend on their observation and memory abilities and can only be based on what players can observe, record and recall. Here are the main not mutually exclusive cases that arise with respect to these, and in each of them players can use bounded or unbounded memory:

• All players have complete information about the model, and in particular they know the underlying concurrent game model and the payoff tables associated at all states in the GCGMP. This is the case we also assume here, but it need not always be the case. Conceivably, the players may have various types of incomplete information: about the state space, or the possible actions, guards, transitions, and the payoffs of the other players. Each of these cases requires detailed further analysis which we cannot reasonably cover within this paper.

• Players can observe only their own local view of the state and their own payoff. This is the case of imperfect information which we will not discuss here, either, but will defer to a future study.

• Players can observe the entire current state and only their own payoff, but not the other players’ actions or payoffs.

• Players can observe the current state and every player’s actions. Using some bounded memory, such players can then compute and keep record of the other players’ current utilities throughout the game, so we can just as well assume that such players can observe the other players’ current utilities, too, and can take them into account in their strategies.

• In the most general case, players’ strategies are based on the entire history of the play.

We make these options precise below.

Definition 4

(Strategies) A strategy of a player $\textsf {a}$ in a GCGMP $\mathcal {M}$ is a mapping $\sigma _{\textsf {a}} : \textsf {Hist} _{\mathcal {M}} \rightarrow \textsf {Act} _\textsf {a}$ which is consistent with the guards for $\textsf {a}$, i.e., such that if $\sigma _{\textsf {a}}(h)=\alpha$ then $h^u[last]_\textsf {a} \models \textsf {grd}_{\textsf {a}}(h^s[last],\alpha )$. That is, actions prescribed by the strategy must be enabled by the guard.

A strategy $\sigma _{\textsf {a}} : \textsf {Hist} _{\mathcal {M}} \rightarrow \textsf {Act} _\textsf {a}$ is:

• state-based, if it only depends on the state histories, i.e. those in $\textsf {Hist} ^s_{\mathcal {M}}$. In the case of state-based strategies we will assume that the guards are also state-based. Formally, a state-based strategy for player $\textsf {a}$ is defined as a mapping $\sigma _{\textsf {a}}: \textsf {Hist} ^s_{\mathcal {M}} \rightarrow \textsf {Act} _\textsf {a}$, consistent with the guards for $\textsf {a}$.

• configuration-based, if it only depends on the configuration histories, i.e. prescribes the same action to any two histories which have the same configuration projections. Formally, a configuration-based strategy is defined as a mapping $\sigma _{\textsf {a}} : \textsf {Hist} ^{c}_{\mathcal {M}} \rightarrow \textsf {Act} _\textsf {a}$, consistent with the guards for $\textsf {a}$.

• memoryless (or, positional), if it only depends on the current configuration². Formally, a memoryless strategy is a mapping $\sigma _{\textsf {a}} : \textsf {Con}_{\mathcal {M}} \rightarrow \textsf {Act} _\textsf {a}$, consistent with the guards for $\textsf {a}$.

• a local view strategy, if it only depends on the player’s local configuration histories, i.e. prescribes the same action to any two histories with the same local projections for the player. Formally, a local view strategy is a mapping $\sigma _{\textsf {a}} : \textsf {Hist} ^{\textsf {a}}_{\mathcal {M}} \rightarrow \textsf {Act} _\textsf {a}$, consistent with the guards for $\textsf {a}$.

The combinations, such as memoryless configuration-based, memoryless local-view, etc., are defined likewise. The class of all (resp. state-based, configuration-based, local-view, and memoryless) strategies is denoted by $\Sigma$ (resp. $\Sigma ^{s}$, $\Sigma ^{c}$, $\Sigma ^{l}$ and $\Sigma ^{m}$). Again, combinations are denoted analogously, e.g. $\Sigma ^{sm}$ refers to state-based memoryless strategies.

The general definition of strategy above extends the notion of strategy from [6] where it is defined only on histories of states—that setting corresponds to state-based strategies combined with state-based guards. That more general notion also includes strategies that are typically considered e.g. in the study of repeated games, where the action prescribed to the player may depend not only on the state history but also on the previous action, or the history of actions, of the other player(s). Such are, for instance, the strategies Tit-for-tat or Grim-trigger in repeated Prisoners Dilemma, as well as strategies for various card games. Also, the strategy of a gambling player could naturally depend not only on his current availability of money, but also on the history of his previous gains and losses, etc. The classification of strategies and comparison of their power is worth a separate study and will not be pursued here further. We only note that the choice of type of strategies affects essentially the computational cost of solving the associated model-checking problems, see e.g. [57].

3.4 Computationally effective strategies

This is an auxiliary subsection, where we introduce a general classification of strategies in terms of the computational resources they require from the agents. Not all notions defined in this subsection will be used further in the paper, but it is intended to serve as a common terminological and notational reference for further follow-up work.

There are at least two ways in which memory resources play a role in strategies: the memory needed to store the input of the strategy and the memory needed to compute the value of the strategy function. Note that, because the configuration graphs of GCGMPs are usually infinite, strategies are generally infinitary objects. For the sake of obtaining effective procedures we focus on “finitary” strategies. Intuitively, a finitary strategy is a program of the type:

If $C_{1}$ apply action $a_{1}$;

...

If $C_{k}$ apply action $a_{k}$;

Otherwise, apply action $a_{k+1}$,

where $C_{1},\ldots C_{k}$ are pairwise exclusive conditions on the configurations or histories which the strategy takes into account. We will make this notion precise in Definition 6.

Note that finitary strategies can be memoryless (when the conditions only refer to the current configuration), finite memory, or perfect recall strategies. Moreover, even finitary strategies can still be non-computable; however, this issue will not be considered further here.

Hereafter we fix a GCGMP $\mathcal {M}$ with a state space $\textsf {St}$, domain of payoffs $\mathbb {D}=\mathbb {Z}$ and a global set of actions $\textsf {Act}$, which we assume to be the union of all players’ sets of actions. In order to precisely define “finitary” and “effective” strategies in $\mathcal {M}$ we introduce a formal language. We call a set $\textsf {B} = \{\beta _{\alpha }\}_{\alpha \in \textsf {Act} _{\textsf {a}}}$ of formulae from $\textsf {ACF} (X,\textsf {Ag})$ strategy-defining for player $\textsf {a}$ at a state $s \in \textsf {St}$ of an GCGMP $\mathcal {M}$ iff each of the following holds:

• 1. For each $\alpha ,\alpha '\in \textsf {Act} _{\textsf {a}}$, if $\alpha \ne \alpha '$ then $\models \lnot (\beta _{\alpha } \wedge \beta _{\alpha '})$;

• 2. $\models \beta _{\alpha } \rightarrow \textsf {grd}_{\textsf {a}}(s,\alpha )$, for each $\alpha \in \textsf {Act} _{\textsf {a}}$;

• 3. $\models \bigvee _{\alpha \in \textsf {Act} _{\textsf {a}}}\beta _{\alpha }$.

Intuitively, $\beta _{\alpha }$ is the condition on current configurations which prescribes to the player to apply action $\alpha$. Then the clauses above state that:

(1) the conditions prescribing different actions are mutually exclusive;

(2) the condition prescribing an action ensures that the guard for that action at state s is satisfied; and

(3) there always exists an enabled action.

An important case of strategy-defining sets of formulae is when each $\beta _{\alpha }$ is a boolean constant ($\top$ or $\bot$). These define state-based strategies.

If the set $\textsf {B}$ above consists of formulae from $\textsf {ACF} (X,\{\textsf {a} \})$ we call it local strategy-defining for player $\textsf {a}$ at a state $s \in \textsf {St}$. Note that, without loss of generality, we can assume that every formula in a strategy-defining set partitions the domain of payoffs $\mathbb {D}$ into a finite set of disjoint intervals.

Now we introduce memory transducers, i.e., finite automata with output, which are usually used as computational means to define finite memory strategies. Fomally, given a GCGMP $\mathcal {M}$ and a finite set (of memory cells) M, a global memory transducer for $\mathcal {M}$ with a memory space M (and memory size |M|) for $\mathcal {M}$ is a tuple $T=(M,m_0,\textsf {next},\textsf {upd})$ where $\textsf {next}:M \times \textsf {Con}_{\mathcal {M}} \rightarrow \textsf {Act}$ and $\textsf {upd}:M\times \textsf {Con}_{\mathcal {M}} \rightarrow M$. A local memory transducer with a memory space M for $\mathcal {M}$ is a tuple $T=(M,m_0,\textsf {next}, \textsf {upd})$ where $\textsf {next}:M \times \textsf {St} \times \mathbb {D}\rightarrow \textsf {Act}$ and $\textsf {upd}:M\times \textsf {St} \times \mathbb {D}\rightarrow M$.

Intuitively, a global (resp., local) transducer reads a current configuration (resp., the local view of the configuration), prescribes an action based on it and on its current internal state (memory cell), and then updates its internal state.

Definition 5

(Effective memory transducers) A global memory transducer $T=(M,m_0,\textsf {next},\textsf {upd})$ is effective for player $\textsf {a}$ iff there is a family of sets of formulae $\big \{\textsf {B}^{s,j}\big \}_{s\in \textsf {St}, j \in M}$ from $\textsf {ACF} (X,\textsf {Ag})$ for a finite set of payoff constants X, where each $\textsf {B}^{s,j} = \{\beta _{\alpha }^{s,j} \mid \alpha \in \textsf {Act} _{\textsf {a}} \}$ is strategy-defining for player $\textsf {a}$ at state s, such that $\textsf {next}(j,(s,\mathbf {u}))=\alpha$ iff $\mathbf {u}$ satisfies $\beta _{\alpha }^{s,j}$. Likewise, a local memory transducer is effective if each $\textsf {B}^{s,j}$ is locally strategy-defining. Finally, an effective transducer as above is n-bounded if $\max \{|c| : c \in X \} =n$ (where |c| is the absolute value of c).

Definition 6

(Effective strategies) A global memory transducer $T = (M,m_0,\textsf {next},\textsf {upd})$ determines a configuration-based strategy $\sigma _{\textsf {a}}^{T} : \textsf {Hist} ^{c}_{\mathcal {M}} \rightarrow \textsf {Act}$ for player $\textsf {a}$, defined for every history $h=c_0 \mathbf {\alpha }_0c_{1}\mathbf {\alpha }_1 \dots c_n\in \textsf {Hist} _{\mathcal {M}}$ as follows: $\sigma _{\textsf {a}}^{T}(h) =\textsf {next}(m_{n},c_{n})$, where $m_{0}, m_{1}, \ldots , m_{n}$ is defined inductively by $m_{i+1}=\textsf {upd}(m_{i},c_{i})$ for $i=1,\dots , n-1$.

Such a configuration-based strategy $\sigma _{\textsf {a}} : \textsf {Hist} ^{c}_{\mathcal {M}} \rightarrow \textsf {Act}$ for player $\textsf {a}$ is (m, n)-effective if it is defined by an n-bounded global transducer T with memory size m; $\sigma _{\textsf {a}}$ is effective if it is (m, n)-effective for some $m,n \in \mathbb {N}$.

Likewise, an n-bounded local memory transducer T with memory size m defines an (m, n)-effective local-view configuration-based strategy by using the projection function $\cdot ^{\textsf {a}}$.

In particular, a (local-view) memoryless strategy is effective if it is (1, n)-effective for some $n\in \mathbb {N}$.

Let $\mathcal {S}$ be some class of strategies from Definition 4, e.g. $\mathcal {S}=\Sigma ^{s}$. Then, we write $\mathcal {S}^{e}$ and $\mathcal {S}^{e(m,n)}$ to refer to all strategies from $\mathcal {S}$ that are effective and (m, n)-effective, respectively. Combinations with earlier defined classes of strategies are defined and denoted as expected, e.g. $\Sigma ^{lme}$ denotes the class of local configuration-based, memoryless, effective strategies.

4 The Logic for combining quantitative and qualitative reasoning $\textsf {QATL}^{*}$

4.1 Syntax and semantics

We now extend the logic ${\textsf {ATL}}^{*}$ with atomic quantitative objectives being arithmetic constraints over the players’ currently accumulated utilities.

Definition 7

(The logic $\textsf {QATL}^{*}$) The language of $\textsf {QATL}^{*}$ consists of state formulae $\varphi$, which constitute the logic, and path formulae $\gamma$, generated as follows, where $A\subseteq \textsf {Ag}$, $\textsf {ac}\in \textsf {AC}$, and $p\in \textsf {Prop}$:

$\varphi {:}{:}{=} {p} \mid \textsf {ac}\mid \lnot \varphi \mid (\varphi \wedge \varphi ) \mid \langle \!\langle {A}\rangle \!\rangle _{_{\! }}\gamma$;

$\gamma {:}{:}{=}\varphi \mid \lnot \gamma \mid (\gamma \wedge \gamma ) \mid \mathbf {X}\,\gamma \mid \mathbf {G}\,\gamma \mid (\gamma \,\mathbf {U}\,\gamma )$.

Outermost parentheses will usually be omitted. The “sometime” operator is defined, as usual, as $\mathbf {F}\,\gamma \equiv \top \,\mathbf {U}\,\gamma$.

We say that a formula is purely qualitative (resp. purely quantitative) if it contains no arithmetic constraints (resp. no propositional symbols).

Now we define some important fragments of $\textsf {QATL}^{*}$:

• The fragment $\textsf {QATL}$ restricts $\textsf {QATL}^{*}$ just like $\textsf {ATL}$ restricts ${\textsf {ATL}}^{*}$.

• By $\textsf {FlatQATL}$ (resp., $\textsf {FlatQATL}^{*}$) we denote the fragment of $\textsf {QATL}$ (reps., $\textsf {QATL}^{*}$) with formulae with no nested cooperation modalities.

• Another natural restriction of $\textsf {QATL}^{*}$, here denoted $\textsf {QATL}_{1}^{*}$, only allows arithmetic constraints comparing the players’ current utilities with constants, but not with each other, i.e. each $\textsf {ac}$ is from $\textsf {AC}_b(X,\{a\})$ for some $a\in \textsf {Ag}$. The fragments $\textsf {QATL}_{1}$ and $\textsf {FlatQATL}_{1}$, $\textsf {FlatQATL}_{1}^{*}$ are defined likewise.

The semantics of $\textsf {QATL}^{*}$ naturally extends the semantics of ${\textsf {ATL}}^{*}$ over GCGMP. In order to make that semantics more realistic from a game-theoretic perspective, we assume that all players have their individual or collective objectives and act strategically in their pursuit; in particular, both proponents and opponents of a given objective follow strategies from given classes. Formally, we consider the semantics of every formula of the type $\langle \!\langle {A}\rangle \!\rangle _{_{\! }}\gamma$ parameterised with the two classes of strategies $\mathcal {S}^p$ for the proponents and $\mathcal {S}^o$ for the opponents, used when evaluating the truth of that formula. Thus, the proponent coalition A selects an $\mathcal {S}^p$-strategy $s_A$ while the opponent coalition $\textsf {Ag} \backslash A$ selects an $\mathcal {S}^o$-strategy $s_{\textsf {Ag} \backslash A}$. Then $\textsf {play} _{\mathcal {M}}(c,(s_A,s_{\textsf {Ag} \backslash A}))$ in a given GCGMP $\mathcal {M}$ refers to the outcome play emerging from the execution of the strategy profile $(s_A,s_{\textsf {Ag} \backslash A})$ from configuration c in $\mathcal {M}$ onward.

Definition 8

(Semantics) Let $\mathcal {M}$ be a GCGMP and let $\mathcal {S}^p$ and $\mathcal {S}^o$ be two fixed classes of strategies. The truth of a $\textsf {QATL}^{*}$ formula at a configuration c, respectively, on a path $\pi$ in $\mathcal {M}$, is defined by mutual recursion on state and path formulae as follows:

$\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)}{p}$:

for $p\in \textsf {Prop}$ iff ${p}\in \textsf {L}(c^s)$;

$\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)}{\textsf {ac}}$:

for $\textsf {ac}\in \textsf {AC}$ iff $c^u\models \textsf {ac}$, (the truth of $\textsf {ac}$ in $c^u$ is defined in standard arithmetic sense)

$\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)}\varphi _1\wedge \varphi _2$:

iff $\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)}\varphi _1$ and $\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)}\varphi _2$,

$\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)}\lnot \varphi$:

iff $\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)} \varphi$,

$\mathcal {M},c\models _{(\mathcal {S}^p,\mathcal {S}^o)} \langle \!\langle {A}\rangle \!\rangle _{_{\! }}\gamma$:

iff there is a collective $\mathcal {S}^p$-strategy $\sigma _A$ for A such that $\mathcal {M},{\textsf {play}}^{\mathcal {M}}(c,(\sigma _A,\sigma _{\textsf {Ag} \backslash A}))\models _{(\mathcal {S}^p,\mathcal {S}^o)}\gamma$ for all collective $\mathcal {S}^o$-strategies $\sigma _{\textsf {Ag} \backslash A}$ for $\textsf {Ag} \backslash A$.

$\mathcal {M},\pi \models _{(\mathcal {S}^p,\mathcal {S}^o)} \varphi$:

iff $\mathcal {M},\pi [0]\models _{(\mathcal {S}^p,\mathcal {S}^o)} \varphi$;

$\mathcal {M},\pi \models _{(\mathcal {S}^p,\mathcal {S}^o)} \mathbf {X}\,\gamma$:

iff $\mathcal {M},\pi [1]\models _{(\mathcal {S}^p,\mathcal {S}^o)} \gamma$,

$\mathcal {M},\pi \models _{(\mathcal {S}^p,\mathcal {S}^o)} \mathbf {G}\,\gamma$:

iff $\mathcal {M},\pi [i]\models _{(\mathcal {S}^p,\mathcal {S}^o)} \gamma$ for all $i\in \mathbb {N}$,

$\mathcal {M},\pi \models _{(\mathcal {S}^p,\mathcal {S}^o)} \gamma _1\,\mathbf {U}\,\gamma _2$:

iff $\mathcal {M},\pi [j]\models _{(\mathcal {S}^p,\mathcal {S}^o)} \gamma _2$ for some $j\in \mathbb {N}$ such that $\mathcal {M},\pi [i]\models _{(\mathcal {S}^p,\mathcal {S}^o)} \gamma _1$ for all $0\le i< j$.

We will write $\models$ for $\models _{(\Sigma ,\Sigma )}$.

4.2 Expressing some properties

Besides capturing all purely qualitative, ${\textsf {ATL}}^{*}$-definable properties, the logic $\textsf {QATL}^{*}$ can also express purely quantitative properties, such as

$$\begin{aligned} \langle \!\langle {\{\textsf {a} \}}\rangle \!\rangle _{_{\! }}\mathbf {G}\,(v_{\textsf {a}} > 0) \end{aligned}$$

meaning “Player $\textsf {a}$ has a strategy to maintain his accumulated utility to be always positive”. Moreover, $\textsf {QATL}^{*}$ can naturally express combined qualitative and quantitative properties, e.g.

$$\begin{aligned} \langle \!\langle {\{\textsf {a} \}}\rangle \!\rangle _{_{\! }}((\texttt {\textsf {a}\ is happy})\ \,\mathbf {U}\,(v_{\textsf {a}} \ge 10^{6})) \end{aligned}$$

saying “Player $\textsf {a}$ has a strategy to stay happy until $\textsf {a}$ becomes a millionaire”, or

$$\begin{aligned} \langle \!\langle {\{\textsf {a},\textsf {b} \}}\rangle \!\rangle _{_{\! }}((v_{\textsf {a}} + v_{\textsf {b}} > v_{\textsf {c}}) \ \,\mathbf {U}\,\mathbf {G}\,(\texttt {\textsf {a}\ is happy})) \end{aligned}$$

saying “Players $\textsf {a}$ and $\textsf {b}$ have a joint strategy to keep their joint accumulated utility greater than the one of $\textsf {c}$ until $\textsf {a}$ becomes always happy thereafter”.

More such examples can be extracted from Examples 3 and 4.

Example 5

The following $\textsf {QATL}^{*}$ state formulae are true at state $s_{1}$ of the GCGMP in Example 1, where $p_{i}$ is an atomic proposition true only at state $s_{i}$, for each $i=1,2,3$. For partial argumentation of these, see Example 3.

• $\langle \!\langle {I,II}\rangle \!\rangle _{_{\! }} \mathbf {F}\,(p_{1} \wedge v_{I}> 100 \wedge v_{II} > 100)$.

• $\lnot \langle \!\langle {I}\rangle \!\rangle _{_{\! }} \mathbf {G}\,v_{I} > 0$.

• $\langle \!\langle {I,II}\rangle \!\rangle _{_{\! }} \mathbf {X}\,\mathbf {X}\,\mathbf {X}\,\langle \!\langle {II}\rangle \!\rangle _{_{\! }} (\mathbf {G}\,(p_{2} \wedge v_{I} = 0) \ \wedge \ \mathbf {F}\,v_{II} >100)$.

• $\langle \!\langle {I,II}\rangle \!\rangle _{_{\! }} \mathbf {X}\,\mathbf {X}\,\lnot \langle \!\langle {I}\rangle \!\rangle _{_{\! }} (\mathbf {F}\,v_{I} \ge 0)$.

• $\lnot \langle \!\langle {I,II}\rangle \!\rangle _{_{\! }} \mathbf {F}\,(p_{3} \wedge \mathbf {G}\,(p_{3} \wedge (v_{I }+ v_{II} > 0)))$.

Example 6

Suppose the objective of the team of robots in Example 2 is that, starting from state base where each robot has energy level 0, the state goal must eventually be reached and then the team must return to the base station.

The following $\textsf {QATL}^{*}$ state formulae are true at the initial configuration $(\textit{base}, 0,0,0)$ in the GCGMP in Example 2, where $\textsf {base}$ is an atomic proposition true only at state base and $\textsf {goal}$ is an atomic proposition true only at state goal. For partial argumentation, see Example 4.

• $\langle \!\langle {}\rangle \!\rangle _{_{\! }} \mathbf {G}\,(v_{\textsf {a}} \ge 0 \wedge v_{\textsf {b}} \ge 0 \wedge v_{\textsf {c}} \ge 0)$

• $\lnot \langle \!\langle {\textsf {a}}\rangle \!\rangle _{_{\! }} \mathbf {F}\,\textsf {goal} \wedge \lnot \langle \!\langle {\textsf {b}}\rangle \!\rangle _{_{\! }} \mathbf {F}\,\textsf {goal} \wedge \lnot \langle \!\langle {\textsf {c}}\rangle \!\rangle _{_{\! }} \mathbf {F}\,\textsf {goal}$.

• $\langle \!\langle {\textsf {b},\textsf {c}}\rangle \!\rangle _{_{\! }} \mathbf {F}\,(\textsf {goal} \wedge \langle \!\langle {\textsf {a},\textsf {b},\textsf {c}}\rangle \!\rangle _{_{\! }} (v_{\textsf {a}}> 0 \wedge v_{\textsf {b}}> 0 \wedge v_{\textsf {c}} > 0) \,\mathbf {U}\,\textsf {base} )$.

• $\langle \!\langle {\textsf {b},\textsf {c}}\rangle \!\rangle _{_{\! }} \mathbf {F}\,(\textsf {goal} \wedge \langle \!\langle {\textsf {b},\textsf {c}}\rangle \!\rangle _{_{\! }} (v_{\textsf {a}}> 0) \,\mathbf {U}\,(\textsf {base} \wedge v_{\textsf {a}} > 0))$.

• $\lnot \langle \!\langle {\textsf {b},\textsf {c}}\rangle \!\rangle _{_{\! }} \mathbf {F}\,(\textsf {goal} \wedge \langle \!\langle {\textsf {b},\textsf {c}}\rangle \!\rangle _{_{\! }} \mathbf {F}\,(\textsf {base} \wedge (v_{\textsf {b}}> 0 \vee v_{\textsf {c}} > 0)))$.

4.3 Reductions of qualitative to quantitative objectives

Here we show that, given a finite GCGMP $\mathcal {M}$ with a state space $\textsf {St}$ one can technically eliminate the qualitative component at the cost of adding a fictitious extra player.

Proposition 1

Let $\mathcal {M}$ be a finite GCGMP. Then there is an effective translation $^{\#}$ from $\textsf {QATL}^{*}$ to a variation of $\textsf {QATL}^{*}$ obtained by removing the propositional symbols and adding an additional agent $\mathbf {s}$, and an effective transformation of $\mathcal {M}$ to a GCGMP ${\mathcal {M}}^*$ expanding $\mathcal {M}$ with the additional agent $\mathbf {s}$, such that for every state formula $\varphi$ of $\textsf {QATL}^{*}$ and a state $q\in \mathcal {M}$:

$$\begin{aligned} \mathcal {M},q\models \varphi \text{ iff } {\mathcal {M}}^*,q\models \varphi ^{\#}. \end{aligned}$$

The size of $\varphi ^{\#}$ is $O(|\varphi | \times |\textsf {St} |)$ where $\textsf {St}$ is the state space of $\mathcal {M}$.

Proof

Here is an informal but precise description of the construction of the expansion of $\mathcal {M}$ to ${\mathcal {M}}^*$ and the translation of $\varphi$ to $\varphi ^{\#}$. We leave the formal details to the interested reader.

• 1. Re-label all states of $\mathcal {M}$ by integers, i.e., assume $\textsf {St} = \{0,\ldots , n-1\}$.

• 2. Introduce an extra player $\mathbf {s}$ with payoff function in $\mathcal {M}$ defined so that the current utility of $\mathbf {s}$ always equals the number $\#$ of the current state. That is done by assigning only one unguarded action to $\mathbf {s}$ at every state and defining its payoffs to be the difference: $\#$(successor state) – $\#$(current state).

• 3. For every $p\in \textsf {Prop}$ define the quantitative formula:

  $$\begin{aligned} \delta _{\mathbf {s}}(p) = \bigvee \{ v_{\mathbf {s}} = i \mid {p \in \textsf {L}(i)}, \text{ for } i \in \textsf {St} \} \end{aligned}$$

  Note that in any play $\pi$, $\delta _{\mathbf {s}}(p)$ is true at a configuration $(i,\mathbf {u})$ iff $p \in \textsf {L}(i)$, for each $i \in \textsf {St}$.

• 4. Translate any $\textsf {QATL}^{*}$-formula $\varphi$ into a purely quantitative one $\varphi ^{\#}$ by replacing every occurrence of each $p\in \textsf {Prop}$ by the respective $\delta _{\mathbf {s}}(p)$.

$\square$

Remark 1

The reduction above only works if negative payoffs are allowed, but it can also be realised in a GCGMP with only non-negative payoffs, by using congruences. The idea is to maintain the current accumulated utility of $\mathbf {s}$ to be always congruent to the number of the current state modulo the number n of all states, and the quantitative formula associated with every $p\in \textsf {Prop}$ is defined likewise, by replacing $v_{\mathbf {s}} = i$ with $v_{\mathbf {s}} \equiv _{n} i$. Moreover, this translation also works in the case of infinitely many states, if each proposition can only occur in the labels of finitely many states.

5 On the model checking of QATL*

5.1 Undecidability results

The GCGMP models are too rich and the language of $\textsf {QATL}^{*}$ is too expressive to expect computational efficiency, or even decidability, of either model checking or satisfiability. In the following we show that model checking of $\textsf {QATL}^{*}$– and even of $\textsf {QATL}$ – in a GCGMP is undecidable under rather weak assumptions, e.g. if the proponents or the opponents can use any effective strategies. These undecidability results are not surprising, as GCGMPs are technically closely related to Petri nets and vector addition systems with states (VASS) and it is known that logic-based model checking over them is generally undecidable. For example, in [34] this is shown for fragments of $\textsf {CTL}$ and (state-based) $\textsf {LTL}$ over Petri nets. Essentially, the reason is that these logics allow encoding a “test for zero” over such models; for Petri nets this means to check whether a place contains a token or not. In our setting undecidability follows for the same reason, and we will sketch some results here. We outline the constructions and arguments in order to illustrate the expressiveness of the present framework, but do not provide full technical details, as they can be essentially retrieved from the references on similar results.

We show that model checking of $\textsf {QATL}$ is undecidable even if the proponents are only permitted to use state-based, local-view, effective strategies (formally: $\mathcal {S}^{p}=\Sigma ^{sle}$). In our construction there will be no opponents; so, it does not matter which class of strategies we fix for them. The reduction can be done by applying ideas from e.g. [34], or from [19]—which are used here—to simulate a two-counter machine (TCM) (aka two-counter automaton, or 2-register Minsky machine [45]). Intuitively, TCM  (see e.g., [40]) can be considered as a transition system equipped with two integer counters that enable/disable transitions. Each step of the machine depends on the current state, the symbol on the tape, and the counters, whether they are zero or not. After each step the counters can be incremented ($+1$), or decremented ($-1$) , the latter only if the respective counter is not zero. An alternative view on a TCM is essentially as a nondeterministic push-down automaton with two stacks and exactly two stack symbols (one of them is the initial stack symbol). It has the same computation power as a Turing machine, cf. [40].

Formally, we define a TCM (in the latter sense), as a tuple $\mathcal {A}=(S,\varGamma ,s^\text {init},S_f,\varDelta )$, where:

• S is a finite non-empty state space,

• $\varGamma$ is a finite input alphabet,

• $s^\text {init} \in S$ is an initial state,

• $S_f$ is a set of final, or accepting states,

• $\varDelta$ is a transition relation, where $\varDelta \subseteq (S\times (\varGamma \cup \{ \epsilon \}) \times \{0,1\}^2)\times (S\times \{-1,0,1\}^2)$ (explained below).

A configuration in $\mathcal {A}$ is a triple $(s,c_1,c_2)$, where $s \in S$ is the current state and $c_1,c_2$ are the (non-negative) current values of the two counters. The initial configuration is $(s^\text {init},0,0)$. The transition relation acts non-deterministically on configurations, as follows: given a current configuration $(s,c_1,c_2)$, $\varDelta$ takes as input $(s,w,E_1,E_2)$, where $w \in \varGamma \cup \{ \epsilon \}$ is the currently read input symbol or the empty word, and for each $i=1,2$, $E_i=1$ if the counter i is non-empty (i.e, $c_i > 0$), respectively, $E_i=0$ if $c_i = 0$. Then $\varDelta$ produces as output a set of triples $(s',C_1,C_2)$ where for each $i=1,2$, $C_i=1$ (resp. $C_i=-1$ and $C_i=0$) denotes that counter i is incremented by 1, decremented by 1 and left unchanged, respectively. The case $C_i=-1$ is allowed only when $c_i > 0$, i.e. $E_i=1$. Every such triple determines a successor configuration $(s',c_1+C_1,c_2+C_2)$. Note that each of the new counter values is non-negative.

The TCM $\mathcal {A}$ reads an input word $\mathbf{w} \in \varGamma ^*$ just like a finite automaton, one symbol at a time, starting from the initial configuration, and makes non-deterministically a sequence of subsequent transitions according to the respective symbols from $\mathbf{w}$ and the transition relation. A computation in $\mathcal {A}$ generated by an input word $\mathbf{w} \in \varGamma ^*$ is a sequence of subsequent configurations effected by transitions according to the input $\mathbf{w}$ and the transition relation.

The word $\mathbf{w} \in \varGamma ^*$ is accepted by $\mathcal {A}$ if there is a computation in $\mathcal {A}$ generated by $\mathbf{w}$ and ending in a configuration $(s,c_1,c_2)$ where $s \in S_f$.

For our present purposes it will suffice to consider computations from the empty input $\epsilon$, where the input alphabet $\varGamma$ can be ignored.

Fig. 5

Encoding of a transition $(s,E_{1},E_{2})\varDelta (s',C_{1},C_{2})$ in $\mathcal {M}^{A}$

Lemma 1

(Reduction) For any two-counter machine $\mathcal {A}$ we can construct a finite, turn based GCGMP $\mathcal {M}^\mathcal {A}$ with two players and proposition $\textsf {halt}$ such that the following holds: $\mathcal {A}$ accepts the empty word iff $\mathcal {M}^\mathcal {A}$ contains a play $\pi$ with $\pi ^{c}=(s_0,(v_1^0,v_2^0))(s_1,(v_1^1,v_2^1))\dots$ such that there exists $j\in \mathbb {N}$ with $\textsf {halt} \in \textsf {L}(s_j)$.

Proof

Let TCM $\mathcal {A}=(S,\varGamma ,s^\text {init},S_f,\varDelta )$ be given. We first outline the construction of the model $\mathcal {M}^{\mathcal {A}}$, and then we provide the full technical details. For the simulation, we associate each counter with a player. The player’s current utility encodes the counter value; actions model the increment/decrement/no change of the counters; guards ensure that the actions respect the state of the counters. The accepting states are labelled by a special proposition $\textsf {halt}$.

As mentioned earlier, since we only need to simulate the runs of $\mathcal {A}$ on the empty input, the input alphabet $\varGamma$ can be ignored and the transition relation can be simplified to $\varDelta \subseteq (S\times \{0,1\}^2)\times (S\times \{-1,0,1\}^2)$.

States of player 1 are given by $S_{1}= S^{1}_{1}\cup S^{2}_{1}$ where $S^{1}_{1}=S$ and $S^{2}_{1}=\{s^{x_{1}x_{2}}\mid x_{1}, x_{2}\in \{0,1\}, s\in S\}$. (Intuitively, player 1 chooses the initial part of a transition $(s,x_1,\cdot )\varDelta (\cdot ,\cdot ,\cdot )$ in states from S, and from a state $s^{{x_{1}x_{2}}}$ player 1 decides how the counter value of counter 1 will change). The states of player 2 are $S_{2}= S^{1}_{2}\cup S^{2}_{2}$ where $S^{1}_{2}=\{s^{x}\mid x\in \{0,1\},s\in S\}$ and $S^{2}_{2}=\{s^{x_{1}x_{2}x_{3}}\mid x_{1},x_{2}\in \{0,1\}, x_{3}\in \{-1,0,1\}, s\in S\}$. (Intuitively, from states $s^{x_{1}}$ player 2 decides which transition $(s,x_{1},x_{2})\varDelta (\cdot ,\cdot ,\cdot )$ to choose. From a state $s^{{x_{1}x_{2}x_{3}}}$ player 2 decides how the counter value of counter 2 will change.)

Actions model the possible transitions of the automaton. An action has the general form (s, x), where $s \in S_1 \cup S_2$ indicates the successor state and $x \in \{-1,0,1\}$ specifies how the payoff of the executing player changes. For example, an action $(s^{E_{1}E_{2}},C_{1})$ is possible in state $s^{E_{1}}$ and simulates the change of counter 1 according to $C_{1}$. Thus, every transition $((s,E_1,E_2),(s',C_1,C_2)) \in \varDelta$ in $\mathcal {A}$ is simulated by a 5-state sequence of transitions in $\mathcal {M}^{\mathcal {A}}$, illustrated in Fig. 5.

Crucial in the encoding are the guards. For example, to a state s we assign the guard $\textsf {grd}_{1}(s,(s,0)) = (v_{1}=0)$ indicating that action (s, 0) is only enabled if counter 1 is indeed zero (i.e. $v_{1}=0$). Similarly, $\textsf {grd}_{1}(s,(s,1))=(v_{1}\ge 1)$ is used to ensure that action (s, 1) is only enabled if counter 1 is non-zero (i.e. $v_{1}\ge 1$). Analogously, for the other states and the other player.

Lastly, we define $s_0 = s^{init}$ and label all states $s\in S_{f}$ with the proposition $\textsf {halt}$.

Here are the technical details of the construction. Given the TCM $\mathcal {A}=(S,\varGamma ,s^\text {init},S_f,\varDelta )$ we construct the turn based GCGMP $\mathcal {M}=(\mathcal {S}, \textsf {payoff}, \textsf {grd})$, where $\mathcal {S} = (\textsf {Ag}, \textsf {St}, \{\textsf {Act} _\textsf {a} \}_{\textsf {a} \in \textsf {Ag}}, \{\textsf {act} _{\textsf {a}}\}_{\textsf {a} \in \textsf {Ag}}, \textsf {out},\textsf {Prop},\textsf {L})$, as follows (cf. also Fig. 5):

• $\textsf {Ag} =\{1,2\}$.

• $\textsf {St} =S_{1}\cup S_{2}$, where:

  • $S_{1}= S^{1}_{1}\cup S^{2}_{1}$ are Player 1’s states, where $S^{1}_{1}=S$ and $S^{2}_{1}=\{s^{x_{1}x_{2}}\mid x_{1}, x_{2}\in \{0,1\}, s\in S\}$.

    Intuitively, Player 1 chooses the initial part of a transition $(s,E_1,\cdot )\varDelta (\cdot ,\cdot ,\cdot )$ in states from S.

    From a state $s^{{x_{1}x_{2}}}$ Player 1 decides how the counter value of counter 1 will change.

  • $S_{2}= S^{1}_{2}\cup S^{2}_{2}$ are Player 2’s states, where $S^{1}_{2}=\{s^{x}\mid x\in \{0,1\},s\in S\}$ and $S^{2}_{2}=\{s^{x_{1}x_{2}x_{3}}\mid x_{1},x_{2}\in \{0,1\}, x_{3}\in \{-1,0,1\}, s\in S\}$.

    Intuitively, from states $s^{x_{1}}$ Player 2 decides which transition relation $(s,x_{1},E_{2})\varDelta (\cdot ,\cdot ,\cdot )$ to chose.

    From a state $s^{{x_{1}x_{2}x_{3}}}$ Player 2 decides how the counter value of counter 2 will change.

• $\textsf {Act} _{1}=\textsf {Act} ^{1}_{1}\cup \textsf {Act} ^{2}_{1}\cup \{\textsf {noop} \}$ where $\textsf {Act} ^{1}_{1}=\{(s,E)\mid (s,E,E')\varDelta (s',C_{1},C_{2})\}$ and $\textsf {Act} ^{2}_{1}=\{(s^{E_{1}E_{2}},C_{1})\mid (s,E_{1},E_{2})\varDelta (s',C_{1},C')\}$,

• $\textsf {Act} _{2}=\textsf {Act} ^{1}_{2}\cup \textsf {Act} ^{2}_{2}\cup \{\textsf {noop} \}$ where $\textsf {Act} ^{1}_{2}=\{(s^{E_{1}},E_{2})\mid (s,E_{1},E_{2})\varDelta (s',C_{1},C_{2})\}$ and $\textsf {Act} ^{2}_{2}=\{(s^{E_{1}E_{2}C_{1}},C_{2},s')\mid (s,E_{1},E_{2})\varDelta (s',C_{1},C_{2})\}$.

• $\textsf {act} _{i}(q)= {\left\{ \begin{array}{ll} \textsf {Act} ^{1}_{i}\cup \{\textsf {noop} \}, &{} q\in S^{1}_{i}\\ \textsf {Act} ^{2}_{1}\cup \{\textsf {noop} \}, &{} q\in S^{2}_{i}\\ \end{array}\right. }$ for $i\in \{1,2\}$

• $\textsf {out} (q,(\alpha _{1},\alpha _{2}))= {\left\{ \begin{array}{ll} q^{E}, &{}\text { if }q\in S\subseteq S_{1}, \alpha _{1}=(q,E), \alpha _{2}=\textsf {noop} \\ s^{E_{1}E_{2}C_{1}}, &{}\text { if } q=s^{E_{1}E_{2}}\in S_{1}, \alpha _{1}=(s^{E_{1}E_{2}},C_{1}), \alpha _{2}=\textsf {noop} \\ s^{E_{1}E_{2}}, &{}\text { if } q=s^{E_{1}}\in S_{2}, \alpha _{2}=(s^{E_{1}},E_{2}), \alpha _{1}=\textsf {noop} \\ s', &{}\text { if } q=s^{E_{1}E_{2}C_{1}}\in S_{2}, \alpha _{2}=(s^{E_{1}E_{2}C_{1}},C_{2},s'), \alpha _{1}=\textsf {noop} \\ q, &{}\text { else} \end{array}\right. }$

• $\textsf {payoff}(1,q,(\alpha _{1},\alpha _{2}))= {\left\{ \begin{array}{ll} C_{1}, &{}\text { if }q\in S_{1}, \alpha _{1}=(s^{E_{1}E_{2}},C_{1})\in \textsf {Act} ^{2}_{^1}\\ 0, &{}\text { else} \end{array}\right. }$

• $\textsf {payoff}(2,q,(\alpha _{1},\alpha _{2}))= {\left\{ \begin{array}{ll} C_{2}, &{}\text { if }q\in S_{2}, \alpha _{1}=(s^{E_{1}E_{2}C_{1}},C_{2})\in \textsf {Act} ^{2}_{^2}\\ 0, &{}\text { else} \end{array}\right. }$

• $\textsf {grd}_{i}(q,\alpha )={\left\{ \begin{array}{ll} v_{i}=0, &{}\text { if } q\in S^{1}_{i}, \alpha =(q,0)\in \textsf {Act} ^{1}_{i}\\ v_{i}\ge 1, &{}\text { if } q\in S^{1}_{i}, \alpha =(q,1)\in \textsf {Act} ^{1}_{i}\\ \top , &{}\text { else} \end{array}\right. }$

• We define $s^{init}$ as initial state and label all states $s\in S_{f}$ with proposition $\textsf {halt}$.

Now, we can show by induction that the automaton accepts the empty word iff $\mathcal {M}^{A}$ contains a path $\pi =(s^0,(v_1^0,v_2^0))(s^1,(v_1^1,v_2^1))\dots$ such that there exists $j\in \mathbb {N}$ with $\textsf {halt}\in \textsf {L}(s_j)$.

To conclude the proof, it is quite straightforward to check that the model $\mathcal {M}^{\mathcal {A}}$ allows a path reaching a state labelled $\textsf {halt}$ starting from $s_0$ iff the automaton accepts the empty word. $\square$

The next theorem states two cases for which the model-checking problem is undecidable. By Lemma 1 it suffices to specify a formula which is true if, and only if, the halting state is reached.

Theorem 1

Model checking of $\textsf {FlatQATL} _{1}$ is undecidable in the 2-agent case where $\mathcal {S}^{o}=\Sigma ^{sle}$ and $\mathcal {S}^{p}$ is fixed arbitrarily. This holds even in each of the following cases:

• (a) formulae not involving arithmetic constraints;

• (b) state-based guards.

Proof

(a) By Lemma 1 and the undecidability of the halting problem of TCMs on an empty input ([40, 45]) it is sufficient to show the following: $\mathcal {M}^{\mathcal {A}}$ contains a path $\pi =(s_0,(v_1^0,v_2^0))\alpha ^{0}(s_1,(v_1^1,v_2^1))\alpha ^{1}\dots$ such that there exists $j\in \mathbb {N}$ with $\textsf {halt} \in \textsf {L}(s_j)$ if, and only if, $\mathcal {M}^{\mathcal {A}},(s^{init},(0,0))\models _{(\Sigma ^{sle},\mathcal {S}^{o})}\langle \!\langle {1,2}\rangle \!\rangle _{_{\! }}\mathbf {F}\,\textsf {halt}$.

The right-to-left direction is clear. For the left-to-right direction, we define the strategy profile $s=({\sigma _{1},\sigma _{2}})$ as follows: For each $i=1,2$, the strategy $\sigma _{i}$ assigns action $\alpha ^{k}$ to the sequence of states $s_{0}\dots s_{k}$ if $s_{k}$ is a player i’s state, for $k=0,\dots , j$, else an arbitrary action. Once the final state $s^{j}$ is reached the action $\textsf {noop}$ that guarantees transition to that same state is performed. Clearly, such strategy needs only finite memory, it is state-based, hence local view, and is effective.

(b) Let $\mathcal {M}^{\mathcal {A}'}$ be defined like $\mathcal {M}^{\mathcal {A}}$ but all guards map to $\top$ (i.e. they are state-based). Moreover, we label all states $s^{x_{1}x_{2}}\in S^{2}_{1}$ with a proposition $\textsf {test}$ and, additionally, with $\textsf {e}_{i}$ iff $x_{i}=0$, for $i=1,2$. In these states the consistency of the choice of the transitions is verified. Then, we have that $\mathcal {M}^{\mathcal {A}}$ contains a path $\pi =(s_0,(v_1^0,v_2^0))\alpha ^{0}(s_1,(v_1^1,v_2^1))\alpha ^{1}\dots$ such that $\textsf {halt} \in \textsf {L}(s_j)$ for some $j\in \mathbb {N}$ iff

$$\begin{aligned} \mathcal {M}^{\mathcal {A}},(s^{init},(0,0))\models _{(\Sigma ^{sle},\mathcal {S}^{o})}\langle \!\langle {1,2}\rangle \!\rangle _{_{\! }}(v_1\ge 0\wedge v_2\ge 0\wedge (\textsf {test}\rightarrow (\textsf {e}_1\leftrightarrow v_1=0\wedge \textsf {e}_2\leftrightarrow v_2=0)))\,\mathbf {U}\,\textsf {halt}. \end{aligned}$$

We illustrate the right-to-left direction by considering the case where the state $s_{k}$ is of the form $s^{0x_{2}}$. Then action $(s_{k-2}^0,0)$ must have been performed in state $s_{k-2}$ and thus $v_{1}^{k-2}=0$. Thus, the guards in $\mathcal {M}^{\mathcal {A}}$ are correctly simulated. The reasoning for the other combinations of $x_{1}x_{2}$ is similar. The remainder of the proof is analogous to (a). $\square$

Corollary 1

Model checking 2-agent $\textsf {QATL}^{*}$ is undecidable, where $\mathcal {S}^{p}=\Sigma ^{sle}$ and $\mathcal {S}^{o}$ is fixed arbitrarily. This holds even in the following cases:

• (a) $\textsf {QATL}$-formulae, not involving arithmetic constraints;

• (b) $\textsf {QATL}$ extended with the release operator³$\mathbf {R}$ and only state-based guards.

Proof

In the proof of Theorem 1 we replace the formulae used in (a) and (b) respectively by $\lnot \langle \!\langle {\emptyset }\rangle \!\rangle _{_{\! }}\mathbf {G}\,\lnot \textsf {halt}$ and $\lnot \langle \!\langle {\emptyset }\rangle \!\rangle _{_{\! }}\lnot ((v_1\ge 0\wedge v_2\ge 0\wedge (\textsf {test} \rightarrow (\textsf {e}_1\leftrightarrow v_a=0\wedge \textsf {e}_2\leftrightarrow v_2=0)))\,\mathbf {U}\,\textsf {halt})$ (note that $\lnot \,\mathbf {U}\,$ can be expressed by means of $\mathbf {R}$). Now, the proofs follows the same lines as in the proof of Theorem 1. $\square$

Remark 2

The undecidability results above essentially use the possibility of negative payoffs, to decrement counters. As we will show later, decidability can be possibly restored if only non-negative payoffs are allowed in the model (cf. Theorem 2). However, if in the language of arithmetical constraints we allow addition and comparison of payoffs of different players, then undecidability can be re-established again, even if only non-negative payoffs are allowed. This can be done by introducing a fictitious new player and using the differences (which can be positive or negative) between his current utility and the current utilities of the other players to play the role of the players’ current utilities used in the undecidability proofs above.

More undecidability results can be obtained likewise, using the formula $\langle \!\langle {1,2}\rangle \!\rangle _{_{\! }}\mathbf {F}\,\textsf {halt}$, for the 2-agent cases with negative payoffs and no guards and any effective strategies, or with configuration based-guards and configuration based strategies. We leave out the technical details.

5.2 Decidability results

Despite the wide-ranging undecidability results, there are some natural semantic and syntactic restrictions of $\textsf {QATL}^{*}$ where decidability of the model checking problem may be restored, by making the configuration space and the strategy search space finite. Such restrictions include: the enabling of only memoryless strategies, imposing non-negative payoffs, constraints on the transition graph of the model, restrictions of the arithmetical constraints and guards ensuring bounded players’ accumulated utilities, etc. Here we outline one such non-trivial case and briefly discuss some others, but a more comprehensive study of decidable cases is left to further work.

Cover unfoldings. As already noted earlier, the GCGMP models are technically closely related to vector addition systems with states (VASS). Karp and Miller introduced in  [44] a compact symbolic representation of an over-approximation of the set of reachable configurations in a given vector addition system $\mathcal {W}$, by means of a finite labelled tree which is often called the cover graph of $\mathcal {W}$ and used it to solve, inter alia, the coverability problem for $\mathcal {W}$, deciding membership in the so called coverability set of $\mathcal {W}$, consisting of all configurations in $\mathcal {W}$ that can be ‘exceeded’, in terms of the lexicographic ordering over the vectors of counter values, by reachable configurations. We will formally define and explain here a version of the cover graph for the class of GCGMP models.

First, let $\mathbb {Z}_{\omega }$ be the set of integers extended with an ‘infinity number’ $\omega$ which is strictly greater than all integers. For each $x\in \mathbb {Z}$ we put $\omega +x = \omega + \omega = \omega$. Now, the arithmetic constraint formulae are readily extended and interpreted over $\mathbb {Z}_{\omega }$.

Let $\kappa \in \mathbb {N}$. Given two vectors $\mathbf {x},\mathbf {x}'\in \mathbb {Z}_{\omega }^{k}$, for some $k\in \mathbb {N}$, we define $\mathbf {x}\le _{\kappa }\mathbf {x}'$ iff $\mathbf {x}_{i}=\mathbf {x}'_i$ or $\kappa<\mathbf {x}_{i}<\mathbf {x}'_{i}$, for each $i=1,\dots ,k$. Then, we define $\mathbf {x}<_{\kappa }\mathbf {x}'$ iff $\mathbf {x}\le _{\kappa }\mathbf {x}'$ and $\mathbf {x} \ne \mathbf {x}'$. Now, we define $\mathbf {x}\oplus \mathbf {x}'$ as the vector $\mathbf {\widehat{x}}\in \mathbb {Z}_{\omega }^{k}$ such that $\mathbf {\widehat{x}}_{i}=\mathbf {x}_{i}$ if $\mathbf {x}_{i}=\mathbf {x}_{i}'$, and $\mathbf {\widehat{x}}_{i}=\omega$ otherwise, for $i=1,\dots ,k$.

Now, given a GCGMP $\mathcal {M}$, a configuration $c\in \textsf {Con}_{\mathcal {M}}$, and a natural number $\kappa \in \mathbb {N}$, the $\kappa$ -cover unfolding of $\mathcal {M}$ from c, denoted $\mathcal {M}_{\kappa }^{c}$, is a CGM essentially obtained by unfolding the initialized configuration graph of $\mathcal {M}$ from the designated initial configuration c, but each time we encounter a configuration $c'=(s,\mathbf {u}')$ after we have already encountered a configuration $c^*=(s,\mathbf {u})$ with $\mathbf {u}\le _{\kappa }\mathbf {u}'$, we add not $c'$ but $(s,\mathbf {u}\oplus \mathbf {u}')$ to $\mathcal {M}_{\kappa }^{c}$. Furthermore, given $c'$, we take a $\le _{\kappa }$-largest such preceding configuration $c^*$. The intuition is as follows: whenever a configuration in $\mathcal {M}$ can be reached which is greater in terms of $\le _{\kappa }$ than a previously reached configuration with the same state, then this ‘increasing step’ can be repeated infinitely, resulting either in a cyclic subsequence of configurations, or in a strictly increasing one on at least one coordinate component. Then $\mathbf {u}''\oplus \mathbf {u}'$ places $\omega$ in each coordinate of strict increase, meaning that unboundedly large values can be reached on that coordinate. To make that formal, we define simultaneously the state space $\textsf {St} _{\kappa }^{c}$ and the outcome function $\textsf {out} _{\kappa }^{c}$ of $\mathcal {M}_{\kappa }^{c}$ as follows. We define the set $\textsf {St} _{\kappa }^{c}$ of generalised configurations reachable from c as the smallest set containing c and closed under $\textsf {out} _{\kappa }^{c}$, which is defined as follows. First, we extend ${\widehat{\textsf {out}}}$ to act on generalised configurations just like it does on standard configurations, but by taking into account the extended interpretation of $+$ and the arithmetic constraint formulae in $\mathbb {Z}_{\omega }$.

Suppose $(s,\mathbf {u})\in \textsf {St} _{\kappa }^{c}$ and $(s',\mathbf {u}') = {\widehat{\textsf {out}}} ((s,\mathbf {u}),\alpha )$.

Then we define $\textsf {out} _{\kappa }^{c}((s,\mathbf {u}),\alpha ){:}{=}(s',\mathbf {\widehat{u}})$, where:

(i) $\mathbf {\widehat{u}}=\mathbf {u}'$, if there is no generalised configuration $(s',\mathbf {u}'')\in \textsf {St} _{\kappa }^{c}$ with $\mathbf {u}''\le _{\kappa }\mathbf {u}'$ which is ${\widehat{\textsf {out}}}$-preceding $(s',\mathbf {u}')$, that is, $(s',\mathbf {u}')$ is an ${\widehat{\textsf {out}}}$-successor of $(s',\mathbf {u}'')$,

else

(ii) $\mathbf {\widehat{u}}=\mathbf {u}''\oplus \mathbf {u}'$ if $(s',\mathbf {u}'')\in \textsf {St} _{\kappa }^{c}$ is ${\widehat{\textsf {out}}}$-preceding $(s',\mathbf {u}')$, such that $\mathbf {u}'' \le _{\kappa }\mathbf {u}'$, and there is no $(s',\mathbf {u}''')\in \textsf {St} _{\kappa }^{c}$ with $\mathbf {u}''<_{\kappa }\mathbf {u}'''\le _{\kappa }\mathbf {u}'$.

We then add $(s',\mathbf {\widehat{u}})$ to $\textsf {St} _{\kappa }^{c}$.

Definition 9

($\kappa$ -cover) Let $\mathcal {M}=((\textsf {Ag}, \textsf {St}, \{\textsf {Act} _\textsf {a} \}_{\textsf {a} \in \textsf {Ag}}, \{\textsf {act} _{\textsf {a}}\}_{\textsf {a} \in \textsf {Ag}}, \textsf {out},\textsf {Prop},\textsf {L}), \textsf {payoff}, \textsf {grd})$ be a GCGMP and let $c\in \textsf {Con}_{\mathcal {M}}$. We define the $\kappa$-cover of the pair $(\mathcal {M},c)$ as the CGM $\mathcal {M}_{\kappa }^{c}=(\textsf {Ag}, \textsf {St} _{\kappa }^{c}, \{\textsf {Act} _\textsf {a} \}_{\textsf {a} \in \textsf {Ag}}, \{\textsf {act} '_{\textsf {a}}\}_{\textsf {a} \in \textsf {Ag}}, \textsf {out} _{\kappa }^{c},\textsf {Prop},\textsf {L}')$ where $\textsf {St} _{\kappa }^{c}$ and $\textsf {out} _{\kappa }^{c}$ are defined as above, and $\textsf {act} _{a}'(s,\mathbf {u})=\{\alpha _{a}\in \textsf {Act} _a\mid \mathbf {u}_{a}\models \textsf {grd}_{a}(s,\alpha _{a})\}$, $\textsf {L}'((s,\mathbf {u}))=\textsf {L}(s)$.

Proposition 2

Let ${\mathcal {M}}$ be a finite GCGMP with non-negative payoffs and ${c}\in \textsf {Con}_{\mathcal {M}}$. Then, $\mathcal {M}_{\kappa }^{c}$ is finite for any $\kappa \in \mathbb {N}$.

Proof

The proof is similar to the corresponding proof for Karp-Miller graphs [44]; cf. also a similar proof for covers of resource bounded models in [18].

Suppose $\mathcal {M}_{\kappa }^{c}$ is infinite (i.e., it has infinitely many states). Note that every $(s,\mathbf {u})\in \textsf {St} _{\kappa }^{c}$ has only finitely many $\textsf {out} _{\kappa }^{c}$-successors. Then, by König’s lemma, there is an infinite play $\pi =c_0\alpha _0c_1\alpha _1\ldots$ in $\mathcal {M}_{\kappa }^{c}$ with $c_i=(s_i,\mathbf {u}_i)$ consisting of distinct states in $\mathcal {M}_{\kappa }^{c}$ (recall, that these are generalised configurations in $\mathcal {M}$). Since the set of states $\textsf {St}$ in $\mathcal {M}$ is finite, there is some state $s\in \textsf {St}$ of $\mathcal {M}$ and an infinite subsequence of distinct configurations $\pi '=c_{i_1}c_{i_2}\dots$ of $\pi$ with $c_{i_j}=(s,\mathbf {u}^{i_j})$ and $i_j<i_{j+1}$ for all $j=1,2,\dots$. Due to the construction of the $\kappa$-cover, it cannot be the case that $\mathbf {u}^{i_{j}}\le _\kappa \mathbf {u}^{i_{j'}}$ for any $1\le j<j'$; otherwise, according to the definition of $\textsf {out} _{\kappa }^{c}$, a configuration $(s,\mathbf {u}^{i_{j}}\oplus \mathbf {u}^{i_{j'}})$ would have been introduced in $\pi '$, forcing each subsequent generalised configuration to be equal from that point on, which contradicts the infinite number of configurations in $\pi$. So, for each $j=1,2,...$ there must be an agent $\textsf {a} _j$ such that $\mathbf {u}^j_{\textsf {a} _j}\ne \mathbf {u}^{j+1}_{\textsf {a} _j}$ and not $\kappa<\mathbf {u}^j_{\textsf {a} _j}<\mathbf {u}^{j+1}_{\textsf {a} _j}$. Since the set of agents is finite, at least one of them, say $\textsf {a}$, will appear infinitely often in ${\textsf {a} _1}, {\textsf {a} _2}, ...$, so we can assume that $\pi '$ has been chosen so that each ${\textsf {a} _j}$ is ${\textsf {a}}$. Thus, $\mathbf {u}^j_{\textsf {a}}\ne \mathbf {u}^{j+1}_{\textsf {a}}$ and not $\kappa<\mathbf {u}^j_{\textsf {a}}<\mathbf {u}^{j+1}_{\textsf {a}}$ for each $j=1,2,...$. Because the payoff vectors are non-negative, this implies that either $\kappa =\mathbf {u}^j_\textsf {a} <\mathbf {u}^{j+1}_\textsf {a}$, or $\mathbf {u}^j_\textsf {a} <\kappa \le \mathbf {u}^{j+1}_\textsf {a}$, or $\mathbf {u}^j_\textsf {a}<\mathbf {u}^{j+1}_\textsf {a} <\kappa$. But, clearly, each of these options can only occur finitely many times – a contradiction with the choice of $\pi '$. Therefore, $\mathcal {M}_{\kappa }^{c}$ must be finite. $\square$

The idea of using $\kappa$-covers is to reduce model checking in a given GCGMP to model checking in its $\kappa$-covers. In order to formally extend the semantics of $\textsf {QATL}^{*}$ to $\kappa$-covers defined as above, note that every $\kappa$-cover can also be seen as a GCGMP with state-based guards and arbitrary payoff function, e.g., one always assigning payoffs 0 to all players. Thus, the set of configurations in $\mathcal {M}_{\kappa }^{c}$ regarded as a GCGMP—denoted $\widehat{\textsf {Con}}(\mathcal {M}_{\kappa }^{c})$ can be identified with the set of states in it and re-defined as $\widehat{\textsf {Con}}(\mathcal {M}_{\kappa }^{c})=\textsf {St} _{\kappa }^{c}$.

Therefore, we can define the satisfaction relation $\widehat{\models }_{(\mathcal {S}^{p}, \mathcal {S}^{o})}$ over $\kappa$-cover models analogously to its state-based version $\models _{((\mathcal {S}^{p})^{s},(\mathcal {S}^{o})^{s})}$ where configurations are drawn from $\widehat{\textsf {Con}}$. Thus, $\mathcal {M}_{\kappa }^{c}$ can be used to give meaningful semantics to $\textsf {QATL}^{*}$-formulae, with the truth definitions of all ${\textsf {ATL}}^{*}$-formulae (which only depend on the state-history) defined as usual (cf. Definition 8), whereas the truth of all atomic formulae $\textsf {ac}\in \textsf {ACF}$ is determined by $\mathbf {u}$, included in the state, with respect to the ordering in $\mathbb {Z}_{\omega }$ as defined above. Formally, we consider arithmetic constraints as atomic propositional formulas and define their truth directly in the model. However, note that comparisons between two players’ utilities may not be possible to evaluate on configurations where both values are $\omega$, so we have to restrict the language to the fragment $\textsf {QATL}_{1}^{*}$ that does not permit comparisons between players’ utility values. The formal definition is given below.

Definition 10

(Extended cover model) Let $\varphi$ be any $\textsf {QATL}_{1}^{*}$-formula. Then we define $C_\varphi =\{\textsf {ac}\in \textsf {ACF} \mid \textsf {ac}\text { occurs in }\varphi \}$ be the set of arithmetic constraints occurring in $\varphi$, and $\mathcal {M}^c_\kappa$ be the $\kappa$-cover of a GCGMP $\mathcal {M}$. The $\varphi$ -extended $\kappa$ -cover $\mathcal {M}^{c,\varphi }_\kappa$ of $\mathcal {M}$ is the same as $\mathcal {M}^c_\kappa$ but the set of atomic propositions is extended by $C_\varphi$ where the labelling function $\textsf {L}$ of $\mathcal {M}^{c,\varphi }_\kappa$ is extended on $C_\varphi$ as follows: for all $\textsf {ac}\in C_\varphi$ and $(s,\mathbf {u})\in \textsf {St}$, $\textsf {ac}\in \textsf {L}((s,\mathbf {u}))$ iff $\mathbf {u}_\textsf {a} \models \textsf {ac}$ where $\textsf {ac}\in \textsf {AC} _b(X,\{\textsf {a} \})$.

Let $\max _{(\mathcal {M},\varphi )}$ be the maximum of all constants occurring in any guard of $\mathcal {M}$ and in any arithmetic constraint occurring in $\varphi$. (If there are none, take any positive integer.) The next result shows that one can reduce truth of formulae of $\textsf {QATL}_{1}^{*}$ in a GCGMP with non-negative payoffs to truth in its $\varphi$-extended $\kappa$-cover for any $\kappa > \max _{(\mathcal {M},\varphi )}$. We first introduce some auxiliary notation and prove a lemma. Given two integers $x,x'\in \mathbb {Z}_{\omega }$ and $\kappa \in \mathbb {N}$ we write $x\equiv ^{\kappa } x'$ iff $x=x'$ or $\kappa < x,x'$. We extend $\equiv ^{\kappa }$ to vectors $\mathbf {u},\mathbf {u}'\in \mathbb {Z}_{\omega }^{n}$ and to sequences $\mathbf {x},\mathbf {x}'\in (\mathbb {Z}_{\omega })^{\omega }$ as follows: $\mathbf {u}\equiv ^{\kappa }\mathbf {u}'$ iff $u_{i}\equiv ^{\kappa }u_{i}'$ for all $i=1,\dots ,n$ and, respectively $\mathbf {x}\equiv ^{\kappa }\mathbf {x}'$ iff $x_{i}\equiv ^{\kappa }x_{i}'$ for all $i=1,2,\dots$. Then, we extend $\equiv ^{\kappa }$ to generalised configurations: $(s,\mathbf {u}) \equiv ^{\kappa } (s',\mathbf {u'})$ iff $s= s'$ and $\mathbf {u}\equiv ^{\kappa }\mathbf {u}'$. Finally, for two plays $\pi$ and $\pi '$ we write $\pi \equiv ^{\kappa }\pi '$ iff $(\pi )^{s}=(\pi ')^{s}$ and $(\pi )^{u}\equiv ^{\kappa }(\pi ')^{u}$, i.e. the sequences of states are identical and the utility values are either pairwise equal or both strictly greater than $\kappa$. The following lemma shows that for a fixed set of basic constraints it is sufficient to consider integers up to a specific size. We note that the result can be extended to simple arithmetic constraints by evaluating addition.

Lemma 2

Let $\kappa$ be the maximum of all constants occurring in an arithmetic constraint $\textsf {ac} \in \textsf {AC} _b(X,\{\textsf {a} \})$. Then, for any $x,x'\in \mathbb {Z}_\omega$ with $x\equiv ^{\kappa } x'$ we have that $x\models \textsf {ac}$ iff $x'\models \textsf {ac}$.

Proof

An arithmetic constraint $\textsf {ac} \in \textsf {AC} _b(X,\{\textsf {a} \})$ is of the form $v_\textsf {a} \sim c$ or $c\sim d$ for $c,d\in X$ and $\sim \in \{<, \le , =, \ge , >\}$. The truth of $c\sim d$ is independent of x and $x'$. It remains to consider $v_\textsf {a} \sim c$. The claim clearly holds if $x=x'$. Finally, suppose that $\kappa <x,x'$. As any constant occurring in $\textsf {ac}$ is at most $\kappa$, it follows that $x\models v_\textsf {a} \sim c$ iff $x'\models v_\textsf {a} \sim c$. $\square$

Lemma 3

Let ${\mathcal {S}^{p},\mathcal {S}^{o}}\in \{\Sigma ,\Sigma ^{e}\}$ and $\mathcal {M}$ be a GCGMP with non-negative payoffs, c be a configuration in $\mathcal {M}$ and $\mathcal {M}^c = (\mathcal {M},c)$ be the respective initialised GCGMP. Then:

• 1. For any state $\textsf {QATL}_{1}^{*}$-formula $\varphi$, $\kappa > \max _{(\mathcal {M},\varphi )}$, and configurations $c'$ in $\mathcal {M}^c$ and $c''$ in $\mathcal {M}_{\kappa }^{c,\varphi }$ such that $c' \equiv ^{\kappa }c''$, it holds that: $\mathcal {M}^c,c' \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\varphi$ if and only if $\mathcal {M}_{\kappa }^{c,\varphi }, c'' \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\varphi$.

• 2. For any path $\textsf {QATL}_{1}^{*}$-formula $\gamma$, and paths $\pi$ in $\mathcal {M}^c$ and $\pi '$ in $\mathcal {M}_{\kappa }^{c,\varphi }$ such that $\pi \equiv ^{\kappa }\pi '$, it holds that: $\mathcal {M}^c,\pi \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\gamma$ if and only if $\mathcal {M}_{\kappa }^{c,\varphi }, \pi ' \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\gamma$.

Proof

We fix arbitrarily $\kappa > \max _{(\mathcal {M},\varphi )}$.

Now, both claims are proved by mutual structural induction on state and path formulae, simultaneously on all configurations $c'$ in $\mathcal {M}^c$ and $c''$ in $\mathcal {M}_{\kappa }^{c,\varphi }$ such that $c' \equiv ^{\kappa }c''$, and all paths $\pi$ in $\mathcal {M}^c$ and $\pi '$ in $\mathcal {M}_{\kappa }^{c,\varphi }$ such that $\pi \equiv ^{\kappa }\pi '$.

The case for atomic formulae follows directly from the semantics of the arithmetic constraints in $\mathcal {M}$ and in $\mathcal {M}_{\kappa }^{c,\varphi }$ and from Lemma 2. The cases of boolean connectives are routine, as usual. The cases of temporal connectives and path formulae follow easily from the respective cases of the inductive hypothesis for state subformulae, applied to all respective pairs of states on the two paths. Now, consider the case where $\varphi =\langle \!\langle {A}\rangle \!\rangle _{_{\! }}\gamma$. By the inductive hypothesis for $\gamma$, for any two plays $\pi$ over $\mathcal {M}^c$ and $\pi '$ over $\mathcal {M}_{\kappa }^{c,\varphi }$ with $\pi \equiv ^{\kappa }\pi '$ we have that ${\mathcal {M}^c},\pi \models \gamma$ iff $\mathcal {M}_{\kappa }^{c,\varphi },\pi '\ {\models }\gamma$. Next, note that every history or play $\pi$ in $\mathcal {M}^c$ generates a respective history or play $\pi '$ in $\mathcal {M}_{\kappa }^{c,\varphi }$ obtained by applying step-by-step $\textsf {out} _{\kappa }^{c}$ instead of ${\widehat{\textsf {out}}}$ to the previous configuration and the same action profile to produce the next generalised configuration in $\mathcal {M}_{\kappa }^{c,\varphi }$. Moreover, $\pi \equiv ^{\kappa }\pi '$ by the definition of $\textsf {out} _{\kappa }^{c}$. Conversely, every history (respectively, path) in $\mathcal {M}_{\kappa }^{c,\varphi }$ is generated in such a way from some history (respectively, path) in $\mathcal {M}^c$. Now, let $\mathcal {S}^{p} = \Sigma$ and suppose that $\mathcal {M}^c,c' \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\varphi$. Then, there is a joint $\mathcal {S}^{p}$-strategy $\sigma _A$ such that for all joint strategies $\sigma _{\textsf {Ag} \backslash A}\in \mathcal {S}^o$ and $\pi \in \textsf {plays} ^{\mathcal {M}}(c',(\sigma _{A},\sigma _{\textsf {Ag} \backslash A}))$ it holds that $\mathcal {M}^c,\pi \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\gamma$. That strategy induces a joint $\mathcal {S}^{p}$-strategy $\sigma _{A}'$ in $\mathcal {M}_{\kappa }^{c,\varphi }$, defined on every history $h'$ starting from $c''$ to prescribe the same joint action for A as the one prescribed by $\sigma _{A}$ on any respective history h starting from $c'$ in $\mathcal {M}^c$ emerging there as a result of the coalition A following their joint strategy $\sigma _{A}$ and generating $h'$. By construction, any play $\pi '\in \textsf {plays} ^{\mathcal {M}_{\kappa }^{c,\varphi }}(c'',(\sigma '_{A},\mathcal {S}^{o}))$ occurring in $\mathcal {M}_{\kappa }^{c,\varphi }$ is generated by some play $\pi \in \textsf {plays} ^{\mathcal {M}}(c',(\sigma _{A},\mathcal {S}^{o}))$ occurring in $\mathcal {M}^c$, and hence $\pi \equiv ^{\kappa }\pi '$. Then, by the inductive hypothesis, applied to $\gamma$, $\pi$ and $\pi '$, we obtain that $\mathcal {M}_{\kappa }^{c,\varphi },\pi ' \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\gamma$. Therefore, $\mathcal {M}_{\kappa }^{c,\varphi },c'' \models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\langle \!\langle {A}\rangle \!\rangle _{_{\! }}\gamma$. The converse implication follows from the fact that every play $\pi '\in \textsf {plays} ^{\mathcal {M}_{\kappa }^{c'',\varphi }}(c,(\sigma '_{A},\mathcal {S}^{o}))$ is generated by some such play $\pi \in \textsf {plays} ^{\mathcal {M}^c}(c',(\sigma _{A},\mathcal {S}^{o}))$ in $\mathcal {M}^c$. The case when $\mathcal {S}^{p} = \Sigma ^{e}$ is analogous, as the construction inducing strategies described above preserves effectiveness. This completes the induction. $\square$

The theorem below states the main result on decidability of the model checking problem, included here.

Theorem 2

Let $\mathcal {M}$ be a finite GCGMP with non-negative payoffs, $c\in \textsf {Con}_{\mathcal {M}}$ and $\varphi$ be a $\textsf {QATL}_{1}^{*}$ -formula. It is decidable whether $\mathcal {M},c\models _{(\mathcal {S}^{p},\mathcal {S}^{o})} \varphi$ for ${\mathcal {S}^{p},\mathcal {S}^{o}}\in \{\Sigma ,\Sigma ^{e}\}$.

Proof

Let $\kappa >\kappa _{(\mathcal {M},\varphi )}$. By Lemma 3 we have that ${\mathcal {M}},{c}\models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\varphi$ if, and only if, $\mathcal {M}_{\kappa }^{c,\varphi },{c} {\models }_{(\mathcal {S}^{p},\mathcal {S}^{o})} \varphi$. As $\mathcal {M}_{\kappa }^{c,\varphi }$ is finite (Proposition 2) we can replace each arithmetic constraint formula $\textsf {ac}$ occurring in $\varphi$ by a new proposition $p_{\textsf {ac}}$ and label all states in $\mathcal {M}_{\kappa }^{c,\varphi }$ in which ${\textsf {ac}}$ holds with $p_{\textsf {ac}}$. We denote the resulting formula by $\widehat{\varphi }$ and the model by $\widehat{\mathcal {M}_{\kappa }^{c,\varphi }}$. The formula $\widehat{\varphi }$ is purely qualitative. Note that in the purely qualitative case, ${\models }$ is simply the classical satisfaction relation of ${\textsf {ATL}}^{*}$, where all versions of $\models _{(\mathcal {S}^{p},\mathcal {S}^{o})}$ for $\mathcal {S}^{p},\mathcal {S}^{p}\in \{\Sigma ,\Sigma ^{s},\Sigma ^{se}\}$ are equivalent, so we can decide the problem of model checking ${\mathcal {M}},{c}\models _{(\mathcal {S}^{p},\mathcal {S}^{o})}\varphi$ by reducing it to ${\textsf {ATL}}^{*}$-model checking of $\widehat{\varphi }$ in $\widehat{\mathcal {M}_{\kappa }^{c,\varphi }}$ [6]. $\square$

There are various other ways to possibly achieve decidability, e.g. by restricting the class of agents strategies to effective strategies with fixed parameters. For instance, it is easy to see that for fixed $m,n\in \mathbb {N}$ there are only finitely many (m, n)-effective strategies. With this observation we conjecture that model checking of $\textsf {FlatQATL}_{1}^{*}$ over GCGMP (without restriction to only non-negative payoffs) is also decidable. The reason is that the configuration graph that can result from effective strategies has some regularity which is sufficient to decide the model checking problem. Formally:

Conjecture 1

Let $m,n\in \mathbb {N}$, $\mathcal {M}$ be a GCGMP, $c\in \textsf {Con}_{\mathcal {M}}$, and $\varphi$ be a $\textsf {FlatQATL}_{1}^{*}$-formula. It is decidable whether $\mathcal {M},c\models _{(\Sigma ^{e(m,n)},\Sigma ^{e(m,n)})}\varphi$.

The semantics presented here is amenable to various further refinements or restrictions, e.g. following approaches from [19] and [11], aiming at obtaining decidable model checking and better complexity results. Further decidability results for cases of model checking of fragments of $\textsf {QATL}^{*}$ over special classes of GCGMP models can also be obtained by adaptation from decidability results for reachability and safety problems and games in Petri nets, VASS, counter machines, and other similar models of computation from [2, 7, 9, 11, 12, 17, 32, 33, 38, 41], etc. We leave these to follow-up work.

6 Concluding remarks

In this paper we have introduced a uniform framework for modelling and formal reasoning about strategic abilities of players and coalitions to achieve qualitative and quantitative objectives in concurrent multi-stage games. We have discussed some modelling and computational issues and have briefly illustrated the use of the proposed framework with two hypothetical examples.

We see our work as not only theoretical but also as providing a technical framework for various potential applications to AI, game theory and multi-agent systems. Detailed modelling and analysis of more concrete scenarios in these areas would be an important direction for further developments. More generic such applications include multi-agent resource-based reasoning, as already indicated in the paper, as well as modelling and verification of multi-agent reinforcement learning (MARL) mechanisms (cf. [22] for a general overview of MARL and [55] for a game-theoretic perspective), where in each transition round the agents in the team perform actions in pursuit of their assigned task and each agent receives a positive or negative reward from the environment or the teaching supervisor. If the agents follow suitably designed efficient (bounded-memory) configuration-based strategies that take into account the recent rewards, they gradually learn by maximising their (possibly discounted) accumulated rewards, while at the same time satisfying specified qualitative objectives e.g. to keep the system within a safe region.

Furthermore, various natural extensions of the presented framework are possible. We briefly outline just a couple here, leaving their exploration to a future research:

• Probabilistic extensions, where the guards or the transitions are defined according to respective probability distributions, rather than deterministically. Such extension can be used, e.g., for an alternative, and more direct, modelling of MARL systems.

• Adding quantitative reasoning about entire plays, by introducing as atomic formulae arithmetic path constraints interpreted over mean payoffs is a natural and important extension that would enable combined quantitative and fully qualitative reasoning over infinite plays. Another natural approach to handling uniformly accumulated payoffs over finite and infinite plays is based on discounted accumulated utilities, by applying discounting factors that depreciate these accumulated utilities over time and enable asymptotic quantitative reasoning.

Finally, the systematic exploration of the purely mathematical and the game-theoretic aspects of games modelled with GCGMP are other important general directions for further research.