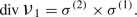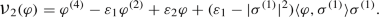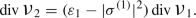Abstract
The variational theory of higher-power energy is developed for mappings between Riemannian manifolds, and more generally sections of submersions of Riemannian manifolds, and applied to sections of Riemannian vector bundles and their sphere subbundles. A complete classification is then given for left-invariant vector fields on three-dimensional unimodular Lie groups equipped with an arbitrary left-invariant Riemannian metric.
Similar content being viewed by others
1 Introduction
In their definitive paper on harmonic mappings of Riemannian manifolds [6], Eells and Sampson remark: “Although the present work is devoted primarily to the (energy) functional E and its extremals, there will be the indications that we will want ultimately to consider other types of energy of maps”. Interestingly, and to the best of our knowledge unbeknown to the authors of [6], a couple of years earlier Skyrme had used one of those “other types of energy” to create a mathematically tractable model for the nucleon [25]. The ‘skyrmion’ model has since gained considerable popularity in the physics and mathematical physics communities; see for example [8, 12, 26,27,28, 30, 31, 41]. However, despite this, and intense interest in the theory of harmonic maps, so far there has been little work on establishing a general theory of the “other types of energy” mentioned in [6]. In this paper, we will make some moves towards such a theory.
Let \(\varphi :(M,g)\rightarrow (N,h)\) be a smooth mapping of Riemannian manifolds, with \(\dim M=m\). Viewing the 2-tensors g and \(\varphi ^*h\) as morphisms \(TM\rightarrow T^*M\), the (Dirichlet) energy of \(\varphi \), which we refer to as its “standard energy”, is obtained by integrating (globally, or locally, depending on whether M is compact) the trace of the tensor field \(\alpha =g^{-1}\varphi ^*h\), sometimes known as the Cauchy–Green tensor [26]. The higher-power energies of \(\varphi \) are a generalisation of the standard energy obtained by integrating the higher-degree elementary invariants of \(\alpha \); the terminology reflects that these correspond to higher exterior powers of \(d\varphi \). Geometrically, therefore, they measure the extent to which \(\varphi \) deforms higher-dimensional infinitesimal volume. In particular, the highest-power energy measures the deformation by \(\varphi \) of full volume, and although different to the volume functional per se it has the same critical points (Remark 2.4), the relationship being analogous to that between energy and length when \(m=1\). Furthermore, higher-power energies generalise to higher dimensions some of well-known properties of standard energy when \(m=2\), such as conformal invariance and area majorisation (see Propositions 2.5 and 2.7, Corollary 2.8, and Example 2.9).
More generally, let \(\pi :(P,k)\rightarrow (M,g)\) be a smooth submersion of Riemannian manifolds, and let \(\sigma :M\rightarrow P\) be a smooth section. At the outset, the Riemannian metrics g, k are not assumed to have any compatibility properties; for example, \(\pi \) is not necessarily a Riemannian submersion [19], or semi-conformal as in the theory of harmonic morphisms [7]. Nor is \(\pi \) assumed to be a fibre bundle, or even locally trivial, and there are no assumptions on the extrinsic geometry of its fibres. Nevertheless, it is possible to define higher-power vertical energies, as measurements of the total twisting of \(\sigma \), in the sense of its deviation from horizontality. The details of these constructions are presented in Sect. 2, where we also introduce the families of Newton tensors associated to \(\varphi \) and \(\sigma \); these play an important rôle in the subsequent variational theory.
In Sect. 3, we derive the Euler–Lagrange equations for the higher-power energy functionals, and thereby characterise their critical points, which we call higher-power harmonic maps. More precisely, for any integer \(r=1,\dots ,m\) we refer to the functional obtained by integrating the r-th elementary invariant of \(\alpha \) as the r-th higher-power energy, and its critical points as r-power harmonic maps, or more briefly r-harmonic maps. (See the Note on nomenclature at the end of this Section.) The Euler–Lagrange operator for this variational problem is denoted by \(\tau _r(\varphi )\), and referred to as the r-th higher-power tension field of \(\varphi \), or more briefly its r-th tension field (Definition 2.10). In contrast to [6], in this paper we make no attempt to explore the analytic properties of \(\tau _r(\varphi )\) (such as existence of solutions, unique continuation, etc.), and simply remark that for \(r>1\) it is a second-order quasi-linear semi-elliptic partial differential operator.
The r-harmonic map equations (Theorem 2.12) emerge as a corollary of more general computations for the first variation of the r-th higher-power vertical energy functional with respect to variations through sections (Theorems 3.3 and 3.6). The Euler–Lagrange equations for this constrained but more general variational problem characterise what we choose to call r-power harmonic sections, or more briefly r-harmonic sections. Our derivation of these equations is analogous to the coordinate-free approach for harmonic maps used in [4], albeit more subtle. Specifically, the analogue in this context of the second fundamental form (of a mapping) is no longer a symmetric tensor, its asymmetry being a manifestation of the curvature of the submersion \(\pi \) (Definition 3.1). This notion of curvature, although somewhat unorthodox at this level of generality, encodes essentially the same geometric and topological information as the second fundamental form of \(\pi \), if \(\pi \) happens to be a Riemannian submersion (see Proposition 3.5, and compare with Lemma 3.11). It also coincides with the standard definition of curvature when, for example, \(\pi \) is a vector bundle with linear connection (Remarks 4.2). Its appearance in the r-harmonic section equations (Theorem 3.6) expresses the interaction of the section with the extrinsic geometry of the fibres of \(\pi \), and means that the equations simplify if \(\pi \) is flat, i.e. its curvature vanishes. Whilst this is an unduly restrictive assumption to make (see Proposition 3.5 and Theorem 5.6), the equations simplify in the same way under the far less onerous condition that \(\pi \) has totally geodesic (t.g.) fibres; for example, if \(\pi \) is a fibre bundle with Kaluza–Klein geometry (Remarks 3.7). The simplified Euler–Lagrange operator is called the r-th vertical tension field (Definition 2.14).
It is also of interest, although perhaps not quite so natural, to study sections that are r-harmonic maps. Since these are critical points of an unconstrained variational problem, the Euler–Lagrange operator, which is now the r-th tension field \(\tau _r(\sigma )\), acquires a horizontal component, which we analyse when \(\pi \) is a Riemannian submersion with t.g. fibres (Theorem 3.14). Interestingly, the curvature of \(\pi \) also appears here. This time a simplification occurs when \(\sigma \) is a flat section (Definition 3.1), a condition that generalises both the flatness of \(\pi \) and the horizontality of \(\sigma \) (Remarks 3.2), although it is still somewhat restrictive (Theorem 5.6). Under the same hypotheses (viz. \(\pi \) a Riemannian submersion with t.g. fibres) the vertical component of \(\tau _r(\sigma )\) fragments into a linear combination of the vertical tension fields of r-th and lower power (Theorem 3.10), prompting the definition of a twisted r-skyrmion (Definition 3.9). It is notable that both the horizontal and vertical components of \(\tau _r(\sigma )\) involve the divergence of a Newton tensor. In contrast to the Newton tensors associated to the shape operator of an isometric immersion or the covariant Hessian of a smooth function [22,23,24], in this case the Newton tensors are not in general solenoidal (i.e. divergence-free) if \(r\geqslant 2\) (see for example Theorem 5.10 and Lemma 5.18). Indeed, for mappings, the divergence of the \((r-1)\)-st Newton tensor is the principle obstruction to a totally geodesic map being r-harmonic when \(r\geqslant 2\) (Remark 2.18). We conclude Sect. 3 with a characterisation of r-harmonicity for flat sections, and in particular a synopsis of the horizontal case (Theorem 3.15).
In Sect. 4, the results of Sect. 3 are interpreted for Riemannian vector bundles, equipped with their natural (Sasaki) geometry. We prove two rigidity results: for bundles with compact base (Theorem 4.5), and for sections of constant length (Corollary 4.15). These generalise various results that are familiar when \(r=1\) [13, 18, 37], where ‘rigid’ sections are those that are parallel; for higher powers r, the ‘rigid’ sections are those that are r-parallel (Definition 4.4), a constraint that becomes increasingly ‘flexible’ as r increases (see for example Theorem 5.8). Nevertheless, rigidity is still a problem. For a section of constant length, this can be side stepped by working within the corresponding sphere subbundle, a proven methodology when \(r=1\) [9]. This further reduces the class of variations, which intuitively increases the likelihood of critical points. In this context, higher-power energies may be regarded as measurements of ‘total bending’ [36]. The Euler–Lagrange equations for this restrained variational problem are derived in Theorem 4.13. When ‘untwisted’ they yield a characterisation of r-harmonic maps into spheres (Corollary 4.17), a first step towards generalising the classic work of R. T. Smith [29]. We illustrate this by showing that the Hopf map is a solution of the 2-power harmonic map equations for mappings \({\mathbb {S}}^3\rightarrow {\mathbb {S}}^2\) (Example 4.19).
The primary example of a Riemannian vector bundle is of course the tangent bundle of a Riemannian manifold, equipped with the Levi–Civita connection. In Sect. 5, we examine in detail the various facets of the general theory for an invariant vector field \(\sigma \) on a 3-dimensional Lie group G endowed with a left-invariant metric. For simplicity we assume that G is unimodular. (This includes all Lie groups that are either compact, nilpotent, or in this dimension, simple.) The geometric classification of such G was achieved by Milnor in [16], and we present it in Sect. 5 as ‘Milnor’s list’. Milnor’s techniques effectively reduce computations to classical vector algebra, and using them simplifies our calculations considerably. To maintain clarity, we adopt a coordinate-free approach as far as possible, aiming for both algebraic and geometric cogency. Assuming without loss of generality that \(\sigma \) has unit length (Corollary 4.16), we refer to r-harmonic sections of the unit tangent bundle \(UG\rightarrow G\) as r-harmonic directions. Then, denoting the set of invariant r-harmonic directions by \({\mathcal {H}}_r\), we obtain a highly geometric classification of \({\mathcal {H}}_2\) (Theorem 5.12), governed by the absolute values of the principal Ricci curvatures. We also recover the classification of \({\mathcal {H}}_1\) obtained in [10], which we recast in a more geometric light (Theorem 5.13). En route we calculate the first vertical Newton tensor of \(\sigma \), and observe precisely when it is solenoidal (Theorem 5.10). We identify the subsets \({\mathcal {Z}}_r\subseteq {\mathcal {H}}_r\) of absolute minimisers of r-th vertical energy, i.e. the r-parallel invariant vector fields. By rigidity, these are precisely the invariant r-harmonic sections of the full tangent bundle \(TG\rightarrow G\) (Theorem 5.8). We also observe that \({\mathcal {H}}_r={\mathcal {H}}_{r-1}\cup {\mathcal {Z}}_r\) for \(r=2,3\) (Corollary 5.15), a feature that we suspect is rather specific to this example. A comprehensive classification, based primarily on the singular values of the Ricci tensor, is then presented (Theorem 5.16), from which we explicitly determine \({\mathcal {H}}_r\) and \({\mathcal {Z}}_r\) for each geometry on Milnor’s list. We then discover which \(\sigma \) are twisted skyrmions (Theorem 5.17), and use this to classify the invariant unit vector fields that are r-harmonic maps \(G\rightarrow UG\) for \(r=1,2,3\) (Theorem 5.21). When \(r=3\) these are precisely the invariant minimal immersions, and we recover results of [33].
This paper is a development of research originally carried out in [21, 37]. All manifolds, mappings, bundles, metrics etc. are assumed smooth (\({\mathscr {C}}^\infty \)), and for notational simplicity all connections are denoted by (undecorated) \(\nabla \), with one notable exception (which is \(\nabla ^v\)). The notation \({\mathfrak {X}}(M)\) is used for the space of (smooth) vector fields on a (smooth) manifold M.
1.1 Note on nomenclature
Phrases such as “r-energy”, “r-harmonic” and “r-th tension field”, and notation such as \(E_r(\varphi )\) and \(\tau _r(\varphi )\), are used in a number of different generalisations of the standard energy functional and its associated harmonic maps; for example [5, Chapter 3], [1, 3, 17]. Whilst this is unfortunate, it is perhaps inevitable, given the nature of these generalisations. The nomenclature “\(\sigma _r\)-energy” and “\(\sigma _r\)-harmonic” has been suggested for the theory under discussion here (to indicate the elementary symmetric polynomials); however, this becomes problematic when applied to sections rather than just mappings. Given the technical complexity of the scenarios in which we will be working, we have opted for nomenclature that is as simple as possible, and which, needless to say, is consistent within the confines of the paper. Whilst there is admittedly a risk of ambiguity, we will not be referencing any of these other theories.
2 Higher-power energy and Newton tensors
In this section, we describe the basic algebraic setup, and its use to define the higher-power energies of mappings and the higher-power vertical energies of sections, along with their associated Newton tensors and tension fields. This is mostly descriptive. However, there are also results concerning the conformal invariance of higher-power energy (Proposition 2.5) and its relation to volume (Proposition 2.7).
2.1 Elementary invariants and Newton polynomials
We begin with a brief description of the essential algebraic background.
Let A be a \(m\times m\) (real) matrix, with characteristic polynomial:

Thus:
and in general the r-th elementary invariant \(\varepsilon _r(A)\) is a \(GL_m\)-invariant homogeneous polynomial of degree r, obtained by summing the leading \(r\times r\) minors of A. The elementary invariants may be characterised recursively, for example:
and in general by the Newton–Girard identity [35, p. 81]:

The r-th Newton polynomial of A is the following interpolant of the characteristic polynomial:

Thus:

and in general  may be characterised by the recurrence relation:
may be characterised by the recurrence relation:

The \(GL_m\)-invariance of elementary invariants and Newton polynomials allows us to define \(\varepsilon _r(\alpha )\) and  for any linear endomorphism \(\alpha \) of an m-dimensional (real) vector space V. Evaluation of the Newton polynomials (of \(\alpha \)) at \(\alpha \) then yields an associated family of Newton endomorphisms
for any linear endomorphism \(\alpha \) of an m-dimensional (real) vector space V. Evaluation of the Newton polynomials (of \(\alpha \)) at \(\alpha \) then yields an associated family of Newton endomorphisms  where:
where:

In particular:

and  by the Cayley–Hamilton Theorem. For future use, we record the following additional identities.
by the Cayley–Hamilton Theorem. For future use, we record the following additional identities.
Lemma 2.1
For all integers \(r=1,\dots ,m\) we have:
-
i)
\(\varepsilon _r(1+\alpha ) =\varepsilon _r(\alpha )+(m-r+1)\varepsilon _{r-1}(\alpha )+\cdots +\textstyle \left( {\begin{array}{c}m-1\\ r-1\end{array}}\right) \varepsilon _1(\alpha )+\textstyle \left( {\begin{array}{c}m\\ r\end{array}}\right) \).
-
ii)
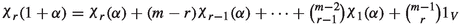 .
. -
iii)
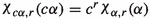 , for all \(c\in {\mathbb {R}}\).
, for all \(c\in {\mathbb {R}}\).
Proof
(i) follows by expanding the characteristic polynomial  and inspecting coefficients, where A is any matrix representing \(\alpha \). Both (ii) and (iii) follow inductively from (2.4), homogeneity of the elementary invariants being used to obtain (iii). \(\square \)
and inspecting coefficients, where A is any matrix representing \(\alpha \). Both (ii) and (iii) follow inductively from (2.4), homogeneity of the elementary invariants being used to obtain (iii). \(\square \)
We record two further useful properties of Newton endomorphisms, the first of which is an immediate consequence of Newton’s identity (2.2).
Lemma 2.2
For all \(r=1,\dots ,m\) we have:

The second property concerns a differentiable 1-parameter family \(\alpha _t\) of endomorphisms of V, with ‘variation vector’ \(\beta _t=d\alpha _t/dt\) (another endomorphism). The elementary invariants of \(\alpha _t\) are then differentiable \({\mathbb {R}}\)-valued functions (of t). Clearly:

and by (2.1):

The following result describes the general situation.
Lemma 2.3
[22, Lem. A] For all \(r=1,\dots ,m\) we have:

2.2 Higher-power harmonic mappings of Riemannian manifolds
Now let \(\varphi :(M,g)\rightarrow (N,h)\) be a (smooth) mapping of (smooth) Riemannian manifolds, with \(\dim M=m\). The Cauchy–Green tensor of \(\varphi \) is the self-adjoint (1, 1)-tensor \(\alpha \) on M metrically dual to \(\varphi ^*h\), which is characterised by:
for all \(X,Y\in {\mathfrak {X}}(M)\). The elementary invariants of \(\alpha \), computed pointwise on tangent spaces, define m smooth \({\mathbb {R}}\)-valued functions on M, which, being dependent primarily on \(\varphi \) (assuming that g and h are fixed) will be denoted by \(\varepsilon _r(\varphi ):M\rightarrow {\mathbb {R}}\) for all \(r=1,\dots ,m\). Likewise, the Newton endomorphisms of \(\alpha \) define a family of self-adjoint (1, 1)-tensors on M, which we denote by \(\nu _r(\varphi )\) and refer to as the Newton tensors of \(\varphi \).
If \(\{e_i\}\) is a local orthonormal tangent frame of (M, g), then:
Furthermore by (2.1) and (2.6):
In general, it follows from Newton’s identity (2.2) that:
where \((d\varphi )^r\) denotes the r-th exterior power:
viewed as an r-form on M with values in \(\wedge ^r(\varphi ^{-1}TN)\), with \(\varphi ^{-1}TN\rightarrow M\) the pullback bundle. Thus, \(\varepsilon _r(\varphi )\) may be interpreted geometrically as the average infinitesimal distortion by \(\varphi \) of squared r-volume, with \(\varepsilon _r(\varphi )_x=0\) precisely when \({{\,\textrm{rank}\,}}d\varphi _x<r\).
The observation that  is the standard (Dirichlet) energy density of \(\varphi \) suggests the following definition of the r-th higher-power energy of \(\varphi \), or more concisely the r-th energy:
is the standard (Dirichlet) energy density of \(\varphi \) suggests the following definition of the r-th higher-power energy of \(\varphi \), or more concisely the r-th energy:
for all integers \(r=1,\dots ,m\), assuming for convenience that M is compact. Then \({\mathcal {E}}_r\) is non-negative, and its zeroes are precisely the mappings \(\varphi \) with \({{\,\textrm{rank}\,}}\varphi <r\) everywhere. Critical points of \({\mathcal {E}}_r\) will be called r-power harmonic maps, or more concisely r-harmonic maps.
Remarks 2.4
-
(1)
In the non-compact case, we proceed (as usual) by considering local r-power energies:
$$\begin{aligned} {\mathcal {E}}_r(\varphi ;U)=\frac{1}{2}\int _U\varepsilon _r(\varphi ){{\,\textrm{vol}\,}}(g), \end{aligned}$$for all relatively compact open subsets \(U\subset M\), and requiring \(\varphi \) to be a critical point with respect to all variations supported on U.
-
(2)
Since \(\varepsilon _m(\varphi )\) is the square of the volume density \(v(\varphi )\), unless \(\varphi \) is an isometric immersion \({\mathcal {E}}_m(\varphi )\) is not the volume of \(\varphi \). In particular, unlike the volume functional, \({\mathcal {E}}_m\) depends on both g and h. Nevertheless the two functionals have the same critical points, see for example Theorem 5.21.
It has been known ab initio [6, p. 126] that when \(m=2\) the energy functional is conformally invariant, that is, dependent only on the conformal structure of the domain. Higher-power energies exhibit this invariance in higher (even) dimensions.
Proposition 2.5
If \(m=2r\) then \({\mathcal {E}}_r(\varphi )\) is conformally invariant. The converse holds provided \({{\,\textrm{rank}\,}}\varphi \geqslant r\) somewhere.
Proof
For clarity in this context, we write \(\varepsilon _r(\varphi )=\varepsilon _r(\varphi ,g)\) and \({\mathcal {E}}_r(\varphi )={\mathcal {E}}_r(\varphi ,g)\). If \(\rho :M\rightarrow {\mathbb {R}}^+\) is a continuous function with \(\rho ^2\) smooth, then by the homogeneity of the elementary invariants we have:
Since the volume element transforms:
it follows that:
which vanishes if \(m=2r\). Conversely, if \({{\,\textrm{rank}\,}}\varphi \geqslant r\) somewhere then \(\varepsilon _r(\varphi ,g)>0\) on an open set, so if (2.8) vanishes for all \(\rho \) then certainly \(m-2r=0\). \(\square \)
It is also well-known that when \(m=2\) the standard energy majorises area, with equality precisely for mappings that are weakly conformal [6, p. 126], [14]. Again, higher-power energies exhibit this in higher (even) dimensions, with the following generalised notion of weak conformality.
Definition 2.6
A mapping \(\varphi \) is r-conformal if \(\varphi \) is a branched conformal immersion with \({{\,\textrm{rank}\,}}\varphi <r\) on the branch set; thus, 1-conformality is equivalent to weak conformality.
Proposition 2.7
If \(m=2r\), then  , with equality precisely when \(\varphi \) is r-conformal.
, with equality precisely when \(\varphi \) is r-conformal.
Proof
Let \(\{e_i\}\) be a local g-orthonormal tangent frame diagonalising \(\alpha \), and set \(\rho _i=\Vert {d\varphi (e_i)}\Vert \); the eigenvalues of \(\alpha \) are therefore \(\rho _i^{\;2}\). Then summing over all permutations of \(1,\dots m\) gives:

If \(\varphi \) is r-conformal, then for all \(x\in M\) either \(\varphi ^*h(x)=\rho (x)^2g(x)\), in which case \(\rho _1(x)=\cdots =\rho _m(x)=\rho (x)\), or \({{\,\textrm{rank}\,}}d\varphi _x<r\), in which case at least \(r+1\) of the \(\rho _i(x)\) vanish. In either case:
for all \(\mu \in S_m\), hence  . Conversely, given the system (2.9), if one of the \(\rho _i(x)\) vanishes then so do at least r others, whereas if no \(\rho _i(x)\) vanishes then all are equal; thus, \(\varphi \) is r-conformal. \(\square \)
. Conversely, given the system (2.9), if one of the \(\rho _i(x)\) vanishes then so do at least r others, whereas if no \(\rho _i(x)\) vanishes then all are equal; thus, \(\varphi \) is r-conformal. \(\square \)
Corollary 2.8
Suppose \(m=2r\) and \(\varphi :M\rightarrow (N,h)\) is an r-conformal map of a compact conformal manifold M. If \(\varphi \) is a local (resp. global) minimiser of volume, then \(\varphi \) is a local (resp. global) minimum of \({\mathcal {E}}_r\) with respect to any Riemannian metric g in the conformal class of M; in particular, \(\varphi \) is an r-harmonic map.
Example 2.9
Let \(\varphi :M\rightarrow (N,h)\) be a calibrated immersion of a compact 2r-manifold into a calibrated Riemannian manifold. Then \(\varphi \) is a minimum of \({\mathcal {E}}_r\) with respect to any metric on M conformal to \(\varphi ^*h\).
The Newton tensors of \(\varphi \) may be used to define its higher-power tension fields, as follows.
Definition 2.10
For all \(r=1,\dots ,m\) the r-th tension field of \(\varphi \) is the following section of \(\varphi ^{-1}TN\):

where \(\{e_i\}\) is any local orthonormal tangent frame of (M, g).
Remark 2.11
Since \(\nu _0(\varphi )\) is the identity, we have:
the usual tension field of harmonic map theory [6].
The tension field is of course the Euler–Lagrange operator for the standard energy functional [6], and the following result, which is in fact a corollary of the more general Theorem 3.3, shows that this relationship between tension and energy persists for higher powers.
Theorem 2.12
For all \(r=1,\dots ,m\), a smooth mapping \(\varphi \) of Riemannian manifolds is an r-power harmonic map if and only if \(\tau _r(\varphi )=0\).
Proof
See Corollary 3.4. \(\square \)
2.3 Higher-power harmonic sections of submersions
We now generalise the situation further as follows. Let \(\pi :(P,k)\rightarrow (M,g)\) be a smooth submersion of Riemannian manifolds, with \(\dim P=p\). The tangent bundle of P then splits as an orthogonal direct sum:
where \({\mathscr {V}}=\ker d\pi \), and we refer (as usual) to \({\mathscr {V}}\) (resp. \({\mathscr {H}}\)) as the vertical (resp. horizontal) distribution over P. Thus, every tangent vector \(A\in TP\) splits:
where \(A^v\in {\mathscr {V}}\) and \(A^z\in {\mathscr {H}}\).
Suppose \(\sigma \) is a smooth section of \(\pi \). The vertical derivative of \(\sigma \) is defined:
for all \(X\in TM\); thus \(d^v\sigma \) is a section of \(T^*M\otimes \sigma ^{-1}{\mathscr {V}}\). The horizontal derivative \(d^z\sigma \) is defined similarly and is a section of \(T^*M\otimes \sigma ^{-1}{\mathscr {H}}\). The vertical energy of \(\sigma \) is then defined:
The zeroes of \({\mathcal {E}}^v\) are precisely the horizontal sections, and stationary points of \({\mathcal {E}}^v\) with respect to variations through sections are usually referred to as harmonic sections; see [38] et seq.
Taking \(\alpha \) now to be the vertical Cauchy–Green tensor of \(\sigma \):
and denoting the elementary invariants of \(\alpha \) by \(\varepsilon _r^v(\sigma ):M\rightarrow {\mathbb {R}}\), we define the r-th higher-power vertical energy of \(\sigma \) for all \(r=1,\dots ,m\) by:

For brevity, we will usually refer to (2.13) as the r-th vertical energy of \(\sigma \).
Definition 2.13
A section is r-horizontal if the rank of its vertical derivative is everywhere less than r.
The zeroes of  are precisely the r-horizontal sections; some examples are given in Theorem 5.8. It follows that
are precisely the r-horizontal sections; some examples are given in Theorem 5.8. It follows that  is trivial for all \(r>p-m\), which is the dimension of the fibres of \(\pi \). (Since \(r\leqslant m\) this possibility can only arise if \(p<2m\); see also Corollary 4.15). Critical points of
is trivial for all \(r>p-m\), which is the dimension of the fibres of \(\pi \). (Since \(r\leqslant m\) this possibility can only arise if \(p<2m\); see also Corollary 4.15). Critical points of  with respect to variations through sections will be called r-power harmonic sections, or r-harmonic sections for short.
with respect to variations through sections will be called r-power harmonic sections, or r-harmonic sections for short.
The Newton endomorphisms of \(\alpha \) once again define a family of self-adjoint (1, 1)-tensors on M, which we call the vertical Newton tensors of \(\sigma \) and denote by \(\nu _r^v(\sigma )\). The higher-power vertical tension fields of \(\sigma \) are then defined as follows.
Definition 2.14
For all \(r=1,\dots ,m\) the r-th vertical tension field of \(\sigma \) is the following section of \(\sigma ^{-1}{\mathscr {V}}\):

for any local orthonormal tangent frame \(\{e_i\}\) of (M, g), where \(\nabla ^v\) is the pullback of the linear connection in the vector bundle \({\mathscr {V}}\rightarrow P\) obtained by orthogonally projecting the Levi–Civita connection of (P, k).
Since \(\nu _0^v(\sigma )\) is the identity, we have:
which is the vertical tension field [39]. Its vanishing characterises harmonic sections in the most commonly encountered situations (viz. fibre bundles with Kaluza–Klein geometry). The harmonic section equations in their full generality (which we believe are not well-known) emerge in Corollary 3.8.
Likewise, the higher-power vertical tension fields appear in the Euler–Lagrange equations for higher-power harmonic sections, and give a complete characterisation in certain situations. This will be fully described in Sect. 3.
We conclude Sect. 2 with some further technical observations about the higher-power (vertical) tension fields.
Definitions 2.15
Let Q be a 2-tensor on M (possibly vector bundle-valued), and let T be a self-adjoint (1, 1)-tensor. Then the T-twisted (metric) trace of Q is the following function (or section):

The divergence of T is the following vector field:

An elementary calculation allows the higher-power vertical tension fields to be expressed using a twisted trace, at the expense of the divergence of the Newton tensor, as follows.
Theorem 2.16
For all \(r=1,\dots ,m\) we have:

where  .
.
A similar calculation may be applied to the higher-power tension fields of a mapping. Alternatively, it may be derived as a corollary of Theorem 2.16, by taking \(\sigma \) to be the graph of a mapping (see the proof of Corollary 3.4).
Corollary 2.17
If \(\varphi :(M,g)\rightarrow (N,h)\) is a smooth map, then for all \(r=1,\dots ,m\) we have:

where  .
.
Remarks 2.18
-
(1)
The Newton tensors of maps/sections are typically not solenoidal, see for example Theorem 5.10 and Lemma 5.18.
-
(2)
If \(\varphi \) is a totally geodesic map, then \(d\varphi \) has constant rank [34], so \(K(\varphi )=\ker d\varphi \) is a vector subbundle of TM. Then \(\varphi \) is an r-harmonic map precisely when
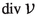 is a section of \(K(\varphi )\), where
is a section of \(K(\varphi )\), where 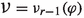 . Thus,
. Thus, 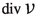 is the obstruction modulo \(K(\varphi )\) for \(\varphi \) to be r-harmonic. In particular, a harmonic map need not necessarily be r-harmonic if \(r\geqslant 2\).
is the obstruction modulo \(K(\varphi )\) for \(\varphi \) to be r-harmonic. In particular, a harmonic map need not necessarily be r-harmonic if \(r\geqslant 2\).
3 Variational calculus of higher-power energy
We continue to work with sections \(\sigma \) of a submersion \(\pi :(P,k)\rightarrow (M,g)\), our main aim being to derive the Euler–Lagrange equations of the higher-power vertical energy functionals (Theorems 3.3 and 3.6). From these, we also obtain the equations for higher-power harmonic maps (Corollary 3.4). We also consider the possibility of sections being higher-power harmonic maps (Theorem 3.10). This introduces twisted higher-power skyrmions (Definition 3.9) and invites a computation of the horizontal component of the higher-power tension fields (Theorem 3.14). The general situation is complicated, but simplifies when the section is flat. This includes the horizontal case and allows us to demonstrate that under favourable conditions horizontal sections are indeed higher-power harmonic sections and maps (Theorem 3.15).
In all of this, an important computational and conceptual rôle is played by a generalised notion of curvature (Definition 3.1 and Proposition 3.5), which we now introduce.
3.1 Curvature of a submersion
Consideration of the variation field of a 1-parameter family of sections of \(\pi \) leads to a natural generalisation of the notion of curvature, for both \(\pi \) and its sections (Definition 3.1). This will expedite our calculations, and provide additional geometric insight.
Let \(\vartheta ^v:TP\rightarrow {\mathscr {V}}\) and \(\vartheta ^z:TP\rightarrow {\mathscr {H}}\) denote the orthogonal projection morphisms:
defined for all \(A\in TP\). An exterior derivative \(d^v\) and coderivative \(\delta ^v\) on the space of \({\mathscr {V}}\)-valued differential forms on P are obtained from the connection \(\nabla ^v\) in the bundle \({\mathscr {V}}\rightarrow P\), in the usual way.
Now let \(\sigma _t\) be a smooth 1-parameter variation of \(\sigma \) through sections, defined for all t in some open interval I about \(0\in {\mathbb {R}}\), with \(\sigma _0=\sigma \) and associated homotopy:
Let \(V_t\) be the variation field:

where \(\partial _t\) is the unit vector field on \(M\times I\) in the positive \({\mathbb {R}}\)-direction. Thus, \(V_t\) is a section of the pullback bundle \(\sigma _t^{\;-1}{\mathscr {V}}\rightarrow M\). In particular, \(V=V_0\) is a section of \(\sigma ^{-1}{\mathscr {V}}\). The vertical second fundamental form of \(\Sigma \) is the following \(\Sigma ^{-1}{\mathscr {V}}\)-valued 2-tensor on \(M\times I\):

defined for all \(E,F\in {\mathfrak {X}}(M\times I)\), where the geometry of \(M\times I\) is that of the Riemannian product, and \(d^v\Sigma \) is the vertical derivative; cf. equation (2.11). Unlike the second fundamental form of a mapping, this is typically not symmetric; its asymmetry is measured by the exterior derivative:
If \(\vartheta ^v\) is viewed as a \({\mathscr {V}}\)-valued 1-form on P, then:

hence:
Definition 3.1
The curvature form \(\Theta \) of \(\pi \) is the following \({\mathscr {V}}\)-valued 2-form on P:
The curvature of a section \(\sigma \) of \(\pi \) is the pullback \(\sigma ^*\Theta \), which is a \(\sigma ^{-1}{\mathscr {V}}\)-valued 2-form on M. The submersion \(\pi \) is flat if \(\Theta =0\), and the section \(\sigma \) is flat if \(\sigma ^*\Theta =0\). The curvature 3-tensor of \(\pi \) is the following 3-tensor on P:
defined for all \(A,B,C\in {\mathfrak {X}}(P)\).
Although the curvature 3-tensor is merely a repackaging of the curvature form, it is occasionally useful to express the curvature of \(\pi \) in this way (for example, Theorem 3.3).
Remarks 3.2
-
1)
If \(\pi \) is flat then clearly so are all its sections. For an interesting converse, see Theorem 5.6.
-
2)
Definition 3.1 agrees with standard terminology in the familiar setting of a vector bundle with linear connection (see Remarks 4.2 (2) and 4.3).
-
3)
The canonical example of a flat submersion is a Riemannian product, projected onto either factor.
-
4)
If \(\pi \) is a Riemannian submersion, then \(\pi \) is flat if and only if \(\pi \) is totally geodesic (see Proposition 3.5 and Lemma 3.11).
-
5)
Evaluating Eq. (3.2) at \(t=0\) shows that a section \(\sigma \) is flat precisely when its vertical second fundamental form \(\nabla ^v d^v\sigma \) is symmetric; see also Remark 4.8 (2). Thus flatness of sections generalises horizontality.
-
6)
Further ramifications of flatness, both of a submersion and its sections, appear in Theorems 3.3 and 3.14.
We will establish some essential technical properties of the curvature form in Section 3.3.
3.2 Euler–Lagrange equations for sections of flat submersions
We obtain an interim expression for the first variation of higher-power vertical energy (Theorem 3.3), which is nonetheless sufficient to derive the equations for higher-power harmonic maps (Corollary 3.4).
For any vector field X on M, let \({\bar{X}}\) denote its natural extension to \(M\times I\):
where \(i_t\) is the inclusion:
Then:

The calculation in the proof of the following result explains the appearance of the higher-power vertical tension fields (Definition 2.14).
Theorem 3.3
For all integers \(r=1,\dots ,m\), we have:

where  and \(\theta \) is the curvature 3-tensor defined in (3.3). Thus, if \(\pi \) is flat then \(\sigma \) is an r-harmonic section precisely when \(\tau _r^{v}(\sigma )=0\).
and \(\theta \) is the curvature 3-tensor defined in (3.3). Thus, if \(\pi \) is flat then \(\sigma \) is an r-harmonic section precisely when \(\tau _r^{v}(\sigma )=0\).
Proof
We first compute the variation tensor \(\beta _t\) of \(\alpha _t\), as follows:

Then by Lemma 2.3:

Finally, by Stokes’ Theorem:

by Definition 2.14 of higher-power vertical tension. \(\square \)
The curvature of \(\pi \) obstructs Theorem 3.3 from presenting the first variation of  in divergence form. However, if \(\pi \) is flat then this is no longer a problem, and whilst the assumption is restrictive it allows us to derive the Euler–Lagrange equations for higher-power harmonic maps, which are presented as Theorem 2.12 in Sect. 2. In this environment, the higher-power vertical tension fields devolve into the higher-power tension fields (Definition 2.10).
in divergence form. However, if \(\pi \) is flat then this is no longer a problem, and whilst the assumption is restrictive it allows us to derive the Euler–Lagrange equations for higher-power harmonic maps, which are presented as Theorem 2.12 in Sect. 2. In this environment, the higher-power vertical tension fields devolve into the higher-power tension fields (Definition 2.10).
Corollary 3.4
For all \(r=1,\dots ,m\), a smooth mapping \(\varphi :(M,g)\rightarrow (N,h) \) of Riemannian manifolds is an r-power harmonic map if and only if \(\tau _r(\varphi )=0\).
Proof
Let (P, k) be the Riemannian product \((M\times N,g\times h)\), fibred over M by projection onto its first factor, and let \(\sigma \) be the graph of \(\varphi \):
defined for all \(x\in M\). Since \(\pi \) is flat the curvature term in Theorem 3.3 drops out, leaving the first variation in divergence form:
where v is the variation field of \(\varphi _t\) at \(t=0\). \(\square \)
3.3 General Euler–Lagrange equations
In order to derive the Euler–Lagrange equations for the higher-power vertical energies when \(\pi \) is not flat we push further the calculation behind Theorem 3.3, leading to an expression for the first variation in divergence form (Theorem 3.6).
We first establish some basic geometric properties of the curvature form \(\Theta \). Let \({\mathcal {A}}\) denote the collective shape operator for the fibres of \(\pi \):

defined for all vertical (resp. horizontal) vector fields V (resp. H) on P. This is tensorial in V and H, and \({\mathscr {V}}\)-valued. The following result generalises (with a twist) a well-known characterisation of the second fundamental form of a Riemannian submersion (cf. Lemma 3.11 and Remark 3.12).
Proposition 3.5
Let V, W (resp. H, K) are vertical (resp. horizontal) vector fields on P. Then:
-
(i)
\(\Theta (V,W)=0\);
-
(ii)
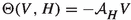 ;
; -
(iii)
\(\Theta (H,K)=-\vartheta ^v[H,K]\).
Thus, \(\pi \) is flat precisely when \(\pi \) has t.g. fibres and integrable horizontal distribution.
Proof
Let \(\vartheta :TP\rightarrow TP\) denote the identity morphism. Then:
hence:
since \(d\vartheta \) is the torsion of the Levi–Civita connection of (P, k). Therefore, for all \(A,B\in {\mathfrak {X}}(P)\):

Now (i) is clear, and (iii) follows since \(\nabla \) is torsion-free. For (ii), we note that:

\(\square \)
The shape operator \({\mathcal {A}}\) may be extended to a \({\mathscr {V}}\)-valued 2-tensor on P, by precomposition with the appropriate projections:

(This is not to be confused with O’Neill’s “A tensor” for Riemannian submersions [19].) We can now recast Theorem 3.3 in a form that is more concise and geometrically meaningful.
Theorem 3.6
Let \(\sigma \) be a section of a submersion \(\pi :(P,k)\rightarrow (M,g)\) of Riemannian manifolds, and let \(\sigma _t\) be a smooth 1-parameter variation of \(\sigma \) through sections, with \(\sigma _0=\sigma \) and variation field V at \(t=0\). Then for all \(r=1,\dots ,m\), we have:

where  . Thus, \(\sigma \) is an r-harmonic section if and only if:
. Thus, \(\sigma \) is an r-harmonic section if and only if:

In particular, if \(\pi \) has t.g. fibres then \(\sigma \) is an r-harmonic section precisely when \(\tau _r^{v}(\sigma )=0\).
Proof
Write  and \(H_i=d^z\sigma (e_i)\). Then by Proposition 3.5 (i), (ii):
and \(H_i=d^z\sigma (e_i)\). Then by Proposition 3.5 (i), (ii):

The result now follows from Theorem 3.3. \(\square \)
Remarks 3.7
-
1)
To deduce that r-horizontal sections are r-harmonic sections from the Euler–Lagrange equations (rather than directly from their r-energy) is surprisingly subtle. If
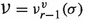 , then we have the following identity (a generalisation of Lemma 2.2 in this situation):
, then we have the following identity (a generalisation of Lemma 2.2 in this situation): 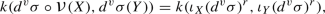
where the interior products on the right-hand side are \((r-1)\)-forms on M with values in the exterior product \(\wedge ^{r-1}(\sigma ^{-1}{\mathscr {V}})\). (The proof is left as an exercise for the reader.) Thus, \(\sigma \) is r-horizontal if and only if
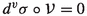 , in which case both terms of the Euler–Lagrange operator vanish.
, in which case both terms of the Euler–Lagrange operator vanish. -
2)
In most applications, \(\pi \) is a fibre bundle with connection and k is a ‘Kaluza–Klein’ metric, in which case \(\pi \) has t.g. fibres [34]. Furthermore, \(\pi \) is usually also a Riemannian submersion, although interestingly this isn’t required for the simplification of the Euler–Lagrange equations (see also Remark 4.2 (3)).
Corollary 3.8
Under the same hypotheses as Theorem 3.6, \(\sigma \) is a harmonic section if and only if:
If \(\pi \) has t.g. fibres, then \(\sigma \) is a harmonic section precisely when \(\tau ^v(\sigma )=0\).
3.4 Sections that are higher-power harmonic maps
We now explore the relationship between higher-power harmonic sections and sections that are higher-power harmonic maps. For this, we introduce the following generalisation of an idea introduced in [25], where the second energy (of a map) was used to perturb the standard (first) energy.
Definition 3.9
A section \(\sigma \) is a twisted r-skyrmion with coupling constants \(c_1,\dots ,c_r\in {\mathbb {R}}\), \(c_i\geqslant 0\), \(c_1,c_r\ne 0\), if \(\sigma \) is a critical point with respect to variations through sections of the hybrid multi-power vertical energy functional:

In order to make the technical details manageable, our comparison between r-harmonic sections and maps will assume that \(\pi \) is a Riemannian submersion with totally geodesic fibres (see Remarks 3.7).
Theorem 3.10
Let \(\sigma \) be a section of a Riemannian submersion with t.g. fibres. Then for all \(r=1,\dots ,m\), we have:
and for all \(r=1,\dots ,m-1\), we have:
Furthermore, the vertical component of \(\tau _r(\sigma )\) is related to the higher-power vertical tension fields by:
Thus, \(\sigma \) is an r-harmonic map precisely when \(\sigma \) is a twisted r-skyrmion with coupling constants \(c_i=\left( {\begin{array}{c}m-i\\ r-i\end{array}}\right) \) and the horizontal component of \(\tau _r(\sigma )\) vanishes.
Proof
For clarity in this context, let \(\alpha \) (resp. \(\alpha ^v\)) denote the Cauchy–Green (resp. vertical Cauchy-Green) tensor of \(\sigma \). Since \(\pi \) is a Riemannian submersion:
Thus, \(\alpha =1+\alpha ^v\), and the expressions for \(\varepsilon _r(\sigma )\) and \(\nu _r(\sigma )\) follow from Lemma 2.1. Then \(\tau _r(\sigma )^v\) follows by expanding \({\mathcal {E}}_r(\sigma )\) as a sum of higher-power vertical energies and comparing the first variations for each using (3.5) and Theorem 3.6. \(\square \)
When \(r=1\), Theorem 3.10 simplifies to:
Thus, \(\sigma \) is a harmonic map precisely when \(\sigma \) is a harmonic section and the horizontal component of \(\tau (\sigma )\) vanishes. This is familiar in, for example, the theory of ‘harmonic unit vector fields’, and in that context the horizontal component of \(\tau (\sigma )\) may be expressed as a ‘twisted Ricci tensor’ [9]. In fact this (second) link with curvature generalises fairly comprehensively (see Theorem 3.14).
To analyse the horizontal component of \(\tau _r(\sigma )\) we will need the following (well-known) decomposition of the second fundamental form of a Riemannian submersion, compiled from results of [11, 19, 34].
Lemma 3.11
Suppose \(\pi :(P,k)\rightarrow (M,g)\) is a Riemannian submersion. Let H, K (resp. V, W) be horizontal (resp. vertical) vector fields on P. Then:
-
(i)
\(\nabla d\pi (H,K)=0\);
-
(ii)
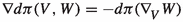 ;
; -
(iii)
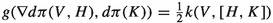 .
.
Remark 3.12
Comparison of Proposition 3.5 with Lemma 3.11 shows that a Riemannian submersion \(\pi \) is flat if and only if \(\pi \) is a t.g. map.
Lemma 3.11 allows us to compute the horizontal component of the second fundamental form of \(\sigma \), as follows.
Lemma 3.13
Let \(\sigma \) be a section of a Riemannian submersion \(\pi :(P,k)\rightarrow (M,g)\) with t.g. fibres. Then for all \(X,Y,Z\in {\mathfrak {X}}(M)\), we have:

where \(\theta \) is the curvature 3-tensor defined in (3.3).
Proof
Successive differentiation of the equation \(\pi \circ \sigma =1_M\) yields:
Applying first Lemma 3.11:

and then Proposition 3.5:
The final identity follows by polarisation. \(\square \)
Applying Lemma 3.13 to Corollary 2.17, in conjunction with Theorem 3.10, yields the following expression for the horizontal component of \(\tau _r(\sigma )\), and allows us to characterise the harmonicity of flat sections.
Theorem 3.14
If \(\sigma \) is a section of a Riemannian submersion \(\pi :(P,k)\rightarrow (M,g)\) with t.g. fibres, then the horizontal component of \(\tau _r(\sigma )\) is given by:

for all \(X\in {\mathfrak {X}}(M)\), where  . In particular, if \(\sigma \) is flat then:
. In particular, if \(\sigma \) is flat then:

Therefore, \(\sigma \) is an r-harmonic map precisely when \(\sigma \) is a twisted r-skyrmion with coupling constants \(c_i=\left( {\begin{array}{c}m-i\\ r-i\end{array}}\right) \) and the full Newton tensor \(\nu _{r-1}(\sigma )\) is solenoidal.
Since horizontal sections are flat (Remarks 3.2), we obtain the following synopsis of the horizontal case.
Theorem 3.15
Let \(\sigma \) be a section of a submersion \(\pi \) of Riemannian manifolds.
-
(i)
If \(\sigma \) is r-horizontal, then \(\sigma \) is an r-harmonic section.
-
(ii)
If \(\pi \) is a Riemannian submersion with t.g. fibres and \(\sigma \) is horizontal, then \(\sigma \) is an r-harmonic map for all \(r=1,\dots ,m\).
Proof
Part (i) follows from the fact that r-horizontal sections are the absolute minima of the r-th vertical energy functional. Part (ii) follows from Theorem 3.14. For, if \(\sigma \) is horizontal then \(\sigma \) is an r-harmonic section for all r, hence a twisted r-skyrmion for any coupling. Furthermore, all vertical Newton tensors of \(\sigma \) vanish, so the full Newton tensor \(\nu _{r-1}(\sigma )\) is a constant multiple of the identity (Theorem 3.10), hence solenoidal. \(\square \)
In certain situations, Theorem 3.15 becomes rigid. This will be one of the topics of the next Section (see Theorem 4.5 and Corollary 4.15).
4 Higher-power harmonic sections of Riemannian vector bundles
We interpret the results of Sect. 3 when the submersion \(\pi \) is a Riemannian vector bundle, that is, a vector bundle \(\pi :{\mathscr {E}}\rightarrow M\) equipped with a linear connection \(\nabla \) and holonomy-invariant fibre metric  . The most natural way to do this is via the connection map, which we briefly review in Sect. 4.1, where we also make the “connection” with the curvature form introduced in Sect. 3.1.
. The most natural way to do this is via the connection map, which we briefly review in Sect. 4.1, where we also make the “connection” with the curvature form introduced in Sect. 3.1.
We use our machinery to prove two rigidity theorems, the first of which (Theorem 4.5) applies when M is compact, and follows directly from the variational characterisation of higher-power harmonicity. The second (Corollary 4.15) applies to sections of constant length, and requires analysis of the higher-power vertical tension fields, which in this context can be viewed as (nonlinear) operators on the space of sections \({\mathscr {C}}({\mathscr {E}})\). These ‘tension operators’ can be expressed in terms of the Riemannian structure of the vector bundle (Theorem 4.7), revealing further detail about the analytic aspects of the Euler–Lagrange equations. We also analyse the horizontal component of the (full) higher-power tension fields (of a section, viewed as a map), noting specifically the appearance of bundle curvature via a Ricci operator (Theorem 4.11).
The higher-power harmonic section equations for sphere subbundles, with induced Sasakian geometry, are derived in Theorem 4.13. As a corollary, we obtain the equations for higher-power harmonic maps into spheres (Corollary 4.17), and in Example 4.19 we apply the model to the Hopf map.
4.1 Connection map and curvature form
Our analysis makes heavy use of the connection map for \(\nabla \), which we briefly review.
The square of \({\mathscr {E}}\) [32] is the pullback bundle \(\pi ^{-1}{\mathscr {E}}\rightarrow {\mathscr {E}}\), where:
This bundle may be equipped with the pullbacks of both \(\nabla \) and the fibre metric. The connection map for \(\nabla \) is then the \(\pi ^{-1}{\mathscr {E}}\)-valued 1-form \(\kappa \) on \({\mathscr {E}}\) defined for all \(A\in T{\mathscr {E}}\) by:

where  is the diagonal section of the square bundle, defined for all \(v\in {\mathscr {E}}\) by:
is the diagonal section of the square bundle, defined for all \(v\in {\mathscr {E}}\) by:

Then \(\kappa \) is surjective, and \(\kappa |_{\mathscr {V}}=\iota \), where \(\iota :{\mathscr {V}}\rightarrow \pi ^{-1}{\mathscr {E}}\) is the canonical isomorphism (obtained by amalgamating the canonical identifications of vertical tangent spaces with the fibre of \({\mathscr {E}}\) to which they are tangent). Given a Riemannian metric g on M, the Riemannian metric of choice on \({\mathscr {E}}\) is the Sasaki metric, defined:
for all \(A,B\in {\mathfrak {X}}({\mathscr {E}})\) (that is, vector fields on \({\mathscr {E}}\)). Then \(\pi \) is a Riemannian submersion, with \({\mathscr {H}}=\ker \kappa \), which is the horizontal distribution of \(\nabla \).
The curvature form K of \(\nabla \) is the exterior covariant derivative of \(\kappa \):

where \(R^\nabla \) is the curvature tensor of \(\nabla \). Thus, K is a \(\pi ^{-1}{\mathscr {E}}\)-valued 2-form on \({\mathscr {E}}\). We note two of its properties, that are of particular relevance.
Proposition 4.1
-
(i)
K is horizontal, that is, \(K(A,B)=0\) whenever A or B is vertical.
-
(ii)
K measures the failure of \(\kappa \) to intertwine the Levi–Civita connection of the Sasaki metric with the linear connection in \({\mathscr {E}}\):
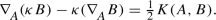
Proof
(i) is standard, and (ii) follows, after some computation, from the Koszul characterisation of the Levi–Civita connection (in which the holonomy-invariance of the fibre metric is crucial). \(\square \)
Remarks 4.2
-
1)
Since \(\kappa |_{\mathscr {V}}=\iota \), it follows from Proposition 4.1 that the canonical isomorphism is connection-preserving:
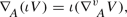 (4.4)
(4.4)for all vertical vector fields V on \({\mathscr {E}}\). This fact is crucial.
-
2)
We can now provide confirmation that Definition 3.1 of the curvature form \(\Theta \) is consistent with established terminology. For:
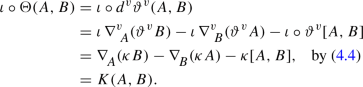 (4.5)
(4.5) -
3)
The Sasaki metric is of Kaluza–Klein type, and placing (4.5) alongside Propositions 4.1 and 3.5 confirms that \(\pi \) has t.g. fibres (see also Remarks 3.7).
4.2 Rigidity theorem
Now let \(\sigma \) be a section of \(\pi \). Equation (4.1) yields the following (well-known) relationship between the differential of \(\sigma \) and its covariant derivative, via the connection map:

for all \(X\in TM\) (after the natural identification of \(\sigma ^{-1}\pi ^{-1}{\mathscr {E}}\) with \({\mathscr {E}}\)). Thus, \(\sigma \) is horizontal precisely when \(\sigma \) is parallel.
Remark 4.3
Equations (4.3) and (4.5) reveal the following relationship between the generalised curvature form and the curvature tensor:
Thus, \(\sigma \) is flat in the sense of Definition 3.1 precisely when  , as we would expect.
, as we would expect.
Plugging (4.6) into (2.12) yields the following characterisation of the vertical Cauchy–Green tensor for \(\sigma \):

It follows from (4.8) that:
where:
is the r-fold exterior product.
Definition 4.4
A section \(\sigma \) is r-parallel if the rank of \(\nabla \sigma \) is strictly less than r at all points of M. Thus, \(\sigma \) is 1-parallel if and only if \(\sigma \) is parallel in the usual sense, and it follows from (4.6) that \(\sigma \) is r-parallel precisely when \(\sigma \) is r-horizontal (Definition 2.13).
When M is compact, Theorem 3.15 becomes rigid, as follows.
Theorem 4.5
Let \(\sigma \) be a section of a Riemannian vector bundle with compact base, equipped with the Sasaki metric. Then for all \(r=1,\dots ,m\) the following rigidity applies.
-
(i)
\(\sigma \) is an r-harmonic section if and only if \(\sigma \) is r-parallel.
-
(ii)
\(\sigma \) is an r-harmonic map if and only if \(\sigma \) is parallel.
Proof
Consider the variation:
Then by (4.9):
Hence, by (2.13):

which yields (i). Now by Theorem 3.10:
Therefore, \(\sigma \) is an r-harmonic map precisely when \(\nabla \sigma =0\). \(\square \)
Remarks 4.6
-
1)
Theorem 4.5 is well-known when \(r=1\), where it says that if M is compact then every harmonic section of \({\mathscr {E}}\) is parallel [13, 18, 37].
-
2)
There is a generalisation of Theorem 4.5 to the non-compact environment, for sections of constant length (see Corollary 4.15).
4.3 Higher-power tension operators
To achieve a general characterisation of r-harmonic sections, applicable when the base is non-compact, we use the canonical isomorphism to realise the higher-power vertical tension fields as sections of \(\pi \). Thus, to each section \(\sigma \) of \({\mathscr {E}}\) we associate another section \({\mathcal {T}}_r(\sigma )\) defined:
for all \(r=1,\dots ,m\). Then \({\mathcal {T}}_r\) may be regarded as an operator:
which turns out to be nonlinear for \(r>1\) (see Remarks 4.10). We refer to \({\mathcal {T}}_r\) as the r-th tension operator.
We also recall the (standard) definition of the second covariant derivative:

which entwines the linear connection in \(\pi \) with the Levi–Civita connection of (M, g).
The following result shows that \({\mathcal {T}}_r\) is a twisted Laplacian with first-order perturbation and provides further insight into the analytic nature of the higher-power harmonic section equations.
Theorem 4.7
Let \(\sigma \) be a section of a Riemannian vector bundle \({\mathscr {E}}\), equipped with the Sasaki metric. The higher-power tension operators are given by:

for all \(r=1,\dots ,m\), where  . Then \(\sigma \) is an r-harmonic section if and only if \({\mathcal {T}}_r(\sigma )=0\).
. Then \(\sigma \) is an r-harmonic section if and only if \({\mathcal {T}}_r(\sigma )=0\).
Proof
Applying the canonical isomorphism to Theorem 2.16, and using (4.6), yields:

By Proposition 4.1:

Hence:

The characterisation of r-harmonic sections follows from Theorem 3.6, since \(\pi \) has t.g. fibres. \(\square \)
Remarks 4.8
-
1)
If \(r=1\) then \({\mathcal {T}}_r(\sigma )=-\nabla ^*\nabla \sigma \), where \(\nabla ^*\nabla =-{{\,\textrm{trace}\,}}\nabla ^2\) is the rough Laplacian. Theorem 4.7 then yields the familiar characterisation \(\nabla ^*\nabla \sigma =0\) for harmonic sections \(\sigma \) of \({\mathscr {E}}\).
-
2)
From Eq. (4.12) in the proof of Theorem 4.7, the curvature
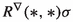 is the antisymmetrisation of the vertical second fundamental form of \(\sigma \); thus, the latter is symmetric if and only if \(\sigma \) is flat (see also Remarks 3.2 and and 4.3).
is the antisymmetrisation of the vertical second fundamental form of \(\sigma \); thus, the latter is symmetric if and only if \(\sigma \) is flat (see also Remarks 3.2 and and 4.3).
Corollary 4.9
With the same hypotheses as Theorem 4.7, if \(\sigma \) is an r-harmonic section of \({\mathscr {E}}\) then so is  for all \(c\in {\mathbb {R}}\).
for all \(c\in {\mathbb {R}}\).
Proof
If  , then \({{\hat{\alpha }}}=c^2\alpha \) by (4.8), and by the homogeneity of the vertical Newton tensor (Lemma 2.1):
, then \({{\hat{\alpha }}}=c^2\alpha \) by (4.8), and by the homogeneity of the vertical Newton tensor (Lemma 2.1):

Therefore, by Theorem 4.7:
from which the result follows. \(\square \)
Remarks 4.10
-
1)
Equation (4.13) shows that \({\mathcal {T}}_r\) is a nonlinear operator on \({\mathscr {C}}({\mathscr {E}})\) if \(r>1\) (see also Remark 5.14).
-
2)
In general, the r-harmonic sections of \({\mathscr {E}}\) generate a linear subspace of \({\mathscr {C}}({\mathscr {E}})\) only if \(r=1\). See however Theorem 5.8 and Remark 5.9 (2) for some interesting exceptions.
We now consider the horizontal component of the full higher-power tension fields \(\tau _r(\sigma )\), for later use (see Theorem 5.21). We would expect this to involve the curvature of \(\nabla \), and to this end introduce the following Ricci operator:
where for any \({\mathscr {E}}\)-valued 1-form \(\eta \) on M the \({\mathscr {E}}\)-valued 1-form \(S_\eta \) is defined:
for any local orthonormal tangent frame \(\{e_i\}\) on (M, g).
Theorem 4.11
The horizontal component of \(\tau _r(\sigma )\) is given by:

for all \(X\in {\mathfrak {X}}(M)\), where  and
and  . In particular, if \({\mathscr {E}}=TM\) equipped with the standard Riemannian structure then:
. In particular, if \({\mathscr {E}}=TM\) equipped with the standard Riemannian structure then:

where:
and R is the Riemann tensor of (M, g).
Proof
From equations (4.6) and (4.7), and the holonomy-invariance of \(\nabla \), we obtain:

Therefore, since  is self-adjoint:
is self-adjoint:

The general result now follows from Theorem 3.14. The simplification achieved for \({\mathscr {E}}=TM\) exploits the additional symmetries of the Riemann tensor. \(\square \)
Remark 4.12
Although the Ricci operator S is linear, the dependence of \(\eta \) on \(\sigma \) in Theorem 4.11 is nonlinear if \(r>1\), since it involves a Newton tensor.
Theorem 4.11 will be used extensively in the final result of the paper (Theorem 5.21).
4.4 Higher-power harmonic sections of sphere bundles
If the bundle has zero Euler class, then the rigidity of Theorem 4.5 can be side-stepped by confining attention to sections of constant length, say \(q>0\), and restricting the entire variational problem to the sphere subbundle:
Thus, we study higher-power harmonic sections of \({\mathscr {S}}{\mathscr {E}}(q)\).
The metric on \({\mathscr {S}}{\mathscr {E}}(q)\) is simply the restriction of the Sasaki metric. It follows from holonomy-invariance of the fibre metric of \({\mathscr {E}}\) that \({\mathscr {S}}{\mathscr {E}}(q)\) is a holonomy-invariant subbundle. The horizontal distribution of \({\mathscr {E}}\) is therefore tangent to \({\mathscr {S}}{\mathscr {E}}(q)\), and hence coincides with the horizontal distribution of \({\mathscr {S}}{\mathscr {E}}(q)\). This simplifies things considerably; for example, the vertical derivative of a section \(\sigma \) of \({\mathscr {S}}{\mathscr {E}}(q)\) is unchanged when \(\sigma \) is regarded as a section of \({\mathscr {E}}\), and consequently so are its higher-power vertical energies and vertical Newton tensors. There will however be an overall change in the higher-power vertical tension fields, which we analyze via the first variation.
Theorem 4.13
Suppose \(\sigma \) is a section of \({\mathscr {E}}\) with constant length \(q>0\). Then \(\sigma \) is an r-harmonic section of the sphere bundle \({\mathscr {S}}{\mathscr {E}}(q)\) if and only if \({\mathcal {T}}_r(\sigma )\) is a pointwise multiple of \(\sigma \). The precise equations are:
where \({\mathcal {T}}_r(\sigma )\) is given by Theorem 4.7.
Proof
By Theorem 3.6 and definition (4.2) of the Sasaki metric:

Now \(\iota V\) is a section \(\zeta \) of \({\mathscr {E}}\), which since \(\sigma _t\) is a variation through sections of constant length satisfies:
Conversely, if \(\zeta \) is a section of \({\mathscr {E}}\) that is pointwise orthogonal to \(\sigma \) then it is possible to construct a variation of \(\sigma \) in \({\mathscr {S}}{\mathscr {E}}(q)\) with variation field \(\iota V=\zeta \); for example, by appropriately rescaling \(\sigma +t\zeta \). It follows that \(\sigma \) is an r-harmonic section of \({\mathscr {S}}{\mathscr {E}}(q)\) if and only if \({\mathcal {T}}_r(\sigma )=f\sigma \) for some smooth function \(f:M\rightarrow {\mathbb {R}}\). Since \(\sigma \) has constant length and the fibre metric is holonomy-invariant:

by (4.8). Therefore, by Theorem 4.7:

by Lemma 2.2 and equation (4.9). \(\square \)
Remarks 4.14
-
1)
When \(r=q=1\) the Euler–Lagrange equations of Theorem 4.13 reduce to:
$$\begin{aligned} \nabla ^*\nabla \sigma =\Vert \nabla \sigma \Vert ^2\sigma , \end{aligned}$$(4.16)which is familiar from [36, 39] and subsequent papers on ‘harmonic unit vector fields’ [9].
-
2)
Theorem 4.13 shows in effect that the higher-power vertical tension fields of a section \(\sigma \) of \({\mathscr {S}}{\mathscr {E}}(q)\) are obtained, not unexpectedly, by orthogonal projection onto the tangent bundle \(T{\mathscr {S}}{\mathscr {E}}(q)\) those of \(\sigma \) when regarded as a section of \({\mathscr {E}}\).
Theorem 4.13 has a number of interesting corollaries. The first is a rigidity result for higher-power harmonic sections of \({\mathscr {E}}\) with constant length, which should be compared with Theorem 4.5.
Corollary 4.15
Suppose that \(\sigma \) is a section of \({\mathscr {E}}\) with constant length. Then \(\sigma \) is an r-harmonic section of \({\mathscr {E}}\) if and only if \(\sigma \) is r-parallel. In particular, \(\sigma \) is an r-harmonic section of \({\mathscr {E}}\) for all \(r\geqslant {{\,\textrm{rank}\,}}{\mathscr {E}}\).
Proof
If \(\sigma \) is a non-zero r-harmonic section of \({\mathscr {E}}\), then it follows from Theorems 4.7 and 4.13 that \(\sigma \) is an r-harmonic section of \({\mathscr {S}}{\mathscr {E}}(q)\) satisfying \((\nabla \sigma )^r=0\). Furthermore, since \(\sigma \) has constant length and the fibre metric is holonomy-invariant, \(\nabla \sigma \) takes values in the corank 1 subbundle  and therefore has rank strictly less than \(p-m\); so \(\sigma \) is r-parallel for all \(r\geqslant p-m\). \(\square \)
and therefore has rank strictly less than \(p-m\); so \(\sigma \) is r-parallel for all \(r\geqslant p-m\). \(\square \)
The next corollary reduces the study of higher-power harmonic sections of sphere bundles to the unit sphere bundle.
Corollary 4.16
Let \(\sigma \) be a section of \({\mathscr {E}}\) with constant length \(q>0\). Then \(\sigma \) is an r-harmonic section of \({\mathscr {S}}{\mathscr {E}}(q)\) if and only if \((1/q)\sigma \) is an r-harmonic section of \({\mathscr {S}}{\mathscr {E}}(1)\).
Proof
If \({{\hat{\sigma }}}=\sigma /q\), it follows from equation (4.13) in the proof of Corollary 4.9 that \({\mathcal {T}}_r(\sigma )\) is a multiple of \(\sigma \) if and only if \({\mathcal {T}}_r({{\hat{\sigma }}})\) is a multiple of \({{\hat{\sigma }}}\). \(\square \)
The final corollary generalises the well-known characterisation of harmonic maps into spheres first given in [29]. Let \({\mathbb {S}}^n\) denote the unit sphere of \({\mathbb {R}}^{n+1}\), equipped with its standard (induced) Riemannian structure.
Corollary 4.17
A mapping \(\varphi :(M,g)\rightarrow {\mathbb {S}}^n\) is r-harmonic precisely when:

where \(H_\varphi \) is the Hessian of \(\varphi \) when viewed as a map into Euclidean \({\mathbb {R}}^{n+1}\), and  .
.
Proof
Let \({\mathscr {E}}\) be the trivial bundle \(M\times {\mathbb {R}}^{n+1}\rightarrow M\), equipped with the trivial connection and Euclidean fibre metric, and let \(\sigma \) be the graph of \(\varphi \) (cf. the proof of Corollary 3.4). Then:

for all \(X\in T_xM\) and \(x\in M\). Now \(\varphi \) is an r-harmonic map (into \({\mathbb {S}}^n\)) if and only if \(\sigma \) is an r-harmonic section of \({\mathscr {S}}{\mathscr {E}}(1)\). It follows from Theorem 4.7 that \({\mathcal {T}}_r(\sigma )\) is the graph of the following \({\mathbb {R}}^{n+1}\)-valued function:

Furthermore, \((\nabla \sigma )^r\) is the graph of \((d\varphi )^r\) (as sections of the r-th exterior product of \({\mathscr {E}}\)). Then extracting the fibre component from the equations of Theorem 4.13 (with \(q=1\)) yields:

as claimed. \(\square \)
Remarks 4.18
-
1)
For clarity, if we denote the composition of \(\varphi :M\rightarrow {\mathbb {S}}^n\) with the inclusion map \({\mathbb {S}}^n \hookrightarrow {\mathbb {R}}^{n+1}\) by \({{\tilde{\varphi }}}\), then comparing Corollary 4.17 with Corollary 2.17 shows that \(\varphi \) is an r-harmonic map if and only if:
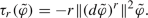
Note that the operator on the left-hand side is nonlinear if \(r>1\) (if \(r=1\) it is the standard Laplacian), so the concept of an ‘eigenmap’ really only makes sense if \(r=1\). (However, see Example 4.19 immediately below for a near miss.)
-
2)
From Corollary 4.15, \({{\tilde{\varphi }}}\) is r-harmonic if and only if \({{\,\textrm{rank}\,}}{{\tilde{\varphi }}}<r\).
Example 4.19
Let \(\varphi :{\mathbb {S}}^3\rightarrow {\mathbb {S}}^2\) be the Hopf map, defined:
for all \(u,v\in {\mathbb {C}}\) satisfying \(|{u}|^2+|{v}|^2=1\), which in Cartesian coordinates is given by:
for all \(x,y,z,w\in {\mathbb {R}}^4\) satisfying \(x^2+y^2+z^2+w^2=1\). For the purposes of calculation, we will use the following global orthonormal tangent frame on \({\mathbb {S}}^3\):
We will need to express the Levi–Civita connection of \({\mathbb {S}}^3\) in terms of this frame, for which we use the Gauss–Weingarten equations. The computations are straightforward, and we record the results in the following connection matrix:

Note that each of \(e_1,e_2,e_3\) is a Hopf vector field.
The Jacobian matrix of \(\varphi \), viewed as a mapping \({\mathbb {R}}^4\rightarrow {\mathbb {R}}^3\), is:
from which it follows after comparison with (4.17) that:
where \(\varphi _1,\varphi _2,\varphi _3\) are the components of \(\varphi \) with respect to the standard coordinates of ambient \({\mathbb {R}}^3\). Note that our frame is not adapted to the vertical/horizontal splitting of \(T{\mathbb {S}}^3\). The Jacobian matrix of \(\varphi \) with respect to \((e_1,e_2,e_3)\) is therefore:
It is now easy to see that:
and after slightly more computation that:
Thus, both the first and second power energy densities of \(\varphi \) are constant.
The Newton tensor of interest is  . To find it, we first need the Cauchy–Green tensor \(\alpha \) of \(\varphi \), which by Eq. (2.6) and some light computation has the following matrix with respect to \((e_1,e_2,e_3)\):
. To find it, we first need the Cauchy–Green tensor \(\alpha \) of \(\varphi \), which by Eq. (2.6) and some light computation has the following matrix with respect to \((e_1,e_2,e_3)\):
It follows from equation (2.5) and the previous paragraph that  , and therefore has matrix:
, and therefore has matrix:
Note that this matrix is symmetric, as expected, i.e.  is self-adjoint.
is self-adjoint.
We now compute the divergence of  , component-wise. Using the fact that the \(e_i\) are geodesic fields, and
, component-wise. Using the fact that the \(e_i\) are geodesic fields, and  is self-adjoint, the \(e_1\)-component is (summing over repeated indices):
is self-adjoint, the \(e_1\)-component is (summing over repeated indices):

Pulling in information from \(M_\nu \) and J then gives:

Similar calculations show that the other components also vanish. Thus, in this case  is solenoidal.
is solenoidal.
Turning now to the vector-valued Hessian \(H_\varphi \), we compute its components \(H_{\varphi _k}\), each of which is a (symmetric) 2-tensor on \({\mathbb {S}}^3\). The computations are numerous but routine, using information from \(M_\nabla \) and J to evaluate:

for all k and \(i\leqslant j\). For example:

In summary, the matrices \(M_k\) for \(H_{\varphi _k}\) are:
It remains to find the  -twisted trace of \(H_\varphi \), which we compute component-wise. For example, using information from \(M_1\) and \(M_\nu \) gives:
-twisted trace of \(H_\varphi \), which we compute component-wise. For example, using information from \(M_1\) and \(M_\nu \) gives:

The other components behave similarly, resulting in:

The fact that this is a multiple of \(\varphi \) is enough to show that \(\varphi \) is a 2-harmonic map. However, our earlier calculation shows that:

as required by Corollary 4.17.
Remarks 4.20
-
1)
It is well-known that the Hopf map is an unstable harmonic map [40]. Whether or not \(\varphi \) is an unstable 2-harmonic map poses an interesting question.
-
2)
Examples of maps whose Newton tensors are not solenoidal are highlighted in Remark 5.20.
-
3)
The r-harmonicity of the Hopf vector field on \({\mathbb {S}}^3\), as a section of the unit sphere bundle, will emerge in Sect. 5.
5 Higher-power harmonic vector fields on three-dimensional Lie groups
Suppose now that M is a three-dimensional Lie group, henceforward denoted G. For simplicity, we assume that G is unimodular (which nevertheless includes all examples that are compact, or simple). Let g be a left-invariant Riemannian metric on G, and let \({\mathscr {E}}=TG\) with the standard Riemannian structure, i.e.  and \(\nabla \) is the Levi–Civita connection. We refer to r-harmonic sections of \({\mathscr {E}}\) as r-harmonic vector fields. Henceforward, we confine our attention to invariant (i.e. left-invariant) vector fields.
and \(\nabla \) is the Levi–Civita connection. We refer to r-harmonic sections of \({\mathscr {E}}\) as r-harmonic vector fields. Henceforward, we confine our attention to invariant (i.e. left-invariant) vector fields.
Section 5.1 is mostly descriptive, and lays out the essential geometric and algebraic features of G, including Milnor’s classification of their Lie algebras.
In Section 5.2, we classify the invariant r-harmonic sections of TG for \(r=1,2\) (Theorem 5.8), which by Corollary 4.15 are the zeroes of r-power vertical energy. The main computation here is that of the first and second vertical energy densities (Lemma 5.5).
In Sect. 5.3, we classify the invariant r-harmonic sections of UG for \(r=1,2\). The main computation is that of the second tension operator, which is to be found in the proof of Theorem 5.12. This is preceded by a computation of the first vertical Newton tensor and its divergence (Theorem 5.10). The computation of the first Newton operator is much simpler (Theorem 5.13). These results, along with those of Sect. 5.2, are combined into a detailed classification, listing the possibilities for each type of Lie algebra and all its possible metrics (Theorem 5.16).
Section 5.4 is computationally intensive, and culminates with the classification of invariant r-power harmonic maps \(G\rightarrow UG\) for \(r=1,2,3\) (Theorem 5.21), preceded by computations of their second vertical Newton tensor and its divergence (Lemma 5.18), and twisted Ricci tensors (Lemma 5.19).
5.1 Geometric and algebraic structure
We briefly review the geometric and algebraic structure of (G, g), following [16] (see also [15]), highlighting features of particular relevance. We will also take the opportunity to recycle some (now redundant) notation from previous Sections.
After an orientation for G has been chosen, the metric determines a unique vector cross product \(\times \) on the Lie algebra \({\mathfrak {g}}\). The Lie structure map \(L:{\mathfrak {g}}\rightarrow {\mathfrak {g}}\) is then the unique linear map satisfying:
for all \(\varphi ,\psi \in {\mathfrak {g}}\). The image of L is the derived subalgebra \({\mathfrak {g}}'\). Furthermore, every non-trivial element of \(\ker (L)\) is orthogonal to a two-dimensional abelian subalgebra, and vice versa. Noting that every two-dimensional subspace containing a non-trivial central element is an abelian subalgebra, we deduce the following list of possibilities for the kernel:
-
K0)
\(\ker (L)\) is zero-dimensional (i.e. L is non-singular) if and only if \({\mathfrak {g}}\) has no two-dimensional abelian subalgebras. In particular, the centre \({\mathfrak {z}}\) of \({\mathfrak {g}}\) is trivial.
-
K1)
\(\ker (L)\) is one-dimensional if and only if \({\mathfrak {g}}\) has a unique 2-dimensional abelian subalgebra \({\mathfrak {h}}\), in which case \({\mathfrak {h}}=\ker (L)^\bot \). In particular, \({\mathfrak {z}}\) is again trivial.
-
K2)
\(\ker (L)\) is two-dimensional if and only if \({\mathfrak {z}}\) is one-dimensional, in which case \({\mathfrak {z}}=\ker (L)^\bot \). In particular, the two-dimensional abelian subalgebras are precisely the two-dimensional subspaces containing \({\mathfrak {z}}\).
-
K3)
\(\ker (L)\) is three-dimensional if and only if \({\mathfrak {g}}\) is abelian.
The unimodularity of G is characterised by L being self-adjoint. Let \((\sigma _1,\sigma _2,\sigma _3)\) be a positively-oriented orthonormal L-eigenbasis of \({\mathfrak {g}}\), with eigenvalues \(\lambda _1,\lambda _2,\lambda _3\). This therefore satisfies the commutation relations:

where \(\epsilon _{ijk}\) is the Levi–Civita symbol. We therefore refer to \(\lambda _1,\lambda _2,\lambda _3\) as the principal structure constants of (G, g), which, being dependent on orientation, are only determined up to sign. The \(\sigma _i\) are then principal (structure) directions.
We say that a two-dimensional subspace \({\mathfrak {p}}\subset {\mathfrak {g}}\) (ie. an invariant plane field on G) is a principal section if \({\mathfrak {p}}\) is spanned by principal directions. The following example shows that principal sections need not be eigenspaces of L.
Example 5.1
Every two-dimensional subalgebra \({\mathfrak {h}}\subset {\mathfrak {g}}\) is a principal section. This is because two-dimensional unimodular Lie algebras are abelian, so \({\mathfrak {h}}\) is orthogonal to an element of \(\ker (L)\). Since L is self-adjoint, the condition:
is equivalent to:
It follows that \({\mathfrak {h}}\) is an ideal; we therefore refer to elements of \({\mathfrak {h}}\) as ideal vectors. From (K1) and (K2) above, the (interesting) possibilities are:
-
i)
If precisely one principal structure constant vanishes, then \({\mathfrak {g}}'\) is two-dimensional and \({\mathfrak {h}}={\mathfrak {g}}'\).
-
ii)
If precisely two principal structure constants vanish, then \({\mathfrak {g}}'={\mathfrak {z}}\) is one-dimensional and \({\mathfrak {h}}\) is any two-dimensional subspace containing \({\mathfrak {g}}'\).
The relative signs of the principal structure constants classify \({\mathfrak {g}}\) algebraically into one of the following six types:
where \({\mathfrak {e}}(2)\) (resp. \({\mathfrak {e}}(1,1)\)) is the Lie algebra of the isometry group of the Euclidean plane \({\mathbb {E}}^2\) (resp. Minkowskian plane \({\mathbb {M}}^2\)), \({\mathfrak {n}}{\mathfrak {i}}{\mathfrak {l}}\) is the three-dimensional Heisenberg algebra and \({\mathfrak {a}}\) is the three-dimensional abelian Lie algebra. The first two are simple, and the others are solvable.
The Milnor numbers of (G, g) are defined (up to sign) as follows:
The Levi–Civita connection is then characterised along principal directions by:

In particular:

so the \(\sigma _i\) are geodesic vector fields (i.e. their integral curves are geodesics).
The Milnor map is the following self-adjoint linear map \(M:{\mathfrak {g}}\rightarrow {\mathfrak {g}}\), whose eigenvalues are the Milnor numbers:

where \((\sigma ^1,\sigma ^2,\sigma ^3)\) is the dual basis; the invariant expression confirms that M is well-defined. For any \(\varphi \in {\mathfrak {g}}\) and \(n\in {\mathbb {N}}\) it is convenient to denote by \(\varphi ^{(n)}\) the n-th iterate of \(\sigma \) under M:
The covariant derivative (5.3) may then be expressed invariantly as follows:

for all \(\sigma \in {\mathfrak {g}}\). (Higher-order iterates will be used extensively in many of our computations.)
The principal structure directions are also principal Ricci directions, with principal Ricci curvatures:
for \(\{i,j,k\}=\{1,2,3\}\). The Ricci curvature is therefore non-degenerate if and only if M is invertible. Furthermore, the vanishing of one principal Ricci curvature implies the vanishing of another, so the Ricci kernel:
cannot be one-dimensional. If \(\dim ({\mathfrak {n}})=2\), then \({\mathfrak {n}}\) is a principal section, although not necessarily a subalgebra or an eigenspace of L. The following result describes the relationship between these different types of principal section.
Proposition 5.2
Suppose \({\mathfrak {p}}\subset {\mathfrak {g}}\) is a principal section.
-
(i)
\({\mathfrak {p}}\) is an eigenspace of \(M^2\), the twice-iterated Milnor map, if and only if \({\mathfrak {p}}\) is either an eigenspace of L or a subalgebra.
-
(ii)
\({\mathfrak {p}}\) is an eigenspace of \({{\,\textrm{Ric}\,}}^2\), the twice-iterated Ricci tensor, if and only if \({\mathfrak {p}}\) is an eigenspace of \(M^2\) or \({\mathfrak {p}}={\mathfrak {n}}\).
Proof
If \(\{i,j,k\}=\{1,2,3\}\), then from (5.2) and (5.6):
If \({\mathfrak {p}}\) is spanned by \(\sigma _i\) and \(\sigma _j\), then (i) follows from (5.7), bearing in mind that \(\lambda _k=0\) precisely when \({\mathfrak {p}}\) is a subalgebra (Example 5.1), and (ii) follows from (5.8), bearing in mind that in the non-flat situation \(\mu _k=0\) precisely when \(\rho _i=\rho _j=0\). \(\square \)
The principal sectional curvatures are:
The Riemann tensor is characterised by its action on principal directions as follows:
The following classification scheme, which we refer to as Milnor’s list, summarises the geometric possibilities for each unimodular Lie algebra. By choice of orientation, it may be assumed that \(\lambda _1\geqslant \lambda _2\geqslant \lambda _3\) with \(\lambda _1,\lambda _2\geqslant 0\), and \(\lambda _1=0\) only if \(\lambda _3=0\).
- \({\mathfrak {a}}:\):
-
all structure constants vanish; all left-invariant metrics are flat.
- \({\mathfrak {n}}{\mathfrak {i}}{\mathfrak {l}}:\):
-
\(\lambda _1>0\) and \(\lambda _2=\lambda _3=0\). Then \(\rho _2=\rho _3<0\) and \(\rho _1=-\rho _2\).
- \({\mathfrak {e}}(1,1):\):
-
\(\lambda _1>0\), \(\lambda _2=0\) and \(\lambda _3<0\). Then \(\rho _1=-\rho _3\) and \(\rho _2<-|{\rho _1}|\), with \(\rho _1=\rho _3=0\) precisely when \(\lambda _1=-\lambda _3\).
- \({\mathfrak {e}}(2):\):
-
\(\lambda _1,\lambda _2>0\) and \(\lambda _3=0\). Then \(\rho _1=-\rho _2\) and \(-|{\rho _1}|<\rho _3<0\), unless \(\lambda _1=\lambda _2\) in which case the metric is flat.
- \({\mathfrak {s}}{\mathfrak {l}}(2):\):
-
\(\lambda _1,\lambda _2>0\) and \(\lambda _3<0\). Then \(\rho _2<0\) and \(\rho _1\rho _3\leqslant 0\), with the \(|{\rho _i}|\) distinct and non-zero unless:
\(\lambda _1=\lambda _2\) in which case \(\rho _1=\rho _2\);
\(\lambda _1=\lambda _2-\lambda _3\) in which case \(\rho _1=\rho _3=0\).
- \({\mathfrak {s}}{\mathfrak {u}}(2):\):
-
\(\lambda _1,\lambda _2,\lambda _3>0\). Then \(\rho _1>0\) and \(\rho _2\rho _3\geqslant 0\), with the \(|{\rho _i}|\) distinct and non-zero unless:
\(\lambda _1=\lambda _2=\lambda _3\) in which case \(\rho _1=\rho _2=\rho _3\);
\(\lambda _1=\lambda _2>\lambda _3\) in which case \(\rho _1=\rho _2>\rho _3>0\);
\(\lambda _1>\lambda _2=\lambda _3\) in which case \(\rho _1>\rho _2=\rho _3\), with \(\rho _3\ne 0\) unless \(\lambda _1=2\lambda _2\);
\(\lambda _1=\lambda _2+\lambda _3\) in which case \(\rho _2=\rho _3=0\).
Notable features of the list are:
-
Metrics with degenerate Ricci curvature occur in every class except \({\mathfrak {n}}{\mathfrak {i}}{\mathfrak {l}}\).
-
Flat metrics are only supported on \({\mathfrak {a}}\) and \({\mathfrak {e}}(2)\).
-
It follows from Example 5.1 that \({\mathfrak {g}}'\) is two-dimensional if and only if \({\mathfrak {g}}={\mathfrak {e}}(2)\) or \({\mathfrak {g}}={\mathfrak {e}}(1,1)\). If G is the isometry group of \({\mathbb {E}}^2\) or \({\mathbb {M}}^2\) then \({\mathfrak {g}}'\) is the Lie algebra of the translation subgroup. Thus, elements of \({\mathfrak {g}}'\) may be regarded as infinitesimal translations; all other elements are infinitesimal (Euclidean or Lorentzian) rotations.
Example 5.3
Let \(G=PSL(2,{\mathbb {R}})\), realised as the unit tangent bundle of the hyperbolic plane \({\mathbb {H}}^2\). If \({\mathbb {H}}^2\) is modelled by the upper half plane then:
The natural left-invariant metric g on G is [2]:

Define a left-invariant orthonormal tangent frame on G by:
(Note that this is not the frame mentioned in [2].) Standard computations of the Lie bracket on vector fields yield:
Therefore, the \(\sigma _i\) are principal structure directions, with:
So g is one of the “exceptional” \({\mathfrak {s}}{\mathfrak {l}}(2)\) metrics on Milnor’s list. From (5.2) and (5.6), its principal Ricci curvatures are:
in accordance with the list.
Remark 5.4
Elements of the Lie algebras \({\mathfrak {e}}(2)\), \({\mathfrak {s}}{\mathfrak {u}}(2)\), \({\mathfrak {s}}{\mathfrak {l}}(2)\) and \({\mathfrak {e}}(1,1)\) may be regarded as infinitesimal isometries, of \({\mathbb {E}}^2\), \({\mathbb {S}}^2\) (under the isomorphism \({\mathfrak {s}}{\mathfrak {u}}(2)\cong {\mathfrak {s}}{\mathfrak {o}}(3)\)), \({\mathbb {H}}^2\) and \({\mathbb {M}}^2\), respectively. However, they are not in general Killing fields when viewed as vector fields on G. Indeed, by (5.5), (5.4) and the antisymmetry of the scalar triple product we have:

So \(\sigma \) is a Killing field on G if and only if the element:
is orthogonal to \(\sigma \) for all \(\varphi ,\psi \in {\mathfrak {g}}\). Since, for example:
if \(\lambda _1\ne \lambda _2\) then \(\sigma _3\) cannot be a Killing field.
5.2 Invariant higher-power harmonic vector fields
Suppose \(\sigma \in {\mathfrak {g}}\), with:
We compute the first and second power vertical energy densities of \(\sigma \), which for notational simplicity we abbreviate to \(\varepsilon _1\) and \(\varepsilon _2\), respectively.
Lemma 5.5
We have:
-
(i)
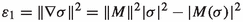 .
. -
(ii)
\(\varepsilon _2=\Vert {\nabla \sigma \wedge \nabla \sigma }\Vert ^2=\tfrac{1}{4}|{{{\,\textrm{Ric}\,}}(\sigma )}|^2\,|{\sigma }|^2\).
Proof
i) From (4.9), (5.5) and a well-known identity of classical vector algebra we compute:

ii) Using (4.9), (5.5) and (5.6) along with various identities of classical vector algebra we compute:

\(\square \)
In general, if a bundle is flat then so are all its sections (see Remark 3.2). The following result shows that the converse holds for the case at hand.
Theorem 5.6
Suppose \(\sigma \) is a non-zero invariant vector field on (G, g). Then:
-
(i)
\(\sigma \) is flat if and only if (G, g) is flat.
-
(ii)
\(\sigma \) is parallel if and only if (G, g) is flat and \(\sigma \) is orthogonal to \({\mathfrak {g}}'\).
Proof
i) If \(\sigma \) is flat (see Remark 4.3), then it follows from (5.10) that at least two principal sectional curvatures vanish. Then by (5.9) two principal Ricci curvatures are equal and the third vanishes. But \(\dim {\mathfrak {n}}\ne 1\) so all the \(\rho _i\) vanish, rendering (G, g) flat.
ii) In the abelian case, all invariant fields are parallel since \(M=0\). In the non-abelian flat case, precisely two Milnor numbers vanish and \(\ker (M)={\mathfrak {g}}'\). It therefore follows from Lemma 5.5 (i), in particular equation (5.11), that \(\sigma \) is parallel if and only if \(\sigma \) is orthogonal to \({\mathfrak {g}}'\). \(\square \)
It follows from Corollary 4.15 that Theorem 5.6 classifies all the invariant harmonic vector fields on G. We now extend that to higher-power harmonicity. First, we clarify some terminology.
Definition 5.7
An invariant vector field \(\sigma \) is Ricci-flat, or a Ricci null vector, if \(\sigma \in {\mathfrak {n}}\) (rather than the weaker condition \({{\,\textrm{Ric}\,}}(\sigma ,\sigma )=0\)).
Theorem 5.8
With the same hypotheses as Theorem 5.6, \(\sigma \) is an r-harmonic vector field in precisely the following cases:
-
(a)
\(r=1:\) (G, g) is flat and \(\sigma \) is orthogonal to \({\mathfrak {g}}'\).
-
(b)
\(r=2:\) \(\sigma \) is Ricci-flat.
-
(c)
\(r=3:\) all \(\sigma \).
Proof
Case (a) is a restatement of Theorem 5.6 (ii), and (c) follows from Corollary 4.15 since TG is a rank 3 vector bundle. By Corollary 4.15, \(\sigma \) is 2-harmonic precisely when \(\sigma \) is 2-parallel, which by Lemma 5.5 (ii) occurs precisely when \(\sigma \) is Ricci-flat. \(\square \)
Remarks 5.9
-
1)
Non-trivial 2-harmonic invariant vector fields exist only if the Ricci curvature degenerates. From ‘Milnor’s list’, there are no such vector fields if, for example, \({\mathfrak {g}}={\mathfrak {n}}{\mathfrak {i}}{\mathfrak {l}}\), or \({\mathfrak {g}}={\mathfrak {e}}(2)\) with a non-flat metric.
-
2)
If \(\sigma \) is Ricci-flat, then the image of \(\nabla \sigma :{\mathfrak {g}}\rightarrow {\mathfrak {g}}\) is orthogonal to \({\mathfrak {n}}\), and since \(\dim {\mathfrak {n}}\ne 1\) therefore lies in a fixed (i.e. independent of \(\sigma \)) rank 1 subbundle. This geometric ‘quirk’ explains why the invariant 2-harmonic vector fields form a linear subspace, contrary to general expectation (Remarks 4.10).
5.3 Invariant higher-power harmonic directions
An invariant vector field \(\sigma \) may be regarded as a section of the sphere bundle \({\mathscr {S}}{\mathscr {E}}(q)\) where \(q=|{\sigma }|\). By Corollary 4.16, it suffices to consider \(q=1\), so we focus on r-harmonic sections of the unit tangent bundle UG, which we refer to as r-harmonic directions, or r-harmonic unit vector fields, depending on whether we wish to emphasise the Lie algebra or the Lie group. In the former case especially, it is convenient to regard invariant unit vector fields as elements of the unit sphere \({\mathcal {S}}\subset {\mathfrak {g}}\).
When \(r=1\), the invariant r-harmonic unit vector fields were classified in [10], which we revisit in Theorem 5.13. When \(r=3\) the classification is tautologous: the third vertical energy of any unit vector field vanishes since the fibres of UG are 2-dimensional. To handle the outstanding case (\(r=2\)), we compute the second tension operator \({\mathcal {T}}_2(\sigma )\). This requires the first vertical Newton tensor, and its divergence (see Theorem 4.7).
Theorem 5.10
Let  where \(\sigma \in {\mathcal {S}}\).
where \(\sigma \in {\mathcal {S}}\).
-
(i)
For all \(\varphi \in {\mathfrak {g}}\), we have:
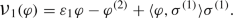
-
(ii)
The divergence of
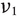 is:
is: 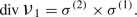
Then  is solenoidal in precisely the following situations:
is solenoidal in precisely the following situations:
-
(a)
The Ricci curvature is non-degenerate and \(\sigma \) is a principal direction.
-
(b)
The Ricci curvature has rank 1 and \(\sigma \) lies in a principal section containing \({\mathfrak {n}}^{\bot }\).
-
(c)
(G, g) is flat.
Proof
i) From (2.4), we have:

where \(\alpha \) is the vertical Cauchy–Green tensor. Using (4.8) and (5.5), for all \(\varphi ,\psi \in {\mathfrak {g}}\) we compute:

Hence:
ii) Since the \(\sigma _i\) are geodesic, we compute (cf. Definition 2.15):

It follows that  if and only if \(M\sigma \) is an eigenvector of M. If the Ricci curvature is non-degenerate, then M is invertible by (5.6); so, since M has the same eigenspaces as L by (5.4), this is the case precisely when \(\sigma \) is a principal direction. If \(\dim {\mathfrak {n}}=2\), then \({\mathfrak {n}}={{\,\textrm{im}\,}}(M)\); so this is the case precisely when \(\sigma \) lies in a principal section containing \(\ker (M)={\mathfrak {n}}^{\bot }\). Finally, if (G, g) is flat then \({{\,\textrm{rank}\,}}(M)\leqslant 1\) by (5.6); so this is the case for all \(\sigma \). \(\square \)
if and only if \(M\sigma \) is an eigenvector of M. If the Ricci curvature is non-degenerate, then M is invertible by (5.6); so, since M has the same eigenspaces as L by (5.4), this is the case precisely when \(\sigma \) is a principal direction. If \(\dim {\mathfrak {n}}=2\), then \({\mathfrak {n}}={{\,\textrm{im}\,}}(M)\); so this is the case precisely when \(\sigma \) lies in a principal section containing \(\ker (M)={\mathfrak {n}}^{\bot }\). Finally, if (G, g) is flat then \({{\,\textrm{rank}\,}}(M)\leqslant 1\) by (5.6); so this is the case for all \(\sigma \). \(\square \)
We also require the second covariant derivative, which is a straightforward consequence of equations (4.11) and (5.5).
Lemma 5.11
For all \(\varphi ,\psi \in {\mathfrak {g}}\), we have:

Theorem 5.12
If \(\sigma \in {\mathcal {S}}\), then:
where \({{\,\textrm{Ric}\,}}^2\) denotes the twice-iterated Ricci tensor. Then \(\sigma \) is a 2-harmonic direction precisely when any of the following hold:
-
(a)
\(\sigma \) is a principal direction;
-
(b)
\(\sigma \) is an ideal direction;
-
(c)
\(\sigma \) is a Ricci null direction.
Note
Conditions (a), (b) and (c) are not mutually exclusive.
Proof
By Theorem 5.10 (i):

Now by Lemma 5.11:

so:

and:

By Lemma 5.11 again:

Applying Theorem 5.10 (ii) and equation (5.5) yields:

where:

after (somewhat remarkably) three pairs of cancellations, including all terms involving \(\Vert {M}\Vert ^4\) and  . Now:
. Now:
Furthermore:

When assembling \({\mathcal {T}}_2(\sigma )\), terms involving \(\Vert {{{\,\textrm{Ric}\,}}}\Vert \) cancel, leaving the stated formula.
Comparing our expression for \({\mathcal {T}}_2(\sigma )\) with Theorem 4.13, it follows that \(\sigma \) is a 2-harmonic direction precisely when \(\sigma \) is a unit eigenvector of \({{\,\textrm{Ric}\,}}^2\). Since \({{\,\textrm{Ric}\,}}\) is symmetric the eigenvalues of \({{\,\textrm{Ric}\,}}^2\) are \(\rho _1^{\,2},\rho _2^{\,2},\rho _3^{\,2}\), and the eigenspaces of \({{\,\textrm{Ric}\,}}^2\) contain those of \({{\,\textrm{Ric}\,}}\). It follows that all one-dimensional eigenspaces of \({{\,\textrm{Ric}\,}}^2\) are principal lines. Furthermore the two-dimensional eigenspaces of \({{\,\textrm{Ric}\,}}^2\) were analysed in Proposition 5.2. If \(\rho _1^{\,2}=\rho _2^{\,2}=\rho _3^{\,2}\), then by (5.8) either precisely two of the \(\mu _i\) vanish, in which case (G, g) is flat (so \(\sigma \) is Ricci-null), or \(\mu _1^{\,2}=\mu _2^{\,2}=\mu _3^{\,2}\). In the latter case, it follows from (5.7) that either \(\lambda _1=\lambda _2=\lambda _3\) (so \(\sigma \) is a principal direction), or precisely two of the \(\lambda _i\) vanish. In the latter case, if \({\mathfrak {l}}\subset {\mathfrak {g}}\) is the line orthogonal to \(\ker (L)\) then every plane containing \({\mathfrak {l}}\) is a subalgebra; so \(\sigma \) is an ideal direction.
\(\square \)
For comparison, we give a similar characterisation of the invariant harmonic unit vector fields on G (cf. [10, Lemma 5.1]).
Theorem 5.13
If \(\sigma \in {\mathcal {S}}\), then:
where \(M^2\) is the twice-iterated Milnor map. Then \(\sigma \) is a harmonic direction precisely when either of the following hold:
-
(a)
\(\sigma \) is a principal direction;
-
(b)
\(\sigma \) is an ideal direction.
Proof
By Remark 4.8 (1) the expression for \({\mathcal {T}}_1(\sigma )\) follows immediately from Eq. (5.13) in the proof of Theorem 5.12. Hence, by Theorem 4.13, \(\sigma \) is a harmonic direction if and only if \(\sigma \) is an eigendirection of \(M^2\). Since the eigenspaces of \(M^2\) contain those of M, all one-dimensional eigenspaces of \(M^2\) are principal lines. The 2-dimensional eigenspaces were determined in Proposition 5.2, and the case \(\mu _1^{\,2}=\mu _2^{\,2}=\mu _3^{\,2}\) was analysed in the proof of Theorem 5.12. \(\square \)
Remark 5.14
Theorems 5.13 and 5.12 clearly show that \({\mathcal {T}}_1\) is a linear operator, whereas \({\mathcal {T}}_2\) is not (cf. Remarks 4.10).
For \(r=1,2,3\) we denote by \({\mathcal {H}}_r\subseteq {\mathcal {S}}\) the invariant r-harmonic directions, and by \({\mathcal {Z}}_r\subseteq {\mathcal {H}}_r\) those of zero r-th vertical energy. Then \({\mathcal {H}}_3={\mathcal {Z}}_3\), and comparing Theorems 5.8, 5.12 and 5.13 for \(r=2\) yields:
Corollary 5.15
We have \({\mathcal {H}}_r={\mathcal {H}}_{r-1}\cup {\mathcal {Z}}_r\) for \(r=2,3\).
It follows from Theorem 5.12 (resp. Theorem 5.13) that the invariant r-harmonic unit vector fields on (G, g) are determined by the singular values of the Ricci tensor (resp. Milnor map) when \(r=2\) (resp. \(r=1\)). To give a unified result, we introduce some further subsets of \({\mathcal {S}}\). If \(\lambda _k\) is distinct from \(\lambda _i\) and \(\lambda _j\) for \(\{i,j,k\}=\{1,2,3\}\) then there is the following principal circle and its poles:
and if the principal structure constants are all distinct then we have the polar set:
Theorems 5.8, 5.12 and 5.13 may now be summarised as follows.
Theorem 5.16
-
(i)
Suppose the \(|{\rho _i}|\) are distinct. Then \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {P}}\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \).
-
(ii)
Suppose \(|{\rho _i}|=|{\rho _j}|\ne |{\rho _k}|\). Then \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {C}}_{ij}\cup {\mathcal {P}}_k\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \), unless \(\rho _i=\rho _j=0\) and \(|{\mu _i}|\ne |{\mu _j}|\) in which case \({\mathcal {H}}_1={\mathcal {P}}\) and \({\mathcal {Z}}_2={\mathcal {C}}_{ij}\).
-
(iii)
Suppose \(|{\rho _1}|=|{\rho _2}|=|{\rho _3}|\). Then \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {S}}\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \), unless (G, g) is flat, in which case:
-
(a)
if G is abelian then \({\mathcal {Z}}_1={\mathcal {Z}}_2={\mathcal {S}}\);
-
(b)
if G is non-abelian, with \(\mu _k\ne 0\), then \({\mathcal {H}}_1={\mathcal {C}}_{ij}\cup {\mathcal {P}}_k\), with \({\mathcal {Z}}_1={\mathcal {P}}_k\) and \({\mathcal {Z}}_2={\mathcal {S}}\).
-
(a)
When Theorem 5.16 is placed alongside ‘Milnor’s list’ the following classification scheme is obtained, which subsumes that of [10, Prop. 5.2].
- \({\mathfrak {a}}:\):
-
\({\mathcal {Z}}_1={\mathcal {Z}}_2={\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {S}}\).
- \({\mathfrak {n}}{\mathfrak {i}}{\mathfrak {l}}:\):
-
\({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {S}}\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \).
- \({\mathfrak {e}}(1,1):\):
-
\({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {C}}_{13}\cup {\mathcal {P}}_2\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \), unless \(\lambda _1=-\lambda _3\) in which case \({\mathcal {Z}}_2={\mathcal {C}}_{13}\).
- \({\mathfrak {e}}(2):\):
-
\({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {C}}_{12}\cup {\mathcal {P}}_3\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \), unless \(\lambda _1=\lambda _2\) in which case \({\mathcal {Z}}_2={\mathcal {H}}_2={\mathcal {S}}\) and \({\mathcal {Z}}_1={\mathcal {P}}_3\).
- \({\mathfrak {s}}{\mathfrak {l}}(2):\):
-
\({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {P}}\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \), unless:
\(\lambda _1=\lambda _2\) in which case \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {C}}_{12}\cup {\mathcal {P}}_3\);
\(\lambda _1=\lambda _2-\lambda _3\) in which case \({\mathcal {H}}_2={\mathcal {C}}_{13}\cup {\mathcal {P}}_2\) and \({\mathcal {Z}}_2={\mathcal {C}}_{13}\).
- \({\mathfrak {s}}{\mathfrak {u}}(2):\):
-
\({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {P}}\) and \({\mathcal {Z}}_1={\mathcal {Z}}_2=\emptyset \), unless:
\(\lambda _1=\lambda _2=\lambda _3\) in which case \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {S}}\);
\(\lambda _1=\lambda _2>\lambda _3\) in which case \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {C}}_{12}\cup {\mathcal {P}}_3\);
\(\lambda _1>\lambda _2=\lambda _3\ne \tfrac{1}{2}\lambda _1\) in which case \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {C}}_{23}\cup {\mathcal {P}}_1\);
\(\lambda _2=\lambda _3=\tfrac{1}{2}\lambda _1\) in which case \({\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {C}}_{23}\cup {\mathcal {P}}_1\) and \({\mathcal {Z}}_2={\mathcal {C}}_{23}\);
\(\lambda _1=\lambda _2+\lambda _3\) and \(\lambda _2\ne \lambda _3\) in which case \({\mathcal {H}}_2={\mathcal {C}}_{23}\cup {\mathcal {P}}_1\) and \({\mathcal {Z}}_2={\mathcal {C}}_{23}\).
Some notable consequences of the classification are:
-
Left-invariant metrics with \({\mathcal {H}}_1\subsetneq {\mathcal {H}}_2\) are supported only on \({\mathfrak {e}}(2)\), \({\mathfrak {s}}{\mathfrak {l}}(2)\) and \({\mathfrak {s}}{\mathfrak {u}}(2)\), and in each case \({\mathcal {H}}_2={\mathcal {H}}_1\cup {\mathcal {Z}}_2\), as expected.
-
If \(G=SU(2)\), realised as the 3-sphere, and g is the standard metric (of constant sectional curvature 1), then \(\lambda _1=\lambda _2=\lambda _3=2\) and \({\mathcal {S}}\) is precisely the set of (left) Hopf vector fields on \({\mathbb {S}}^3\). These are all 1-harmonic, and 2-harmonic. (It follows from Theorem 5.10 that the vertical newton tensor \(\nu _1^v(\sigma )\) is solenoidal.)
-
If \({\mathfrak {g}}={\mathfrak {e}}(2)\) or \({\mathfrak {g}}={\mathfrak {e}}(1,1)\) then the infinitesimal translations are 1-harmonic and 2-harmonic, for all choices of metric. (The vertical Newton tensor is solenoidal only for the flat metric on \({\mathfrak {e}}(2)\).)
-
From Example 5.3, in addition to \(\partial _\theta \) we obtain the following 1-parameter family of 1-harmonic and 2-harmonic unit vector fields on \(U{\mathbb {H}}^2\):
$$\begin{aligned} \sigma _t&=\cos t\,\sigma _1+\sin t\,\sigma _2 \\&=y\cos (\theta +t)\,\partial _x +y\sin (\theta +t)\,\partial _y -\cos (\theta -t)\,\partial _\theta . \end{aligned}$$(The vertical newton tensor \(\nu _1^v(\sigma _t)\) is solenoidal for all t.)
5.4 Invariant higher-power harmonic maps
We conclude with a classification of all left-invariant unit vector fields that are higher-power harmonic maps \(G\rightarrow UG\), making use of Theorem 3.10. This requires an analysis of twisted skyrmions (Definition 3.9) for the case at hand. Since \({\mathcal {H}}_1\subseteq {\mathcal {H}}_2\), all invariant 1-harmonic directions are twisted 2-skyrmions in the bundle \(UG\rightarrow G\), for all coupling constants. The following result shows that there are no others.
Theorem 5.17
An element \(\sigma \in {\mathcal {S}}\) is a twisted 2-skyrmion in the unit tangent bundle precisely when \(\sigma \in {\mathcal {H}}_1\).
Proof
By Eq. (4.15) for the first variation of higher-power vertical energy of sections of vector bundles, and the argument used to prove Theorem 4.13, \(\sigma \) is a twisted 2-skyrmion if and only if \({\mathcal {T}}_1(\sigma )+c\,{\mathcal {T}}_2(\sigma )\) is a pointwise multiple of \(\sigma \) for some \(c>0\), and by Theorems 5.12 and 5.13 this is the case precisely when \(\sigma \) is an eigenvector of:
Now:

where by (5.6):

for \(\{i,j,k\}=\{1,2,3\}\). Then:

hence \(\eta _i=\eta _j\) if and only if \(|{\mu _i}|=|{\mu _j}|\). So by Theorem 5.13 the classification scheme is identical to that for \({\mathcal {H}}_1\). \(\square \)
We also require the second vertical Newton tensor  of \(\sigma \). (We computed
of \(\sigma \). (We computed  in Theorem 5.10.)
in Theorem 5.10.)
Lemma 5.18
Let  where \(\sigma \in {\mathcal {H}}_1\).
where \(\sigma \in {\mathcal {H}}_1\).
-
(i)
For all \(\varphi \in {\mathfrak {g}}\), we have:
-
(ii)
Furthermore:
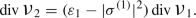
Proof
i) From (2.4):

where \(\alpha \) is the vertical Cauchy–Green tensor, calculated in (5.12). It follows from Theorem 5.13 that \(\sigma \) is an eigenvector of \(M^2\):

This yields the following simplification:
ii) Since the \(\sigma _i\) are geodesic, we compute:

and the result follows from Theorem 5.10 (ii). \(\square \)
Finally, we will need the various twisted Ricci tensors from Theorem 4.11. For \(r=1,2,3\), we define:
and abbreviate:
Lemma 5.19
If \(\sigma \in {\mathcal {H}}_1\), then:
Proof
i) Since \(\nu _0(\sigma )\) is the identity, it follows from (5.5) and (5.10) that:

Now by (5.10) again, and (5.9), we compute:

Therefore:
ii) By Theorem 3.10:

Therefore, by Theorem 5.10 and equation (5.5):
since by (5.14) the covariant derivative of \(\sigma \) along \(\sigma ^{(1)}\) vanishes. Hence, by (5.15):

and by (5.16):

The result now follows from (i).
iii) By Theorem 3.10 and Eq. (5.17):

Therefore, by Lemma 5.18 (i) along with equations (5.5) and (5.18) we have:

Hence, by (5.15):

and by (5.16):

The result now follows from (i) and (ii). \(\square \)
Remark 5.20
It follows from Eq. (5.17) and Theorem 5.10 that the first Newton tensor \(\nu _1(\sigma )\) of \(\sigma \) is not in general solenoidal. By Eq. (5.19), Lemma 5.18 and Theorem 5.10, the same is true of \(\nu _2(\sigma )\).
Theorem 5.21
An invariant unit vector field \(\sigma \) is an r-harmonic map \(G\rightarrow UG\) if and only if \(\sigma \) is a principal direction (\(r=1,2\)), or \(\sigma \in {\mathcal {H}}_1\) (\(r=3\)).
Proof
It follows from Theorems 3.10 and 5.17, bearing in mind that \(\tau _3^v(\sigma )=0\), that \(\sigma \) is an r-harmonic map precisely when \(\sigma \in {\mathcal {H}}_1\) and \(d\pi \circ \tau _r(\sigma )=0\). By Theorem 4.11 and equations (5.17) and (5.19):

Assuming henceforward that \(\sigma \in {\mathcal {H}}_1\), it follows from Theorem 5.10, Lemma 5.18 (ii) and equation (5.14) that:

Comparing these with Lemma 5.19, \(d\pi \circ \tau _r(\sigma )\) is a multiple of \(\sigma \times \sigma ^{(1)}\), and therefore vanishes if \(\sigma \) is a principal direction. So by Theorem 5.13, it suffices to consider ideal directions \(\sigma \). Thus, \(\lambda _k=0=a_k\) for some k (Example 5.1). Assuming without loss of generality that \(k=1\), it then follows from (5.2) that:
Referring to Lemma 5.5 and equation (5.6), this yields the following simplifications:
i) \(r=1\). By Lemma 5.19 (i):
Since \(a_1=0\), it follows from (5.20) that \(\mu _2\) vanishes only when \(\sigma \) is a principal direction.
ii) \(r=2\). By Lemma 5.19 (ii):

which by (i) vanishes precisely when \(\sigma \) is a principal direction.
iii) \(r=3\). We have:

and by Lemma 5.19 (iii):
Therefore, \(d\pi \circ \tau _3(\sigma )=0\). \(\square \)
Remark 5.22
The characterisation of invariant harmonic maps \(\sigma :G\rightarrow UG\) agrees with that of [10, Thm. 5.2]. Furthermore, it was shown in [33, Proposition 3.1] and [10, Cor. 5.3] that \(\sigma \) is a minimal immersion precisely when \(\sigma \) is a harmonic unit vector field, i.e. \(\sigma \in {\mathcal {H}}_1\).
References
Baird, P., Gudmundsson, S.: \(p\)-harmonic maps and minimal submanifolds. Math. Ann. 294, 611–624 (1992)
Baird, P., Wood, J.C.: Harmonic Morphisms Between Riemannian Manifolds, LMS Monographs, vol. 29. Oxford University Press, Oxford (2003)
Branding, V., Montaldo, S., Oniciuc, C., Ratto, A.: Higher order energy functionals. Adv. Math. 370, 107236 (2020)
Eells, J., Lemaire, L.: Selected Topics in Harmonic Maps. C.B.M.S. Regional Conference Series in Mathematics, vol. 50. American Math Society, Providence, RI (1983)
Eells, J., Lemaire, L.: Another report on harmonic maps. Bull. Lond. Math. Soc. 20, 385–524 (1988)
Eells, J., Sampson, J.H.: Harmonic mappings of Riemannian manifolds. Amer. J. Math. 86, 109–160 (1964)
Fuglede, B.: Harmonic morphisms between Riemannian manifolds. Ann. Inst. Fourier Grenoble 28, 107–144 (1978)
Gillard, M., Harland, D., Speight, M.: Skyrmions with low binding energies. Nuclear Phys. B 895, 272–287 (2015)
Gil-Medrano, O.: Unit vector fields that are critical points of the volume and of the energy: characterization and examples. In: Kowalski, O., Musso, E., Perrone, D. (eds.) Complex, Contact and Symmetric Manifolds Progress in Mathematics, vol. 234. Birkhäuser, Boston (2005)
González-Davila, J.C., Vanhecke, L.: Invariant harmonic unit vector fields on Lie groups. Boll. Un. Mat. Ital. 5B, 377–403 (2002)
Hermann, R.: A sufficient condition that a mapping of Riemannian manifolds be a fibre bundle. Proc. Amer. Math. Soc. 11, 236–242 (1960)
Houghton, C., Manton, N., Sutcliffe, P.: Rational maps, monopoles and Skyrmions. Nuclear Phys. B 510, 507–537 (1998)
Ishihara, T.: Harmonic sections of tangent bundles. J. Math. Tokushima Univ. 13, 23–27 (1979)
Lemaire, L.: Applications harmoniques de surfaces Riemanniennes. J. Diff. Geom. 13, 51–78 (1978)
Meeks, W.H., Pérez, J.: Constant mean curvature surfaces in metric Lie groups. In: Pérez, J., Gálvez, J.A. (eds.) Geometric Analysis: Partial Differential Equations and Surfaces. Contemporary Mathematics, vol. 13, pp. 25–110 (2012)
Milnor, J.: Curvature of left invariant metrics on Lie groups. Adv. Math. 21, 293–329 (1976)
Misawa, M.: Regularity for the evolution of \(p\)-harmonic maps. J. Diff. Eqns. 264, 1716–1749 (2018)
Nouhaud, O.: Applications harmoniques d’une variété riemannienne dans son fibré tangent. Généralisation. C. R. Acad. Sci. Paris Sér. A-B 284, A815–A818 (1977)
O’Neill, B.: The fundamental equations of a submersion. Mich. Math. J. 13, 459–469 (1966)
Palais, R.: The principle of symmetric criticality. Comm. Math. Phys. 69, 19–30 (1979)
Ramachandran, A.: Higher power harmonic unit vector fields on 3-dimensional Lie groups. PhD thesis, University of York (2012)
Reilly, R.C.: Variational properties of functions of the mean curvatures for hypersurfaces in space forms. J. Diff. Geom. 7, 465–477 (1973)
Reilly, R.C.: On the Hessian of a function and the curvatures of its graph. Michigan Math. J. 20, 373–383 (1973)
Reilly, R.C.: Applications of the Hessian operator in a Riemannian manifold. Indiana Math. J. 26, 459–472 (1977)
Skyrme, T.H.R.: A unified field theory of mesons and baryons. Nuclear Phys. 31, 556–569 (1962)
Slobodeanu, R.: On the geometrized Skyrme and Faddeev models. J. Geom. Phys. 60, 643–660 (2010)
Slobodeanu, R.: Perfect fluids from high power sigma models. Int. J. Geom. Meth. Mod. Phys. 8, 1763–1782 (2011)
Slobodeanu, R., Svensson, M.: Skyrme-Faddeev instantons on complex surfaces. Comm. Math. Physics 335, 83–91 (2015)
Smith, R.T.: Harmonic mappings of spheres. Amer. J. Math. 97, 364–385 (1975)
Speight, J.M., Svensson, M.: On the strong coupling limit of the Faddeev–Hopf model. Comm. Math. Phys. 272, 751–773 (2007)
Speight, J.M., Svensson, M.: Some global minimizers of a symplectic Dirichlet energy. Oxford Q. J. Math. 62, 737–745 (2011)
Steenrod, N.: Topology of Fibre Bundles. Princeton Math. Series 14, Princeton Univ. Press (1951 & 1999)
Tsukuda, K., Vanhecke, L.: Invariant minimal unit vector fields on Lie groups. Period. Math. Hungar. 40, 123–133 (2000)
Vilms, J.: Totally geodesic maps. J. Diff. Geom. 4, 73–79 (1970)
van der Waerden, B.L.: Algebra, vol. 1. Springer Verlag (2003)
Wiegmink, G.: Total bending of vector fields on Riemannian manifolds. Math. Ann. 303, 325–344 (1995)
Wood, C.M.: Some energy-related functionals, and their vertical variation theory. PhD thesis, University of Warwick (1983)
Wood, C.M.: The Gauss section of a Riemannian immersion. J. Lond. Math. Soc. 33, 157–168 (1986)
Wood, C.M.: The energy of Hopf vector fields. Manuscripta Math. 101, 71–88 (2000)
Xin, Y.-L.: Some results on stable harmonic maps. Duke Math. J. 47, 609–613 (1980)
Zhang, S., et al.: Reciprocal space tomography of 3D skyrmion lattice order in a chiral magnet. Proc. Nat. Acad. Sci. 115, 6386–6391 (2018)
Acknowledgements
The authors thank the referees for their thoughtful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
In memoriam Anand.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ramachandran, A., Wood, C.M. Higher-power harmonic maps and sections. Ann Glob Anal Geom 63, 6 (2023). https://doi.org/10.1007/s10455-022-09875-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10455-022-09875-9
Keywords
- Higher-power energy
- Higher-power harmonic maps
- Minimal immersion
- r-conformal map
- Higher-power harmonic sections
- r-horizontal section
- Newton polynomials
- Newton’s identities
- Newton tensor
- Curvature of a submersion
- Twisted skyrmion
- Riemannian vector bundle
- r-parallel section
- Sphere subbundle
- Hopf map
- Three-dimensional unimodular Lie group
- Left-invariant metric
- Invariant (unit) vector field
- Milnor map
- Principal Ricci curvatures



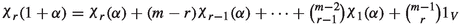 .
.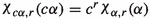 , for all
, for all 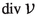 is a section of
is a section of 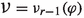 . Thus,
. Thus, 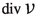 is the obstruction modulo
is the obstruction modulo 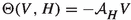 ;
;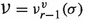 , then we have the following identity (a generalisation of Lemma
, then we have the following identity (a generalisation of Lemma 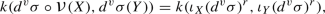
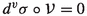 , in which case both terms of the Euler–Lagrange operator vanish.
, in which case both terms of the Euler–Lagrange operator vanish.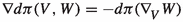 ;
;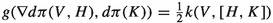 .
.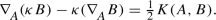
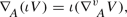
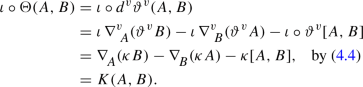
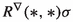 is the antisymmetrisation of the vertical second fundamental form of
is the antisymmetrisation of the vertical second fundamental form of 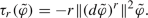
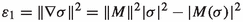 .
.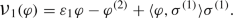
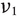 is:
is: