Escobar constants of planar domains

Abstract

We initiate the study of the higher-order Escobar constants $I_k(M)$, $k\ge 3$, on bounded planar domains M. The Escobar constants $I_k$ of the unit disk and a family of polygons are provided.

1 Introduction

Escobar [6] introduced the isoperimetric constant $I_2(M)$ of a Riemannian manifold (M, g) with non-empty boundary. In terms of this constant, he gave a lower bound for the first nonzero eigenvalue $\sigma _1$ of the Dirichlet-to-Neumann operator. Recently, this theory has been extended by Hassannezhad and Miclo [9] who introduced analogous isoperimetric constants $I_k(M)$ for any $k\in \mathbb {N}_+$ and used them to provide lower bounds on the higher-order eigenvalues $\sigma _k$ of the Dirichlet-to-Neumann operator. In what follows, we call the isoperimetric constant $I_k(M)$, where $k\in \mathbb {N}_+$, the k-th Escobar constant (of M).

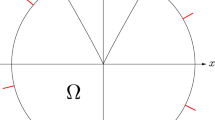
Escobar constants Let M be a Riemannian manifold with Lipschitz boundary and $\mathcal {A}(M)$ denote the family of all non-empty open subsets $\Omega$ of M with piecewise smooth (or more generally rectifiable) boundary $\partial \Omega$, i.e.,

$$\begin{aligned} \mathcal {A}(M)=\{\Omega \subset M\,|\,\Omega \ne \emptyset , \partial \Omega \,\,\text{ piecewise } \text{ smooth }\}. \end{aligned}$$

We use $\mathcal {A}$ instead of $\mathcal {A}(M)$ when there is no possibility of confusion. For $\Omega \in \mathcal {A}$, we write the boundary of $\Omega$ as $\partial \Omega =\partial _I\Omega \cup \partial _E\Omega ,$ where

$$\begin{aligned} \partial _I\Omega :=\partial \Omega \cap M\quad \text{ and }\quad \partial _E\Omega :=\partial \Omega \cap \partial M \end{aligned}$$

are the so-called interior boundary and exterior boundary of $\Omega$, respectively (Fig. 1).

Fig. 1

Setting

For $\Omega \in \mathcal {A}$ let $\eta^{\partial} (\Omega )$ be the isoperimetric ratio given by

$$\begin{aligned} \eta^{\partial} (\Omega ):= \frac{|\partial \Omega \cap M|}{|\partial \Omega \cap \partial M|}= \frac{|\partial _I\Omega |}{|\partial _E\Omega |}, \end{aligned}$$

where $|\cdot |$ denotes the Riemannian volume of the set. By convention, when $\partial _E\Omega =\emptyset$ then $\eta^{\partial} (\Omega )=\infty$. For any $k\in \mathbb {N}$, we introduce the k-th Escobar constant as

$$\begin{aligned} I_k(M)\ :=\ \inf _{(\Omega _1,\ldots ,\Omega _k)\in \mathcal {A}_k}\max _j\eta^{\partial} (\Omega _j).\end{aligned}$$

Here, $\mathcal {A}_k=\mathcal {A}_k(M)$ is the family of all mutually disjoint k-tuples $(\Omega _1,\ldots ,\Omega _k)$ such that ${\emptyset \ne }\Omega _j\in \mathcal {A}$, $j=1,\ldots ,k$. The k-th Escobar constant $I_k(M)$ is a scaling invariant quantity.

It is easy to check that the definition of $I_2(M)$ does not change if we assume that $(\Omega _1,\Omega _2)\in \mathcal {A}_2$ is a partition of M instead of just a disjoint 2-tuple. Hence, the definition for $I_2$ given here coincides with the definition given by Escobar [6]. It also has a functional characterization:

$$\begin{aligned} I_2(M)=\inf _{f\in H^1( M)}\frac{\int _M|\nabla f|}{\int _{\partial M} |f-f_\mathrm{med}|}, \end{aligned}$$

where $f_\mathrm{med}$ is the median of f on $\partial M$:

$$\begin{aligned} f_\mathrm{med}:=\sup \left\{ t\in \mathbb {R}: \mathcal {H}^{n-1}\{x\in \partial M: f(x)> t\}|> |\partial M|/2\right\} . \end{aligned}$$

Here, $\mathcal {H}^{n-1}(\cdot )$ denotes the $(n-1)$-Hausdorff measure of the set. In other words, $I_2(M)$ gives the geometric description of the optimal constant C in the Poincaré trace inequality

$$\begin{aligned}\parallel f-f_\mathrm{med}\parallel _{L^{1}(\partial M)}\le C^{-1} \parallel \nabla f\parallel _{L^1(M)}.\end{aligned}$$

See [5, 6] for more details. However, there is no interpretation for $I_k$, $k\ge 3$, as the optimal constant of some functional inequalities.

The k-th Escobar constant together with another isoperimetric ratio closely related to the k-th Cheeger constant $h_k$ appear in lower bounds for the k-th Steklov eigenvalues [9]. This has been the primary motivation for the definition of $I_2(M)$ in [6, 7] (see also [11] for a closely related isoperimetric constant) and $I_k(M)$, $k\ge 3$ in [9]. The k-th Cheeger constant is given by

$$\begin{aligned} h_k(M)\ :=\ \inf _{(\Omega _1,\ldots ,\Omega _k)\in \mathcal {A}_k}\max _j \eta (\Omega _j),\end{aligned}$$

where

$$\begin{aligned} \eta (\Omega ):= \frac{|\partial \Omega \cap M|}{| \Omega |}=\frac{|\partial _I\Omega |}{| \Omega |}.\end{aligned}$$

The main motivation for the study of the higher Cheeger constants stems from the fact that they are used for bounding eigenvalues of the Laplace operator.¹ This relationship has been intensively studied in the literature, see [4, 14, 15] and the references therein.

We now restrict to planar domains. The study of the higher-orders Escobar constants is a largely unexplored field. In this paper, we establish fundamental properties of the Escobar constants of planar domains. More precisely, the aim of this manuscript is to investigate the relation between $I_k(M)$, $k\ge 3$, and the geometry of a planar domain M. We are in particular interested in the behavior of $I_k(M)$ for k large and the configuration of optimal k-tuples. This may share some similarities with the study of optimal Cheeger clusters, see [1, 2, 12] and reference therein for more details. A quantity similar to the second Escobar constant $I_2(M)$ also appears in the study of longtime existence result for the curve shortening flow [8, 10].

Main results Escobar [7] and Kusner–Sullivan [13] independently proved that the unit disk maximizes $I_2$ among all bounded domains M in $\mathbb {R}^2$ with rectifiable boundary, i.e.,

$$\begin{aligned} I_2(M)\le I_2(\mathbb {D}).\end{aligned}$$

(1.1)

It also holds in higher dimensions. For the discussion on the higher dimensional version of this inequality we refer to [5].

We conjecture that this inequality also holds for higher Escobar constants.

Conjecture 1

Let $M\subset \mathbb {R}^2$ be bounded domain with rectifiable boundary then for every $k\ge 3$

$$\begin{aligned} I_k(M)\le I_k(\mathbb {D}). \end{aligned}$$

(1.2)

We prove this conjecture for M being a polygon in $\mathbb {R}^2$ and k being greater or equal than the number of vertices of M. Further, we provide a similar result for a family of curvilinear polygons. The general case, however, remains open.

In order to prove inequality (1.2) for polygons in $\mathbb {R}^2$ and curvilinear polygons, respectively, we first provide the value of $I_k(\mathbb {D})$.

Theorem 1.3

(Disks) The k-th Escobar constant of the unit disk $\mathbb {D}\subset \mathbb {R}^2$ centered at the origin is given by

$$\begin{aligned} I_k(\mathbb {D})=\frac{\sin (\pi /k)}{\pi /k}, \end{aligned}$$

where $k\in \mathbb {N}$.

Then we can prove inequality (1.2) for a regular n-polygon M in $\mathbb {R}^2$ when k is either greater than or equal to the number of vertices of M, or k is a divisor of n.

Theorem 1.4

(Regular polygons) Let $n\ge 3$. The regular n-gon $D_n$ satisfies

• (i) the identity

  $$\begin{aligned} I_k(D_n)= \cos \left( \pi /n\right) \le I_k(\mathbb {D}), \end{aligned}$$

  for all $k\ge n$;

• (ii) and

  $$\begin{aligned} I_k(D_n)=\sin (\pi /k)\cot (\pi /n)k/n\le I_k(\mathbb {D}), \end{aligned}$$

  if $n=m k$, where $m\in \mathbb {N}$.

The main idea for the proof of (i) is that the domains $\Omega _j$ of the k-tuples concentrate at the vertices of $D_n$—also see Fig. 3. Subsequently we provide the inequality (1.2) for some cases with $k<n$ and M being a regular n-gon.

Afterward, we address the above conjecture for Euclidean n-gon.

Theorem 1.5

(Euclidean n-gon) Let M be a Euclidean n-gon and assume that the interior angles of M are ordered as follows

$$\begin{aligned} 0<\theta _1\le \theta _2\le \cdots \le \theta _n<2\pi . \end{aligned}$$

Then we have

$$\begin{aligned} I_k(M)\le \sin (\theta _1/2)\le \cos \left( \pi /n\right) ,\qquad \text{ for } \text{ all }\,\,\,\, k\ge 3. \end{aligned}$$

In particular, we have

$$\begin{aligned} I_k(M)\le I_k(\mathbb {D}) \end{aligned}$$

when either $k\ge n$ or $n\le 4$.

The proof is a modification of the proof for Theorem 1.4. However, as an additional obstacle we no longer have control over the lengths of the edges of the polygons. We also prove that we have equality $I_k(M)=\sin (\theta _1/2)$ if k is ‘sufficiently large’.

Finally, we generalize these considerations to curvilinear polygons. This is done by adapting the proof of Theorem 1.5 in order to find a suitable family of k-tuples near the vertix with smallest angle.

Theorem 1.6

(Curvilinear Polygons) Let $M\subset \mathbb {R}^2$ be a curvilinear n-gon with at least one interior angle $<\pi$. Order the interior angles of M in an increasing order

$$\begin{aligned} 0<\theta _1\le \theta _2\le \cdots \le \theta _n<2\pi . \end{aligned}$$

Then we have the inequality

$$\begin{aligned} I_k(M)\le \sin (\theta _1/2), \end{aligned}$$

for all $k\ge 3$.

2 Elementary properties of the Escobar constants

In this section we collect elementary properties of the Escobar constants $I_k(M)$, where M is a bounded domain of $\mathbb {R}^2$ with piecewise smooth boundary $\partial M$.

First we show that the Escobar constants $I_k(M)$ are bounded from above by 1. For $k=2$ this result has already been stated in [7] in a more general setting.

Lemma 2.1

For a bounded domain M of $\mathbb {R}^2$ with piecewise smooth boundary $\partial M$, we have

$$\begin{aligned} I_k(M)\le 1 \end{aligned}$$

for any $k\in \mathbb {N}_+$.

Proof

Since $I_1(M)=0$, below we consider $I_k(M)$ for $k\ge 2$ only. Indeed, take a connected smooth arc U of $\partial M$ with length $|U|=\ell$. Consider k disjoint connected arcs $B_i\subset U$, $i=1,\ldots ,k$, each of length smaller than $\ell /k$, i.e., $|B_i|<\ell /k$. Define

$$\begin{aligned} F:U\times [0,\epsilon ] \rightarrow M, (p,t)\mapsto p-t\nu , \end{aligned}$$

where $\nu$ is the unit outward normal direction along $\partial M$ and $\epsilon$ is chosen small enough so that $F(\cdot ,t)$ is a diffeomorphism for any $t\in [0,\epsilon ]$. Then we can consider $(\Omega _1^\epsilon ,\ldots , \Omega _k^\epsilon )\in \mathcal {A}_k$, where $\Omega _i^\epsilon =F(B_i\times (0,\epsilon ))$. Thus, we have $I_k(M)\le {\max _j\eta^{\partial} (\Omega _i^\epsilon )\rightarrow 1}$ when $\epsilon$ tends to 0. $\square$

Remark 2.2

There is however no universal, positive lower bound on the Escobar constants. Indeed, let

$$\begin{aligned} M_\epsilon =[-\epsilon ,\epsilon ]\times [-1/2,k+1/2] \end{aligned}$$

be a thin rectangle and

$$\begin{aligned} \Omega _i=(-\epsilon ,\epsilon )\times (i-1,i), \end{aligned}$$

$i\in \{1,\ldots k\}$ rectangles therein. Then $\eta^{\partial} (\Omega _i)=2\epsilon$. Therefore, $I_k(M_\epsilon )$ goes to 0 as $\epsilon \rightarrow 0$.

Next we prove that the Escobar constants $I_k(M)$ are increasing in k.

Lemma 2.3

For a bounded domain M of $\mathbb {R}^2$ with piecewise smooth boundary $\partial M$, the Escobar constants are increasing in k, i.e., we have

$$\begin{aligned} I_{k+1}(M)\ge I_k(M) \end{aligned}$$

for all $k\in \mathbb {N}_+$.

Proof

By definition of $I_{k_0+1}(M)$, there exists a sequence $\{(\Omega _1^i,\ldots ,\Omega _{k_0+1}^i)\}_{i\in \mathbb {N}}$ in $\mathcal {A}_{k_0+1}$ satisfying

$$\begin{aligned} I_{k_0+1}(M)=\lim _{i\rightarrow \infty } \max _{1\le j\le k_0+1}\eta^{\partial} (\Omega _j^i). \end{aligned}$$

Associate to each element $(\Omega _1^i,\ldots , \Omega _{k_0+1}^i)\in \mathcal {A}_{k_0+1}$ an element $(\tilde{\Omega }_1^i,\ldots , \tilde{\Omega }_{k_0}^i)\in \mathcal {A}_{k_0}$ by erasing exactly one $\Omega _l^i$ in $(\Omega _1^i,\ldots , \Omega _{k_0+1}^i)$ which attains the minimum $\min _{1\le j\le k_0+1}\eta^{\partial} (\Omega _j^i)$. If the minimum is attained by several elements, erase the $\Omega _l^i$ with the smallest index l. By construction we have

$$\begin{aligned} I_{k_0}(M)\le \lim _{i\rightarrow \infty }\max _{1\le j\le k_0}\eta^{\partial} (\tilde{\Omega _j^i})=\lim _{i\rightarrow \infty }\max _{1\le j\le k_0+1}\eta^{\partial} (\Omega _j^i)=I_{k_0+1}(M), \end{aligned}$$

which proves the statement. $\square$

3 Bounds on the Escobar constants of planar domains

In this section we prove the main results, Theorems 1.3–1.6.

3.1 Escobar constants $I_k$ for disks

We start by providing $I_k(\mathbb {D})$, i.e., by proving Theorem 1.3. Note that since $I_k(M)$, $M\subset \mathbb {R}^2$, is invariant under scaling and translation of M, this theorem also gives $I_k$ for disks in $\mathbb {R}^2$. For $k=2$, this result was proven by Escobar [7].

Proof

It is easy to show that

$$\begin{aligned} I_k(\mathbb {D})\le \sin (\pi /k)/(\pi /k). \end{aligned}$$

(3.1)

Indeed, let $z_j=e^{i(j-1)\frac{2\pi }{k}}$, $1\le j\le k$ on $\mathbb {S}^1=\partial \mathbb {D}$. Then the k-tuple constituted by the k domains enclosed by the arcs and the corresponding segments $\overline{z_jz_{j+1}}$, $1\le j\le k$, consists of k isometric domains $\mathcal {D}$. Since $\eta^{\partial} (\mathcal {D})=\frac{\sin (\pi /k)}{\pi /k}$, this establishes inequality (3.1).

We now prove that equality holds in (3.1).

Let ${\tilde{\mathcal {A}}}_k(\mathbb {D})$ be the collection of all $(\Omega _1,\ldots ,\Omega _k)\in \mathcal {A}_k(\mathbb {D})$ satisfying

• (1) $\eta^{\partial} (\Omega _j)\le \frac{\sin (\pi /k)}{\pi /k}$ for each $1\le j\le k$,

• (2) each $\Omega _j$ is connected, and

• (3) the interior boundary of each $\Omega _j$ consists of a disjoint union of straight segments.

We first show that

$$\begin{aligned} I_k(\mathbb {D})\ =\ \inf _{(\Omega _1,\ldots ,\Omega _k)\in {\tilde{\mathcal {A}}}_k(\mathbb {D})}\max _j\eta^{\partial} (\Omega _j).\end{aligned}$$

(3.2)

Assume that $\Omega _j$, for a $j\in \{1,\dots ,n\}$, consists of two connected components $C_1$ and $C_2$. If

$$\begin{aligned} \frac{|\partial _IC_1|}{|\partial _EC_1|}=\frac{| \partial _IC_2|}{|\partial _EC_2|}, \end{aligned}$$

we substitute $\Omega _j$ by $C_1$, i.e., by a connected set. Clearly, this substitution leaves $\max _j\eta^{\partial} (\Omega _j)$ invariant. Therefore, let us assume that w.l.o.g. we have

$$\begin{aligned} \frac{|\partial _IC_1|}{|\partial _EC_1|}<\frac{| \partial _IC_2|}{|\partial _EC_2|}. \end{aligned}$$

Since $a/b<c/d$ implies $a/b<(a+b)/(c+d)<c/d$ for $a,b,c,d\in \mathbb {R}_+$, we can substitute $\Omega _j$ by $C_1$. This substitution decreases $\max _j\eta^{\partial} (\Omega _j)$, what is permitted since in the definition of the Escobar constant the infimum is taken over all admissible k-tuples.

If $\Omega _j$ consists of more than two components, the same argument allows us to substitute $\Omega _j$ by its connected component $C_i$ with smallest fraction $\frac{|\partial _IC_i|}{|\partial _EC_i|}$.

Now, assume that the interior boundary of a domain $\Omega _j$ is not a straight line. Then

$$\begin{aligned} \eta^{\partial} (\Omega _j) \ge \eta^{\partial} ({\tilde{\Omega }}_j)\end{aligned}$$

(3.3)

where ${\tilde{\Omega }}_j$ has the same exterior boundary as $\Omega _j$ but its interior boundary consists of disjoint straight lines connecting the corresponding endpoints on $\partial _E\Omega _j$. By the same argument as in the previous paragraph, we can simultaneously substitute all $\Omega _j$ whose interior boundary does not consist of union of straight lines with ${\tilde{\Omega }}_j$. The new collection belongs to $\tilde{\mathcal {A}}_k(\mathbb {D})$ and inequality (3.3) shows that $\max _j\eta^{\partial} (\Omega _j)$ can decrease with this procedure. The discussion above proves (3.2).

For $\Omega \in \tilde{\mathcal {A}}(\mathbb {D})={\tilde{\mathcal {A}}}_1(\mathbb {D})$, we say that $\Omega$ is of type n when $\partial _E\Omega$ has n connected components.

Let us first assume that $\Omega _j$ is of type 1. Then

$$\begin{aligned} \eta^{\partial} (\Omega _j)=\frac{2\sin (\alpha _j/2)}{\alpha _j}, \end{aligned}$$

where $\alpha _j= |\partial _E\Omega _j|$. Assume $\alpha _j\le \pi$ and note that the function $f:\mathbb {R}_+\rightarrow \mathbb {R}$ given by

$$\begin{aligned} f(\alpha )=\frac{2\sin (\alpha /2)}{\alpha } \end{aligned}$$

is decreasing on $(0,\pi )$. Since assumption (1) can be written as

$$\begin{aligned} f(\alpha _j)=\eta^{\partial} (\Omega _j)\le f(2\pi /k), \end{aligned}$$

it implies $\alpha _j\ge \frac{2\pi }{k}$ for $\alpha _j\in (0,\pi )$.

If $\alpha _j=|\partial _E\Omega _j|\ge \pi$, then $\eta^{\partial} (\Omega _j)=\frac{2\pi -\alpha _j}{\alpha _j}f(2\pi -\alpha _j)\le f(2\pi /k)$.

If $\Omega _j$ is of type n, $n\ge 2$, then each connected component of $\mathbb {S}^1{\setminus }\partial _E\Omega _j$ should contain the exterior boundary of at least one $\Omega _t$ for some $t\ne j$. Otherwise, we can add this arc to the exterior boundary of $\Omega _j$ and remove the corresponding segment in the interior boundary, see Fig. 2. This decreases $\eta^{\partial} (\Omega _j)$.

Fig. 2

This example shows how one can replace type 2 domains by type 1 domains and decrease $\eta^{\partial} (\Omega _j),\,j=1,2$

We now consider the following cases:

Case 1. All $\Omega _j$, $1\le j\le k$, are of type 1. Then $\alpha _j= |\partial _E\Omega _j|\ge \frac{2\pi }{k}$. Since $\sum _{j=1}^k\alpha _j\le 2\pi$, the only possible situation is that the domains $\Omega _j$ are all isometric to $\mathcal {D}$.

Case 2. There exists at least one $j\in \{1,\dots ,k\}$ such that $\Omega _j$ is of type $n\ge 2$. We claim that each connected component of $\mathbb {S}^1{\setminus }\partial _E\Omega _j$ contains the boundary of a type 1 domain $\Omega _k$. Indeed, if a connected component of $\mathbb {S}^1{\setminus }\partial _E\Omega _j$ contains the boundary of only one element in the k-tuple, then it is clear that this element is of type 1. By induction, it is easy to show that if it contains the exterior boundary of more than one element, then at least one of them is of type 1 or can be substituted by an element of type 1. This substitution is possible for the same reason discussed above and depicted in Fig. 2. Hence, we get that

$$\begin{aligned} |\partial _I\Omega _j|\ge 2\sin (\alpha _1/2)+\dots 2\sin (\alpha _n/2)\ge 2n\sin (\pi /k). \end{aligned}$$

Here $\alpha _i$, $i\in \{1,\dots , n\}$, denote the centric angles of the connected components of $\partial _I\Omega _j$. Since $\eta^{\partial} (\Omega _j)\le f(2\pi /k)$ by assumption (1), we have $|\partial _E\Omega _j|\ge n\frac{2\pi }{k}$. On the other hand we have $\sum _{j=1}^k|\partial _E\Omega _j|\le 2\pi$. Therefore, it is impossible to have any type except type 1 domains if we want to decrease the value of $\eta^{\partial} (\cdot )$. Hence, only case 1 gives us an optimal k-tuple. This completes the proof. $\square$

3.2 Escobar constants $I_k$ for regular n-gon and $k\ge n$

In this subsection, we will prove Theorem 1.4. For the considerations below, it is convenient to introduce the following notations: let $\mathcal {K}_n$ denote the set of all convex polygons with n vertices. For $K\in \mathcal {K}_n$, let ${\tilde{\mathcal {A}}}_k(K)$ denote the collection of all k-tuple $(\Omega _1,\ldots ,\Omega _k)\in \mathcal {A}_k(K)$ such that

• (1) each $\Omega _j$ is connected, and

• (2) the closure of each $\partial _I\Omega _j$ made of disjoint union of straight segments.

We say that a domain $\Omega \in \tilde{\mathcal {A}}(K):=\tilde{\mathcal {A}}_1(K)$ is of type $\ell$, if $\partial _E\Omega$ has components in exactly $\ell$ edges of K.

Lemma 3.4

Let $K\in \mathcal {K}_n$ . Then there are at most $n-2$ domains $\Omega _j\in \tilde{\mathcal {A}}(K)$ which are of type $\ell$ with $\ell \ge 3$ and $(\Omega _1,\dots ,\Omega _{n-2})\in {\tilde{\mathcal {A}}}_{n-2}(K).$

Proof

We prove the claim by induction. Let $n=3$, i.e., $K\in \mathcal {K}_3$. Assume that there exists a domain $\Omega _1\in \tilde{\mathcal {A}}(K)$ of type 3. Then $K{\setminus }\Omega _1$ consists of connected sets which contain components of at most two edges of K. Hence, there can be no other domain of type greater or equal than three. This settles the induction beginning.

We now assume that the claim holds true for all $n\le n_0$, where $n_0$ is some integer with $n_0\ge 3$. Consider a set $K\in \mathcal {K}_{n_0+1}$ and suppose that there are at least $n_0$ domains $\Omega _j\in \tilde{\mathcal {A}}(K)$ of type at least three. Then there exists a $\Omega _{j_0}$, such that one connected component of $K{\setminus }\Omega _{j_0}$ contains all the remaining $\Omega _j$ of type greater or equal than three. This is indeed the case:

Consider a fixed $\Omega _{k_1}$ of type greater or equal than three and denote the connected components of $K{\setminus }\Omega _{k_1}$ by $C^1_{1},\dots ,C^1_{m_1}$. If one of these connected components contains all the remaining $\Omega _j$ of type equal to or greater than three, the claim follows. Otherwise there exists at least two $C^1_i$ which contain sets of such types. W.l.o.g. we assume this to be the sets $C^1_1$ and $C^1_2$. Let $\Omega _{k_2}\in C^1_1$ and denote the connected components of $C^1_1{\setminus }\Omega _{k_2}$ by $C^2_{1},\dots ,C^2_{m_2}$. If one of these connected components contains all the remaining $\Omega _j$ of type equal to or greater than three, the claim follows. Otherwise we repeat this process finitely many times to find $\Omega _{j_0}$.

Due to the existence of $\Omega _{j_0}$, there exists an edge which is disjoint from the remaining $\Omega _j$. We now collapse this edge to one point. Note that this neither changes the number of the remaining $\Omega _j$ of type greater or equal than three nor does this procedure change their type. Furthermore, $\Omega _j$ stay disjoint. Hence, this process leaves us with a set in $\mathcal {K}_{n_0}$ which has at least $n_0-1$ domains $\Omega _j$ of type at least three. This, however, yields a contradiction to the induction assumption and hence the claim is established. $\square$

We now prove Theorem 1.4, i.e., we provide $I_k$ for regular n-gons with $n\ge 3$, which will henceforth be denoted by $D_n$. Since the Escobar constants $I_k(D_n)$ are invariant under translation and scaling of $D_n$, we assume w.l.o.g. that $D_n$ is centered at the origin and its vertices lie on the unit circle.

Proof of Theorem 1.4

We start by proving (i). We first prove the inequality

$$\begin{aligned} I_k(D_n)\le \cos \left( \pi /n\right) . \end{aligned}$$

(3.5)

It is sufficient to construct a k-tuple $(\Omega _1,\ldots ,\Omega _k)\in \mathcal {A}_k(D_n)$ such that $\max \eta ^{\partial }(\Omega _j)\le \cos \left( \pi /n\right) .$ Recall that for a regular convex n-gon, each interior angle is given by $\theta =\pi -2\pi /n$. Near a fixed corner of $D_n$, consider the k-tuple $(\Omega _1,\ldots ,\Omega _k)$ depicted in Figure 3, where

$$\begin{aligned} \delta _j=\epsilon ^{-\frac{1}{k-j+1}}. \end{aligned}$$

Fig. 3

k-Tuple concentrating at a corner

A straightforward calculation yields

$$\begin{aligned} \eta^{\partial} (\Omega _1)=\sin (\theta /2),\quad \text {and}\quad \eta^{\partial} (\Omega _j)=\frac{\delta _{j-1}+2\left( 1+\delta _1+\ldots +\delta _{j-2}\right) }{\delta _{j-1}}\sin (\theta /2). \end{aligned}$$

Consequently, for $j=2,\dots ,k$, we have

$$\begin{aligned} \eta^{\partial} (\Omega _1)<\eta^{\partial} (\Omega _j)\end{aligned}$$

(3.6)

and

$$\begin{aligned} \eta^{\partial} (\Omega _j)=\sin (\theta /2)+O(\epsilon ^{\frac{1}{(k-j+3)(k-j+2)}}).\end{aligned}$$

(3.7)

This entails that

$$\begin{aligned} I_k(D_n)\le \max _{j=2,\dots ,k}\eta^{\partial} (\Omega _j)\le \sin (\theta /2)+C \epsilon ^{\frac{1}{k(k+1)}}=\cos (\pi /n)+C \epsilon ^{\frac{1}{k(k+1)}}, \end{aligned}$$

which establishes the claimed inequality by the arbitrariness of $\epsilon$.

Next, we show the reverse inequality, i.e.,

$$\begin{aligned} I_k(D_n)\ge \cos (\pi /n). \end{aligned}$$

(3.8)

Let ${\tilde{\mathcal {A}}}_k(D_n)$ denote the collection of all k-tuple $(\Omega _1,\ldots ,\Omega _k)\in \mathcal {A}_k(D_n)$ such that

• (1) $\eta^{\partial} (\Omega _j)<1,~1\le j\le k,$

• (2) each $\Omega _j$ is connected, and

• (3) the closure of each $\partial _I\Omega _j$ consist of disjoint union of straight segments. In particular, any two connected component of $\partial _I\Omega _j$ have no intersection on $\partial D_n$.

With a similar argument as in the proof of Theorem 1.3, we show that

$$\begin{aligned} I_k(D_n)=\ \inf _{(\Omega _1,\ldots ,\Omega _k)\in {\tilde{\mathcal {A}}}_k(D_n)}\max _j\eta^{\partial} (\Omega _j). \end{aligned}$$

(3.9)

Having inequality (3.5), w.l.o.g we can assume that all $\Omega _j$ satisfy (1).

By a verbatim argument as on page 6, we can assume that each $\Omega _j$ is connected. Assume that the interior boundary of some of $\Omega _j$ is not a collection of disjoint straight segments with endpoints on the boundary of $D_n$. We show that we can replace $(\Omega _1,\ldots ,\Omega _k)$ with a new collection $({\tilde{\Omega }}_1,\ldots ,{\tilde{\Omega }}_k)\in {\tilde{\mathcal {A}}}_k(D_n)$ such that $\max _j\eta^{\partial} (\Omega _j)\ge \max _j\eta^{\partial} ({\tilde{\Omega }}_j)$. We consider two cases: Case 1.  The two endpoints of each connected component of $\partial _I\Omega _j$, $1\le j\le k$, belong to distinct edges of $D_n$. Then we can simultaneously substitute all $\Omega _j$ by ${\tilde{\Omega }}_j$ whose interior boundary consists of disjoint union of straight segments. Clearly $({\tilde{\Omega }}_1,\ldots ,{\tilde{\Omega }}_k)\in {\tilde{\mathcal {A}}}_k(D_n)$ and as explained on page 6, we have $\eta^{\partial} (\Omega _j) \ge \eta^{\partial} ({\tilde{\Omega }}_j)$.

Fig. 4

Domains in a do not satisfy property (1). The domain on the left in b can be replace by a new domain (the domain on the right) such that each component of the interior boundary has endpoints on distinct edges

Case 2.  Some of the connected components of $\partial _I\Omega _j$ have two endpoints on the same edge of $D_n$. We can immediately rule out the situation when $\partial _E\Omega _j$ only consists of one or two connected components with all endpoints on the same edge, see Fig. 4a. Because in this case $\eta^{\partial} (\Omega _j)>1$. Hence, since we have more than one domain in the collection, at least one of the components of $\partial _I\Omega _j$ has endpoints on two distinct edges. For each $\Omega _j$, we can remove those boundary components whose endpoints are on the same edge and get a new collection of domains in $\mathcal {A}_k(D_n)$ which satisfies the assumption of Case 1, see Fig. 4b. This process increases the length of the exterior boundary and decreases the length of the interior boundary of each $\Omega _j$. Now we do the same procedure as in Case 1 to get a new collection $({\tilde{\Omega }}_1,\ldots ,{\tilde{\Omega }}_k)\in {\tilde{\mathcal {A}}}_k(D_n)$ satisfying $\eta^{\partial} (\Omega _j) \ge \eta^{\partial} ({\tilde{\Omega }}_j)$. Therefore, we have identity (3.9).

To prove inequality (3.8), we show that any k-tuple $(\Omega _1,\ldots ,\Omega _k)\in {\tilde{\mathcal {A}}}_k(D_n)$ contains an element $\Omega _j$ such that $\eta ^{\partial }(\Omega _j)\ge \cos (\pi /n)$.

For the considerations below, it is convenient to introduce the following notation: we say that a domain $\Omega \subset D_n$ is of type $\ell$, if $\partial _E\Omega$ has components in exactly $\ell$ edges of $D_n$. Notice that each $\Omega \in {\tilde{\mathcal {A}}}(D_n):={\tilde{\mathcal {A}}}_1(D_n)$ is of type $\ell \ge 2$.

Lemma 3.4 implies that there are at most $n-2$ disjoint domains $\Omega _j$ which are of type $\ell$ with $\ell \ge 3$.

Consequently, any k-tuple $(\Omega _1,\ldots ,\Omega _k)\in {\tilde{\mathcal {A}}}_k(D_n)$ with $k\ge n$, has at least two elements of type 2. Assume w.l.o.g. that $\Omega _1$ is of type 2. If the boundary components of $\Omega _1$ lie on edges which are not adjacent (it can be only the case when $n\ge 4$), then we have $\eta ^{\partial }(\Omega _1)\ge 1$—compare Fig. 5.

Fig. 5

Type 2 domain in $D_5$ with non-adjacent edges

Thus, we assume w.l.o.g. that the boundary components of $\Omega _1$ lie on adjacent edges $e_1$ and $e_2$. Denote the corner which is the intersection point of the edges $e_1$ and $e_2$ by C. There are now two possible cases: either $C\in \partial _E\Omega _1$ or $C\notin \partial _E\Omega _1$—compare Fig. 6.

Fig. 6

C covered by a triangle—C not covered at all

If $C\notin \partial _E\Omega _1$ then there exists a domain $\Omega _j$ of the k-tuple $(\Omega _1,\ldots ,\Omega _k)$ which is of type 2 and closest to C. Notice that $\Omega _j$ can be equal to $\Omega _1$. Let T be the triangle which covers C and two of its edges are subset of $e_1$ and $e_2$ and the third one is subset of $\partial _I\Omega _j$. We can then substitute $\Omega _j$ by the union of $\Omega _j$ and T since $\eta ^{\partial }(\Omega _j)\ge \eta ^{\partial }(\Omega _j\cup T)$ by construction. Note that $\Omega _j\cup T$ is a triangle covering the corner C. An elementary calculation shows $\eta ^{\partial }(\Omega _j\cup T)$ attains its minimum $\cos (\pi /n)$ when $\Omega _j\cup T$ is an isosceles triangle. We conclude that for any given k-tuple $(\Omega _1,\ldots ,\Omega _k)\in {\tilde{\mathcal {A}}}_k(D_n)$, we have

$$\begin{aligned} \max _j\eta^{\partial} (\Omega _j)\ge \cos (\pi /n). \end{aligned}$$

This establishes inequality (3.8).

To complete the proof of (i), we are left with proving the inequality

$$\begin{aligned} \cos \left( \pi /n\right) \le I_k(\mathbb {D})=\sin (\pi /k)k/\pi \end{aligned}$$

(3.10)

for all $k\ge n$. For this purpose, we introduce the function

$$\begin{aligned} f:\mathbb {R}^{+}\rightarrow \mathbb {R},\qquad x\mapsto \sin (\pi /x)/(\pi /x), \end{aligned}$$

which satisfies $f(k)=I_k(\mathbb {D})$ for $k\in \mathbb {N}$. Since f is strictly increasing it is sufficient to prove the inequality (3.10) for $k=n$. This is however equivalent to the inequality $\tan (\pi /n)\ge \pi /n$ which clearly holds for all $n\ge 3$. Thus, (i) is established.

We now turn to the proof of (ii) and start by showing the inequality

$$\begin{aligned} I_k(D_n)\le \sin (\pi /k)\cot (\pi /n)k/n. \end{aligned}$$

(3.11)

It is sufficient to construct a k-tuple $(\Omega _1,\ldots ,\Omega _k)\in {\tilde{\mathcal {A}}}_k(D_n)$ such that the inequality $\max \eta ^{\partial }(\Omega _j)\le \sin (\pi /k)\cot (\pi /n)k/n$ is satisfied. We inscribe a regular k-gon into the n-gon as follows: consider the midpoints of the edges of the n-gon. The vertices of the k-gon are given by taking every m-th of the midpoints. Recall that $n=mk$ by the assumption. The k-gon hence divides $D_n$ into $k+1$ domains. Those of these domains which cover the corners of $D_n$ yield a k-tuple ${(\Omega _1,\dots ,\Omega _k)}\in \mathcal {A}_k(D_n)$. See Fig. 7 in which the situation is demonstrated for $n=6$ and $k=3$.

Fig. 7

k-Tuple for $n=6$ and $k=3$

All $\Omega _j$ are congruent to a domain which we denote by ${\tilde{\Omega }}$. The exterior boundary of ${\tilde{\Omega }}$ is given by m times the length of one side of the n-gon $D_n$. Straightforward elementary calculations yield

$$\begin{aligned} {|\partial _E{\tilde{\Omega }}|}=2{m}\sin (\pi /n)\qquad \text{ and }\qquad |{\partial _E{\tilde{\Omega }}}|=2\cos (\pi /n)\sin (\pi /k). \end{aligned}$$

Therefore,

$$\begin{aligned} { \eta^{\partial} (\Omega _j)=\eta^{\partial} ({\tilde{\Omega }})}=\sin (\pi /k)\cot (\pi /n)k/n \end{aligned}$$

(3.12)

and it proves (3.11). We are thus finally left with proving $\sin (\pi /k)\cot (\pi /n)k/n\le I_k(\mathbb {D})$. This is an immediate consequence of $\cot (\pi /n)\pi /n\le 1$ and Theorem 1.3.

We now prove the equality case. Let $(\Omega _1,\ldots ,\Omega _k)$ be a k-tuple in ${\tilde{\mathcal {A}}}_k(D_n)$ such that

$$\begin{aligned} \max _j\eta ^{\partial }(\Omega _j)\le \sin (\pi /k)\cot (\pi /n)k/n.\end{aligned}$$

(3.13)

W.l.o.g. we assume that all vertices are covered. We consider two cases.

Case 1.  Assume that for every $j\in \{1,\ldots ,k\}$, the exterior boundary $\partial _E\Omega _j$ is connected. Then there exists at least one j such that $\frac{|\partial D_n|}{n}\le |\partial _E\Omega _j|\le |\partial D_n|/k=|\partial _E{\tilde{\Omega }}|$. By Proposition 3.22, and inequalities (3.19) and (3.20) in Appendix, we get $\eta^{\partial} (\Omega _j)\ge \sin (\pi /k)\cot (\pi /n)k/n$. Hence, we have equality in (3.13).

Case 2.  Assume that there is at least one $j_0$ for which $\partial _E\Omega _{j_0}$ is not connected. By assumption, all vertices are covered. Hence, in each connected component of $D_n{\setminus }\Omega _{j_0}$, there is at least one domain $\Omega _j$ with connected $\partial _E\Omega _j$. If $|\partial _E\Omega _j|\le |\partial _E{\tilde{\Omega }}|$ for some $\Omega _j$, we repeat the same argument as in Case 1. Let us assume that for all $\Omega _j$ with connected exterior boundary, $|\partial _E\Omega _j|>|\partial _E{\tilde{\Omega }}|$. We claim that the length of each connected component of $\partial _I\Omega _{j_0}$is bounded below by $2\cos (\pi /n)\sin (\pi /k)$. Let L be a connected component of $\partial _I\Omega _{j_0}$. It divides $\partial D_n$ into two parts $L_1$ and $L_2$. Note that in each component of $D_n{\setminus } L$, there is $\Omega _j$ with connected $\partial _E\Omega _j$. Hence, $|L_i|>|\partial _E{\tilde{\Omega }}|$, $i=1,2$. Let $L_1$ be the one with $|L_1|\le |\partial D_n|/2$ and consider the domain $\Omega$ enclosed by L and $L_1$. Then we can use Proposition 3.22 in Appendix (taking $\Omega _0={\tilde{\Omega }}$) to get

$$\begin{aligned} |L|=|\partial _I\Omega |\ge |\partial _I{\tilde{\Omega }}|=2\cos (\pi /n)\sin (\pi /k). \end{aligned}$$

Since L was arbitrary, the above inequality holds for each connected component of $\partial _I\Omega _{j_0}$. Let $m\ge 2$ be the number of connected components of $\partial _I\Omega _{j_0}$. Then we have $|\partial _I\Omega _{j_0}|\ge 2m\cos (\pi /n)\sin (\pi /k)$. By assumption, $\eta^{\partial} (\Omega _{j_0})\le \sin (\pi /k)\cot (\pi /n)k/n$ which implies

$$\begin{aligned} |\partial _E\Omega _{j_0}|\ge m|{\partial D_n}|/k. \end{aligned}$$

As a result we get $\sum _{j=1}^k|\partial _E\Omega _j|>|\partial D_n|$ which is impossible. Therefore, condition (3.13) only holds in Case 1. This completes the proof of (ii). $\square$

3.3 Escobar constants $I_k$ for Euclidean and curvilinear polygons

In this subsection we first give upper bounds for $I_k(M)$ where M is a Euclidean n-gon, i.e., we prove Theorem 1.5. Afterward, we generalize these considerations to curvilinear polygons, i.e., we show Theorem 1.6.

Proof of Theorem 1.5

The idea of the proof is the same as the proof of inequality (3.5) (see the proof of Theorem 1.4), i.e., the domains of a k-tuple will concentrate at the corner with the smallest interior angle.

Clearly, there exists $1\le n_0\le n$ such that

$$\begin{aligned} 0<\theta _1\le \theta _2\le \cdots \le \theta _{n_0}<\pi<\theta _{n_0+1}\le \dots \le \theta _n<2\pi . \end{aligned}$$

For every $\theta \in \{\theta _j:1\le j\le n_0\}$, we consider the k-tuple $(\Omega _1,\ldots , \Omega _k)$ illustrated in Fig. 3 near the corner of angle $\theta$. Consequently, we get the same estimate as in (3.6) and (3.7):

$$\begin{aligned} \eta^{\partial} (\Omega _j)=\sin (\theta /2)+O(\epsilon ^{\frac{1}{(k-j+3)(k-j+2)}}),\qquad 1<j\le k. \end{aligned}$$

This entails that

$$\begin{aligned} I_k(M)\le \max _{j=2,\dots ,k}\eta^{\partial} (\Omega _j)\le \sin (\theta /2)+O(\epsilon ^{\frac{1}{(k+1)k}}). \end{aligned}$$

By the arbitrariness of $\epsilon$, we thus get

$$\begin{aligned} I_k(M)\le \max _{j=2,\dots ,k}\eta^{\partial} (\Omega _j)\le \sin (\theta /2). \end{aligned}$$

Therefore, we have

$$\begin{aligned} I_k(M)\le \displaystyle {\min _{1\le j\le n_0}} \sin (\theta _j/2)=\sin (\theta _1/2). \end{aligned}$$

Since the sum of interior angles of any n-gon is $(n-2)\pi$, the maximum value for $\theta _1$ is attained when M is a regular n-gon and it is equal to $\frac{(n-2)\pi }{n}$. Consequently, we obtain

$$\begin{aligned} \sin (\theta _1/2)\le \sin \left( \pi /2-\pi /n\right) =\cos \left( \pi /n\right) , \end{aligned}$$

which establishes the claim. $\square$

In what follows let $\mathcal {P}_n$ be the family of n-gons.

Corollary 3.14

For every $M\in \mathcal {P}_n$ , we have the inequality

$$\begin{aligned} I_k(M)\le I_k(D_n)\le I_k(\mathbb {D}),\qquad \text{ for } \text{ all }\quad k\ge n.\end{aligned}$$

(3.15)

Remark 3.16

• (1) The statement of Theorem 1.5 can be extended to any polygon in the hyperbolic plane. The proof uses the same k-tuple as in the proof of Theorem 1.5 and the Toponogov theorem.

• (2) Note that we have equality in Theorem 1.5 when M is a regular polygon and $k\ge n$. However, for any fixed $k\ge 2$ there is no lower bound for $I_k(M)$, compare Remark 2.2.

It is an interesting question whether among all n-gons, $I_k$ is maximized by $D_n$ for all $k\ge 2$.

Open Question.Let $D\in \mathcal {P}_n$. Does inequality

$$\begin{aligned} I_k(D)\le I_k(D_n), \end{aligned}$$

hold for all $k\ge 2$?

From Theorem 1.4, we know that it holds for $k\ge n$ and $k=3,4$.

The following theorem demonstrates that if we fix $M\in \mathcal {P}_n$ then we have equality in Theorem 1.5 when ‘k is large enough’.

Theorem 3.17

Let $M\in \mathcal {P}_n$ be given. There exists $n_0\ge n$ such that $I_k(M)=\sin (\theta _1/2)$ for all $k\ge n_0$. Here $\theta _1$ is given as in Theorem 1.5.

Proof

As in the proof of Theorem 1.4, we say that a domain $\Omega \subset M$ is of type $\ell$, if $\partial _E\Omega$ has components in exactly $\ell$ edges of M. By Lemma 3.4 there can be at most $n-2$ domains $\Omega _j$ which are of type $\ell$ with $\ell \ge 3$. Hence, any k-tuple $(\Omega _1,\ldots ,\Omega _k)\in A_k(M)$ with $k\ge n$, has at least two elements of type 2. Assume w.l.o.g. that $\Omega _1$ is of type 2. If the boundary components of $\Omega _1$ lie on adjacent edges $e_1$ and $e_2$, then proceed as in the proof of Theorem 1.4 to get $\eta ^{\partial }(\Omega _1)\ge \sin (\theta _j/2)\ge \sin (\theta _1/2),$ where $\theta _j$ denotes the angle enclosed by $e_1$ and $e_2$. Therefore, we assume w.l.o.g. that the boundary components of $\Omega _1$ lie on non-adjacent edges $e_1$ and $e_2$. Let $d=\text{ dist }(e_1,e_2)$. Thus the interior boundary of $\Omega _1$ is at least 2d. When k increases, the number of type 2 domains necessarily increases. Consequently, there can not exist a uniform lower bound on the lengths of their exterior boundaries. Hence, for large enough k, there has to exist a domain $\Omega _i$ of type 2 with exterior boundary less than $2d/ \sin (\theta _1/2)$. Consequently, $\eta ^{\partial }(\Omega _i)\ge \sin (\theta _1/2)$. By Theorem 1.5, we know $I_k(M)\le \sin (\theta _1/2)$. This establishes the claim. $\square$

Finally, we generalize the preceding considerations to curvilinear polygons and prove Theorem 1.6.

Fig. 8

A curvilinear 6-gon

Let us first recall the definition of a curvilinear polygon. Let M be a simply connected domain in $\mathbb {R}^2$ whose boundary $\partial M$ consists of union n-smooth curve and n vertices. The vertices are point were two smooth parts of the boundary meet and the angle of each vertex is in $(0,2\pi ){\setminus }\{\pi \}$, see Fig. 8. We call such domain M a curvilinear n-gon.

Proof of Theorem 1.6

The strategy is essentially the same as that of the proof of Theorem 1.4. Since the boundaries of the polygons are now possibly more general curves than lines, we need to modify the construction a bit.

For every $\varepsilon >0$, there exists a neighborhood $U\subset M$ of the vertex $\mathcal {V}$ with interior angle $\theta _1$ which lies inside a cone C of angle $\theta _1+\varepsilon$ centered at $\mathcal {V}$, see Fig. 9. Let $\mathcal {C}_1,\dots ,\mathcal {C}_k$ be the circles centered at $\mathcal {V}$ with radii $\delta _0\epsilon , (\delta _0+\delta _1)\epsilon ,\ldots ,\sum _{j=0}^k\delta _j\epsilon$, respectively. Here $\delta _0=1$, $\delta _j:=\epsilon ^{-\frac{1}{k-j+1}}$ for $j=1,\dots , k$ and $\epsilon >0$ is chosen small enough such that the intersection with M is contained in U. Denote by $E_1$ and $E_2$ the two edges of the cone. Among the intersection points of M and $\mathcal {C}_j$, we choose $p_1^j$ and $p_2^j$ to be the closest point to $E_1$ and $E_2$, respectively. Further, denote by $\ell _j$ straight line which connects $p_1^j$ and $p_2^j$. We now define the k-tuple $(\Omega _1,\ldots ,\Omega _k)$. Let $\Omega _j$, $1\le j\le k$, be the intersection of the strip between $\ell _j$ and $\ell _{j-1}$ and M. Note that $\ell _0$ is a point and is equal to $\mathcal {V}$. The interior boundary of $\Omega _j$ consists of union of segments which are subset of $\ell _j\cup \ell _{j-1}$. Hence, $\partial \Omega _j\cap M=|\partial _I\Omega _j|\le |\ell _j|+|\ell _{j-1}|.$ It is clear that the length of the exterior boundary $|\partial _E\Omega _j|\ge 2\epsilon \delta _{j}$. Also see Fig. 9, where $\Omega _1$ and $\Omega _2$ are depicted. The interior boundary of $\Omega _2$ is given by the two blue lines.

Next we construct a k-tuple $(\Omega _1^C,\dots , \Omega _k^C)$ for the cone C. In analogy to the above construction, the intersection points of the circles $\mathcal {C}_j$ with the cone C give rise to the exterior boundaries of $\Omega _j^C$—see Fig. 9, where they are depicted in red. The exterior boundary of $\Omega _j^C$ is then simply given by the Euclidean distance between $\mathcal {C}_j$ and $\mathcal {C}_{j-1}$ which is $2\epsilon \delta _j$. Note that we assume $\mathcal {C}_0=\mathcal {V}$. Since $U\subset C$, the interior boundary of $\Omega _j$ is smaller than or equal to that of $\Omega _j^C$. Further, the exterior boundary of $\Omega _j$ is larger than that of $\Omega _j^C$. Hence, $\eta^{\partial} (\Omega _j)\le \eta^{\partial} (\Omega ^C_j)$. Therefore,

$$\begin{aligned}I_k(M)\le \sin \left( \frac{\theta _1+\varepsilon }{2}\right) ,\end{aligned}$$

which establishes the claim, by arbitrariness of $\epsilon$. $\square$

Fig. 9

k-Tuple for a curvilinear polygon near a vertex

Appendix: Calculation of \(\eta^{\partial}\) for a domain in \(D_n\)

Consider $\Omega \subset D_n$ with connected exterior boundary $\partial _E\Omega$ of length $L=|\partial _E\Omega |$. We define the type I symmetrization of $\Omega$ to be the domain $\Omega ^{*}$ with the same exterior length L, obtained by the following symmetrization process. Pick the mid-point p of an edge of $D_n$ and mark two points A, B on the boundary with same distance from p such that the part $\mathcal {B}_{AB}$ of the boundary of $\partial D_n$ which lies between A and B has length L. We denote by $\Omega ^{*}$ the connected domain whose interior boundary is the segment AB and its exterior boundary is given by $\mathcal {B}_{AB}$. Similarly, we define the type II symmetrization of $\Omega$ to be a domain $\Omega ^\star$ when instead of taking p to be the mid-point of an edge, we choose p to be a vertex and A, B on the boundary with same distance from p such that the part of the boundary $\partial D_n$ between A and B has length L.

Proposition 3.18

Let $\Omega \in {\tilde{\mathcal {A}}}(D_n)$ be a domain with connected exterior boundary $\partial _E\Omega$ of length $L=|\partial _E\Omega |\le |\partial D_n|/2$ . Let $\Omega ^{*}$ and $\Omega ^\star$ with $|{\partial _E\Omega ^{*}}|=|{\partial _E\Omega ^\star }|=L$ be the type I and type II symmetrization of $\Omega$ , respectively. Then we have

$$\begin{aligned}{|\partial _I\Omega |\ge \min \{|\partial _I\Omega ^{*}|,|\partial _I\Omega ^\star |\}.}\end{aligned}$$

In particular,

$$\begin{aligned}\eta^{\partial} (\Omega )\ge \min \{\eta^{\partial} (\Omega ^{*}),\eta^{\partial} (\Omega ^\star )\}.\end{aligned}$$

Proof

Let P and Q be the intersection points of the interior boundary $\partial _I\Omega$ of $\Omega$ with $\partial D_n$. W.l.o.g., we assume that P and Q belong to different edges of $D_n$. Let P and Q move clockwise or anticlockwise maintaining distance L from each other along the boundary $\partial D_n$ until they make a symmetric configuration $\Omega ^{*}$ or $\Omega ^\star$ for a first time. Notice that their displacement $\delta$ will be between 0 and the length of the half of an edge, see Fig. 10. We can always choose the moving direction of P and Q so that they do not cross a vertex. Then it is easy to check that the length of dotted line in Figure 10 is less than L. The resulting domain, after moving P and Q to new positions, is either $\Omega ^{*}$ or $\Omega ^\star$. Therefore, the statement follows: $\square$

Fig. 10

Displacement of P and Q to get a symmetric configuration

Fig. 11

Symmetric configuration

If $|{\partial _E\Omega _1^{*}}|=L_1\le L_2=|{\partial _E\Omega _2^{*}}|\le |\partial D_n|/2$, see Figure 11, then an easy calculation shows that

$$\begin{aligned} \eta^{\partial} (\Omega _2^{*})\le \eta^{\partial} (\Omega _1^{*}). \end{aligned}$$

(3.19)

The same holds if we replace ${*}$ by $\star$, i.e.,

$$\begin{aligned} \eta^{\partial} (\Omega _2^\star )\le \eta^{\partial} (\Omega _1^\star ). \end{aligned}$$

(3.20)

Remark 3.21

In some cases, we can calculate the minimum of $\eta^{\partial} (\Omega ^{*})$ and $\eta^{\partial} (\Omega ^\star )$ depending on the value of L. Let $s:=|\partial D_n|/n$ and $c:=\frac{2s\sin ^2(\pi /n)}{1+\cos (\pi /n)-\cos ^2(\pi /n)}$. Then

$$\begin{aligned}{\left\{ \begin{array}{ll} \eta^{\partial} (\Omega ^{*})\le \eta^{\partial} (\Omega ^\star )&{} c\le L\le 2s\\ \eta^{\partial} (\Omega ^{*})\ge \eta^{\partial} (\Omega ^\star )&{} L<c \end{array}\right. }.\end{aligned}$$

Indeed, if $L\le 2s$, then $\Omega ^{*}$ is an isosceles trapezoid and $\Omega ^\star$ is an isosceles triangle with $\eta^{\partial} (\Omega ^\star )=\cos (\pi /n)$. Then we calculate $\eta^{\partial} (\Omega ^{*})$ and find c for which the statement above holds.

Proposition 3.22

Let $\Omega _0$ be a domain in $\tilde{\mathcal {A}}(D_n)$ with connected exterior boundary $\partial _E\Omega _0$ of length $s\le L_0\le \frac{sn}{2}$ , where s is the edge length of $D_n$ . Assume that the endpoints of ${\partial _E\Omega _0^{*}}$ or of ${\partial _E\Omega _0^\star }$ position at the midpoint of two edges. We denote the corresponding symmetrization by $\Omega _0^*$ . Then for any domain $\Omega {\in \tilde{\mathcal {A}}(D_n)}$ with connected exterior boundary of length L

• (i) with $L \le L_0$ we have

  $$\begin{aligned}\eta^{\partial} (\Omega )\ge \eta^{\partial} ( \Omega _0^*);\end{aligned}$$

• (ii) with $L_0\le L\le \frac{sn}{2}$ we have

  $$\begin{aligned}|\partial _I\Omega |\ge |\partial _I\Omega _0^*|.\end{aligned}$$

When $n=\ell k$ and $L_0=\ell s$, then $\Omega _0^*={\tilde{\Omega }}$, where ${\tilde{\Omega }}$ is defined on page 3.2 and

$$\begin{aligned} \eta^{\partial} ( \Omega _0^*)=\sin (\pi /k)\cot (\pi /n)k/n. \end{aligned}$$

Proof Let assume that the endpoints of ${\partial _E\Omega _0^{*}}$ position at the midpoint, i.e., $\Omega _0^*=\Omega _0^{*}$. Thus the endpoints of ${\partial _E\Omega _0^\star }$ are two vertices of $D_n$. An easy calculation shows that $\eta^{\partial} (\Omega _0^{\star })\ge \eta^{\partial} (\Omega _0^{{*}})$. Similarly, if $\Omega _0^*=\Omega _0^\star$, then one can show that $\eta^{\partial} (\Omega _0^{*})\ge \eta^{\partial} (\Omega _0^{{ \star }})$. Since $L\le L_0$, then we have (3.19) and (3.20). We conclude

$$\begin{aligned}\min \{\eta^{\partial} (\Omega ^{*}), \eta^{\partial} (\Omega ^\star )\}\ge \min \{\eta^{\partial} (\Omega _0^{{*}}), \eta^{\partial} (\Omega _0^{\star })\}=\eta^{\partial} (\Omega _0^*).\end{aligned}$$

Combining with Proposition 3.18 proves the first inequality.

We now prove the second inequality. By Proposition 3.18, we have

$$\begin{aligned}|\partial _I\Omega |\ge \min \{|\partial _I\Omega ^{*}|,|\partial _I\Omega ^\star |\}|.\end{aligned}$$

Since $\frac{s}{2}\le L_0\le L\le \frac{sn}{2}$, we get $|\partial _I\Omega ^\star |\ge |\partial _I\Omega _0^\star |$ by considering $\Omega ^\star$ and $\Omega _0^\star$ from a same vertex p. Similarly, we have $|\partial _I\Omega ^{*}|\ge |\partial _I\Omega _0^{*}|$, see Fig. 12 for an illustration. Therefore,

$$\begin{aligned}|\partial _I\Omega |\ge \min \{|\partial _I\Omega _0^{*}|,|\partial _I\Omega _0^\star |\}=|\partial _I\Omega _0^*|.\end{aligned}$$

$\square$

Fig. 12

In the notation of Proposition 3.22, we consider $\Omega _0\subset D_{10}$ with $L_0=3s$