1 Introduction

A batch adsorption experiment from the liquid phase, also known as immersion experiment, is one of the most common tests used to measure adsorption equilibrium and kinetics from solutions. It consists of the addition of a known mass of sample to a fixed volume of liquid at an initial concentration. The liquid is mixed either using a stirrer or the entire cell is agitated to mix the liquid phase. The liquid is sampled or is circulated to a detector and the evolution of the liquid concentration in time is monitored up to equilibrium. This is schematically shown in Fig. 1 for a single cell.

Fig. 1
figure 1

Schematic representation of a liquid phase batch adsorption experiment

Full size image

To obtain an adsorption isotherm the experiment is repeated varying either the amount of solid or the initial concentration of the solution or both. Everett (1986) provides an excellent discussion of the different methods to measure adsorption isotherms from the liquid phase, along with recommendations on issues that may be sources of uncertainty.

Here the focus will be on kinetic measurements and consider two general industrially relevant cases:

  1. a

    Physisorption in porous beads where internal mass transfer is governed by diffusion;

  2. b

    Chemisorption represented by a shrinking core mechanism.

For chemisorption one can develop more complex kinetic schemes, but these are system dependent and are beyond the scope of this contribution. Furthermore, as diffusion in the stagnant liquid in the macropores is relatively slow, the shrinking core model has been shown to describe well, for example, ion-exchange from concentrated solutions (Phelps and Ruthven 2001) and protein adsorption in porous particles (Zhu and Carta 2016) and is a very relevant limiting case to consider. The uptake curves obtained from the two mechanisms become mathematically very similar when dealing with very sharp isotherms, i.e. the limit of the rectangular isotherm (Teo and Ruthven 1986; Ruthven 2000; Do 1998). Therefore, to confirm which mechanism is relevant imaging of carefully cut beads can be used to determine if the shrinking core model applies (Phelps and Ruthven 2001; Zhu and Carta 2016; Dominguez et al. 2019).

The main scope of this work is to use these phenomenological models to generate liquid batch sorption uptake curves that can then be used to demonstrate the potential pitfalls of correlating these kinetic processes using empirical models that are widely used because they lead to linear plots. The models considered are pseudo first order and pseudo second order kinetic models (Ho and McKay 1998) and the Elovich chemisorption kinetics (Low 1960; Aharoni and Ungarish 1977; Cheung et al. 2000). Although diffusion in a particle would be a phenomenological model, the typical approach is to use the solution valid for short times, crediting either Boyd et al. (1947a) or Weber and Morris (1963). What makes this also an empirical approach is the fact that the analytical solution used applies to the case of constant fluid concentration and linear isotherm and both these assumptions do not apply in the batch adsorption experiment.

These models are widely used in the literature because of the ability to obtain their parameters using unconstrained linear regression, which is easily accessible. The fact that this is a very common methodology in adsorption from solution is evidenced by the fact that (Ho and McKay 1998; Cheung et al. 2000; Boyd et al. 1947a) are cited well over 1000 times. Only considering issues of the journal Adsorption since 2015, 16 contributions reporting parameters based on linearized plots of these empirical models could be found (Câmara et al. 2020; Kong et al. 2016; Lupul et al. 2015; Peralta et al. 2019; Rincon-Silva et al. 2016; Shen et al. 2018; van der Heyden et al. 2018; Bartczak et al. 2016; Bazargan et al. 2017; Ciesielczyk et al. 2016; Marques Fraga et al. 2020; Hubetska et al. 2020; Morales-Perez et al. 2016; Popugaeva et al. 2019; De Smedt et al. 2015; Yuan et al. 2019). This shows that significant effort is being devoted to determining the kinetics of adsorption in liquid systems and it is therefore important to be able to interpret these results correctly and arrive at physical parameters that are directly applicable in the design and simulation of adsorption separation processes.

The paper presents a description of the phenomenological models and a brief outline of the empirical approaches and the corresponding linearised plots. Two well characterised systems that are examples of physisorption and chemisorption will be used to generate batch adsorption curves for dilute and concentrated solutions. Physisorption of xylenes in beads of Y zeolite are well characterised by Santacesaria et al. (1982a), who have also shown the portability of the parameters obtained to the prediction of breakthrough curves (Santacesarla et al. 1982b) and chromatographic pulses (Santacesarla et al. 1982c). For chemisorption Cu++ uptake on a commercial ion-exchange resin was investigated in detail (Phelps and Ruthven 2001) and also in this case the parameters obtained where used to predict breakthrough curves and the performance of an endless belt adsorber (Phelps and Ruthven 2002). Teo and Ruthven (1986) also predict breakthrough curves based on the kinetic measurements for water from an aqueous ethanol solution and use a rectangular isotherm for water on 3A molecular sieves.

1.1 Common basis for batch adsorption from the liquid phase

In a batch adsorption experiment, starting from a fully regenerated adsorbent, the mass balance in the system is given by

$${V}_{F}{c}_{0}={V}_{F}{\bar{c}}\left(t\right)+{V}_{S}{\bar{Q}}\left(t\right)$$
(1)

where \(c\) is the concentration of the fluid and \(Q\) is the concentration in the solid, while \({V}_{F}\) and \({V}_{S}\) are the volumes of the fluid and solid. The overbar indicates the average over the corresponding volume.

$$c(t)={c}_{0}-\frac{{V}_{S}}{{V}_{F}}{\bar{Q}}\left(t\right)={c}_{0}-\alpha {\bar{Q}}(t)\quad {\text{with}}\quad \alpha =\frac{{V}_{S}}{{V}_{F}}$$
(2)

Therefore an uptake curve of \({\bar{Q}}(t)\) vs. \(t\) is easily obtained from \(c(t)\) vs. \(t\).

The typical experiment uses a solid that is initially dry, but alternatively the solid could be equilibrated with the pure solvent and then added to the solution. With a dry solid, the initial part of the experiment will have a transient associated with the wetting of the adsorbent and a temperature rise of the solid. This is typically neglected because the thermal mass of the fluid limits the temperature rise and the initial adsorption of the solvent is fast compared to the process being studied. An alternative improved configuration would be to pack a small column with the adsorbent and pump the fluid mixture through the column at high rate (Teo and Ruthven 1986; Babić et al. 2008; Wegmann et al. 2011). In this case the column could be exposed to the pure solvent prior to the start of the experiment. In all the configurations mixing is achieved either with a stirrer or through the rapid circulation. In what follows we make the assumption that the liquid is well mixed and the fluid is considered to be at a uniform concentration, i.e. \(c(t)=\bar{c}(t)\).

With a liquid system, the solute molecules will have to reach the solid through a boundary layer. Whatever mass transport mechanism is considered in the solid phase, there will always be a film resistance and

$$\frac{d{\bar{q}}}{dt}={k}_{F}{a}_{S}\left(c-{c}_{s}\right)$$
(3)

where \({c}_{s}\) is the fluid concentration at the external surface of the solid and \({k}_{F}\) is the film mass transfer coefficient and \({a}_{S}\) is the surface to volume ratio for the solid. Experiments at different stirrer speeds are normally performed, but one should not assume that \({k}_{F}\) is negligible once the kinetic response becomes independent of the speed of the stirrer. At high stirrer speeds and corresponding high fluid velocities the particles will be fully fluidized and therefore the relative velocity between the fluid and the particles will become effectively independent of the speed of the stirrer. This is one advantage of the use of a fixed bed with a circulation pump, where the relative velocity is always the fluid velocity and results that become independent of the circulation rate could be used to indicate a negligible film resistance (Teo and Ruthven 1986). A further advantage of the fluid circulation system is a reduction in particle attrition (Teo and Ruthven 1986). A simple method to assess the relative importance of the film resistance is to estimate the worst case scenario, where the Sherwood number is 2, which corresponds to the case of a stagnant liquid film.

For the solid phase we consider a biporous adsorbent, with macropores that lead to the adsorbing material. In the macropores a normal liquid solution is present and there is no selectivity to any molecule. The overall concentration in the particles is then

$${\bar{Q}}={\varepsilon }_{P}{\bar{c}}_{P}+\left(1-{\varepsilon }_{P}\right){\bar{q}}$$
(4)

where \({\varepsilon }_{P}\) is the macropore void fraction of the particles.

Having defined the fluid phase concentration at the surface of the particle, it is possible to define the adsorbed phase concentration that would be at equilibrium with this fluid concentration, \({\bar{Q}}_{eq}\).

$${\bar{Q}}_{eq}={\varepsilon }_{P}{c}_{s}+\left(1-{\varepsilon }_{P}\right){\bar{q}}_{eq}$$
(5)

For the purposes of this contribution the Langmuir isotherm will be used

$${\bar{q}}_{eq}={q}_{S}\frac{b{c}_{s}}{1+b{c}_{s}}$$
(6)

The Langmuir saturation capacity, \({q}_{S}\), and the affinity \(b\) are constants and should be determined independently, regressing accurately the final equilibrium data at different fluid concentrations.

\({\bar{Q}}_{eq}\) varies during the experiment because the measurement is based on determining the variation of the fluid phase concentration in time, therefore the equilibrium isotherm becomes an integral part of the dynamic model.

To close the problem it is necessary to describe mass transport in the solid using a phenomenological model. Here the emphasis is on models that allow to determine meaningful physical parameters from pure component immersion experiments which can be used to predict reliably multicomponent separations.

1.2 Linear rate model

The linear rate model is the simplest case to consider

$$\frac{d\bar{Q}}{dt}={k}_{S}{a}_{S}\left({\bar{Q}}_{eq}-\bar{Q}\right)$$
(7)

As an example, this model has been used to describe biosorption of dyes and corresponding binary breakthrough curves (Fernandez et al. 2015).

Glueckauf (1955) showed that the surface resistance constant, \({k}_{S}\), can be expressed in terms of the internal diffusion coefficient. For a sphere, \({k}_{S}=\frac{5D}{{R}_{P}}\). This model can be generalised to multiple resistances in series and becomes a lumped model approach. The relationships needed to include external film resistance, surface resistance, diffusion in macropores, and diffusion in micropores can be obtained from the moments of chromatographic or kinetic experiments and can be found in Ruthven (1984). The film and surface resistances can be combined into a linear driving force constant, \({k}_{LDF}\), given by

$$\frac{1}{{k}_{LDF}}=\frac{1}{{k}_{S}}+\frac{\frac{d{\bar{Q}}_{eq}}{d{c}_{S}}}{{k}_{F}}\approx \frac{1}{{k}_{S}}+\frac{\frac{{Q}_{\infty }}{{c}_{\infty }}}{{k}_{F}}$$
(8)

For the case of strong adsorption, where the accumulation in the macropores is negligible compared to the adsorbed amount, i.e. \({\bar{Q}}_{eq}={\bar{q}}_{eq},\) the LDF model can be solved analytically to obtain

$$\text{ln}\left(\frac{{q}_{+}}{{q}_{+}-\bar{q}}\right)+A\text{ln}\left[\frac{{q}_{-}}{{q}_{+}}\frac{\left({q}_{+}-\bar{q}\right)}{\left({q}_{-}-\bar{q}\right)}\right] ={k}_{LDF}{a}_{S}t \quad {\text{if}}\quad 1+b{c}_{0}>\alpha b{q}_{s}$$
(9a)
$$\text{ln}\left(\frac{{q}_{-}}{{q}_{-}-\bar{q}}\right)-A\text{ln}\left[\frac{{q}_{-}}{{q}_{+}}\frac{\left({q}_{+}-\bar{q}\right)}{\left({q}_{-}-\bar{q}\right)}\right]={k}_{LDF}{a}_{S}t\quad {\text{otherwise}}$$
(9b)

where

$$A=\frac{\sqrt{{\phi }^{2}-4\gamma }}{2\phi }+\frac{1}{2}\quad {\text{with}}\quad \phi =\sqrt{{\left(1+b{c}_{0}+\gamma \right)}^{2}-4\gamma b{c}_{0}}$$
(9c)

and

$${q}_{\pm }=\frac{1+b{c}_{0}+\gamma \pm \phi }{2\alpha b}\quad {\text{with}}\quad \gamma=\alpha b q_{s}$$
(9d)

with the final equilibrium concentration \({\bar{q}}_{eq}\left(\infty \right)={\bar{q}}_{\infty }={q}_{-}\). When matching this model to data the uptake curve vs. the dimensionless time is generated varying \(\bar{q}\) between 0 and a value close to \({\bar{q}}_{\infty }\). The regression of the data can be carried out by a simple determination of the scaling factor for the time axis.

1.3 Diffusion in a biporous particle

If one considers the fact that normally materials are optimized for a specific separation, the case of macropore diffusion control is the most likely controlling mass transport mechanism in commercial beads. Here we limit the discussion to macropores where the fluid has the same properties as a bulk liquid.

The mass balance in a spherical bead can be written as

$${\varepsilon }_{P}\frac{\partial {c}_{P}}{\partial t}+\left(1-{\varepsilon }_{P}\right)\frac{\partial q}{\partial t}=\frac{{\varepsilon }_{P}}{\tau }\frac{{D}_{m}}{{r}^{2}}\frac{\partial }{\partial r}\left({r}^{2}\frac{\partial {c}_{P}}{\partial r}\right)$$
(10)

where \({c}_{P}\) is the concentration in the fluid inside the pores and \(q\) is the concentration in the adsorbed phase. The porosity \({\varepsilon }_{P}\) and the tortuosity \(\tau\) are used to relate the diffusion coefficient to the molecular diffusivity \({D}_{m}\) in the fluid phase.

If transport in the microporous material is fast compared to the effective diffusional time constant of the macropores, the adsorbed phase can be considered to be at local equilibrium with \({c}_{P}\) and

$$\frac{\partial {c}_{P}}{\partial r}=\frac{1}{\frac{dQ}{d{c}_{P}}}\frac{\partial Q}{\partial r}$$
(11)

and Eq. 10 can be rearranged to

$$\frac{\partial Q}{\partial t}=\frac{1}{{r}^{2}}\frac{\partial }{\partial r}\left(\frac{{\varepsilon }_{P}}{\tau }\frac{{r}^{2}{D}_{m}}{\frac{dQ}{d{c}_{P}}}\frac{\partial Q}{\partial r}\right)=\frac{1}{{r}^{2}}\frac{\partial }{\partial r}\left({D}_{P}^{Eff}{r}^{2}\frac{\partial Q}{\partial r}\right)$$
(12)

This is coupled to the boundary conditions.

$${\left(\frac{\partial Q}{\partial r}\right)}_{r=0}=0 \quad {\text{and}}\quad {\left(Q\right)}_{r={R}_{P}}={\bar{Q}}_{eq}\left(t\right)$$
(13)

Equation 12 shows how a concentration dependent effective pore diffusivity \({D}_{P}^{Eff}\) is obtained in this case.

What is important to note is that this model, although mathematically more complex than what seen previously, has only the tortuosity that cannot be measured independently. The adsorption isotherm has to be measured in any case and porosity is a known parameter in commercial materials or can be measured using mercury porosimetry (Lowell et al. 2006). Complexity can be added by including surface diffusion, but this will not be considered here. If surface diffusion can be neglected, once kinetic results for one molecule are interpreted correctly and the tortuosity is determined, the kinetic response of other molecules as well as mixtures can be predicted if the adsorption isotherm is known.

For strongly adsorbed components \(\frac{dQ}{d{c}_{P}}\) decreases rapidly with increasing concentration. Therefore, in an immersion experiment under highly nonlinear conditions the outer layer of the particle will equilibrate rapidly (high diffusivity), while the inner layer will still have a relatively slow transport process. Under these conditions the kinetic response of this model will be qualitatively very similar to a shrinking core model. This can also be seen considering the Langmuir isotherm in the limit of infinite affinity, where the rectangular isotherm (Ruthven 2000) is obtained.

1.4 Shrinking core model

The assumption in this case is that the process is controlled by diffusion in the external layer of the particle with a rapid reaction that effectively takes place at a surface which moves towards the centre of the particle. While more complex mechanisms can be considered, this is in fact a reasonable model for liquid phase systems with chemisorption. It is adopted here given the fact that also in this case particle porosity and tortuosity are the only physical parameters needed, once the equilibrium concentration of the adsorbed phase is known.

As discussed by Ruthven and Phelps (2001) the assumption of finite volume and a shrinking core lead to the following relationship.

$$\frac{{D}_{S}}{{R}_{P}^{2}}\frac{{c}_{0}}{{Q}_{S}}t={\int }_{z}^{1}\frac{z\left(1-z\right)}{1-\delta +\delta {z}^{3}}dz\quad {\text{with}}\quad \delta =\frac{{V}_{S}{Q}_{S}}{{V}_{F}{c}_{0}}$$
(14)

The parameter \(\delta\) represents the ratio of the moles that are chemisorbed by the solid compared to the initial moles in the system when the final fluid concentration is not zero, which is normally the case in immersion experiments where a stoichiometric excess of adsorbate is used, i.e. \(\delta <1\).

Analytical solutions to the shrinking core model are available for both the infinite system (Brauch and Schlünder 1975) and the finite volume/variable concentration case (Teo and Ruthven 1986; Do 1998). To use a consistent notation the integral can either be calculated numerically by a suitable quadrature formula or from.

$${\int }_{z}^{1}\frac{z\left(1-z\right)}{1-\delta +\delta {z}^{3}}dz=\frac{\sqrt[3]{{\Lambda }}}{6\delta }\left\{\frac{2}{\sqrt[3]{{\Lambda }}}\text{ln}\left(1-\delta +\delta {z}^{3}\right)-2\text{ln}\left(\frac{\sqrt[3]{{\Lambda }}+1}{z\sqrt[3]{{\Lambda }}+1}\right)+\text{ln}\left(\frac{\sqrt[3]{{{\Lambda }}^{2}}-\sqrt[3]{{\Lambda }}+1}{{z}^{2}\sqrt[3]{{{\Lambda }}^{2}}-z\sqrt[3]{{\Lambda }}+1}\right)+\sqrt{12}\left[\text{atan}\left(\frac{2\sqrt[3]{{\Lambda }}-1}{\sqrt{3}\sqrt[3]{{\Lambda }}}\right)-\text{atan}\left(\frac{2z\sqrt[3]{{\Lambda }}-1}{\sqrt{3}\sqrt[3]{{\Lambda }}}\right)\right]\right\} \quad {\text{with}} \quad {\Lambda }=\frac{\delta }{1-\delta }=\frac{{V}_{S}{Q}_{S}}{{V}_{F}{c}_{\infty }}$$
(15)

At the end of the experiment \({z}_{\infty }=0\) for \(\delta <1\), while for \(\delta \ge 1\), the shrinking core will stop at \({z}_{\infty }=\frac{-1}{\sqrt[3]{{\Lambda }}}\) and \({c}_{\infty }=0\), i.e. all the adsorbate will be consumed. This reaction model will have a finite uptake rate at the end of the experiment.

2 Empirical models

2.1 Pseudo first order model

The pseudo first order (PFO) model is derived from the linear rate model assuming that the equilibrium amount is constant throughout the experiment and equal to the final concentration in the solid

$$\frac{d\bar{Q}}{dt}={k}_{1}\left({\bar{Q}}_{\infty }-\bar{Q}\right)$$
(16)

Here the kinetic constant of the PFO model is explicitly defined as a different parameter from \({k}_{LDF}\) to avoid confusion between the two models. Only for a rectangular isotherm (irreversible adsorption), \({\bar{Q}}_{eq}\) is a constant if the accumulation in the macropores is negligible.

Equation 13 can be solved analytically using the initial condition (\({\bar{Q}}_{0}=0; {t}_{0}=0\)) to obtain

$$\text{ln}\left(1-\frac{\bar{Q}}{{\bar{Q}}_{\infty }}\right)=-{k}_{1}t$$
(17a)

or

$$\text{ln}\left({\bar{Q}}_{\infty }-\bar{Q}\right)=\text{ln}\left({\bar{Q}}_{\infty }\right)-{k}_{1}t$$
(17b)

While equivalent these two relationships are shown explicitly because Eq. 17a leads to a linear plot that is constrained to start at the origin, while Eq. 17b leads to a linear plot that is unconstrained. This distinction is in fact very important, because if \({\ln}({\bar{Q}}_{\infty })\) is not fixed to the actual equilibrium value the PFO model can be used to fit in a semilogarithmic plot any process which results in an exponential decay to equilibrium. Given that in physisorption any mass transport process will eventually conform to an exponential decay to equilibrium, selecting a portion of the uptake for the unconstrained regression of the parameters will lead to the square of the correlation coefficient, R2, close to unity if the points selected are close to the final equilibrium point. Without the test of actually plotting the original data on a linear uptake plot (McLintock 1967), R2 close to unity has very little value in determining which model applies.

We note also that the only apparent advantage of using the approximate Eq. 17 over Eq. 9 is due to the fact that the first allows to convert the data to a form that can be linearized. The kinetic curve from Eq. 9 can be computed easily by setting the value of \(\bar{q}\left(t\right)\), which varies from 0 to \({\bar{q}}_{\infty }\), and calculating the corresponding time. Thus a nonlinear regression of the data with Eq. 9 would be straightforward and to be preferred over the PFO model.

2.2 Pseudo second-order model

The pseudo second order (PSO) model is derived from the quadratic driving force (QDF) model

$$\frac{d\bar{Q}}{dt}={k}_{QDF}{\left({\bar{Q}}_{eq}-\bar{Q}\right)}^{2}={k}_{QDF}\left({\bar{Q}}_{eq}-\bar{Q}\right)\left({\bar{Q}}_{eq}-\bar{Q}\right)$$
(18)

One should note that Vermeulen suggested the use of the following driving force relationship for irreversible equilibrium (Vermeulen 1953)

$$\frac{d\bar{Q}}{dt}={k}_{V}\left({\bar{Q}}_{Eq}^{2}-{\bar{Q}}^{2}\right)={k}_{V}\left({\bar{Q}}_{eq}+\bar{Q}\right)\left({\bar{Q}}_{eq}-\bar{Q}\right)$$
(19)

Glueckauf showed that this model was the best approximation for nearly rectangular isotherms (Glueckauf 1955), when \({k}_{V}\) could be related to the internal diffusion coefficient. Eq. 19 is significantly different from the QDF model and is in fact a concentration dependent LDF model, with the mass transfer coefficient increasing with concentration, which is typically true for systems with a Langmuir isotherm. Note that in a batch adsorption experiment \(\left({\bar{Q}}_{eq}+{\bar{Q}}\right)\approx 2{\bar{Q}}_{\infty }\) apart from the very initial uptake, therefore Eq. 19 will not be discussed further.

Equation 18 is a kinetic model that has a rate of adsorption that decreases in time monotonically because \(\left({\bar{Q}}_{eq}-\bar{Q}\right)\) is constantly decreasing throughout the experiment. The QDF model can be seen as a concentration dependent LDF model where the mass transfer coefficient goes to zero at equilibrium. While the QDF expression could be physically representative of a particular chemisorption process, in the opinion of the author it is not a physically realistic kinetic model of physisorption, where the mass transfer coefficient is not zero at equilibrium.

If the equilibrium concentration is assumed to be constant and equal to the final value, the PSO model is obtained

$$\frac{d\bar{Q}}{dt}={k}_{2}{\left({\bar{Q}}_{\infty }-\bar{Q}\right)}^{2}$$
(20)

This can be solved analytically using the initial condition (\({\bar{Q}}_{0}=0; {t}_{0}=0\)) to obtain

$${\bar{Q}}=\frac{{\bar{Q}}_{\infty }^{2}{k}_{2}t}{1+{\bar{Q}}_{\infty }{k}_{2}t}=\frac{{\bar{Q}}_{eq}^{\infty }{K}_{2}t}{1+{K}_{2}t}\quad {\text{with}}\quad {K}_{2}={\bar{Q}}_{\infty }{k}_{2}$$
(21)

This shows that there are in fact two possible definitions of the pseudo-second order kinetic constant. It is important to note that if \({k}_{2}\) is indeed a constant, then \({K}_{2}\) would depend on the initial concentration in the fluid and the amount of solid added and vice versa.

Equation 21 has a similar structure to the Langmuir isotherm equation and can be linearized as

$$\frac{1}{\bar{Q}}=\frac{1}{{\bar{Q}}_{\infty }{K}_{2}}\frac{1}{t}+\frac{1}{{\bar{Q}}_{\infty }}$$
(22)

or

$$\frac{t}{\bar{Q}}=\frac{1}{{\bar{Q}}_{\infty }{K}_{2}}+\frac{t}{{\bar{Q}}_{\infty }}$$
(23)

Note that any kinetic model that is based on a driving force will conform to Eq. 23 as the system approaches equilibrium. For fast systems limited data will be available far from equilibrium and Eq. 23 will give the false impression of accuracy because it will have R2 close to unity. Similarly to the PFO model, further incorrect interpretations of results arise when \({\bar{Q}}_{\infty }\) is used as an adjustable parameter.

2.3 Langmuir kinetics

Neglecting the accumulation in the macropores, one can consider adsorption and desorption kinetics (Azizian 2004) expressed as

$$\frac{d\bar{q}}{dt}={k}_{A}c\left({q}_{S}-\bar{q}\right)-{k}_{D}\bar{q}$$
(24)

where \({k}_{A}\) and \({k}_{D}\) are the adsorption and desorption kinetic constants. While this appears to be a two parameter model, the two constants are related to the affinity in the Langmuir isotherm. At equilibrium one obtains \({k}_{A}=b{k}_{D}\). It is useful to rearrange Eq. 24 to

$$\frac{d\bar{q}}{dt}={k}_{D}\left(1+bc\right)\left({\bar{q}}_{eq}-\bar{q}\right)$$
(25)

Equation 25 shows that Langmuir kinetics are similar to the LDF model with a linear concentration dependence of the kinetic coefficient. In an immersion experiment the apparent LDF mass transfer coefficient will decrease in time between \({k}_{D}\left(1+b{c}_{0}\right)\) and \({k}_{D}\left(1+b{c}_{\infty }\right)\), consistent with two apparent kinetic regimes. When \(bc\ll 1\) the model reduces to Eq. 9 with \({k}_{LDF}{a}_{S}={k}_{D}\).

Azizian’s analytical solution (Azizian 2004) can be expressed in a more convenient form using the terms defined in Eq. 9b

$$\frac{1}{\phi }\text{ln}\left[\frac{{q}_{-}}{{q}_{+}}\frac{\left({q}_{+}-\bar{q}\right)}{\left({q}_{-}-\bar{q}\right)}\right] ={k}_{D}t$$
(26)

As was the case for the LDF model, also here \(\bar{q}\) can be varied between 0 and \({\bar{q}}_{\infty }\) to obtain the corresponding time.

Azizian has shown that Eq. 26 can be used to show convergence to either PFO or PSO models depending on the concentrations in the fluid (Azizian 2004). The main result was to show that both models could match the more general model but resulted in concentration dependent \({k}_{1}\) values (linear dependence on \({c}_{0}\)) and \({k}_{2}\) (more complex dependence on \({c}_{0}\)). Here the approach is quite different, because the aim is to warn against use of these models in systems where the transport mechanisms are known to be not Langmuir kinetics.

2.4 The Elovich model

The Elovich model is discussed in detail by Low (1960) and Aharoni and Ungarish (1977), who also consider the possible derivation from reaction kinetic models and the fact that it does not conserve the number of surface sites, i.e. it is not compatible with the assumptions of Langmuir kinetics. The general expression for the rate is

$$\frac{d\bar{q}}{dt}={k}_{E}{e}^{-B\bar{q}}$$
(27)

This expression is not a “driving force” model since the rate is zero only for \(\bar{q}=\infty\). This is not a feasible model for physisorption because the rate will not be zero at equilibrium. In the simulation of an adsorption process one would need to couple Eq. 27 with the equilibrium isotherm and switch to \(\frac{d\bar{q}}{dt}=0\) when the equilibrium concentration is achieved. As such this model should only be used for chemisorption and should give a shape of the response similar to the shrinking core model.

The solution to Eq. 27 is

$$\frac{1}{B}{e}^{B\bar{q}}={k}_{E}t$$
(28)

This can be re-arranged into.

$$\bar{q}=\frac{1}{B}\text{ln}\left({Bk}_{E}t+1\right)=\frac{1}{B}\text{ln}\left({Bk}_{E}\right)+\frac{1}{B}\text{ln}\left(t+{t}_{0}\right)\quad {t}_{0}=\frac{1}{{Bk}_{E}}$$
(29)

In this case the data are time shifted varying \({t}_{0}\) to obtain a linear plot and an unconstrained linear regression is then applied (Cheung et al. 2000).

Qualitatively Eq. 27 corresponds to an initially fast rate, \({k}_{E}\), that progressively decreases. As such one can intuitively suggest that a time-shifted diffusion process should give a linear Elovich plot in a region not close to final equilibrium. The qualitative behaviour away from the final equilibrium is not dissimilar to the PSO model and Langmuir kinetics.

2.5 Linear diffusion model

This model assumes linearity even when the system follows a nonlinear isotherm like the Langmuir isotherm and the immersion experiment is carried out far from the region where Henry’s law applies. As such it is included in the list of empirical models, especially when the short time linear plot that results from this model is used to fit batch adsorption experiments.

For the case where the external film resistance is negligible an analytical solution is readily available (Do 1998; Ruthven 1984; Crank 1975) and is given by

$$\frac{\bar{Q}}{{Q}_{\infty }}=1-{\sum }_{n}\frac{6\text{exp}\left(-{\beta }_{n}^{2}\frac{{D}_{P}^{EL}}{{R}_{P}^{2}}t\right)}{9{\lambda }^{2}+9\lambda +{\beta }_{n}^{2}}$$
(30a)

where

$$\frac{{D}_{P}^{EL}}{{R}_{P}^{2}}=\frac{{\varepsilon }_{P}}{\tau }\frac{{D}_{m}}{K}$$
(30b)

and

$${\beta }_{n}\text{cot}{\beta }_{n}-1-\frac{1}{3\lambda } {\beta }_{n}^{2}=0\quad {\text{with}}\quad \lambda =\alpha K$$
(30c)

and

$$K=\frac{\Delta Q}{\Delta c}=\frac{{Q}_{\infty }}{{c}_{\infty }}={\varepsilon }_{P}+\left(1-{\varepsilon }_{P}\right)\frac{{q}_{S}b}{1+b{c}_{\infty }}$$
(30d)

In a truly linear system \(K\) becomes the Henry law constant of the particle when \(b{c}_{\infty }\ll 1\).

Equation 30c has a root in each π interval, except the first and requires only a few terms to converge apart from the region close to \(t=0\). It is therefore useful also to derive the short time expression valid in this region

$$\frac{\bar{Q}}{{Q}_{\infty }}\approx \left(1+\lambda \right)\left[6\sqrt{\frac{{D}_{P}^{EL}}{{R}_{P}^{2}}\frac{t}{\pi }}-3\left(1+3\lambda \right) \frac{{D}_{P}^{EL}}{{R}_{P}^{2}}t+12\lambda \left(1+3\lambda \right) \frac{{D}_{P}^{EL}}{{R}_{P}^{2}}t\sqrt{\frac{{D}_{P}^{EL}}{{R}_{P}^{2}}\frac{t}{\pi }}+\dots \right]$$
(31)

Equation 31 suggests the plot of the dimensionless uptake response vs. \(\sqrt{t}\), which should be linear for short times.

While the finite volume solution is readily available, as a first approximation one could consider using the solution to the diffusion equation subject to a step change in surface concentration, which corresponds to the limiting case of \(\lambda =0\) and \({\beta }_{n}=n\pi\). There are however important differences between Eq. 30 and

$$\frac{{\bar{Q}}_{0}}{K{c}_{0}}=1-{\sum }_{n}\frac{6\text{exp}\left(-{n}^{2}{\pi }^{2}\frac{{D}_{P}^{App}}{{R}_{P}^{2}}t\right)}{{n}^{2}{\pi }^{2}}$$
(32)

and the corresponding

$$\frac{{\bar{Q}}_{0}}{K{c}_{0}}\approx 6\sqrt{\frac{{D}_{P}^{App}}{{R}_{P}^{2}}\frac{t}{\pi }}-3 \frac{{D}_{P}^{App}}{{R}_{P}^{2}}t+0 \frac{{D}_{P}^{App}}{{R}_{P}^{2}}t\sqrt{\frac{{D}_{P}^{App}}{{R}_{P}^{2}}\frac{t}{\pi }}+\dots$$
(33)

The short time behaviour differs by a coefficient \(1+\lambda\), therefore the apparent diffusivity, \({D}_{P}^{App}\), will be higher by a factor \({\left(1+\lambda \right)}^{2}\) compared to \({D}_{P}^{EL}\) and will depend on both the isotherm and the volume of solid added to the solution since \(\lambda =\frac{{V}_{S}}{{V}_{F}}K\). Note also that the third term of this series expansion is zero which indicates that the finite volume solution deviates from the initial linear trend more rapidly than the constant concentration solution.

To see more clearly the origin of this difference consider that for short times the external concentration is close to \({c}_{0}\) and the fact that in the constant concentration case \({Q}_{\infty }=K{c}_{0}\). The initial trend should be similar, but the normalization to 1 is different. Writing this explicitly

$$\frac{\bar{Q}}{K{c}_{\infty }}=\frac{\bar{Q}}{K{c}_{0}}\frac{{c}_{0}}{{c}_{\infty }}\approx \frac{{\bar{Q}}_{0}}{K{c}_{0}}\frac{{c}_{0}}{{c}_{\infty }}\approx \left(1+\lambda \right)6\sqrt{\frac{{D}_{P}^{EL}}{{R}_{P}^{2}}\frac{t}{\pi }}$$
(34)

The other important difference is the final approach to equilibrium where

$$1-\frac{\bar{Q}}{{Q}_{\infty }}\approx \frac{6}{9{\lambda }^{2}+9\lambda +{\beta }_{1}^{2}}\text{exp}\left(-{\beta }_{1}^{2}\frac{{D}_{P}^{EL}}{{R}_{P}^{2}}t\right)$$
(35)
$$1-\frac{{\bar{Q}}_{0}}{K{c}_{0}}\approx \frac{6}{{\pi }^{2}}\text{exp}\left(-{\pi }^{2}\frac{{D}_{P}^{App}}{{R}_{P}^{2}}t\right)$$
(36)

From Eq. 30c it is possible to see that \(1<\frac{{\beta }_{1}}{\pi }<1.4302\) as \(\lambda\) varies between 0 and \(\infty\). The long-time asymptote will yield an apparent diffusivity that will be up to double the value of \({D}_{P}^{EL}\) and different from the value obtained from the short time uptake, Eq. 33. The incorrect use of the constant concentration equations, could therefore lead to identifying two apparent kinetic regimes for strongly adsorbed species.

What limits further the validity of results found in the literature is the fact that uptake data are regressed using the short time \(\bar{Q}\) vs. \(\sqrt{t}\) with the empirical expression

$${\bar{Q}}\approx {A}_{D}\sqrt{t}+C$$
(37)

which is often attributed to Weber and Morris (1963) but no distinction is made with respect to the assumption of constant volume or constant concentration. Note also that often Eq. 37 is applied to separate segments of the uptake curve, linking this to the presence of an initial fast process followed by a much slower second kinetic regime. It is not clear how such an interpretation originated, but the \(\bar{Q}\) vs. \(\sqrt{t}\) plot should only be used in the very first part of the uptake, i.e. for \(\bar{Q}<0.5\).

Boyd et al. (1947a) are also often referenced as the basis for Eq. 37. It is very instructive to read this reference in detail and realise the efforts made to achieve conditions of constant external concentration and linear equilibrium, which are the basis for the model adopted in that study. Boyd’s system was not a fixed volume system, but a shallow bed with once-through flow of the solution. This ensured constant external concentration, while the measurement of tracer exchange ensured linearity of the equilibrium isotherm. Using radioactive tracers the adsorbed amounts were measured directly from the particles, not calculated indirectly from the external concentration. Provided that the concentration change across the shallow bed is small, Eq. 32 or the equivalent for diffusion and external film resistance is perfectly valid. The shallow bed with varying concentration in linear conditions would be similar to a liquid phase zero length column system (Brandani and Ruthven 1995). Boyd et al. confirmed that the uptake of different ions on an Amberlite ion-exchange resin could be either controlled by internal diffusion (Eq. 32) for strongly adsorbed species or a film resistance (Eq. 7 or the PFO model). This is consistent with an internal mechanism of macropore diffusion control leading to a strongly concentration dependent internal diffusion coefficient.

The series of papers by Boyd et al. are still today an excellent example of how to characterize rigorously the equilibrium properties (1947b) in ion-exchange processes and then carry out careful kinetic experiments (Boyd et al. 1947a) and subsequent breakthrough experiments (Boyd et al. 1947c), checking the independent measurements for consistency. Their aim was the design of ion-exchange separation processes and anything more advanced than what Boyd et al. presented would have required numerical computational power not available between 1943 and 1946 when their work was carried out. Today, one would possibly consider extending the analysis introducing diffusion models that include the interactions between charged species (Wesselingh et al. 1995; Krishna and Wesselingh 1997), but this will not be discussed further as it is beyond the scope of this contribution.

3 Results and discussion

In the description of the empirical models the qualitative discussion of potential pitfalls of the use of linearized plots to extract kinetic information was introduced. To give a quantitative setting to the arguments made, specific examples will be presented based on generating “data” from the full non-linear model and then applying the empirical approaches to see if the models appear to fit the data well and if any of the models produce parameters that could be considered to be physically meaningful.

3.1 Physical adsorption on zeolites: xylenes on Y zeolite beads

The first in a series of three papers by Santacesaria et al. (1982a) covered immersion experiments to obtain equilibrium properties and formulate a mass transport model based on combined film resistance and diffusion inside the beads (Table 1).

Table 1 The parameters used in this study
Full size table

The supplementary information includes all the results. Here we discuss in greater detail the case of pure diffusion for p-xylene (\({c}_{0}=500\) mol m−3 and \({M}_{S}=40\) gr) and m-xylene (\({c}_{0}=250\) mol m−3 and \({M}_{S}=40\) gr). p-Xylene and m-xylene were chosen because they are the strongest and weakest adsorbate respectively.

While these are specific examples, the shape of the kinetic response of macropore diffusion control with a Langmuir adsorption isotherm will always conform to being between close to linear (m-xylene example) and strongly nonlinear (p-xylene example). A measure of the nonlinearity is the ratio of the equilibrium concentration of the solid to the value at complete saturation of the adsorbed phase (Brandani 1998), which in this case is given by

$${\Gamma }=\frac{{Q}_{\infty }}{{\varepsilon }_{P}{c}_{\infty }+\left(1-{\varepsilon }_{P}\right){q}_{S}}$$
(38)

A value of \({\Gamma }<0.5\) is an indication of mild nonlinearity (Brandani 1998). The nonlinearity increases as \({\Gamma }\) approaches 1.

Figure 2 shows the uptake curves for the two cases of interest. Qualitatively the shapes of the curves are similar, even when nonlinearity is considered. As expected, the surface resistance modifies the take-off from zero and in general results in a smoother shape. It is interesting to note though that overall, on the uptake plot, the worst case scenario, Sh = 2, is not significantly different from the case of pure diffusion, Sh \(=\infty\). Therefore particular care should be used in analysing results with the combined film resistance and diffusion model when experimental scatter will give a large uncertainty on the individual values of the two mass transfer resistances, but the overall effect should still be estimated with sufficient accuracy. To discriminate better between the two mechanisms it would be better to modify the configuration of the experimental system so that the relative velocity between the particles and the fluid can be controlled directly. Examples of these systems are discussed in Kärger and Ruthven (1992).

Fig. 2
figure 2

Batch adsorption uptake curves for p-xylene (\({c}_{0}=500\) mol m−3 and \({M}_{S}=40\) gr) and m-xylene (\({c}_{0}=250\) mol m−3 and \({M}_{S}=40\) gr). Full lines diffusion model (Sh \(=\infty\)); dashed lines combined model and Sh = 2

Full size image

Figure 3 shows the simulated kinetic response for p-xylene, \({\Gamma }=0.90\). The data between 3 and 25 min are used to apply the PFO, PSO and Elovich empirical approaches. Figure 3 shows the relevant plots along with the linear regression trend-line. In the Elovich kinetics case one has to plot the data varying \({t}_{0}\), which introduces a small potential bias from the analyst. The data with \({t}_{0}=45\) s, conform well to the linear plot, even though there are no chemical reactions involved

Fig. 3
figure 3

Linearized plot and linear regression of data using the PFO, PSO and Elovich models. Filled points are those used in establishing the trendline. Lower right plot shows the linear plot of the uptake data with the curves calculated from the parameters obtained from the unconstrained linear regression. For the PFO model an additional curve is shown with the correct final concentration. p-Xylene \({c}_{0}=500\) mol m−3 and \({M}_{S}=40\) gr

Full size image

The order in which one would rank the models in terms of goodness of fit is PFO > PSO > Elovich. There is very little to discriminate between the three given that the range of R2 is between 0.9982 and 0.9993. Experimental scatter of the data would reduce R2, possibly modifying the order. What is important to emphasise though is that the trend observed is perfectly consistent with the qualitative observations made previously. All models fit well the data in the linearized plots even though they do not represent the correct transport phenomena.

Figure 3 shows also the test of the fits (McLintock 1967), where the regression parameters are used to generate the actual uptake curves to compare the models to the original data. We now see that the PFO model is in fact a very poor match to the data, whether the equilibrium concentration from the fit is used or the actual equilibrium concentration is used. In the long time region the PSO model appears to be the best match, but in the short time deviations close to 100% can be observed with the actual response being much faster. The Elovich kinetic model matches the initial part well but as expected cannot describe the final approach to equilibrium. This is in fact the best model if one decouples the kinetics from the final equilibrium. Plotting the uptake data on linear scales would lead to the incorrect conclusion that one of the two physically unrealistic models describes this system well. It should be clear in this case that the parameters of these models are not physical parameters and therefore of very limited portability to other systems, if any.

Figure 4 shows the \(\bar{Q}\) vs. \(\sqrt{t}\) plot of the data. Here only the data over the first 10 min are used in the linear regression. Again a high R2 is obtained, 0.9896, but this is the lowest for all models. It is worth emphasizing again that the fact that R2 is close to unity cannot be used to identify the mechanism of mass transport. If anything, this measure leads to the wrong conclusion, given that in this case it would be better to use the linear diffusion model, even though the match to the data is not as good. This crucial consideration can be understood if the particle size is changed and only the diffusion model would capture the quadratic dependence of the kinetic time constant on the radius of the particles. The empirical models are only correlative and not predictive, they cannot be used for conditions different from those used in the actual experiment from which the parameters were obtained.

Fig. 4
figure 4

Regression of uptake data based on linear diffusion model. Filled points are those used in establishing the trendline. Uptake predicted using Eq. 30 passing through the first two points. p-Xylene \({c}_{0}=500\) mol m−3 and \({M}_{S}=40\) gr

Full size image

The intercept of the linear regression in Fig. 4 is a significant deviation from 0 and this would be interpreted as evidence of combined surface resistance and internal diffusion (Câmara et al. 2020; Kong et al. 2016; Lupul et al. 2015; Peralta et al. 2019; Rincon-Silva et al. 2016; Shen et al. 2018; Heyden et al. 2018), even though if this was the case the intercept should be negative. The positive intercept is actually a result of the fact that the points used are already outside the range where the first term in the series expansion is sufficient to describe the response. Assuming a contribution from film resistance leads again to identifying the incorrect transport mechanism.

Additional information can be inferred when the slope of the short time regression is converted to a diffusional time constant

$$\frac{{R}_{P}^{2}}{{D}_{P}^{App}}={\left(\frac{6{Q}_{\infty }}{{A}_{D}\sqrt{\pi }}\right)}^{2}$$
(39)

to obtain approximately 289 min. The PFO fit of the data can also be interpreted as the long-time asymptote of the linear diffusion equation. From the slope of the PFO regression curve and Eq. 36, it is possible to estimate a value of the apparent time constant of approximately 104 min. This simple check would allow to confirm that the system is strongly non-linear and that the data should be analysed with the full model.

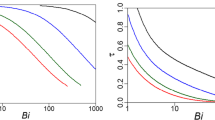
The nonlinearity of this system is also evident from the comparison of the data and the linear model that includes variable fluid concentration, Eq. 30. This comparison, shown in Fig. 4, provides much more information than the empirical linear regression and should always be preferred over the linear short time approach. The practical barrier to generating the curve from Eq. 30 are the roots of Eq. 30c. The simplest and most robust method of generating the \({\beta }_{n}\) values is the bisection method applied in each \(\pi\) interval after the first, given that the sign of the function is always positive to the left of the root and negative to the right. Any solver of a single nonlinear equation will also work, provided that the search for the solution is kept within the correct \(\pi\) interval. Note that \(\lambda\) is the ratio of the moles in the solid to those in the fluid at equilibrium, and is a constant which allows the calculation of \({\beta }_{n}\) before the attempt to estimate the time constant is carried out. Therefore, rate of convergence to a solution is not an issue and robustness is key.

Figure 5 shows the internal concentration profiles at 3 and 30 min. Note how the profiles are qualitatively similar to a shrinking core model. On close inspection there are however two main differences: the sharp but continuous transition to the initial concentration in the inner part and the fact that the plateau close to the surface shifts down with time because of the decrease in concentration in the fluid phase, i.e. there is desorption taking place in the outer layer of the particle.

Fig. 5
figure 5

Internal concentration profiles after 3 and 30 min. Note strong nonlinearity as evidenced by the sharp inflection in the profiles. p-Xylene \({c}_{0}=500\) mol m−3 and \({M}_{S}=40\) gr

Full size image

Without a detailed analysis of the kinetic response or a comparison with the full solution of the diffusion equation, the strong nonlinearity could be detected from results over a range of adsorbed phase concentrations, always taking into account the finite volume and variable fluid concentration during the experiment.

Given the importance of the nonlinearity of the isotherm on the resulting kinetic responses, an alternative that could be useful to consider would be a desorption experiment. This could be carried out by allowing the solution to equilibrate first and then adding a known quantity of solvent after the adsorption step. Note that this additional experiment is not common, but would allow to distinguish between reversible and irreversible adsorption. It would be recommended when enough sensitivity is available in the concentration detector.

Figure 6 shows the results for m-xylene, \({\Gamma }=0.44\). Here the nonlinearity is mild as can be seen from the concentration profiles shown in Fig. 7. Also in this case the trends observed match closely the observations made for the p-xylene example. Again R2 values close to unity are obtained for all the unconstrained linear regressions and the values range from 0.996 to 0.999. When the linear uptake plot is used to check results, the PFO model is seen to match poorly the data. The PSO and Elovich kinetic models would be chosen to represent this system.

Fig. 6
figure 6

Linearized plot and linear regression of data using the PFO, PSO and Elovich models. Filled points are those used in establishing the trendline. Lower right plot shows the linear plot of the uptake data with the curves calculated from the parameters obtained from the unconstrained linear regression. For the PFO model an additional curve is shown with the correct final concentration. m-Xylene \({c}_{0}=250\) mol m−3 and \({M}_{S}=40\) gr

Full size image
Fig. 7
figure 7

Internal concentration profiles after 3 and 30 min. m-Xylene \({c}_{0}=250\) mol m−3 and \({M}_{S}=40\) gr

Full size image

It is possible to see now that the PSO and Elovich models will match the pure diffusion uptake curves with both strong and mild nonlinearity in the isotherm. This simply reflects the nature of the models that start with a fast rate and approach equilibrium with a significantly lower rate. This is a result of the shape that these empirical kinetic models can reproduce and the fact that this is consistent with the diffusion model and what happens in the batch adsorption experiment. However, both empirical models are not physically meaningful for physisorption and should not be used to correlate the data.

Figure 8 shows the comparison of the data and the linear diffusion model. Equation 30 is now seen to match closely the data over the entire kinetic response. In this case the linear model would provide an accurate method to determine the tortuosity of the particles.

Fig. 8
figure 8

Regression of uptake data based on linear diffusion model. Filled points are those used in establishing the trendline. The model shown is calculated from Eq. 30. m-Xylene \({c}_{0}=250\) mol m−3 and \({M}_{S}=40\) gr

Full size image

The addition of a film resistance to mass transport will affect primarily the short time response where the rate is faster. The worst case scenario for external film resistance can be estimated from the Sherwood number set to 2, i.e. \({k}_{F}=\frac{{D}_{m}}{{R}_{P}}\). The uptake curves for the diffusion with and without film resistance cases are qualitatively similar as shown in Fig. 2. Therefore the same trends already observed will apply to the empirical models. The only noticeable difference is the more gradual transition from a fast initial rate to a slower final approach to equilibrium, and this in turn will favour the PSO model for nonlinear systems which becomes the model of choice based on the goodness of fit. Figure 9 shows the uptake response for the p-xylene case with Sh = 2 along with the match to the Langmuir kinetics and LDF models. Due to the effect of the variation in fluid concentration on the apparent mass transfer coefficient, the Langmuir kinetics model is a very good match to the data and the best model in Fig. 9. Even by eye one can see that the R2 is very close to unity, but again there are no reactions taking place and Langmuir kinetics is not the physical mechanism of mass transport. The excellent match to the data is only the result of the shape of the uptake curves obtained from Langmuir kinetics.

Fig. 9
figure 9

Uptake curves for p-Xylene \({c}_{0}=500\) mol m−3 and \({M}_{S}=40\) gr and Sh = 2. Langmuir kinetics and LDF models are calculated adjusting \({q}_{S}\) to give the same fluid phase concentration at equilibrium. The PSO model is calculated from the parameters obtained from the unconstrained linear regression

Full size image

Very similar results are obtained for the m-xylene case with Sh = 2. This shows that a diffusion process with or without some surface film resistance can be incorrectly interpreted to conform to the PSO, Elovich and Langmuir kinetic models simply due to the characteristic shape of the uptake curves in a batch adsorption experiment. Figure 10 shows the \(\bar{Q}\) vs. \(\sqrt{t}\) plot of the data for m-xylene with Sh = 2.

Fig. 10
figure 10

Regression of uptake data based on linear diffusion model. Filled points are those used in establishing the trendline. m-Xylene \({c}_{0}=250\) mol m−3 and \({M}_{S}=40\) gr and Sh = 2

Full size image

Note that in Fig. 10 the intercept is negative, as one would expect in this case. A recent example of Cu++ kinetics in a coke derived porous carbon (Yuan et al. 2019) shows R2 values close to unity for the unconstrained linear regressions from all empirical models considered here, with the Elovich being the worst. The data also lead to a negative intercept of the linear diffusion regression. All these results seem to suggest that this particular system was in fact limited primarily by a film resistance, especially because the PFO model shows a calculated equilibrium concentration that is close to the actual measured value. This is very similar to the case p-Xylene \({c}_{0}=500\) mol m−3, \({M}_{S}=10\) gr, \({\Gamma }=0.94\) and Sh = 2 shown in fig. S-2.

We turn now briefly to a case where adsorption is irreversible and generate the data with the shrinking core model. There were no substantial differences observed compared to the p-xylene case, therefore the curves and linear regressions are shown in the Supplementary Information for one of the experiments reported by Phelps and Ruthven (2001). The linear regressions give R2 values of 0.9978, 0.9989, 0.9959 for the PFO, PSO and Elovich models respectively. Also in this case there is very little to discriminate between the models based on this figure of merit. Figure 11 shows the uptake curve and the calculated responses, including Langmuir kinetics. There is very little difference between the shapes of the PSO and the Langmuir kinetics models. The unconstrained regression of the parameters of the PFO model is shown to be the worst model.

Fig. 11
figure 11

Uptake curves for Cu++ in Ionac SR-5 Cation Exchange Resin. \({C}_{0}=0.0059\) gr Cu/ml; \({V}_{F}=100\) ml; \({M}_{S}=3.6\) gr; \({Q}_{S}=0.09\) gr Cu/gr resin. Langmuir kinetics are calculated setting \(b={10}^{6}\). The other models are calculated from the parameters obtained from the unconstrained linear regression

Full size image

Based on Fig. 11 the PSO model would be selected as the kinetic model in this case, but again this would be inconsistent with the actual mechanism, given that Phelps and Ruthven report experiments carried out with different bead sizes that show that for this system uptake is a diffusion controlled process, which at high concentrations is well described by the shrinking core model (Phelps and Ruthven 2001).

4 Conclusions and recommendations

The analysis carried out has shown that empirical models, that lead to linear regression of uptake data from batch adsorption experiments, can match the data well if the goodness of fit is based on how close to unity R2 is. This can be very misleading especially if unconstrained regression of data is applied, particularly for the pseudo first order model. The models and the data should always be shown on a full uptake plot to avoid the incorrect interpretation of the results.

For two nonlinear models, namely macropore controlled diffusion in beads with a Langmuir isotherm and the shrinking core model, the empirical approaches lead to the incorrect identification of the mechanism if only one uptake experiment is carried out. Experiments in a wide range of conditions will result in coefficients that vary significantly, generating a confusing picture of the kinetic behaviour. This can lead to inefficient experimentation, given that the effect of many different parameters has to be investigated, even when the actual physical mechanism contains only one or two parameters that need to be determined.

When uptake curves conform to the pseudo second order model and the pseudo first order model has an R2 close to unity, but a low calculated equilibrium amount, it is likely that a diffusion model coupled with an appropriate isotherm will match the data very well. It would be important to carry out experiments with particles of different sizes to confirm that this is indeed the case.

When using the linear plot based on the solution of the diffusion equation for short times, a positive intercept is an indication that the initial rate of uptake is fast and that the data selected are already beyond the range of validity of the approximate model. The resulting apparent diffusivity will be lower than the true value. It is preferable to use the full solution, Eq. 30, in this case. Furthermore, identifying multiple linear regions in the \(\bar{Q}\) vs. \(\sqrt{t}\) plot is inconsistent with the diffusion model.

All the approximate models should be used only to arrive at an initial estimate of the mass transfer coefficients. This may be sufficient if the scope of the investigation is a direct qualitative comparison between materials tested in the same experimental system.

For a more accurate determination of the mass transfer coefficients the full nonlinear models should be used with the measured equilibrium isotherm parametrised independently. Furthermore, given that the experiment relies on measuring the variation of the fluid concentration in time, models based on the assumption of constant fluid concentration should not be used.

Phenomenological models should be preferred over empirical kinetic expressions. This is particularly important when the scope of the investigation is the measurement of kinetic responses to aid the design of separation processes or reactors. In such applications the models used and the corresponding parameters have to be applicable also to multicomponent mixtures and to conditions that can be far from those explored in the batch experiments.