Fast numerical integration of highly oscillatory Bessel transforms with a Cauchy type singular point and exotic oscillators

Abstract

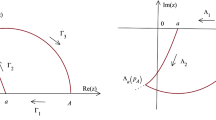
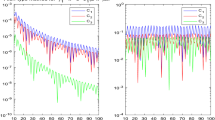
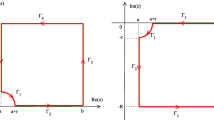
In this article, we propose an efficient hybrid method to calculate the highly oscillatory Bessel integral $\int _{0}^{1} \frac{f(x)}{x-\tau } J_{m} (\omega x^{\gamma } )\textrm{d}x$ with the Cauchy type singular point, where $0< \tau < 1, m \ge 0, 2\gamma \in N^{+}.$ The hybrid method is established by combining the complex integration method with the Clenshaw– Curtis– Filon– type method. Based on the special transformation of the integrand and the additivity of the integration interval, we convert the integral into three integrals. The explicit formula of the first one is expressed in terms of the Meijer G function. The second is computed by using the complex integration method and the Gauss– Laguerre quadrature rule. For the third, we adopt the Clenshaw– Curtis– Filon– type method to obtain the quadrature formula. In particular, the important recursive relationship of the required modified moments is derived by utilizing the Bessel equation and the properties of Chebyshev polynomials. Importantly, the strict error analysis is performed by a large amount of theoretical analysis. Our proposed methods only require a few nodes and interpolation multiplicities to achieve very high accuracy. Finally, numerical examples are provided to verify the validity of our theoretical analysis and the accuracy of the proposed methods.