1 Introduction

Lightning strikes are a naturally occurring phenomenon that interact with airliners approximately once per year [1]. A lightning strike is a combination of several interacting physics, including electrical, thermal and mechanical loading behaviours. Lightning strikes have been characterised into four test Waveforms (A-D) which have then been used as the inputs for simulation and experimental research. These are proposed in SAE-ARP5412B where each waveform has its own time period and peak current profile [2].

A small number of experimental works have been conducted to attempt to study lightning strike damage in a controlled environment, e.g. [1, 3,4,5,6,7]. Research is on-going to model the plasma developed during a strike using Finite element or CFD simulations and the resulting loading to the specimen [8, 9, 18,19,20,21, 10,11,12,13,14,15,16,17]. The majority of simulation authors have modelled specimen behaviour only and assumed a surface load, employing FE models to characterise the thermal damage [8, 10, 11, 14, 16, 20] or damage as a result of pressure loading [11,12,13]. More recent works have incorporated thermal expansion effects [15, 17]. However, a modelling approach using all three of these loads has not been developed and the vast majority of models with individual loads have assumed / idealised surface loads which do not represent the complexities of the lightning plasma. Moreover, lightning is understood to result in high strain, high heating rates, high temperatures, and both thermal and mechanical damage to the fibres and resin. However, the representation of composite material damage in the published works is typically incomplete (with omitted physical phenomena). To accurately predict material degradation and failure the appropriate behaviours must be represented. Works have included damage initiation models [13] and progressive failure models [12, 17, 22]. However, none of these models have incorporated the strain and heating rate effects which are generally expected for a lightning strike event.

Therefore, the objective of this paper is to generate a failure model including damage initiation, progressive failure and strain and heating rate effects and use this to model lightning strike damage. In addition, to avoid the use of assumed specimen loading conditions, where possible plasma simulation for SAE test Waveforms will be used to demonstrate a complete modelling framework – representing specific artificial lightning strike test arrangements.

2 Background

Lightning strike simulations have typically focussed on thermal-electric models to predict the effects of resistive heating due to current loading [8, 10, 13, 16, 19, 23, 24] and have attempted to replicate the experimental work of Hirano et al. [1]. Foster et al. defined moderate (wide and shallow area of sharp and shiny resin, fibre fracture, matrix cracking, delamination and fibre blow out) and severe damage (narrow but deep region with char residue, fibre fracture and fibre blow out) areas using simulation temperature boundaries of 300 °C and 500 °C [14]. Using these boundaries a summary of the damage predictions of preceding thermal-electric works can be established [14]. Generally speaking these works under predict both moderate damage areas (from −97% [20] to −71% [10]), and severe damage areas (−83% [23] to −57% [10]). However, damage depth is generally over predicted, 2% [10, 24] to 80% [10, 24]. These significant under and over predictions for damage suggest that other physics, beyond the modelled resistive heating, play an important role in the damage of the test specimen.

As noted in the introduction, authors have attempted to model the other contributors to damage (pressure and thermal expansion due to resistive heating). However, comparisons with experimental results are limited. Foster et al. [13], using the damage modelling strategy of Phadnis et al. [25], for their lightning strike pressure loading simulations, used Hashin/Puck criteria but no damage evolution to predict failure. Instead the damage initiation criteria was used to delete elements. The peak pressure load for Waveform A was calculated and uniformly applied over a central radius of 5 mm [13], where the upper bound loading (200 MPa) was almost enough to cause some mechanical damage alone. Yao et al. [22] and Dong et al. [17] used continuum damage mechanics (CDM) to model progressive damage evolution for scaled SAE test Waveform A, with peak current magnitudes of 10, 30, 50 and 40 kA. Hashin and Yeh failure initiation criteria were used with an exponential damage evolution law. A combined thermal and mechanical constitutive relationship was used in both UMAT and VUMAT subroutines. Yao compared their results with the experimental work of Feraboli and Miller [3] while Dong compared their results with the work of Hirano et al. [1]. Yao focussed on thermal and pressure loading damage while Dong conducted thermal and thermal-expansion analyses. While the results of both works were closer to experimental results than thermal damage alone, both have neglected one of the three key physics involved, either pressure or thermal expansion. Constrained thermal expansion was also considered by Foster et al. using the outputs of a preceding thermal-electric simulation to generate the temperature profile during the simulated strike [15]. Karch et al. [12] conducted an extensive study for Waveform D (96.4kA, 20 MPa peak) pressure loading using a progressive damage model with four bilinear softening laws. However, while Foster et al. included cohesive zones between plies to represent interlaminar failure, Karch et al. did not consider this failure mode.

Beyond lightning strike simulations, failure models have typically been developed in the high and low velocity impact research fields with many authors using criteria for damage initiation and different relations for degradation [25,26,27,28,29,30,31]. The majority of studies in this area have used the Hashin or Puck failure criteria or a combination of both, however some authors have used the Tsai-Wu criteria [30]. Phadnis et al. [25] used a combination with the criteria adjusted for rate dependency using the equations of Daniel et al. [32]. Long et al. [28] used the Hashin criteria only with a linear damage evolution model, as did Shi et al. [27]. However, this set of authors used Hashin for fibre tension and compression and matrix tension with Puck for matrix compression. Tan et al. [26] modelled low velocity impact and compression-after-impact (CAI) damage using a more advanced initiation criteria proposed by Catalanotti et al. [33] and compared this with Hashin. Tan et al. noted that the inclusion of in-situ effects required more detailed study and material testing, beyond the scope of both that and this work. A similar bilinear damage evolution model was used by Tan et al. as other authors [27, 28].

Foster et al. [15] indicated that, to best knowledge, no single material data set was available within literature which incorporated the combined heating rates, high temperatures and high strain-rates expected in a composite material during a lightning strike event. Foster incorporated these effects individually to analyse their influence. Surface damage area varied by 30 and 50% respectively for heating rate and strain rate dependent material properties [15]. More generally, studies have been conducted to experimentally determine the influence of strain on composite material properties [32, 34,35,36,37,38,39,40] however significantly less have focused on the combined effects of strain and heating rates [41, 42]. Zhang et al. [41] experimentally compared the effects of temperature and strain rate for 3D braided composites. A heater and split-Hopkinson pressure bar (SHPB) were used in tandem between 23 and 210 °C and 1200s−1 to 2400 s−1. Results showed that compression modulus, failure stress and specific energy absorption decreased with increasing temperature while failure strain increased. Conversely the failure stress, failure strain and specific energy increased with strain rate. Interestingly, compression modulus was particularly sensitive to combined strain rate and temperature effects. These experiments were conducted at constant temperatures and thus did not include any effects from heating rate; which could reasonably be expected to be present and to be large during a lightning strike event.

2.1 Summary

Literature has shown that progressive damage models have been under development for a number of years and are beginning to find application within lightning strike simulations. However, to-date these have typically been confined to simulations of a single type of lightning strike physics (thermal-electric, pressure-displacement, thermal-displacement) and have not accounted for the strain and heating rate effects observed during a lightning strike event. Preceding works which have studied the various physics individually indicated that mechanical damage plays an important role during Waveform A and thermal damage plays an important role under Waveform B conditions [15, 21]. In general, given the individual physics studied in preceding works, there is limited understanding of the combined role or ratio of damage for the range of physical loading types. Moreover, how damage mechanisms change with waveform is also unknown. The hypothesis of this work is that by introducing a more complete simulation framework it will become possible to model each waveform type and quantify the relevant ratio of each damage mechanism and thereby enable better understanding of the critical behaviour for each. Hence herein a coupled thermal-mechanical damage model is proposed which can incorporate strain and heating rate effects to better characterise damage as a result of lightning strikes. Damage will be predicted in a two-phase process with thermal ablation damage predicted in the first phase, and coupled thermal-mechanical behaviour in the second. As preceding literature has not represented the full range of damage modes possible this approach will create new understanding on lightning strike damage. Moreover, by loading the damage models with plasma simulations (in a three-step simulation process; a plasma simulation to predict specimen loading, a thermal-electric simulation to predict thermal ablation, a dynamic, coupled temperature-displacement, explicit model to predict thermal-mechanical damage) this approach will create new understanding on waveform effects on composite material damage. Development of the material and damage modelling strategy will now be discussed along with benchmarking of the individual component parts.

3 Implementation and Verification/Validation

This section will cover the theory behind the generation of a VUMAT subroutine to model damage. Composite specimens, subjected to lightning strikes, have two broad failure modes: intralaminar - characterised by thermal decomposition of the fibres and resin deterioration, and interlaminar - characterised by delamination [14]. According to the constitutive relationship for an orthotropic composite material the stress, σ, and strain, ε, can be related using:

$$ \left\{\sigma \right\}=\overline{C}\left\{\varepsilon \right\}=\left[\begin{array}{ccc}\frac{1-{\nu}_{23}{\nu}_{32}}{E_2{E}_3\Delta }\kern0.5em \frac{\nu_{21}+{\nu}_{31}{\nu}_{23}}{E_2{E}_3\Delta }\kern0.5em \frac{\nu_{32}+{\nu}_{21}{\nu}_{32}}{E_2{E}_3\Delta }& & \kern0.5em \\ {}\begin{array}{ccc}\kern5.5em & \frac{1-{\nu}_{31}{\nu}_{13}}{E_1{E}_3\Delta }& \frac{\nu_{32}+{\nu}_{31}{\nu}_{12}}{E_1{E}_3\Delta }\end{array}& & \begin{array}{cc}& \end{array}\\ {}\begin{array}{ccc}\begin{array}{c}\\ {}\\ {}\begin{array}{c}\\ {}\end{array}\end{array}& \begin{array}{c}\kern9.75em \\ {}\\ {}\begin{array}{c}\\ {}\end{array}\end{array}& \begin{array}{c}\begin{array}{c}\frac{1-{\nu}_{12}{\nu}_{21}}{E_2{E}_1\Delta }\\ {}\end{array}\\ {}\\ {}\end{array}\end{array}& \begin{array}{c}\\ {}{G}_{12}\\ {}\begin{array}{c}\\ {}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\\ {}\\ {}\begin{array}{c}{G}_{23}\\ {}\end{array}\end{array}& \begin{array}{c}\\ {}\\ {}\begin{array}{c}\\ {}{G}_{13}\end{array}\end{array}\end{array}\end{array}\right]\left\{\varepsilon \right\} $$
(1)

where \( \overline{C} \) is the stiffness matrix and Δ is given by the following:

$$ \Delta =\frac{\left(1-{\nu}_{12}{\nu}_{21}-{\nu}_{23}{\nu}_{32}-{\nu}_{13}{\nu}_{31}-2{\nu}_{21}{\nu}_{32}{\nu}_{13}\right)}{\left({E}_1{E}_2{E}_3\right)} $$
(2)

and where Ei (i = 1,2,3) is the elastic modulus, νij is Poisson’s ratio and Gij is the shear modulus. The strain in this case is the sum of the mechanical and thermal strains:

$$ \varepsilon ={\varepsilon}_{Mechanical}+{\varepsilon}_{Thermal} $$
(3)

where the thermal strain is the product of the thermal expansion coefficient, α, and ΔT, the change in temperature.

3.1 Influence of Strain and Heating Rates

Authors have typically observed that strain rates affect moduli, fracture toughness and strength properties while heating rates affect the moduli of the material [15]. The incorporation of these parameters will now be discussed individually.

3.1.1 Influence of Heating Rate

Heating rate effects were identified as a key influence on material behaviour for lightning strike simulations by several authors [10, 14, 24]. With increasing heating rate the decomposition or mass loss curves were shown to offset, i.e. a lag in the temperature at which decomposition occurs [10]. The offsets were typically represented in the material definition by modifying the temperature at which a material change occurred. An example was reported by Foster et al. [14] who took Abdelal and Murphy’s [20] data and modified the temperatures for property changes to reflect the heating rate using the observed offset of approximately 200 °C from the work of Ogasawara et al. [10]. When the work of Ogasawara et al. was studied more closely for a heating rate between 11 and 20 °C/min the offset was 35 °C with the other offsets and heating ranges shown in Table 1. Herein the same approach was used within the VUMAT using the material data from Chen et al. [18]. Chen’s data was selected because it provided the most complete set of mechanical properties to compliment the electrical and thermal properties from Foster et al. for the same material [14]. The offset was used to adjust the temperature at which the moduli and strength of the material changed. Within each temperature limit the moduli were linearly interpolated. State variables were defined and used with a min() function to prevent the scale factors and therefore modulus increasing if the element cooled down after heating. The scale factor ω was used to scale the material properties with the relevant heating rate effects. For example, for E2 the scale factor was determined as follows:

$$ \omega =\left\{\begin{array}{c}1.0\kern14.00em if\ T\le \left(200+ OFF\right)\\ {}\begin{array}{cc}\frac{\left(T-\left(200+ OFF\right)\right)\left(0.8-1\right)}{\left(260+ OFF\right)-\left(200+ OFF\right)}+1& if\ \left(200+ OFF\right)<T\le \left(260+ OFF\right)\end{array}\\ {}\begin{array}{c}\begin{array}{cc}\vdots \kern20.75em & \vdots \end{array}\\ {}\begin{array}{cc}0.00005& \kern11.25em if\ T>\left(3316+ OFF\right)\end{array}\end{array}\end{array}\right. $$
(4)

where T was the temperature (°C) and OFF was the offset.

Table 1 Temperature offset with corresponding heating rate ranges
Full size table

3.1.2 Influence of Strain Rate

Three strain rate regimes are typically defined in literature; quasi-static (QS) taken as 0.1 s−1 or less, high-rate (HR) defined as 100 s−1 or higher and the intermediate zone between these values [32, 34,35,36,37,38, 43]. Strain rate effects have been represented in the material definition by Foster et al. [15] where the transverse modulus was scaled uniformly with increasing strain rate for example by a factor of 1.5 for a strain rate 1x103s−1. Herein, to incorporate the effects of strain rate on the material the rate was first calculated and used to determine the strain rate regime. The choice of regime then determined the scale factors for the material properties which were collated from a variety of sources, with experiments conducted at both QS and HR conditions, using a SHPB [32, 35, 36]. The results of these studies were used to generate the scale factors shown in Table 2 and implemented in the material subroutine. In the intermediate zone the scale factors were linearly interpolated, as with heating rate effects, as the strain rate changed. Strain rate effects were incorporated into E2, E3 and the intralaminar strength and fracture toughness properties. These properties were transformed as follows using the strain rate scale factor β where for E2:

$$ \beta =\left\{\begin{array}{c}1.0\kern12.7em if\ {\dot{\varepsilon}}_2\le 0.1\\ {}\frac{\left({\dot{\varepsilon}}_2-0.1\right)\left(1.29-1\right)}{100-0.1}+1\kern5.25em if\ 0.1<{\dot{\varepsilon}}_2<100\\ {}1.29\kern12em if\ {\dot{\varepsilon}}_2\ge 100\end{array}\right. $$
(5)
Table 2 Scale factors for strain rate effects. [32, 35, 36]
Full size table

Once both scale factors (heating rate and strain rate) had been determined the material properties were updated where, for scaled E2 (\( {\overline{E}}_2\Big) \):

$$ {\overline{E}}_2=\omega\ \beta\ {E}_2 $$
(6)

3.2 Failure Initiation

Failure initiation has been included in the majority of lightning strike simulations using the Hashin or Puck failure criteria or a combination of both. For example, Foster et al. used a combination of both [13]. Hashin failure criteria was used for both compression and tension in the fibre direction and transverse tensile failure. The Puck [44] criteria was used for compressive failure in the transverse and through-thickness directions [13]. Herein, the same combination of Hashin/Puck was used. Thus in the material subroutine, Hashin tensile and compressive fibre failure were represented using:

$$ F=\left\{\begin{array}{c}{\left(\frac{\sigma_{11}}{X_T}\right)}^2+{\left(\frac{\sigma_{12}+{\sigma}_{13}}{S_{12}}\right)}^2,\kern0.5em {\sigma}_{11}\ge 0\\ {}{\left(\frac{\sigma_{11}}{X_C}\right)}^2\kern7.5em ,\kern0.5em {\sigma}_{11}<0\end{array}\right. $$
(7)

where F was the failure index. The Hashin in-plane transverse matrix tension and Puck in-plane transverse matrix compression were calculated using:

$$ F=\left\{\begin{array}{c}{\left(\frac{\sigma_{22}}{Y_T}\right)}^2+{\left(\frac{\sigma_{12}}{S_{12}}\right)}^2+{\left(\frac{\sigma_{13}}{S_{12}}\right)}^2,\kern0.5em {\sigma}_{22}\ge 0\\ {}{\left(\frac{\sigma_{33}}{Y_T}\right)}^2+{\left(\frac{\sigma_{13}}{S_{12}}\right)}^2+{\left(\frac{\sigma_{23}}{S_{12}}\right)}^2,\kern0.5em {\sigma}_{22}<0\end{array}\right. $$
(8)

In the case of Puck through-thickness matrix compression failure, this was given by:

$$ F=\left\{{\left(\frac{\sigma_{11}}{X_T}\right)}^2+\left(\frac{{\sigma_{33}}^2}{Y_T+{Y}_C}\right)+{\left(\frac{\sigma_{23}}{S_{12}}\right)}^2+\left(\frac{\sigma_{33}}{Y_T+{Y}_C}\right)\right. $$
(9)

if σ33 < 0.

Finally, if damage had occurred and the failure index reached a value of F ≥ 0.99 then further modifications to the material properties by strain or heating rate effects were skipped and the model representation moved directly to damage evolution.

3.3 Progressive Damage Evolution

Progressive damage evolution models the stiffness degradation of the material after failure initiation. Tan et al. [26] used a linear damage evolution model which occurred after the failure initiation criteria, Hashin, was greater than 0.99.. Herein, the same approach was used as shown in Fig. 1. The damage parameter for damage evolution was given by the following equation [26]:

$$ d=\frac{\varepsilon_f}{\varepsilon_f-{\varepsilon}_i}\left(1-\frac{\varepsilon_i}{\varepsilon}\right),\kern0.5em \varepsilon >{\varepsilon}_i $$
(10)

where d is the damage parameter, εf is the failure strain, εi is the initiation strain and ε is the current strain on the element. The initiation strain was determined from the failure strength and modulus in the corresponding direction, εi = XT/E11 while the failure strain was determined using the appropriate fracture toughness, strength in the relevant orientation and the characteristic length of the given element, εf = 2Γ/XTl∗. When initiation occurred the damage area grew and the stress was gradually reduced to zero at the failure strain using Eq. 11.

$$ \sigma =\left(1-d\right)\overset{\sim }{\sigma } $$
(11)
Fig. 1
figure 1

Bilinear Law for Tensile Failure

Full size image

3.3.1 Characteristic Length Calculation

The characteristic length was used to incorporate the crack-band theory of Ba\( \overset{\check{} }{\mathrm{z}} \)ant and Oh [45] to avoid mesh objectivity allowing the model to be more mesh independent. The characteristic length of the element was determined from the cube root of the element volume and was given an upper limit in order to avoid negative behaviours such as distorted elements or snap-back behaviour. This limit was given by,

$$ {l}^{\ast }=\frac{V}{A}\le \frac{2\varGamma E}{X^2} $$
(12)

where the variables Γ, E and X in Eq. 12 are the intralaminar fracture toughness, elastic modulus or strength for the fibre or matrix [26]. Using the values in Table 3 and Table 4 the maximum element size was calculated as l∗≤0.71 mm.

Table 3 Temperature dependent mechanical properties of CFRP [18]
Full size table
Table 4 Strain rate effects on intralaminar strength and fracture toughness [23]
Full size table

3.4 Interlaminar Failure

Delamination was modelled using ABAQUS/Explicit cohesive surfaces incorporating the bi-linear traction-separation law. This reduced the total number of elements required as opposed to cohesive elements [46]. In this law failure initiation was governed by the quadratic stress criterion.

$$ {\left(\frac{\tau_1}{\tau_1^0}\right)}^2+{\left(\frac{\tau_2}{\tau_2^0}\right)}^2+{\left(\frac{\left\langle {\tau}_3\right\rangle }{\tau_3^0}\right)}^2\le 1 $$
(13)

where τi(i = 1, 2, 3) are the stresses in each material orientation and \( {\tau}_i^0 \) is the maximum stress in each orientation. Delamination was then modelled to propagate using the mixed-mode relationship proposed by Benzeggagh and Kenane (B-K) [13, 47].

$$ {G}_c={G}_{Ic}+\left({G}_{IIc}-{G}_{Ic}\right){B}^{\eta } $$
(14)

where Gc is the mixed-mode fracture toughness, B is the local mixed-mode ratio defined as B = Gshear/(GI + Gshear) where Gshear = GII and η is the mixed-mode interaction typically determined from experiments but taken as 1.45 in this work [13]. Penalty interface stiffness values, K, were left default [46]. Kamiyama et al. [48] proposed relationships for each interlaminar property against pyrolysis degrees of 0, 10 and 100%. These were correlated with temperatures of 25, 300 and 3000 °C respectively, incorporated herein and showed that the interlaminar properties became infinitely small at and above 300 °C.

3.5 Other Model Considerations and Assumptions

Some other considerations and assumptions should be noted:

  • Tensile softening in the through-thickness direction was ignored since propagation occurred in the interface and the cohesive region was weaker than the ply.

  • Offset (OFF) values were not interpolated but were considered constant values for each heating rate band. Further experimental work would be required to improve these offsets although this approach provided a good first approximation.

  • The same scale factor was used for S12 and YT as shear is a matrix dominated failure.

  • No strain rate effects were considered on E1 as literature did not report any effects.

Figure 2 shows the flowchart for the developed subroutine. Benchmarking of the subroutine will now be discussed.

Fig. 2
figure 2

Flowchart of VUMAT subroutine

Full size image

3.6 Benchmarking Failure Model

During and after generation of the failure model the component parts were benchmarked against published works. This established that the individual components of the VUMAT behaved correctly and could replicate a variety of applications and test cases with comparatively short run-times compared to the full scale simulations. These benchmarking tests will now be briefly discussed prior to the main application within lightning strike simulations.

Firstly, damage evolution was checked using a single element and the material data used by Tan et al. [26]. Damage evolution was assessed using peak stress, initiation and failure strains, volumetric strain energy density and element deletion occurrence. The final VUMAT implementation performed within 10% of the expected values.

The second benchmark was the sensitivity of scale factors & characteristic length. Using the material properties of Foster et al. [13] the effect of intralaminar fracture toughness was assessed. Properties were adjusted by ±10% and tested using a single element under transverse compression, the limiting factor for characteristic length. When \( {\varGamma}_{22}^C \) was increased by 10% energy regulation improved since the failure strain had increased by 7.2%. However, when \( {\varGamma}_{22}^C \) was reduced by 10% energy regularisation became more difficult, since the failure strain had reduced by 15% and approached a snapback condition.

Next YC properties were modified by ±10% with effects on stress-strain plots checked, Fig. 3. In this test \( {\varGamma}_{22}^C \) was reverted to its original value. Firstly, when YC was reduced by 10% the peak stress reduced by 10%, as would be expected. However, when YC was increased by 10% this resulted in a snapback failure of the element i.e. the element was unable to regulate the energy involved in transverse compression. Therefore, to attempt to correct this condition, the scale factor for E2 was reduced by 10%. This increased the initiation strain by 9.4% and decreased the failure strain by 0.4% and eliminated snapback. Consequently, to prevent snapback and avoid problems in the regularisation of the energy the scale factor for the modulus and corresponding strength were made equal herein. One drawback of this approach was the potential incorrect strength, modulus and initiation strain combination, however failure strain was still accurate and element deletion would still occur at the correct strain.

Fig. 3
figure 3

Effects of modifications to YC

Full size image

Strain rate effects were tested against the work of Koerber et al. for both quasi-static and high rate tests for a single ply specimen [35, 36]. Compression tests were replicated and peak stresses were compared. These results were again within 10% of the expected values. This was deemed suitable since only one ply was modelled and no other damageable surfaces such as cohesive elements/surfaces were incorporated.

The final stage of benchmarking checked the heating rate and temperature boundary behaviour of the VUMAT. The experimental work of Pinto et al. [42] was used to test temperature effects. Four DEN test cases were replicated using one 90o and one 0o ply with peak load predictions compared with the published experimental results. The model was able to predict the peak load with errors between −1% and − 5.6%.

3.6.1 Benchmarking Summary

The benchmarking results presented in this section illustrate the capability of the developed damage model and subroutine to capture the desired behaviours, individually, in a variety of designs and using a variety of composite material properties. Each aspect of the damage model has been tested individually and has predicted the required results within 10% in all cases. The main simulations for this work will now be discussed.

4 Lightning Strike Simulations

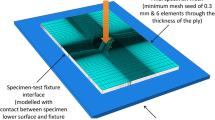
A two-phase damage modelling process was completed using ABAQUS. Firstly, a coupled thermal-electric simulation was used to generate a temperature profile throughout the specimen subjected to the lightning plasma electric loading. The composite specimen measured 150 × 100 mm with a total thickness of 4.704 mm and had a layup of [45/0/−45/90]4s (replicating the experimental work of Hirano et al. [1], Table 5). Temperature dependent material properties were represented, taken from Foster et al. [14]. A transient, fully coupled, thermal-electric step with DC3D8E elements was initially completed. A zero electrical potential boundary condition was applied to the side and bottom surfaces of the specimen to replicate the experimental conditions [1, 14, 20]. The mesh was optimised to adhere to the characteristic length requirements noted previously. A mesh of 33,478 elements, with two elements through the thickness of each ply, was developed. Results of a previous publication indicated that most of the moderate and severe damage, generated by thermal-electrical loading, was confined to a region 30 mm from the centre of the specimen [21]. This region enclosed 87% of the moderate damage volume (and all moderate damage below ply two) and 99% of the severe damage (and all severe damage below ply one) as shown in Fig. 4 along with the final mesh density. In order to reduce the number of elements, but still comply with the characteristic length conditions, two material definitions were used. In the central area, where most thermal damage occurred and pressure loading was applied, the main material, designated “inner material,” which featured damage evolution was used. At the extremities of the specimen, a simpler material, designated “outer material,” which neglected damage evolution was used. For the “outer material,” damaged elements were deleted when the initiation criteria was ≥0.99. The mesh was established such that it could be used for both the thermal-electric and temperature-displacement simulations. The second analysis was a dynamic, temperature-displacement, explicit analysis step completed in ABAQUS Explicit using C3D8RT elements [46]. Temperature dependent material properties were represented, taken from Chen et al. [18] (Table 3). Strain rate dependent fracture and strength properties were represented, taken from Wang et al. [23] (Table 4). In this simulation the specimen was placed on a copper plate, which was constrained in the z direction, to represent the experimental conditions [1]. The interlaminar properties from Kamiyama et al. [48] were also incorporated into the model, Table 6. The same python script methodology, proposed by Foster et al. [15], was used to transfer the temperature profile from the thermal-electric to the dynamic, temperature-displacement, explicit simulation.

Table 5 Hirano et al. [1] Experimental Damage Summary
Full size table
Fig. 4
figure 4

Severe damage area for each ply for thermal-electric simulation with inner material region marked (top) and final simulation mesh density (bottom)

Full size image
Table 6 Traction and fracture toughness properties for IMS60/133 [48]
Full size table

A Waveform B simulation was undertaken by loading the mesh with the plasma simulation outputs from previous publications [21, 49]. In this case the temperature-displacement simulation was run for a total of 0.03 ms because at this point the thermal damage had stopped increasing and pressure loading had normalised to atmospheric pressure. This pressure load was applied by means of a VDLOAD user-subroutine developed previously [50].

A scaled Waveform A simulation was also undertaken, using the same model mesh and material and boundary conditions as the published works of Foster et al. [13,14,15]. In this case the loading developed by Foster et al. [13,14,15] was applied as there was no published plasma simulation output for Waveform A in which the plasma properties were predicted from initial room temperature conditions. To the author’s best knowledge, Foster’s work represented the most complete time and space varying loading data set available in the literature. The three previous works of Foster et al. [13,14,15] were therefore combined in this single analysis. Foster’s Waveform A pressure load was assumed to expand every 2.5 × 10−6s, at a rate defined by Chemartin et al. [51]. Therefore in both cases (Waveform B and A), axisymmetric and expanding plasma loading was applied, which would aid in comparison between the simulation results. The peak pressure was assumed to be 50 MPa as this was quoted by Foster et al. as the peak corresponding with the experimental works of Hirano, Munoz and Chemartin et al. and which was considered herein for simulation prediction verification [1, 11, 13, 51]. Although Foster’s loading data set for scaled Waveform A was based on a series of argued assumptions [13,14,15] and the loading data for Waveform B was based on simulation output [19, 49] each was considered as the best available to-date for this study. The same temperature dependent mechanical properties, strain rate dependent fracture and strength properties, interlaminar properties and specimen boundary conditions were therefore used in the Waveform A analysis (matching the Waveform B analysis), Tables 3, 4 and 6.

These simulations were chosen as the Waveform A variant allowed for the prediction of damage due to short time period, high peak current loads and comparison with the published, single physics simulations from Foster et al. [13, 15], as well as the experimental results of Hirano et al. [1]. The Waveform B simulation allowed for the prediction of damage due to long time period, low peak current loads but with accurate predictions of the surface loading due to the preceding plasma model [19]. The damage simulation results are presented in the following section.

5 Results

This section will present the results for both Waveforms B and A. First the physics occurring in both simulations will be described and discussed, followed by details of the damage predictions. Comparisons between the predictions, preceding simulation studies and experimental test campaigns will then be presented and discussed. In these results critical damage is the hole generated in the specimen due to material removal and element deletion while interlaminar delamination is the delamination between plies. The calculation of both damage types considers the impact of strain rate and temperature effects.

5.1 Waveform B Thermal-Electric Results

Initially when current was applied to the top surface of the composite specimen it flowed predominantly in the fibre direction due to a comparatively high conductivity in this orientation compared with the transverse and through thickness directions. As the temperature of the top ply increased, due to resistive heating, ply resin decomposition occurred between 500 and 800 °C [14]. At this point through-thickness conductivity increased which allowed current to reach the second ply and beyond. A pattern of damage therefore formed through the specimen thickness based on the fibre orientation of each ply. The size of the damaged area reduced with each ply as less current reached each subsequent ply through the specimen thickness. Thermal damage for this model extended to five plies deep within the specimen. Figure 5 shows the severe damage volume (310mm3) for the specimen and Table 7 presents the moderate damage volume and moderate and severe damage areas on the top ply.

Fig. 5
figure 5

Thermal damage, delamination and damage initiation contours for Waveform B specimen

Full size image
Table 7 Predicted peak stresses and strains compared between models and published works [13, 15]
Full size table

5.2 Waveform B Multiple-Physics Stresses/Strains

Stresses, strains and strain rates through the thickness of the centre of the specimen were analysed during loading as they progressed over time. Waveform B strain rates ranged between 1 × 102 and 1 × 103 s−1 which placed them in the bar impact region as noted by Lindholm [43]. Table 7 shows the key intralaminar stresses and strains predicted for Waveform B conditions. Fibre, transverse and through-thickness stresses were all compressive in nature at the top of the specimen before becoming tensile further through the specimen and finally reducing to zero due to the limited thermal loading towards the specimen’s bottom surface. The predicted transverse and through-thickness stresses peaked at magnitudes of approximately 219 and 91 MPa respectively. Likewise the strains followed the trend of their respective stresses and were highest at the specimen surface, as this point was at the highest temperature. In general the shear stresses and strains were negligible in the specimen.

None of the peak stresses predicted in the specimen were high enough to cause significant critical damage to the specimen. Therefore, there was no predicted critical damage area for Waveform B, Fig. 5. Focussing on one-time point in both models (i.e. thermal-electric and temperature-displacement models), this behaviour can be illustrated. A time point 15% through the simulation was chosen to allow comparison. At this time the transverse strain rate \( {\dot{\varepsilon}}_{yy} \) for Waveform B was 285 s−1 at the specimen surface. At the same point the temperature was 222 °C. The heating rate at this time was 21,233 °C/min. Therefore, using the scale factor ranges developed previously the scale factors for strength were: 1.0 due to heating rate, and 1.37 due to strain rate. Therefore, YC which was used in the transverse direction scaled to 263 MPa. However, the peak transverse stress was only 43 MPa and therefore the predicted stress state was not enough to cause critical damage.

Delamination occurred in the top five plies with a total area of 1437mm2. The amount of both thermal damage and delamination reduced through-the-thickness of the specimen. Figure 5 shows the thermal damage and delamination for each of the top five plies in the specimen at the end of the simulation. The damage initiation contours in Fig. 5 show the low amount of critical damage that had initiated in the top five plies of the specimen. The dominant damage mode for Waveform B was delamination due to thermal expansion resulting from thermal loading. Most of the damage for Waveform B was caused by tension due to the thermal expansion of the top plies and the low pressure load.

5.3 Waveform A Thermal-Electric Results

The same physical electric and thermal behaviours as described for Waveform B (Section 5.1) were seen in the Waveform A results. In this case thermal damage extended to four plies deep within the specimen. Figure 6 shows the severe damage volume (7.53mm3) for the specimen. Under Waveform A conditions the moderate damage volume and moderate damage area resulting from Joule heating on the top ply were both significantly larger while severe damage area and volume were significantly smaller than predicted under the Waveform B conditions, Table 7.

Fig. 6
figure 6

Thermal damage, delamination and damage initiation contours for Waveform A specimen (elements deleted above 0.99)

Full size image

5.4 Waveform A Multiple-Physics Stresses/Strains

Stresses, strains and strain rates through the thickness of the centre of the specimen were again analysed as they progressed over time. Under the Waveform A conditions the strain rates were in the region of 1 × 104 to 1 × 105 s−1, which placed them in the high velocity impact region as noted by Lindholm [43]. Table 7 shows a comparison between the predicted peak stresses and strains for Waveform A and the previous works of Foster et al. [13, 15]. The predicted peak magnitudes for the transverse and through-thickness stresses were approximately 457 and 413 MPa respectively. Strains followed the trend of their respective stresses and were highest at the specimen surface, as this point was at the highest temperature. Shear stresses and strains were again negligible in the specimen.

Now looking at the damage prediction using the new user-subroutine for Waveform A it can be seen that the predicted critical damage area was 121 mm2 which was a decrease of 71% from the observed area from the experiment of Hirano et al. [1]. Considering the same location and time point as examined in detail during Waveform B - the transverse strain rate \( {\dot{\varepsilon}}_{yy} \) was 32,316 s−1, the temperature was 759 °C and the heating rate was 242,819 °C/min. Therefore, the scale factor for strength was 0.29 due to heating rate and 1.37 due to strain rate. As a result YC scaled to 78 MPa. On this occasion the transverse stress was 214 MPa therefore critical damage had occurred and the element had been deleted. Most of the damage for Waveform A was caused by compression due to the high peak pressure load acting on the top ply.

The critical damage depth had reached 8 plies or 1.18 mm, an underestimate of 4.8% from the average experimental value of 1.24 mm, Table 5. Considering delamination, the total predicted delaminated area for this simulation was 2099 mm2. This was approximately 4.4% above the average measured delamination area (2010 mm2, Table 5) from Hirano’s C-scan of the specimen, but within the upper and lower bounds of approximately 1800 and 2260 mm2 respectively [1, 14]. Delamination depth was predicted as 1.47 mm, 18.5% above the observed experimental depth of 1.24 mm. The predicted delamination area in this analysis can be seen side by side with the experimental C-scan in Fig. 7. Also illustrated in Fig. 7 is the cross-sectional damage comparison between the experiment and the simulation taken through the middle of each specimen. The general shape of damage was recreated in the simulation and was comparable with the experimental results, excluding the material displaced upwards in the experimental specimen. This was potentially related to an electrical-magnetic effect or a dynamic ablation effect not represented in the finite element model. The resin deterioration area also called the moderate damage area was 3709 mm2 which is 85% larger than the average experimental value (2007 mm2) from Hirano. This was potentially due to the assumed loading used in the thermal-electric model as currently there is no plasma simulation output available for Waveform A but it could also be contributed by the temperature boundaries defined by Foster et al. [14]. If the moderate area was defined by 324 °C rather than 300 °C the error with the average experimental value would be less than 1%.

Fig. 7
figure 7

Damage/Delamination plots for Waveform A and Hirano Experiment [1]

Full size image

5.5 Results Comparison

The results presented here clearly illustrate the difference in damage prediction between waveforms. Table 7 shows a comparison between the predicted peak stresses and strains for Waveform B, the work of Foster et al. for Waveform A [13, 15], the loading approach using a combination of Foster’s models [13,14,15] and ratios of severe thermal to critical damage areas. Comparing the Waveform A and B combined models, it is clear that the stresses and strains for Waveform A were much higher than Waveform B, on occasion by at least one order of magnitude.

Looking at the effects of modelling only pressure or thermal expansion (first three columns of results in Table 7, Waveform A - Foster et al. [13, 15]) versus combined loading - the results suggested the combined loading produces a tensile stress in the fibres (1046 MPa) rather than compressive for pure pressure loading (−78.9 MPa). The peak transverse stresses were predicted to be compressive in all cases however for Waveform A with combined loading the magnitude is significantly larger (−457 vs −201 MPa). The transverse stress for Waveform B was 77% smaller than Waveform A. The predicted delamination area for Waveform B was significantly smaller (32%) than that predicted under Waveform A. Additionally, the predicted depth of interlaminar damage was 50% smaller under Waveform B conditions. The results in Table 7 also enabled quantification of the ratio of damage type (thermal damage/critical damage). Waveform B was dominated by severe thermal damage (ratio of 1.00) while Waveform A had a combination of both thermal and critical damage, with a ratio of 0.28.

Since it was unclear how the combined effects of heating and strain rate interact, the Waveform A multiple-physics simulation was rerun with all strain rate scale factors set to one, i.e. no strain rate effects. Under these conditions the predicted critical damage area increased from 121 mm2 to 491 mm2, Table 7. This was due to the removal of strain rate scale effects on the material strength properties i.e. strength did not increase with strain rate and therefore failure initiation occurred at a lower value compared with the previous cases with strain rate effects. It is interesting to note that by not modelling the strain rate effects the percentage difference from the experimental results has reduced (from 71% to 17%). Consequently, this suggests that the scale factors represented in the model may be too severe for this case.

Considering delamination, removing the strain rate effects has decreased the predicted area of delamination from 2099 mm2 to 1696 mm2; falling below the lower bound of Hirano’s published experimental results [1]. Delamination in all cases initiated at approximately 300 °C. However, as this final result and the maximum element temperatures predicted at the edge of the interlaminar delamination area, for both original Waveforms A and B (25 °C to 300 °C) shows, delamination is not solely controlled by the thermal properties within Table 6, but rather a combination of different physics (thermal, pressure loading and thermal-expansion). That is to say without the effects of thermal expansion, delamination would not propagate. Therefore, there appears to be a complex interaction between the strain rate effects and the predicted intralaminar and critical damage, requiring further modelling research.

5.6 Results Summary

The results presented have accurately predicted the damage depth and delamination area for a specimen subjected to lightning test Waveform A. Fibre damage depth and delamination area have both been predicted within 5% of experimental values. However, the shape of the predicted delamination area and the fibre damaged area were inaccurate, Fig. 7. In order to improve this experimental effort is required to characterise the material under combined strain and thermal loading at rates suitable for lightning strikes, particularly in the matrix dominated directions. This would improve the strain rate scale factors used in this work and could significantly improve the damage area predictions.

In order to improve the failure model and modelling approach in general, several developments are required. A Waveform A plasma model would be beneficial to accurately predict the peak and rate of expansion of the shock wave pressure load on the surface of the specimen. Currently the mesh is governed by the thermal-electric model however, Foster et al. [13] showed that for pressure loading there were six elements required through-the-thickness.

These results illustrate four observations of the damage between Waveforms A and B and between the new failure model and preceding literature:

  • Stresses, strains and strain rates were all lower for Waveform B,

  • Interlaminar damage was larger for Waveform A,

  • The user-subroutine approach underestimated the critical damage area for Waveform A,

  • The user-subroutine approach more accurately predicted delamination area and critical damage depth.

Finally while the damage for Waveform B was made of thermal and delamination the damage for Waveform A was more severe and interactive between thermal, expansion and pressure loading.

6 Conclusions

This work has detailed the generation of a novel VUMAT user subroutine to better represent failure of a composite specimen during a lightning strike event. In this failure model, failure initiation, damage evolution, and strain and heating rate effects were all incorporated. This criteria has been benchmarked in component parts against relevant literature before being implemented for the assessment of lightning strike damage. This work for the first time has presented a model capable of incorporating thermal, pressure loading and thermal expansion induced damage for a lightning strike test. Results illustrated that for test Waveform B, damage took the form of thermal (resin deterioration) and delamination due to thermal expansion. Limited critical damage was predicted during a Waveform B event due to the low stresses and strains produced and the low magnitude of the incident pressure load. Waveform A created a much more severe combination of interactive thermal, expansion and pressure loading physics and the developed model was capable of accurately predicting the damage depth and delamination area, both within 5% of the experimental values.

Further development of the subroutine will be required in order to better represent the explosive strain rates of 1x104s−1 possible from high energy waveforms such as A or D. However, in order to do this, further experimental work and a considerable research effort is needed to determine the composite material behaviour under lightning strike conditions, with extreme heating and strain rates. Moreover, local material loading conditions (compressive, tensile and shear) and the state of material degradation, will influence many of the modelled material properties. Herein, for example, fibre properties where modelled as equivalent whether the material was loaded in tension or compression. Further experimental work should aid in determining if such idealisations are appropriate. However, designing an experimental arrangement for this purpose is highly complex. In addition further experimental investigation of the resin deterioration behaviour with heating rate would also aid the definition of damage zones. Future work should also consider the use of a more advanced three-dimensional failure criteria capable of fully considering in-situ effects and shear strain.