1 Introduction

In 2020 a global agreement on climate change is due to come into force with the intention of avoiding dangerous climate change by limiting global warming to well below 2 °C. Renewable energy will play a critical role and wind energy is becoming the preferred modality - every year 1 MW of wind energy can offset approximately 2600 tonnes of CO2 emissions [1, 2]. A wind turbine is mainly made up of rotor blades, rotor hub, gearbox, nacelle, generator, electrical systems, tower and foundation. In service, sufficient wind drives the blades to rotate and subsequently leads the motors to generate electricity. Nowadays, glass fibre-reinforced polymer (GFRP) composites are widely used for the blade manufacturing, as glass fibre composites provide improved strength, better corrosion resistance, reduced total weight and larger sizes for higher wind energy harvest. The blades comprise 15–20 % of the total wind turbine cost. During a likely 20-year life cycle, the GFRP blades are subjected to various hazards, such as fatigue induced degradation caused by cycling loads [3], strong winds, lightning, hailstones and bird strikes [4]. It was found that blade failure accounts for most accidents and damage to wind turbines [5]. Some typical types of blade damage are delamination, skin/adhesive debonding, sandwich debonding and buckling induced skin/adhesive debonding [6]. The minor blade damage could cause severe secondary damage to the whole system if immediate repair action is not taken.

For this reason, extensive attention has been given to structural health monitoring and fault diagnosis of the wind turbine blades. The information gathered from structural monitoring can be used in a condition-based maintenance schedule to better plan the inspection intervals, minimise the unnecessary replacements and offer practical guidance for future design. A number of non-destructive testing (NDT) techniques have been employed [7, 8], such as, conventional strain gauges, ultrasonic testing, acoustic emission, thermography, optical fibre sensors and X-ray imaging. However, most of the existing condition monitoring systems are not suitable for long-term and continuous examination in the field [9]. For example, the strain gauges are vulnerable to electrical interference. Couplants (e.g., water or gel) are required in ultrasonic testing, as the ultrasonic waves attenuate strongly in air and thick GFRP. The acoustic emission sensors should be placed near the damage source for accurate measurement [10]. For thermography, the possibility of unwanted thermal damage to the structures should be taken into account caused by the inspection technique. In optical fibre sensing systems, the weight penalty, possibility of failures in the wiring network, manufacturing and installation costs are significant. X-ray imaging is not practical for larger structures, as it requires a particular setup to prevent ionising radiation.

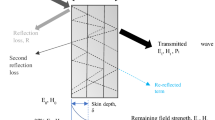
An alternative method for damage detection is the microwave technique [11–14]. Microwaves can propagate in air and dielectric materials with low attenuation. The amplitude and phase of the received signals can be affected by the variations of thickness or the electromagnetic properties of the materials (e.g., permittivity and permeability) due to internal damage/defects. Microwave NDT has various attributes, such as non-contact, one-sided scanning, no need for transducers or couplants and no safety concerns due to low power of the signal (milliwatts) [15, 16]. For the detection of defects in glass fibre composites, microwave techniques have proved to be superior to some other NDT methods [17]. Hosoi et al. [18] detected a slit and thin film inserted in thin and thick GFRP laminates. The experimental results indicated that microwaves had a potential to detect defects in the laminates of at least 30 mm thickness. Green et al. [19] employed a near-field microwave scanning technique to detect the disbonds and impact damage in GFRP composites.

However, few studies have been reported on the detection of damage in wind turbine blades using microwave techniques. In this paper, microwave imaging with an open-ended waveguide is applied to the detection of delamination in GFRP T-joints of wind turbine blades. Discussions on the effect of the inspection frequency on the performance and the selection of the damage indicator are presented. In addition, electromagnetic simulation is employed to identify optimum operating frequency range and standoff distance for delamination detection. The electromagnetic simulation requires the knowledge of the permittivity of the T-joint (the magnetic permeability is equal to that of free space). Samples were cut from representative positions of the glass fibre T-joint and their dielectric properties were characterised for simulation. Parametric studies were then performed to determine the minimum detectable size of delamination.

2 Glass Fibre Composite T-Joints

As illustrated in Fig. 1a, the T-joints in the blade provide the vital connection between the web and the skin. The T-joint under test, as presented in Fig. 1b, is made up of web, flange, skin and stiffener [20]. The delamination between the flange and the skin is the common damage type in the field due to the relatively low interlaminar strength [21]. In the present case, the delamination in T-joint-1 and T-joint-2 (Fig. 2) was induced by pull-out test.

Fig. 1
figure 1

Schematic diagram of the GFRP composite T-joint: (a) locations of T-joints in a wind turbine blade; (b) structure of the T-joint under test (reduced thickness near the flange ends)

Full size image
Fig. 2
figure 2

Photographs of two GFRP T-joint specimens (a) T-joint-1 (b) T-joint-2

Full size image

For T-joint-1, 3D woven 4 layer-to-layer stitched (3D4L) T-joint fabric was utilised to make the web and flange. For T-joint-2, the stacking sequence of the flange and skin was [45°/-45°]5, and the web was a [45°/-45°]10 laminate. The stiffener consisted of five-layer unidirectional [0°]5 to prevent large deflections during the pull-out test. The specifications of the two specimens are listed in Table 1. Two different types of glass fibres were used: unidirectional E glass fibre (FGE664) for the stiffener and ±45° glass fibre (FGE104) for the web, flange and skin. Epoxy resin Araldite LY 564 and hardener XB 3486 were used with the recommended ratio of 100:34 by weight. Detailed information about the fabrication process and the pull-out test can be referred to in [22].

Table 1 Specifications of the T-joints under test
Full size table

3 Experimental Study of Delamination Detection

3.1 Experimental Setup

Microwave imaging with an open-ended waveguide was employed because of its easy setup, capability of non-contact inspection and no need for signal processing or significant operator expertise [23]. In the test, a K band (18.0–26.5 GHz) rectangular waveguide adapter was used. The dimensions of the waveguide aperture are presented in Fig. 3a. The waveguide assembly was mounted on an X-Y-Z scanning stage and connected to an HP 8720D vector network analyser (VNA) (50 MHz-20 GHz) by a semi-rigid coaxial cable. A personal computer (PC) was connected to a PIC18C452 Microchip® microcontroller for logic control of the stepper motors. VEE software® was employed for precise and reproducible movements of the sensor. In addition, the analyser was connected to the PC by a IEEE-488 cable for data acquisition. The frequency range employed in the test was 18–20 GHz.

Fig. 3
figure 3

Experimental setup using the microwave imaging with an open-ended waveguide (a) size of the waveguide aperture (b) schematic diagram of the setup

Full size image

As shown in Fig. 4, a raster (2D) scan was performed over the top surface with an effective scanning area of 141.67 mm × 27.26 mm. The step size used for the scanning was 1 mm with a standoff distance of 5 mm. T-joint-1 was inspected first to thoroughly study the characteristics of the microwave imaging. It should be noted that there are some slight thickness variations from the edge to the central region due to fabrication. The distances between the centre of the waveguide at the origin and the locations of interest are demonstrated in Fig. 5.

Fig. 4
figure 4

2D scan over the top surface of T-joint-1

Full size image
Fig. 5
figure 5

Locations of interest in T-joint-1 with respect to the starting point of the scan

Full size image

3.2 Experimental Results

As a one-port measurement, only the reflection coefficients (S11) were acquired from the analyser. The distribution of the phase at each sampling position is plotted. As seen in Fig. 6, at an inspection frequency of 19 GHz, both the delamination and the variation of the thickness can be detected. In addition, the presence of the web is well presented. It is shown that the size of the blue region is slightly larger than the real size of the web, which is primarily due to the intrinsic limited resolution that is dependent on the waveguide dimensions [24].

Fig. 6
figure 6

Microwave inspection of T-joint-1 at 19 GHz

Full size image

As presented in Fig. 7, a similar result is found in T-joint-2. The colour difference in the delamination region reveals the severity of the defects inside the joint. However, the same colour in Figs.6 and 7 is not comparable, and the colour differences indicating varied signal responses are only meaningful for a specific T-joint.

Fig. 7
figure 7

Microwave inspection of T-joint-2 at 19 GHz. Lay-up and dimensions are shown in Table 1; colour contours are affected by layup and thickness

Full size image

3.3 Discussions

  1. (1)

    The detection performances at four other frequencies (i.e.,18 GHz, 18.5 GHz, 19.5 GHz and 20 GHz) for the T-joint-1 case are examined. In Fig. 8, there is no clear difference between the phase distribution for the frequencies below 19.5 GHz. However, at 20 GHz, the size of the delaminated region is around 40 % larger than that in the cases with smaller frequencies. The location of the web can still be identified, although two unexpected blue strips exist on each side. The selection of an optimal frequency for the delamination detection will be studied in the simulation in detail.

    Fig. 8
    figure 8

    Inspection of T-joint-1 at different frequencies (a) 18 GHz (b) 18.5 GHz (c) 19.5 GHz (d) 20 GHz. Location and extent of delamination is better identified at the lower frequency

    Full size image
  2. (2)

    Here, the images of magnitude and phase for the delamination inspection are compared. As presented in Fig. 9, the location of the web in T-joint-1 is captured by the magnitude image, while only the boundaries of the delamination can be identified. As little electromagnetic energy is attenuated in the delamination (air gaps), the magnitude is more sensitive to the variation of the thickness when compared with the phase information. In addition, it is seen that the dynamic range given by the phase is higher than that by the magnitude. Therefore, only the phase response will be analysed in the following simulation section.

    Fig. 9
    figure 9

    Microwave image of T-joint-1 represented by the magnitude distribution at 18 GHz, where delamination boundaries are identified but not its severity that is more evident in the phase image

    Full size image

4 Permittivity Profiling of the T-Joint

4.1 Setup of the Permittivity Measurement

Three small pieces with the inner dimensions of the K-band waveguide at the typical positions of T-joint-1 shown in Fig. 10a were cut. The permittivity of the samples was measured over 18-26 GHz using the transmission line method as schematically illustrated in Fig. 10b. The HP 8510C VNA was calibrated before the test using the thru-reflect-line (TRL) standard [25]. A MATLAB® programme was developed for acquisition of the S-parameters from the VNA and subsequent permittivity calculation. The transmission coefficients (S21) were retrieved for calculation, as it was suggested that the transmission measurement was generally more reliable than the reflection measurement [25].

Fig. 10
figure 10

Permittivity measurement of three representative samples cut from T-joint-1 (a) positions of the samples (b) experimental setup of the permittivity measurement

Full size image

4.2 Permittivity Results

The S21 obtained from the measurement are shown in Fig. 11. In practice, the relative permittivity (ε r) of materials with respect to free space is commonly characterised by dielectric constant (ε′r) and loss tangent (tanδ), i.e., ε r = ε′r (1-j tanδ). The calculated dielectric constants and loss tangents of all the three samples are presented in Fig. 12.

Fig. 11
figure 11

Measured S21 in the form of magnitude and phase over the measured frequency range (a) magnitude (b) phase

Full size image
Fig. 12
figure 12

Calculated dielectric properties of the three samples (a) dielectric constant (b) loss tangent

Full size image

It is seen that the dielectric constant of Sample A is the largest, which is followed by Sample B and Sample C (lay-up effect). The curve for Sample A is close to that of Sample B. All the three curves remain stable over the frequency range. In addition, all the loss tangents are within 0.04, which indicates the low-loss characteristic of the glass fibre composites. For simplicity of simulation, the dielectric properties of the materials are assumed independent of frequency and averaged over the range as listed in Table 2. The penetration depth of the microwave signal (d p) into dielectrics can be calculated by:

$$ {d}_p=\frac{c}{\sqrt{2}\pi f{\left\{{\varepsilon}_r^{\prime}\left[\sqrt{1+{\left( \tan \delta \right)}^2}-1\right]\right\}}^{1/2}} $$
(1)

where f is the inspection frequency, and c is the speed of light in free space. Due to the near-field characteristic of this technique, the effect of the standoff distance is not considered here. The calculated penetration depths given in Table 2 indicate that the microwave signal over K-band is capable for internal damage detection in relatively thick glass fibre-epoxy composite components (signal can travel to a depth of almost 142 mm).

Table 2 Average dielectric properties and microwave penetration depth
Full size table

5 Electromagnetic Simulation of Delamination Detection

5.1 Modelling of the T-Joint Structure

As illustrated in Fig. 13a, the T-joint structure and K-band rectangular waveguide adapter are modelled in electromagnetic simulation software CST MWS 2014. Electromagnetic waves are excited through the waveguide port defined on the top of the waveguide. The dimensions of the simulated T-joint structure are shown in Fig. 13b, where the sizes of the original T-joint-1 are rounded for easy modelling. Three regions making up the T-joint are evidently distinguished: red region for the stiffener and skin on the edge, yellow region for the stiffener, skin and flange and blue region for the web. The occurrence of the flange tapering during the actual fabrication process is reflected in the raised central region.

Fig. 13
figure 13

CST model of a glass-fibre T-joint with simulated delamination (a) CST model (b) side view (not to scale)

Full size image

The results from the permittivity measurement of Sample A, B and C are used to set the dielectric properties of red, yellow and blue regions, respectively. Here, the delamination is simulated by a narrow air gap located in the centre of the yellow region. The length and width of the delaminated region are denoted by L and W, respectively. As seen in Fig. 13b, there are three positions of interest associated with the variation of thickness and discontinuity of the materials: Position I (boundary between the red region and the yellow region), Position II (left end of the simulated delamination) and Position III (left end of the web). The location of each position with respect to the origin of the scanning is listed in Table 3.

Table 3 The locations of positions of interest with respect to the origin of the line scanning
Full size table

The standoff distance of the waveguide with respect to the top of the central region is represented by h. Initially, the parameters L, W and h are set to 25 mm, 0.6 mm (10 % of the thickness of the central region) and 5 mm, respectively. In this case, Position II is located at X = 58.3 mm. The ability to detect this combination will be taken as a reference in the following parametric studies, where the effect of these three variables is investigated.

5.2 Modelling of the Inspection Process

As illustrated in Fig. 14, due to the symmetry of the CST model, only a quarter of the surface is scanned so as to speed up the simulation process. Hence, the effective scanning area in the simulation is 70.80 mm × 13.80 mm. The simulation is carried out with a frequency range of 18 - 26 GHz and a step size of 1 mm.

Fig. 14
figure 14

Top-view of the 2D scan over the modelled glass fibre T-joint

Full size image

The methodology of using MATLAB to control CST [26] is adopted here. In order to perform an automatic scan across the simulated structure, a MATLAB-CST interaction technique involving data exchange between the two types of software is proposed, and the flowchart of this method is shown in Fig. 15. MATLAB is utilised to control the simulation process via Visual Basic for Application (VBA), which is the programming language in the CST environment. Specifically, MATLAB first calls the VBA programme to modify the parameter values and update the model. Then, a new calculation is performed and the resultant reflection coefficients are saved in a designated file. Afterwards, a new computation cycle starts at a new waveguide location. The CST simulation will finish when all the simulation positions are visited. Finally, another MATLAB programme will run to generate images at a given frequency. By using this joint computation technique, the simulated scanning process becomes more efficient and less time-consuming.

Fig. 15
figure 15

Flowchart of the proposed MATLAB-CST interaction technique for efficient simulation of microwave scanning

Full size image

5.3 Simulation Results

The signal response at 19 GHz is plotted in Fig. 16, where both the delamination and the variation of the thickness are captured. As there is little variation in the phase values along the Y direction, only the performance along the bottom edge of the scanned 2D area (shaded region) in Fig. 14 is studied in later sections for clarity.

Fig. 16
figure 16

Phase distribution for the simulated T-joint at 19 GHz

Full size image

5.4 Parametric Studies

5.4.1 Effect of the Inspection Frequency

Here, the effect of the inspection frequency is examined, which is shown in Fig. 17. The sensitivity of the signal is evaluated by comparing the phase difference between the origin and the present position. It is seen that the value of the plateau in the sensitivity curve (between Position I and Position II) decreases when the frequency increases to 22.5 GHz, which is in good agreement with the experimental results. Beyond 22.5 GHz, the plateau value increases with increasing frequency. The curves at the frequencies above 24.5 GHz become higher than that at 18 GHz. The highest sensitivity occurs at 26 GHz, and the performances at this frequency will be examined in the following sections.

Fig. 17
figure 17

Effect of the inspection frequency on the detection sensitivity

Full size image

The trend of each sensitivity curve with respect to the scanning distance is similar: increases at approximately 10 cm, decreases at approximately 55 cm and then increases again at approximately 65 cm. These changes correspond to Position I, Position II and Position III, respectively. For the present setup, the span of the gradual increase/decrease stage is associated with the narrow inner dimension of the waveguide, as the most effective sensing position is where the discontinuity boundary in the material (e.g., Position II) is under the waveguide aperture. For example, for the case where the delamination length L is 25 mm, the relative distances between the delamination and the two edges of the waveguide aperture at the origin are illustrated in Fig. 18.

Fig. 18
figure 18

Illustration of the distance between the left end of the delamination and the two edges of the waveguide aperture at the origin

Full size image

5.4.2 Effect of the Size of the Delamination

The effects of the length and width of the simulated delamination are studied separately. First, detection performances are computed at a fixed width W = 0.6 mm, a fixed standoff distance h = 5 mm and four varied lengths, i.e., 45 mm, 35 mm, 15 mm and 5 mm. The simulation results are presented in Fig. 19. The responses to the thickness and material discontinuities at Position I are the same among the five cases as expected. However, the location of the sharp drop around Position II shifts leftwards as the delamination length increases. It should be noted that the distance between the adjacent two curves is approximately equivalent to a half of the total delamination length difference.

Fig. 19
figure 19

Parametric study of the effect of the delamination length on the detection performance

Full size image

Similarly, signal responses are computed at L = 25 mm, h = 5 mm and four other widths, i.e., 1.0 mm, 0.8 mm, 0.4 mm and 0.2 mm. As presented in Fig. 20, there is a negligible variation between the five sensitivity curves before the waveguide scans across Position II. Beyond that point, the sensitivity drops lower as the delamination width increases, but the sensitivity difference between the adjacent two curves is not equal. The relationship between the delamination width (W) and the sensitivity drop (ΔSsd) is evaluated by the sensitivity difference between the average plateau value and the sensitivity value at Position II. Regression analysis is further carried out. As seen in Fig. 21, a linear line is offered with the given correlation coefficient R 2 = 0.99, which demonstrates a high reliability of the approximation over the delamination width range investigated in the simulation.

Fig. 20
figure 20

Parametric study of the effect of the delamination width on the detection performance

Full size image
Fig. 21
figure 21

Relationship between the delamination width (W) and the corresponding sensitivity drop (ΔSsd)

Full size image

5.4.3 Effect of the Standoff Distance

A parametric study is performed to evaluate the effect of the standoff distance with the sizes of the delamination region being kept the same (L = 25 mm and W = 0.6 mm). Four standoff distances are used, i.e., 1 mm, 2 mm, 10 mm and 20 mm. In Fig. 22, it is shown that the setup with a standoff distance of 20 mm is relatively insensitive to the simulated defect. The sensitivity starts to increase as the standoff distance decreases. Among the five cases, the setup with a standoff distance of 1 mm provides the highest sensitivity and resolution, as the location of the sharp increase in the curve coincides with Position II.

Fig. 22
figure 22

Parametric study of the effect of the standoff distance on the detection performance

Full size image

6 Concluding Remarks

Non-contact microwave imaging with an open-ended waveguide has been successfully employed for the detection of delamination in glass fibre T-joints used in wind turbine blades. The regions of the delamination and variation of the thickness (due to flange tapering and the presence of the web underneath the skin) can be identified from the images produced by the microwave scanning. It has been found that the phase of the reflection coefficient is most useful for delamination detection, whereas the magnitude is more sensitive to thickness variation.

Permittivity characterisation measurements were made on samples from the T-joint. The dielectric properties were used in an electromagnetic MATLAB-CST model of the detection system. The effects of the inspection frequency, the length and width of the delamination and the standoff distance were studied in detail. The sensitivity decreases when the frequency increases towards 22.5 GHz, while the sensitivity starts to increase when the frequency is beyond that critical frequency. For the K-band (18–26 GHz) scanning, the highest sensitivity is recorded at 26 GHz. As the delamination length is increased, the drift distance of the peak of interest is equivalent to a half of the total delamination length difference. From the study of the delamination width, it is indicated that there is a linear relationship between the delamination width and the sensitivity drop at the left end of the delamination. The parametric studies of the delamination length and width demonstrate the great potential of the open-ended waveguide inspection for damage quantification. In addition, it is revealed that the decreased standoff distance could significantly improve the sensitivity, and the starting location of the delamination region can be readily recognised from the sensitivity curve.

The promising results from the microwave imaging technique suggests that it can be extended to other applications for the wind turbine system, for example, monitor the manufacturing process for quality control (e.g., air voids and lack of thickness uniformity). In addition, it could be used for off-line monitoring, where the machinery is taken down from the tower to allow inspection by maintenance personnel. It could be difficult to perform in-service microwave inspection considering the height of the wind turbine (the tower height ranges from 40 m up to more than 100 m). In terms of on-line/in-service monitoring, the built-in sensors (e.g., Lamb wave sensing and electromechanical sensor) could be a preferable option. Further work is required to validate the simulation results related to the sensor’s sensitivity.