Limits and Dynamics of Randomly Connected Neuronal Networks

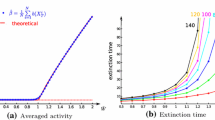
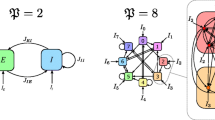
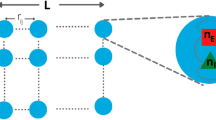
Abstract

Networks of the brain are composed of a very large number of neurons connected through a random graph and interacting after random delays that both depend on the anatomical distance between cells. In order to comprehend the role of these random architectures on the dynamics of such networks, we analyze the mesoscopic and macroscopic limits of networks with random correlated connectivity weights and delays. We address both averaged and quenched limits, and show propagation of chaos and convergence to a complex integral McKean-Vlasov equations with distributed delays. We then instantiate a completely solvable model illustrating the role of such random architectures in the emerging macroscopic activity. We particularly focus on the role of connectivity levels in the emergence of periodic solutions.

Appendix A: Randomly Connected Neural Fields

We now extend the above results to the mesoscopic case of spatially-extended neural fields with random correlated connectivity weights and delays. In this case, following [29], we consider that the number of populations in a network of size N is P(N), and this quantity diverges when N tends to infinity covering, in the limit N→∞, a piece of cortical tissue Γ which compact set of $\mathbb{R}^{\delta}$ (generally δ=1,2). In this interpretation, a population index represents the location r _α ∈Γ of a microcolumn on the neural field, which are assumed to be independent random variables with distribution λ on Γ. For the sake of simplicity and consistency with other works about neural fields, we include the dependence on the neural populations in the drift and diffusion functions. We therefore introduce three maps:

• the measurable functions $f: \varGamma\times \mathbb{R}\times E\mapsto E$ and $g: \varGamma\times \mathbb{R}\times E \mapsto E^{m}$

• the map $b:\varGamma\times\varGamma\times \mathbb{R}\times E \times E\mapsto E$ which is assumed measurable,

and rewrite the network equations as:

$$\begin{aligned} dX_t^{i,N} =&f(r_{\alpha},t,X_t^{i,N}) \\ &{}+\frac{1}{P(N)} \sum_{\gamma =1}^{P(N)}\sum_{p(j)=\gamma}\frac{1}{N_\gamma}b(r_{\alpha},r_{\gamma },w_{ij},X_t^{i,N},X_{t-\tau_{ij}}^{j,N})dt+g(r_{\alpha },t,X_t^{i,N})\cdot dW_t^i. \end{aligned}$$

(14)

These equations are clearly well-defined as proved in Proposition 1. As described in the macroscopic framework 2, the two sequences of random variables (w _ij ) and (τ _ij ) for fixed $i\in \mathbb{N}$ are independent, and for fixed (i,j), τ _ij and w _ij are correlated. Their law depend on the locations r _α and r _γ of the microcolumns neurons i and j belong to. We denote $\varLambda_{r_{\alpha},r_{\gamma}}$ this law. We assume that this law is measurable with respect to the Borel algebra of Γ, i.e. for any $A \in \mathcal{B}(\mathbb{R}\times \mathbb{R}_{+})$ the Borel algebra of $\mathbb{R}\times \mathbb{R}_{+}$, the map (r,r′)↦Λ _r,r′(A) is measurable with respect to $\mathcal{B}(\varGamma\times\varGamma)$. We assume that assumptions (H1)–(H4) are valid uniformly in the space variables, and consider the neural field limit given by the condition:

$$ \varepsilon(N)=\frac{1}{P(N)} \sum_{\gamma=1}^{P(N)} \frac{1}{N_{\gamma }}\mathop{\longrightarrow}\limits_{N\to\infty} 0. $$

(15)

Elaborating on the proofs provided (i) in the finite-population case treated in the present manuscript and (ii) in the neural field limit for non random synaptic weights or delays, we will show that the network equations converge towards a spatially-extended McKean-Vlasov equation:

$$\begin{aligned} dX_t(r) =&f(r,t,X_t(r))\,dt+g(r,t,X_t(r))\cdot dW_t(r) \\ &{}+\int_{\varGamma}\int_{\mathbb{R}}\int_{-\tau}^0 \mathbb{E}_{Z}[b(r,r',j,X_t(r),Z_{t+s}(r'))] d\varLambda_{r,r'}(j,s) d\lambda(r') dt. \end{aligned}$$

(16)

In these equations, the process (W _t (r)) is a chaotic Brownian motion (as defined in [29]), i.e. a stochastic process indexed by space r∈Γ, such that for any r∈Γ, the process W _t (r) is a standard m-dimensional Brownian motion and for any r≠r′∈Γ ², W _t (r) and W _t (r′) are independent. These processes are singular functions of space, and in particular not measurable with respect to the Borel algebra of Γ, $\mathcal{B}(\varGamma)$. Therefore, the solutions are themselves not measurable, which raise questions on the definition of the mean-field equation (16) in particular for the definition of the integral on space of the mean-field term. However, it was shown in [29], making sense of this equation amounts showing that the law of the solution is $\mathcal{B}(\varGamma)$-measurable. Once this is proved, the integral is well defined. In the spatial case, we make the following assumptions, that are directly corresponding to the assumptions (H1)–(H4) of the finite-population case:

• (H1’) f and g are uniformly Lipschitz-continuous functions with respect to their last variable.

• (H2’) For almost all $w\in \mathbb{R}$ and any (r,r′)∈Γ ², b(r,r′,w,⋅,⋅) is L-Lipschitz-continuous, i.e. for any (x,y) and (x′,y′) in E×E, we have:

  $$|b(r,r',w,x,y)-b(r,r',w,x^\prime,y^\prime)|\leq L(|x-x^\prime |+|y-y^\prime|). $$

• (H3’) There exists a function $\bar{K} : \mathbb{R}\mapsto \mathbb{R}^{+}$ such that for any (r,r′)∈Γ ²,

  $$|b(r,r',w,x,y)|^2\leq\bar{K}(w)\quad\mbox{and}\quad \mathcal{E}_{\varLambda _{r,r'}}[\bar{K}(w)]\leq\bar{k}<\infty. $$

• (H4’) The drift and diffusion functions satisfy the uniform (in r) monotone growth condition:

  $$x^Tf(r,t,x)+\frac{1}{2}|g(r,t,x)|^2\leq K(1+|x|^2). $$

The initial conditions we consider for the mean-field equations are processes $(\zeta_{t}(r), t\in[-\tau,0])\in\mathcal{X}_{0}$ the space of spatially chaotic square integrable process with measurable law, processes such that the regularity conditions are satisfied:

• for any r∈Γ, ζ _t (r) is square integrable in $\mathcal{C}_{\tau}$

• for any r≠r′, the processes ζ(r) and ζ(r′) are independent

• for fixed t∈[−τ,0], the law of ζ _t (r) is measurable with respect to $\mathcal{B}(\varGamma)$, i.e. for any $A\in \mathcal{B}(E)$, $p_{\zeta _{t}}(r)=\mathbb{P}(\zeta_{t}(r)\in A)$ is a measurable function of $(\varGamma,\mathcal{B}(\varGamma))$ in [0,1].

We will denote $\mathcal{X}_{T}$ the set of processes (ζ _t (r),t∈[−τ,T]) satisfying the above regularity conditions on [−τ,T].

Proposition 6

Under assumptions (H1’)–(H4’), for any initial condition $\zeta\in \mathcal{X}$, there exists a unique, well-defined strong solution to the mean-field equations (16).

The proof classically starts by showing square integrability of possible solutions, then considers equation (16) as a fixed point equation X _t =Φ(X _t ), and shows a convergence property of iterates of the map Φ starting from an arbitrary chaotic process $X^{0}_{t}(r)\in\mathcal{X}_{T}$. It is easy to see that the function Φ maps $\mathcal{X}_{T}$ in itself. The sequence of processes X ^k=Φ ^k(X ⁰) is therefore well-defined. Estimates similar to those proved in Proposition 1 and Theorem 2 allow concluding on the existence and uniqueness of solutions. The proof being classical, it is left to the interested reader extending the argument of [29, Theorem 2] to our random environment setting.

The convergence result of the network equations towards the mean-field equations can be stated as follows:

Theorem 7

Let $\zeta\in\mathcal{X}_{0}$ a chaotic process. Consider the process $(X^{i,N}_{t}, t\in[-\tau,T])$ solution of the network equations (14) with independent initial conditions identically distributed for neurons in the same population located at r∈Γ with law equal to (ξ _t (r),t∈[−τ,0]). Under assumptions (H1’)–(H4’) and the neural field limit assumption (15), the process $(X^{i,N}_{t}, t\in[-\tau,T])$ converges in law towards (X _t (r),t∈[−τ,T]) solution of the mean-field equations with initial conditions ζ.

The proof of this result proceeds as that of [29, Theorem 3] including the refinements brought in the proof of Theorem 2 to take into account random connectivities and delays.