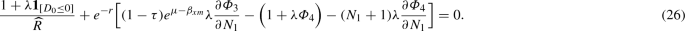Abstract
This paper explores the effects of a firm’s cash flow systematic risk on its optimal capital structure. In a model where firms are allowed to borrow resources from a competitive lending sector, those with cash flows more correlated with the aggregate economy (i.e., firms with riskier assets in place) choose a lower leverage given their higher expected financing costs. On the other hand, less risky firms, having lower expected financing costs, optimally choose to issue more debt to exploit a tax advantage. The model predicts that cash flow systematic risk is negatively correlated with leverage and corporate bond yields.




Similar content being viewed by others
Notes
Differently from George and Hwang (2010), who focus exclusively on book-leverage, Gomes and Schmid (2010) and Ozdagli (2012) also study the relation between market leverage and equity returns. In both models, investment and financing choices are endogenous, but while in Ozdagli (2012) corporate debt is risk-free, in Gomes and Schmid (2010) firms can issue risky corporate debt.
A more realistic setting with costly debt restructuring at time 1 will only complicate the analysis without changing the key predictions of the model.
The cash flow produced at time \(t=1\) is discounted using the factor
$$\begin{aligned} M_1= & {} e^{m_{1}}=e^{-r -\frac{1}{2}\sigma _z^2-\sigma _z \varepsilon _{z,1}}, \end{aligned}$$where \(\varepsilon _{z,1}\sim N(0,1)\) is the aggregate shock at time \(t=1\). The above formulation implies \(E_0[M_1]=e^{-r}=1/R\). The pay-off produced by the risky asset at time 1 is \(e^{x_{1}}\), where \(x_{1}\) is equal to
$$\begin{aligned} x_{1}=\mu -\frac{1}{2}\sigma _x^2+\sigma _x \varepsilon _{x,1}. \end{aligned}$$The cash flow shock, \(\varepsilon _{x,1}\sim N(0,1)\), is correlated with \(\varepsilon _{z,1}\), thus making the cash flows produced by the asset in place risky. In what follows, we assume that \(COV(\varepsilon _{z,1},\varepsilon _{x,1})=\sigma _{x,z}\) and, as a consequence, \(COV(x_{1},m_{1})=-\sigma _x\sigma _z\sigma _{x,z}\). As in Berk et al. (1999), the systematic risk of a project’s cash flow, \(\beta _{xm}\), is equal to \(\sigma _x\sigma _z\sigma _{x,z}\).
See “Appendix A.1” for the derivation.
\(\frac{ds_1(N_1)}{dN_1}=(1-\tau )R \left[ \frac{\varPhi _2'(\sigma _x(N_1-\overline{L_1}))^{-1} }{(1-\varPhi _2)^2}\right] >0\), \(\frac{ds_1(N_1)}{d\beta _{xm}} =(1-\tau )R\left[ \frac{\varPhi _2'(\sigma _x )^{-1} }{(1-\varPhi _2)^2}\right] >0\), and \(\frac{ds_1(N_1)}{d\mu }=(1-\tau )R\left[ \frac{-\varPhi _2'(\sigma _x )^{-1} }{(1-\varPhi _2)^2}\right] <0\).
The first derivative of \(\hat{R} +s_1(N_1)\) is \(\frac{ds_1(N_1)}{dN_1}\), while the first derivative of \(N_1\frac{ds_1(N_1)}{dN_1}\) is \(\frac{ds_1(N_1)}{dN_1}+N_1\frac{ds_1(N_1)}{dN_1dN_1} \), which is larger for each value of \(N_1>\overline{L_1}\) given the convexity of the credit spread. An alternative argument is the following. Let us assume that there is more than one maximum. It follows that there must be two values of \(N_1\), \(N_1^a\) and \(N_1^b\) with \(\overline{L_1}<N_1^a < N_1^b\), such that \(B_1(N^a_1)=B_1(N^b_1)=\overline{B}\) and \(B_1(N_1)<\overline{B}\) for all \(N_1 \in (N_1^a,N_1^b)\). In the interval \((N_1^a,N_1^b)\), \(B_1\) is first decreasing and then increasing in \(N_1\); it follows that the credit spread \(N_1/B_1\) is not increasing at an increasing rate over \((N_1^a,N_1^b)\). This violates the convexity of the credit spread function.
Consider the following result:
$$\begin{aligned} \frac{d\varPhi \left( f(x)-\sigma _x\right) }{dx}=\phi (f(x) -\sigma _x)f_x(x)=\frac{1}{\sqrt{2\pi }}e^{-\frac{(f(x)-\sigma _x)^2}{2}}f_x(x) =\phi (f(x))e^{f(x)\sigma _x-\frac{\sigma _x^2}{2}}f_x(x), \end{aligned}$$where \(\phi \) is the probability distribution of a standard normal variable. If we set \(f(x)=\varepsilon _{i}+\frac{\beta _{xm}}{\sigma _x}\), then
$$\begin{aligned} (1-\tau )e^{\mu -\beta _{xm}}\frac{\partial \varPhi _3}{\partial N_1} =\frac{1-\tau }{\sigma _x}\phi \left( \varepsilon _{i}+\frac{\beta _{xm}}{\sigma _x}\right) =(N_1+1)\frac{\partial \varPhi _4}{\partial N_1}. \end{aligned}$$This allows us to simplify the first-order condition in Eq. (26):
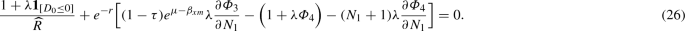
References
Bagnoli, M., Bergstrom, T.: Log-concave probability and its applications. Econ Theory 26(2), 445–469 (2005)
Barlow, R.E., Marshall, A.W., Proschan, F.: Properties of probability distributions with monotone hazard rate. Ann Math Stat 34(2), 375–389 (1963)
Berk, J.B., Green, R.C., Naik, V.: Optimal investment, growth options, and security returns. J Finance 54(5), 1553–1607 (1999)
Bhamra, H.S., Kuehn, L.A., Strebulaev, I.A.: The levered equity risk premium and credit spreads: \(a\) unified framework. Rev Financ Stud 23(2), 645–703 (2010)
Epstein, L., Zin, S.: Substitution, risk aversion, and the temporal behavior of consumption and asset returns: a theoretical framework. Econometrica 57, 937–969 (1989)
Garlappi, L., Yan, H.: Financial distress and the cross-section of equity returns. J Finance 66(3), 789–822 (2011)
George, T.J., Hwang, C.Y.: A resolution of the distress risk and leverage puzzles in the cross section of stock returns. J Financ Econ 96, 56–79 (2010)
Glover, B.: The expected cost of default. J Financ Econ (forthcoming) (2015)
Gomes, J.F., Schmid, L.: Levered returns. J Finance 65(2), 467–494 (2010)
Hackbarth, D., Miao, J., Morellec, E.: Capital structure, credit risk, and macroeconomic conditions. J Financ Econ 82, 519–550 (2006)
Imrohoroglu, A., Tuzel, S.: Firm level productivity, risk, and return. Manag Sci 60(8), 2073–2090 (2014)
Kuehn, L.A., Schmid, L.: Investment-based corporate bond pricing. J Finance 69(6), 2741–2776 (2014)
Leland, H.E.: Corporate debt value, bond covenants, and optimal capital structure. J Finance 49(4), 1213–1252 (1994)
Merton, R.C.: On the pricing of corporate debt: the risk structure of interest rates. J Finance 29(2), 449–470 (1974)
Ozdagli, A.K.: Financial leverage, corporate investment, and stock returns. Rev Financ Stud 25(4), 1033–1069 (2012)
Ross, S.A.: Debt and taxes and uncertainty. J Finance 60(3), 637–657 (1985)
Acknowledgements
I am very grateful to Rui Albuquerque, Harjoat Bhamra, Barbara Bukhvalova, Andrea Buffa, Gian Luca Clementi, Dirk Hackbart, Siamak Javadi, Evgeny Lyanders, David McLean, Angelo Mele, Allen Michel, Ali Ozdagli, Marco Rossi, Lukas Schmid, Philip Strahan, Adam Zawadowski, as well as seminar attendants at Boston University, Green Line Macroeconomics Meeting, Midwest Finance Association, Society for Economics Dynamics, University of Alberta, and BI Oslo for their comments and suggestions. The views expressed are those of the author and do not necessarily reflect those of the Federal Reserve Board or the Federal Reserve System.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
In this appendix, we provide proofs for the results discussed in Sects. 2 and 3.
1.1 A.1: Continuation value for the firm’s problem
Note that it is never optimal for the firm to issue debt and save the proceeds because the internal accumulation rate is lower than the risk-free rate (i.e., cash is negative debt). For this reason, we can use net leverage as the unique choice variable and the problem of the firm becomes
subject to the constraints described in Eqs. 9–11. To derive the continuation value \(E_0[M_1V_1]\), we rely on Result A.1.
Result A.1
Let \(M_1\) be the SDF defined in footnote 3, \(x_1\) the stochastic process for the cash flow also defined in footnote 3, and A and B any two variables whose values are known at time 0. Then
where \(\varPhi \) is the cumulative distribution function of a standard normal variable, \(\varepsilon _{\overline{x}}\) is equal to \(\frac{\overline{x}-\mu +0.5\sigma ^2_x}{\sigma _x}\), and \(\varepsilon _{\underline{x}}\) is equal to \(\frac{\underline{x}-\mu +0.5\sigma ^2_x}{\sigma _x}\).
The continuation value \(E_0[M_1V_1]\) can be explicitly rewritten as
By virtue of Result A.1., the continuation value takes the following form
where \(\varepsilon _{di}=\frac{\kappa _{di} -\mu +0.5\sigma ^2_x}{\sigma _x}\), \(\varepsilon _{i} =\frac{\kappa _{i}-\mu +0.5\sigma ^2_x}{\sigma _x}\), \(\varepsilon _{dn}=\frac{\kappa _{dn}-\mu +0.5\sigma ^2_x}{\sigma _x}\) and
The quantities \(\kappa _{di}\), \(\kappa _{i}\), and \(\kappa _{dn}\) are defined in Sect. 2.2.1. The continuation value for the risk-free debt case can be derived setting \(\varPhi _1=\varPhi _2=0\) in Eq. (36).
1.2 A.2: The bond pricing equation and credit spread: properties
The bond pricing equation can be rewritten as
where
is the firm’s credit spread. The credit spread is Eq. (21) is strictly increasing in \(N_1\), strictly increasing in \(\beta _{xm}\), and strictly decreasing in \(\mu \).Footnote 5
If the credit spread is a convex function, then \(B_1\) has a unique interior maximum, \(B^{max}_1\). we first provide a condition that ensures a convex credit spread, namely a credit spread value increasing at an increasing rate. The second derivative of the credit spread is
and the credit spread is convex if the following condition is satisfied:
where \(y=\varepsilon _{di}+\frac{\beta _{xm}}{\sigma _x}\) and h(x) is the strictly increasing hazard rate of a standard normal distribution (see Barlow et al. 1963; Bagnoli and Bergstrom 2005, among others). Then a sufficient condition for a (globally) convex credit spread is to have \(\sigma _x<2(h(y^*)-0.5y^*)=1.5176\), where \(y^*\) is such that \(h'(y^*)=0.5\).
Now we can show that if the credit spread is convex in \(N_1\), then the bond pricing equation has a unique maximum. The first-order condition for the bond pricing equation is
and a maximum satisfies
For \(N_1\) that converges to \(\overline{L_1}\), the term \(\hat{R} +s_1(N_1)\) converges to \(\hat{R}\), while \(N_1\frac{ds_1(N_1)}{dN_1}\) goes to zero. On the other hand, if \(N_1\) goes to infinity then both terms also go to infinity. It follows that there is only one value satisfying Eq. (25) because \(N_1\frac{ds_1(N_1)}{dN_1}\) grows faster than \(\hat{R} +s_1(N_1)\).Footnote 6
1.3 A.3: The risk-free case: the Euler equation and optimal net leverage policy
The firm’s problem in the risk-free case satisfies the first order condition belowFootnote 7
When time 0 net worth is positive, then the Euler equation is
In this case, the firm chooses \(N_1\) over the interval \([-W_0, \overline{N_1}]\). Notice that the RHS is smaller than the LHS when \(N_1=-1\) (in such a case \(\varPhi _4=0\)) and it is also strictly increasing in \(N_1\). It follows that an interior solution is always unique. Firms with an RHS value smaller than \(1/\widehat{R}\) when \(N_1= \overline{L_1}\) optimally choose to borrow up to their debt limit so that optimal leverage equals \(\overline{L_1}\). On the other hand, firms with an RHS value larger than \(1/\widehat{R}\) when \(N_1= \overline{L_1}\) optimally choose a net leverage value in \((-1, \overline{L_1})\). Notice that firms that have an unconstrained optimal value of net leverage smaller than \(-W_0\) optimally choose \(N_1=-W_0\) because it is not optimal to raise external financing and save the proceeds.
When time 0 net worth is negative (\(W_0<0\)), then the Euler equation is
If liabilities do not exceed the debt limit, then it is optimal to repay them by issuing debt. In this case, firms with an RHS value larger than \(1/\widehat{R}\) when \(N_1=-W_0\) optimally choose not to borrow any additional amount, while firms with an RHS value smaller than \(1/\widehat{R}\) when \(N_1= \overline{L_1}\) optimally choose to borrow up to their debt limit. To conclude, firms with an RHS value smaller than \(1/\widehat{R}\) when \(N_1=-W_0\) and an RHS value larger than \(1/\widehat{R}\) when \(N_1= \overline{L_1}\), choose an optimal leverage in the interval \(-W_0, \overline{L_1}\). If liabilities exceed \(\overline{L_1}\), firms will always issue debt up to \(\overline{L_1}\) and then issue equity to repay the remaining amount.
When an interior solution exists, the optimal net leverage policy is increasing in the mean of the cash flow process \(\mu \), decreasing in the cost of external financing \(\lambda \), and decreasing in the firm’s riskiness \(\beta _{x,m}\). These properties can be derived taking the total differential implied by the Euler equation with respect to \(N_1\) and the relevant parameters.
1.4 A.4: The risky case: the Euler equation and optimal net leverage policy
An interior solution for the firm problem in the risky case satisfies the first-order condition below:
Given that \(\varPhi _2\) matters only if \(N_1\) exceeds the risk-free debt limit \(\overline{L_1}\), we can rewrite the Euler equation as
I have already illustrated that the optimal net leverage is decreasing in the firm’s riskiness when \(N_1\le \overline{L_1}\), so we only need to check if the total differential of \(N_1\) w.r.t. \(\beta _{xm}\) is negative using the following version of the Euler equation for values of \(N_1\) larger than \(\overline{L_1}\).
The LHS in Eq. (30) is the marginal benefit of issuing debt, which equals the sum of the marginal increase in time 0 dividend distribution (or the marginal decrease in time 0 equity issuance costs if the firm has negative net worth) and the benefit of defaulting given by the missed time 1 repayment. The RHS is the marginal cost of issuing debt, which equals the time 1 debt repayment and the corresponding marginal increase in the probability of being financially constrained plus the cost related to the possibility of foregoing a time 1 growth option with positive net present value.
Sensitivity analysis this figure depicts the optimal net leverage as a function of the firm’s riskiness \(\sigma _{xz}\) for different values of the parameters \(\mu \), \(\sigma _x\), \(C_2\), \(\lambda \), \(\sigma _z\), and R. In the top left panel, \(\mu \) varies from 0.5 to 2. In the top right panel, \(\sigma _x\) varies from 0.1 to 1.5. In the central left panel, \(C_2\) varies from 1.144 to 2.5. In the central right panel, \(\lambda \) varies from 0.02 to 0.24. In the bottom left panel, \(\sigma _z\) varies from 0.1 to 1.2. In the bottom right panel, R varies from 1 to 1.15. The baseline case parameter values are \(\mu =1.5\), \(\sigma _x=0.5\), \(C_2=1.5\), \(\lambda =0.10\), \(\sigma _z=0.4\), \(\tau =0.30\), and \(R=1.04\)
If the LHS is decreasing in \(\beta _{xm}\) and the RHS is increasing in \(\beta _{xm}\), then an increase in the firm’s riskiness causes a downward shift of the marginal benefit curve and an upward shift of the marginal cost curve. The result is a lower optimal net leverage value. This is the same as having the below term decreasing in \(\beta _{xm}\):
Let us assume that the optimal default probability is low, so that both \(\varPhi _4\) and \(\varPhi _2\) are less than 0.50. Because of the convexity of credit spreads, \(\frac{dB_1}{dN_1}\) is decreasing in the cash flow riskiness; in addition, also \(\lambda (\varPhi _2-\varPhi _4)\) is decreasing in \(\beta _{xm}\) because if \(\varPhi _4\) and \(\varPhi _2\) are less than 0.50, then \(\varepsilon _{i}>\varepsilon _{di}\) implies \(\varPhi '_4> \varPhi '_2\). If the quantity \(\varPhi _2 - \frac{\varPhi '_2e^{-r}C_2}{\sigma _x(N_1-\overline{L_1} )} \) is also decreasing in \(\beta _{xm}\), then the optimal net leverage is decreasing in the firm’s riskiness also when \(N_1> \overline{L_1}\). The derivative of the latter quantity w.r.t. \(\beta _{xm}\) is negative if the following condition is satisfied:
Note that for \(N_1\) that goes to \(\overline{L_1}\), the LHS of Eq. (32) converges to zero, while the RHS goes to \(+\infty \). It follows that for small values of \(N_1\) (i.e., \(N_1\rightarrow \overline{L_1}\)), the optimal net leverage is decreasing in the firm’s riskiness. Figure 5 shows that the negative relation between optimal net leverage and risk is robust across different parameter values.
1.5 A.5: Credit spreads and equity returns
The expected equity return in Eq. (14) can be rewritten as \(f(\sigma _{xz})/g(\sigma _{xz})\), so the first-order condition w.r.t. \(\sigma _{xz}\) is
Equation (33) is positive if we assume a time 0 ex-dividend value of the firm decreasing in cash flow riskiness (i.e., \(g'(\sigma _{xz})<0\)). This assumption is sufficient to generate expected equity returns increasing in \(\sigma _{xz}\) because \(f(\sigma _{xz})\) is also increasing in \(\sigma _{xz}\).
The expected value of future dividends at time 0 is
Using Result A.1., Eq. (34) can be rewritten as
where
Using the same argument described in footnote 7, we can write the derivative of \(E_0[V_1]\) w.r.t. \(\sigma _{xz}\) as
The quantity in the square brackets is positive because \(\widehat{\varPhi }_4>\widehat{\varPhi }_2\), while \(\frac{dN^*_1}{d\sigma _{xz}}\) is negative because the optimal net leverage is decreasing in cash flow riskiness. It follows that the expected future dividends are increasing in \(\sigma _{xz}\).
Rights and permissions
About this article
Cite this article
Palazzo, B. Cash flows risk, capital structure, and corporate bond yields. Ann Finance 15, 401–420 (2019). https://doi.org/10.1007/s10436-018-00342-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10436-018-00342-9