Skip to main content
SpringerLink
Log in

Nonlinear forced vibrations of a slightly curved nanotube conveying fluid based on the nonlocal strain gradient elasticity theory

  • Research Paper
  • Published:
Microfluidics and Nanofluidics Aims and scope Submit manuscript

Abstract

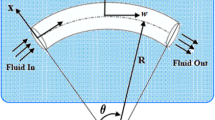
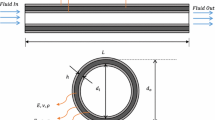
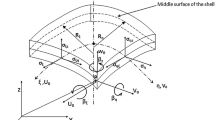
Advances in miniaturization of medical and engineering equipment made nanotubes and nanopipes to be very important components for these devices. A nonlinear mechanical behaviour of nonlocal strain gradient of a slightly curved tube conveying pressurized fluid under thermal loading subjected to forced vibration is investigated in this study. The microtube’s viscoelasticity of the material is assumed using the Kelvin–Voigt model. First the effects of scale due to fluid and solid are considered. Then using Hamilton’s principle, and the nonlocal strain gradient elasticity, the nonlinear size-dependent governing partial integro-differential equation (PDE) is derived. Two different methods are used to solve this problem. These are; (1) finite difference method (FDM), is used to solve the PDE, and (2) the Eigenfunction expansion methods was combined using Runge–Kutta and Heun schemes to solve the resulting ODE in time. The results of pipe’s midpoint displacement and frequency are almost indistinguishable with Runge–Kutta and Heun schemes. However, comparing FDM with RK, the displacement is within 16% while frequency is within 2% respectively. Results show that particularly the effect of initial curvature have profound effects on the resonance of the system. For the linear analysis, the slip, nonlocal and thermal parameters degraded the natural frequency of the nanotube. For forced vibration, when initial curvature is zero, one distinct resonant frequency was obtained. However, for slightly curved pipe, two distinct resonant frequencies were obtained for flow velocity between 3.7 and 4.5 respectively. Slightly curved nanopipes with slip boundary condition behave very differently from those without slip boundary condition. There are no comparable results in the study of micropipes conveying fluids in the oil and gas industry.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  • Adebusoye AT, Oyediran AA (2016) Analytical solutions of two models of thermal-mechanical vibration of pinned-pinned fluid-conveying single-walled carbon nanotubes resting on a two-parameter elastic foundation. J Eng Res 21(1):31–40

    Google Scholar 

  • Ansari R, Ramezannezhad H, Gholami R (2012) Nonlocal beam theory for nonlinear vibrations of embedded multiwalled carbon nanotubes in thermal environment. Nonlinear Dyn 67(4):2241

    Article  MathSciNet  MATH  Google Scholar 

  • Ashley H, Haviland G (1950) Bending vibration of a pipe line containing flowing fluid. J Appl Mech 17(3):229–232

    Article  MathSciNet  Google Scholar 

  • Burden RL, Faires JD (2011) Numerical analysis, 9th edn. Cengage Learning, Brooks

    MATH  Google Scholar 

  • Dehghan M (2006) Solution of a partial integro-differential equation arising from viscoelasticity. Int J Comput Math 83(1):123–129

    Article  MathSciNet  MATH  Google Scholar 

  • Dehrouyeh-Semnani AM, Nikkhah-Bahrami M, Yazdi MRH (2017a) On nonlinear stability of fluid-conveying imperfect micropipes. Int J Eng Sci 120:254–271

    Article  MathSciNet  MATH  Google Scholar 

  • Dehrouyeh-Semnani AM, Mostafaei H, Dehrouyeh M, Nikkhah-Bahrami M (2017b) Thermal pre- and post-snap-through buckling of a geometrically imperfect doubly-clamped microbeam made of temperature-dependent functionally graded materials. Compos Struct 170:122–134

    Article  MATH  Google Scholar 

  • Deng J, Liu Y, Zhang Z, Liu W (2017) Stability analysis of multi-span viscoelastic functionally graded material pipes conveying fluid using a hybrid method. Eur J Mech 65:257–270

    Article  MathSciNet  MATH  Google Scholar 

  • Ding H, Chen L (2019) Nonlinear vibration of a slightly curved beam with quasi-zero-stiffness isolators. Nonlinear Dyn 95:2367–2382

    Article  MATH  Google Scholar 

  • Eringen AC, Edelen DGB (1973) On nonlocal elasticity. Int J Eng Sci 10(3):233–248

    Article  MathSciNet  MATH  Google Scholar 

  • Eringen A, Wegner J (2003) Nonlocal continuum field theories. Springer, New York

    Google Scholar 

  • Farajpour A, Farokhi H, Ghayesh MH, Hussain S (2018) Nonlinear mechanics of nanotubes conveying fluid. Int J Eng Sci 133:132–143

    Article  MathSciNet  MATH  Google Scholar 

  • Farajpour A, Farokhi H, Ghayesh MH (2018) Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. Eur J Mech 74:281–296

    Article  MathSciNet  MATH  Google Scholar 

  • Farajpour A, Ghayesh MH, Farokhi H (2019) Super and subcritical nonlinear nonlocal analysis of NSGT nanotubes conveying nanofluid. Microsyst Technol 25:4693–4707

    Article  Google Scholar 

  • Farajpour A, Ghayesh MH, Farokhi H (2020) Local dynamic analysis of imperfect fluid-conveying nanotubes with large deformations incorporating nonlinear damping. J Vib Control 26:1–17

    Article  MathSciNet  Google Scholar 

  • Farokhi H, Ghayesh MH, Amabili M (2013) Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int J Eng Sci 68:11–23

    Article  MathSciNet  MATH  Google Scholar 

  • Ghayesh MH, Farajpour A (2008) Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int J Eng Sci 129:84–95

    Article  MathSciNet  MATH  Google Scholar 

  • Ghayesh MH, Farokhi H, Alici G (2016) Size-dependent performance of microgyroscopes. Int J Eng Sci 100:99–111

    Article  MathSciNet  MATH  Google Scholar 

  • Ghayesh MH, Farokhi H, Farajpour A (2018) Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid. Microfluid Nanofluid 22(72):1–17

    Google Scholar 

  • Ghayesh MH, Farajpour A, Farokhi H (2019) Viscoelastically coupled mechanics of fluid-conveying microtubes. Int J Eng Sci 145:1–16

    Article  MathSciNet  MATH  Google Scholar 

  • Ghayesh MH, Farajpour A, Farokhi H (2019) Chaos in fluid-conveying NSGT nanotubes with geometric imperfections. Appl Math Model 74:708–730

    Article  MathSciNet  MATH  Google Scholar 

  • Ghayesh MH, Farajpour A, Farokhi H (2020) Effect of flow pulsations on chaos in nanotubes using nonlocal strain gradient theory. Commun Nonlinear Sci Numer Simul 83:105090

    Article  MathSciNet  MATH  Google Scholar 

  • Gholipour A, Ghayesh MH (2020) Nonlinear coupled mechanics of functionally graded nanobeams. Int J Eng Sci 150:1–14

    Article  MathSciNet  MATH  Google Scholar 

  • Karniadakis G, Beskok A, Aluru N (2006) Microflows Nanoflows. Springer, New York

    MATH  Google Scholar 

  • Kauthen JP (1992) The method of lines for parabolic partial integro-differential equations. J Integral Equ Appl 4(1):69–81

    Article  MathSciNet  MATH  Google Scholar 

  • Kiani Keivan (2014) Nonlinear vibrations of a single-walled carbon nanotube for delivering of nanoparticles. Nonlinear Dyn 76(4):1885–1903

    Article  MathSciNet  MATH  Google Scholar 

  • Li L, Hu Y (2016) Wave propagation in fluid-conveying viscoelastic carbon nanotubes based on nonlocal strain gradient theory. Comput Mater Sci 112:282–288

    Article  Google Scholar 

  • Li L, Hu Y, Li X, Ling L (2016) Size-dependent effects on critical flow velocity of fluid-conveying microtubes via nonlocal strain gradient theory. Microfluid Nanofluid 5(20):1–12

    Google Scholar 

  • Liu HS, Mote CD (1974) Dynamic response of pipes transporting fluids. ASME J Eng Ind 96(2):591–596

    Article  Google Scholar 

  • Mattheij RMM, Rienstra SW, Ten Thije JHM(2005) Boonkkamp. In: Partial differential equations: modeling, analysis, computation (Siam Monographs on Mathematical Modeling and Computation). SIAM, USA

  • Mohammadi H, Mahzoon M, Mohammad M, Mohammadi M (2014) Postbuckling instability of nonlinear nanobeam with geometric imperfection embedded in elastic foundation. Nonlinear Dyn 76(4):2005–2016

    Article  MathSciNet  MATH  Google Scholar 

  • Nematollahi MS, Mohammadi H, Taghvaei S (2019) Fluttering and divergence instability of functionally graded viscoelastic nanotubes conveying fluid based on nonlocal strain gradient theory. Chaos 29(3):1–11

    Article  MathSciNet  MATH  Google Scholar 

  • Ni Q, Zhang ZL, Wang L (2011) Application of the differential transformation method to vibration analysis of pipes conveying fluid. Appl Math Comput 217:7028–7038

    MathSciNet  MATH  Google Scholar 

  • Orolu KO, Fashanu TA, Oyediran AA (2019) Cusp bifurcation of slightly curved tensioned pipe conveying hot pressurized fluid. J Vib Control 25(5):1109–1121

    Article  MathSciNet  Google Scholar 

  • Owoseni OD, Orolu KO, Oyediran AA (2017) Dynamics of slightly curved pipe conveying hot pressurized fluid resting on linear and nonlinear viscoelastic foundations. ASME J Vib Acoust 140(2):021005

    Article  Google Scholar 

  • Oyelade AO, Oyediran AA (2020) The effect of various boundary conditions on the nonlinear dynamics of slightly curved pipes under thermal loading. Appl Math Model 87:332–350

    Article  MathSciNet  MATH  Google Scholar 

  • Oyelade AO, Oyediran AA (2020) Imperfect bifurcation and chaos of slightly curved carbon nanotube conveying hot pressurized fluid resting on foundations. ASME J Fluids Eng 142(11):111204

    Article  Google Scholar 

  • Oyelade AO, Ikhile OG, Oyediran AA (2020) On stability of a slightly curved Maxwell viscoelastic pipe conveying fluid resting on linear viscoelastic foundation. Aust J Mech Eng 40:1–8

    Google Scholar 

  • Sanz-Serna JM (1988) A numerical method for partial integro-differential equation. SIAM J Numer Anal 25(2):319–327

    Article  MathSciNet  MATH  Google Scholar 

  • Sloan IH, Thomée V (1986) Time discretization of integro-differential equation of parabolic type. SIAM J Numer Anal 23(5):1052–1061

    Article  MathSciNet  MATH  Google Scholar 

  • Soliman AF, El-Asyed AMA, El-Azab MS (2012) On the numerical solution of partial integro-differential equations. Math Sci Lett 1(1):71–80

    Article  Google Scholar 

  • Qian Q, Wang L, Ni Q (2009) Instability of simply supported pipes conveying fluid under thermal loads. Mech Res Commun 36(3):413–417

    Article  MATH  Google Scholar 

  • Yi-Min H, Seng G, Wei W, Jie H (2012) A direct method of natural frequency analysis on pipeline conveying fluid with both ends supported. Nucl Eng Des 253:12–22

    Article  Google Scholar 

  • Yun-dong Li, Yang Yi-ren (2017) Nonlinear vibration of slightly curved pipe with conveying pulsating fluid. Nonlinear Dyn 88(4):2513–2529

    Article  Google Scholar 

  • Zhong-min W, Zhan-wu Z, Feng-qun Z (2005) Stability analysis of viscoelastic curved pipes conveying fluid. Appl Math Mech 26(6):807–813

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Engineering, Department of Civil and Environmental Engineering, University of Lagos, Lagos, Nigeria

    Akintoye O. Oyelade

  2. Faculty of Science, Department of Mathematics, University of Lagos, Lagos, Nigeria

    Julius O. Ehigie

  3. Faculty of Engineering, Department of Mechanical Engineering, University of Lagos, Lagos, Nigeria

    Ayo A. Oyediran

Authors
  1. Akintoye O. Oyelade
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Julius O. Ehigie
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ayo A. Oyediran
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Akintoye O. Oyelade.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Oyelade, A.O., Ehigie, J.O. & Oyediran, A.A. Nonlinear forced vibrations of a slightly curved nanotube conveying fluid based on the nonlocal strain gradient elasticity theory. Microfluid Nanofluid 25, 95 (2021). https://doi.org/10.1007/s10404-021-02493-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10404-021-02493-0

Keywords

Search

Navigation