Interfacial instability of liquid films coating the walls of a parallel-plate channel and sheared by a gas flow

Abstract

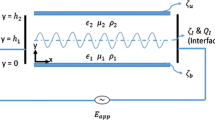
The stability and coupling of liquid films coating the walls of a parallel-plate channel and sheared by a pressure-driven gas flow along the channel center plane is studied. The films are susceptible to a long-wavelength instability. For sufficiently low Reynolds numbers and thick gas layers, the dynamic behavior is found to be described by two coupled nonlinear partial differential equations. A linear stability analysis is conducted under the condition that the material properties and the initial undisturbed liquid-film thicknesses are equal. The linear analysis is utilized to determine whether the interfaces are predominantly destabilized by the variations of the shear stress or by the pressure gradient acting upon them. The analysis of the weakly nonlinear equations performed for this case shows that instabilities corresponding to a vanishing Reynolds number are absent from the system. Moreover, for this configuration, the patterns emerging along the two interfaces are found to be identical in the long-time limit, implying that the films are fully synchronized. A different setup, where the liquid films have identical material properties but their undisturbed thicknesses differ, is studied numerically. The results show that, even for this configuration, the interfacial waves remain phase-synchronized and closely correlated for an extended period of time. These findings are particularly relevant for gaseous flow through narrow ducts with liquid-coated walls.

Appendices

Appendix 1: Evolution equations

Herein, the method of obtaining the evolution equations Eqs. (7) and (8) is summarized. At first, the following discussion considers a system where the $1/M^2\ll 1$ condition is not assumed. In this case, one solves Eqs. (1)–(6) for the zeroth and first order of $\epsilon$ separately, and assumes that $(\epsilon {\textit{Re}})^2,\epsilon ^2\ll 1$. At $O(\epsilon ^0)$, one obtains the solution corresponding to solving the Stokes equation in all layers while neglecting the effect of the capillary pressure (as $Ca=O(1)$, capillary effects enter at $O(\epsilon ^1)$). To zeroth order in $\epsilon$, an evolution equation for the film thicknesses can be obtained by utilizing the kinematic boundary conditions [Eq. (6)]. Afterwards, these solutions are applied to obtain the first-order solutions in $\epsilon$ for the governing equations. This approach has been applied in many studies, for example to the related problem of liquid stability during spin coating (Reisfeld et al. 1991).

To implement the condition $1/M^2\ll 1$, one solves all equations arising from the previously summarized method only up to order 1 / M. If higher order terms in the viscosity ratio were also included in the equations, Eq. (7) would take the form

$$\begin{aligned} \frac{\partial H_1}{\partial \overline{\tau }}&=-\frac{\partial }{\partial \overline{X}}\left\{ \frac{H_1^2(3+H_1-3H_2)}{\epsilon (1-H_1-H_2)^3}\right. \\&\quad +{\textit{Re}}\sqrt{3}{{\textit{Ca}}}\frac{3H_1^2(1+5H_1-H_2)}{35(1-H_1-H_2)^3}\left( \frac{\partial H_1}{\partial \overline{X}}+\frac{\partial H_2}{\partial \overline{X}}\right) \\&\quad \left. +\frac{H_1^3}{3}\frac{\partial ^3 H_1}{\partial \overline{X}^3}\right\} -\frac{1}{{\textit{M}}}\frac{\partial }{\partial \overline{X}}\left\{ \frac{-6 H_1^5-H_1^6+H_1^4 (3+6 H_2{}^2)}{\epsilon (1-H_1-H_2){}^6}\right. \\&\quad +\frac{3 H_2^3 (-2+H_2+H_2^3)+H_1^3(-12+42H_2)}{\epsilon (1-H_1-H_2){}^6} \\&\quad \left. +\frac{H_1^3H_2^2 (-42+8 H_2)}{\epsilon (1-H_1-H_2){}^6}+O(\epsilon ^0)\right\} \\&\quad +O\left( \frac{1}{{\textit{M}}^2}\right) +\cdots . \end{aligned}$$

(38)

A similar equation would govern the time evolution of $H_2$. These equations imply that Eqs. (7) and (8) give a good approximation to the evolution of the system as long as $O(\epsilon )\gg O(1/M)$, in particular if $O(\epsilon ^2)\ge O(1/M)$. This corresponds to all the numerical simulations performed for the current paper. It is notable that if $O(\epsilon )\approx O(1/M)$, the additional terms expressed in detail in Eq. (38) would also be necessary for a valid description of the system. However, to the first order in $\epsilon$, these terms would transform to additional linear terms of the weakly nonlinear equations. In this sense, they only modify the first terms on the right-hand side of Eqs. (13) and (14). Especially, for symmetric systems, these terms correspond to the propagation velocity of interfacial waves. As this velocity only affects the coupling term between the symmetric and the antisymmetric instability, it is expected that the main results discussed in the related sections of this paper remain qualitatively valid and quantitatively reasonably accurate even in the $O(\epsilon )=O(1/M)$ regime.

To demonstrate this, Fig. 8 depicts the evolution of the symmetric and antisymmetric instability for a) silicone oil and b) water. The line plots were calculated by evolving the film interfaces according to Eqs. (7) and (8). The point plots correspond to Eq. (38) and to its analogue for $H_2$. The simulation parameters for Fig. 8a) are the same as used for Fig. 6. Since, in this case $1/M\ll \epsilon$, the two plots match very well, in agreement with the expectations. For the simulation with water films displayed in Fig. 8b), the parameters were chosen as $d=200~\upmu \text{m}$, $H_0=0.07$, $u=3.5~\text{m/s}^{-1}$. For this case, according to Eq. (23), the errors of the assumption of semi-rigidness are $\varDelta \sigma _+=0.08$ and $\varDelta \sigma _-=0.01$. Thus, the parameters are at the limit of the applicability range of the method presented in the paper. Moreover, $\epsilon =0.07$ and $1/M\approx 0.02$, i.e., they are comparable. Considering these facts, it is especially remarkable that the two sets of graphs remain highly similar. Hence, Eqs. (7) and (8) give a quantitatively good description for the system even in this case, while they remain extremely helpful in retaining a physically understandable picture of the problem. A number of additional simulations indicated that the quantities $\varDelta \sigma _+$ and $\varDelta \sigma _-$ generally give a good estimate for the validity of semi-rigidness. Performing such a detailed verification of this assumption is considerably more complicated for asymmetric systems. However, intuitively it is still expected that the effects of the additional term in Eq. (38) are overshadowed by the first terms of Eqs. (13) and (14).

Fig. 8

Evolution of the symmetric instability for a silicone oil ($H_0 = 0.2$, ${\textit{Re}}= 23.46$, ${\textit{Ca}}= 0.15$, $\epsilon =0.12$, and $1/M=0.002$) and b water ($H_0 = 0.07$, ${\textit{Re}}= 37.70$, ${\textit{Ca}}= 0.14$, $\epsilon =0.07$, $1/M=0.02$) films. The lines correspond to Eqs. (7) and (8); the points to the corrected evolution equations according to Eq. (38)

Appendix 2: Linear growth rate for arbitrary viscosities

The growth rates from the linear stability analysis of Sect. 3.1 for arbitrary viscosities are given by

$$\begin{aligned} \text{Re}(\sigma _{+})&=\frac{(1-2 H_0){}^2 H_0^2}{210 ({\textit{M}}-6 ({\textit{M}}-1) H_0 +12 ({\textit{M}}-1) H_0^2-8 ({\textit{M}}-1) H_0^3){}^5} \\&\quad \times\, \{k^2 18 Ca^{1/3}({\textit{M}}-1) {\textit{Re}}(1-2 H_0)[2 {\textit{M}}^4-4 {\textit{M}}^3 (-3+7 {\textit{M}}) H_0 \\&\quad -\,{\textit{M}}^2(-63+4 (37-36 {\textit{M}}){\textit{M}}) H_0^2-6{\textit{M}}^2(105+4{\textit{M}}(-17+8{\textit{M}}) \\&\quad -\,56{\textit{R}})H_0^3-2 {\textit{M}}(2 {\textit{M}}(-133+12 {\textit{M}}(-51+28 {\textit{M}}))+7 (-63 \\&\quad +\,178 {\textit{M}}){\textit{R}}) H_0^4-(-756{\textit{R}}+4 {\textit{M}}(21 (60+49{\textit{R}})-2 {\textit{M}}(1981 \\&\quad +\,4 {\textit{M}}(-673+252 {\textit{M}})+753{\textit{R}}))) H_0^5-12 (21 (15+7{\textit{R}}) \\&\quad +\,{\textit{M}}(-3255-179{\textit{R}}+4 {\textit{M}}(1743+4 {\textit{M}}(-373+112 {\textit{M}}) \\&\quad +\,44{\textit{R}}))) H_0^6-(48 (-420+53{\textit{R}})+16 {\textit{M}}(7210-1027{\textit{R}} \\&\quad +\,2 {\textit{M}}(-5999+132 (31-8{\textit{M}}) {\textit{M}}+422{\textit{R}}))) H_0^7-(64 (-1 \\&\quad +\,{\textit{M}}) {\textit{M}}(1925+28 {\textit{M}}(-59+18 {\textit{M}})-345{\textit{R}})+96 (-1+{\textit{M}}) (-385 \\&\quad +\,97{\textit{R}})) H_0^8-128 (-1+{\textit{M}}) (210-54{\textit{R}}+{\textit{M}}(-595+68 (7-2 {\textit{M}}) {\textit{M}} \\&\quad +\,99{\textit{R}})) H_0^9-64 (-1+{\textit{M}}) (8 {\textit{M}}(35-28 {\textit{M}}+8 {\textit{M}}^2-5{\textit{R}})+5 (-21 \\&\quad +\,5{\textit{R}})) H_0^{10}]+k^4 35 H_0 [(4{\textit{M}}-3) H_0-2{\textit{M}}] [{\textit{M}}-2({\textit{M}}-1) H_0 (3 \\&\quad -\,6 H_0+4 H_0^2)]{}^4\}, \end{aligned}$$

(39)

$$\begin{aligned} \text{Re}(\sigma _{-})&=\frac{H_0^3}{30 \text{Ca}^{2/3} ({\textit{M}}+2 (1-{\textit{M}}) H_0){}^3 ({\textit{M}}+2 (1-{\textit{M}}) H_0 (3-6 H_0+4 H_0^2)){}^2} \\&\quad \times\, \{k^2[18 \text{Ca} (-1+{\textit{M}}) {\textit{Re}}(1-2 H_0) H_0 (5 {\textit{M}}^2+2 {\textit{M}}^2(-15 \\&\quad +\,18{\textit{R}}) H_0+2 {\textit{M}}({\textit{M}}(30-32{\textit{R}})+7{\textit{R}}) H_0^2+4 ({\textit{R}}-7 {\textit{M}}{\textit{R}} \\&\quad +\,2 {\textit{M}}^2 (-5+8{\textit{R}})) H_0^3)]+k^4[5 \text{Ca}^{2/3} (-2 {\textit{M}}-(1-4 {\textit{M}}) H_0) ({\textit{M}}^2 \\&\quad -\,8 (-1+{\textit{M}}) {\textit{M}}H_0+12 (1-3 {\textit{M}}+2 {\textit{M}}^2) H_0^2-8 (3-7 {\textit{M}} \\&\quad+\,4 {\textit{M}}^2) H_0^3+16 (-1+{\textit{M}})^2 H_0^4){}^2]\}, \end{aligned}$$

(40)

where R is the ratio of the mass densities, defined in Sect. 2.

These formulas were compared with the results of the numerical calculations of Renardy (1987). The corresponding results are summarized in Fig. 3. To match with the nondimensional parameters used in the paper referred to, the material properties were taken as $\mu _1=\mu _2=1.56605\times 10^{-6}~\text{Pa}\,\text{s}$, $\rho _1=\rho _2=\rho _g=1~\text{kg}\,\text{m}^{-3}$, and a channel width of $200~\upmu \text{m}$ was chosen. Renardy (1987) has performed her numerical calculations for vanishing surface tension, whereas the scaling introduced in the current paper is based on a finite capillary number. For this purpose, the surface tension of the silicone oil listed in Table 2 was used. Subsequently, the effects of the surface tension can be eliminated by omitting the terms in the growth rates (39) and (40) scaling with $k^4$. In Fig. 3, the growth rates for the wavenumber $0.01/H_0$ are plotted for a pressure gradient of $\partial p_g/\partial x=19.62~\text{Pa}\,\text{m}^{-1}$ as a function of the nondimensional film thickness.

Papaefthymiou et al. (2013) discussed that the weakly nonlinear equations describing systems of arbitrary viscosity ratios should still take a qualitatively similar form as Eqs. (13) and (14). However, expression (40) indicates that for arbitrary viscosities the antisymmetric mode is not necessarily linearly stable in this case. Therefore, for such systems, the mirror symmetry can break down dynamically. A similar feature for the related problem of core-annular flows was obtained numerically by Hu and Patankar (1995).

Appendix 3: Weakly nonlinear analysis

Most linear terms of Eqs. (13) and (14) drop out after substitution of the ansatz for the solution (24). This is a direct consequence of employing a generalized form of the solution used for the linearized equation to describe the weakly nonlinear behavior. For instance, Eq. (13) takes the form

$$\begin{aligned}&\int \limits _{-\infty }^{\infty }{\left( \frac{\partial A_+}{\partial \tau } {\mathrm{e}}^{\sigma _+\tau }+\frac{\partial A_-}{\partial \tau }{\mathrm{e}}^{\sigma _-\tau } \right) {\mathrm{e}}^{{{\text{i}}}kX}{\mathrm{d}}k} \\&\quad =-\frac{\partial }{\partial X}\left[ \left\{ \int \limits _{-\infty }^{\infty } {\left( A_+{\mathrm{e}}^{\sigma _+\tau }+A_-{\mathrm{e}}^{\sigma _-\tau }\right) {\mathrm{e}}^{{{\text{i}}}kX}{\mathrm{d}}k} \right\} ^2 \right. \\&\qquad \times\, \frac{3(1-H_0)[1+H_0(3-2H_0)]}{(1-2H_0)^5} \\&\qquad +\,\left\{ \int \limits _{-\infty }^{\infty }{\left( A_+{\mathrm{e}}^{\sigma _+\tau }+ A_-{\mathrm{e}}^{\sigma _-\tau }\right) {\mathrm{e}}^{{{\text{i}}}kX}{\mathrm{d}}k}\right\} \\&\qquad \times\, \left\{ \int \limits _{-\infty }^{\infty }{\left( A_+{\mathrm{e}}^{\sigma _+\tau } -A_-{\mathrm{e}}^{\sigma _-\tau }\right) {\mathrm{e}}^{{{\text{i}}}k'X}{\mathrm{d}}k'}\right\} \\&\qquad \times\, \frac{6H_0(2+H_0-2H_0^2)}{(1-2H_0)^5}+ \left\{ \int \limits _{-\infty }^{\infty }{\left( A_+ {\mathrm{e}}^{\sigma _+\tau }-A_-{\mathrm{e}}^{\sigma _-\tau }\right) {\mathrm{e}}^{{{\text{i}}}kX}{\mathrm{d}}k}\right\} ^2 \\&\qquad \left. \times\, \frac{3H_0^2(3+2H_0)}{(1-2H_0)^5}\right] . \end{aligned}$$

(41)

Since multiplication in the position space transforms to convolution in Fourier space, one finds that

$$\begin{aligned}&\frac{\partial A_+}{\partial \tau }{\mathrm{e}}^{\sigma _+\tau }+\frac{\partial A_-}{\partial \tau }{\mathrm{e}}^{\sigma _-\tau } \end{aligned}$$

(42)

$$\begin{aligned}&\quad =-{{\text{i}}}k\left[ \frac{3(1+6H_0)}{(1-2H_0)^5}(A_+{\mathrm{e}}^{\sigma _+\tau })\underset{k}{*}(A_+{\mathrm{e}}^{\sigma _+\tau }) \right. \\&\qquad +\frac{6(1+4H_0)}{(1-2H_0)^4}(A_+{\mathrm{e}}^{\sigma _+\tau })\underset{k}{*}(A_-{\mathrm{e}}^{\sigma _-\tau }) \end{aligned}$$

(43)

$$\begin{aligned}&\qquad \left. +\frac{3(1+2H_0)}{(1-2H_0)^3}(A_-{\mathrm{e}}^{\sigma _-\tau })\underset{k}{*}(A_-{\mathrm{e}}^{\sigma _-\tau })\right] . \end{aligned}$$

(44)

A similar calculation can be performed for Eq. (14). A straightforward simplification of these two equations leads to the form of Eq. (25).

Appendix 4: Instabilities at vanishing Reynolds number

There are two known instabilities appearing during stratified film flows at zero Reynolds numbers. The first one is the kinetic alpha effect which appears from the resonance-like coupling of the interfaces. According to the results of Kliakhandler and Sivashinsky (1995), this instability is significant for configurations where the intermediate layer is thin. However, Assumption 3 of Sect. 2.2 is only justified if the mean gas velocity is much larger than the velocities at the gas–liquid interfaces. This is not fulfilled for thin gas layers. Thus, the kinetic alpha effect is automatically excluded from the analysis described in this paper.

As it was indicated Kliakhandler and Sivashinsky (1995) as well as by Papaefthymiou et al. (2013), another form of instability could also appear in the system. This instability is induced by the coupling between capillary forces and advective effects, and it has been implied to be a generalization of the Majda–Pego instability (Majda and Pego 1985). It is noted that the validity of this assumption is currently an open question: The Majda–Pego instability has been derived for systems where, instead of a fourth-order spatial derivative, there is only a second-order spatial derivative in the evolution equations for the film thicknesses. Given the limited importance of the instability for the current analysis, herein, only a brief comparison between the corresponding results and those of Papaefthymiou et al. (2013) will be presented. As it was mentioned in the discussion of Eqs. (31) and (32), in symmetric systems, the surface tension always decreases the deformations of the interfaces, and thus, no Majda–Pego instability appears. This agrees with the expectations, as the instability criteria discussed by Canic and Plohr (1995) and assumed by Papaefthymiou et al. (2013) to be valid for quartic dissipative systems cannot be fulfilled. Formally, according to Eqs. (13) and (14), the dissipation matrix of the Majda–Pego instability is defined by

(45)

Since this is a positive multiple of the identity matrix, the system under study is not expected to be unstable in the sense of Majda and Pego. For asymmetric systems, the diagonal elements of D are no longer equal; thus, the kinetic instability may appear in such systems. In principle, such a secondary instability could also lead to the observed decoupling of the liquid layers for intermediate values of $\delta$ captured by the numerical simulations of Sect. 4. In the light of the yet unproven applicability of the Majda–Pego instability for the asymmetric systems addressed in this work, the explanation given in the main text appears to be the more profound one.

Appendix 5: Numerical simulations

To support the argument that the antisymmetric mode disappears if the system is initially mirror-symmetric, numerical simulations were performed. The parameters of the simulations are summarized in Sect. 3.2. The results are given in Table 3. The simulated time intervals were set to $\tau _{\mathrm{max}}$, the value of which was chosen large enough for $\langle \zeta _+^2\rangle$ to reach an asymptotic state, i.e., it just oscillates around its asymptotic value. At the last time step, the ratio of $\langle \zeta _+^2\rangle$ and $\langle \zeta _-^2\rangle$ is calculated. The results confirm that, after a sufficiently long time, the magnitude of the antisymmetric mode is considerably smaller than that of the symmetric one.

Table 3 Results of the numerical simulations for symmetric configurations

Appendix 6: Reduction to single evolution equation

Equations (29) and (30) are reducible to a single evolution equation, even without assuming that $\zeta _-\ll \zeta _+$. To show this, one introduces

$$\begin{aligned} Z_-(Y)=\int \limits _{-\infty }^Y{\zeta _-}\,{\mathrm{d}}X. \end{aligned}$$

(46)

After integrating Eq. (30) with respect to X, one finds

$$\begin{aligned} \zeta _+\Big |_X=-\left\{ \frac{(1-2H_0)^4}{6(1+4H_0)Z_-} \left[ \frac{1}{\epsilon }\frac{\partial Z_-}{\partial \tau }+\frac{H_0^3}{3}\frac{\partial ^4Z_-}{\partial X^4}\right] \right\} {\Bigg |}_{X+\frac{12H_0^2}{(1-2H_0)^4}\tau }. \end{aligned}$$

(47)

Substituting this into (29) and using $\zeta _-=\partial Z_-/\partial X$, one arrives at a single evolution equation for $Z_-$. The resulting equation is considerably more complicated than the Kuramoto–Sivashinsky equation. Nevertheless, after solving this single equation, one can directly calculate the deformations of the interfaces.

As an equivalent approach, one can also reduce the number of equations by integrating Eq. (29) instead of (30). Subsequently, $\zeta _-$ can be computed. This can be applied to arrive at a single evolution equation for the spatial integral of $\zeta _+$. Since, in general, $\zeta _-\ll \zeta _+$, in certain cases, it may be beneficial to use this equation for the simulations to avoid numerical inaccuracies.