1 Introduction

Algae are a diverse set of simple plants which are found in water almost everywhere on Earth. Most algae use photosynthesis to obtain energy and require access to light and nutrients to live. The availability and characteristics of the light and nutrients, along with other properties of the local environment, play a strong role in the species dynamics of algae populations; this means that algae dynamics can also be used as an indicator of environmental changes. A rapid increase in nutrients can lead to the development of algae blooms, where one species rapidly grows, typically to the point where the algal mass is visible by eye. These blooms can cause environmental and/or economic harm through negative impacts on other aquatic organisms (Landsberg 2002), aquaculture (Lewitus et al. 2012), or by introducing toxins into drinking or recreational water (Hinder et al. 2011; Fleming et al. 2011). Even otherwise benign species can impact their surroundings during a bloom by consuming nutrients and blocking light.

The gold standard for the identification of algae is manual sample collection and microscopy-based identification (here, we use the general term “algae” to refer specifically to microscopic phytoplankton). Manual cell identification is slow and limits the spatio-temporal resolution of sampling, so technology which automates the identification process would be useful for monitoring and understanding algae species dynamics, particularly for the identification of blooms or toxin-producing species (Anderson et al. 2001, 2012). Technical solutions to automated algae identification have been presented, including microfluidic or lab-on-a-chip devices intended to be suitable for portable use (Benazzi et al. 2007; Hashemi et al. 2011a, b; Schaap et al. 2012a, b). However, algae cells can have characteristic dimensions from a few microns to hundreds of microns, and the need to accurately identify cells over a size range of two orders of magnitude limits the approaches which can be used in this technology.

The ability to pre-sort algae by size and/or shape can thus be a key component in sample preparation for microfluidic algae identification systems. To this end, we present a size- and shape-sensitive algae sorting method using inertial microfluidics. This work complements the size- and shape-sensitive optical identification methods we have presented previously (Schaap et al. 2011, 2012b). To motivate the use of shape as a relevant measurement for algae monitoring, we first review the use of morphology in algae classification before presenting previous work on inertial microfluidics for other applications.

Our exploration of this technique for algae sorting is of interest to both the microfluidics community and the phycological community. Sorting and measuring algae is not only a relevant end application in its own right, but the complex shapes and ease of handling of algal cells also make them attractive specimens for the development and evaluation of microfluidic techniques. Current microfluidic research demonstrating the handling, sorting, or measurement of single cells has focused primarily on mammalian cells (for example, blood cells) rather than plant cells. Inertial microfluidics has not, to our knowledge, been demonstrated as a focusing or sorting technique for plant cells, and the morphology-based sorting of highly non-spherical cells using secondary Dean flows with inertial microfluidics has not been previously demonstrated.

1.1 Relevance of algae morphology

Size- and shape-sensitive algae sorting is motivated by the phenetic approach to algae taxonomy. In a phenetic system, organisms are grouped according to similarities in observable traits like morphology (shape, size, patterns, etc.). This is in contrast to molecular or genetic classifications, which can provide information on the complex relationships between species from an evolutionary perspective but which do not necessarily correspond to predictable behaviour in response to environmental stimuli. For applications like predicting and measuring planktonic blooms, a phenetic approach may yield valuable information while requiring simpler or cheaper technology.

Interest in phenetic classification of algae has recently enjoyed a resurgence, triggered by a paper by Reynolds et al. (2002) in which 31 groups of phytoplankton are defined on their shared adaptive features. Kruk et al. (2010, 2011) proposed a scheme that defines algal groups using a combination of seven primarily morphological traits, including the surface-to-volume ratio and the maximum linear dimension. Various studies have used phenetic classifications to characterize the seasonal variations in algae communities in water or to compare the communities in ecologically similar bodies of water (Naselli-Flores et al. 2007; Abonyi et al. 2012). The distribution of algae cell sizes in a body of water can also provide insight into the population dynamics, the functional behaviour of the algae, or the ecosystem properties. For example, the spectra of size distributions of organisms in an environment usually follow a power function N = M α where N is the abundance of a given size range, M the size of cells in that range, and α a size-scaling exponent. Huete-Ortega et al. (2010) found that this exponent α changed for different oceanographic conditions and concluded that size distributions could thus provide an efficient description of the transient state of an ecosystem. Correlations have also been suggested between the number of species present and the size distribution (Cermeno and Figueiras 2008). It has also been shown that the algae dynamics in a body of water could be described by the size distribution of the community (Marquis et al. 2011) and that photosynthetic behaviour changes as a function of algae cell size (Kaiblinger et al. 2007). Further motivation for size-based measurements comes from the need to correlate models of algae–environment interactions to measurements (Baird and Suthers 2007).

Phenetic approaches to algae bloom characterization do have some limitations. For example, the production of toxins by cyanobacteria does not depend solely on the species of the cyanobacteria, but also on the strain of the species and even on genetic mutations within the strain. That is, the same species can have both toxic and non-toxic versions (see, for example, Meiβner et al. 1996; Schembri et al. 2001). Further, morphological data may need to be coupled to local environmental or physiological traits to form a fuller understanding of the phytoplankton community (Litchman and Klausmeier 2008).

In addition to its use in monitoring or classification, size-sorting of algae may also be useful as a technique for pre-concentrating and isolating individual cells to be used in growing algal culture.

1.2 Inertial microfluidics for particle sorting

Inertial microfluidics provides a promising tool with which to rapidly screen an algae sample by morphological features, by manipulating particles in a microchannel using only forces arising from the system’s fluid dynamics (shear forces, lift forces, etc.), without applying external fields. One of the commonly cited properties of microfluidics is the ability to work at such low Reynolds numbers that inertial effects are negligible. However, it is possible to create laminar flow conditions in a microchannel where inertial forces are non-negligible and can be used for particle sorting.

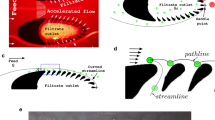
When a fluid entraining small, neutrally buoyant particles flows along a straight channel, two forces cause the particles to cross the fluidic streamlines. The particle experiences an asymmetric shear force from the Poiseuille flow profile which pushes the particles towards the channel walls. This force competes with the wall-induced lift forces, which push the particles away from the walls. This combination of forces defines a set of equilibrium positions for the particles in the channel cross section. In a circular channel, there is an annulus of equilibrium positions at a fixed distance from the centre of the channel. A straight channel with a square cross section has four equilibrium positions along the walls, and a straight rectangular channel (Fig. 1) has two equilibrium positions (Di Carlo 2009).

Fig. 1
figure 1

(Top) Particle sorting in a straight channel using inertial effects: particles in a rectangular channel with Re > 1 self-align to equilibrium positions due to inertial forces. (Bottom) A spiral channel (geometry not to scale) creates a counter-rotating secondary Dean flow, which provides an asymmetrical bias to the particle equilibrium positions that are now collapsed onto one single point

Full size image

Di Carlo et al. have presented some practical design rules which can be used to determine whether the geometry of a given system is adequate to inertially sort particles (Amini et al. 2014). The first rule covers the ratio of particle size to channel size, and the second covers the required length of the channel.

In order for the shear forces to be large enough to have significant effect, the particle diameter a must have a minimum size compared to the channel dimensions. This criterion can be evaluated with the use of the particle Reynolds number

$$Re_{P} = \frac{{\rho UD_{H} }}{\mu }\left( {\frac{a}{{D_{H} }}} \right)^{2}$$
(1)

which depends on the fluid density ρ, average velocity U, viscosity µ, and the channel hydraulic diameter

$$D_{H} = \frac{2HW}{H + W}$$
(2)

which is a function of the channel height H and width W. For inertial focusing in a square or rectangular channel to occur, Re P should be on the order of one or larger.

The required focusing length of a rectangular channel

$$L_{f} = \frac{{\pi \mu D_{\text{ch}} }}{{\rho U_{\text{m}} a^{2} f_{L} }}$$
(3)

depends on the maximum velocity U m ~ 1.5 U and a dimensionless lift coefficient f L which is between 0.02 and 0.05 for channels of aspect ratio between 0.5 and 2; the value D ch is the dimension of the face along which the particles are focusing (either the channel height or width) (Di Carlo 2009).

This particle focusing effect in a straight channel has been demonstrated in numerous works, for example from the Di Carlo group. This group showed that, for example, 9-µm particles at channel Reynolds number Re = ρUD H /μ = 90 in 50-µm square channels reached an equilibrium position after 1 cm of channel (Di Carlo et al. 2007).

1.3 Using Dean flows to bias equilibrium positions

In a straight channel with a symmetric cross section (circular or rectangular, for example), the inertial sorting effect creates a symmetric set of equilibrium positions. In order to sort particles into one unique position according to their size or shape, a biasing force must be applied which collapses the multiple equilibrium solutions to a single point.

This can be accomplished with the use of a curved channel, in which two counter-rotating secondary flows (“Dean flows”) form in the direction perpendicular to the main flow direction (Fig. 1). The combination of drag forces from the Dean flow and the previously described shear and wall lift forces create a single particle-size-dependent equilibrium position in the channel cross section.

The Dean flow is characterized by the dimensionless Dean number

$${\text{De}} = Re\sqrt {\frac{{D_{H} }}{2R}} = \frac{{\rho UD_{H} }}{\mu }\sqrt {\frac{{D_{H} }}{2R}}$$
(4)

and depends on the channel radius of curvature R. The drag force imposed by the Dean flow on a particle works with or against the lift forces described above, depending on the particle’s position in the channel. At flow rates just high enough to focus the particles, particles above a certain size will assume an equilibrium position in the cross section near the radially inward vertical wall of the channel, where there are balanced forces pushing on the particle from all four directions in the channel cross section: in the height direction, the particles are brought to the middle of the channel height by the drag of the counter-rotating Dean flows. In the width direction, the Dean flow drag and wall lift forces are pushing the particle towards the channel centre, while the force from the asymmetric shear flow pushes the particle towards the wall. This equilibrium position moves towards the channel centre as the flow rate increases.

Previous work has shown that particles in curved channels tend to focus at a position not too near the wall, and thus the shear gradient lift F L is the predominant force counteracting the drag forces from the Dean flow F D. That observation led to the expression of an inertial force ratio

$$R_{f} = \frac{{F_{\text{L}} }}{{F_{\text{D}} }} = \frac{{2Ra^{2} }}{{D_{h}^{3} }}f$$
(5)

which depends on a dimensionless constant f which ranges from 0.02 to 0.03 for 20 < Re < 95 (Gossett and Di Carlo 2009). If this ratio is much greater than one, the particles will be unaffected by the secondary flow; if it is too low, the particle’s behaviour will be dominated by drag from the secondary flow. For R f on the order of 1, an equilibrium between the two forces can be reached. This ratio, together with the channel Reynolds number Re, can provide an indication of the width of a focused stream of particles through the use of a state diagram (see Fig. 5 in Gossett and Di Carlo 2009). Details can be seen in the original work but in general, conditions with R f  ≥ 0.05 and Re < 200 focus to a tight stream, and some conditions with R f on the order of 0.01 and Re < 250 will focus, albeit to a broader stream. At 0.01 < R f  < 0.1, particles focus up to a certain value of channel Reynolds number (Re ≈ 200), but above that become unfocused. Based on the parameters used in our experiments, which are detailed below, we can thus predict that 5-µm-diameter particles will not focus in our experiments, that 20-µm particles will focus well, and that 10-µm-diameter particles will focus but not as tightly as the 20-µm particles.

Previous work by other groups has studied this approach to particle focusing and demonstrated it in practice: for example, an asymmetrically wavy channel was used to induce Dean flows to manipulate particles from 2 to 17 µm in diameter (Di Carlo et al. 2007). Two limitations in the migration of particles were observed: a loss of focusing occurred at a/D H  < 0.07 and at De > 20. In both of these cases, the Dean drag becomes much larger than the lift forces, i.e. R f  ≪ 1, pulling the particles out of the equilibrium positions and dragging them around the channel with the secondary flows. The same group has demonstrated the focusing of small particles in asymmetric wavy channels at high throughput rates (Re = 27; 41,000 particles/second)(Gossett and Di Carlo 2009) and has used inertial microfluidics in straight channels to sort particles by deformability (Hur et al. 2011b) and aspect ratio (Hur et al. 2011a; Masaeli et al. 2012).

Spiral microchannels have also been used to introduce a Dean flow in an inertial microfluidic device to sort particles. This approach has been successfully used to sort microspheres by size as well as to separate neuroblastoma cells (~15 µm diameter) from glioma cells (~8 µm diameter) with 80 % efficiency and with a high throughput rate of ~1 million cells/min (Bhagat et al. 2008; Kuntaegowdanahalli et al. 2009). Similar devices have been used to separate red blood cells and white blood cells with 95 % efficiency (Nivedita and Papautsky 2013) and to isolate circulating tumour cells (Hou et al. 2013; Warkiani et al. 2014b). A similar device was used to sort sperm cells from red blood cells; the design of the channel was based on models of sperm as 5-µm spheres and the red blood cells as 9-µm spheres. While the sperm cells were only weakly focused due to the polydispersity in their sizes, repeating the sorting process several times led to a removal of 100 % of the blood cells from the sample (Son et al. 2015). The sorting of larger particles has also been demonstrated, for example, using 40- and 60-µm particles in a 5-loop spiral channel with flow rates >1 mL/min. This technique has been further improved upon by creating a spiral channel with a trapezoidal cross section (Warkiani et al. 2014a). This geometry moved the location of the Dean vortex which improved the sorting resolution.

2 Materials and methods

The microchannel used for the experiments presented here was 350 µm wide and 100 µm high. It was in the shape of an Archimedean spiral with three full turns, an initial radius of 5 mm, and a final radius of 10 mm, making a total channel length of approximately 14 cm. The Dean number is a function of the radius of curvature and thus varies over the channel length, but an average value can be calculated for a given flow rate. The flow rates in our experiments were all between 0.4 and 4 mL/min, yielding average Dean numbers between De = 7.9 and De = 31.5 and Reynolds numbers between 30 < Re < 300, respectively. The channel is long enough that the focusing length criterion L f is met in all cases tested.

The Archimedean spiral was chosen for practical space considerations, as it keeps the total footprint of the separation device to a minimum. The width, height, and channel length were chosen such that the larger two particle or algae sizes could be focused and separated, as a compromise between experimental practicalities and separation. The channel size was kept relatively large as the mask was prepared with an ordinary laser printer (see “Microchannel fabrication”) and the flow rates were constrained by needing to be low enough for the objects to be imaged while moving but high enough to ensure that the particles would not settle out of the flow. The criteria used to establish these parameters were the ones described in Eqs. 1, 3, and 5; i.e. Re P  > 1, channel length >L f, and the combination of R f and Re in the range where some focusing would occur. Experiments were done at room temperature, so the viscosity of water was taken as 1 mPa s.

2.1 Microchannel fabrication

The microchannel was fabricated using soft lithography. First, a negative mask of the channel design was printed on a transparency sheet with an ordinary office laser printer. Photoresist (SU-8) was spin-coated onto a silicon wafer using the manufacturer’s recommended parameters for a 100-µm-thick layer. The photoresist was exposed to ultraviolet light through the printed mask, so that the channel pattern was cross-linked and the remaining photoresist could be removed by developer. More information on this well-established technique can be found in other publications (Ng et al. 2002; Friend and Yeo 2010).

PDMS silicone was prepared at a 1:10 hardener/base ratio and poured on the wafer/photoresist mould. After being cured in an oven at 90 °C for 1.5 h, the PDMS was removed from the mould and access holes were punched at the channel inlet and outlets. The PDMS channel and a glass microscope slide were both exposed to oxygen plasma and then put in contact with one another, bonding them permanently together.

2.2 Samples

Experiments were run with three sizes of polystyrene latex (PSL) microspheres (nominal diameters 5, 10, and 20 µm, from Corpuscular Inc., USA) and with three species of algae, two of which had non-spherical shapes. The algae used were Chlorella vulgaris, Cyanothece aeruginosa, and Monoraphidium griffithii; pictures of the species are in Fig. 3. The algae were obtained from the Norwegian Water Research Institute; their culture numbers from that supplier were NIVA-CYA 258/2, NIVA-CHL 19, and NIVA-CHL 8, respectively. In all cases, water was the working fluid, with the algal or particle concentration sufficiently low that particle–particle interactions could be ignored.

Optical microscope images of the spheres and algae were taken and measured before use. At least 20 examples of each type of specimen were measured; the dimensions are reported in Table 1. Estimates of the concentrations of the samples were made from the micrographs taken during the experiments.

Table 1 Dimensions of the microspheres and algae used in this work
Full size table

2.3 Setup

The experimental setup (Fig. 2) consisted of the spiral microchannel, a syringe pump which flowed the sample through the channel at a user-selected flow rate, and a camera with a microscope objective positioned directly above the channel at the end of the spiral.

Fig. 2
figure 2

a Experimental setup for particle sorting in a spiral channel and b–e example of image analysis for the photographs taken of the channel. b shows a background image and c an image with particles. d shows the result of the background subtraction and e the result of the low-pass filter to remove noise from the image produced in (d). This example is using the algae Monoraphidium with a flow rate of 3.2 mL/min

Full size image

The transparent channel was illuminated from below. The camera was set to capture 120 frames/s. A total of 240 frames were captured at each flow rate (0.4–3.6 mL/min in increments of 0.2 mL/min) for each sample type.

2.4 Data analysis

The images collected by the camera at the end of the channel were primarily used for measuring the position of the particles over the channel width. The analysis of the images was automated using MATLAB. The steps for identifying the distribution of particles in the channel cross section are as follows and are illustrated in Fig. 2.

  1. (a)

    Create a background. The background image is formed by taking the mean value of each pixel over 100 images from the same dataset. This needs to be repeated separately for each dataset because whenever the sample was changed, the channel could move slightly with respect to the camera’s field of view.

  2. (b)

    Background subtraction. Identify the mean value of the background image in a rectangle on the far right of the image (Fig. 2a) and in the same location on the image with particles (Fig. 2b). Find the difference between the two and subtract this constant value from the particle image. Then, create a new background-subtracted image where the value of each pixel is

    $${\text{Final}}\,{\text{image}}\,(i,j) = {\text{particle}}\,{\text{image}}\,(i,j)^{2} - {\text{bgimage}}\,(i,j)^{2}$$

(Figure 2d). Finally, use a low-pass filter to remove the background noise from the image (Fig. 2e).

  1. (c)

    Sum over many images. Step b is repeated for all images in the set. The images are summed together and then summed column-wise and normalized to create a plot of the particle distribution across the channel (see examples in Fig. 3).

    Fig. 3
    figure 3

    a Micrographs of the three different sizes of microspheres (left set) and species of algae (right set) used in this study; the dimensions of the algal species are given in Table 1. b Examples of images captured at the end of the spiral channel at a flow rate of 1.6 mL/min. c Normalized distributions of the particles/algae across the channel cross section at 1.6 mL/min, each combining the particles in 240 images. The small secondary peaks in the 10-µm sphere and Cyanothece data are noise caused by a few clusters of 4–5 particles entering the channel over the course of the experiment

    Full size image
  2. (d)

    Image registration subtraction. The datasets are not all in exactly the same x–y position due to small shifts in the channel position with respect to the camera. To account for this in the data analysis, MATLAB’s image registration tool is used to identify the translation that best aligns each background image to a reference background image. The values are used to shift the particle distributions in the x direction (see Fig. 2) to make them comparable.

No analysis of the location of the particles/algae in the channel depth direction was done, as our target was separation in the channel width. These measurements could be done by confocal or narrow depth of field imaging, but this is outside of the scope of this paper.

3 Results

An example of the particle focusing at 1.6 mL/min flow rate is shown in Fig. 3. At this flow rate, the smallest particles (the 5-µm spheres and the Chlorella algae) do not focus but remain spread across the channel. In these cases, the particles do not fulfil the size criteria for inertial focusing (i.e. for these samples Re P  < 1 for all flow rates tested) and the drag forces from the Dean flow are significantly larger than the lift forces (R f  ≪ 1). Consequently, the particles and algae end up scattered around the channel cross section. The medium-sized particles (10-µm spheres and Monoraphidium) focus but not as strongly as the largest particles (20-µm spheres and Cyanothece). The 20-µm particles and Cyanothece both focus to a position closer to the channel wall than the smaller particles/cells. Both the Monoraphidium and the Cyanothece are more spread out and further from the wall than the 10- and 20-µm spheres.

The average positions of the microspheres and algae in the channel as a function of flow rate are shown in Fig. 4. The larger particles (10, 20 µm) and algae (Monoraphidium and Cyanothece) can be focused and can be mostly distinguished from one another over a specific range of flow rates. Of particular interest for morphology-based sorting, the Monoraphidium and Cyanothece have similar equivalent spherical diameter to one another, but can still be separated because of their very different shapes. The Cyanothece, which are prolate spheroids of 10–15 µm, behave very similarly to the spherical 10- and 20-µm particles. They are initially focused near one edge of the channel, and the position of this focus moves towards and across the channel centre with increasing flow rate.

Fig. 4
figure 4

Equilibrium position of the microspheres (top plot) and algae cells (bottom plot) in the channel width as a function of the fluid flow rate. The data points represent the peak position in the particle distribution, with the error bars representing its full-width half-maximum (FWHM) width. The centre of the channel is marked with the dashed gray line (colour figure online)

Full size image

The collected images were also used for estimating the concentration of the particles. The frame rate of the camera is sufficiently slow (240 fps) that any given particle is not visible in multiple frames. The total number of particles counted in all of the frames thus provides a reasonably accurate estimate of the concentration of algae: 438 ± 28 cells/µL for the Monoraphidium and 576 ± 48 cells/µL for the Cyanothece.

The collected images were also used to look at the orientation of highly non-spherical particles at the lower flow rates. In the lower half of the flow rates tested, the shutter time of the camera was quite short compared to the characteristic transport times of the flow. Qualitatively, the particles and cells in this regime (<2 mL/min) were well focused and clear, indicating that the finite shutter time did not bias the particle length measurements in this regime. To confirm this quantitatively, the length and aspect ratio of each Monoraphidium cell were measured and the average length of all cells in the top tenth percentile of length was calculated at each flow rate. The results showed that these cells had nearly identical length statistics, independent of the flow rate, in the <2 mL/min regime, with an increase in the apparent particle length for higher flow rates. This proves that for flow rates <2 mL/min, the measured cell length equals the actual length, i.e. the finite shutter time indeed did not bias the length measurement, and 2 mL/min is a good cut-off flow rate for looking at particle orientation.

4 Discussion

As seen in the results, the smallest particles (the 5-µm spheres and the Chlorella algae) do not focus but remain spread across the channel at all flow rates tested, as the particles do not fulfil the size criteria for inertial focusing and the drag forces from the Dean flow are significantly larger than the lift forces (Eq. 5). However, changes to the geometry and test conditions allow the system to be tuned to fulfil these criteria for a given set of test specimen. For the 5-µm spheres and Chlorella algae in particular, decreasing the channel height and width dimensions by a factor of 4 (to 25 µm high and 87.5 µm wide) and using a flow rate of >1.4 mL/min would cause these small particles to be focused into a narrow stream.

To evaluate the results, a separation efficiency was defined for the separation of two species and applied to the measurements of the particle positions in the channel. Separation efficiencies can be defined in many ways, often focusing on the retention or removal of one specific category of specimen. Since we are separating two species, either of which may be of interest to a user, we define a separation efficiency based on the maximum concentration achievable by both specimens in the channel. The separation efficiency η is defined by identifying the point x sep in the channel width where a certain fraction η of one species would pass to the left of x sep and the same fraction of the other species would pass to the right of x sep. In other words, a separation efficiency of 90 % indicates that a point in the channel width exists where 90 % of one species is to the left of that point and 90 % of the other species is to the right. While this approach could lead to lower apparent efficiencies than ones based on the purification of only one specimen from a background, it offers a balance by not assuming one specimen is more important than the other.

This separation efficiency was found for the separation of the 10-µm spheres from the 20-µm spheres, and of the Monoraphidium from the Cyanothece (Fig. 5). The microspheres could be separated with an efficiency of >90 % for many of the flow rates tested, with the best results at 1.6 mL/min (η = 96 %). The flow rate of 1.6 mL/min is the lowest for which both the 10- and 20-µm spheres fulfilled the conditions of adequate particle Reynolds number and channel length (Eqs. 1, 3). However, the separation efficiency was above 85 % for the whole range of 0.6–3 mL/min, demonstrating that the system holds some robustness against fluctuations in the flow rate. At higher flow rates (around 3 uL/min and Re ≈ 220), the width of the focused particle streams began to increase, which is in line with the results expected from the Rf–Re state diagram in (Gossett and Di Carlo 2009).

Fig. 5
figure 5

Separation efficiency of the 10- and 20-µm-diameter microspheres (“microspheres” series) and of Monoraphidium and Cyanothece cells (“algae” series). The monodisperse microspheres have high separation efficiency over a large range of flow rates, whereas the polydisperse algal cells have a lower efficiency

Full size image

The Monoraphidium and Cyanothece were best separated at 3.2 mL/min, which yielded η = 77 %. The higher separation efficiency of the microspheres compared to the algae is likely due to the algae’s higher polydispersity. This can be seen in the coefficient of variation of measurements of the samples’ physical dimensions (Table 1). The Monoraphidium have a COV of 0.25 in the length and 0.20 in the diameter, and the Cyanothece have a COV of 0.15 along the long axis and 0.09 in the short axis. In contrast, the COV of the 10- and 20-µm spheres diameters is 0.02 and 0.06, respectively.

The shape of the algae affected their behaviour in the channel. The Cyanothece are nearly spherical: they have short axes of ~11 µm and a long axis of ~15 µm (Table 1). The Cyanothece positions in the channel are very similar to those of the 10-µm microspheres. In contrast, the Monoraphidium have the equivalent spherical volume of an 8-µm-diameter sphere but they behave very differently to the 10-µm spheres. Compared to the 10-µm spheres, the Monoraphidium require a higher flow rate to achieve their narrowest focusing and they focus to a position much further from the radially inward channel wall. This suggests that the ratio of lift to drag forces (R f , Eq. 5) of these particles is smaller. This makes sense given the geometry: in the plane perpendicular to the flow, the Monoraphidium have 3.14 µm diameter and so they experience smaller lift forces due to fluid shear than the 10-µm spherical particles do; they also experience more drag as their cross-sectional profile perpendicular to the Dean flow is nearly twice that of the 10-µm spheres. The other effect which could be playing a role in the Monoraphidium position is particle tumbling, as previous investigations into the inertial focusing of non-spherical particles in straight channels showed high-aspect-ratio microparticles tumbling as they travelled the channel (Hur et al. 2011a; Masaeli et al. 2012).

To examine whether the Monoraphidium particles were tumbling a discernible amount while travelling the channel, the orientation and aspect ratio of each cell were determined. Masaeli et al. (2012) reported tumbling occurring around multiple axes, with the axis of tumbling converging with increasing Re P to the axis parallel to the longer channel wall and perpendicular to the flow direction, i.e. the x axis, in our setup (see Fig. 2 for illustration). Since this tumbling axis lies on the plane of the field of view of the camera, any rotation about this axis is not easily recorded. However, this tumbling would result in a spread in the apparent aspect ratio of particles, ranging from the aspect ratio of the cell viewed from its broad side (17.4 ± 2.7) to the aspect ratio of the cell viewed from the end (~1).

The image processing and binarization process affect the absolute measurement of the aspect ratio, but tumbling about the x axis could still be identified by looking at the coefficient of variation (COV) of the distribution of aspect ratios measured at various flow rates. If the Monoraphidium are not tumbling, the COV should not change over different flow rates, and if there is some tumbling, then this value should increase with increased tumbling. As the cells in the <2 mL/min flow rate regime are not blurred (due to their relatively slow motion compared to the shutter time of the camera), only these flow rates were included in this analysis. The COV of the Monoraphidium aspect ratios decreases with increasing flow speed, from 0.38 at the lowest flow rate (0.4 mL/min) to 0.25 at 1.8 mL/min, indicating that some tumbling is indeed occurring at these flow speeds. The decrease is approximately linear over this range (R 2 = 0.94). This indicates that at lower flow rates, the Monoraphidium cells are tumbling about the x axis more than at higher flow rates.

Finally, to consider the possibility of particle rotation about the z axis, the orientation of each Monoraphidium cell in the x–y plane was determined. At all flow rates, the mean cell orientation was aligned with the y axis, but the standard deviation of the cell alignment decreases from 16° at the lowest flow rate (0.4 mL/min) to below 5° for all flow rates at or above 1.0 mL/min. This indicates that there is also some rotation of particles around the z axis at low flow rates, but this effect is not significant at the flow rates that yielded focusing.

This data on the spread of particle aspect ratios indicate that there is little to no tumbling of Monoraphidium cells about the y axis. The data on tumbling about the x axis shows that the spread of apparent particle aspect ratio is not as broad as would be expected for a continuously tumbling particle. Hur et al. found that doublets in a straight channel were not continuously tumbling, but that they resided longer at an orientation aligned with the main flow direction than at an orientation perpendicular to it, with larger particles more likely to be aligned with the flow (Hur et al. 2011a). Our data show that particles in a faster-moving flow were also more likely to remain oriented along the main channel axis. Together these data suggest that the amount of time a particle spends aligned to the main channel axis is correlated with the particle Reynolds number. It is also possible that there are some further effects on tumbling from the secondary Dean flow in the spiral device presented here, but since that flow is slow compared to the axial flow and perpendicular to the direction of cell tumbling, it is unlikely to be exerting a large influence.

A major advantage of inertial sorting is the ability to use constant flow combined with throughput rates that are relatively high compared to many other microfluidic sorting techniques (Gossett et al. 2010). To better quantify this and to evaluate the suitability of this technology for use in typical field conditions, the concentration of particles/algae, and thus the throughput rate, was estimated from the captured images. Both the Monoraphidium and Cyanothece had concentrations of around 500 cells/µL, which, in the best sorting conditions (3.2 mL/min), yields a throughput of 2.7 × 104 cells/s. These concentrations indicate that this technique would be useful at naturally occurring concentrations: more than 99 % of the test sites at the 2007 National Lakes Survey (US Environmental Protection Agency) had a concentration of algae lower than this range (United States Environmental Protection Agency 2007).

To ultimately use this device in a field setting, some engineering work would be required to solve a problem common to many microfluidic devices: that of replacing the benchtop fluidic and measurement technologies. Commercial or custom pumps appropriate for field work already exist, but the particle position reading in particular would need to be addressed carefully. While the miniaturization of a microscope would be an option, a more elegant solution could perhaps be found through time-of-flight measurements, using, for example, optical or electrical impedance measurements.

5 Conclusions

We presented an inertial microfluidics approach to sorting live algal cells by shape and size, leading to a separation by species. The sorting of cells by shape and size is of particular interest in algal studies, since statistics on cell morphologies can be used as a shorthand for population dynamics.

The inertial microfluidic approach to particle sorting has several advantages. It has low instrumentation requirements: the only requirements are a pump and the appropriate choice of channel geometry. Inertial sorting also has a higher throughput rate than other passive sorting techniques, such as those using optical or gravitational forces. Its main drawback is a relative lack of flexibility compared to, for example, optical force sorting. However, the inertial system can be tuned by changing the flow rate to manipulate the cut-off size of the focused particles. To use this technology in a field-deployable sorting device, the size-dependent focusing of particles would have to be exploited either by an in situ measurement of the particle position or by separating the channel into multiple outlets.

In these experiments, the high polydispersity in the cell dimensions within each algal species led to a lower separation efficiency than that of more monodisperse microspheres. Nevertheless, this is a powerful method which could serve as a low-cost, technologically simple pre-sorting technique, to be combined with downstream on-chip measurements.