1 Introduction

Consumption heterogeneity plays a crucial role in influencing the transmission of macroeconomic policies such as monetary and fiscal policies. The impact of these policies varies among consumers with different income levels, wealth levels, debt levels, education, age, and so on. Therefore, understanding consumption heterogeneity is vital for accurately assessing the overall consequences of macroeconomic policies. Failure to account for the heterogeneity may result in an incomplete or inaccurate evaluation of policy transmission, leading to less effective policy decisions. Nevertheless, most modern macroeconomic theories were built based on the assumption that all economic agents, including consumers, are homogeneous in terms of preferences, endowments, and face the same constraints. For example, the Representative Agent New Keynesian (RANK) is constructed on the assumption that all consumers are identical. They are expected to behave optimally in a way that maximizes their utilities. The representative agent framework is convenient for analytical purposes, but it leads to an incomplete and partial understanding of economic behavior. In fact, consumers and households have heterogeneous behaviors, preferences, incomes, and demographic characteristics among many others. For example, Kaplan et al. (2018) consider agents’ heterogeneity in holding assets with different degrees of liquidity to investigate its importance to monetary policy transmission, including the relative contribution of direct and indirect effects. Also, Kaplan and Violante (2022) conduct a systematic investigation of the size and determinants of the aggregate marginal propensity to consume (MPC) in models with different preferences, dimension of ex-ante heterogeneity, income processes, and asset structure. The paper shows that the most important factor influencing the MPC, thus affecting the transmission mechanism of monetary policy and the size of fiscal multipliers, is the share and type of hand-to-mouth households.

In terms of the heterogeneity of consumption behaviors, two common forms of behaviors have been introduced to consumption models to improve predictability in the literature: (i) habit formation (HF) behavior (Deaton 1992; Campbell and Mankiw 1989; Dynan 2000; Carroll et al. 2011); and (ii) hand-to-mouthFootnote 1 (HtM) behavior (Campbell and Mankiw 1989, 1990). A growing body of literature acknowledges the significance of heterogeneous consumption behaviors in the realm of macroeconomic policies. For example, researchers have studied the impacts of HtM behavior on fiscal policy (Galí et al. 2007; Mankiw 2000; Callegari 2007; Cho and Kim 2013; Forni et al. 2009); the HtM behavior on monetary policy (Amato and Laubach 2003; Gali et al. 2004; Bilbiie 2008; Rossi 2014; Bartolomeo and Rossi 2007); the HF behavior on fiscal policy (Karayalçin 2003; Bouché and De Miguel 2019); and the HF behavior on monetary policy (Edge 2007; Amato and Laubach 2004; Bouakez et al. 2005). These two heterogeneous behaviors are typically integrated into the standard utility function of consumers, thus altering the Euler equation and IS curve function. Although these consumption behaviors are not novel in the literature, the effects of the combination of HtM and HF behaviors on monetary policy have received scant attention, especially in developing countries where the heterogeneity of consumption behaviors is assumed to be more prevalent. In this paper, we first theoretically examine how the interaction between HtM and HF behaviors influences the effectiveness of monetary policy by letting HtM consumers follow the former behavior and optimizing consumers follow the latter one. We then estimate a version of the Two-Agent New Keynesian (TANK) model that integrates both HtM and HF behaviors, utilizing quarterly data from three Association of Southeast Asian Nations (ASEAN) countries, namely Indonesia, the Philippines, and Thailand. Aside from examining the effects of heterogeneous consumption behaviors on monetary policy, the TANK model enables the exploration of how the existence of these behaviors shapes the reactions of macroeconomic variables to external shocks. Although the TANK model may not incorporate the intricate heterogeneity features in the more recent Heterogeneous Agent New Keynesian (HANK) model, it has the advantage of facilitating a straightforward analytical explanation of the impacts of consumer behavior heterogeneity (Chen et al. 2023). Debortoli and Galí (2017) also demonstrate that a basic TANK model is able to provide a reasonable approximation of the outcomes observed in a HANK model concerning the impact of shocks on aggregate output. Furthermore, estimating HANK models necessitates powerful computers and high-quality microdata, resources that are often unavailable in developing countries.

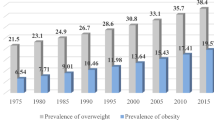
Influenced by the studies of Lusardi et al. (2011) and Bracco et al. (2021), we indirectly identify HtM consumers from the Global Findex Database as those who are not able to cope with a financial shockFootnote 2. According to Fig. 1, all three countries initially experienced an increase in HtM households from 2014 to 2017 but showed a substantial decrease in 2021, possibly due to economic factors, changes in employment patterns, or social welfare conditions. In 2014, Indonesia had 22% HtM consumers, which increased to 47% in 2017 and then decreased to 38% in 2021. Similar to Indonesia, the Philippines started with 36% HtM consumers in 2014, which then increased to 50% in 2017 before decreasing to 41% in 2021. Thailand witnessed the most fluctuation in the share of HtM consumers with a notable rise in HtM consumers in 2017 and a substantial decrease in 2021. Hence, it is essential to investigate how macroeconomic variables respond to external shocks in these three economies, especially given the increasing fluctuation in the ratio of HtM consumers.

Fig. 1
figure 1

Hand-to-mouth consumers and financial exclusion. Source: Global Findex Database 2014, 2017, 2021

Full size image

To the best of my knowledge, this is the first study investigating HtM and HF behaviors in the context of three ASEAN economies. The contribution of the paper is fourfold. Firstly, we theoretically show that both HtM and HF behaviors play crucial roles in causing the demand regime inversion discussed in the seminal study by Bilbiie (2008). Secondly, it estimates HtM and HF parameters in the three ASEAN countries using the Bayesian technique. Thirdly, it delves into the relationship between heterogeneous consumption behaviors and monetary policy and examines how macroeconomic variables respond to external shocks (i.e., monetary shock, demand shock, and supply shock) when both HtM and HF behaviors coexist. Finally, we do a simple policy experiment by fixing the share of HtM consumers at different values to investigate how the responses of macroeconomic variables to external shocks change.

The remainder of the paper is organized as follows. Section 2 briefly reviews related literature on this topic. Section 3 outlines the theoretical model and some calibrations that help to understand the model’s features more deeply. The empirical findings are reported and discussed in Section 4. The last section—Section 5—contains our conclusions.

2 Related literature

2.1 Theoretical studies

To date, the relative importance of heterogeneous consumption behaviors, especially HtM behavior, on macroeconomic models and the conduct of monetary policy has been subject to considerable debate. Whereas some studies confirm that the presence of consumption behaviors heterogeneity can significantly affect the monetary policy (Amato and Laubach 2003; Gali et al. 2004; Bilbiie 2008; Motta and Tirelli 2012; Rossi 2014), others argue that it does not matter (Ascari et al. 2011; Colciago 2011; Ocampo 2013; Albonico et al. 2023).

Amato and Laubach (2003) is considered one of the first studies reviewing the linkage between HtM behavior and monetary policy. In this study, the authors investigated the implications of both the rule-of-thumb behavior of producers and the HtM behavior of consumers for optimal monetary policy and simple interest rate rules. They assumed that instead of behaving optimally and forward-looking, a fraction of consumers follow a hand-to-mouth (HtM consumers), and a fraction of producers set prices by following a rule of thumb (ROT price-setters). For the HtM consumers, changes in interest rates do not affect their inter-temporal consumption decisions as predicted by the Permanent Income Hypothesis (PIH). Hence, the effectiveness of monetary policy is significantly affected by the proportion of HtM consumers in an economy. Employing a small structural model derived from optimizing the behavior of households and imperfectly competitive suppliers, the study showed that the implications of ROT price-setters for monetary policy are trivial. In contrast, the interest rate is more sensitive following a shock to the degree of HtM consumers.

Another important theoretical work investigating the impact of HtM consumers on monetary policy is Gali et al. (2004). In this paper, HtM consumers are defined as agents who do not borrow or save to smooth consumption but instead follow a simple rule: they consume all their current labor income each period. The research derived two main results by introducing HtM consumers to a standard sticky-price model. Firstly, the Taylor rule no longer guarantees a unique equilibrium when the fraction of HtM consumers reaches a certain level. For a given change in the inflation rate, as the ratio of HtM consumers goes up, the nominal interest rate must rise by more to ensure equilibrium is determined. In other words, Gali et al. (2004) proposed a “modified” Taylor principle in which the response of the nominal interest rate to changes in inflation increases as the share of HtM consumers increases. Thus, the Taylor rule does not necessarily guarantee stability when HtM consumers exist. The intuition behind this result is clear. The presence of HtM consumers makes part of the aggregate demand directly unrelated to the real interest rate. An upswing in aggregate demand leads to an increase in nominal wages and, thereby, a decrease in countercyclical mark-ups (ratio of price to marginal cost) because of nominal price rigidities. The real wage goes up and allows HtM consumers to increase their consumption. Hence, to guarantee the system’s stability, the increase in the nominal interest rate on the consumption of forward-looking consumers must be strong enough to dominate the rise in consumption of HtM consumers. Secondly, the central bank’s tasks become more complicated with HtM consumers’ presence. Gali et al. (2004) showed that the effectiveness of monetary policy depends not only on intertemporal allocation decisions but also on the behavior of constrained consumers. The paper showed that if the central bank follows a Taylor rule when the proportion of HtM consumers in an economy is high enough, the response coefficient should be bigger than that suggested by the Taylor principle.

Bilbiie (2008) modified the Gali et al. (2004) model by incorporating the Limited Asset Markets ParticipationFootnote 3 (LAMP) in the Dynamic General Equilibrium. But unlike Gali et al. (2004), his model did not consider capital accumulation. Moreover, his study is also different from the paper of Gali et al. (2004) regarding assumptions, girth, and message. The asset market, labor market, and their interaction which are absent from the analysis of Gali et al. (2004) are explicitly modeled. Bilbiie (2008) added sticky prices in the model, which is called a LAMP Sticky-Price model. The study indicated that aggregate demand falls when the interest rate increases in the standard model with the full-participation economy (λ = 0). It, in turn, leads to lower output levels, consumption, and real wage. Suppose there is limited participation in an economy, but λ < λ∗ either because participation is not restricted “enough” or labor supply is not inelastic enough. Because non-asset holders simply consume their wage income, it implies a further fall in demand, shifting labor demand to the new equilibrium with even lower output, consumption, and real wage. Next, Bilbiie (2008) considered the third case with more limited participation (λ > λ∗) where an additional distribution dimension is introduced. It stems from the fact that non-asset holders affect firms’ profits because changes in real wage impact both marginal cost and sales (output and hours). The net effect on profits depends on the share of non-asset holders (λ) and labor supply elasticity. If the fraction of non-asset holders is high enough and/or the labor supply elasticity is low enough, profits would increase, thus generating a positive income effect on asset holders. This effect offsets and overturns the initial impact of interest rates on aggregate demand, thus raising aggregate demand. Hence, the IS curve changes its sign, and the Taylor rule is inverted when allowing for limited assets markets participation. Bilbiie (2008) also confirmed that the required share of non-asset holders for these results is much smaller than those suggested by Campbell and Mankiw (1989). His research highlighted that central banks in developing countries should pay more attention to the aggregate demand side of the economy under low participation in financial markets. However, this theoretical study does not take into account HF behavior and its potential effects, as HF behavior is not integrated into the utility function of the model of Bilbiie (2008).

Motta and Tirelli (2012) seem to have compensated for this shortcoming by allowing consumers to follow HF behavior. Their study confirmed that the combination of LAMP and HF behavior can generate indeterminacy and revive Bilbiie’s inverted Taylor principle for empirically plausible values of the HtM consumers share. Motta and Tirelli (2012) demonstrate how HF amplifies the impact of changes in aggregate demand on the marginal rate of substitution between consumption and labor effect, thus increasing the elasticity of real wages with respect to employment. Therefore, HF behavior should always be considered for determinacy analysis of models that account for LAMP. Unlike the study of Motta and Tirelli (2012), this paper focuses on examining how the interaction of HtM and HF behaviors influences the effectiveness of monetary policy, as presented by the slope of the IS curve. By extending the study of Leeper (1991) and (Bilbiie 2008), Rossi (2014) studied how the presence of HtM consumers affects the interaction between monetary and fiscal policies in a small-scale New Keynesian model. He introduced a positive level of steady-state public debt (Leeper 1991) and a share of HtM consumers (Bilbiie 2008) to the standard setting. Rossi (2014) integrated the share of HtM consumers and the inverse of the Frisch elasticity of labor supplyFootnote 4 into the dynamic IS equation via a parameter identifying the elasticity of aggregate demand to real interest rates and taxes. The size and sign of this parameter can strongly alter the model’s transmission mechanism and local determinacy properties. The study concluded that policymakers should consider the steady-state level of government debt and the fraction of HtM consumers to ensure determinate equilibrium dynamics.

In contrast to earlier findings, however, Ascari et al. (2011) argued that once wage stickiness is taken into account, the HtM behavior does not matter for monetary policy. The Taylor rule is restored as a necessary condition for equilibrium determinacy regardless of asset market participation. According to Ascari et al. (2011), the implications of HtM behavior for the design of optimal monetary policy are pretty small. Moreover, optimal interest rate rules become active regardless of the degree of HtM behavior. In the same way, the result (Colciago 2011) had a similar conclusion. As shown in his study, the Taylor principle implies equilibrium determinacy for any level of the share of HtM agents. Colciago (2011) suggested that the determinacy properties of the model with HtM consumers rely strongly on the form of nominal rigidities considered. The study of Ocampo (2013), which is similar to Colciago (2011), strongly argues that in the presence of nominal wage rigidities, HtM consumers and price rigidities do not cause a modification in the Taylor principle, as suggested by Gali et al. (2004).

2.2 Empirical studies

Whereas the above papers have theoretically studied the HtM behavior and its implications for monetary policy individually, few attempts have empirically explored how the combination of the HtM and HF behaviors influences monetary policy. Fuhrer (2000) is considered one of the first studies doing this and found that the responses of both spending and inflation to monetary policy actions are considerably improved. In other words, this modified model replicates key dynamic correlations in the data better than traditional ones. Thus, it is more suitable for conducting monetary policy analysis. However, the paper places greater emphasis on HF behavior and its implications for monetary policy, rather than on HtM behavior.

Di Bartolomeo et al. (2011) integrated agents who cannot smooth consumption (HtM consumers) and are affected by external consumption habits into the standard New Keynesian Dynamic Stochastic General Equilibrium (DSGE) model. This approach is similar to the study of Gali et al. (2004), but like Bilbiie (2003), Di Bartolomeo et al. (2011) did not consider capital accumulation. The paper proposed two different demand regimes corresponding with two different versions of IS curve. A standard demand regime implies a standard negatively sloped IS curve. An increase in the real interest rate reduces output. This regime is consistent with the theory of the Permanent Income Hypothesis. In contrast, an inverse demand regime dominated by HtM behavior means a positively sloped IS curve. The study confirmed a positive relationship between the probability of an inverse regime and the size of the share of HtM consumers. Moreover, the inversion also depends on the presence of HF. This mechanism can be explained by analyzing and comparing the direct effect (by smoothing consumption) and indirect effect (by the labor market and real wage) of the interest rateFootnote 5. Utilizing the Bayesian parameters estimates for quarterly data in the period from 1963 to 2003 of the Group of Seven (G7) economies, the empirical results indicated that even though the share of HtM consumers in seven countries is 26% on average, none of them is high enough to cause the regime inversion.

Bilbiie and Straub (2013) estimate an extended version of Bilbiie (2008) with HF behavior on US data by using Bayesian techniques, distinguishing between the pre-Volcker and Volcker-Greenspan periods. The paper argues that LAMP is important in explaining US macroeconomic performance and monetary policy. It also demonstrates that the share of HtM agents has changed between the two periods, leading to a significant change in the sign of the IS curve. Unlike Di Bartolomeo et al. (2011) and Bilbiie and Straub (2013), this paper argues that HF behavior is irrelevant to HtM consumers who are solely concerned with the current period. Therefore, in our model, only optimizing consumers follow HF behavior. In a similar study, Furlanetto and Seneca (2012) introduce HtM and HF behaviors into a basic New Keynesian model and investigate how the former behavior can affect the transmission of technology shocks in the economy. The authors conclude that including HtM consumers, interacting with nominal rigidities, in the model can improve the transmission of these shocks. The combination of these two behaviors might explain a significant decline in hours worked and a trivial response of output after a positive productivity shock. However, this study does not consider the impacts of HF and HtM behaviors on monetary policy effectiveness.

Employing Bayesian inference methods for the Euro area from Q1-1985 to Q2-2010, Coenen et al. (2012) discover that the share of HtM households is 18%, which is somewhat smaller than the estimates reported in Coenen and Straub (2005) and Albonico et al. (2019). In another research, Marto (2014) estimates a New Keynesian DSGE model with HtM consumers for the Portuguese economy. The estimated share of HtM consumers is relatively high (58%). Moreover, the author calibrates the ratio of HtM consumers at different levels and finds out that estimates of parameters and responses of macroeconomic variables to external shocks are particularly sensitive to the level of HtM ratio. In the recent publication of Albonico et al. (2023), the authors estimate a medium-scale DSGE model with and without HtM consumers and find evidence that HtM consumers are irrelevant to explain aggregate US business cycle fluctuations. In summary, previous empirical studies have primarily focused on developed economies, such as the US or the Euro area. There has been limited attention given to estimating the share to HtM consumers in developing countries, particularly in Asia.

3 Theoretical model

The model closely follows a modified New Keynesian DSGE model integrating the HtM behavior developed by Bilbiie (2008) but letting only optimizing consumers follow the HF behavior. The modification allows us to explore how the combination of these two common behaviors theoretically affects monetary policy effectiveness and empirically influences responses of macroeconomic variables to external shocks, i.e., monetary policy shock, demand shock, and supply shock. Figure 2 illustrates the interactions among the different agents in a basic DSGE model.

Fig. 2
figure 2

Basic DSGE model

Full size image

3.1 Demand side

This paper considers a continuum of infinitely lived heterogeneous consumers in a closed economy, normalized to a population size of 1. A fraction λ of them are HtM agents who consume all their current disposable income. The remaining fraction (1 − λ) comprises optimizing consumers who accumulate wealth and allocate their income during their lifetime by optimization subject to their inter-temporal budget constraint. HtM consumers are indexed by H, and optimizing consumers are indexed by O. For the sake of tractability, we do not consider capital accumulation.

  1. a.

    Optimizing consumers

Each optimizing consumer tries to maximize the following utility function:

$${E}_t\sum_{i=0}^{\infty }{\beta}^iU\left({C}_{t+i}^O,{N}_{t+i}^O\ \right),$$
(1)

where β ∈ (0, 1) is the discount factor; \({C}_t^O\) and \({N}_t^O\) are consumption and labor supply of optimizing consumers at time t. The utility function takes the additively separable log-Constant Relative Risk Aversion (CRRA) form, which has been used in many DSGE studies:

$$U\left(\bullet \right)=\mathit{\ln}\left({C}_t^O-\gamma {C}_{t-1}\right)-\kappa \frac{{\left({N}_t^O\right)}^{1+\phi }}{1+\phi }$$
(2)

subject to the sequence of constraints:

$${B}_t^O+{\varOmega}_{t+1}^O{V}_t+{P}_t{C}_t^O\le {Z}_t^O+{\varOmega}_t^O\left({V}_t+{P}_t{D}_t\right)+{W}_t{N}_t^O,$$
(3)

where κ > 0 is the value of leisure relative to consumption, ϕ > 0 is the inverse of the labor supply elasticity, and γ is the external HF parameter. \({B}_t^O\) is the nominal value of a portfolio of all state-contingent assets held, except for shares in firms, at the end of period t. \({\Omega}_t^O\) are shareholdings at time t. Vt is average market value at time t shares in intermediate good firms; Dt are real dividend payoffs. \({Z}_t^O\) is beginning of period wealth, not including the payoff of shares.

Optimality conditions for optimizing consumers are:

$$\frac{1}{R_t}=\beta {E}_t\left[\frac{C_t^O-\gamma {C}_{t-1}}{C_{t+1}^O-\gamma {C}_t}\ \frac{P_t}{P_{t+1}}\right],$$
(4)
$$\kappa {\left({N}_t^O\right)}^{\phi }=\frac{1}{C_t^O-\gamma {C}_{t-1}}\ \frac{W_t}{P_t}.$$
(5)

Log-linearizing Eq. 4 and Eq. 5 around the steady state, we get the Euler equation (Eq. 6) and labor supply (Eq. 7) for optimizing consumers:

$${c}_t^O-\gamma {c}_{t-1}={E}_t{c}_{t+1}^O-\gamma {c}_t-\left(1-\gamma \right)\left({i}_t-{E}_t{\pi}_{t+1}\right)$$
(6)
$$\phi {n}_t^O={w}_t-\frac{1}{1-\gamma}\left({c}_t^O-\gamma {c}_{t-1}\right)$$
(7)

where a lowercase x denotes the log deviation of variable X from its steady state. Accordingly, ct is total consumption; \({c}_t^O\) is optimizing consumption; it is the gross nominal interest rate; πt is the gross inflation rate; \({n}_t^O\) is optimizing labor supply; and wt is the real wage.

  1. b.

    Hand-to-mouth consumers

The HtM consumers do not save and borrow to smooth consumption but consume all their labor income; and therefore at each period, they solve a static problem. Moreover, HtM consumers obviously do not follow habit formation behavior. Hence, their period utility function is given by:

$$\underset{C_t^H,{N}_t^H}{\max}\ln \left({C}_t^H\right)-\kappa \frac{{\left({N}_t^H\right)}^{1+\phi }}{1+\phi }$$

subject to

$${C}_t^H=\frac{W_t}{P_t}{N}_t^H$$
(8)

The first-order condition is

$$\kappa {\left({N}_t^H\right)}^{\phi }=\frac{1}{C_t^H}\ \frac{W_t}{P_t}.$$
(9)

Log-linearizing Eq. 8 and Eq. 9 around the steady state, we get the budget constraint equation and labor supply equation for HtM consumers as follows:

$${c}_t^H={w}_t+{n}_t^H$$
(10)

and

$$\phi {n}_t^H={w}_t-{c}_t^H$$
(11)

where \({c}_t^H\) is HtM consumption and \({n}_t^H\) is HtM labor supply. Since the HtM labor supply is fixed \(\left({n}_t^H=0\right)\), the HtM consumption exhausts the real wage \(\left({c}_t^H={w}_t\right)\).

  1. c.

    Aggregate consumption and labor

Aggregate consumption takes the following form:

$${c}_t=\lambda {c}_t^H+\left(1-\lambda \right){c}_t^O,$$
(12)

where yt = ct is the market clearing condition. Similarly, aggregate labor is given by:

$${n}_t=\lambda {n}_t^H+\left(1-\lambda \right){n}_t^O.$$
(13)

Since \({n}_t^H=0\), Eq. 13 can be simplified as \({n}_t=\left(1-\lambda \right){n}_t^O\). Aggregating and then manipulating above equations, we get the modified IS equation:

$${y}_t=\frac{\varGamma_1}{\varGamma_1+{\varGamma}_2}{E}_t{y}_{t+1}+\frac{\varGamma_2}{\varGamma_1+{\varGamma}_2}{y}_{t-1}-\frac{1-\gamma }{\varGamma_1+{\varGamma}_2}\left({i}_t-{E}_t{\pi}_{t+1}\right),$$
(14)

where

$${\Gamma}_1=\frac{1-\gamma }{1-\gamma +\gamma \lambda}\left[\frac{\left(1+\mu \right)\left(1-\lambda \right)-\lambda \phi}{\left(1+\mu \right)\left(1-\lambda \right)}\right]$$
$${\Gamma}_2=\gamma -\left[\frac{\lambda \gamma}{1-\gamma +\gamma \lambda}\right]$$

3.2 Supply side

The supply side is completely standard in macroeconomic literature. There are two types of sectors: the intermediate goods sector and the final goods sector. Each firm in the former produces intermediate goods, which will be bought and transformed into one single final goods by the firm in the latter. The final goods, in turn, will be consumed by economic agents.

  1. a.

    Final goods firm

The perfectly competitive firm produces the final goods, with a CES production function taking the Dixit-Stiglitz aggregator (Dixit and Stiglitz 1977).

$${Y}_t={\left({\int}_0^1{Y}_{s,t}^{\frac{\varepsilon -1}{\varepsilon }} ds\right)}^{\frac{\varepsilon }{\varepsilon -1}},$$
(15)

where Yt is the product of the final firm in period t, and Ys, t for s ∈ [0, 1] is the product of the intermediate firm s, and ε > 1 is the elasticity of substitution between intermediate goods. Given the price of each intermediate goods, the representative final firm tries to maximize its profit Πt.

$${\varPi}_t={P}_t{Y}_t-{\int}_0^1{P}_{s,t}{Y}_{s,t} ds$$
(16)

where Pt is the price of final goods and Ps, t is the price of intermediate goods s. Substituting (15) into (16), we get:

$$\underset{\left\{{Y}_{s,t}\right\}}{\mathit{\max}}{P}_t{\left({\int}_0^1{Y}_{s,t}^{\frac{\varepsilon -1}{\varepsilon }} ds\right)}^{\frac{\varepsilon }{\varepsilon -1}}-{P}_{s,t}{\int}_0^1{Y}_{s,t} ds$$
(17)

Taking the first-order condition for the above problem and doing some manipulations, we obtain the demand function for the immediate goods s.

$${Y}_{s,t}={Y}_t{\left(\frac{P_t}{P_{s,t}}\right)}^{\varepsilon }$$
(18)

and the mark-up/pricing rule for final goods.

$${P}_t={\left[{\int}_0^1{P_{s,t}}^{1-\varepsilon } ds\right]}^{\frac{1}{1-\varepsilon }}$$
(19)
  1. b.

    Intermediate goods firms

We assume that a continuum of intermediate goods firms is indexed by s ∈ [0, 1]. An intermediate firm solves its optimization problem in two stages. First, it takes wages as the price of labor and determines the amount of labor that it will hire to minimize the total production cost: \(\underset{N_{s,t}}{\min }{W}_t{N}_t(s)\) subject to the following production function: Yt(s) = Nt(s). Using the Lagrangian methodology to solve the above problem, we can easily derive the marginal cost:

$${MC}_t(s)=\frac{\partial {TC}_t(s)}{\partial {Y}_t(s)}={W}_t$$
(20)

In the second stage, the intermediate firm will identify the price of its goods. It is assumed that the intermediate firm has a ρ probability of keeping the price fixed in the next period (Pt(s) = Pt − 1(s)) and a (1 − ρ) probability of changing its price to maximize:

$$\mathit{\max}\ {E}_t\sum_{i=0}^{\infty}\left[{\rho}^i{\Lambda}_{t,t+i}\left({P}_t(s){Y}_{t,t+i}(s)-M{C}_{t+i}{Y}_{t,t+i}(s)\right)\right]$$

subject to the demand equation. Λt, t + i is the relevant stochastic discount factor for nominal payoffs. To solve the above problem, we derive the following first-order conditions:

$${P}_t^{\ast }(s)={E}_t\sum_{i=0}^{\infty}\frac{\rho^i{\Lambda}_{t,t+i}{P}_{t+i}^{\varepsilon -1}{Y}_{t+i}}{E_t{\sum}_{k=0}^{\infty }{\rho}^k{\Lambda}_{t,t+k}{P}_{t+k}^{\varepsilon -1}{Y}_{t+k}}{MC}_{t+i},$$

where \({P}_t^{\ast }(s)\) is the same price for all the (1 − ρ) intermediate firms that reset their prices at time t. Using the mark-up rule Eq. (19), the final goods’ mark-up rule is obtained as follows:

$${P}_t={\left[{\rho P}_{t-1}^{1-\varepsilon }+\left(1-\rho \right){P}_t^{\ast 1-\varepsilon}\right]}^{\frac{1}{1-\varepsilon }}$$
(21)
  1. c.

    New Keynesian Phillips curve

Based on the above derivations, we can obtain the well-known log-linearized New Keynesian Phillips curve after several substitutions and manipulationsFootnote 6:

$${\pi}_t=\beta {E}_t{\pi}_{t+1}+{\varPsi w}_t$$
(22)

where Ψ = (1 − ρ)(1 − βρ)ρ−1.

3.3 Central bank

To complete the model, we introduce the simple feedback Taylor rule:

$${i}_t={\rho}_i{i}_{t-1}+\left(1-{\rho}_i\right)\left[{\phi}_{\pi }{E}_t{\pi}_{t+1}+{\phi}_y{y}_t\right]+{\varepsilon}_t^i,$$
(23)

where ϕπ and ϕy are inflation and output coefficients, respectively, ρi is the degree of interest rate smoothing, and \({\varepsilon}_t^i\) is a white-noise monetary disturbance.

3.4 Hand-to-mouth, habit formation, and demand regimes

Let \(\Omega =-\frac{1-\gamma }{\Gamma_1+{\Gamma}_2}\). This parameter is the slope of the IS curve (Eq. 14) which measures the effectiveness of monetary policy, as Ω reflects the responsiveness of output to the real interest rate \(\left(\left|\frac{\partial {y}_t}{\partial {i}_t}\right|=\Omega \right)\). Ω, in turn, depends on the HtM consumers’ fraction (λ), HF parameter (γ), the inverse of the labor supply elasticity (ϕ), and net markup which is identified as μ ≡ ε(ε − 1)−1 − 1, where ε is the elasticity of substitution between intermediate goods. As a result, Ω becomes highly nonlinear, and the model becomes more complicated if we consider both λ and γ. Hence, we do a simulation by assigning different values for μ and ϕ, and observe how the combinations of the HF parameter (γ) and the ratio of the HtM consumers (λ) determine the demand regimes.

In Fig. 3, yellow areas represent the combination of (γ) and (λ), where the traditional regime holds (Ω < 0), and dark blue areas represent the inverse regime (Ω > 0). Given the values of μ and ϕ, the inversion is likely to be observed with relatively high values of λ and low values of γ. Interestingly, the HF parameter (γ) plays an important role in causing the inverse regime because the probability of observing the inverse regime changes much when γ alters. In addition, the combinations of low values of μ and high values of ϕ seem to have a higher chance of observing the inverse regime. In other words, the size of the dark blue region appears to extend as μ decreases and ϕ increases. However, the net markup (μ) plays a lesser role in causing the inverse regime, as indicated by the relatively stable dark blue areas that do not change significantly as μ varies.

Fig. 3
figure 3

Parameter combinations and demand regime inversions

Full size image

3.5 Linearized model

The stochastic structural model is fully described by the 12 below equations (Table 1). To avoid stochastic singularity, we set the number of shocks equal to the number of observable variables. Accordingly, three external shocks are considered, namely monetary policy shock \(\left({\varepsilon}_t^i\right)\), demand shock \(\left({\varepsilon}_t^g\right)\), and supply shock \(\left({\varepsilon}_t^z\right)\).

Table 1 Model summary
Full size table

4 Bayesian estimation

4.1 Methodology and data

4.1.1 Methodology

We employ the Bayesian inference method to undertake the DSGE estimation. In principle, the Bayesian method combines the prior distribution P(θ), which is our initial belief about the model parameters (θ), and the observed data P(YT| θ) to get the posterior distribution P(θ| YT) by employing the well-known Bayes’ rule:

$$P\left(\boldsymbol{\uptheta} |{Y}_T\right)\propto P\left({Y}_T|\boldsymbol{\uptheta} \right)P\left(\boldsymbol{\uptheta} \right)$$

However, simple and closed-form solutions are typically not available when dealing with complex models or high-dimensional spaces. Hence, the Metropolis-Hasting algorithm is applied to explore and approximate the posterior distribution of the model parametersFootnote 7.

4.1.2 Data

The paper uses three main macroeconomic variables on a quarterly basis in three ASEAN countriesFootnote 8, including real GDP per capita growth rate, inflation growth rate, and policy rate. The real GDP per capita is defined as real GDP divided by the population. Since the quarterly population is not available, the paper interpolates it from yearly data using the quadratic match average. The study uses the monetary policy-related interest rate defined by the IMF as a policy rate. All data is collected from the International Financial Statistics – IMF Data, and seasonally adjusted by the X-13 ARIMA SEATS before applying one-side HP filter. Based on data availability, the period for Indonesia spans from Q2-2006 to Q4-2022, for the Philippines, it covers from Q4-2002 to Q4-2022, and for Thailand, it extends from Q4-2003 to Q4-2022.

4.2 Priors

Table 2 provides information about the prior distribution of 14 parameters which consists of 11 structural parameters and three fixed parameters. The prior densities for estimated parameters are mostly based on the standard literature unless otherwise stated. There are three types of prior distribution, namely beta (B), gamma (G), and inverse gamma (I). Accordingly, the beta distribution is used for the HtM parameter, HF parameter, persistence parameter of demand shock, persistence parameter of supply shock, and degree of interest rate smoothing. Meanwhile, the gamma distribution is used for the inverse of the labor supply elasticity, Taylor parameters on output, and inflation. Moreover, the inverse gamma is used for the standard error of structural shocks (i.e., monetary shock, demand shock, and supply shock).

Table 2 Prior distributions for the structural parameters
Full size table

In particular, the HtM parameter and HF parameter are assumed to follow the beta distribution as in the standard literature with means of 0.5 and 0.7, respectively. Regarding the Taylor rule parameters on inflation and output gap, we assume that the mean value for the former is 1.5 and for the latter it is 0.125 as in studies of Smets and Wouters (2007), Zams (2021), and Di Bartolomeo et al. (2011). The prior shape of the distribution of both parameters is gamma. Following An and Schorfheide (2007), the persistence parameters for demand shock and supply shock follow the beta distribution. Their mean and standard deviation equal 0.85 and 0.1, respectively. The degree of interest rate smoothing also follows beta distribution (Smets and Wouters 2007). Finally, the standard errors of the monetary policy, demand, and supply shocks are assumed to follow the inverse gamma distribution with a mean of 0.15 and a standard deviation of 0.2.

Due to the insufficiency of data points, we fix two parameters, namely net markup and Calvo price stickiness. We also found that adding them to the estimation leads to identification issues which might generate incorrect results. Moreover, they are not our major interests. Accordingly, the net markup is set to be 0.2 which is equivalent to the elasticity of substitution between intermediate goodsFootnote 9 of 6 which is also used in several studies, such as Gali et al. (2004), Di Bartolomeo et al. (2011), and Takyi and Leon-Gonzalez (2020). Following the standard literature, the Calvo price stickiness is fixed at 0.75.

4.3 Empirical analysis

We estimate the posterior distributions of the parameters using the Metropolis-Hastings algorithm. For each country, two independent Markov chains with 500,000 draws are employed and the first 250,000 draws are discarded. The results of Brooks and Gelman (1998) convergence diagnostics and trace plots suggest that the two chains have converged in terms of both the univariate and multivariate convergence diagnostics.

4.3.1 Posterior estimates

Table 3 shows the Bayesian estimates of the structural parameters for three ASEAN economiesFootnote 10. Remarkably, while the estimated parameter for HF behavior consistently hovers around 0.5 implying that consumers rely on approximately 50% of past consumption information to determine their current consumption in three countries, there is notably greater variability observed in HtM behavior. In particular, the posterior means of the HtM parameter are 22% in Indonesia, 34% in the Philippines, and 27% in Thailand.

Table 3 MCMC estimates of the structural parameters
Full size table

Based on the estimated values, the likelihood of regime inversion occurring in all three countries is relatively low. Regarding Fig. 4, calibrated with estimated parameters, under the assumption of a stable HF parameter at 0.5, the inversion only transpires when the ratio of HtM consumers exceeds approximately 0.6Footnote 11.

Fig. 4
figure 4

Estimated parameters and demand regime inversions

Full size image

However, this result remains surprising since the ratio of HtM consumers is typically regarded as a proxy for the level of development in the financial sector. Given that Indonesia, the Philippines, and Thailand are developing countries with relatively constrained financial development, one might anticipate a higher HtM parameter. Interestingly, the Global Findex database partially addresses this concern by indicating that a higher financial inclusion does not necessarily lead to a lower proportion of HtM consumers. According to Fig. 1, despite consistent downward trends in the ratio of respondents without accounts at financial institutions, signifying decreased financial exclusion, from 2014 to 2021, the percentage of HtM consumers exhibited considerably more fluctuation. Particularly noteworthy is its increase in 2017, followed by a substantial decline in 2021. Therefore, our findings emphasize the importance of not conflating HtM consumers with financially excluded consumers, a common mistake that some recent studies have made. Furthermore, additional factors, such as unique psychological or cultural elements, may provide explanations for the relatively low ratio of HtM consumers. Delving into these determinants could prove to be an intriguing subject for future research.

The results also reveal that the Taylor rule parameter for output is about 0.20 which is significantly different from its prior (0.125). In contrast, the Taylor rule parameters for inflation fluctuate around 1.50–1.55, slightly surpassing its prior of 1.5. Notably, the estimated inverse Frisch labor elasticity parameter is heterogeneous among countries. Indonesia demonstrates the highest estimated parameter at 1.48, which is approximately half of its prior value, suggesting a labor supply elasticity with respect to real wage of 0.68. Thailand and the Philippines exhibit lower estimated values, standing at 1.25 and 1.02 respectively. The persistence of demand shock and supply shock is relatively low, with parameters of 0.38–0.52 and 0.52–0.59, respectively. Additionally, the degree of interest rate smoothing is about 0.9, indicating a substantial degree of interest rate smoothing in three countries.

4.3.2 Bayesian impulse response analysis

  1. a.

    Monetary policy shock

We investigate how three economies respond to one standard deviation of monetary policy shock by using the Bayesian impulse response analysis (Fig. 5). Interestingly, the impulse response functions exhibit similarities across the three countries. Given the relatively low share of HtM behavior, a positive monetary shock has the standard effects on main macroeconomic variables, despite some degree of heterogeneity at the country level. Particularly, a monetary shock leads to higher real interest rate due to higher nominal interest rate and lower inflation. It, in turn, decreases aggregate output/consumption. Consequently, aggregate laborFootnote 12 and real wage also significantly decline in response to the shock. However, the magnitudes of response vary among countries. Indonesia, which has the lowest ratio of HtM consumers, exhibits the least response in aggregate consumption and aggregate labor to the monetary shock. Two groups of consumers behave differently in terms of both their consumption and labor supply when facing such a shock. HtM consumption reacts much more fiercely in comparison to its counterpart. While the initial response of the HtM consumption is around 50 bps, the initial response of the optimizing consumption is only 10 bps before reaching the highest response of 15 bps in the second quarter. Likewise, Thailand and the Philippines have stronger responses than Indonesia in both optimizing and HtM consumption.

Fig. 5
figure 5

Responses to monetary shock

Full size image

A less aggressive response of optimizing consumption is understandable because of the ability to smooth consumption during the lifetime of optimizing consumers. Meanwhile, we should recall that HtM consumption is not directly affected by changes in real interest rate. Instead, they determine their consumption based on current income, which mainly depends on the real wage. Hence, HtM consumers simply cut down their consumption due to a lower wage income. Consequently, a monetary policy shock widens the consumption gap between optimizing and HtM consumers as confirmed in the studies of Albonico et al. (2019) and Bhatnagar (2023). Therefore, introducing HtM consumers is likely to result in monetary policy shocks having redistributive effects, which underscores the importance of fiscal stabilization policies that should be closely coordinated with central bank actions. Unlike Bhatnagar (2023), this paper uses a small-scale DSGE model that does not include the government sectorFootnote 13. The empirical findings confirm a strong linkage even in a small-scale DSGE model without government transfers.

  1. b.

    Demand shock

Figure 6 represents the shock to the demand side. As an initial response to the shock, aggregate output/consumption growth shrinks by 45 bps in Indonesia and by 80 bps in both Thailand and the Philippines. The Indonesian optimizing consumption initially responds to the shock by a decline of 25 bps in the first quarter and reaches the highest level of 28 bps in the second quarter which is much smaller than that of the HtM consumption (120 bps) before gradually decaying. Optimizing consumptions in Thailand and the Philippines follow similar patterns but exhibit significantly higher levels compared to Indonesia. Therefore, in spite of the relatively low ratio of HtM consumers, the presence of these consumers still intensifies the negative impacts of the demand shock on output/consumption in all countries. Like the case of monetary shock, a demand shock also creates a temporary inequality in consumption between two consumer groups.

Fig. 6
figure 6

Responses to demand shock

Full size image

A similar trend is observed in labor supply, with an immediate decline of 38 basis points in Indonesia right after the shock, while Thailand and the Philippines experience declines of 68 basis points each. Owing to the weak demand, firms lower their prices, and so does inflation. Central bank might react to this situation by decreasing nominal interest rate as suggested by the Taylor rule.

  1. c.

    Supply shock

Responses of variables to a negative supply shock are shown in Fig. 7. In general, macroeconomic variables react to the shock by lowering their levels except for inflation and interest rates. Understandably, inflation rate strongly surges right after the shock. We can imagine the supply shock is activated by a strong increase in oil prices. The monetary authorities immediately raise interest rate according to the Taylor rule. Consequently, the inflation rate quickly returns back to its steady-state levels after about four quarters. However, it pushes the real interest rate to higher levels because of the high persistence of nominal interest rate. Following that, aggregate output/consumption decreases by around 10 bps after four quarters. Moreover, the supply shock also leads to reductions in aggregate labor and real wage which definitely link to lower output. Two types of consumers share similar patterns but different levels of response. While optimizing consumers lower their consumption by 6–8 bps after four quarters, HtM consumers made a much stronger reaction. In conclusion, like the demand shock, the existence of HtM consumers exaggerates the negative effects of the supply shock on economic growth. This is probably because HtM consumers are much more sensitive to income fluctuations than optimizing consumers.

Fig. 7
figure 7

Responses to supply shock

Full size image

4.4 Policy experiment

In this section, we do a policy experiment by fixing the share of HtM consumers (λ) at different levels and investigate how the HtM behavior affects the economy’s responses to a monetary shock via the impulse response analysisFootnote 14. Given the changeability of the HtM consumer ratio, the experiment serves as a useful tool for policymakers to explore how macroeconomic variables respond to shocks as λ varies over time. We omit HF behavior from consideration due to its estimated parameters being relatively homogeneous, consistently around 0.5 across the three economies (Table 3). Furthermore, HF behavior is less likely to change over time compared to HtM behavior. All parameters used for the experiment are from the above Bayesian estimation results of the Thai economyFootnote 15. Simulation procedures have been obtained with Dynare for MATLAB software.

We simulate the effects of a unit standard deviation monetary shock in three different models: (i) λ = 0.2; (ii) λ = 0.3; and (iii) λ = 0.4. In general, the share of HtM consumers does not change responding patterns but significantly affects responding magnitudes of endogenous variables (Fig. 8). The higher the ratio of HtM consumers, the stronger the macroeconomic variables response to the monetary policy shock. Hence, the findings imply that a higher share of HtM consumers strengthens the impacts of monetary shock. This observation is consistent with our analysis in Section 4 where we show that monetary policy effectiveness is an increasing function of the HtM consumers ratio in the standard regime. However, this observation interestingly suggests that policies resulting in lower HtM ratios might have unexpected effects on monetary policy effectiveness.

Fig. 8
figure 8

Monetary shock experiment

Full size image

5 Conclusion

The study’s primary purpose is to investigate how the presence of the HtM and HF behaviors theoretically influences the monetary policy effectiveness and empirically affects the responses of three ASEAN economies to external shocks using a modified New Keynesian DSGE model. The paper demonstrates that both HtM and HF behaviors play significant roles in determining the effectiveness of monetary policy. The Bayesian estimation using quarterly data from three ASEAN countries reveals that the HtM parameter is estimated at 22% in Indonesia, 34% in the Philippines, and 27% in Thailand, while the HF parameter consistently fluctuates around 50%. The combination of relatively low HtM parameters and median HF parameters implies that the policy inversion suggested by Bilbiie (2008) is unlikely to occur in all three countries. The empirical findings provide an important recommendation for policymakers. Accordingly, given the relatively low HtM parameter, financial stimulus packages designed to raise disposable income during recessions might not effectively boost private spending since current income plays a limited role in consumption growth. Most consumers are optimizing instead of HtM. Hence, policymakers may need to explore alternative measures, such as implementing monetary stimulus packages.

The impulse response analysis strongly confirms that the integration of HtM behavior into a standard DSGE model intensifies the adverse effects of structural shocks on aggregate consumption/output growth because the HtM consumption seems to be more responsive to structural shocks than its counterpart. Hence, a temporary consumption inequality between two consumer groups is created after every shock. The current share of HtM consumers should not be overlooked by policymakers when implementing macroeconomic policies because it significantly influences how robust the economy responds to external shocks or policies. Regarding the policy experiment where the ratio of HtM consumers is fixed at different values, whereas a higher ratio of HtM consumers significantly exaggerates the negative effects of monetary shock on macroeconomic variables, it does not modify much the adverse impacts of demand and supply shocks. Thus, policymakers should be cautious when dealing with external shocks. Different policies should be implemented for different shocks faced by each country referring to the particular popularity of HtM consumers in each period.