Introduction

In a context in which urbanised areas are globally increasing (Helbling and Meierrieks 2022), studies show how the expansion of sealed surfaces is directly correlated to green area reduction (Hilbert et al. 2019) to the detriment of the area available for urban tree growth (Roy et al. 2012). Furthermore, it is well documented how replacing natural green areas corresponds to the onset of the urban heat island (UHI) phenomena in cities (Cui and Shi 2012). Urban forests play an essential role in microclimate regulation, helping to tackle UHI and the heat waves that are becoming more and more frequent (Wang et al. 2018; Zhao et al. 2020). Urban trees contribute positively to the surrounding environment by providing multiple ecosystem services (ES), such as cooling by shading and evapotranspiration and improving the urban surface’s thermic properties by intercepting solar radiation (Morini et al. 2018; Detommaso et al. 2021). In addition, they contribute to climate change mitigation at a larger scale through CO2 absorption, improving the heat balance of houses (leading to reduce CO2 emissions) acting as air pollution removers (Grote et al. 2016; Ko 2018; Silveira et al. 2020), and preserving human health (Wolf et al. 2020). However, the ES-providing capacity mostly depends on the trees’ dimension (Semenzato et al. 2011), which in the urban environment is not as predictable as it could seem. In forestry, tree dimension is easily estimated starting from simple collecting parameters such as the trunk diameter at 1.3 m, the so-called diameter at breast height (DBH), and tree height (TH), with good intra-species predictability, even if with some site-related variability (Fortin et al. 2019). DBH-based models have largely been employed also in urbanised contexts (Semenzato et al. 2011; McPherson et al. 2016), but urban environments differ entirely from natural ones, and besides geographical influence, they present high variability in growth conditions even within a few metres. In early studies, Berrang et al. (1985) identified over 80 variables of five different environmental factors typology that influence tree health (i.e. tree interaction with its physical environment, care received and chemical site parameters). Nevertheless, studies that collected urban tree dendrometrical data to assess their growth potential are few and scattered (Semenzato et al. 2011; McPherson et al. 2016; Pretzsch et al. 2015), especially for the southern European areas, where Sanesi et al. (2007), Semenzato et al. (2011), and Marziliano et al. (2013) represent the leading figures. However, the combined effect of the tree’s health status, maintenance practice, and little space availability often characterising urban green infrastructure have not yet been sufficiently investigated. Moreover, studies carried out in very different climatic areas could present inaccuracies due to the lack of a proper adaptation of the models to a completely different context (Maco and Nowak 2011), showing the need for more studies in Mediterranean urban environments. In this study we aim to analyse tree growth data of a medium-sized Italian city with a methodology realised within the Life Clivut project (LIFE18 GIC/IT/001217) and compare the results obtained with another well-proven methodology: the one that McPherson et al. (2016) used to realise the urban tree Growth Models for the USDA Forest Service (USDA-GM from now on). However, this research aims to introduce a methodology to simultaneously consider the effect of urban environment, maintenance practices and designed space on tree growth in order to estimate the expected tree size reduction in cities and the implications on their ES-providing capacity. Therefore, we used a methodology approach that combines two of the methodologies seen in literature. The first is based on the findings of the studies by Grabosky and Gilman (2004), Sanders et al. (2013), and Sanders and Grabosky (2014) regarding the influence of the tree pit designed space (the “Apparent Available Soil”, AAS) on the overall tree growth. The second, similar to the methodology utilised in other studies (Iakovoglou et al. 2001), considers the impact of near-grown vegetation, human-induced mechanical injury and physical obstacles on the urban tree development. Thus, the main objective of this study was to investigate the effect of different urban limiting conditions on the TH/DBH ratio of well-established trees and their maximum dimensional potential, considering their status.

Methods

This study was based on the comparison between the tree census carried out in 2022 in Casalecchio di Reno as part of the Life Clivut project (LIFE18 GIC/IT/001217) and the tree census performed by the municipality in 2008 to evaluate the 14-year growth of trees in an urban environment. During the first census of Casalecchio in 2008, measurements were taken in metres for the TH and in centimetres for the DBH of each tree with DBH >20 cm. Also, trees’ localisation, health status and management intervention were accurately described, and a unique id was assigned to each tree by a label attached to the trunk.

Site description

Casalecchio di Reno, province of Bologna, is a medium-sized city located in the Pianura Padana plain in the northwest of Italy with a humid subtropical (Cba) climate according to the Köppen and Geiger classification (Kottek et al. 2006), so it could be described as warm and temperate with significant rainfalls throughout the year. The average yearly rainfall is 825 mm with the minimum number of rainy days being expected in July (6.60 days) and the maximum in April (10.57 days). The yearly average temperature measured in the last 31-year period (1991-2021) in Casalecchio di Reno is 14.3°C, and the highest average monthly temperature is recorded in July (25.5°C).

Data collection

Trees dendrometric parameters from the 2008 census campaign were provided by the Casalecchio di Reno municipality, and a further survey campaign was realised during the 2022 vegetative season from May to July. In particular, this study surveyed 264,872.53 m2 of 33 green areas in total, comprising gardens, urban parks, historical green areas, schools, equipped green and special areas according to Cvejić et al. (2015) green infrastructure categorisation (Table 1).

Table 1 Tree sampling description with mean values and standard deviation (SD) of tree height and DBH
Full size table

For the 2022 census activities, the Treedb platform (https://lifeclivut.treedb.eu/) of the Life Clivut project was used as a tool for specialised personnel and volunteers to register the tree-related parameters. The instruments used included: a clinometer, a roll-up metre, a diameter tape and a tablet for data entry on the web app. During the surveys, tree species, DBH, TH, plant conservation and health status, damage typology and pruning typology were re-measured over the same trees censused in 2008, following the web app board criteria (https://www.lifeclivut.eu/public_download/download/8/file_download_en.pdf). The space available for each tree was considered as well and verified to be unchanged since 2008. Thus, the parameters collected have been used to build several models assessing the TH/DBH ratio of trees grown in an urban environment.

Constraints classification and assumption

The large variability that characterises urban conditions has been simplified and parametrised in order to bring back all conditioning variables to three main aspects that will be discussed in depth in the following paragraphs: the health status of the tree (both health status and conservation status); the tree’s management (pruning); the tree’s available space. These three constraints categories (CC) encountered during census activities have been classified by binomial response: the letter A or B to point out the tree health status and conservation status, the letter C or D to indicate the maintenance pruning treatment and the letter E or F to trace the boundaries between non-limiting space condition and limiting space conditions. Table 2 shows the acronyms that will be used from now on and the full meaning of these.

Table 2 Classification and description of the constraints categories (CC)
Full size table

Tree health and conservation status parameters

Tree health status is intended as the tree conditions on the basis of possible pathogen attacks. The visible presence of pathogens affecting the tree may determine a “poor” health status, while a “sufficient” one when the presence of pathogens is minimally significant and a “good” status when they are absent. The details of the classification applied in this study in defining the conservation status as “good”, “sufficient”, and “poor”, were defined in the protocol developed by Life Clivut Project (https://www.lifeclivut.eu/public_download/download/8/file_download_en.pdf). The censused tree falls in the “A” category indicating a generally good condition when the health and conservation status are both defined as “good” or “sufficient”. In contrast, it falls in the “B” category, which indicates a suffering condition when one of the two tree’s statuses (or both) is indicated as “poor”.

Tree management parameters

The pruning techniques encountered during the trees survey have been subdivided into light and heavy pruning interventions. In this study, maintenance pruning and no pruning have been grouped in the “C” category for “light pruning”. Heavy pruning techniques were classified in the “D” category and included control pruning, aimed at containing the tree crown shape and dimension through the removal of a consistent part of it, and pollard pruning, which foresees the removal of big tree branches. Usually, pollard pruning does not involve coniferous species, but, wherever big lateral branches have been cut from these species (even without apex removal), they have been included in the “heavy pruning” category.

Tree space parameters

In the present study, to assess space constrictions to which trees are subjected, we take the “apparent available soil” (Sanders and Grabosky 2014) as the leading indicator to set tree space availability. However, in an urban environment, trees can go against numerous limitations of their living space, even when not confined in a tree isle. Therefore, to consider the possible limitation due to the nearby physical constraints we elaborated a parameter, the tree available area (TAA). The TAA concurrently considers two factors (when present). First, the distance of the tree from elements that may limit crown and root system expansion, such as asphalt-sealed surface (pavement or the road lane border, depending on the cases) and important fences that constitute vertical barriers. Secondly, the distance (from trunk to trunk) of the closest tree, which may compete for sun or space. In this way, it has been assumed that each tree has the possibility to explore half of the distance from the nearest tree before starting to compete. Considering the root system and crown’s adaptability, when several limiting conditions occurred, it was chosen to give to all elements the same weight and to calculate the area available based on the mean distance from the different space-limiting elements. In particular, in the presence of a well-defined tree pit area (i.e. Fig. .1a), the TAA has been considered equal to its border dimension area measured in m2 (Sanders and Grabosky 2014). While, when the permeable area around the trees does not present a border, we calculated the TAA considering the distance (and the possible interaction) with the nearest urban infrastructure (fence and street or pavements) or other trees.

Fig. 1
figure 1

Definition of the tree available area (TAA) in four different cases: a—confined trees with presence of clearly bordered tree pit area; b—not-confined tree nearby other trees; c—not confined trees near sealed surfaces and other trees; d—not-confined trees, close to other trees, sealed surfaces, and deep fences

Full size image

In parks (Fig. 1b), where there are no paved surfaces, we consider as TAA the surface surrounding the tree within a radius equal to half the distance to the nearest tree. In case of absence of a specific demarcation of the planting area but with the presence of limiting conditions infrastructure (paved surface as in Fig. 1c or in addition to deep fences as in Fig. 1d), the TAA has been approximated to a circle with a radius equal to the mean between the road/pavements distance and fence distance and half of the distance to the nearest tree. Considering the average size of the planting areas collected and the potential tree growth, a range of TAA values was calculated on the basis of the observed data. Street trees (the worst-case urban scenario regarding space) had a TAA range of approximately 8–16 times the mean trunk area at DBH (TAD). On the basis of this evidence, an average value of 12 times was then chosen as the threshold value (i.e. 30 cm of tree DBH corresponds to 100 cm of pit area diameter or 0.85 m2). So, the trees were sorted into the “E” category (non-limiting space conditions) when TAA/TAD > 12. On the other hand, when the ratio TAA/TAD is smaller than 12, they were classified into the “F” category indicating limited-space conditions.

Data analysis and growth model construction

Data analysis focused on the most present trees sampled during 2022 field surveys. Species with similar habitus and few sampled individuals were clustered and considered as “tree groups” composed of multiple species belonging to the same genus: Quercus robur and Q. cerris were grouped in the “Quercus spp.” group as Cedrus atlantica, C. deodara and C. libani were grouped in “Cedrus spp.”, while Platanus acerifolia, P. hybrida and P. orientalis compose the “Platanus spp.” group. In contrast, the species that present more sampled individuals (Tilia cordata Mill., Acer negundo L.) were the only species considered inside their tree group.

These five tree groups (two species and three genus) represent 51% of the total censused trees. A quartile-based technique was used to describe the variation in the differential DBH (ΔDBH22-08) and TH (ΔTH22-08) of the tree groups to show the various growth rates within each quartile.

Moreover, the DBH and TH pairs of observations for each tree group were charted by the graphical analysis open-source software DESMOS (Ebert 2015). The equations to be used to interpolate the data were chosen from those most commonly used in this field of research: a linear regression (y ~ ax + b); a logarithmic regression (y ~ a + b (log (log (x + c)))); and a logistic one (y ~ k/(1+a · e^(-b · x))).

Once the equations were defined, the coefficients that maximised the percentage of explained variance (highest R2 values) were identified using the graphical analysis software to carry out the best fitting models.

Each tree group’s different CC frequencies among DBH and TH quartiles were evaluated to highlight potential growth rate differences. Therefore, the census data were further analysed considering the CC within the tree groups, if represented by at least 20 pairs of observations, and the best-fitting regression coefficients were carried out. Finally, the one-way analysis of variance (ANOVA) was used to evidence any statistically significant differences between the CC groups of each tree species.

“Census-growth model" and "USDA-growth model" comparison

The Growth Models carried out in the present study (Census-GM from now on) for each tree group, were compared with the growth models for the same tree groups in North American geographical areas (USDA-GM by McPherson et al. 2016). The comparison with US geographical areas assimilable to the Mediterranean basin climate was made only in respect of the total tree census database, and it was considered as a starting point for creating additional tree subsets based on different limitations (CC).

Results

Table 3 shows the mean values of the differential DBH (ΔDBH22-08), tree height (ΔTH22-08) and ΔTH/ΔDBH ratio for all the five studied tree groups subdivided into quartiles (Q1, Q2, Q3, Q4). Among these, T. cordata trees showed the most variable TH increment (ΔTH22-08) with a mean value ranging from 77.69 cm in Q1 to 875.64 cm in Q4 (corresponding, respectively, to 5.55 cm and 62 cm of average yearly height growth). Also, the DBH development of the Tilia group presented the highest variable mean values among quartiles, considering that the Q1 individuals had a yearly development of only 0.21 cm, while the fastest in Q4 showed a DBH growth of 0.95 cm/year. Quercus spp. and Platanus spp. were the tree groups with the highest ratio between TH and DBH development (Mean ΔTH/ΔDBH) of all the five groups.

Table 3 Quartiles mean values of total (14 years) and annual increment (AI) realized with ΔTH22-08 and ΔDBH22-08 of each tree groups (both expressed in cm)
Full size table

Moreover, a more in-depth analysis was realised considering the ΔDBH22-08 and ΔTH22-08 quartiles to ascertain the different CC distributions inside them. Below are the results of the Tilia cordata group, the most widespread species in the investigated area with the presence of several individuals in each constraint category.

The analysis of ΔDBH22-08 quartiles concerning the CC frequencies showed that the Tilia cordata trees with the smallest DBH development during the last 14 years (Q1 and Q2), were mainly characterised by the presence of plants limited by heavy pruning (ADE, BDE) and by limitations in the TAA (ADF, BDF). On the other hand, Q4 (with the highest DBH growth) presents 66% of individuals with no constraints (ACE). The quartiles based on ΔTH22-08 showed the presence of different constraints on vertical tree growth. In the Tilia species, the effect of the limiting constraints decreased from Q1 to Q4. Indeed, in Q4, the plants with no constraints (ACE) exceeded 60%, and the ADE-BDE and ADF-BDF constraints were jointly lower than 30% (Fig. 2).

Fig. 2
figure 2

Different CC distribution among ΔDBH22-08 and ΔTH22-08 quartiles for Tilia cordata group

Full size image

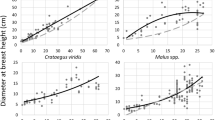
Table 4 shows the USDA urban tree growth models (USDA-GM) (McPherson et al. 2016) compared to the growth models which best interpret the data derived from the Casalecchio census (Census GM), also corresponding to the curves drawn in Fig. 3. The USDA equations for each species were only considered to compare them to our total databases (trees with and without conditioning). Further subdivision into subsets (different CC) for the different species allowed us to generate specific models to analyse the effects of growing conditions. Among the available USDA models the equation for the Lower Midwest (LoMidW), Indianapolis, Indiana for Tilia cordata and Acer negundo has been selected, as well as the curves of the Central Florida (Cen Fla), Orlando geographic area for the Platanus spp. tree group and that related to the Sacramento Valley area (SacVal), California, for Cedrus spp. These USDA models when utilised to interpret the Casalecchio data carried out lower statistical significance (R2) in comparison with the growth models provided by DESMOS interpretation. In Fig. 3, for each tree group, the total TH and DBH data sampled during both census campaigns were represented in the ordinates and x-axis, together with the Census-GM and USDA-GM for the tree species considered.

Table 4 Census-GM and USDA-GM with the respective statistical significance and coefficient values for the four tree groups analysed
Full size table
Fig. 3
figure 3

Total height (H) and DBH values sampled during both census campaigns for each tree group (Census-GM). Regression lines by DESMOS and the curves derived by US Department of Agriculture, Forest Service (USDA-GM)

Full size image

The Tilia cordata linear equations shown in Fig. 3a, present an angular coefficient of values very close to each other (a = 0.223 vs a = 0.239), although the USDA-GM curve is shifted downwards. The graphic interpretation in Fig. 3b highlights the difficulty of USDA-GM in interpreting the Platanus spp. Casalecchio census data, especially for DBH values higher than 60 cm. In addition, the USDA-GM shown in Fig. 3c for the Cedrus tree growth describes a TH/DBH ratio averagely higher than that actually resulting from the census operation; thereafter, Casalecchio data appear to be better described by linear regression for this tree group. Figure 3d shows the similarity of TH vs DBH growth ratios between Census-GM and USDA-GM, although the latter is shifted downwards. Even the best regression line of the A. negundo Census-GM shows a rather modest R2 (R2 = 0.268) due to the great variability of plant growth and a concentrated range of DBH values.

Census growth model in different CC

In order to further our study, we have clustered the census data according to different growth constraint conditions (CC). Table 5 shows the best-fitting model (census-GM) for each tree group, and each CC carried out through graphic interpretation (DESMOS software). Table 5 presents an R2 of 0.525 with an angular coefficient a = 0.320 for the Tilia tree group developed without constraints (ACE group), while logarithmic and logistic equations for the same CC showed slightly higher R2 values. Tilia trees subjected to heavy pruning (ADE-BDE) were interpreted by linear regression (R2 = 0.458) yielding a lower angular coefficient (a = 0.214) compared to the precedent group (ACE). In Figs. 4 and 5, the DBH-TH pairs of observations sampled in 2008 and 2022 of each tree group are reported as different datasets on the base of the CC identified during the 2022 census. In Fig. 4c, the Tilia cordata trees affected by heavy pruning and limiting “TAA” (ADF-BDF) showed the lowest R2 for all the considered equations. Figure 6 reports the three Census-GM of Cedrus genus, the first (Fig. 6a) constructed with trees not limited in their dimensional growth (ACE), the second (Fig. 6b) with trees affected by heavy pruning conditioning effect (ADE) and the third (Fig. 6c) with trees limited TAA (ACF). Moreover, Acer negundo trees showed only two groups of DBH-TH pairs of observations (Fig. 7), the first representing ACE condition and the second (ADE) only affected by heavy pruning (but with not limiting TAA). In Table 5, the limited group (ADE-BDE) of the Platanus genus practically showed individuals with a constant TH despite the different DBH values; the R2 was very low for all the considered equations.

Table 5 Census-GM (linear, I; logarithmic, II; logistic, III) derived by the graphical interpretation (DESMOS software) for each species and the different constraints categories (CC)
Full size table
Fig. 4
figure 4

DBH and TH observations pairs of Tilia cordata trees sampled in 2008 and 2022 reported on the base of the urban constraints (CC) identified during the 2022 census. Linear, I; logarithmic, II; logistic, III regression equations are shown

Full size image
Fig. 5
figure 5

DBH and TH observations pairs of Cedrus spp. trees sampled in 2008 and 2022 reported on the base of the urban constraints (CC) identified during the 2022 census. Linear, I; logarithmic, II; logistic, III regression equations are shown

Full size image
Fig. 6
figure 6

DBH and TH observations pairs of Acer negundo trees sampled in 2008 and 2022 reported on the base of the urban constraints (CC) identified during the 2022 census. Linear, I; logarithmic, II; logistic, III regression equations are shown

Full size image
Fig. 7
figure 7

DBH and TH observations pairs of Platanus spp. trees sampled in 2008 and 2022 reported on the base of the urban constraints (CC) identified during the 2022 census. Linear, I; logarithmic, II; logistic, III regression equations are shown

Full size image

To quickly identify the effects of the CC groups on tree growth rates we can highlight the tree height increments in cm corresponding to each DBH increment (cm).

  • Tilia cordata growth rates in height, considering linear regressions with different CC, corresponding to each DBH growth rate (cm) are: ACE 32 cm, ADE-BDE 24 cm, ADF-BDF 15 cm.

  • Cedrus spp growth in height for each DBH (cm), respectively: ACE 26 cm, ADE 24 cm, ACF 9 cm.

  • Acer negundo growth in height for each DBH (cm), respectively: ACE 36 cm, ADE 12 cm.

  • Platanus spp. growth in height for each DBH (cm), respectively: ACE 33 cm, ADE-BDE 4 cm.

The Census-GM carried out for the different tree groups using the regression lines, allowed a graphical analysis of the TH/DBH ratios for different constraints (CC) at different DBH. In this way, by considering a reference diameter of 70 cm, in the absence of conditioning (ACE), the model output for T. cordata expresses a height of 23 m. The model constructed for T. cordata trees subject to heavy pruning (ADE-BDE) presents a height of 20 m, while that for trees subject to the maximum number of constraints (ADF-BDF) shows a height of only 17.5 m. The Census-GM for the Platanus species expresses a height of 25 m in the absence of conditioning (ACE), and the model output for Platanus trees subject to ADE-BDE pruning presents a height of 20 m. Finally, Census-GM for the ACE Cedrus trees shows a height of 21 m, while the model built for ADE condition expresses a height of 19 m. The Census-GM for Acer negundo species, considering instead a reference DBH of 40 cm (this species does not commonly reach a high DBH value in an urban environment) expresses a height of 15.5 m for ACE and 11.5 m height for trees subjected to ADE condition. Although assessed at a lower DBH growth rate, the Acer species shows a high vertical development reduction following heavy pruning interventions. When subjected to one-way ANOVA for comparing height means in the different CC groups at a reference DBH, the considered species showed no statistically significant differences, even if the Cedrus genus generally evidenced reduced growth in the studied urban areas compared to other species.

Discussion

A correct evaluation of the ecosystem services provided by woody species depends on tree size and health status, conditioned by both biotic and abiotic stresses such as anthropogenic factors (Vaz Monteiro et al. 2017), so the estimation of tree growth potential in urban environments is of primary importance. However, it is limited by the availability of tree growth equations, which are widely used for forest trees but are not directly transferable to open-grown urban trees due to their different growth patterns (McPherson et al. 2016). Therefore, numerous worldwide studies developed allometric equations to describe the urban tree dimension in relation to easily measurable morphological features such as DBH (McPherson et al. 2016). For example, Pretzsch et al. (2015) developed allometric equations to describe crown diameter variation depending on DBH and species on a worldwide analysis of different urban tree databases with a focus on the growth of not-pruned isolated trees in order to assess the species-specific maximum tree crown dimension. However, studies about the South Europe region are still rare. With respect to the results of our study, the analysis carried out by Sanesi et al. (2007), Semenzato et al. (2011) and Marziliano et al. (2013) in Parco Nord of Milano, show trees are more affected by competition with other trees than by the typical constraints of the urban environment i.e. heavy pruning, restricted rooting volume, limited access to water or the intense sunlight that characterises the cities' surfaces (Celestian and Martin 2005). Moreover, coherently with the increased mortality and reduced growth evidenced by another study (Schwets and Brown 2000), space limitation seems to be the most restricting condition to growth, while trees planted on turf present growth more similar to the design expectation. The present study merged the methodology approach of Sanders and Grabosky (2014) (also found in previous works i.e. Grabosky and Gilman 2004; Sanders et al. 2013), who correlated the reduction of tree growth in parking areas and limited availability of soil (AAS), with a spatial wide investigation of nearby biotic (nearby trees, disease, human-induced injuries) and abiotic (pavements) interference to tree expansion, similar to Iakovoglou et al. (2001) approach. The results of our model Census-GM for interpreting the different CC, appear coherent with both previous studies, showing a decreased growth rate in trees characterised by limited space availability regardless of the limiting-space factors. Moreover, USDA-GM showed an interpretative effectiveness of the total DBH-TH pairs of observations for each tree group similar to that of our study in case of the inclusion of all the urban constraints (CC) in growth models building, providing a mean growth rate despite the tree growth conditions. On the other hand, the subdivision in different CC subsets determined a decrease in USDA-GM accuracy. Among the different urban abiotic stresses, heavy pruning stands out as the main growth-limiting factor, manifested by the fact that in the quartile corresponding to both the greatest diametrical and vertical growth, most of the plants (over 60%) belong to the unconditioned ACE category.

The evaluation of the space and pruning effects on different tree groups showed that in Tilia cordata trees pruning alone causes a 35% of height growth reduction, while when combined with limited space availability, the reduction reaches about 50%. For this species the condition of limited space does not occur alone, as trees in avenues are generally subject to heavy pruning. Moreover, Cedrus spp. is particularly affected by limited space with a reduction of about 70% in its height growth rate, while the reduction due to heavy pruning is limited to about 10%, probably due to the fact that apex removal is generally avoided in coniferous species. The most widespread Acer negundo species in the Casalecchio parks shows a drastic reduction in growth, greater than 60%, following heavy pruning, while it is not subject to limited space availability. Finally, the Platanus spp. in the study areas, considering the restricted individuals availability, is also extremely affected by heavy pruning with a growth reduction of more than 80%.

Therefore, the ACE category showed the highest growth rates, confirming the evidences of previous studies that urban trees grown in park-like conditions, characterised by an unsealed surface, were not as limited by urban heat island and increased pollution as those found in more restrictive urban spaces (Monn et al. 1995; Roger and Clark 1992; Grimmond 2007; Vaz Monteiro et al. 2017). Based on these considerations, it might be possible to select the ACE trees to assume an average annual DBH growth rate for unconditioned individuals of different ages. At the same time, the worst-case BDF conditioned trees could be selected to calculate their respective growth rates at different ages. Consequently, for each CC a different tree growth rate might be evaluated. In the first few years of life, a tree has a high growth rate due to the presence of no limiting conditions; successively, at the onset of constraints, the tree growth rate decreases until it reaches major limitations (pruning or others), which cause the growth rate to drop dramatically. These kinds of dynamics are the reason why it was not possible to ascertain the exact age of a tree through the Census-GM, as we have yet to determine its exact growth rate period by period due to the increasing effects of conditioning as the tree grows. Moreover, the combined effect generated by the presence of contemporary constraints conditions is of difficult interpretation, while the possibility that a tree may not be subjected to the same severity of CC for its entire life must be considered.

Conclusion

The first results of the tree census data elaboration have highlighted the importance of correctly interpreting tree growth rates for the most widespread species in urban environments considering their different response to various constraints. This is of fundamental importance for future plantings in urban areas and for accurately evaluating the tree's ecosystem services providing capacity.

In addition, the tree census (still a rare practice among Italian municipalities) should be considered as an important tool for surveying the urban forest management in order to define the timing and intensity of the abiotic stress events.

Moreover, in an urban environment, some tree species may never be subjected to certain urban constraints (CC), being typically planted in parks where the growing conditions are not limiting. In addition, the results evidenced the importance of breaking down the different tree growth phases into periods during which the same tree will be subjected to differential conditioning. In this way, further census activities will be realised, focusing our attention on the plants with DBH of less than 20 cm not previously surveyed, helpful to study the first stage of tree development. The same tree growth curves in the scientific literature also show various problems in reconstructing morphological parameters in the early stages of growth, often introducing validity limits on the equations themselves. Moreover, further investigations will be carried out to interpret how the crown radius and crown projection area may change with DBH.