Skip to main content
SpringerLink
Log in

Regular Position-Oriented Method for Mesh Smoothing

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

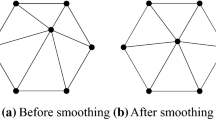
Mesh smoothing is an essential technique for the improvement of mesh quality in finite element analysis, due to the fact that mesh quality has a large impact on the convergence of the computational scheme and the accuracy of the numerical results. A novel mesh smoothing method based on regular-position-guided operations is presented in this paper. The method introduced here contains two main stages: The first stage computes the regular position of each vertex based on the shape of the element and conducts regular-position-oriented-based element transformations independently; the second stage determines the finial position of each vertex according to its surrounding elements with an assembly strategy. This method is not limited to planar triangular mesh, but applicable to surface polygonal mesh. Numerical experiments on various mesh models demonstrate the effectiveness and potential of this method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Basaran C. Solving large-scale problems in mechanics: the development and application of computational solution methods. Int J Numer Anal Methods Geomech. 1994;18(2):139–40.

    Article  Google Scholar 

  2. Plassmann LAFP. Local optimization-based simplicial mesh untangling and improvement. Int J Numer Methods Eng. 2000.

  3. Freitag L, Leurent T, Knupp P. MESQUITE design : issues in the development of a mesh quality improvement toolkit; 2002.

  4. Durand R, Pantoja-Rosero BG, Oliveira V. A general mesh smoothing method for finite elements. Finite Elem. Anal. Des. 2019;158:17–30.

    Article  MathSciNet  Google Scholar 

  5. Vartziotis D, Wipper J. The geometric element transformation method for mixed mesh smoothing. Eng. Comput. 2009;25(3):287–301.

    Article  Google Scholar 

  6. Sun S, Zhang M, Gou Z. Smoothing algorithm for planar and surface mesh based on element geometric deformation. Math. Probl. Eng. 2015;2015:1–9.

    MathSciNet  MATH  Google Scholar 

  7. Field DA. Laplacian smoothing and Delaunay triangulations. Commun. Appl. Numer. Methods. 1988;4(6):709–12.

    Article  Google Scholar 

  8. Ji Z, Liu L, Wang G. A global Laplacian smoothing approach with feature preservation. In: IEEE 9th international conference on computer aided design and computer graphics; 2005.

  9. Zhihong M, Lizhuang M, Mingxi Z, Zhong L. A modified Laplacian smoothing approach with mesh saliency. In: Smart graphics, 6th international symposium, SG 2006, Vancouver, Canada, July 23–25, Proceeding, 2006.

  10. Vollmer J, Mencl R, Muller H. Improved Laplacian smoothing of noisy surface meshes. Comput Graph Forum. 1999;18(3):131–8.

    Article  Google Scholar 

  11. Xu H, Newman TS. An angle-based optimization approach for 2D finite element mesh smoothing. Finite Elem Anal Des. 2006;42(13):1150–64.

    Article  MathSciNet  Google Scholar 

  12. Vartziotis D, et al. Mesh smoothing using the geometric element transformation method. Comput Methods Appl Mech Eng. 2008;197(45–48):3760–7.

    Article  Google Scholar 

  13. Sun S, Gou Z, Geng M. Simultaneous smoothing and untangling of 2D meshes based on explicit element geometric transformation and element stitching. Appl Sci. 2020. 10(14).

  14. Frey PJ, Borouchaki H. Geometric surface mesh optimization. Comput Vis Sci. 1998;1(3):113–21.

    Article  Google Scholar 

  15. Wang D, et al. Enhanced remeshing from STL files with applications to surface grid generation. Commun Numer Methods Eng. 2006;23(3):227–39.

    Article  MathSciNet  Google Scholar 

  16. Huang Y, Qin H, Wang D. Centroidal Voronoi tessellation-based finite element superconvergence. Int J Numer Methods Eng. 2008;76(12):1819–39.

    Article  MathSciNet  Google Scholar 

  17. Ahmed AGM, et al. A simple push-pull algorithm for blue-noise sampling. IEEE Trans Vis Comput Graph. 2017;23(12):2496–508.

    Article  Google Scholar 

  18. Chen L. Mesh smoothing schemes based on optimal Delaunay triangulations. In: Proceedings of the 13th international meshing roundtable, pp. 109–120, Sandia National Laboratories, 2004.

  19. Liu J, Li S, Chen Y. A fast and practical method to pack spheres for mesh generation. Acta Mech Sin. 2008;24(4):439–47.

    Article  MathSciNet  Google Scholar 

  20. Shimada K, Gossard DC. Bubble mesh: automated triangular meshing of non-manifold geometry by sphere packing. In: Proceedings. Third symposium on solid modeling and applications, 1995; 409–419.

  21. Yagou H, Ohtake Y, Belyaev A. Mesh smoothing via mean and median filtering applied to face normals. In: IEEE proceedings of the geometric modeling and processing, 2002.

  22. Knupp PM. Algebraic mesh quality metrics. SIAM J Sci Comput. 23(1), 193–218.

  23. Lo DSH. Finite element mesh generation. Boca Raton: CRC Press; 2015.

    MATH  Google Scholar 

  24. University RA. OpenMesh. http://www.openmesh.org/.

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics and Engineering Science, Peking University, Beijing, 100871, China

    Yongqing Hai

  2. X Lab, Second Academy of China Aerospace Science and Industry Corporation, Beijing, 100854, China

    Yufei Guo

  3. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin, 300072, China

    Siyuan Cheng

  4. College of Electromechanical Engineering, Qingdao University of Science and Technology, Qingdao, 266061, China

    Yunpeng Hai

Authors
  1. Yongqing Hai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yufei Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Siyuan Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yunpeng Hai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yufei Guo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hai, Y., Guo, Y., Cheng, S. et al. Regular Position-Oriented Method for Mesh Smoothing. Acta Mech. Solida Sin. 34, 437–448 (2021). https://doi.org/10.1007/s10338-020-00201-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-020-00201-z

Keywords

Search

Navigation