Vessel radius mapping in an extended model of transverse relaxation

Abstract

Objectives

Spin dephasing of the local magnetization in blood vessel networks can be described in the static dephasing regime (where diffusion effects may be ignored) by the established model of Yablonskiy and Haacke. However, for small capillary radii, diffusion phenomena for spin-bearing particles are not negligible.

Material and methods

In this work, we include diffusion effects for a set of randomly distributed capillaries and provide analytical expressions for the transverse relaxation times T2* and T2 in the strong collision approximation and the Gaussian approximation that relate MR signal properties with microstructural parameters such as the mean local capillary radius.

Results

Theoretical results are numerically validated with random walk simulations and are used to calculate capillary radius distribution maps for glioblastoma mouse brains at 9.4 T. For representative tumor regions, the capillary maps reveal a relative increase of mean radius for tumor tissue towards healthy brain tissue of $128 \pm 23 \%$ (p < 0.001).

Conclusion

The presented method may be used to quantify angiogenesis or the effects of antiangiogenic therapy in tumors whose growth is associated with significant microvascular changes.

Appendices

Appendix A: Single-vessel approximation model (SVM)

In this appendix, the random vessel distribution model (RVM) is compared to the single-vessel approximation model (SVM). Static dephasing limit, an exact solution of the Bloch-Torrey equation in the SVM and the SCA in the SVM were summarized and compared to the obtained results in the RVM.

Geometrical model

The Bloch-Torrey equation can be solved for uniformly arranged capillaries by applying Krogh’s capillary supply model [21] to reduce the vessel network geometry to one single vessel. In this model, only one single capillary with radius R is considered, which is surrounded by a second concentric cylinder, or Krogh cylinder, that accounts for the surrounding tissue. The outer radius $R_\text {D}$ is chosen such that the capillary blood volume $\eta$ corresponds to:

$$\begin{aligned} \frac{N\pi R^2}{V} = \eta = \frac{R^2}{R_\text {D}^2}\,. \end{aligned}$$

(38)

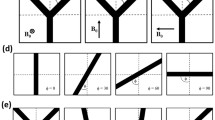
Reflecting boundary conditions are chosen at the surface of the Krogh cylinder (see e.g. Fig. 1 in [90]). A schematic illustration of the SVM is shown in Fig. 1c.

This simplistic geometrical model provides an exact solution of the Bloch-Torrey Eq. (1) for spin dephasing around capillaries, as demonstrated recently (see also below and [22, 24, 26]).

Static dephasing regime

In the static dephasing regime (index 0), where diffusion effects are neglected, the free induction decay in the SVM can be found as the signal around a single blood vessel (see [18] and Eq. (36) in [10]):

$$\begin{aligned} M_{0,\text {SVM}}(\eta ,t)&= \frac{h(\eta \delta \omega t)-\eta h(\delta \omega t)}{1-\eta } = \frac{\eta }{1-\eta } \int \limits _{\eta }^{1} \frac{\mathrm {d}x}{x^2} J_0(x\delta \omega t)\end{aligned}$$

(39)

$$\begin{aligned}&= \frac{2}{\pi } \left[ \int \limits _\eta ^1 \!\!\! \mathrm {d}x \frac{\sin (x\,\delta \omega \,t) \sqrt{x^2 - \eta ^2}}{x^2[1-\eta ]} + \int \limits _1^\infty \!\!\! \mathrm {d}x \frac{\sin (x\,\delta \omega \, t)\left[ \sqrt{x^2-\eta ^2} + \eta \sqrt{x^2-1} \right] [1+\eta ]}{\displaystyle {x^2[1+\eta ^2] + 2\eta \left[ \sqrt{[x^2-\eta ^2][x^2-1]} - \eta \right] }}\right] \,, \end{aligned}$$

(40)

where $J_0(x\delta \omega t)$ denotes the Bessel function of first kind with an index of zero. The function h(x) can be expressed in terms of the hypergeometric function as given in Eq. (26). Equation (40) follows from Eq. (29) in [25] and allows calculating the mathematical limits $\eta \rightarrow 0$ and $\eta \rightarrow 1$.

The frequency distribution $p(\omega )$ is defined as the Fourier transform of the free induction decay:

$$\begin{aligned} p(\omega ) = \frac{1}{2\pi }\int \limits _{-\infty }^{+\infty } \mathrm {d}t M(t) \mathrm {e}^{-\mathrm {i}\omega t}\,. \end{aligned}$$

(41)

Since $M(0) = 1$ [see Eq. (3)], $p(\omega )$ is normalized to:

$$\begin{aligned} \int \limits _{-\infty }^{+\infty } \mathrm {d}\omega \, p(\omega ) = 1\,. \end{aligned}$$

(42)

The frequency distribution in the static dephasing limit for the SVM was found as [18]:

$$\begin{aligned} p(\omega ) = \frac{\eta }{1-\eta } \frac{\delta \omega }{\pi \omega ^2} \left\{ \begin{array}{ll} \sqrt{1-\left[ \frac{\omega }{\delta \omega }\right] ^2} &{\quad} \text {for } -\delta \omega \le \omega \le -\eta \delta \omega \; \text {or} \; +\eta \delta \omega \le \omega \le +\delta \omega \\ \\ \sqrt{1-\left[ \frac{\omega }{\delta \omega }\right] ^2} - \sqrt{1-\left[ \frac{\omega }{\eta \, \delta \omega }\right] ^2} &{\quad} \text {for } -\eta \delta \omega<\omega < +\eta \delta \omega \\ \\ 0 &{\quad} \text {elsewhere} \,. \end{array} \right. \end{aligned}$$

(43)

Evidently, $p(\omega )$ exhibits two prominent peaks at $\omega = \pm \eta \delta \omega$. The frequency distribution from Eq. (43) possesses a local minimum at $\omega = 0$, whereas $p(\omega )$ in the RVM peaks globally at $\omega = 0$ (as shown in the blue lines in Fig. 6). The mean relaxation time approach to determine the relaxation rate $R_2^{*}$ [see Eq. (4)], however, translates into the Fourier domain as follows [91]:

$$\begin{aligned} R_2^{*} = \frac{1}{\pi p(0)} = \frac{2\eta \delta \omega }{1+\eta }\,. \end{aligned}$$

(44)

Thus, it follows that the relaxation rate for the SVM in the static dephasing regime is twice as large as that for the RVM, while both frequency distributions exhibit a similar lineshape, i.e. both distributions have the same width:

$$\begin{aligned} \langle \omega ^2 \rangle = \int \limits _{-\infty }^{+\infty } \mathrm {d}\omega p(\omega ) \omega ^2 = \frac{\eta }{2}\delta \omega ^2\,. \end{aligned}$$

(45)

In the limit of static dephasing, Yablonskiy and Haacke could connect the free induction decay of N randomly distributed capillaries, $M_{0,\text {RVM}}$, with the free induction decay around one single blood vessel, $M_{0,\text {SVM}}$, as in [10]:

$$\begin{aligned} M_{0,\text {RVM}}(t) = \left[ M_{0,\text {SVM}}\left( \frac{\eta }{N},t\right) \right] ^N\,, \end{aligned}$$

(46)

where $M_{0,\text {SVM}}$ is given in Eq. (39). In the statistical limit $N\rightarrow \infty$, the gradient echo signal in the RVM is then given in Eq. (10).

Exact solution of the Bloch-Torrey equation in the SVM

An analytical solution of the local magnetization and the free induction decay in the SVM can be obtained with an eigenfunction expansion of the Bloch-Torrey equation [22, 24].

$$\begin{aligned} M_{\text {SVM}}(t) = \sum \limits _{m=0}^{\infty }\sum \limits _{n=1}^{\infty }d_{nm}\mathrm {e}^{-\lambda _{nm}^2\frac{Dt}{R^2}}\,. \end{aligned}$$

(47)

The eigenvalues $\lambda _{nm}$ in the SVM are, in general, complex and obey the following condition:

$$\begin{aligned} Y^{\prime }_{k_m}(\lambda _{nm}) J^{\prime }_{k_m}\left( \frac{\lambda _{nm}}{\sqrt{\eta }}\right) = J^{\prime }_{k_m}(\lambda _{nm}) Y^{\prime }_{k_m}\left( \frac{\lambda _{nm}}{\sqrt{\eta }}\right) \,. \end{aligned}$$

(48)

Here $J_{k_m}$ and $Y_{k_m}$ are Bessel functions of the first and second kind and $J^{\prime }_{k_m}$ and $Y^{\prime }_{k_m}$ are derivations of Bessel functions, respectively. The index $k_m$ relates to the interplay between diffusion and susceptibility effects, since:

$$\begin{aligned} k_m^2 = a_{2m} \left( \frac{\mathrm {i}}{2}\delta \omega \frac{R^2}{D}\right) \,, \end{aligned}$$

(49)

where $a_{2m}$ denotes the characteristic values of the Mathieu functions [92]. The expansion coefficients $d_{nm}$ are given as:

$$\begin{aligned} d_{nm}=\frac{8\eta }{1-\eta }\left[ A_0^{(2m)} \right] ^2\frac{\left[ J^{\prime }_{k_m}(\lambda _{nm}) s^{\prime }_{1,k_m}\left( \frac{\lambda _{nm}}{\sqrt{\eta }}\right) -J^{\prime }_{k_m}\left( \frac{\lambda _{nm}}{\sqrt{\eta }}\right) s^{\prime }_{1,k_m}\left( \lambda _{nm}\right) \right] ^2}{\left[ J^{\prime }_{k_m}(\lambda _{nm})\right] ^2 \left[ \lambda _{nm}^2-\eta k_m^2 \right] -\left[ J^{\prime }_{k_m}\left( \frac{\lambda _{nm}}{\sqrt{\eta }}\right) \right] ^2 \left[ \lambda _{nm}^2-k_m^2 \right] }\,, \end{aligned}$$

(50)

with $s^{\prime }_{1,k_m}$ denoting the first derivative of the Lommel function $s_{1,k_m}$ (see also [93]). The symbol $A_0^{(2m)}$ represents the first Fourier coefficient of the even $\pi$-periodic Mathieu functions $\text {ce}_{2m}$ and also depends on the parameter $\delta \omega R^2/D$. This expansion uses angular eigenvalues $\kappa _m$ and associated eigenvectors with an index m, as well as radial eigenvalues $\lambda_{nm}$ and associated eigenvectors with indices m and n. The indices n and m are therefore analogues of the radial and angular quantum numbers in quantum mechanics. The total magnetization is then given as sum over all eigenfunctions and corresponding eigenvalues as given in Eq. (47). One could argue against such an expansion since the Bloch-Torrey operator, $D\Delta -\mathrm {i}\omega$, is non-hermitian. However, an operator does not necessarily need to be hermitian to allow for an eigenfunction expansion as e.g. exemplified in [94, 95]. Furthermore, Herberthson et al. provided proof that the eigenfunctions of the Bloch-Torrey operator for a linear field gradient are self-dual [96]. This proof can easily be generalized for arbitrary magnetic field inhomogeneities for reflecting boundary conditions:

Lemma 1

Suppose u and v are eigenfunctions of the operator $\Delta +z(\mathbf {r})$ with the eigenvalues $\upmu$ and $\lambda$, respectively, which fulfill reflecting boundary conditions at the surface $\partial \Omega$ of the volume $\Omega$. The function $z(\mathbf {r})\in \mathbb {C}$ is an arbitrary complex function. Then, the eigenfunctions are self-dual, e.g. if $\upmu \ne \lambda$, then$\int _\Omega \mathrm {d}\Omega \, uv = 0$.

Proof

Suppose $\upmu \ne \lambda$.

$$\begin{aligned} \upmu \int _{\Omega } \mathrm {d}\Omega \,vu&= \int _{\Omega } \mathrm {d}\Omega \,v\left[ \Delta u +z(\mathbf {r}) u \right] \end{aligned}$$

(51)

$$\begin{aligned}&= \int _{\Omega } \mathrm {d}\Omega \,u \left[ \Delta v\right] - \underbrace{\int _{\partial \Omega } \hat{n} \mathrm {d}s [v\nabla u-u\nabla v]}_{=0}+\int _{\Omega } \mathrm {d}\Omega \,z(\mathbf {r})\, u v\,, \end{aligned}$$

(52)

where the second term vanishes due to the reflecting boundary conditions and Green’s identity was applied. Hereby, $\hat{n}$ denotes a unity vector that is orthogonal to the surface $\partial \Omega$ of the volume $\Omega$, $\mathrm {d}\Omega$ symbolizes the volume integration and $\mathrm {d}s$ symbolizes the integration over the surface $\partial \Omega$. Finally, one obtains:

$$\begin{aligned} \upmu \int _{\Omega } \mathrm {d}\Omega \,uv = \int _{\Omega } \mathrm {d}\Omega \,u [\Delta +z(\mathbf {r})]v = \lambda \int _{\Omega } \mathrm {d}\Omega \,uv\,. \end{aligned}$$

(53)

Thus, the statement follows. $\square$

In the special case $z(\mathbf {r}) \propto -\mathrm {i}\omega (\mathbf {r})$, where the function z takes purely imaginary values, the eigenfunctions of the Bloch-Torrey operator are self-dual. This agrees with Eq. (4) in [92] and Eqs. (9) and (12) in [24]. In addition, an actual eigenfunction expansion for the Bloch-Torrey equation has been successfully developed in several publications, e.g. [97,98,99,100]. A more detailed account is given in [101].

Fig. 6

Frequency distributions for $\eta = 0.05$ and $\delta \omega = 1000/\text {s}$, which correspond to $B_0=9.4\, \text {T}$ and $D=1\,\upmu \text {m}^2/\text {ms}$ for different capillary radii. The solid lines present the strong collision approximation (SCA) of the randomly positioned capillary model obtained from Eq. (82), and exact solutions in the single-vessel approximation are shown as dashed lines [see Eq. (47)]. In the static dephasing limit, both distributions exhibit the same width [see Eq. (45)]. The frequency distribution in the SVM, however, possesses a local minimum at $\omega = 0$ for large capillary radii, whereas the RVM contains a global maximum at $\omega = 0$. This difference gives different estimations of the relaxation rate $R_2^{*}$, as shown in Eq. (44)

According to Eq. (4), the relaxation rate in this model can be found as:

$$\begin{aligned} R_2^{*} = \frac{D}{R^2}\left[ \sum \limits _{m=0}^{\infty }\sum \limits _{n=1}^{\infty } \frac{d_{nm}}{\lambda _{nm}^2}\right] ^{-1}\,. \end{aligned}$$

(54)

Strong collision approximation (SCA)

In the static dephasing limit, the free induction decay is given in Eq. (39); its Laplace transform then follows as:

$$\begin{aligned} \hat{M}_{0,\text {SVM}}(s)=\frac{1}{1-\eta }\frac{1}{s} \left[ \sqrt{1+\frac{\eta ^2\delta \omega ^2}{s^2}}-\eta \sqrt{1+\frac{\delta \omega ^2}{s^2}}\right] \,, \end{aligned}$$

(55)

where the $\hat{}$ symbol denotes the Laplace transform of a quantity as defined in Eq. (72) in “Appendix C”. We then find the SCA relaxation rate as [25]:

$$\begin{aligned} R_2^{*}=\frac{\sqrt{1+\left[ \eta \tau _{\text {SVM}}\delta \omega \right] ^2}+\eta \sqrt{1+\left[ \tau _{\text {SVM}}\delta \omega \right] ^2}}{\tau _{\text {SVM}}[1+\eta ]}-\frac{1}{\tau _{\text {SVM}}}\,. \end{aligned}$$

(56)

In the SVM, the correlation time $\tau$, as given in Eq. (73) in “Appendix C”, can be obtained as [18]:

$$\begin{aligned} \tau _{\text {SVM}} =\frac{R^2}{4D}\frac{\mathrm {ln}(\eta )}{\eta -1}\, \end{aligned}$$

(57)

and the spin echo relaxation rate is determined by [19]:

$$\begin{aligned} R_2 = \frac{R_2^{*}}{1+\tau R_2^{*}}\,, \end{aligned}$$

(58)

with the gradient echo relaxation rate $R_2^{*}$ from Eq. (56) and the correlation time $\tau$ from Eq. (57). Thus, the spin echo relaxation rate in the SCA reads:

$$\begin{aligned} R_2 = \tau _{\text {SVM}}^{-1} \left[ 1-\frac{1+\eta }{\sqrt{1+[\eta \tau _{\text {SVM}}\delta \omega ]^2}+\eta \sqrt{1+[\tau _{\text {SVM}}\delta \omega ]^2}} \right] \,. \end{aligned}$$

(59)

Appendix B: Weak field approximation

In analogy to Jensen et al. [15], the correlation function for a randomized distribution of permeable capillaries is given as [18, 38, 106]:

$$\begin{aligned} K(t) = \frac{1}{V}\int _V \mathrm {d}^2 \mathbf {r} \int _V \mathrm {d}^2 \mathbf {s}\, \omega (\mathbf {r}) \frac{1}{4\pi D t} \mathrm {e}^{-\frac{|\mathbf {r}-\mathbf {s}|^2}{4Dt}} \omega (\mathbf {s})\,, \end{aligned}$$

(60)

where the free diffusion of spin-bearing particles was assumed, which is a good approximation for small capillary blood volume fractions $\eta$. The correlation function at the initial time point $t = 0$ takes the value: $K(0) = \langle \omega ^2(\mathbf {r}) \rangle$. Using the local Larmor frequency given in Eq. (7), we can simplify K(t) to:

$$\begin{aligned} K(t) = \frac{\eta \delta \omega ^2 R^2}{4\pi ^2 D t }\int _{|\mathbf {r}|>R} \mathrm {d}^2 \mathbf {r}\int _{|\mathbf {s}|>R} \mathrm {d}^2 \mathbf {s} \,\mathrm {e}^{-\frac{|\mathbf {r}-\mathbf {s}|^2}{4Dt}} \frac{2[\hat{x}\mathbf {r}]^2-r^2}{r^4}\frac{2[\hat{x}\mathbf {s}]^2-s^2}{s^4}\,, \end{aligned}$$

(61)

where $\hat{x}$ is the unit vector in the spatial x direction and a random distribution of capillaries in a plane is assumed. This approximation, however, allows for an overlap of capillary positions. Yet, for low capillary blood volume fractions $\eta$, the occurrences of capillary overlaps are very scarce and, thus, can be neglected. With the representation of the diffusion propagator in Fourier space

$$\begin{aligned} \mathrm {e}^{-\frac{|\mathbf {r}-\mathbf {s}|^2}{4Dt}} = \frac{Dt}{\pi } \int \mathrm {d}^2 \mathbf {k}\, \mathrm {e}^{\mathrm {i}\mathbf {k}[\mathbf {r}-\mathbf {s}]}\mathrm {e}^{-Dtk^2}, \end{aligned}$$

(62)

we find

$$\begin{aligned} K(t)&= \frac{\eta \delta \omega ^2 R^2}{4\pi ^3} \int \mathrm {d}^2 \mathbf {k} \mathrm {e}^{-Dtk^2} \left| \int _{r>R} \mathrm {d}^2 \mathbf {r} \frac{2[\hat{x}\mathbf {r}]^2-r^2}{r^4} \mathrm {e}^{\mathrm {i}\mathbf {k}\mathbf {r} } \right| ^2\end{aligned}$$

(63)

$$\begin{aligned}& \qquad= \frac{\eta \delta \omega ^2 R^2}{4\pi ^3} \int \mathrm {d}^2 \mathbf {k} \mathrm {e}^{-Dtk^2} \left| \int _{R}^{\infty } \mathrm {d}r r \int _{0}^{2\pi } \mathrm {d}\phi \frac{\cos (2\phi )}{r^2} \mathrm {e}^{\mathrm {i}k r \cos (\phi -\vartheta )} \right| ^2\,, \end{aligned}$$

(64)

where $\phi$ is the angle between the position vector $\mathbf {r}$ and the transverse component of the magnetic field (see Fig. 1) and $\vartheta$ denotes the angle between the reciprocal vector $\mathbf {k}$ and the magnetic field. Evaluating the angular part $\phi$ of the integral, we find:

$$\begin{aligned} K(t)&= \frac{\eta \delta \omega ^2 R^2}{\pi } \int \mathrm {d}^2\mathbf {k} \cos ^2(2\vartheta ) \mathrm {e}^{-Dtk^2} \left[ \int _{R}^{\infty } \frac{\mathrm {d}r}{r} J_2(kr)\right] ^2\end{aligned}$$

(65)

$$\begin{aligned}&=\frac{\eta \delta \omega ^2}{\pi } \int _{0}^{2\pi } \mathrm {d}\vartheta \cos ^2(2\vartheta ) \int _{0}^{\infty } \frac{\mathrm {d}k}{k}\mathrm {e}^{-Dtk^2} [J_1(kR)]^2\,, \end{aligned}$$

(66)

where $J_1$ and $J_2$ are Bessel functions of the first kind. By evaluating the integrals over $\vartheta$ and k, the correlation function follows as:

$$\begin{aligned} K(t)= \frac{\eta \delta \omega ^2}{2} \left[ 1-\mathrm {e}^{-\frac{R^2}{2Dt}}\left[ I_0\left( \frac{R^2}{2Dt}\right) +I_1\left( \frac{R^2}{2Dt}\right) \right] \right] \,, \end{aligned}$$

(67)

where $I_0$ and $I_1$ are modified Bessel functions of the first kind. The prefactor $\eta \delta \omega ^2/2 = \langle \omega ^2 \rangle$ equals the width of the frequency distribution as demonstrated below [see Eq. (45)]. For very long or short times, the correlation function can be approximated as:

$$\begin{aligned} K(t) \approx {\left\{ \begin{array}{ll} \frac{\eta \delta \omega ^2}{2}\,& \text {for}\, \frac{R^2}{2D}\gg t \\ \\ \frac{\eta \delta \omega ^2R^2}{8Dt} \,& \text {for}\, \frac{R^2}{2D}\ll t\,. \end{array}\right. } \end{aligned}$$

(68)

According to [15], the weak field approximation (WFA) is valid for

$$\begin{aligned} R_2^{*} < \frac{D}{R^2}\,. \end{aligned}$$

(69)

Since $R_2^{*} \approx \frac{\eta }{2}\tau \delta \omega ^2$ in the motional narrowing regime, the WFA is valid for $\eta \frac{R^4}{D^2}\delta \omega ^2 < 3.72$. Non-Gaussian spin behaviour was analyzed in [107].

In Fig. 7, the calculated correlation function is compared with the correlation function of Sukstanskii and Yablonskiy as obtained in the RVM for impermeable vessel walls [17, 38]:

$$\begin{aligned} K(t) = \frac{16}{\pi ^2}\eta \delta \omega ^2\int \limits _{0}^{\infty } \frac{\mathrm {d}x}{x^5} \frac{\exp \left( -\frac{Dt}{R^2}x^2\right) }{\left[ {J_2^{\prime }}(x)\right] ^2+\left[ {Y_2^{\prime }}(x)\right] ^2}\,, \end{aligned}$$

(70)

where $J_2^{\prime }$ is the first derivative of the Bessel functions of the first kind with index 2 and $Y_2^{\prime }$ is the first derivative of the Bessel functions of the second kind with index 2.

Fig. 7

Comparison of the correlation function in the RVM for permeable vessel walls, given in Eq. (67), with the correlation function in the RVM for impermeable vessels (yellow line), given in Eq. (70) and the correlation function in the SVM (see Ref. [106], red line). All functions coincide for short times. The blue dotted line shows the monoexponential approximation of the correlation function with the correlation time given in Eq. (76)

As shown in Fig. 7, the correlation function in the RVM for impermeable vessels is similar to the correlation function in the RVM for permeable vessels. Especially, both curves exhibit the same asymptotic behaviour for long times that is shown in Eq. (68).

Random walk simulations were performed to validate the correlation functions. Therefore, 100,000 random walk trajectories were simulated in a volume with 17,500 randomly distributed cylindrical vessels with capillary volume fraction $\eta =0.05$. The obtained correlation function is compared in Fig. 7 with the correlation functions in the SVM and RVM for permeable and impermeable vessels.

Appendix C: strong collision approximation (SCA) in the random vessel distribution model (RVM)

In the SCA, the diffusion operator in the Bloch-Torrey equation is replaced by a simpler Markov operator. In a Markov process, the diffusion transition rate between different positions is only dependent on the equilibrium probability of the final state. One of the main results of the SCA condenses in the connection between the Laplace transform of the free induction decay with the Laplace transform of the static dephasing free induction decay and the correlation time $\tau$ [see Eq. (20) and [28]]:

$$\begin{aligned} \hat{M}(s) = \frac{\hat{M}_0(s+\tau ^{-1})}{1-\tau ^{-1}\hat{M}_0(s+\tau ^{-1})}\,, \end{aligned}$$

(71)

where the Laplace transform is defined as:

$$\begin{aligned} \hat{M}(s) = \int \limits _{0}^{\infty } \mathrm {d}t \mathrm {e}^{-st} M(t)\,. \end{aligned}$$

(72)

Lerch’s uniqueness theorem guarantees the uniqueness of the inverse Laplace transform of $\hat{M}(s)$, even if the function M(t) is only piecewise continuous [102]. With the strong collision assumption, the correlation function exhibits monoexponential decay with the correlation time $\tau$ of the form [107]:

$$\begin{aligned} K(t) = K(0) \mathrm {e}^{-\frac{t}{\tau }}\,. \end{aligned}$$

(73)

The correlation time $\tau$ can then be obtained with the least squares method by minimizing the functional difference between the correlation function K(t) with its monoexponential approximation [see Eq. (19)]. For permeable vessel boundaries, we obtained with the correlation function K(t) in Eq. (67) the correlation time $\tau _\text {per}$ as a solution of the equation:

$$\begin{aligned} \frac{3}{4}\sqrt{\pi } = G_{1,3}^{2,1}\left( \frac{R^2}{D}\tau _{\text {per}}^{-1}\left |\frac{1}{2}; 0,2,0 \right) + G_{1,3}^{2,1}\left( \frac{R^2}{D}\tau _{\text {per}}^{-1}\right|\frac{1}{2}; 1,2,-1 \right) \,, \end{aligned}$$

(74)

where G denotes Meijers G-function. The correlation time $\tau _{\text {per}}$ can then obtained as

$$\begin{aligned} \tau _{\text {per}} \approx 0.5374\,\frac{R^2}{D}\,. \end{aligned}$$

(75)

For impermeable vessels, the correlation time $\tau$ is also defined by minimizing the expression given in Eq. (19):

$$\begin{aligned} \tau \approx 0.6902\frac{R^2}{D}\,, \end{aligned}$$

(76)

where K(t) is given in Eq. (70). Since impermeable vessel walls provide a more realistic tissue model than permeable vessels walls, the correlation time of impermeable vessels is used for the SCA in the RVM.

Details about the derivation of Eq. (71) are presented in appendix A in Ref. [18], or in [64, 103, 104]. For the static dephasing magnetization in the RVM given in Eq. (28), the Laplace transform follows as:

$$\begin{aligned} \hat{M}_{0,\text {RVM}}(s) = \sqrt{\frac{\pi }{\eta }}\frac{\mathrm {e}^{\frac{s^2}{\eta \delta \omega ^2}}}{\delta \omega }\mathrm {erf}\left( \frac{s}{\sqrt{\eta }\delta \omega },\frac{s}{\sqrt{\eta }\delta \omega }+\frac{3\sqrt{\eta }}{4}\right) +\frac{\mathrm {e}^{-\frac{3s}{2\delta \omega }-\frac{\eta }{2}}}{\eta \delta \omega +s}\,, \end{aligned}$$

(77)

where $\mathrm {erf}(z_0,z_1) = \mathrm {erf}(z_1)- \mathrm {erf}(z_0)$. When inserting the Laplace transform of the RVM static dephasing free induction decay into Eq. (71), one finds:

$$\begin{aligned} \hat{M}_{\text {RVM}}(s) = \tau \frac{\frac{1}{\tau \delta \omega }\sqrt{\frac{\pi }{\eta }}\mathrm {e}^{\frac{1}{\eta }\left[ \frac{\tau s+1}{\tau \delta \omega }\right] ^2}\mathrm {erf}\left( \frac{\tau s+1}{\sqrt{\eta }\tau \delta \omega },\frac{\tau s+1}{\sqrt{\eta }\tau \delta \omega }+\frac{3\sqrt{\eta }}{4}\right) +\frac{\mathrm {e}^{\frac{3\tau s+3-\eta \tau \delta \omega }{2\tau \delta \omega }}}{\eta \tau \delta \omega + \tau s+1}}{1- \frac{1}{\tau \delta \omega }\sqrt{\frac{\pi }{\eta }}\mathrm {e}^{\frac{1}{\eta }\left[ \frac{\tau s+1}{\tau \delta \omega }\right] ^2}\mathrm {erf}\left( \frac{\tau s+1}{\sqrt{\eta }\tau \delta \omega },\frac{\tau s+1}{\sqrt{\eta }\tau \delta \omega }+\frac{3\sqrt{\eta }}{4}\right) -\frac{\mathrm {e}^{\frac{3\tau s+3-\eta \tau \delta \omega }{2\tau \delta \omega }}}{\eta \tau \delta \omega +\tau s+1}}\,. \end{aligned}$$

(78)

The monoexponential relaxation rate $R_2^{*}$ is defined in Eq. (4):

$$\begin{aligned} R_2^{*}&=\left[ \hat{M}(0)\right] ^{-1}\end{aligned}$$

(79)

$$\begin{aligned}&= \frac{1}{\hat{M}_0(\tau ^{-1})} - \tau ^{-1}\,. \end{aligned}$$

(80)

Inserting the definition of the Laplace transform given in Eq. (72), one finds Eq. (20). Finally, the gradient echo relaxation rate can be obtained as:

$$\begin{aligned} R_2^*=\frac{\delta \omega }{\mathrm {e}^{\frac{1}{\eta [\tau \delta \omega ]^2}}\sqrt{\frac{\pi }{\eta }}\mathrm {erf}\left( \frac{1}{\sqrt{\eta }\tau \delta \omega },\frac{1}{\sqrt{\eta }\tau \delta \omega }+\frac{3\sqrt{\eta }}{4}\right) +\frac{\tau \delta \omega }{\eta \tau \delta \omega +1}\mathrm {e}^{-\frac{3}{2\tau \delta \omega }-\frac{\eta }{2}}}-\frac{1}{\tau }\,. \end{aligned}$$

(81)

A Taylor expansion with respect to the capillary blood volume fraction $\eta$ leads to Eq. (30). Both gradient echo relaxation rate $R_2^{*}$ and spin echo relaxation rate $R_2$ are shown in Figs. 8 and 9 for different magnetic field strengths $B_0$, for a blood volume fraction of $\eta = 0.05$, a dipole field strength of $\delta \omega \approx 100 \frac{1}{\text {s} \text {T}} B_0$ in accordance with Eq. (8) and a diffusion coefficient of $D=1\,\upmu \text {m}^2 \text {ms}^{-1}$ in accordance with [41]. A change of the blood volume fraction would linearly scale the ordinates in Figs. 8 and 9, while the abscissas show a dependence on the product $\delta \omega R^2/D$ [105].

Fig. 8

Gradient echo relaxation rate $R_2^{*}$ for different magnetic field strength $B_0$. The static dephasing regime is valid for large vessel radii and the weak field approximation in the opposite limit for small vessel radii. The strong collision approximation (SCA) agrees very well with random walk simulations for arbitrary vessel radii

Fig. 9

Spin echo relaxation rate $R_2$ for different magnetic field strengths $B_0$. The slow diffusion approximation is valid for large vessel radii and its accuracy increases with increasing magnetic field strengths. The weak field approximation is valid in the opposite limit for small vessel radii and small magnetic field strengths. The strong collision approximation (SCA) can only qualitatively describe the shape of the $R_2$ simulation data points

With the Laplace transform of the free induction decay, $\hat{M}_{\text {RVM}}(s)$, the frequency distribution follows as:

$$\begin{aligned} p(\omega ) = \frac{1}{\pi } \mathrm{Re} \left( \hat{M}(\mathrm {i}\omega )\right) \,. \end{aligned}$$

(82)

In Fig. 6, the frequency distribution is shown for different capillary radii; evidently, with increasing capillary radius, the frequency distribution broadens.

So far, the gradient echo signal was analyzed for a fixed angle $\theta$ between the main magnetic field and vessel orientation. An averaging over all possible orientations (index RO) is therefore a natural step to account for the intrinsic inhomogeneities of blood vessel networks. In this limit, Yablonskiy and Haacke obtained an expression for the static dephasing magnetization given in Eq. (33). Using a similar procedure as above, we can obtain the Laplace transform

$$\hat{M}_{0,\text {RO}}(s) = \frac{\mathrm {e}^{- \frac{3s}{2\overline{\delta \omega }}-\frac{\eta }{2}}}{s+\eta \overline{\delta \omega }}+\sqrt{\frac{5\pi }{6\eta }}\frac{ \mathrm{e}^{\frac{5s^2}{6\eta \overline{\delta \omega }^2 }}}{\overline{\delta \omega }}\text {erf}\left(\frac{ s}{\overline{\delta \omega }}\sqrt{\frac{5}{6\eta }},\frac{s}{\overline{\delta \omega}}\sqrt{\frac{5}{6\eta }}+\frac{9}{2}\sqrt{\frac{\eta }{30}}\right)$$

(83)

and, eventually, the SCA relaxation rate $\overline{R_2^{*}}$ as:

$$\begin{aligned} \tau \overline{R_2^*}= \left[ \sqrt{\frac{5\pi }{6\eta }}\frac{\mathrm {e}^{\frac{5}{6 \eta [\tau \overline{\delta \omega }]^2}}}{\tau \overline{\delta \omega }} \text {erf}\left( \frac{1}{\tau \overline{\delta \omega }}\sqrt{\frac{5}{6\eta }},\frac{1}{\tau \overline{\delta \omega }}\sqrt{\frac{5}{6\eta }}+\frac{9}{2}\sqrt{\frac{\eta }{30}}\right) +\frac{\mathrm {e}^{-\frac{3}{2\tau \overline{\delta \omega }}-\frac{\eta }{2}}}{1+\eta \tau \overline{\delta \omega }}\right] ^{-1}-1. \end{aligned}$$

(84)

A Taylor expansion in order of $\eta$ again leads to Eq. (34).