Regional ionospheric correction generation for GNSS PPP-RTK: theoretical analyses and a new interpolation method

Abstract

The regional ionospheric corrections have become one of the critical parts of Precise Point Positioning (PPP)-based Real-Time-Kinematic (RTK) services to achieve fast positioning convergence. Several methods for regional ionospheric corrections supporting PPP-RTK have been developed and implemented over recent years, but little attention is given to the theoretical foundation of existing ionospheric correction methods and their performance comparison to find an optimal method in some sense. The optimality criterion of such methods should not only be based on the precision of the ionospheric correction itself, but also on its broadcasting strategies, and implementation aspects. This contribution studies ionospheric correction generation methods within the best linear unbiased predictor (BLUP) framework. Comparing the accuracy performances of the methods, we demonstrate that the Kriging method with trend, as a special case of BLUP, is the most appropriate method for large-scale networks (above 500 km). A strategy for the evaluation of the uncertainty of the grid-interpolated ionospheric corrections is also developed. In contrast to other empirical methods, this new method is rigorous in the sense that it avoids the underestimation of the uncertainty of predicted ionospheric corrections, especially when reference stations are close to a grid point.

Introduction

Currently, the Global Navigation Satellite System (GNSS) provides location-based services for users globally. While this service can generate huge advantages for various applications, the accuracy achieved by the single point positioning (SPP) technique is still insufficient for many purposes, such as precision agriculture, autonomous driving, geodetic surveying, and more. Compared with the SPP technique whose positioning accuracy is limited by the large noise of the pseudorange data, the technology of using the carrier phase measurements for positioning aiming to achieve higher accuracy has been developed in recent decades. At the same time, in order to achieve higher accuracy, the error in the GNSS observations also needs to be handled more properly. Accordingly, GNSS positioning techniques including the RTK and the PPP methods are proposed for this purpose.

The RTK method aims to remove or mitigate model errors by observation differencing through a base station. As a result, a short inter-station distance between the base station and the user is needed to guarantee the assumption of having almost identical errors between the rover and the base stations. The network-based RTK (NRTK) method interpolates such model errors via continuously operating reference stations (CORS). This method allows one to work with larger distances between the network stations and the user compared to the traditional RTK method. However, a large communication burden is required as the data link between multiple users and the server for data transmission has to be established. Note also that the NRTK performance can still deteriorate, the larger the distance between the user and the involved network stations becomes. Therefore, the RTK and the NRTK methods have considerable restrictions in several marketing applications, such as smartphones and automotive industries.

Another method, PPP, achieves high accuracy positioning by modeling the errors experienced by the single-receiver GNSS measurements. However, compared with the RTK method, which largely eliminates the stated errors by differencing, PPP requires a longer convergence time to achieve high accuracy (Li et al. 2024). As an extended version of PPP, PPP-AR recovers the integer characteristics of the carrier phase by using strategies for estimating uncalibrated phase delay (UPD) (Ge et al. 2008; Li and Zhang 2012), decoupled clock (DCK) model (Collins et al. 2008, 2010), integer recovery clock (IRC) (Laurichesse et al. 2009), and observation-specific bias (OSB) (Banville et al. 2020) so as to obtain single-receiver user ambiguity resolution. While PPP-AR methods can decrease the positioning convergence time, the corresponding reduction in the convergence time is often not considerable to address the needs of the market.

The main reason for PPP-AR’s long convergence time is that the atmospheric delays are difficult to be accurately modelled, hindering successful integer ambiguity resolution of the carrier phase measurements. It is thus necessary to employ rigorous parameter estimation methods to largely mitigate the impact of atmospheric errors. Augmenting the PPP-AR corrections with extra atmospheric corrections leads to the methods of PPP-RTK. The PPP-RTK technology based on the regional network stations is proposed to overcome this issue (Wübbena et al. 2005; Zhang et al. 2011; Teunissen and Khodabandeh 2015). Except for biases to recover integer ambiguities, the PPP-RTK method can generate atmospheric delay corrections, especially ionospheric corrections, to users for improving the model strength and fast or sometimes instantaneous ambiguity fixing (Li et al. 2021; Zhang et al. 2022a; Zhang and Wang 2023).

The process of computing and disseminating PPP-RTK ionospheric corrections to users can be roughly divided into two phases: ionospheric delay estimation and interpolation. For estimating the ionospheric delay at each station, it is proven by existing research (e.g., Ciraolo et al. 2007; Zhang 2016) that the PPP-based method will have an improvement compared to the carrier-to-code leveling (CCL) method (Hernández-Pajares et al. 1999, 2011). To estimate the ionospheric delay more accurately, the PPP ionospheric method based on the ambiguity-fixed solutions can be used and it has been verified that they can achieve millimeter-level (Banville et al. 2014, 2022; Wang et al. 2020a).

In order to interpolate user ionospheric corrections from the network-derived ionospheric solution, methods of NRTK error interpolations are employed in PPP-RTK. Accordingly, the commonly used interpolation methods comprise the Distance-based linear interpolation method (DIM) (Gao et al. 1997), the Linear combination model (LCM) (Han and Rizos 1996; Han 1997), the Lower-order surface model (LSM) (Wübbena et al. 1996; Fotopoulos and Cannon 2001), the Least-squares collocation (LSC) method (Tscherning 1974; Raquet 1997; Marel 1998), and the Kriging interpolation methods (Oliver and Webster 1990). The DIM, LCM, and LSM models are very easy and convenient to use, but they are not suitable for generating stochastic models. The LSC method requires prior knowledge of regional ionospheric characteristics, while Kriging interpolation may involve a relatively large computational burden. These methods are used in PPP-RTK ionospheric delay interpolations (Zha et al. 2021; Zhang et al. 2022b) and recent studies improved these models by using other information such as rate of total electron content index (ROTI) and the elevation of satellites (Li et al. 2023). In the case of small-scale networks, the corresponding performances are similar. Wang et al. (2020b) compared the DIM and LSM methods in some cases of small-scale networks and concluded that the results were relatively similar. Studies on the performance of these methods under larger scale networks do, however, deserve further investigation.

In addition to the ionospheric correction itself, studies have shown that the uncertainty of the ionospheric correction has an important impact on positioning accuracy and integrity monitoring (Du et al. 2021; Li et al. 2022; Psychas et al. 2022; Zhang et al. 2023; Zhang and Wang 2024). Wang et al. (2022a) used simulation results showing that the properly estimated uncertainty can improve the performance of integrity monitoring. Furthermore, Wang et al. (2022b) presented that even using a simplified method for uncertainty estimation, user positioning results can improve compared to a pre-defined fixed uncertainty. Thus, generalized uncertainty estimation and prediction methods should also be studied. In contrast to the usual RTK data link, PPP needs to deliver the correction unidirectionally. The performance of broadcast methods, such as the broadcasting by grid points, are also to be evaluated, quantifying their impacts on the ionospheric corrections. Moreover, the performance of user PPP-RTK positioning via such ionospheric corrections should be properly studied.

In this study, we aim at proposing a new methodology and procedure for regional ionospheric modeling and uncertainty estimation for PPP-RTK from the ionospheric delay interpolation to broadcast to users. First, common methods available for high-precision PPP-RTK ionospheric delay interpolation will be compared by their accuracy to explore the best method for regional ionospheric modeling. Second, the regional characteristics prediction uncertainty and its performance versus the true error are analyzed. Moreover, the impact on accuracy and uncertainty after broadcasting the corrections is also investigated. Building upon the research in Chapter 4 of the first author's PhD thesis (Zhang 2023), we propose a new broadcasting method with the BLUP theory and further analyze this new method in comparison with existing procedures in several case studies. This new method is theoretically rigorous and produces promising results.

Ionospheric delay estimation with PPP-AR

The linearized form of GNSS observations based on approximate values of the unknown parameters can be expressed as:

$$ \begin{array}{*{20}c} {E\left( {P_{r,j}^{s} } \right) = \rho_{0r}^{s} + G_{r}^{s} u_{r} + c\left( {dt_{r,sys} + dt^{s} } \right) + b_{r,j} - b_{j}^{s} + T_{r}^{s} + \mu_{j} I_{r,1}^{s} } \\ \end{array} $$

(1)

$$ \begin{array}{*{20}c} {E\left( {L_{r,j}^{s} } \right) = \rho_{0r}^{s} + G_{r}^{s} u_{r} + c\left( {dt_{r,sys} + cdt^{s} } \right) + \lambda_{j} \left( {N_{r,j}^{s} + B_{r,j} - B_{j}^{s} } \right) + T_{r}^{s} - \mu_{j} I_{r,1}^{s} } \\ \end{array} $$

(2)

where $P$ and $L$ stand for the measurements of pseudorange and carrier observations in meters; E(*) is the notation of mathematical expectation, $G$ is the matrix of unit vectors from the receiver to the satellite and $u$ is the increments from estimated positions to the linearized point; $s$ and $r$ represent the satellite and receiver respectively; $sys$ identifies different constellations; the subscript $j$ denotes the frequency ${\uprho }$ is the distance between respective satellite and receiver pair in meters (m); $c$ and $dt$ are the speed of light in vacuum in meters per second (m/s) and time offsets in seconds (s) respectively;$\lambda$ is the wavelength in meters and $N$ is the integer ambiguity; $b$ and $B$ represent the hardware and phase delay in meters, respectively; $T$ and $I$ represent tropospheric delay and ionospheric delay in meters, respectively; $\mu_{j} = \frac{{f_{1}^{2} }}{{f_{j}^{2} }}$ is the coefficient of ionospheric delay projected from the first frequency. Other errors including relativistic effects, solid tides, antenna offsets and variation, phase wind-up effects, earth rotation, ocean loading and so on are corrected by models, and remaining errors are assumed with zero-mean distributions.

Meanwhile, precise satellite clock and orbit products estimated by the global network could be used at the user end for positioning. Besides, the fractional bias products in the UPDs or IRCs forms have been proven that they can be used to obtain the OSB format bias products (Banville et al. 2020). Considering that bias product estimated by a global network can provide a global consistency of satellite-related parameter. As a result, the biases corrected by the OSB format products provided by Centre National D'Etudes Spatiales (CNES) are used in this study. After such products are corrected, the observations re-parameterized with full rank could be written as:

$$ \begin{array}{*{20}c} {E\left( {\hat{P}_{r,j}^{s} } \right) = G_{r}^{s} u_{r} + d\overline{t}_{r,sys} + \overline{b}_{r,sys,j} + M_{r}^{s} Z_{r} + \mu_{j} \overline{I}_{r,1}^{s} } \\ \end{array} $$

(3)

$$ \begin{array}{*{20}c} {E\left( {\hat{L}_{r,j}^{s} } \right) = G_{r}^{s} u_{r} + d\overline{t}_{r,sys} + \lambda_{j} \overline{N}_{r,j}^{s} + M_{r}^{s} Z_{r} - \mu_{j} \overline{I}_{r,1}^{s} } \\ \end{array} $$

(4)

$$ \left\{ {\begin{array}{*{20}l} {cd\overline{t}_{r,sys} = cdt_{r,sys} + b_{r,sys,IF} } \hfill \\ {\overline{b}_{r,sys,j} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\left( {j \le 2} \right) } \hfill \\ {b_{r,sys,j} - \mu_{j} \frac{{f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}b_{r,sys,GF} - b_{r,sys,IF} } \hfill & {\left( {j > 2} \right)} \hfill \\ \end{array} } \right.} \hfill \\ {\lambda_{j} \overline{N}_{r,j}^{s} = \lambda_{j} N_{r,j}^{s} + \lambda_{j} B_{r,sys,j} + b_{r,sys,IF} + \mu_{j} \frac{{f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}b_{r,sys,GF} } \hfill \\ {\overline{I}_{r,1}^{s} = I_{r,1}^{s} + \frac{{f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}b_{r,sys,GF} } \hfill \\ \end{array} } \right. $$

(5)

with

$$ \begin{array}{*{20}c} {\left( {\begin{array}{*{20}l} {\left( * \right)_{IF} = \alpha_{IF,12} b_{r,1} + \beta_{IF,12} b_{r,2} } \hfill \\ {\left( * \right)_{GF} = \left( * \right)_{2} - \left( * \right)_{1} } \hfill \\ \end{array} } \right.} \\ \end{array} $$

(6)

The slant tropospheric delay is modeled as the product of the mapping function $M_r^s$ and the zenith tropospheric delay $Z_r$. The ionospheric term $\overline{I}_{r,1}^{s}$ can be estimated in the optimal estimator since this is a full rank equation. The estimable ionospheric delay $\overline{I}_{r,1}^{s}$ and the ambiguities $\lambda_{j} \overline{N}_{r,j}^{s}$ in Eq. (5) are biased by the receiver-specified bias term (Odijk et al. 2015). Thus, after correcting the satellite biases, only between-satellite single-differencing ambiguities could be fixed into integers (Liu et al. 2022).

Obviously, the ionospheric delays estimated by the PPP estimator with fixed ambiguities can eliminate receiver bias by single-differenced form, which could be written as:

$$ \begin{array}{*{20}c} {\overline{I}_{r,1}^{pq} = I_{r,1}^{pq} } \\ \end{array} $$

(7)

with $\left( * \right)^{pq} = \left( * \right)^{p} - \left( * \right)^{q}$. Thus, these single-differenced ionospheric delays could be used for interpolation. Notably, the user can use any one satellite as reference satellite in processing.

Generalized and customary models for regional ionospheric modeling

Regional ionospheric modeling can be based on the slant total electron content (STEC) or vertical total electron content (VTEC). As the ionospheric delays need to be mapped onto the zenith direction as VTEC, the accuracy may be considerably decreased. VTEC models would have a limited accuracy that can reach 1 TECU (0.16m in L1) even when ionosphere is calm (Psychas et al. 2018). We thus only discuss methods for directly interpolating ionospheric delays in the slant direction.

The regional ionospheric modeling can be implemented on the basis of either single-differenced ionospheric delays of each satellite pair or undifferenced ionospheric delays of all the involved satellites and receivers with adding parameters of receiver biases (Banville et al. 2022). Since the methods of DIM, LCM, and LSM are often based on the single-differenced ionospheric delays of each satellite pair, the present study develops a model based on the single-differenced ionospheric delays of each satellite pair. The formulation of the modeling method will not be changed with different forms. In the following, we provide an overview of the ionospheric correction generation methods within the best linear unbiased predictor (BLUP) framework (Teunissen 2007).

Let $i_{j}$ denotes the ionospheric delay estimated at the $jth$ station, where $j = 0$ corresponds to the user location. The primary objective of regional ionospheric modeling is to derive the ionospheric delay $i_{0}$ by utilizing $i_{1} , \ldots ,i_{n}$ estimated by $n$ stations within the network. Hence, the generalized unbiased linear model, as formulated by Odijk (2002), is expressed as:

$$ \begin{array}{*{20}c} {\widehat{{i_{0} }} = WI } \\ \end{array} $$

(8)

with:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {W = \left[ {\begin{array}{*{20}c} {w_{1} } & \ldots & {w_{n} } \\ \end{array} } \right]} \\ {I = \left[ {\begin{array}{*{20}c} {i_{1} } \\ \vdots \\ {i_{n} } \\ \end{array} } \right]} \\ {\mathop \sum \limits_{i}^{n} w_{i} = 1} \\ \end{array} } \right.} \\ \end{array} $$

(9)

Upon acquiring the weight matrix $W$, calculating the ionospheric delay $i_{0}$ becomes straightforward. The weight matrix can be obtained by employing the best linear unbiased estimator (BLUE) and best linear unbiased predictor (BLUP), techniques aimed at minimizing prediction variance (Tscherning 1974; Raquet 1997; Marel 1998).

The linear system of equations for ionospheric delays could be written as:

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} I \\ {i_{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} A \\ {A_{0} } \\ \end{array} } \right]x + \left[ {\begin{array}{*{20}c} {\varepsilon_{I} } \\ {\varepsilon_{{i_{0} }} } \\ \end{array} } \right] } \\ \end{array} $$

(10)

where $A$ and $A_{0}$ are design matrices, and $x$ is the vector for deterministic parameters. $\varepsilon$ is the zero-mean random vector with:

$$ \begin{array}{*{20}c} {D\left( {\left[ {\begin{array}{*{20}c} {\varepsilon_{I} } \\ {\varepsilon_{{i_{0} }} } \\ \end{array} } \right]} \right) = D\left( {\left[ {\begin{array}{*{20}c} I \\ {i_{0} } \\ \end{array} } \right]} \right) = \left[ {\begin{array}{*{20}c} {Q_{II} } & {Q_{{Ii_{0} }} } \\ {Q_{{i_{0} I}} } & {Q_{{i_{0} i_{0} }} } \\ \end{array} } \right] } \\ \end{array} $$

(11)

Here, $D\left( * \right)$ represents the dispersion operator, and $Q$ is the variance–covariance (VC) matrix. According to the BLUP theory, in order to minimize both prediction and estimation variance, the expression for the vector of deterministic parameters and the estimated ionospheric delay can be formulated as (Teunissen 2007):

$$ \left\{ {\begin{array}{*{20}l} {\hat{x} = \left( {A^{T} Q_{II}^{ - 1} A} \right)^{ - 1} A^{T} Q_{II}^{ - 1} I} \hfill \\ {\widehat{{i_{0} }} = A_{0} \hat{x} + Q_{{i_{0} I}} Q_{II}^{ - 1} \left( {I - A\hat{x}} \right) = WI} \hfill \\ {W = \left( {\left( {\left( {A_{0} - Q_{{i_{0} I}} Q_{II}^{ - 1} A} \right)\left( {A^{T} Q_{II}^{ - 1} A} \right)^{ - 1} A^{T} + Q_{{i_{0} I}} } \right)Q_{II}^{ - 1} } \right)} \hfill \\ \end{array} } \right. $$

(12)

With the exception of the estimated ionospheric delay, the variance of the estimated errors can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {Q_{{\hat{x}\hat{x}}} = \left( {A^{T} Q_{II}^{ - 1} A} \right)^{ - 1} } \hfill \\ {Q_{{\widehat{{l_{0} }}\widehat{{l_{0} }}}} = Q_{{i_{0} i_{0} }} - Q_{{i_{0} I}} Q_{II}^{ - 1} Q_{{Ii_{0} }} + \left( {A_{0} - Q_{{i_{0} I}} Q_{II}^{ - 1} A} \right)Q_{{\hat{x}\hat{x}}} \left( {A_{0} - Q_{{i_{0} I}} Q_{II}^{ - 1} A} \right)^{T} } \hfill \\ \end{array} } \right. $$

(13)

Moreover, it is evident that $Q_{II}$ can be subdivided into two components, encompassing the computation of uncertainty and spatial properties:

$$ \begin{array}{*{20}c} {Q_{II} = Q_{{\hat{I}}} + Q_{d} } \\ \end{array} $$

(14)

In this context, where $Q_{{\hat{l}}}$ is VC matrix for the estimated ionospheric delays and $Q_{d}$ is the VC matrix for the ionospheric characteristics associated with the location. $Q_{{\hat{l}}}$ can be determined during the process of PPP-AR estimation and given that the accuracy of single-differenced estimated ionospheric delay with ambiguity-fixed results can achieve millimeter-level precision (Wang et al. 2020a), it is thereby negligible in this study. Consequently, $Q_{II}$ in this study primarily addresses the spatial correlations of regional ionospheric delays.

The DIM method

The DIM method, also known as the inverse distance weighting (IDW) method, involves assigning weights directly based on the distance between the target position and reference stations (Gao et al. 1997). As a result, the conventional formulation of the weight within the DIM method can be expressed as:

$$ \begin{array}{*{20}c} {w_{i} = \frac{{\frac{1}{{d_{i,0}^{\alpha } }}}}{{\mathop \sum \nolimits_{i}^{n} \frac{1}{{d_{i,0}^{\alpha } }}}} } \\ \end{array} $$

(15)

where $d_{i,j}$ represents the distance between the $ith$ and $jth$ stations, and $\alpha$ denotes the order of the DIM model, typically set to $1$ or $2$.

The LSM method and the LCM method

The LSM model employs a lower-order surface mapping function to accommodate the ionospheric delay in each region (Wübbena et al. 1996; Fotopoulos and Cannon 2001). For the function characterized by $m$ coefficient $a_{1} , \ldots ,a_{m}$, the surface function $f_{s}$ can be formulated as:

$$ \begin{array}{*{20}c} {f_{s,i} = a_{1} \beta_{1,i} + a_{2} \beta_{2,i} + \cdots + a_{m} \beta_{m,i} } \\ \end{array} $$

(16)

where $b_{1} , \ldots ,b_{m}$ represent the terms estimated by the coordinates of station $i$. In the scenario where $f_{s,i} = a_{1} + a_{2} X_{i} + a_{3} Y_{i} + a_{4} X_{i} Y_{i}$ with $X_{i}$ and $Y_{i}$ denoting the coordinates in the horizontal direction, the coefficients are expressed as $\beta_{1,i} = 1$, $\beta_{2,i} = X_{i}$, $\beta_{3,i} = Y_{i}$ and $\beta_{4,i} = X_{i} Y_{i}$. In the conventional LSM model, the weight matrix for each station in the LSM model can be articulated as:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {W = H_{0} \left( {H^{T} H} \right)^{ - 1} H^{T} } \\ {H = \left[ {\begin{array}{*{20}c} {H_{1} } \\ \vdots \\ {H_{n} } \\ \end{array} } \right]} \\ {H_{i} = \left[ {\begin{array}{*{20}c} {\beta_{1,i} } & \ldots & {\beta_{m,i} } \\ \end{array} } \right]} \\ \end{array} } \right.} \\ \end{array} $$

(17)

The LCM method is a specific type of the LSM model that incorporates a lower-order surface function characterized by:

$$ \begin{array}{*{20}c} {f_{s,i} = a_{1} + a_{2} X_{i} + a_{3} Y_{i} } \\ \end{array} $$

(18)

For a demonstration of the equivalence between the LSM model and the LCM model, one can refer to Wang et al. (2020b).

The LSC method

Equation (12) is regarded as the initial form of the LSC method. In the LSC method for regional ionospheric delay modeling, it is crucial to appropriately define the VC matrix to capture the spatial characteristics. This matrix can be expressed as:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {D\left( I \right) = Q_{II} = \left[ {\begin{array}{*{20}c} {\sigma_{0}^{2} } & \cdots & {q_{n,1} } \\ \vdots & \ddots & \vdots \\ {q_{1,n} } & \cdots & {\sigma_{0}^{2} } \\ \end{array} } \right]} \\ {Q_{{i_{0} I}} = \left[ {\begin{array}{*{20}c} {q_{0,n} } & \cdots & {q_{n,0} } \\ \end{array} } \right]} \\ \end{array} } \right.} \\ \end{array} $$

(19)

where $q_{i,j}$ denotes the element for the VC matrix for the $\left( {i,j} \right)th$ station pairs and $q_{i,j} = \sigma_{0}^{2}$ when $i = j$; The prior variance factor $\sigma_{0}^{2}$ in this context represents the variance of the ionospheric delay based on the mapping function.

The Kriging interpolation method

Various Kriging methods come with distinct assumptions. The simple Kriging method posits that the variable of interest in the region has a zero mean, except for a known constant. In contrast, ordinary Kriging assumes that the variable of interest has an unknown mean value. Finally, the universal Kriging method assumes the inclusion of a trend function in the variable of interest.

Using the ordinary Kriging method as an example, the initial expression of the Kriging method for estimating the weight matrix can be formulated as:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} W \\ {\mathcal{L}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\gamma_{11} } & \ldots & {\gamma_{1n} } & 1 \\ \vdots & \ddots & \vdots & \vdots \\ {\gamma_{n1} } & \ldots & {\gamma_{nn} } & 1 \\ 1 & \ldots & 1 & 0 \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {\gamma_{10} } \\ \vdots \\ {\gamma_{n0} } \\ 1 \\ \end{array} } \right]} \\ {\gamma_{ij = } \Upsilon \left( {d_{i,j} } \right)} \\ \end{array} } \right.} \\ \end{array} $$

(20)

where $\gamma_{ij}$ represents the semi-variance and ${\Upsilon }$ is the semi-variogram function employed to model the semi-variance based on the inter-station distances; ${\mathcal{L}}$ stands for the Lagrange multiplier.

Methods under the BLUP model

In summary, each specific instance of the BLUP can be completely defined by three essential components:

(1) the full design matrix $\left[ {\begin{array}{*{20}c} A \\ {A_{0} } \\ \end{array} } \right]$; (2) the nonnegative elements $q_{i,j} \left( {i,j = 1, \ldots ,n,0} \right)$ constituting the $\left( {n + 1} \right) \times \left( {n + 1} \right)$ full variance–covariance matrix $\left[ {\begin{array}{*{20}c} {Q_{II} } & {Q_{{Ii_{0} }} } \\ {Q_{{i_{0} I}} } & {Q_{{i_{0} i_{0} }} } \\ \end{array} } \right]$. Table 1 provides a synopsis of various models within the BLUP framework. In this table, $e_{k}$ is the (1 × $k$) matrix $\left[ {1, \ldots , 1} \right]_{k}$; $g_{lsc} \left( {d_{i,j} } \right)$ is the function defining the spatial correlation in the LSC method; $F_{sv}$ is the applied function for the semi-variogram, where various functions can be employed for the semi-variogram function. In the Kriging method, $S_{0}$ is referred to as sill, representing the defined maximum value of the semi-variogram function; $R_{0}$ is termed range; $C_{0} = {\Upsilon }\left( 0 \right)$ is known as nugget with $C_{0}$ often considered as $C_{0} = 0$.

Table 1 Concise summary of different models within the BLUP framework

Broadcasting methods for interpolation models

Due to the notable advantage of PPP-RTK in minimizing data transmission load compared to NRTK, direct broadcasting of corrections to users based on their locations is not appropriate. Additionally, in the open message format for satellite-based GNSS correction services, such as those defined by 3GPP and SPARTN, only interpolated corrections (functional or grid) are accommodated (Hirokawa et al. 2021). Consequently, there is still a need to interpolate ionospheric delays at users' end based on their respective locations.

Among the regional ionospheric interpolation methods discussed earlier, only the LSM method has the capability to directly broadcast the interpolated coefficients to users. Users can utilize these coefficients along with roughly estimated positions to derive ionospheric corrections. In contrast, other methods necessitate knowledge of the user's location during the interpolation process.

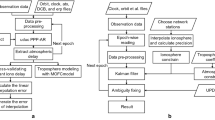
To address this challenge, the grid-point method is employed for regional broadcasting. In this approach, ionospheric delays of each satellite are initially estimated individually at predefined grid points. Subsequently, users can interpolate the ionospheric delays based on the nearest grid point to their approximate location. The procedural steps, from generating regional ionospheric corrections to implementing these corrections in PPP-RTK processing, are illustrated in the flowchart presented in Fig. 1.

Fig. 1

The procedure from generating corrections to user implementation

It is evident from the procedure that users are required to perform regional modeling, also known as interpolation, to acquire the ionospheric correction specific to their locations. Unlike directly employing results from stations for interpolation, this method helps alleviate the impact of irregular station distribution and offers greater convenience in organizing data structures.

Existing methods for user interpolation

In previous research, where grid points are systematically arranged, a commonly employed method is bilinear interpolation (Takasu 2013; Banville et al. 2022), which can be expressed as:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}l} {i_{user} = \left( {1 - p} \right)\left( {1 - q} \right)i_{A} + p\left( {1 - q} \right)i_{B} + pqi_{C} + \left( {1 - p} \right)qi_{D} } \hfill \\ {p = \frac{{\left| {X_{user} - X_{A} } \right|}}{{\left| {X_{B} - X_{A} } \right|}}} \hfill \\ {q = \frac{{\left| {Y_{user} - Y_{A} } \right|}}{{\left| {Y_{D} - Y_{A} } \right|}}} \hfill \\ \end{array} } \right.} \\ \end{array} $$

(21)

where $A, B, C, D$ denote the four vertices of the square grid, starting from the northwest in a clockwise direction.; It is important to note that while this method serves as a practical solution for engineering applications, the formula in this section is not a rigorously derived mathematical expression.

In addition to accounting for ionospheric delay, it is essential to re-evaluate the uncertainty associated with the interpolated ionospheric delay during the user interpolation process. Banville et al. (2022) suggest utilizing a weighted average standard deviation (STD) to estimate the STD post-interpolation by grid points. Similarly, the weighted average variance method presents an alternative for uncertainty interpolation. Sparks et al. (2011) employ the maximization of STD from all utilized measurements, excluding the weighted average method, to compute the interpolated uncertainty. These methods, commonly employed for estimating uncertainty by grid points, are notably not deviated from both BLUE and BLUP theories, constituting empirically-based approximation methods lacking rigor. Consequently, the procedure for user interpolation based on BLUP theory will be discussed.

The BLUP method for user interpolation

Considering that four grid points are used for user interpolation, the matrices related to the interpolated location $A_{0}$, $Q_{{i_{0} I}}$, and $Q_{{i_{0} i_{0} }}$, which has a size of $\left( {1 \times m} \right)$, $\left( {1 \times n} \right)$, and $\left( {1 \times 1} \right)$, respectively in Eqs. (12–13) could be written with a size of $\left( {4 \times m} \right)$, $\left( {4 \times n} \right)$, and $\left( {4 \times 4} \right)$, respectively, which yields:

$$ \left\{ {\begin{array}{*{20}l} {A_{0} = \left[ {\begin{array}{*{20}l} {A_{0gridA} } \hfill \\ {A_{0gridB} } \hfill \\ {A_{0gridC} } \hfill \\ {A_{0gridD} } \hfill \\ \end{array} } \right]} \hfill \\ {Q_{{i_{0} I}} = \left[ {\begin{array}{*{20}l} {Q_{{i_{0} IgridA}} } \hfill \\ {Q_{{i_{0} IgridB}} } \hfill \\ {Q_{{i_{0} IgridC}} } \hfill \\ {Q_{{i_{0} IgridD}} } \hfill \\ \end{array} } \right]} \hfill \\ {Q_{{i_{0} i_{0} }} = \left[ {\begin{array}{*{20}l} {Q_{{i_{0} gridAi_{0} gridA}} } \hfill & {Q_{{i_{0} gridAi_{0} gridB}} } \hfill & {Q_{{i_{0} gridAi_{0} gridC}} } \hfill & {Q_{{i_{0} gridAi_{0} gridD}} } \hfill \\ {Q_{{i_{0} gridBi_{0} gridA}} } \hfill & {Q_{{i_{0} gridBi_{0} gridB}} } \hfill & {Q_{{i_{0} gridBi_{0} gridC}} } \hfill & {Q_{{i_{0} griBi_{0} gridD}} } \hfill \\ {Q_{{i_{0} gridCi_{0} gridA}} } \hfill & {Q_{{i_{0} gridCi_{0} gridB}} } \hfill & {Q_{{i_{0} gridCi_{0} gridC}} } \hfill & {Q_{{i_{0} gridCi_{0} gridD}} } \hfill \\ {Q_{{i_{0} gridDi_{0} gridA}} } \hfill & {Q_{{i_{0} gridDi_{0} gridB}} } \hfill & {Q_{{i_{0} gridDi_{0} gridC}} } \hfill & {Q_{{i_{0} gridDi_{0} gridD}} } \hfill \\ \end{array} } \right]} \hfill \\ \end{array} } \right. $$

(22)

where $\left( * \right)_{gridA}$, $\left( * \right)_{gridB}$, $\left( * \right)_{gridC}$, $\left( * \right)_{gridD}$ represent the notation of the four grid points, respectively. Subsequently, the ionospheric corrections at four grid points and their VC matrix could be estimated based on Eq. (12–13). Since the VC matrix of grid points are symmetric matrix, only 6 more parameters need to be broadcast inside these grid points.

At the user end, after receiving such information broadcast by the network, the ionospheric corrections could also be interpolated based on the BLUP theory as Eqs. (12–13). Notably, $Q_{II}$ in Eq. (14) only considered the effect of spatial properties because the accuracy of ionospheric delays extracted by PPP ambiguity-fixed solutions is considered significantly smaller than the effect of spatial properties. But differently, the interpolated ionospheric corrections at grid points are not ignorable; therefore, it could be written as:

$$ \begin{array}{*{20}c} {Q_{II} = Q_{{\hat{I}grid}} + Q_{d} } \\ \end{array} $$

(23)

where $Q_{{\hat{I}grid}}$ is the VC matrix of estimated ionospheric corrections of grid points.

Numerical results

Due to the unique temporal and geographical characteristics of the ionosphere, employing the same processing method may yield different results for various datasets. This study utilizes three distinct datasets, each situated in different locations, to demonstrate methods for processing ionospheric corrections in PPP-RTK. Dataset A utilizes a GNSS network situated in Europe, as depicted in Fig. 2. Dataset B encompasses GNSS stations located in Southern Australia, as illustrated in Fig. 3. Dataset C involves GNSS stations from the US, as shown in Fig. 4. For each station, eleven days of GNSS observations are selected. Dataset A spans from March 13rd to March 23rd, 2021, dataset B covers January 1st to January 11st, 2022, and dataset C encompasses observations from February 19th to March 1st, 2022. Considering that data is collected at 30-s intervals, the actual volume of data tested is already quite substantial, which should be sufficient to reflect certain trends.

Fig. 2

The experiment's station locations for Network A, with the rover indicated by the red point and network stations represented by blue points

Fig. 3

The experiment's station locations for Network B, with the rover indicated by the red point and network stations represented by blue points

Fig. 4

The experiment's station locations for Network C, with the rover indicated by the red point and network stations represented by blue points

Given that numerous stations in the datasets are unable to track dual-frequency Beidou signals and ionospheric delays of GLONASS are biased by inter-frequency biases, the experiments will exclusively utilize GPS and Galileo observations. The processing strategies on the network side are outlined in Table 2. As emphasized earlier, due to the potential for significant errors in float solutions of estimated ionospheric delays, this study opts to utilize only ambiguity-fixed ionospheric delays for interpolation. A relatively high elevation mask is used in the study to reduce the potential effect caused by ionospheric delays extracted from a very low elevation angle with large outliers. To mitigate the impact of exceptionally large errors stemming from results obtained by a limited number of stations located far from the user, satellites with ionospheric delays estimated by fewer than three stations will be excluded from the analysis.

Table 2 Processing strategies on the network side

Comparison between different methods for interpolation

Different models are compared numerically to assess their performances in this section. Details of some key parameters of different models used in the numerical analysis are as follows:

LSM1 LSM method with the surface function of $a_{0} + a_{1} X_{i} + a_{2} Y_{i}$.

LSM2 LSM method with the surface function of $a_{0} + a_{1} X_{i} , + a_{2} Y_{i} + a_{3} X_{i} Y_{i}$

DIM1 distance-related weight is based on $p_{i} = \frac{1}{{d_{i0} }}$.

DIM2 distance-related weight is based on $p_{i} = \frac{1}{{d_{i0}^{2} }}$.

LSC coefficient of the VC matrix is determined by $q_{ij} = \sigma_{0}^{2} {\text{exp}}\left( { - \left( {\frac{{d_{ij} }}{{d_{0} }}} \right)^{2} } \right)$ and $d_{0} = 200km$ (Wang et al. 2022a).

Kriging1 Ordinary Kriging method with a semi-variogram model using the spherical function to fit the semi-variance.

Kriging2 Universal Kriging method with a trend model $a_{0} + a_{1} X_{i} + a_{2} Y_{i}$ and the semi-variogram model using the spherical function to fit the semi-variance.

We evaluate the performance of different models using the estimated ionospheric delay from all stations in the network, as well as from only the four closest stations that can surround the user, representing a small-scale network. As the quality control process may vary for different models, it is important to note that the quality control process is not applied in this analysis to eliminate potential faults in the ionospheric delay extraction. The comparative results for the three networks are presented in Table 3.

Table 3 Root Mean Squared Errors (RMSE) of different interpolation methods (unit: cm)

Based on the results, we could draw such conclusions:

• In a small-scale network, all methods exhibit relatively similar performance.

• The LSM method's performance significantly deteriorates as the network size increases. This is attributed to the low-order surface's inability to adequately capture the ionospheric characteristics when the network scale becomes too large.

• The DIM method with first order is negatively impacted by stations at longer distances.

• The DIM method with a second order demonstrates an ability to mitigate the effects caused by stations distant from the interpolation point.

• The Kriging and LSC methods outperform other methods in large-scale networks, as they account for spatial correlation in the model.

• The Kriging method typically exhibits the best performance, benefiting from proper modeling of spatial correlation through the semi-variogram function. Similar outcomes are also presented in Lyu et al. (2023).

• After incorporating the trend model, the Kriging model exhibits comparable or, in some cases, even worse performance (especially evident when the user position is near the edge of the network) compared to the original Kriging method. This phenomenon may be attributed to the location at the network's periphery and the impact of faults originating from stations situated at long distances.

Uncertainty estimated by different models

In accordance with the BLUE and BLUP theories, all methods have the capacity to estimate the STD of predicted ionospheric delays based on their underlying assumptions. In the DIM, LSM, LSC methods, the stochastic model is pre-defined, resulting in a fixed trend within the network; however, from Eqs. (13, 16, 19), reveal the presence of a prior factor $\sigma_{0}^{2}$ in these methods. While this factor does not impact the estimation of ionospheric delays, it does influence the predicted STD.

Given the variability in the ionospheric characteristics across different locations, elevation angles, ionospheric activity intensities, etc., the prior factor is expected to change. This necessitates a comprehensive modeling approach using extensive historical data. However, in this study, we opted for a simplified model for the prior factor. It is determined by the root mean square error (RMSE) estimated by the user station, allowing us to discern the trends associated with different models.

To illustrate the characteristics of different methods, a region measuring $700\;{\text{km}} \times 500\;{\text{km}}$ within Network B is examined. The colormaps in Figs. 5 and 6 depict the uncertainty of the DIM1 and DIM2 methods, respectively, with asterisks indicating station locations. Notably, the uncertainty is minimal when in proximity to network stations (indicated by cold spots). Additionally, the cold spot cycle size in the DIM2 model is relatively larger than in the DIM1 model. This discrepancy arises from the user's location having a much smaller RMSE estimated by the DIM2 model compared to the DIM1 model. Consequently, the uncertainty of the higher degree DIM model is less influenced by observations located far away from the user's position.

Fig. 5

The estimated uncertainty in network B using the DIM1 model

Fig. 6

The estimated uncertainty in network B using the DIM2 model

The uncertainty colormaps of the LSM1 and LSM2 methods are depicted in Figs. 7 and 8, respectively. In contrast to the DIM model, there are no distinct variations in uncertainty in close proximity to the reference stations. The uncertainty across the entire area generally remains consistent, except for gradient variations from the central region of the network to the network's periphery. Notably, the gradient of the LSM model employing a higher degree function (LSM2 model) is observed larger than that of the LSM model using a lower degree function (LSM1 model).

Fig. 7

The estimated uncertainty in network B using the LSM1 model

Fig. 8

The estimated uncertainty in network B using the LSM2 model

The uncertainty of the LSC model is comparatively illustrated in Fig. 9 in relation to the DIM and LSM models. The primary trend observed is that the closer a point is to a reference station, and the greater the number of reference stations nearby, the smaller the uncertainty becomes.

Fig. 9

The estimated uncertainty in network B using the LSC model

In contrast, the stochastic models of Kriging methods exhibit variability with the fitting functions at different epochs. Consequently, the trend of these methods is not consistently uniform. In Kriging methods, the absolute value of uncertainty can be directly determined without the need for further understanding. To assess the performance of predicted uncertainty versus predicted errors, the Cumulative Distribution Function (CDF) of predicted errors divided by the STD of predicted uncertainty is analyzed. This analysis is presented in Fig. 10 for the Kriging1 method and Fig. 11 for the Kriging2 method.

Fig. 10

The CDF of prediction errors divided by the estimated STD versus the standard normal distribution (SND) with the Kriging1 model

Fig. 11

The CDF of prediction errors divided by the estimated STD versus the SND with the Kriging2 model

The observed CDF curves of the Kriging2 model closely align with the standard normal distribution function, in stark contrast to the Kriging1 model. This alignment suggests that the predicted uncertainty of the Kriging2 model is more reasonable. The discrepancy arises from the semi-variogram model assumed in the Kriging method, which should plateau after a certain distance. However, in the Kriging1 model, this trend may not be very pronounced in certain cases. Consequently, there is a tendency to overestimate the sill and range in the semi-variogram model, leading to an overestimation of uncertainty.

Effects of broadcasting by grid

To assess the impact of grid point interpolation at the user end, the grid points and the user location are presented in Fig. 12. In this section, results are simulated based on the same processing flow as real-time processing. As previously mentioned, the Kriging2 model demonstrates commendable performance in both accuracy and uncertainty prediction. Consequently, the results presented in this section are based on the Kriging2 model.

Fig. 12

The locations of the user and grid points generated by the network with varying intervals

First, the effect of the grid interval is analyzed. The difference between using different intervals of gird points and direct estimation at user location is present in Fig. 13. It can be noticed that even if the grid point interval increases to 100 km, the RMSE for the worse case only improves by less than 15% compared to the RMSE for direction estimation at the user end. This showed that the grid point method can still preserve a high accuracy of ionospheric delay prediction in PPP-RTK.

Fig. 13

RMSE absolute variation compared to the direct estimation at users’ location

The impact of grid interval variation is analyzed, and the differences between using different grid point intervals and direct estimation at the user location are depicted in Fig. 13. Notably, even when the grid point interval increases to 100 km, the RMSE for the worst case only improves by less than 15% compared to the RMSE for direct estimation at the user end. This indicates that the grid point method can maintain a high accuracy in ionospheric delay prediction for PPP-RTK.

In addition to analyzing the accuracy of ionospheric delay, the uncertainty accuracy of using grid points is also examined. For instance, considering the 100 km interval grid point, the impact of interpolated uncertainty via grid points versus direct estimation is examined. The CDF of prediction errors divided by the predicted uncertainty before and after using grid point interpolations is compared. Figures 14 and 15 depict the results using the weighted average standard deviation (STD) and weighted average variance methods, respectively. Notably, both methods demonstrate a tendency to underestimate the uncertainty in comparison to direct estimation. Moreover, the weighted average variance method exhibits slightly closer alignment to the direct estimation compared to the weighted average STD method.

Fig. 14

The CDF of prediction errors divided by the estimated STD for direct estimation at user station and estimation by grid point using a weighted average for STD

Fig. 15

The CDF of prediction errors divided by the estimated STD for direct estimation at user station and estimation by grid point using a weighted average for variance

Conversely, the CDF of prediction errors divided by the predicted uncertainty using maximization methods reveals a trend of overestimating uncertainty, as illustrated in Fig. 16. An obvious overestimation of predicted uncertainty is observed in this method.

Fig. 16

The CDF of prediction errors divided by the estimated STD for direct estimation at user station and estimation by grid point using maximal STD of grid points

In the method under the BLUP framework, the semi-variogram function can still be modeled using the spherical function, as demonstrated in previous studies. Users can estimate it with the aid of broadcasted range and sill parameters. On the contrary, when employing a bounded linear function, only a gradience factor needs to be broadcasted. Figure 17 illustrates that the performance of this method closely resembles the original distribution.

Fig. 17

The CDF of prediction errors divided by the estimated STD for direct estimation at user station and estimation by grid point using the BLUP method

Among the four methods considered, only the maximization method exhibits a significant variation compared to the original results in the graphs. Both the weighted average method and the BLUP method seem to offer reliable solutions for uncertainty prediction. However, when grid points are positioned near reference stations—specifically in Network B, where grid point distances to the nearest reference stations are 3 km, 6 km, 24 km, and 70 km, respectively—the results of all methods are depicted in Fig. 18. It is apparent that the weighted-average method struggles to handle this scenario. Moreover, in extreme cases where all grid points are exceptionally close to the reference stations, the maximization method tends to notably underestimate uncertainty.

Fig. 18

The CDF of prediction errors divided by the estimated STD for different methods when the grid points are close to the reference stations

The disparity in root mean squared standardized errors (errors divided by STDs) between direct estimation and broadcasting by grid points serves as a measure of the consistency between the two methods. This difference is employed as a criterion to assess the performance of broadcasting methods, as presented in Table 4. Notably, the results for Network A, B, and C indicate a certain degree of comparability across different methods. However, when grid points are situated close to reference stations, the difference observed with the BLUP method is notably smaller compared to other methods. Consequently, the BLUP method is recommended for uncertainty prediction after interpolation by grid points.

Table 4 Difference of root mean squared standardized errors of different methods

Conclusion

Regional high-accuracy ionospheric correction holds a crucial role in PPP-RTK, playing a pivotal role in accelerating ambiguity fixing and reducing convergence time compared to PPP-AR and traditional PPP float solutions. This study delves into the analysis of the regional ionospheric correction generation procedure for PPP-RTK. The approach involves estimating ionospheric delays at each station within the network, with the primary objective of identifying the most effective method and procedure to generate high-accuracy regional ionospheric correction, complete with appropriately predicted uncertainty, and broadcasting it to users under the BLUP framework.

Our numerical case study results have revealed some interesting findings. In small-scale networks, interpolation methods displayed comparable accuracy, while in larger networks, the Kriging methods notably outperformed others. Uncertainty prediction analyses indicated that DIM, LSC, and Kriging methods tended to exhibit smaller uncertainties near reference stations and larger uncertainties farther away. In contrast, LSM methods showcased increasing uncertainties moving outward from the network's center. Except for Kriging methods, other techniques relied on empirical values to define stochastic models for uncertainty determination. Among Kriging interpolation methods, those integrating trend functions demonstrated the most consistent predicted uncertainties with actual values. Regarding broadcasting procedures, only LSM methods could broadcast coefficients to users; other methods required grid point methods for broadcasting. Analysis of grid point methods revealed that even with a 100 km grid point interval, the RMSE increase remained under 15%. Additionally, in uncertainty estimation, the proposed method based on the BLUP theory was deemed the superior method compared to weighted average and maximization methods, especially when grid points were near well-observed reference stations.