Introduction

The development of the Global Navigation Satellite System (GNSS, Montenbruck et al. 2017, 2018) and the availability of station-based data through the International GNSS Service (IGS, Johnston et al. 2017) and orbital products through the Crustal Dynamics Data Information System (CDDIS, Noll 2010) have facilitated accurate results for Precise Point Positioning (PPP, Kouba et al. 2017). Further improvement of PPP solutions can be obtained by modeling the receiver clock parameter provided that the GNSS receiver is connected to an ultra-stable atomic clock. In multi-GNSS solutions, one common clock parameter can be derived for all systems with additional parameters accounting for hardware delays. The receiver hardware delays vary with the selected constellations and are known as inter-system biases (ISBs). ISBs can be estimated as the differences between the common clock in the specified system and the clocks of the other systems (Hong et al. 2019; Mi et al. 2019). Typically, a common clock is determined from the GPS and ISBs are estimated for the other systems (G + ISB, Mikoś et al. 2023a).

To stabilize the PPP solutions, proper stochastic modeling must be applied to the common clock parameter (Weinbach and Schön 2011; Ge et al. 2023) and ISBs (Li et al. 2023). In this paper, we propose the stochastic clock model in the form of a random walk (RW) constraint imposed on the common clock parameter and ISBs. In the proposed model, the clock parameter varies in a limited range between neighboring observation epochs, while the clock stability is guaranteed by a stable receiver atomic clock. For the first epoch, white noise is assumed for both the common clock and ISB. The results are compared to solutions with no clock constraints denoted as reference values (RV). RV is a strategy based on white noise for the common clock parameter and ISB.

Clocks used at IGS stations have different characteristics and noise levels. For internal crystal oscillator (XO) clocks, stochastic modeling may not provide significant improvement due to higher noise in observations. However, for atomic clocks such as rubidium (Rb), cesium (Cs), and especially for hydrogen maser (HM), the effect of stochastic modeling can lead to some improvements (Wang and Rothacher 2013; Krawinkel and Schön 2016, 2021). HM clocks exhibit better short- and long-term stability than other types of clocks (Mikoś et al. 2023b). Malys et al. (1992) proposed stochastic receiver and satellite clock modeling in the so-called NEPTUNE algorithm. The statistical properties for the clock parameter were adjusted according to the frequency standards used, including XO, Rb, Cs, and HM in the sequential least-squares PPP. The NEPTUNE algorithm provided results with precision better by about 50% than the GASP algorithm which employed differenced phase observations (Malys et al. 1992). However, NEPTUNE was very sensitive to receiver clock fluctuations, and thus, partitioning of the data was indispensable for some receivers with unstable clocks, as opposed to GASP.

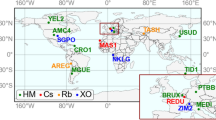
The goal of this paper is to derive optimum constraints for the receiver clock stochastic process for GNSS stations equipped with different types of clocks in Galileo-only and multi-GNSS kinematic and static PPP solutions. We consider selected IGS stations for multi-GNSS static and kinematic PPP based on GPS (G), GLONASS (R), Galileo (E), and BeiDou-3 (C). We utilize four types of clocks at GNSS stations: XO, Rb, Cs, and HM. The selected stations are part of the Multi-GNSS Experiment (MGEX) pilot project (Montenbruck et al. 2017), which allows for the tracking of all global GNSS systems for system-specific clock error analysis. We show results for a solution using only observations of Galileo-only with one receiver clock parameter, and then, for the multi-GNSS solutions with ISBs. The Galileo constellation is equipped with the most homogeneous clocks of similar type and performance as opposed to other GNSS. Consequently, we conducted analyses focusing on a single system and multi-GNSS solutions with different clock and ISB constraining.

Methodology

We process multi-GNSS dual-frequency pseudorange (code) \(P\) and carrier phase \(L\) observations using the undifferenced uncombined model (Schönemann 2014) of the PPP technique:

$$P_{i}^{s} - \rho_{0}^{{\text{s}}} + c\delta t^{s} - \Delta_{P}^{s} = {{\varvec{e}}_{\varvec{r}}^{\varvec{s}}} \cdot {\boldsymbol{\delta} \varvec{X}}_{{\varvec{r}}} + c\left( {\delta t_{r}^{M} + {\text{ISB}}_{M}^{G} } \right) + m^{s} \cdot T + \frac{{f_{1}^{2} }}{{f_{i}^{2} }} \cdot I^{s}$$
(1)
$$L_{i}^{s} - \rho_{0}^{{\text{s}}} + c\delta t^{s} - \Delta_{L}^{s} = {{\varvec{e}}_{\varvec{r}}^{\varvec{s}}} \cdot {\boldsymbol{\delta} \varvec{X}}_{{\varvec{r}}} + c\left( {\delta t_{r}^{M} + {\text{ISB}}_{M}^{G} } \right) + m^{s} \cdot T - \frac{{f_{1}^{2} }}{{f_{i}^{2} }} \cdot I^{s} + \lambda_{i} \cdot N_{i}^{s}$$
(2)

with

$${{\varvec{e}}_{\varvec{r}}^{\varvec{s}}} = \left[ {\begin{array}{*{20}c} {\frac{{X_{{\text{r}}} - X^{{\text{s}}} }}{\rho_{{0}}^{{\text{s}}}}} & {\frac{{Y_{{\text{r}}} - Y^{{\text{s}}} }}{{\rho_{{0}}^{{\text{s}}} }}} & {\frac{{Z_{{\text{r}}} - Z^{{\text{s}}} }}{{\rho_{{0}}^{{\text{s}}} }}} \\ \end{array} } \right]$$
(3)
$${\boldsymbol{\delta} \varvec{X}}_{{\varvec{r}}} = \left[ {\begin{array}{*{20}c} {\delta X_{{\text{r}}} } & {\delta Y_{{\text{r}}} } & {\delta Z_{{\text{r}}} } \\ \end{array} } \right]^{{\text{T}}}$$
(4)

where \(s\) denotes the satellite number and \(M\) is the corresponding GNSS (\(M\in \left\{G,R,E,C\right\}\)); \(i\) is the number of the frequency\(f\); \(\rho_{{0}}^{{\text{s}}}\) is the geometric distance between the position of the satellite \(s\) antenna phase center \(\left( {X^{{\text{s}}} ,Y^{{\text{s}}} ,Z^{{\text{s}}} } \right)\) and the a priori position of the receiver \(r\) antenna phase center \(\left( {X_{{\text{r}}} ,Y_{{\text{r}}} ,Z_{{\text{r}}} } \right)\); \(c\) is the speed of light; \(\delta t^{{\text{s}}}\) and \(\delta t_{r}^{M}\) are satellite and system-specific receiver clock offsets, respectively; \(T\) is the troposphere delay and \({m}^{s}\) is its corresponding mapping function; \({\Delta }_{P}^{s}\) and \({\Delta }_{L}^{s}\) are satellite, receiver, and site displacement effect corrections for \(P\) and \(L\) measurements, respectively; \({\text{ISB}}_{M}^{G}\) is the receiver inter-system bias between M and \(G\) (for \(M=G\) it is set to 0); Is is the slant ionosphere delay; \({N}_{i}^{s}\) is the carrier-phase ambiguity that corresponds to its original wavelength \({\lambda }_{i}\); \({{\varvec{e}}_{\varvec{r}}^{\varvec{s}}}\) is the direction vector and \({\boldsymbol{\delta} \varvec{X}}_{{\varvec{r}}}\) is the position correction vector. For system-specific clock estimation, all \({\text{ISB}}_{M}^{G} = 0\). For the solutions with \({\text{ISB}}_{M}^{G}\) determination, one common \(\delta t_{r}^{M}\) parameter is derived, i.e., \(\delta t_{r}^{G} = \delta t_{r}^{R} = \delta t_{r}^{E} = \delta t_{r}^{C}\).

We apply a one-dimensional Markov process (Weiss 1960), due to its simplicity of understanding and implementation (Hadas et al. 2017). The correlation time in our solutions is + ∞. Therefore, the Markov process is completely equivalent to a random walk process. In the Markov process, the expected translation distance S after n steps (or t epochs), each being of length \(\Phi\), is expressed by the following formula:

$$E\left( {\left| {S_{n} \left( \Phi \right)} \right|} \right) = \Phi \sqrt n .$$
(5)

Adopting (5) to the clock parameter \({\delta t}_{r}^{M}\) for i and i + 1 epochs, whose time difference is equal to t, we obtain:

$$E\left( {\left| {\delta t_{r, i + 1}^{M} - \delta t_{r,i}^{M} } \right|} \right) = \Phi \sqrt t$$
(6)

which means that the expected change in \({\delta t}_{r}^{M}\) after the specific time interval t depends on the interval length and defined translation distance \(\Phi\), which can be considered as RW process. The stochastic modeling of the common clock parameter and ISBs for the receiver is achieved by imposing constraint:

$$E(\Phi_{r} )\sqrt t = \left| {\delta t_{r, i + 1}^{M} - \delta t_{r,i}^{M} } \right|$$
(7)

where \({\Phi }_{r}\) is the RW constraint, t denotes the time interval between consecutive observations which in this work is equal to 30 s. The RW is imposed 1) only for the common clock parameter, and 2) for the common clock parameter and ISBs. To determine the parameter of the common clock and ISBs, the RW constraint is taken into consideration for the clock (\({\Phi }_{r}\)) and ISB (\({\Phi }_{ISB}\)):

$$E(\Phi_{r} ) = {{\left| {\delta t_{r, i + 1}^{M} - \delta t_{r,i}^{M} } \right|} \mathord{\left/ {\vphantom {{\left| {\delta t_{r, i + 1}^{M} - \delta t_{r,i}^{M} } \right|} {\sqrt t }}} \right. \kern-0pt} {\sqrt t }}$$
(8)
$$E(\Phi_{{{\text{ISB}}}} ) = {{\left| {{\text{ISB}}_{M, i+1}^{G} - {\text{ISB}}_{M, i}^{G} } \right|} \mathord{\left/ {\vphantom {{\left| {{\text{ISB}}_{M, i}^{G} - {\text{ISB}}_{M, i - 1}^{G} } \right|} {\sqrt t }}} \right. \kern-0pt} {\sqrt t }} .$$
(9)

In the case where RW constraint is solely applied to the common clock parameter, then ISB is estimated as a constant parameter with errors provided by the least-squares Markov estimation process only. Moreover, due to the discontinuity at the day boundaries (Guo and Zhang 2014; Lyu et al. 2019), a common receiver clock and ISB parameters should be reset for continuous postprocessing calculations (Mikoś et al. 2023a). The discontinuity is caused by changing the tracked satellites and selecting a different reference clock. This reset helps to avoid unnecessary parameter discontinuities at the beginning of the next day for both RV strategy and RW solutions.

Data and software

Multi-GNSS stations were selected based on the analysis of clock stability for different types of clocks and their distribution across multiple locations (Mikoś et al. 2023b). We included ten MGEX stations that track four systems: G, R, E, and C. Table 1 shows the relevant information for each station, with the stations sorted according to the type of clock employed.

Table 1 Basic information about the selected MGEX stations
Full size table

All PPP solutions in this study are computed using the GNSS-WARP (Wroclaw Algorithms for Real-Time Positioning) software (Hadaś 2015). This software is capable of processing undifferenced and uncombined dual-frequency GNSS observations in real-time and post-processing modes. The solution computation is performed using the sequential least squares method (Hadas et al. 2019).

Processing characteristics

The analyses are conducted in the kinematic and static PPP modes, as specified in the strategy described in Table 2. The estimated station coordinates and troposphere parameters are common to all GNSS systems for all strategies.

Table 2 Processing strategy in the GNSS-WARP software
Full size table

Strategies

The stochastic modeling of the common clock parameter and ISB is analyzed using four different RW strategies and the reference RV strategy with no clock constraints to find the optimal Galileo-only and multi-GNSS PPP processing strategy, see Table 3. The unit of the random walk process is typically given in \(m/\sqrt{s}\). The constraints in this paper are given always in millimeters for the sake of simplification and readability. This means that the constraint of, e.g., 10 mm between neighboring observation epochs corresponds in fact to \(\frac{10 \;mm}{{\sqrt {30s} }} = 1.83 \cdot 10^{ - 3} \frac{m}{\sqrt s }\).

Table 3 Constraints used in RW strategies for the clock parameters and ISB
Full size table

In the first strategy, RW is applied only to the common clock (RWG). The common clocks RW from the strategy RWG are also used in the Galileo-only processing. In the next three strategies, the constraint is also applied to the ISB, and the value depends on each specific strategy. However, in each of these three strategies, the same constraint as for RWG is imposed for the common clock. In the case of RWG+ISB(1) strategy, the identical RW is imposed for both the common clock and ISB, \(\Phi_{r} :\Phi_{{{\text{ISB}}}} = 1:1\). In the case of RWG+ISB(2) strategy, the RW value for ISB is ten times smaller than for the common clock, i.e., \(\Phi_{r} :\Phi_{{{\text{ISB}}}} = 1:0.1\). For the RWG+ISB(3) strategy, the RW value for ISB is one hundred times smaller than for the common clock, i.e., \(\Phi_{r} :\Phi_{{{\text{ISB}}}} = 1:0.01\).

Results

The following four sections show results for stochastic clock modeling in Galileo-only and multi-GNSS solutions for kinematic and static PPP. We also indicate the influence of modeling on the Zenith Tropospheric Delay (ZTD). Afterward, results from different RWG+ISB constraining tests are provided.

Analysis for RWG strategy using Galileo-only kinematic PPP

Figure 1 shows the estimated clock parameters in the form of epoch-wise differences for the selected RWG and RV strategies in the Galileo-only solution. The results include all analyzed stations with the same vertical axis range. The largest epoch-to-epoch noise is observed for stations ZIM2 and AREG, where the noise for the RV strategy exceeds the ± 5 cm range. ZIM2 and AREG are equipped with XO and Rb clocks, respectively. The REDU station with a Cs clock also exhibits higher noise compared to stations with an HM clock. The interquartile range (IQR, i.e., the spread between the 75th (Q3) and 25th (Q1) percentiles of the data) value for stations with the worst clock parameter stability is 37, 18, and 46 mm for AREG, REDU, and ZIM2, respectively, in the RV strategy. Three RW solutions with 10, 15, and 20 mm constraints show a similar estimated clock stability level. For the RW of 15 mm, IQR value for the same set of stations is 9, 2, and 6 mm. For AMC4, BRUX, CRO1, PTBB, TID1 stations, the value of IQR for RW solutions is below one millimeter. These results show that the clock modeling effectively enables noise reduction.

Fig. 1
figure 1

Epoch-wise differences of clock parameters between adjacent epochs for RWG and RV strategies from Galileo-only kinematic PPP solutions

Full size image

Figure 2 shows IQR values for RV and RWG strategies using all RW solutions for coordinate components: North (N), East (E), and Up (U). For AMC4, BRUX, CRO1, and PTBB stations, RW solutions achieve more accurate results than RV. The best solutions for these four stations are obtained for RW of about 20 mm. For the remaining stations, the IQR value for RV yields the most accurate outcome. In the case of AREG (Rb), REDU (Cs), and ZIM2 (XO) stations, the improvement is unnoticeable and the solution is deteriorated, mainly due to the less stable clock used. For the four GNSS stations, where RW solutions demonstrate more precise results than the RV strategy, improvements are especially observed for the U component, e.g., from 36 to 25 mm in BRUX or from 56 to 41 mm in AMC4. Depending on the station, the most stable result is achieved by a different constraint. In the case of the N and E components, there is either no improvement or it is rather small up to 5 mm for AMC4.

Fig. 2
figure 2

IQR values of estimated station coordinates in RWG and RV strategies for each station from Galileo-only kinematic PPP solutions

Full size image

Figure 3 illustrates an analysis of the U component in the form of box plots with a level of RWG constraints and RV strategies for each station. For stations: AREG, MGUE, REDU, YEL2, and ZIM2, RW solutions instead of improving the results, lead to a substantial deterioration, which is also evident in Fig. 2. For the stations without HM clocks, the RW solutions lead to a decrease in the number of correctly estimated PPP epochs compared to the RV strategy. Oppositely, the greatest improvement from RW is observed for the CRO1 station, where the difference between the RV strategy and the best RW solution reaches a 20-mm difference in terms of IQR. For the most stable clocks: AMC4, BRUX, CRO1, and PTBB, each RW solution achieves a more stable result than the RV strategy, irrespective of the constraint imposed. For these four stations, the RW of 20 mm solution provides the best outcome in terms of the IQR of the station U component.

Fig. 3
figure 3

The quality of the U coordinate in RWG and RV strategies for each station from Galileo-only kinematic PPP solutions

Full size image

Figure 4 shows estimated N, E, and U station components from the RWG and RV strategies for the BRUX station. On the left-hand side, we indicate the time series for each coordinate for the first nine days, while on the right-hand side, we provide a zoom on the boundary between the ninth and tenth days. A significant improvement can be observed for the U component. When comparing the time series, RW solutions are clearly less noisy than the reference RV strategy. The standard deviation (STD) value for the U component is 29, 29, 29, and 38 mm for the RW 10 mm, RW 15 mm, RW 20 mm, and RV strategy, respectively.

Fig. 4
figure 4

Estimated coordinates (N, E, and U components) for the BRUX station using the RWG and RV strategies for the first nine days (on the left) and zoomed-in view of the boundary between two days (on the right) from Galileo-only kinematic PPP solutions

Full size image

Figure 5 shows the results for the same data range as in Fig. 4 for the U coordinate component of the AMC4, CRO1, PTBB, and TID1 stations. For the indicated time series, the STD value for the U coordinate at the AMC4 station is 48, 45, 44, and 51 mm for RW 10, 15, 20 mm, and RV, respectively. For the CRO1 station, the STD value for the U component is 74, 67, 63, and 101 mm for RW 10, 15, 20 mm, and RV, respectively. In the case of the AMC4, CRO1, and PTBB stations, each RW solution stabilizes the results. For the TID1 station, RW shows a slight deterioration from the level of 62 mm in RV to 64 mm in RW 15 mm.

Fig. 5
figure 5

Estimated U component for the AMC4, CRO1, PTBB, and TID1 stations using the RWG and RV strategies for the first nine days (on the left) and zoomed-in view of the boundary between two days (on the right) from Galileo-only kinematic PPP solutions

Full size image

Stochastic modeling applied to the clock also affects the ZTD results. Figure 6 shows ZTD estimates for the RWG and RV strategies, as well as the differences of RWG with respect to RV for BRUX, CRO1, PTBB, and TID1. For the CRO1 and TID1 stations, systematic ZTD offsets occur when compared to the RV strategy. The systematic offsets increase with the strength of the clock constraint, achieving the maximum value for the constraint of 10 mm. The observed differences are caused by strong correlations between receiver clocks, U component, and the ZTD parameter. For TID1, a systematic coordinate offset occurs for the solutions with clock constraints in Fig. 5. For the BRUX and PTBB stations, the ZTD differences between RW solutions and RV strategy are minor. The stochastic modeling applied to the clock parameter leads to differences in ZTD estimates, indicating specific correlations between these parameters which depend on the observation geometry.

Fig. 6
figure 6

Estimated ZTD and differences of ZTD relative to RV strategy for the BRUX, CRO1, PTBB, and TID1 stations using the RWG and RV strategies from Galileo-only kinematic PPP solutions

Full size image

Analysis for RWG strategy using Galileo-only static PPP

Now, we discuss Galileo-only results from the static PPP. Figure 7 shows the epoch-wise differences for the clock parameters between adjacent epochs from the RWG and RV strategies. The dependencies in terms of data characteristics are similar to the results shown in Fig. 1. The noise for the RV strategy is again larger compared to the solutions with clock constraining, however, the noise for RV is smaller in static PPP than in kinematic PPP (cf. Figs 7 and 1). The clock difference converges to a zero value during the first epochs of each day, which is visible for RW solutions and stations with HM clocks. Static PPP solution is reinitialized every day, therefore each estimated parameter requires a certain station-dependent time to achieve stable estimates. However, for the stations without HM clocks, the clock convergence to mm-level does not occur at all.

Fig. 7
figure 7

Epoch-wise differences of clock parameters between adjacent epochs for RWG and RV strategies from Galileo-only static PPP solutions

Full size image

Figure 8 shows the time transfer results between the PTBB station and the BRUX and AMC4 stations in the form of Modified Allan Deviation (MDEV). The MDEV analysis shows better short-term stability for RW solutions than RV strategy. In the case of time transfer between PTBB and BRUX, the RV strategy achieves the MDEV level of \({1.0 \cdot 10}^{-11}\) for 30 s intervals, while RW solutions achieve results a factor of four smaller of \(2.5\cdot{10}^{-12}\) for the same intervals. Analyzing the long-term intervals beyond 104 s, both RW solutions and the RV strategy achieve very similar stabilities. For the time transfer between PTBB and AMC4 from different continents, the RV strategy achieves an MDEV level of \(1.3\cdot{10}^{-11}\) for short-term stability of 30 s, while RW solutions achieve MDEV values of \(6.7\cdot{10}^{-12}\). PTBB and BRUX are located on the same continent, thus, observe the same set of Galileo satellites, whereas PTBB and AMC4 typically track different satellites at the same time, hence, high-quality reference satellite clocks are needed to allow for the state-of-the-art inter-continental time transfer.

Fig. 8
figure 8

Analysis of the stability of clock parameters using MDEV for RWG and RV strategies from Galileo-only static PPP excluding the first 4 h of clock parameters from each day of the week

Full size image

Figure 9 shows the results for ZTD in the same manner as Fig. 6. Interestingly, both in Fig. 6 and Fig. 9, for the CRO1 and TID1 stations, RW 10 mm solution exhibits much larger offsets than the other two RW solutions, which shows that the stochastic clock modeling has a systematic impact on the estimated troposphere parameters via correlations.

Fig. 9
figure 9

Estimated ZTD and the differences of ZTD relative to RV strategy for the BRUX, CRO1, PTBB, and TID1 stations using the RWG and RV strategies from Galileo-only static PPP solutions

Full size image

Analysis for RWG strategy using multi-GNSS kinematic PPP

Now, we discuss the results for multi-GNSS kinematic PPP solutions with stochastic clock modeling. Figure 10 illustrates epoch-wise differences of the common clock parameter from the RWG and RV strategies. Compared to Fig. 1, the use of multi-GNSS results in a reduced clock noise, especially for the RV strategy, which is a result of an increased number of observations contributing to the multi-GNSS solutions compared to Galileo-only in Fig. 1. In the case of RW solutions, the clock noise reduction also occurs but to a lesser extent. The largest discrepancy for HM clocks between Fig. 1 and Fig. 10 is observed for the YEL2 and MGUE stations, where RW solutions using multi-GNSS are remarkably stabilized compared to Galileo-only solutions. In the case of YEL2, the increased noise from RV solutions is effectively eliminated in RW solutions, indicating a positive impact of the receiver clock modeling. IQR value for stations with the worst clock parameter stability is 36, 14, and 44 mm for AREG, REDU, and ZIM2, respectively, in the RV strategy. For RW of 15 mm, the IQR value for the same set of stations is 13, 3, and 9 mm. For AMC4, BRUX, CRO1, PTBB, TID1 stations, the value of IQR for RW solutions is below one millimeter.

Fig. 10
figure 10

Epoch-wise differences of clocks between adjacent epochs for RWG and RV strategies for each station for multi-GNSS kinematic PPP solutions

Full size image

Figure 11 shows the station coordinate IQR values for each RV and RWG strategies using RW solutions with different constraints for all stations. The benefits of RW solutions can be observed for almost all stations equipped with HM, especially AMC4, BRUX, CRO1, PTBB, and TID1. For the U component, RW solutions achieve the greatest improvement compared to the RV strategy. The RW of 15 mm seems to be optimal for best-performing HM clocks, reducing the IQR of the U component from 25 to 20 mm for BRUX, from 31 to 25 mm for AMC4, from 30 to 24 mm for PTBB, and from 38 to 28 mm for CRO1. Therefore, the proper clock modeling leads to an improvement of about 25% in terms of the station coordinate repeatability for the up component of the GNSS stations connected to stable HM. Contrary, low-quality receiver clocks deteriorate the PPP solutions when compared to RV even when applying loose clock constraints.

Fig. 11
figure 11

IQR values of estimated station coordinates in RWG and RV strategies from multi-GNSS kinematic PPP solutions

Full size image

Figure 12 shows the U component in the form of box plots for different constraints in RWG as well as for the RV strategies. In the case of the stations: AREG, MGUE, REDU, YEL2, and ZIM2, RW solutions do not improve the results with respect to RV, which is also evident in Fig. 11. For the three stations without HM clocks, RW solutions lead to a small decrease in the number of solution epochs compared to the RV strategy. Once again, the greatest improvement can be observed at the CRO1 station, where the difference between the RV strategy and the best RW solution leads to an improvement of 11 mm of the U component IQR. For the other stations with stable HM: AMC4, BRUX, and PTBB, each RW solution achieves a more stable result than the RV strategy. Analyzing the results for AMC4, BRUX, CRO1, and PTBB stations, the RW of 15 mm in the RWG strategy provide the most accurate results. For Galileo-only kinematic PPP solutions, the best results were obtained for the constraint of 20 mm.

Fig. 12
figure 12

The quality of the U coordinate in RWG and RV strategies for each station from multi-GNSS kinematic PPP solutions

Full size image

Figure 13 shows the results for the N, E, and U components from the RWG and RV strategies for the BRUX station, similar to Fig. 4 showing Galileo-only solutions. Despite good observation geometry in multi-GNSS solutions, which include multiple satellite observations from each constellation, stochastic clock modeling still improves results for the U component. The STD value for U is 28, 28, 28, and 32 mm for the RW 10, 15, 20 mm, and RV, respectively.

Fig. 13
figure 13

Estimated station coordinates (N, E, and U components) for the BRUX station using the RWG and RV strategies for the first nine days (on the left) and zoomed-in view of the boundary between the ninth and tenth days (on the right) from multi-GNSS kinematic PPP

Full size image

Figure 14 displays the results for the same data range as in Fig. 13 for the U component of the AMC4, CRO1, PTBB, and TID1 stations. Eg., for CRO1, the STD is 18, 17, 17, and 23 mm for RW 10, 15, 20 mm, and RV, respectively. For TID1, the STD value is 26, 24, 24, and 25 mm for RW 10, 15, 20 mm, and RV, respectively. For AMC4, CRO1, and PTBB, each RW solution stabilizes the U station component. For the TID1 station, RW 10 mm shows a deterioration compared to the RV strategy, but the other RW solutions exhibit improvement with respect to RV, which was not the case in Galileo-only solutions (cf. Fig. 5).

Fig. 14
figure 14

Estimated U component for the AMC4, CRO1, PTBB, and TID1 stations using the RWG and RV strategies for the first nine days (on the left) and zoomed-in view of the boundary between two days (on the right) from multi-GNSS kinematic PPP

Full size image

Analysis for RWG strategy using multi-GNSS static PPP

Figure 15 illustrates the epoch-wise differences for the common clock parameter from multi-GNSS static PPP based on the RWG and RV strategies. Compared to Fig. 7, the HM clock convergence time for the RW solutions is slightly shorter, despite that in both solutions all parameters are reset at the day boundary.

Fig. 15
figure 15

Epoch-wise differences of clock parameters between adjacent epochs for RWG and RV strategies for each station from multi-GNSS static PPP

Full size image

Figure 16 shows the time transfer results between the PTBB station and the BRUX and AMC4 stations. As opposed to the Galileo-only solution, the MDEV analysis for multi-GNSS demonstrates better short-term as well as long-term stability for RW solutions compared to the RV solution. For clock differences between PTBB and BRUX, the RV strategy achieves MDEV values of \(2.2\cdot10^{ - 11}\) in 30 s intervals, while RW solutions result in \(1.3\cdot10^{ - 11}\). For the time transfer between PTBB and AMC4, the RV strategy results in an MDEV of \(2.8\cdot10^{ - 11}\) for short-term stability of 30 s, while RW solutions achieve \(1.8\cdot10^{ - 11}\). In contrast to Fig. 8, Fig. 16 shows a better accuracy for the long-term stability for both cases when using RW solutions. However, the short-term stability was better in Galileo-only RW solutions than in multi-GNSS RW solutions, which can be related to very stable and homogeneous clocks in the Galileo constellation as opposed to other GNSS.

Fig. 16
figure 16

Analysis of the stability of clock parameters using MDEV for RWG and RV strategies from multi-GNSS static PPP excluding the first 4 h of clock parameters from each day of the week

Full size image

Comparison of kinematic PPP results with different ISB constraining

Stations without HM clocks exhibit no improvement or even a deterioration in the solutions with clock constraining. Therefore, Table 4 shows aggregated results for stations using the most stable HM clocks for multi-GNSS and Galileo-only solutions. The best results are obtained for multi-GNSS with RW of 15 mm. For the Galileo system, the best solution is for RW 20 mm. In both cases, the RW results are more accurate than the RV.

Table 4 Median value of the IQR for the coordinates based on kinematic PPP for the entire month from the RW solutions and RV strategy for AMC4, BRUX, CRO1, and PTBB stations
Full size table

Comparing different ISB constraining approaches in multi-GNSS solutions, RWG and RWG+ISB(3) consistently achieve the most favorable results with the lowest IQR values of station coordinates. The RWG+ISB(3)strategy yields almost identical results to RWG but requires more matrix operations. Therefore, it can be inferred that the RWG strategy is the most optimal approach for clock modeling due to its performance, accuracy, and simplicity.

Table 5 shows the IQR analysis for the U component of the four stations with the most stable clocks. Only the results for constraints of 15 mm for multi-GNSS and 20 mm for Galileo-only are shown, as these solutions provide the best results. As opposed to Table 4, Table 5 provides statistics for the first five hours of each day which are typically affected by much larger noise to verify possible improvements in terms of the solution convergence time. Once again, the results for the RWG and RWG+ISB(3) strategies are very similar with the best performace, whereas all other strategies result in inferior solutions.

Table 5 IQR values for the U coordinate component from the best RW solution with a constraint of 15 mm for multi-GNSS and 20 mm for Galileo-only for each strategy from kinematic PPP solutions. First 5 h means the first 5 h of observation from each day
Full size table

Conclusion

Modeling the clock parameter in solutions using a single satellite system or the common clock parameter in multi-GNSS solutions enables the stabilization of the determined position, especially the up component of the station coordinates. Reducing the noise for the clock parameter consistently improves the stability of other parameters that are correlated with receiver clocks, such as troposphere delays and station coordinates.

In this manuscript, stochastic modeling is tested for the receiver clock, common clock, and ISB parameters in PPP solutions using Galileo-only and multi-GNSS data. In both cases, tests were conducted for kinematic and static positioning modes. The clock and ISB modeling involved the application of a one-dimensional Markov process using stochastic modeling in the form of a random walk with different constraints. Additionally, we have defined various strategies, where the constraint was imposed: 1) on the clock or the common clock, 2) on the common clock and ISB with a ratio of 1:1, 3) with a ratio of 1:0.1, 4) and finally, with a ratio of 1:0.01. The most optimal stochastic modeling is 1), in which the clock is constrained, whereas ISBs are calculated as constant parameters for each day.

Superior results with stochastic clock modeling can be obtained for stations utilizing a stable hydrogen maser. In our case, stochastic modeling had a beneficial impact on kinematic solutions for the AMC4, BRUX, CRO1, and PTBB stations. The clock modeling resulted in reduced noise for the estimated clock or the common clock in the Galileo-only and multi-GNSS solutions, respectively. Consequently, the North, East, and Up coordinate components were also stabilized in kinematic PPP solutions with clock modeling. For the Galileo system, the most favorable random walk constraining is 20 mm, while for multi-GNSS, it is 15 mm. The improvement in the North and East coordinates is marginal, but there is a significant improvement in the Up component. The CRO1 station achieved the most substantial improvement of 29% for both Galileo-only and multi-GNSS, between solutions with and without stochastic clock modeling. For AMC4, BRUX, and PTBB stations, the improvement ranges from 18 to 31% with different results for Galileo-only and multi-GNSS solutions.

In the static PPP solution, the results obtained from stochastic modeling reduce the clock or common clock noise. The constrained solutions exhibit better short-term stability and time transfer results for the Galileo system and both short-term and long-term stability for multi-GNSS solutions. Clock modeling in the static PPP solutions does not remarkably affect the stabilization of coordinates compared to the reference solution.

Analyzing ZTD for Galileo-only kinematic and static PPP, the influence of clock constraining is evident, as observed through the offsets of respective results. For multi-GNSS solutions, this effect is less pronounced, which results from weaker correlations between ZTD and clock parameters in multi-GNSS solutions than in Galileo-only.

In the case of the kinematic PPP, clock modeling has a large impact on epoch-wise station coordinates. On the other hand, the coordinates in static PPP solutions are already stable, so the influence of stochastic clock modeling may not necessarily have a prominent effect on estimated parameters. In both cases, the proposed stochastic modeling can be effective only for high-performing hydrogen maser clocks, whereas introducing stochastic modeling for other clock types leads to a substantial deterioration of the solution.